-
原子自旋成像技术对气室内温度分布、旋光角检测以及镀膜抗弛豫特性测量至关重要, 其关键在于精确捕捉并解析原子自旋极化的复杂时空动态特性, 这些特性直接关系到磁强计带宽的扩展及磁梯度检测的灵敏度提升. 传统的气室内分割成像方法因静态特性限制, 无法实时捕捉原子自旋极化态的动态演变过程, 制约了量子测量仪器的性能提升. 针对这一挑战, 本研究提出了一种实时调控原子自旋极化态的碱金属原子气室动态自旋成像方法, 在空间分布上实时控制光束阵列中不同位置激光束的连续通断; 在时间序列上控制光束阵列中每束光的通断频率变化, 从而生成具有特定空间分布和频率特性的激光, 分别与气室内部不同位置的碱金属原子相互作用, 诱导原子自旋极化程度的变化. 通过对激光特性的精细调节, 当泵浦光的调制频率与原子在磁场中的拉莫尔频率相匹配时, 原子自旋极化达到最大值, 系统处于共振状态; 当调制频率与拉莫尔频率不匹配时, 原子自旋极化程度降低. 通过这种频率调制方法实现了对原子自旋极化状态地动态操控. 实验结果表明, 该方法达到95.9 μm的空间分辨率和355帧的时间分辨率, 显著优于传统静态自旋成像方法. 此方法增强了对原子自旋极化动态特性的认知, 能更精确地观测并分析磁场分布的动态特征, 从而为量子仪表性能的进一步优化提供坚实的实验依据与有力支持.With the state-of-the-art quantum measurement devices, such as atomic clocks, atomic gyroscopes, and atomic magnetometers, as their central components, the spatiotemporal evolution of atomic spin polarization in the atomic vapor cell has a major effect on both increasing the bandwidth of magnetometer and improving the accuracy of magnetic gradient measurements. However, the major factor impeding the further improvement of the performance of quantum measurement instrument is the inherent static nature of the traditional intra-vapor cell segmentation imaging technique, which makes it challenging to achieve the real-time capture of the dynamic evolution of atomic spin states. In this work, we suggest a dynamic spin imaging method for alkali metal atomic vapor cells with real-time modification of atomic spin polarization states in order to overcome this technological difficulty. In particular, to ensure that the laser can precisely act on the alkali metal atoms in various regions in the vapor cell, we employ a complex beam array management system to modify the on/off state of the laser beams at various positions in the spatial dimension in real time. In the meantime, we generate laser fields with particular spatial distribution and frequency characteristics by using frequency modulation techniques in the time series to accurately regulate the on-off frequency of each laser beam in the beam array. These laser beams cause dynamic changes in the atomic spin polarization state by interacting with alkali metal atoms at various points in the vapor cell. Through precise adjustment of the laser properties, we can see and study the dynamic evolution of the atomic spin-polarization state in real time. According to the experimental data, the technology outperforms the traditional static spin imaging techniques by achieving an excellent temporal resolution of 355 frames per second and a spatial resolution of 95.9 micrometers. The effective use of this method enables us to monitor and evaluate the dynamic aspects of magnetic field distribution with unprecedented precision, also greatly enhance our understanding of the dynamic characteristics of atomic spin polarization.
[1] Albert M, Cates G, Driehuys B, Happer W, Saam B, Springer Jr, Wishnia A 1994 Nature 370 199
Google Scholar
[2] Chupp T, Hoare R, Walsworth R, Wu B 1994 Phys. Rev. Lett. 72 2363
Google Scholar
[3] Navon G, Song Y Q, Room T, Appelt S, Taylor R, Pines A 1996 Scienc 271 1848
Google Scholar
[4] Ishikawa K, Anraku Y, Takahashi Y, Yabuzaki T 1999 J. Opt. Soc. Am. B 16 31
Google Scholar
[5] 郝传鹏 2022博士学位论文(合肥: 中国科学技术大学)
Hao C P 2022 Ph. D. Dissertation (Hefei: University of Science and Technology of China
[6] Savukov I, Romalis M 2005 Phys. Rev. Lett. 94 123001
Google Scholar
[7] Xu S J, Yashchuk V, Donaldson M, Rochester S, Budker D, Pines A 2006 PNAS 103 12668
Google Scholar
[8] Savukov I, Karaulanov T 2014 J. Magn. Reson. 249 49
Google Scholar
[9] Young A, Appelt S, Baranga A, Erickson C, Happer W 1997 Appl. Phys. Lett. 70 3081
Google Scholar
[10] Skalla J, Wackerle G, Mehring M 1997 Opt. Commun. 143 209
Google Scholar
[11] Skalla J, Wackerle G, Mehring M, Pines A 1997 Phys. Lett. A 226 69
Google Scholar
[12] Baranga A, Appelt S, Erickson C, Young A, Happer W 1998 Phys. Rev. A 58 2282
Google Scholar
[13] Giel D, Hinz G, Nettels D, Weis A 2000 Opt. Express 6 251
Google Scholar
[14] Savukov I 2015 J. Magn. Reson. 256 9
Google Scholar
[15] Ito Y, Sato D, Kamada K, Kobayashi T 2014 IEEE Trans. Magn. 50 4006903
Google Scholar
[16] Nishi K, Ito Y, Kobayashi T 2018 Opt. Express 26 1988
Google Scholar
[17] Johnson C, Schwindt P 2010 IEEE International Frequency Control Symposium Newport Beach, CA, USA, June 4–6, 2010 p371
[18] Johnson C, Schwindt P, Weisend M 2010 Appl. Phys. Lett. 97 243703
Google Scholar
[19] Kominis I, Kornack T, Allred J, Romalis M 2003 Nature 422 596
Google Scholar
[20] Gusarov A, Levron D, Paperno E, Shuker R, Baranga A 2009 IEEE Trans. Magn. 45 4478
Google Scholar
[21] Kim K, Begus S, Xia H, Lee S, Jazbinsek V, Trontelj Z, Romalis M 2014 NeuroImage 89 143
Google Scholar
[22] Xia H, Baranga A, Hoffman D, Romalis M 2006 Appl. Phys. Lett. 89 211104
Google Scholar
[23] Mamishin Y, Ito Y, Kobayashi T 2017 IEEE Trans. Magn. 53 4001606
Google Scholar
[24] Dolgovskiy V, Fescenko I, Sekiguchi N, Colombo S, Lebedev V, Zhang J, Weis A 2016 Appl. Phys. Lett. 109 023505
Google Scholar
[25] Weis A, Colombo S, Dolgovskiy V, Grujic Z, Lebedev V, Zhang J 2017 J. Phys.: Conf. Ser. 793 012032
Google Scholar
[26] Taue S, Toyota Y, Fujimori K, Fukano H 2017 22nd Microoptics Conference Tokyo, Japan, November 19–22, 2017 p212
[27] Dong H F, Chen J L, Li J M, Liu C, Li A X, Zhao N, Guo F Z 2019 J. Appl. Phys. 125 243904
Google Scholar
[28] 曹益平, 苏显渝, 向立群 2002 激光杂志 23 16
Google Scholar
Cao Y P, Su X Y, Xiang L Q 2002 Laser J 23 16
Google Scholar
[29] Ding Z C, Yuan J, Long X 2018 Sensors 18 1401
Google Scholar
[30] Wyllie R 2012 Ph. D. Dissertation (Madison: University of Wisconsin-Madison
[31] Dong H F, Yin L X, Li A X, Zhao N, Chen J L, Sun M J 2019 J. Appl. Phys. 125 023908
Google Scholar
[32] Mitsunaga T, Nayar S 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Fort Collins, CO, USA, July 6–9, 1999 p374
-
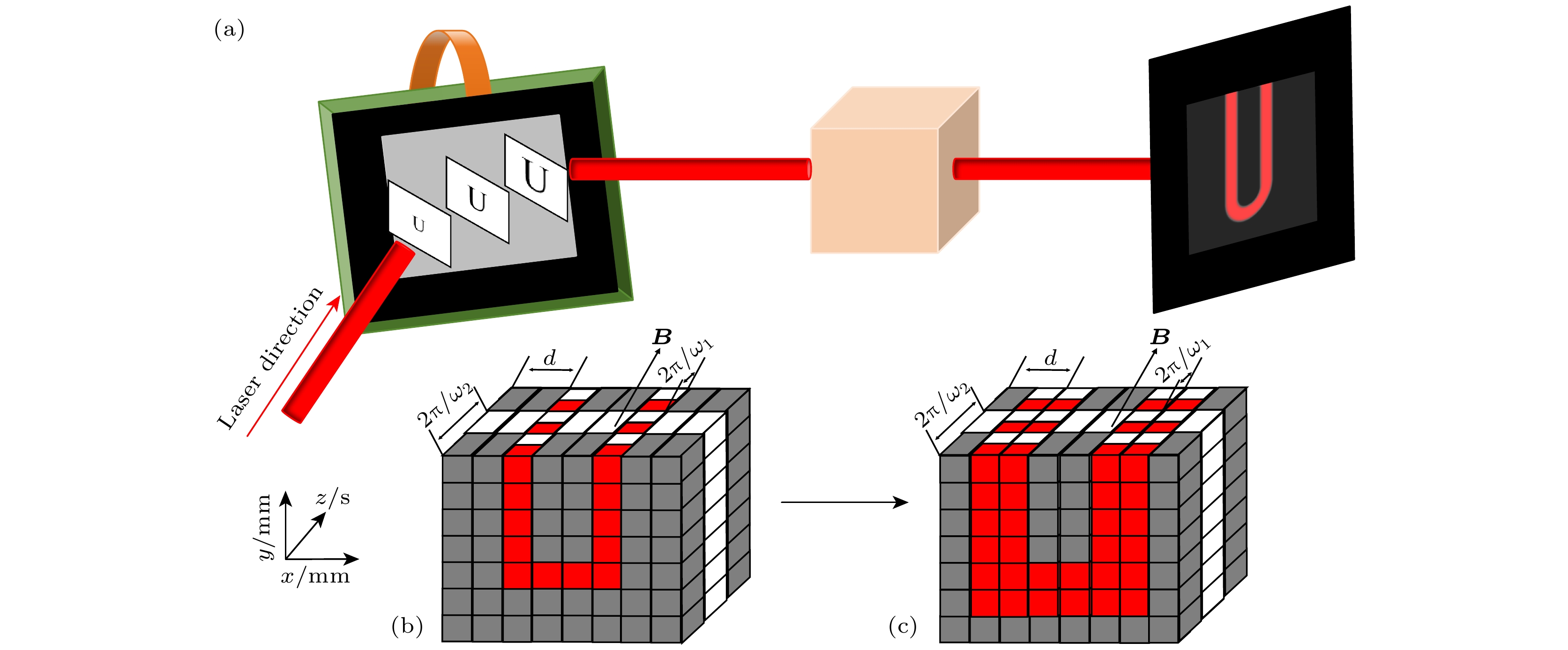
图 2 (a) DMD加载图片示意图; (b)气室内光强时空分布示意图(一列镜子); (c)气室内光强时空分布示意图(两列镜子), 其中d为空间周期, B为磁场强度, ${{2{\text{π}}}}/{{{\omega _1}}}$和${{2{\text{π}}}}/{{{\omega _2}}}$为时间周期, 本实验中B ≈ 1427 nT, ${{2{\text{π}}}}/{{{\omega _1}}} = 200\;{\text{μs}}$, ${{2{\text{π}}}}/{{{\omega _2}}} = 400\;{\text{μs}}$
Fig. 2. (a) Schematic of DMD loading images; (b) schematic of spatiotemporal distribution of light intensity inside the vapor cell (one column of mirrors); (c) schematic of spatial-temporal distribution of light intensity inside the vapor cell (two columns of mirrors), d represents spatial periodicity; B represents magnetic field intensity, ${{2{\text{π}}}}/{{{\omega _1}}}$, ${{2{\text{π}}}}/{{{\omega _2}}}$ represent time period, in this experiment B ≈ 1427 nT, ${{2{\text{π}}}}/{{{\omega _1}}} = 200\;{\text{μs}}$, ${{2{\text{π}}}}/{{{\omega _2}}} = 400\;{\text{μs}}$.
图 3 碱金属原子的自旋进动示意图
Fig. 3. Schematic diagram illustrating the advance process of spin in alkali metal atoms.
图 4 真实亮度的对数($\ln (Et)$)与灰度值百分比之间的函数关系
Fig. 4. Logarithm of true luminance ($\ln (Et)$) as a function of percent gray value.
图 5 调制光场时需加载入DMD的图片 (a)字符大小对应于7列镜子宽度的二进制图片; (b)字符粗细增加, 字符大小对应于15列镜子宽度的二进制图片; (c)字符粗细再次增大, 字符大小对应于23列镜子宽度的二进制图片
Fig. 5. Pictures to be loaded into the DMD when modulating the light field: (a) The character size corresponds to a binary picture of 7 column mirror widths; (b) the character thickness increases, the character size corresponds to a binary picture of 15 column mirror widths; (c) the character thickness increases again, the character size corresponds to a binary picture of 23 column mirror widths.
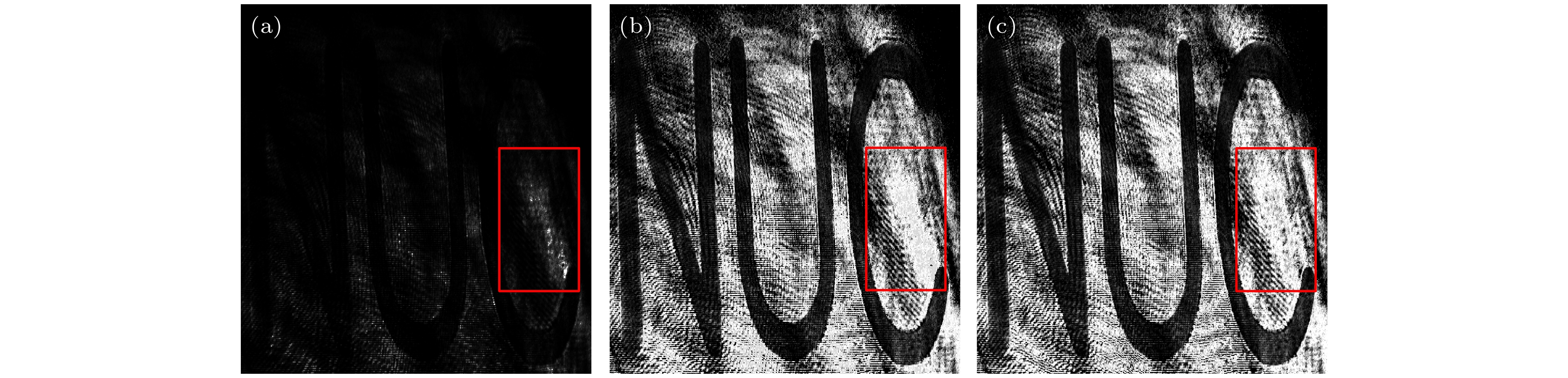
图 6 原子气室中自旋极化的二维成像 (a)未加磁场得到的背景图即激光光场直接成像; (b)加入磁场后的原子自旋极化图; (c)原子自旋极化图像减去激光光场成像的结果
Fig. 6. Two-dimensional imaging of spin polarization in an atomic vapor cell: (a) The background image obtained without applying a magnetic field, namely, the direct imaging of the laser light field; (b) the atomic spin polarization image after applying a magnetic field; (c) the result of subtracting the laser light field imaging from the atomic spin polarization image.
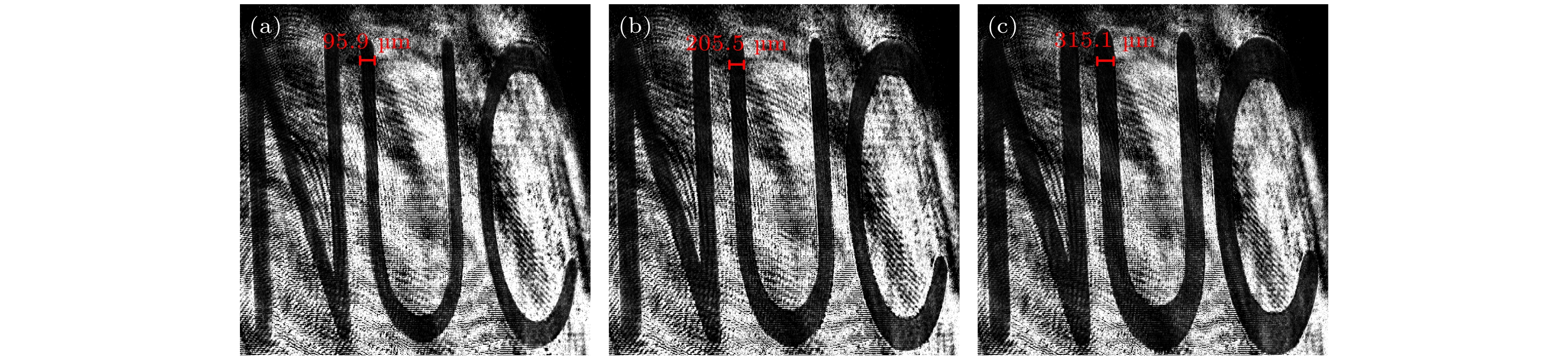
图 7 极化原子动态成像图 (a)—(c)字符大小不断增大的原子自旋极化图, 图(a)中条纹的线宽对应7个柱状微镜, 宽度为95.9 μm
Fig. 7. Two-dimensional spin diagrams of atomic vapor cell: (a)–(c) Atomic spin polarization with increasing character sizes, the line width of the stripes in the panel (a) corresponds to 7 columnar micromirrors with a width of 95.9 μm.
图 8 不同帧率下原子极化图 (a) 30 fps; (b) 150 fps; (c) 355 fps
Fig. 8. Atomic polarization plots at different frame rates: (a) 30 fps; (b) 150 fps; (c) 355 fps.
图 9 (a) 相机帧率在30—385 fps时直线A上像素值极差变化; (b)帧率分别在345, 355, 365, 375, 385 fps时直线A上像素值变化曲线图
Fig. 9. (a) Variation of pixel value extremes on line A at camera frame rates from 30 fps to 385 fps; (b) graph of pixel value changes on line A at frame rates of 345, 355, 365, 375, and 385 fps respectively.
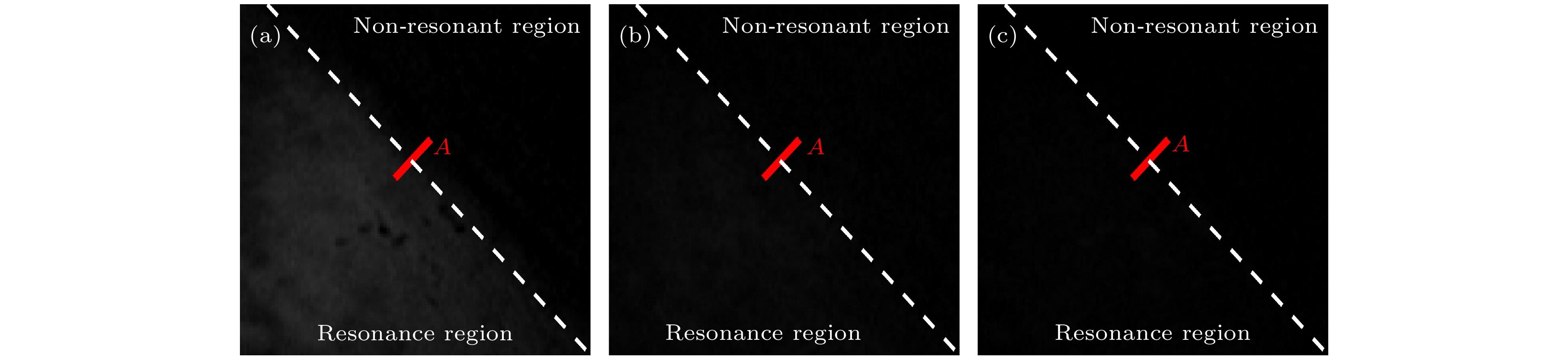
图 10 气室内高质量原子动态自旋成像图, 蚂蚁内部黑色部分为原子低极化态区域, 外部为高极化态区域, 自旋成像图分别展示了在帧率为355 fps时, 不同时间下的蚂蚁运动轨迹
Fig. 10. Dynamic spin-imaging maps of atoms inside the vapor cell. The black part inside the ants is the region of low-polarized state of atoms, the outside is the region of high-polarized state, and the spin-imaging maps show the ants’ motion trajectories at different times at a frame rate of 355 fps, respectively.
-
[1] Albert M, Cates G, Driehuys B, Happer W, Saam B, Springer Jr, Wishnia A 1994 Nature 370 199
Google Scholar
[2] Chupp T, Hoare R, Walsworth R, Wu B 1994 Phys. Rev. Lett. 72 2363
Google Scholar
[3] Navon G, Song Y Q, Room T, Appelt S, Taylor R, Pines A 1996 Scienc 271 1848
Google Scholar
[4] Ishikawa K, Anraku Y, Takahashi Y, Yabuzaki T 1999 J. Opt. Soc. Am. B 16 31
Google Scholar
[5] 郝传鹏 2022博士学位论文(合肥: 中国科学技术大学)
Hao C P 2022 Ph. D. Dissertation (Hefei: University of Science and Technology of China
[6] Savukov I, Romalis M 2005 Phys. Rev. Lett. 94 123001
Google Scholar
[7] Xu S J, Yashchuk V, Donaldson M, Rochester S, Budker D, Pines A 2006 PNAS 103 12668
Google Scholar
[8] Savukov I, Karaulanov T 2014 J. Magn. Reson. 249 49
Google Scholar
[9] Young A, Appelt S, Baranga A, Erickson C, Happer W 1997 Appl. Phys. Lett. 70 3081
Google Scholar
[10] Skalla J, Wackerle G, Mehring M 1997 Opt. Commun. 143 209
Google Scholar
[11] Skalla J, Wackerle G, Mehring M, Pines A 1997 Phys. Lett. A 226 69
Google Scholar
[12] Baranga A, Appelt S, Erickson C, Young A, Happer W 1998 Phys. Rev. A 58 2282
Google Scholar
[13] Giel D, Hinz G, Nettels D, Weis A 2000 Opt. Express 6 251
Google Scholar
[14] Savukov I 2015 J. Magn. Reson. 256 9
Google Scholar
[15] Ito Y, Sato D, Kamada K, Kobayashi T 2014 IEEE Trans. Magn. 50 4006903
Google Scholar
[16] Nishi K, Ito Y, Kobayashi T 2018 Opt. Express 26 1988
Google Scholar
[17] Johnson C, Schwindt P 2010 IEEE International Frequency Control Symposium Newport Beach, CA, USA, June 4–6, 2010 p371
[18] Johnson C, Schwindt P, Weisend M 2010 Appl. Phys. Lett. 97 243703
Google Scholar
[19] Kominis I, Kornack T, Allred J, Romalis M 2003 Nature 422 596
Google Scholar
[20] Gusarov A, Levron D, Paperno E, Shuker R, Baranga A 2009 IEEE Trans. Magn. 45 4478
Google Scholar
[21] Kim K, Begus S, Xia H, Lee S, Jazbinsek V, Trontelj Z, Romalis M 2014 NeuroImage 89 143
Google Scholar
[22] Xia H, Baranga A, Hoffman D, Romalis M 2006 Appl. Phys. Lett. 89 211104
Google Scholar
[23] Mamishin Y, Ito Y, Kobayashi T 2017 IEEE Trans. Magn. 53 4001606
Google Scholar
[24] Dolgovskiy V, Fescenko I, Sekiguchi N, Colombo S, Lebedev V, Zhang J, Weis A 2016 Appl. Phys. Lett. 109 023505
Google Scholar
[25] Weis A, Colombo S, Dolgovskiy V, Grujic Z, Lebedev V, Zhang J 2017 J. Phys.: Conf. Ser. 793 012032
Google Scholar
[26] Taue S, Toyota Y, Fujimori K, Fukano H 2017 22nd Microoptics Conference Tokyo, Japan, November 19–22, 2017 p212
[27] Dong H F, Chen J L, Li J M, Liu C, Li A X, Zhao N, Guo F Z 2019 J. Appl. Phys. 125 243904
Google Scholar
[28] 曹益平, 苏显渝, 向立群 2002 激光杂志 23 16
Google Scholar
Cao Y P, Su X Y, Xiang L Q 2002 Laser J 23 16
Google Scholar
[29] Ding Z C, Yuan J, Long X 2018 Sensors 18 1401
Google Scholar
[30] Wyllie R 2012 Ph. D. Dissertation (Madison: University of Wisconsin-Madison
[31] Dong H F, Yin L X, Li A X, Zhao N, Chen J L, Sun M J 2019 J. Appl. Phys. 125 023908
Google Scholar
[32] Mitsunaga T, Nayar S 1999 IEEE Computer Society Conference on Computer Vision and Pattern Recognition Fort Collins, CO, USA, July 6–9, 1999 p374
下载:
计量
- 文章访问数: 421
- PDF下载量: 15
- 被引次数: 0
