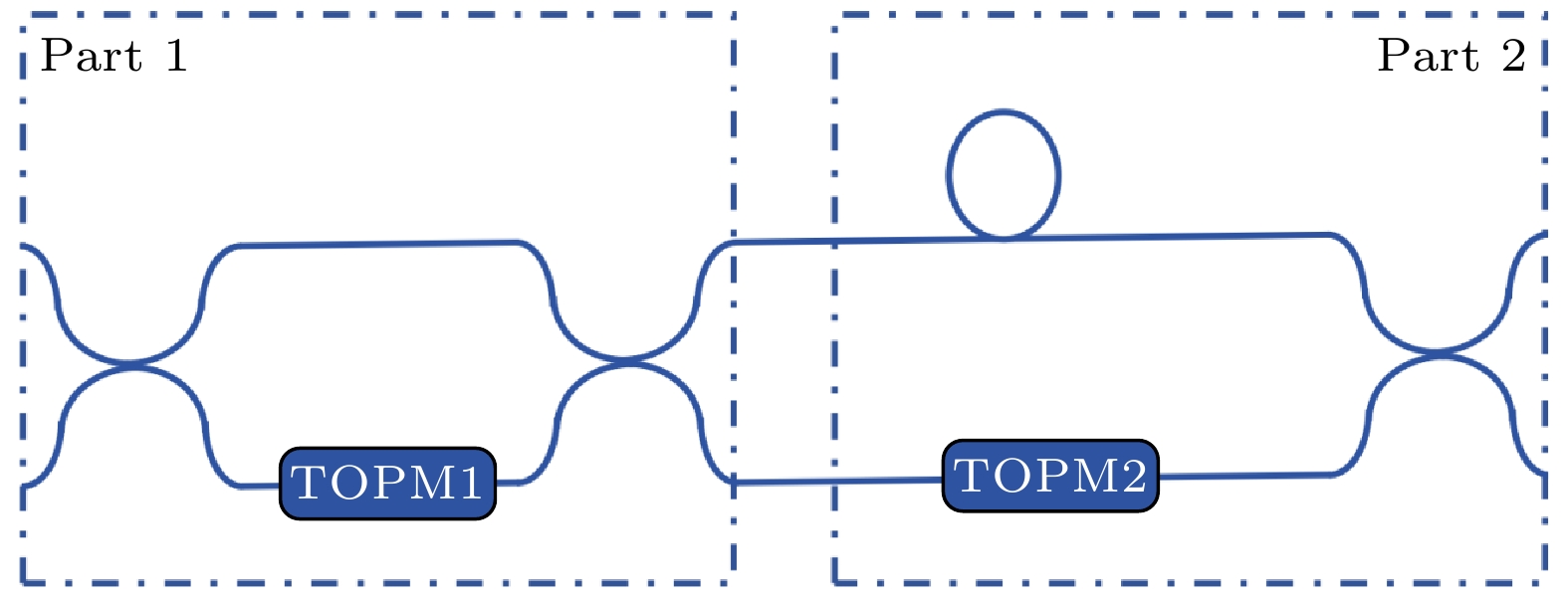
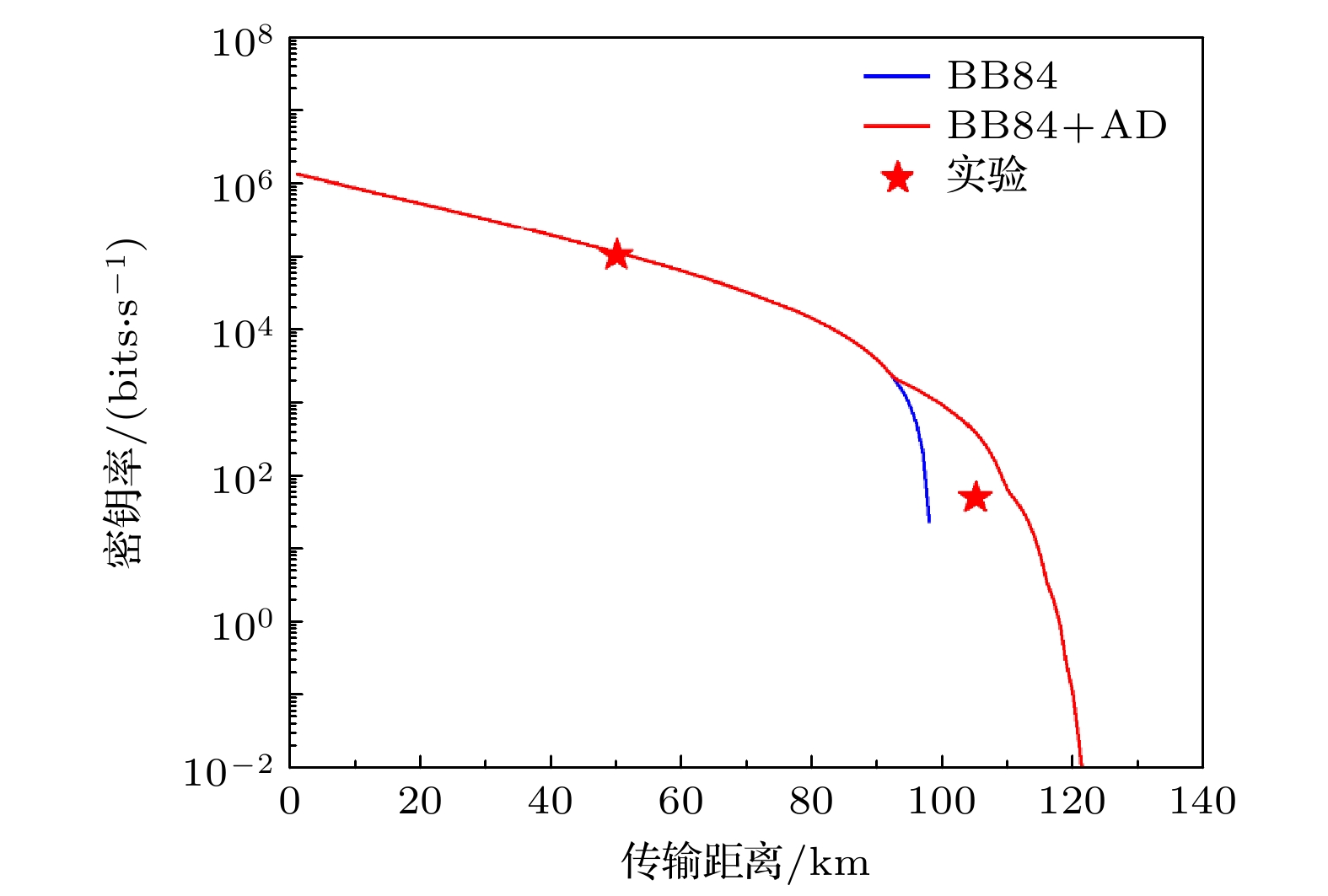
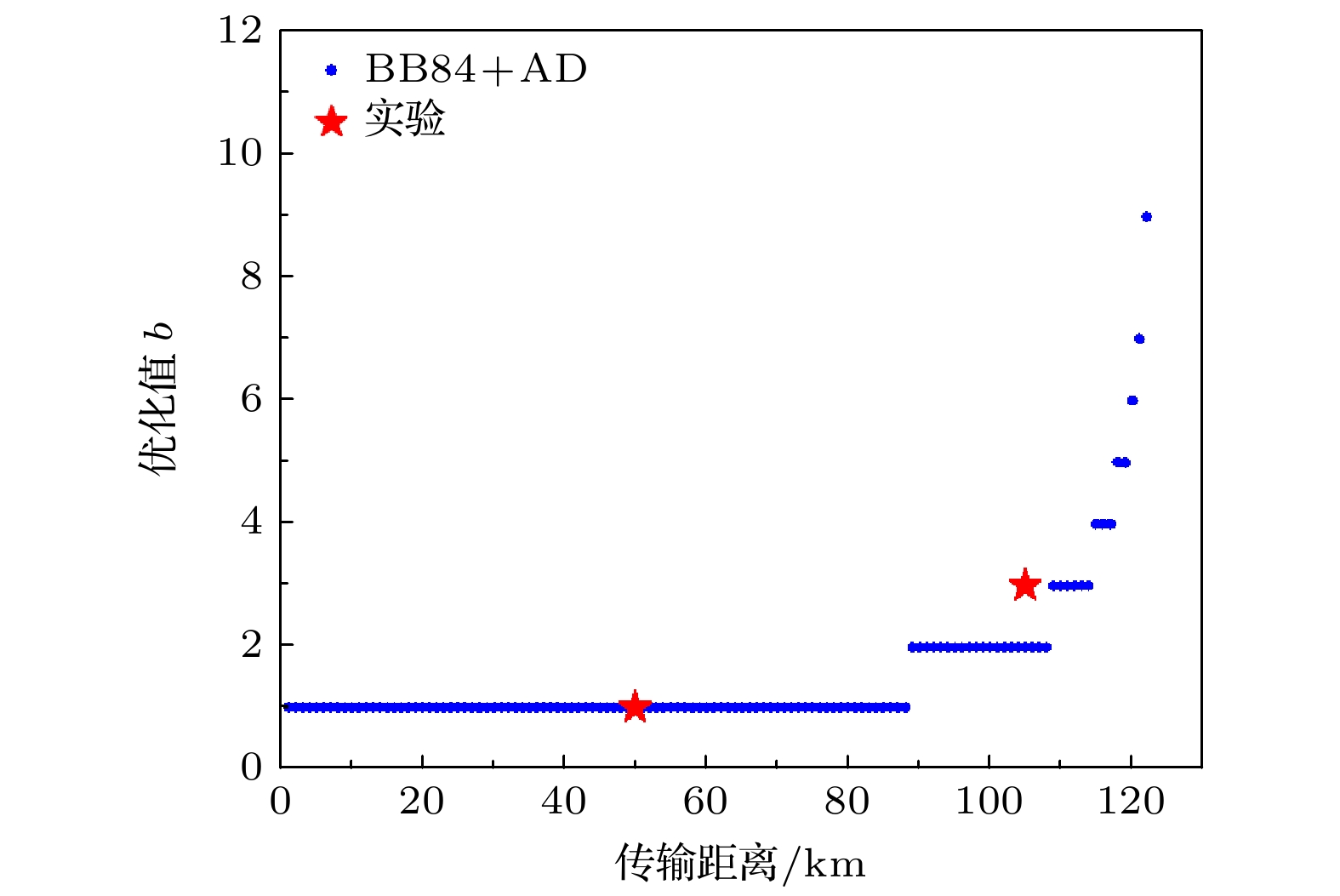
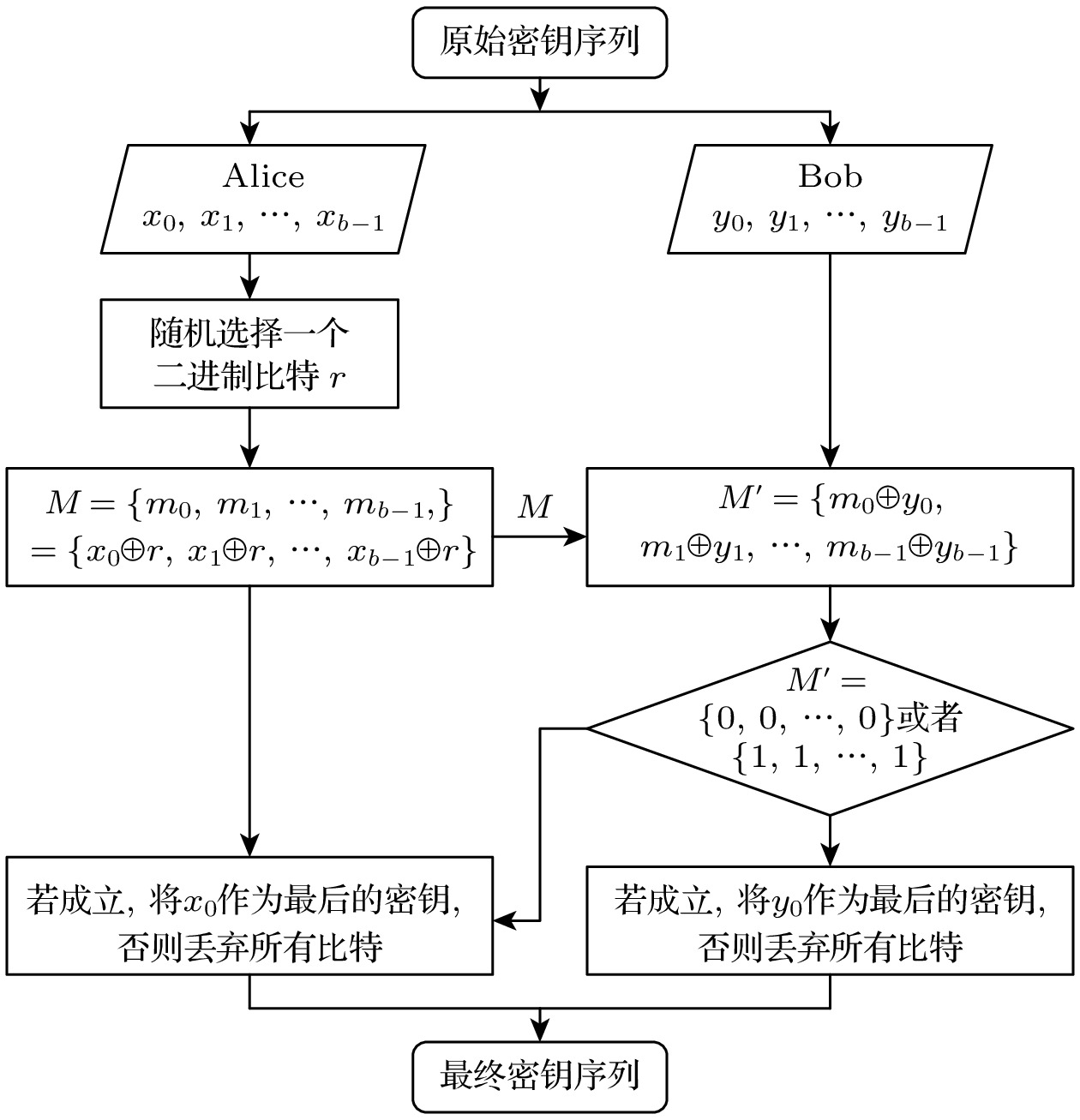
-
Quantum key distribution (QKD) has been extensively studied for practical applications. Advantage distillation (AD) represents a key technique to extract highly correlated bit pairs from weakly correlated ones, thus improving QKD protocol performance, particularly in large-error scenarios. However, its practical implementation remains under-explored. In this study, the AD is integrated into the three-intensity decoy-state BB84 protocol and its performance is demonstrated on a high-speed phase-encoding platform. The experimental system employs an asymmetric Mach-Zehnder interferometer (AMZI) fabricated on a silicon dioxide optical waveguide chip for phase encoding, which is benefited from its low coupling loss and minimum waveguide transmission loss. Phase-randomized weak coherent pulses, generated by a distributed feedback laser at 625 MHz, are modulated into decoy states of varying intensities. The signals are encoded via an AMZI and attenuated to single-photon levels before transmission. At the receiver, another AMZI demodulates the signals detected by avalanche photodiodes in gated mode. Experiments conducted at 50 km and 105 km demonstrate secure key rates of 104 kbits/s and 59 bits/s, respectively. The results at shorter distances closely match theoretical predictions, while slight deviations at 105 km are attributed to signal attenuation and noise. Despite these challenges, the results obtained at 105 km highlight the effectiveness of AD in enhancing secure key rates in the large-error scenario. This study confirms the potential of AD in extending secure communication range of QKD. By leveraging the high integration and scalability of silicon dioxide photonic chips, the proposed system lays a foundation for large-scale QKD deployment, paving the way for developing advanced protocols and real-world quantum networks.
[1] Bennett C H, Brassard G 2014 Theoret. Comput. Sci. 560 7
Google Scholar
[2] Lo H K, Chau H F 1999 Science 283 2050
Google Scholar
[3] Shor P W 2000 Phys. Rev. Lett. 85 441
Google Scholar
[4] Mayers D 2001 Journal of the ACM 48 3
Google Scholar
[5] Wang X B 2005 Phy. Rev. Lett. 94 230503
Google Scholar
[6] Lo H K, Ma X F, Chen K 2005 Phy. Rev. Lett. 94 230504
Google Scholar
[7] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[8] Braunstein S L, Pirandola S 2012 Phys. Rev. Lett. 108 130502
Google Scholar
[9] Lucamarini M, Yuan Z L, Dynes J F, Shields A 2018 Nature 557 400
Google Scholar
[10] Wang X B, Yu Z W, Hu X L 2018 Phys. Rev. A 98 062323
Google Scholar
[11] Cui C, Yin Z Q, Wang R, Chen W, Wang S, Guo G C, Han Z F 2019 Phys. Rev. Appl. 11 034053
Google Scholar
[12] Curty M, Azuma K, Lo H K 2019 npj Quantum Inf. 5 64
Google Scholar
[13] Ma X F, Zeng P, Zhou H Y 2018 Phys. Rev. X 8 031043
Google Scholar
[14] Zeng P, Zhou H Y, Wu W, Ma X 2022 Nat. Commun. 13 3903
Google Scholar
[15] Xie Y M, Lu Y S, Weng C X, Yin H L, Chen Z B 2022 PRX Quantum 3 020315
Google Scholar
[16] Maurer U M 1999 IEEE Trans. Inf. Theory 39 733
Google Scholar
[17] Renner R 2008 Int. J. Quantum Inf. 6 1
Google Scholar
[18] Li H W, Zhang C M, Jiang M S, Cai Q Y 2022 Commun. Phys. 5 53
Google Scholar
[19] Wang R Q, Zhang C M, Yin Z Q, Li H W, Wang S, Chen W, Guo G C, Han Z F 2022 New J. Phys. 24 073049
Google Scholar
[20] Li H W, Wang R Q, Zhang C M, Cai Q Y 2023 Quantum 7 1201
Google Scholar
[21] Zhang K, Liu J, Ding H, Zhang C H, Wang Q 2023 Entropy 25 1174
Google Scholar
[22] Boaron A, Boso G, Rusca D, Vulliez C, Autebert C, Caloz M, Perrenoud M, Gras G, Bussiѐres F, Li M J, Nolan D, Martin A, Zbinden H 2018 Phys. Rev. Lett. 121 190502
Google Scholar
[23] Yuan Z, Plews A, Takahashi R, Doi K, Tam W, Sharpe A, Dixon A, Lavelle E, Dynes J, Murakami A, Kujiraoka M, Lucamarini M, Tanizawa Y, Sato H, Shields A 2018 J. Light. Technol. 36 3427
Google Scholar
[24] Li W, Zhang L K, Tan H, Lu Y C, Liao S K, Huang J, Li H, Wang Z, Mao H K, Yan B Z, Li Q, Liu Y, Zhang Q, Peng C Z, You L X, Xu F H, Pan J W 2023 Nat. Photonics 17 416
Google Scholar
[25] Zhang G W, Chen W, Fan-Yuan G J, Zhang L, Wang F X, Wang S, Yin Z Q, He D Y, Liu W, An J M, Guo G C, Han Z F 2022 Sci. China Inf. Sci. 65 200506
Google Scholar
[26] Wu D, Zhang C X, Zhang J S, Wang Y, Chen W, Wu Y D, An J M 2024 Opt. Commun. 564 130597
Google Scholar
[27] Zhu J L, Zhou X Y, Ding H J, Liu J Y, Zhang C H, Li J, An J M, Wang Q 2025 Phys. Rev. A 111 012608
Google Scholar
-
图 2 BB84 QKD系统实验装置结构示意图, 其中Laser为激光器模块, IM为强度调制器, AMZI为非对称马赫-曾德尔干涉仪, APD为探测器模块, TDC为时间数字转换器
Fig. 2. Schematic diagram of the experimental setup for BB84 QKD system, where Laser is the laser module, IM is the intensity modulator, AMZI is the low-loss unbalanced Mach-Zehnder interferometer chip, APD denotes the avalanche photodiode detector module, and TDC is the time-to-digital converter.
图 3 非对称马赫-曾德尔干涉仪原理图
Fig. 3. Schematic diagram of the asymmetric Mach-Zehnder interferometer.
图 4 非对称马赫-曾德尔干涉仪实物图
Fig. 4. Physical picture of the asymmetric Mach-Zehnder interferometer.
图 5 基于AD技术的BB84协议的理论与实验密钥率对比图
Fig. 5. Comparison between theoretical and experimental key rates of BB84 protocol based on AD technology.
图 6 基于AD技术的BB84协议的理论与实验最优值$ b $
Fig. 6. Theoretical and experimental optimal values $ b $ of BB84 protocol based on AD technology.
表 1 实验数据
Table 1. Experimental data.
50 km (10 dB) 105 km (21 dB) 类型 理论数值 实验数据 理论数值 实验数据 $u$ 0.66653 0.64151 $v$ 0.04537 0.07259 ${P_u}$ 0.97000 0.94795 ${P_v}$ 0.02190 0.03627 $ Q_{u} $ $ 7.195\times {10}^{-4} $ $ 7.1084\times {10}^{-4} $ $ 5.692\times {10}^{-5} $ $ 5.2736\times {10}^{-5} $ $ Q_{v} $ $ 8.006\times {10}^{-5} $ $ 7.5179\times {10}^{-5} $ $ 1.714\times {10}^{-5} $ $ 1.6844\times {10}^{-5} $ $ E_{u} $ $ 0.01403 $ $ 0.01220 $ $ 0.06510 $ $ 0.085985 $ $ E_{v} $ $ 0.04623 $ $ 0.05180 $ $ 0.1930 $ $ 0.2109 $ $ Y_{1} $ $ 9.481\times {10}^{-4} $ $ 8.756\times {10}^{-4} $ $ 7.719\times {10}^{-5} $ $ 7.7438\times {10}^{-5} $ $ e_{1} $ $ 0.02064 $ $ 0.02562 $ $ 0.0715 $ $ 0.0974 $ $ R $ $ 115700 $ $ 104260 $ $ 389.0636 $ $ 59.3501 $ 
下载: 导出CSV
-
[1] Bennett C H, Brassard G 2014 Theoret. Comput. Sci. 560 7
Google Scholar
[2] Lo H K, Chau H F 1999 Science 283 2050
Google Scholar
[3] Shor P W 2000 Phys. Rev. Lett. 85 441
Google Scholar
[4] Mayers D 2001 Journal of the ACM 48 3
Google Scholar
[5] Wang X B 2005 Phy. Rev. Lett. 94 230503
Google Scholar
[6] Lo H K, Ma X F, Chen K 2005 Phy. Rev. Lett. 94 230504
Google Scholar
[7] Lo H K, Curty M, Qi B 2012 Phys. Rev. Lett. 108 130503
Google Scholar
[8] Braunstein S L, Pirandola S 2012 Phys. Rev. Lett. 108 130502
Google Scholar
[9] Lucamarini M, Yuan Z L, Dynes J F, Shields A 2018 Nature 557 400
Google Scholar
[10] Wang X B, Yu Z W, Hu X L 2018 Phys. Rev. A 98 062323
Google Scholar
[11] Cui C, Yin Z Q, Wang R, Chen W, Wang S, Guo G C, Han Z F 2019 Phys. Rev. Appl. 11 034053
Google Scholar
[12] Curty M, Azuma K, Lo H K 2019 npj Quantum Inf. 5 64
Google Scholar
[13] Ma X F, Zeng P, Zhou H Y 2018 Phys. Rev. X 8 031043
Google Scholar
[14] Zeng P, Zhou H Y, Wu W, Ma X 2022 Nat. Commun. 13 3903
Google Scholar
[15] Xie Y M, Lu Y S, Weng C X, Yin H L, Chen Z B 2022 PRX Quantum 3 020315
Google Scholar
[16] Maurer U M 1999 IEEE Trans. Inf. Theory 39 733
Google Scholar
[17] Renner R 2008 Int. J. Quantum Inf. 6 1
Google Scholar
[18] Li H W, Zhang C M, Jiang M S, Cai Q Y 2022 Commun. Phys. 5 53
Google Scholar
[19] Wang R Q, Zhang C M, Yin Z Q, Li H W, Wang S, Chen W, Guo G C, Han Z F 2022 New J. Phys. 24 073049
Google Scholar
[20] Li H W, Wang R Q, Zhang C M, Cai Q Y 2023 Quantum 7 1201
Google Scholar
[21] Zhang K, Liu J, Ding H, Zhang C H, Wang Q 2023 Entropy 25 1174
Google Scholar
[22] Boaron A, Boso G, Rusca D, Vulliez C, Autebert C, Caloz M, Perrenoud M, Gras G, Bussiѐres F, Li M J, Nolan D, Martin A, Zbinden H 2018 Phys. Rev. Lett. 121 190502
Google Scholar
[23] Yuan Z, Plews A, Takahashi R, Doi K, Tam W, Sharpe A, Dixon A, Lavelle E, Dynes J, Murakami A, Kujiraoka M, Lucamarini M, Tanizawa Y, Sato H, Shields A 2018 J. Light. Technol. 36 3427
Google Scholar
[24] Li W, Zhang L K, Tan H, Lu Y C, Liao S K, Huang J, Li H, Wang Z, Mao H K, Yan B Z, Li Q, Liu Y, Zhang Q, Peng C Z, You L X, Xu F H, Pan J W 2023 Nat. Photonics 17 416
Google Scholar
[25] Zhang G W, Chen W, Fan-Yuan G J, Zhang L, Wang F X, Wang S, Yin Z Q, He D Y, Liu W, An J M, Guo G C, Han Z F 2022 Sci. China Inf. Sci. 65 200506
Google Scholar
[26] Wu D, Zhang C X, Zhang J S, Wang Y, Chen W, Wu Y D, An J M 2024 Opt. Commun. 564 130597
Google Scholar
[27] Zhu J L, Zhou X Y, Ding H J, Liu J Y, Zhang C H, Li J, An J M, Wang Q 2025 Phys. Rev. A 111 012608
Google Scholar
下载:
计量
- 文章访问数: 573
- PDF下载量: 16
- 被引次数: 0
