-
本文研究了具有Stark势的一维相互作用任意子模型. 通过数值计算能谱统计、半链纠缠熵和粒子非平衡态占据数等来观测有限尺寸下的多体局域化现象. 随着线性势强度的增强, 系统的能谱统计分布从高斯系综向泊松系综过渡, 过渡区域的平均能级差比率表现为强烈依赖于统计角的非单调行为. 平均半链纠缠熵服从体积律到面积律转变且转变点对统计角有非单调依赖关系, 遍历相的半链纠缠熵随时间线性增长, 而在局域相中随时间呈对数增长, 其演化行为也与统计角有关. 最后随着线性势增大, 长时极限下粒子非平衡态占据数由零变为有限值, 有限值的大小与任意子统计角的取值有关, 这种演化行为进一步验证了任意子模型中统计角的重要性. 该研究结果为任意子系统中多体局域化的研究提供了新的视角.
In this paper, we study a one-dimensional interacting anyon model with a Stark potential in the finite size. Using the fractional Jordan Wigner transformation, the anyons in the one-dimensional system are mapped onto bosons, which are described by the following Hamiltonian: $ \begin{aligned} \hat{H}^{\text{boson}}=-J\sum_{j=1}^{L-1}\left( \hat{b}_{j}^{\dagger}\hat{b}_{j+1}e^{i\theta \hat{n}_{j}}+h.c.\right)+\frac{U}{2}\sum_{j=1}^{L}\hat{n}_{j}\left( \hat{n}_{j}-1\right)+\sum_{j=1}^{L}{h}_{j}\hat{n}_{j},\;\;\;\;\;\;\;\;(7)\end{aligned}$ where θ is the statistical angle, and the on-site potential is $h_{j}=-\gamma\left(j-1\right) +\alpha\left( \dfrac{j-1}{L-1}\right)^{2}$ with γ representing the strength of the Stark linear potential and α being the strength of the nonlinear part. Using the exact diagonalization method, we numerically analyze the spectral statistics, half-chain entanglement entropy and particle imbalance to investigate the onset of many-body localization (MBL) in this interacting anyon system, induced by the increasing of the linear potential strength. As the Stark linear potential strength increases, the spectral statistics transition from a Gaussian ensemble to a Poisson ensemble. In the ergodic phase, except for $\theta=0$ and π, where the mean value of the gap-ratio parameter $\left\langle r\right\rangle\approx 0.53$, due to the broken time reversal symmetry, the Hamiltonian matrix becomes a complex hermit one and $\left\langle r\right\rangle\approx 0.6$. In the MBL phase, $\left\langle r\right\rangle\approx 0.39$, which is independent of θ. However, in the intermediate γ regime, the value of $\left\langle r\right\rangle$ strongly depends on the choice of θ. The average of the half-chain entanglement entropy transitions from a volume law to an area law, which allows us to construct a θ-dependent MBL phase diagram. The time evolution of the half-chain entanglement entropy $S(t)$ increases linearly with time in the ergodic phase. In the MBL phase, $S(t)$ grows logarithmically with time, reaching a stable value that depends on the anyon statistical angle. The localization of particles in a quench dynamics can provide evidence for the breakdown of ergodicity and is experimentally observable. We observe that with the increasing of γ, the even-odd particle imbalance changes from zero to non-zero values in the long-time limit. In the MBL phase, the long-time mean value of the imbalance is dependent on the anyon statistical angle θ. From the Hamiltonian $\hat{H}^{\text{boson}}$, it can be inferred that the statistical behavior of anyon system equally changes the hopping interactions in boson system, which is a many-body effect. By changing the statistical angle θ, the many-body interactions in the system are correspondingly altered. And the change of the many-body interaction strength affects the occurrence of the MBL transition, which is also the reason for MBL transition changes with the anyon statistical angle θ. Our results provide new insights into the study of MBL in anyon systems and whether such phenomena persist in the thermodynamic limit needs further discussion in the future. -
Keywords:
- anyon /
- Stark potential /
- many-body localization
-
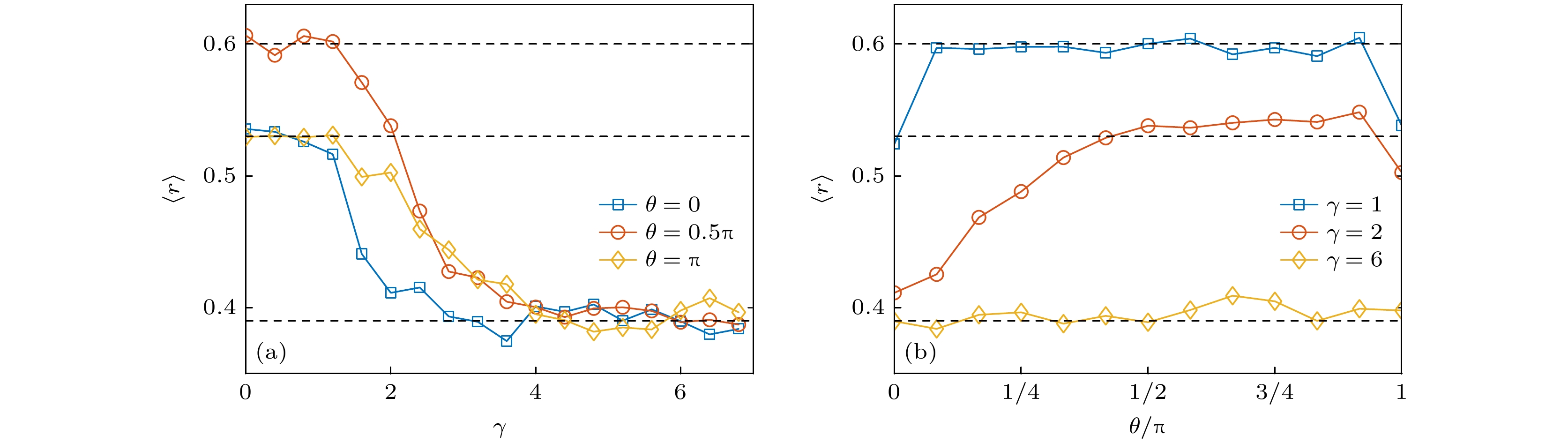
图 1 (a) 不同统计角θ下平均能级差比率$ \langle r\rangle $与Stark线性势强度γ的关系. (b) 平均能级差比率$ \langle r\rangle $在不同线性势强度γ下与统计角θ的关系. 这里选取$ L=12 $
Fig. 1. (color line) (a) The mean value of the gap-ratio parameter $ \langle r\rangle $ as a function of the Stark linear potential strength γ for different statistical angles θ. (b) $ \langle r\rangle $ as a function of the statistical angle θ for different γ. Here, $ L=12 $.
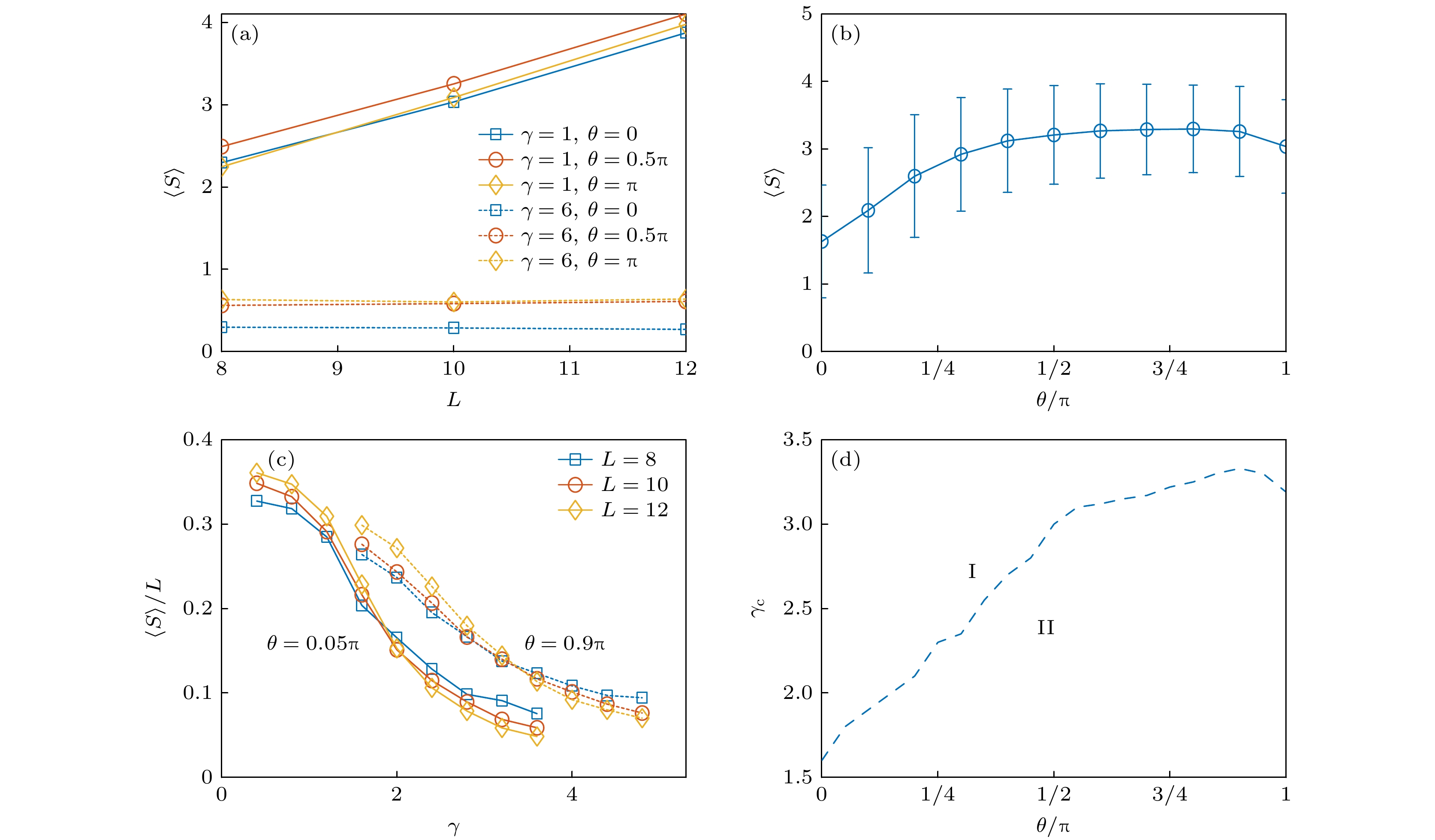
图 2 (a) 线性势强度分别为$ \gamma=1 $和6时, 不同统计角的平均半链纠缠熵与系统尺寸L的关系图. (b)当$ L=12 $, $ \gamma=2 $时, 平均半链纠缠熵随统计角θ的变化趋势. (c) 任意子统计角分别为$ \theta=0.05\pi $和$ 0.9\pi $时, 不同尺寸的平均半链纠缠熵$ \langle S\rangle /L $随线性势强度γ的变化. (d) 多体局域化转变点$ \gamma_c $随着统计角θ变化的情况. I和II区域分别为多体局域相和遍历相
Fig. 2. (color line) (a) The average half-chain entanglement entropy $ \langle S\rangle $ as a function of the system size L for different θ with $ \gamma=1 $ and $ 6 $. (b) $ \langle S\rangle $ as a function of θ with $ \gamma=2 $ and $ L=12 $. (c) $ \langle S\rangle /L $ as a function of γ for $ \theta=0.05\pi $ and $ 0.9\pi $. (d) The many-body transition points $ \gamma_c $ as a function of θ, where region I and region II correspond to many-body localization and ergodic phases, respectively.
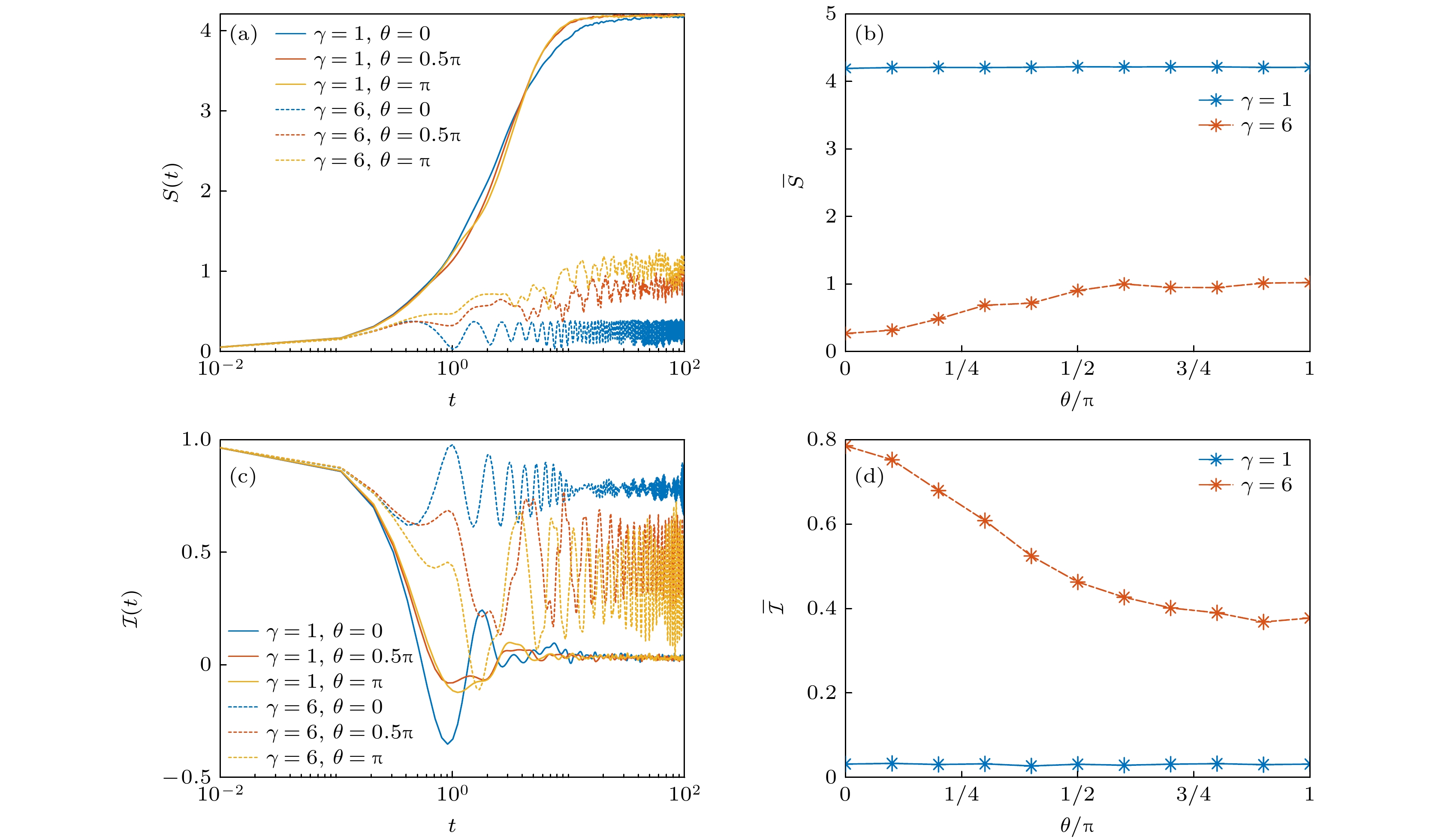
图 3 (a) 不同θ和γ时半链纠缠熵$ S(t) $随时间t的演化行为. (b) 对于不同的γ, 半链纠缠熵平均值$ \overline{S} $随统计角θ的变化情况. (c) 不同θ和γ时, 粒子非平衡态占据数$ \mathcal{I}\left( t\right) $随时间演化的情况. (d) 对于不同的γ, 非平衡态占据数平均值$ \overline{\mathcal{I}} $随统计角θ的变化情况. 这里选取$ L=12 $
Fig. 3. (color line) (a) The evolution of the half-chain entanglement entropy $ S(t) $ for different θ and γ. (b) $ \overline{S} $ as a function of θ for different γ. (c) The evolution of the particle imbalance $ \mathcal{I}\left( t\right) $ for different θ and γ. (d) $ \overline{\mathcal{I}} $ as a function of θ for different γ. Here, $ L=12 $.
-
[1] Schreiber M, Hodgman S S, Bordia P, Lüschen H P, Fischer M H, Vosk R, Altman E, Schneider U, Bloch I 2015 Science 349 842
Google Scholar
[2] Bordia P, Lüschen H P, Hodgman S S, Schreiber M, Bloch I, Schneider U 2016 Phys. Rev. Lett. 116 140401
Google Scholar
[3] Smith J, Lee A, Richerme P, Neyenhuis B, Hess P W, Hauke P, Heyl M, Huse D A, Monroe C 2016 Nat. Phys. 12 907
Google Scholar
[4] Xu K, Chen J J, Zeng Y, Zhang Y R, Song C, Liu W, Guo Q, Zhang P, Xu D, Deng H, Huang K, Wang H, Zhu X, Zheng D, Fan H 2018 Phys. Rev. Lett. 120 050507
Google Scholar
[5] Guo Q, Cheng C, Sun Z H, Song Z, Li H, Wang Z, Ren W, Dong H, Zheng D, Zhang Y R, Mondaini R, Fan H, Wang H 2021 Nat. Phys. 17 234
Google Scholar
[6] Guo Q, Cheng C, Li H, Xu S, Zhang P, Wang Z, Song C, Liu W, Ren W, Dong H, Mondaini R, Wang H 2021 Phys. Rev. Lett. 127 240502
Google Scholar
[7] Morong W, Liu F, Becker P, Collins K S, Feng L, Kyprianidis A, Pagano G, You T, Gorshkov A V, Monroe C 2021 Nature 599 393
Google Scholar
[8] Scherg S, Kohlert T, Sala P, Pollmann F, Hebbe Madhusudhana B, Bloch I, Aidelsburger M 2021 Nat Commun 12 4490
Google Scholar
[9] Liu J H, Xu Z H 2023 Phys. Rev. B 108 184205
Google Scholar
[10] Leinaas J M and Myrheim J 1977 Nuovo Cimento Soc. Ital. Fis. B 37 1
[11] Tsui D C, Stormer H L, Gossard A C 1982 Phys. Rev. Lett. 48 1559
Google Scholar
[12] Laughlin R B 1983 Phys. Rev. Lett. 50 1395
Google Scholar
[13] Nayak C, Simon S H, Stern A, Freedman M, Das Sarma S 2008 Rev. Mod. Phys. 80 1083
Google Scholar
[14] Kitaev A 2006 Ann. Phys. 321 2
Google Scholar
[15] Stern A 2008 Ann. Phys. 323 204
Google Scholar
[16] Haldane F D M 1991 Phys. Rev. Lett. 67 937
Google Scholar
[17] Vitoriano C, Coutinho-Filho M D 2009 Phys. Rev. Lett. 102 146404
Google Scholar
[18] Keilmann T, Lanzmich S, McCulloch I, Roncaglia M 2011 Nat Commun 2 361
Google Scholar
[19] Greschner S, Santos L 2015 Phys. Rev. Lett. 115 053002
Google Scholar
[20] Sträter C, Srivastava S C L, Eckardt A 2016 Phys. Rev. Lett. 117 205303
Google Scholar
[21] Zuo Z W, Li G L, Li L 2018 Phys. Rev. B 97 115126
Google Scholar
[22] Liu F, Garrison J R, Deng D L, Gong Z X, Gorshkov A V 2018 Phys. Rev. Lett. 121 250404
Google Scholar
[23] Zhang G Q, Zhang D W, Li Z, Wang Z D, Zhu S L 2020 Phys. Rev. B 102 054204
Google Scholar
[24] Wang Y Y, Sun Z H, Fan H 2021 Phys. Rev. B 104 205122
Google Scholar
[25] 王利, 贾丽芳, 张云波 2022 71 130501
Google Scholar
Wang L, Jia L F, Zhang Y B 2022 Acta. Rhys. Sin. 71 130501
Google Scholar
[26] 刘敬鹄, 徐志浩 2024 73 077202
Google Scholar
Liu J H, Xu Z H 2024 Acta. Rhys. Sin. 73 077202
Google Scholar
[27] Wu H, Vallières M, Feng D H, Sprung D W L 1990 Phys. Rev. A 42 1027
Google Scholar
[28] Hamazaki R, Kawabata K, Kura N, Ueda M 2020 Phys. Rev. Research 2 023286
Google Scholar
[29] Oganesyan V, Huse D A 2007 Phys. Rev. B 75 155111
Google Scholar
[30] Serbyn M, Papić Z, Abanin D A 2013 Phys. Rev. Lett. 111 127201
Google Scholar
[31] Van Nieuwenburg E, Baum Y, Refael G 2019 Proc. Natl. Acad. Sci. U.S.A. 116 9269
Google Scholar
下载:
计量
- 文章访问数: 457
- PDF下载量: 23
- 被引次数: 0
