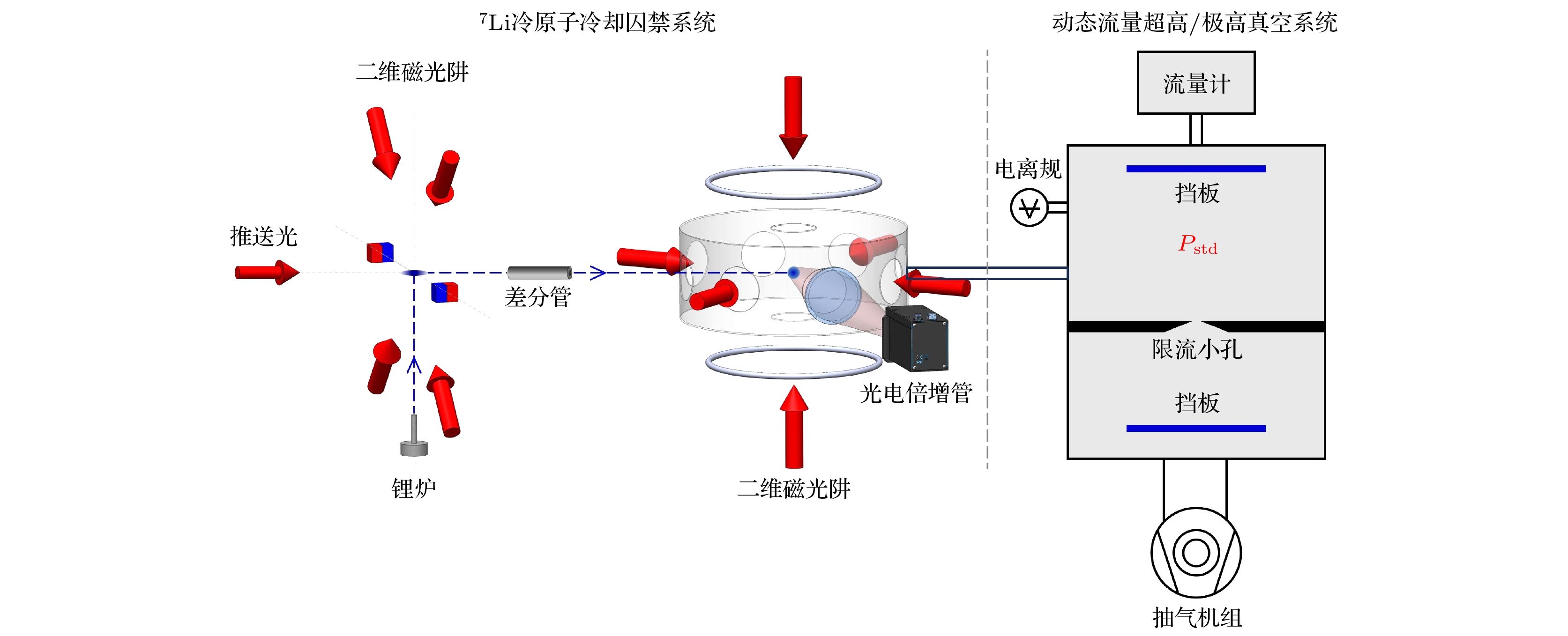
-
国际单位制的重新定义促进真空计量体系向量子化转变, 真空参数的量子化是国际真空测量学领域目前最具引领性、前瞻性和颠覆性的研究方向之一, 量子真空测量是基于微观粒子体系的量子效应, 利用光学手段和量子力学理论实现真空参数的精密测量. 本文通过自主研制的冷原子真空测量装置操控7Li原子, 利用锂冷原子在磁光阱和磁阱中的逃逸损失特性开展了超高真空测量实验研究, 结果表明, 针对N2, Ar, He, H2四种真空常用气体分子, 在3×10–8—4×10–5 Pa真空范围, 7Li冷原子真空测量的不确定度最大为7.6%—6.0% (k = 2), 7Li冷原子的真空反演结果与传统电离真空计的测量结果具有良好的一致性, 其相对灵敏度因子的最大偏差小于8%, 验证了冷原子量子真空测量的准确性和可靠性, 研究成果对促进全新跨代真空测量技术发展, 满足空间科学探测、超精密测量与高端装备制造等需求具有重要意义.The redefinition of the International System of Units (SI) promotes the transformation of the vacuum measurement system toward quantization, and the quantization of vacuum parameters is one of the most leading, prospective and subversive research directions in the field of international vacuum metrology, and the quantum vacuum measurement is based on the quantum effect of the microscopic particle system, and the use of optical means and the theory of quantum mechanics to realize the precision measurement of the vacuum parameters. We develop a lithium-cooled atom vacuum measurement apparatus, which mainly consists of a 7Li atom trap system and a continuous expansion vacuum system. In this work, an experimental study of ultrahigh vacuum measurement is carried out by manipulating 7Li atoms and utilizing the loss characteristics of lithium cold atoms in magneto-optical and magnetic traps, and the results show that for the four commonly used gas molecules in vacuum, namely N2, Ar, He, and H2, in the vacuum range of (3×10–8–4×10–5) Pa, the maximum measurement uncertainty is 7.6%–6.0% (k = 2) based on 7Li cold atoms, and the cold atom vacuum measurement results are in good agreement with those of the traditional ionization vacuum gauges, and their relative sensitivities are in good agreement with those of the ionization vacuum gauges, and the maximal deviation of the relative sensitivity factor is less than 8%, which verifies the accuracy and reliability of the cold-atom quantum vacuum measurements. The research results are of great significance in promoting the development of new cross-generation vacuum measurement technology and meeting the needs of space science exploration, ultra-precision measurement and high-end equipment manufacturing.
-
Keywords:
- ultra-high vacuum measurement /
- cold atom /
- magneto-optical trap /
- magnetic trap
[1] 李得天, 成永军, 冯焱, 卢耀文, 赵澜, 徐婕 2009 真空科学与技术学报 29 522
Google Scholar
Li D T, Cheng Y J, Feng Y, Lu Y W, Zhao L, Xu J 2009 Chin. J. Vac. Sci. Technol. 29 522
Google Scholar
[2] Li D T, Wang Y J, Zhang H Z, Xi Z H, Li G 2021 Space Sci. Tech. 23 7592858
[3] 刘见, 王刚, 胡一鸣, 张腾, 罗子人, 王晴岚, 邵立晶 2016 科学通报 61 1502
Google Scholar
Liu J, Wang G, Hu Y M, Zhang T, Luo Z R, Wang Q L, Shao L J 2016 Chin. Sci. Bull 61 1502
Google Scholar
[4] 王欲知, 陈旭 2007 真空技术 (北京: 北京航空航天大学出版社) 第6页
Wang Y Z, Chen X 2007 Vacuum Technology (Beijing: Beihang University Press) p6
[5] Jenninger B, Anderson J, Bernien M, Bundaleski M, Dimitrova H, Granovskij M, Illgen C, Setina J, Jousten K, Kucharski P, Reinhardt C, Scuderi F, Silva R A S, Stöltzel A, Teodoro O M N D, Trzpil-Jurgielewicz B, Wüest M 2021 Vacuum 183 109884
Google Scholar
[6] Fedchak J A, Abbott P J, Hendricks J H, Arnold P C, Peacock N T 2018 J. Vac. Sci. Technol. A 36 030802
Google Scholar
[7] Prentiss M, Cable A, Bjorkholm J E, Chu S, Raab E L, Pritchard D E 1988 Opt. Lett. 13 452
Google Scholar
[8] Scherschligt J, Fedchak J A, Barker D S, Eckel S, Klimov N, Makrides C, Tiesinga E 2017 Metrologia 54 125
Google Scholar
[9] Eckel S, Barker D S, Fedchak J A, Klimov N N, Norrgard E, Scherschligt J, Makrides C, Tiesinga E 2018 Metrologia 55 182
Google Scholar
[10] Makrides C, Barker D S, Fedchak J A, Eckel S, Tiesinga E 2019 Phys. Rev. A 99 042704
Google Scholar
[11] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2020 Phys. Rev. A 101 012702
Google Scholar
[12] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2022 Phys. Rev. A 105 029902
Google Scholar
[13] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2022 Phys. Rev. A 105 039903
Google Scholar
[14] Barker D S, Klimov N N, Tiesinga E, Fedchak J A, Scherschligt J, Eckel S 2021 Measurement: Sensors 18 100229
Google Scholar
[15] Barker D S, Acharya B P, Fedchak J A, Klimov N N, Norrgard E B, Scherschligt J, Tiesinga E, Eckel S 2022 Rev. Sci. Instrum. 93 121101
Google Scholar
[16] Barker D S, Fedchak J A, Kłos J, Scherschligt J, Sheikh A A, Tiesinga E, Eckel S 2023 AVS Quantum Sci. 5 035001
Google Scholar
[17] Kłos J, Tiesinga E 2023 J. Chem. Phys. 158 014308
Google Scholar
[18] Booth J L, Shen P, Krems R V, Madison K W 2019 New J. Phys. 21 102001
Google Scholar
[19] Shen P, Madison K W, Booth J L 2020 Metrologia 57 025015
Google Scholar
[20] Shen P, Madison K W, Booth J L 2021 Metrologia 58 022101
Google Scholar
[21] Makhalov V B, Martiyanov K A, Turlapov A V 2016 Metrologia 53 1287
Google Scholar
[22] Jousten K 2016 Handbook of Vacuum Technology (Weinheim: Wiley-VCH) p634
[23] Dongen J V, Zhu C, Clement D, Dufour G, Booth J, Madison K 2011 Phys. Rev. A 84 022708
Google Scholar
[24] Kawanaka J, Shimizu K, Takuma H 1993 Appl. Phys. B 57 113
Google Scholar
[25] 张苏钊, 孙雯君, 董猛, 武海斌, 李睿, 张雪姣, 张静怡, 成永军 2022 71 094204
Google Scholar
Zhang S Z, Sun W J, Dong M, Wu H B, Li R, Zhang X J, Zhang J Y, Cheng Y J 2022 Acta Phys. Sin. 71 094204
Google Scholar
[26] Wu X M, Cheng Y J, Dong M, Sun W J, Zhang S Z, Ma Z Y, Li Y P, Jia W J, Feng T Y, Wu C Y 2023 Vacuum 207 111561
Google Scholar
[27] Sun W J, Wu X M, Cheng Y J, Ma Z Y, Jia W J, Zhang Y F, Zhang R F, Wu C Y, Feng C, Luo H G 2024 Vacuum 222 113079
Google Scholar
[28] Hajime Yoshida, Kenta Arai 2018 J. Vac. Sci. Technol. A 36 031604
Google Scholar
[29] Alper Elkatmis, Rifat Kangi 2019 Measurement 131 269
Google Scholar
[30] Yoshida H, Arai K, Kobata T 2014 Vacuum 101 433
Google Scholar
[31] Bich W 2014 Metrologia 51 S155
Google Scholar
-
图 2 碰撞体系的损失率系数kloss与阱深U的关系曲线
Fig. 2. Loss rate coefficient kloss versus trap depth U for the collision system.
图 3 7Li冷原子真空测量装置原理图
Fig. 3. Schematic diagram of the 7Li cold atom measurement apparatus.
图 4 3D MOT真空腔体中7Li冷原子团拍摄照片
Fig. 4. Photo of 7Li cold atom clusters in 3D MOT vacuum cavity.
图 5 7Li原子2S基态和2P激发态能级图
Fig. 5. Energy level diagrams of 2S ground state and 2P excited state of 7Li atom.
图 6 磁光阱和磁阱中冷原子损失率测量控制时序
Fig. 6. Timing sequence of the cold atom loss rate measurements in MOT and MT.
图 7 磁光阱和磁阱中冷原子损失率测量曲线
Fig. 7. Measurement curves of the loss rate of cold atoms in MOT and MT.
图 8 损失率Γloss与冷原子测量真空度p的关系曲线
Fig. 8. Curve of loss rate Γloss versus cold atom measurement vacuum pressure p.
图 9 分离规灵敏度因子与冷原子测量真空度的关系曲线
Fig. 9. Curve of the sensitivity factor of the extractor gauge versus the vacuum pressure of the cold atom measurement.
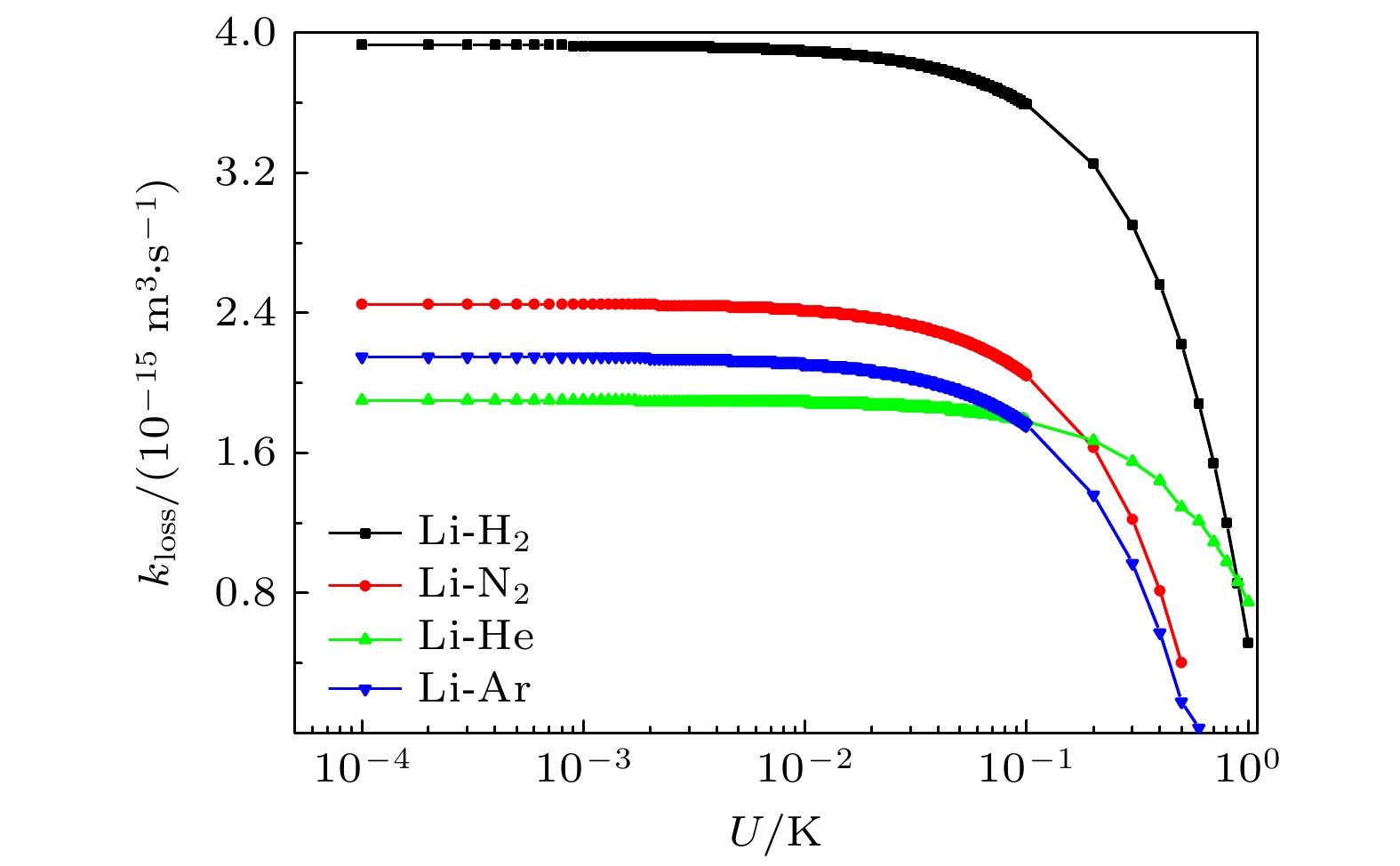
表 1 ab initio第一性原理实验测量的损失率系数kloss和半经典理论计算值比对
Table 1. Comparison of the loss rate coefficient kloss measured by the ab initio first principle experiment and the calculated value of the semiclassical theory.
碰撞体系 第一性原理测量值
kloss/(10–15·m3·s–1)半经典理论计算值
kloss/(10–15·m3·s–1)7Li-N2 1.36 0.27 7Li-Ar 1.21 0.059 7Li-He 1.04 1.29 7Li-H2 1.56 2.12 
下载: 导出CSV
表 2 冷原子校准的分离规相对N2的灵敏度因子
Table 2. Sensitivity factors of extractor gauge relative to N2 by cold atom calibration.
下载: 导出CSV
表 3 冷原子真空测量不确定度汇总表
Table 3. Summary of cold atom vacuum measurement uncertainties.
不确定度来源 评定方法 不确定度分量 损失率不确定度$ {u_{\text{r}}}({\varGamma _{{\text{loss}}}}) $ A类 10–8 Pa 0.03%@N2; 0.02%@Ar 10–7 Pa 0.07%@N2;0.05%@Ar;0.05%@He;0.04%@H2 10–6 Pa 0.04%@N2; 0.1%@Ar; 0.02%@He;0.04%@H2 10–5 Pa 0.06%@N2;0.04%@Ar;0.07%@He;0.08%@H2 B类 0.6% 损失率不确定度$ {u_{\text{r}}}({\varGamma _{{\text{MT}}}}) $ A类 1.6%@N2; 1.7%@Ar; 1.5%@He; 1.5%@H2 B类 0.6% 损失率不确定度$ {u_{\text{r}}}({\varGamma _{{\text{MOT}}}}) $ A类 0.05%@N2; 0.07%@Ar; 0.09%@He; 0.06%@H2 B类 0.6% 损失率系数不确定度$ {u_{\text{r}}}({k_{{\text{tot}}}}) $ — 0.8%@N2; 0.3%@Ar; 2.4%@He; 1.9%@H2 玻尔兹曼常数不确定度$ {u_{\text{r}}}({k_{\text{B}}}) $ — 忽略不计 气体分子温度不确定度$ {u_{\text{r}}}(T) $ B类 0.3% 本底真空波动不确定度$ {u_{\text{r}}}(w) $ A类 10–8 Pa 2.5%@N2; 2.5%@Ar; 2.0%@He; 2.7%@H2 10–7 Pa 0.5%@N2; 0.7%@Ar; 0.6%@He; 0.8%@H2 10–6 Pa 0.07%@N2;0.07%@Ar;0.08%@He;0.1%@H2 10–5 Pa 忽略不计 合成标准不确定度 10–8 Pa 3.3%@N2; 3.2%@Ar; 3.6%@He;3.8%@H2 10–7 Pa 2.2%@N2; 2.2%@Ar; 3.1%@He;2.8%@H2 10–6 Pa 2.1%@N2; 2.0%@Ar; 3.0%@He;2.7%@H2 10–5 Pa 2.1%@N2; 2.0%@Ar;3.0%@He; 2.7%@H2
下载: 导出CSV
-
[1] 李得天, 成永军, 冯焱, 卢耀文, 赵澜, 徐婕 2009 真空科学与技术学报 29 522
Google Scholar
Li D T, Cheng Y J, Feng Y, Lu Y W, Zhao L, Xu J 2009 Chin. J. Vac. Sci. Technol. 29 522
Google Scholar
[2] Li D T, Wang Y J, Zhang H Z, Xi Z H, Li G 2021 Space Sci. Tech. 23 7592858
[3] 刘见, 王刚, 胡一鸣, 张腾, 罗子人, 王晴岚, 邵立晶 2016 科学通报 61 1502
Google Scholar
Liu J, Wang G, Hu Y M, Zhang T, Luo Z R, Wang Q L, Shao L J 2016 Chin. Sci. Bull 61 1502
Google Scholar
[4] 王欲知, 陈旭 2007 真空技术 (北京: 北京航空航天大学出版社) 第6页
Wang Y Z, Chen X 2007 Vacuum Technology (Beijing: Beihang University Press) p6
[5] Jenninger B, Anderson J, Bernien M, Bundaleski M, Dimitrova H, Granovskij M, Illgen C, Setina J, Jousten K, Kucharski P, Reinhardt C, Scuderi F, Silva R A S, Stöltzel A, Teodoro O M N D, Trzpil-Jurgielewicz B, Wüest M 2021 Vacuum 183 109884
Google Scholar
[6] Fedchak J A, Abbott P J, Hendricks J H, Arnold P C, Peacock N T 2018 J. Vac. Sci. Technol. A 36 030802
Google Scholar
[7] Prentiss M, Cable A, Bjorkholm J E, Chu S, Raab E L, Pritchard D E 1988 Opt. Lett. 13 452
Google Scholar
[8] Scherschligt J, Fedchak J A, Barker D S, Eckel S, Klimov N, Makrides C, Tiesinga E 2017 Metrologia 54 125
Google Scholar
[9] Eckel S, Barker D S, Fedchak J A, Klimov N N, Norrgard E, Scherschligt J, Makrides C, Tiesinga E 2018 Metrologia 55 182
Google Scholar
[10] Makrides C, Barker D S, Fedchak J A, Eckel S, Tiesinga E 2019 Phys. Rev. A 99 042704
Google Scholar
[11] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2020 Phys. Rev. A 101 012702
Google Scholar
[12] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2022 Phys. Rev. A 105 029902
Google Scholar
[13] Makrides C, Barker D S, Fedchak J A, Scherschligt J, Eckel S, Tiesinga E 2022 Phys. Rev. A 105 039903
Google Scholar
[14] Barker D S, Klimov N N, Tiesinga E, Fedchak J A, Scherschligt J, Eckel S 2021 Measurement: Sensors 18 100229
Google Scholar
[15] Barker D S, Acharya B P, Fedchak J A, Klimov N N, Norrgard E B, Scherschligt J, Tiesinga E, Eckel S 2022 Rev. Sci. Instrum. 93 121101
Google Scholar
[16] Barker D S, Fedchak J A, Kłos J, Scherschligt J, Sheikh A A, Tiesinga E, Eckel S 2023 AVS Quantum Sci. 5 035001
Google Scholar
[17] Kłos J, Tiesinga E 2023 J. Chem. Phys. 158 014308
Google Scholar
[18] Booth J L, Shen P, Krems R V, Madison K W 2019 New J. Phys. 21 102001
Google Scholar
[19] Shen P, Madison K W, Booth J L 2020 Metrologia 57 025015
Google Scholar
[20] Shen P, Madison K W, Booth J L 2021 Metrologia 58 022101
Google Scholar
[21] Makhalov V B, Martiyanov K A, Turlapov A V 2016 Metrologia 53 1287
Google Scholar
[22] Jousten K 2016 Handbook of Vacuum Technology (Weinheim: Wiley-VCH) p634
[23] Dongen J V, Zhu C, Clement D, Dufour G, Booth J, Madison K 2011 Phys. Rev. A 84 022708
Google Scholar
[24] Kawanaka J, Shimizu K, Takuma H 1993 Appl. Phys. B 57 113
Google Scholar
[25] 张苏钊, 孙雯君, 董猛, 武海斌, 李睿, 张雪姣, 张静怡, 成永军 2022 71 094204
Google Scholar
Zhang S Z, Sun W J, Dong M, Wu H B, Li R, Zhang X J, Zhang J Y, Cheng Y J 2022 Acta Phys. Sin. 71 094204
Google Scholar
[26] Wu X M, Cheng Y J, Dong M, Sun W J, Zhang S Z, Ma Z Y, Li Y P, Jia W J, Feng T Y, Wu C Y 2023 Vacuum 207 111561
Google Scholar
[27] Sun W J, Wu X M, Cheng Y J, Ma Z Y, Jia W J, Zhang Y F, Zhang R F, Wu C Y, Feng C, Luo H G 2024 Vacuum 222 113079
Google Scholar
[28] Hajime Yoshida, Kenta Arai 2018 J. Vac. Sci. Technol. A 36 031604
Google Scholar
[29] Alper Elkatmis, Rifat Kangi 2019 Measurement 131 269
Google Scholar
[30] Yoshida H, Arai K, Kobata T 2014 Vacuum 101 433
Google Scholar
[31] Bich W 2014 Metrologia 51 S155
Google Scholar
下载:
计量
- 文章访问数: 368
- PDF下载量: 27
- 被引次数: 0
