-
近年来, 基于宇称-时间(parity-time, PT)对称的非厄密物理机制在磁谐振式无线电能传输(wireless power transfer, WPT)领域取得了显著进展. 非厄密物理不仅有效地解释了当前WPT领域基于电路理论分析的主要实验结果, 而且为进一步提升WPT器件的传输效率、距径比、鲁棒性等方面提供了全新的原理支撑. 本文主要综述了基于PT对称、高阶PT对称、高阶Anti-PT对称等条件下的高效稳定磁谐振式WPT的研究进展, 揭示了非厄密物理在该领域的独特作用机制及重要应用. 最后对非厄密物理在WPT领域的应用前景进行了展望.
In recent years, wireless power transfer (WPT) leveraging parity-time (PT) symmetry has made significant progress , in terms of enhancing efficiency, transfer distance, and robustness. This paper overviews magnetic resonance WPT systems utilizing ideal, asymmetric, high-order, and anti-PT symmetry. The first section discusses the second-order PT symmetry, evolving from inductive to resonant WPT. Active tuning and nonlinear saturation gain techniques optimize frequency and spontaneously achieve efficient WPT. These methods improve transmission efficiency, especially with the change of dynamic transfer distance. The second section focuses on the third-order PT and anti-PT symmetry. The third-order PT systems maintain a fixed eigenfrequency, making stable energy transfer possible. Generalized PT symmetry harnesses bandgaps for further efficiency. The BIC in asymmetric systems reveals a pure real mode for stable WPT. The anti-PT symmetry’s ‘level pinning’ maintains stability in dynamic changes. The final section summarizes high-order PT symmetry for long-range WPT. Heterojunction coupling and topologically non-trivial chains enhance efficiency and stability. Examples include long-range WPT via relay coils and directional WPT using asymmetric topological edge states. In summary, this review emphasizes the pivotal role of various forms of PT symmetry in improving the performance and reliability of magnetic resonance WPT systems. By improving transmission efficiency, range, and stability, these symmetries pave the way for wider applications in fields such as smart homes, medical devices, and electric vehicles. The synthesis of current research results provides valuable insights and references for the future development of WPT technology. -
Keywords:
- wireless power transfer /
- non-Hermitian physics /
- parity-time symmetry /
- near-field manipulation and application
[1] Tesla N 1914 U. S. Patent 1 119 732 [1914-12-1]
[2] Hui S Y R, Zhong W X, Lee C K 2013 IEEE Trans. Power Electron. 29 4500
[3] Wang C S, Covic G A, Stielau O H 2004 IEEE Trans. Ind. Electron. 51 148
 Google Scholar
Google Scholar
[4] Ho S L, Wang J, Fu W N, Sun M 2011 IEEE Trans. Magn. 47 1522
 Google Scholar
Google Scholar
[5] Shen D, Du G P, Zeng W, Yang Z J, Li J J 2020 IEEE Access 8 59648
 Google Scholar
Google Scholar
[6] Kurs A, Karalis A, Moffatt R, Joannopoulos J D, Fisher P, Soljacic M 2007 Science 31 75834
[7] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
 Google Scholar
Google Scholar
[8] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S, Christodoulides D N 2018 Nat. Phys. 14 11
 Google Scholar
Google Scholar
[9] Li A, Wei H, Cotrufo M, Chen W, Mann S, Ni X, Xu B, Chen J, Wang J, Fan S, Qiu C W, Alù A, Chen L 2023 Nat. Nanotechnol. 18 706
 Google Scholar
Google Scholar
[10] Feng L, El-Ganainy R, Ge L 2017 Nat. Photonics 11 752
 Google Scholar
Google Scholar
[11] Özdemir K, Rotter S, Nori F, Yang L 2019 Nat. Mater. 18 783
 Google Scholar
Google Scholar
[12] Zhang S M, Jin L, Song Z 2022 Chin. Phys. B 31 010312
 Google Scholar
Google Scholar
[13] 唐原江, 梁超, 刘永椿 2022 71 171101
 Google Scholar
Google Scholar
Tang Y J, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101
 Google Scholar
Google Scholar
[14] 祝可嘉, 郭志伟, 陈鸿 2022 71 131101
 Google Scholar
Google Scholar
Zhu K J, Guo Z W, Chen H 2022 Acta Phys. Sin. 71 131101
 Google Scholar
Google Scholar
[15] Cao W, Wang C, Chen W, Hu S, Wang H, Yang L, Zhang X 2022 Nat Nanotechnol. 17 262
 Google Scholar
Google Scholar
[16] Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101(R
[17] Li H, Yin S, Galiffi E, Alù A 2021 Phys. Rev. Lett. 127 153903
 Google Scholar
Google Scholar
[18] Yang X, Li J, Ding Y, Xu M, Zhu X F, Zhu J 2022 Phys. Rev. Lett. 128 065701
 Google Scholar
Google Scholar
[19] Chen P Y, Sakhdari M, Hajizadegan M, Cui Q, Cheng M M C, El-Ganainy R, Alù A 2018 Nat. Electron. 1 297
 Google Scholar
Google Scholar
[20] Zeng C, Guo Z W, Zhu K J, Fan C F, Li G, Jiang J, Li Y H, Jiang H T, Yang Y P, Sun Y, Chen H 2022 Chin. Phys. B 31 010307
 Google Scholar
Google Scholar
[21] Song M, Jayathurathnage P, Zanganeh E, Krasikova M, Smirnov P, Belov P, Kapitanova P, Simovski C, Tretyakov S, Krasnok, A 2021 Nat. Electron. 4 707
 Google Scholar
Google Scholar
[22] Song M, Belov P, Kapitanova P 2017 Appl. Phys. Rev. 4 021102
 Google Scholar
Google Scholar
[23] Sakhdari M, Hajizadegan M, Chen P Y 2020 Phys. Rev. Res. 2 013152
 Google Scholar
Google Scholar
[24] Guo Z W, Chen H 2024 Physics 53 33 [郭志伟, 陈鸿 2024 物理 53 33]
 Google Scholar
Google Scholar
Guo Z W, Chen H 2024 Physics 53 33
 Google Scholar
Google Scholar
[25] Miri M A, Alù A 2019 Science 363 7709
 Google Scholar
Google Scholar
[26] Ding K, Fang C, Ma G 2022 Nat. Rev. Phys. 4 745
 Google Scholar
Google Scholar
[27] Sample A P, Meyer D T, Smith J R 2010 IEEE Trans. Ind. Electron. 58 544
[28] Park J, Tak Y, Kim Y, Kim Y, Nam S 2011 IEEE Trans. Antennas Propag. 59 1769
 Google Scholar
Google Scholar
[29] Li Y, Wang M, Zhang W, Zhao M, Liu J 2019 Energies 12 2626
 Google Scholar
Google Scholar
[30] Song M, Baryshnikova K, Markvart A, Belov P, Nenasheva E, Simovski C, Kapitanova P 2019 Phys. Rev. Appl. 11 054046
 Google Scholar
Google Scholar
[31] Lerosey G 2017 Nature 546 354
 Google Scholar
Google Scholar
[32] Assawaworrarit S, Yu X, Fan S 2017 Nature 546 387
 Google Scholar
Google Scholar
[33] Guo Z, Jiang H, Li Y, Chen H, Agarwal G. S 2018 Opt. Express 26 627
 Google Scholar
Google Scholar
[34] Fan S H , Suh W, Joannopoulos J D 2003 J. Opt. Soc. Am. A 20 569
[35] Zhou J, Zhang B, Xiao W, Qiu D, Chen Y 2019 IEEE Trans. Ind. Electron. 66 4097
 Google Scholar
Google Scholar
[36] Assawaworrarit S, Fan S 2020 Nat. Electron. 3 273
 Google Scholar
Google Scholar
[37] Zeng C, Sun Y, Li G, Li Y, Jiang H, Yang Y, Chen H 2020 Phys. Rev. Appl. 13 034054
 Google Scholar
Google Scholar
[38] Guo Z, Jiang J, Wu X, Zhang H, Hu S, Wang Y, Li Y, Yang Y, Chen H 2023 Fundam. Res. 11 2667
[39] Xie Y, Zhang Z, Lin Y, Feng T, Xu Y 2021 Phys. Rev. Appl. 15 044024
 Google Scholar
Google Scholar
[40] Zhang H, Guo Z, Li Y, Yang Y, Chen Y, Chen H 2024 Front. Phys. 19 43209
 Google Scholar
Google Scholar
[41] Wu Y, Kang L, Douglas H. Werner 2022 Phys. Rev. Lett. 129 200201
 Google Scholar
Google Scholar
[42] Hao X, Yin K, Zou J, Wang R, Huang Y, Ma X, Dong T 2023 Phys. Rev. Lett. 130 077202
 Google Scholar
Google Scholar
[43] Zhang G Q, You J Q 2019 Phys. Rev. B 99 054404
 Google Scholar
Google Scholar
[44] Wu H C, Jin L, Song Z 2021 Phys. Rev. B 103 235110
 Google Scholar
Google Scholar
[45] Peng P, Cao W, Shen C, Qu W, Wen J, Jiang L, Xiao Y 2016 Nat. Phys. 12 1139
 Google Scholar
Google Scholar
[46] Zhang H, Huang R, Zhang S D, Li Y, Qiu C W, Nori F, Jing H 2020 Nano Lett. 20 7594
 Google Scholar
Google Scholar
[47] Ke S, Zhao D, Liu J, Liu Q, Liao Q, Wang B, Lu P 2019 Opt. Express 27 13858
 Google Scholar
Google Scholar
[48] Guo Z, Yang F, Zhang H, Wu X, Wu Q, Zhu K, Jiang J, Jiang H, Yang Y, Li Y, Chen H 2024 Natl. Sci. Rev. 11 172
 Google Scholar
Google Scholar
[49] Ozaki T, Ohta N, Jimbo T, Hamaguchi K 2021 Nat. Electron. 4 845
 Google Scholar
Google Scholar
[50] Kim H, Yoo S, Joo H, Lee J. An D, Nam S, Han H, Kim D H, Kim S 2022 Sci. Adv. 8 4610
 Google Scholar
Google Scholar
[51] Shu J C, Cao M S, Zhang M, Wang X X, Cao W Q, Fang X Y, Cao M Q 2020 Adv. Funct. Mater. 30 1908299
 Google Scholar
Google Scholar
[52] Gutruf P, Krishnamurthi V, Vázquez-Guardado A, Xie Z, Banks A, Su C J, Xu Y, Haney C R, Waters E A, Kandela I, Krishnan S R, Ray T, Leshock J P, Huang G Y, Chanda D, Rogers J A 2018 Nat. Electron. 1 652
 Google Scholar
Google Scholar
[53] Gutruf P, Yin R T, Lee K B, Ausra J, Brennan J A, Qiao Y, Xie Z, Peralta R, Talarico O, Murillo A, Chen S W, Leshock J P, Haney C R, Waters E A, Zhang C X, Luan H, Huang Y G, Trachiotis G, Efimov I R, Rogers J A 2019 Nat. Commun. 10 5742
 Google Scholar
Google Scholar
[54] Lyu H, John M, Burkland D, Greet B, Post A, Babakhani A, Razavi M 2020 Sci. Rep. 10 2067
 Google Scholar
Google Scholar
[55] Yoo S, Lee J, Joo H, Sunwoo S H, Kim S, Kim D H 2021 Adv. Healthcare Mater. 10 2100614
 Google Scholar
Google Scholar
[56] Kim J, Banks A, Xie Z, Heo S Y, Gutruf P, Lee J W, Xu S, Jang K I, Liu F, Brown G, Choi J, Kim J H, Feng X, Huang Y, Paik U Rogers, J A 2015 Adv. Funct. Mater. 25 4761
 Google Scholar
Google Scholar
[57] Khan S R, Pavuluri S K, Cummins G, Desmulliez M P 2020 Sensors 20 3487
[58] Zhong W X, Lee C K, Ron Hui S Y 2013 IEEE Trans. Ind. Electron. 60 261
 Google Scholar
Google Scholar
[59] Song J, Yang F, Guo Z, Wu X, Zhu K, Jiang J, Sun Y, Li Y, Jiang H, Chen H 2021 Phys. Rev. Appl. 15 014009
 Google Scholar
Google Scholar
[60] Yang F, Song J, Guo Z, Wu X, Zhu, K, Jiang J, Sun Y, Jiang H, Li Y, Chen H 2021 Opt. Express 29 7844
 Google Scholar
Google Scholar
[61] Zhang L, Yang Y, Jiang Z, Chen Q, Yan Q, Wu Z, Zhang B, Huangfu J, Chen H, 2021 Sci. Bull. 66 974
 Google Scholar
Google Scholar
[62] Lu L, Joannopoulos J D, Soljacic M 2014 Nat. Photonics 8 821
 Google Scholar
Google Scholar
[63] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
[64] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
 Google Scholar
Google Scholar
[65] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
[66] Guo Z, Wang Y, Ke S, Su X, Ren J, Chen H 2024 Adv. Phys. Res. 3 2300125
 Google Scholar
Google Scholar
[67] Guo Z, Zhang T, Song J, Jiang H, Chen H 2021 Photonics Res. 9 574
 Google Scholar
Google Scholar
[68] Zangeneh‐Nejad F, Fleury R 2020 Adv. Mater. 32 2001034
 Google Scholar
Google Scholar
[69] Feis J, Solymar L, Shamonina E 2023 J. Appl. Phys. 133 22
[70] Puchnin V M, Matvievskaya O V, Slobozhanyuk A P, Shchelokova A V, Olekhno N A 2023 Phys. Rev. Appl. 20 024076
 Google Scholar
Google Scholar
[71] Guo Z, Jiang H, Sun Y, Li Y, Chen H 2018 Opt. Lett. 43 51425
[72] Wu H C, Xu H S, Xie L C, Jin L 2024 Phys. Rev. Lett. 132 083801
 Google Scholar
Google Scholar
[73] Lu C C, Yuan H Y, Zhang H Y, Zhao W, Zhang N E, Zheng Y J, Elshahat S, Liu Y C 2022 Chip 1 100025
 Google Scholar
Google Scholar
[74] Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature 548 187
 Google Scholar
Google Scholar
[75] Maamache M, Kheniche L 2020 Prog. Theor. Exp. Phys. 12 123A01
[76] Li Y, Peng Y G, Han L, Miri M A, Li W, Xiao M, Zhu X F, Zhao J, Alù A, Fan S, Qiu C W 2019 Science 364 170
 Google Scholar
Google Scholar
[77] Yang Y, Wang Y P, Rao J W, Gui Y S, Yao B M, Lu W, Hu C M 2020 Phys. Rev. Lett. 125 147202
 Google Scholar
Google Scholar
[78] Kim D H, Ahn D 2019 IEEE Trans. Power Electron. 35 11391
[79] Ma W, Liu Z, Kudyshev Z A, Boltasseva A, Cai W, Liu Y 2021 Nat. Photonics 15 77
 Google Scholar
Google Scholar
[80] Genty G, Salmela L, Dudley J M, Brunner D, Kokhanovskiy A, Kobtsev S, Turitsyn S K 2021 Nat. Photonics 15 91
 Google Scholar
Google Scholar
[81] Nadell C C, Huang B, Malof J M, Padilla W J 2019 Opt. Express 27 27523
 Google Scholar
Google Scholar
-
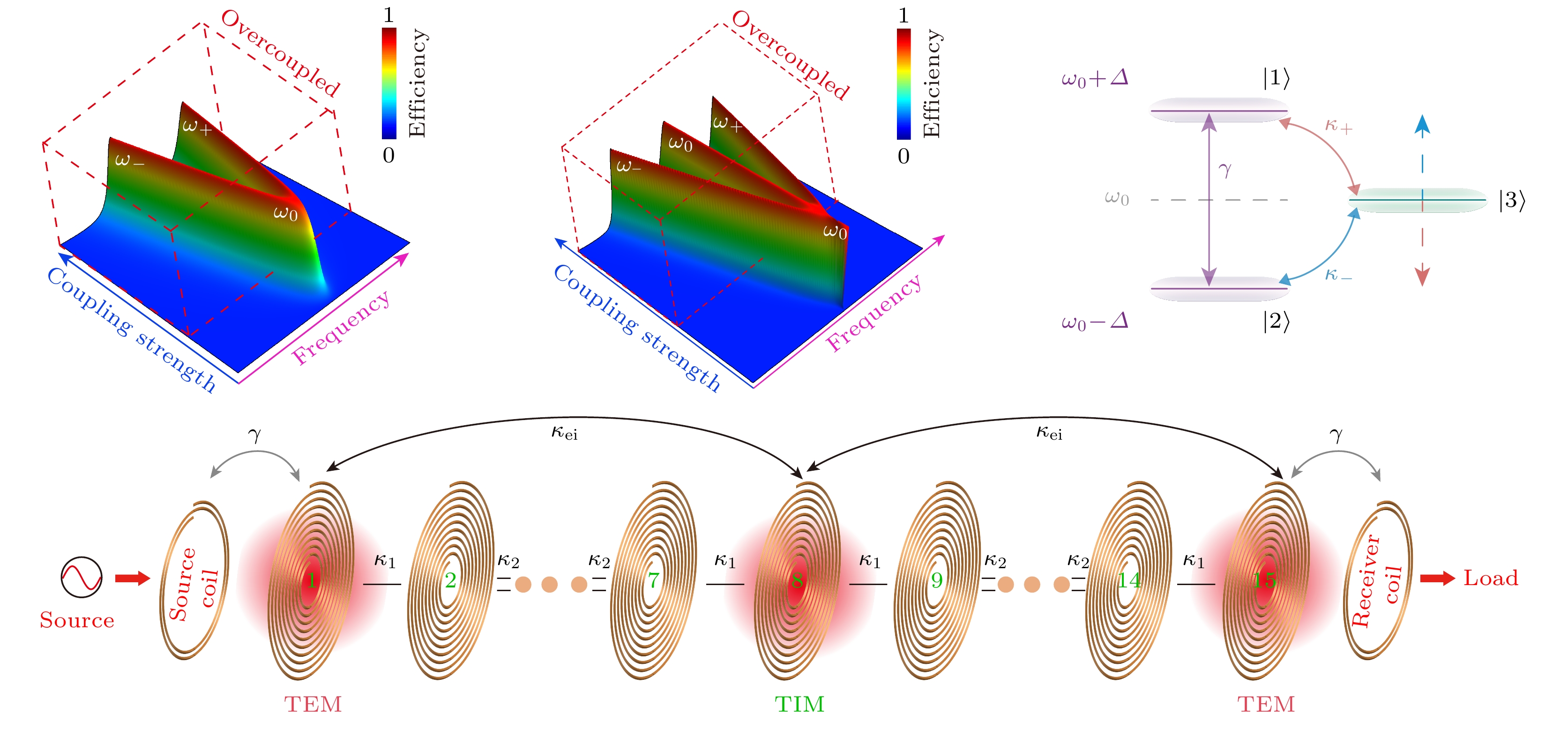
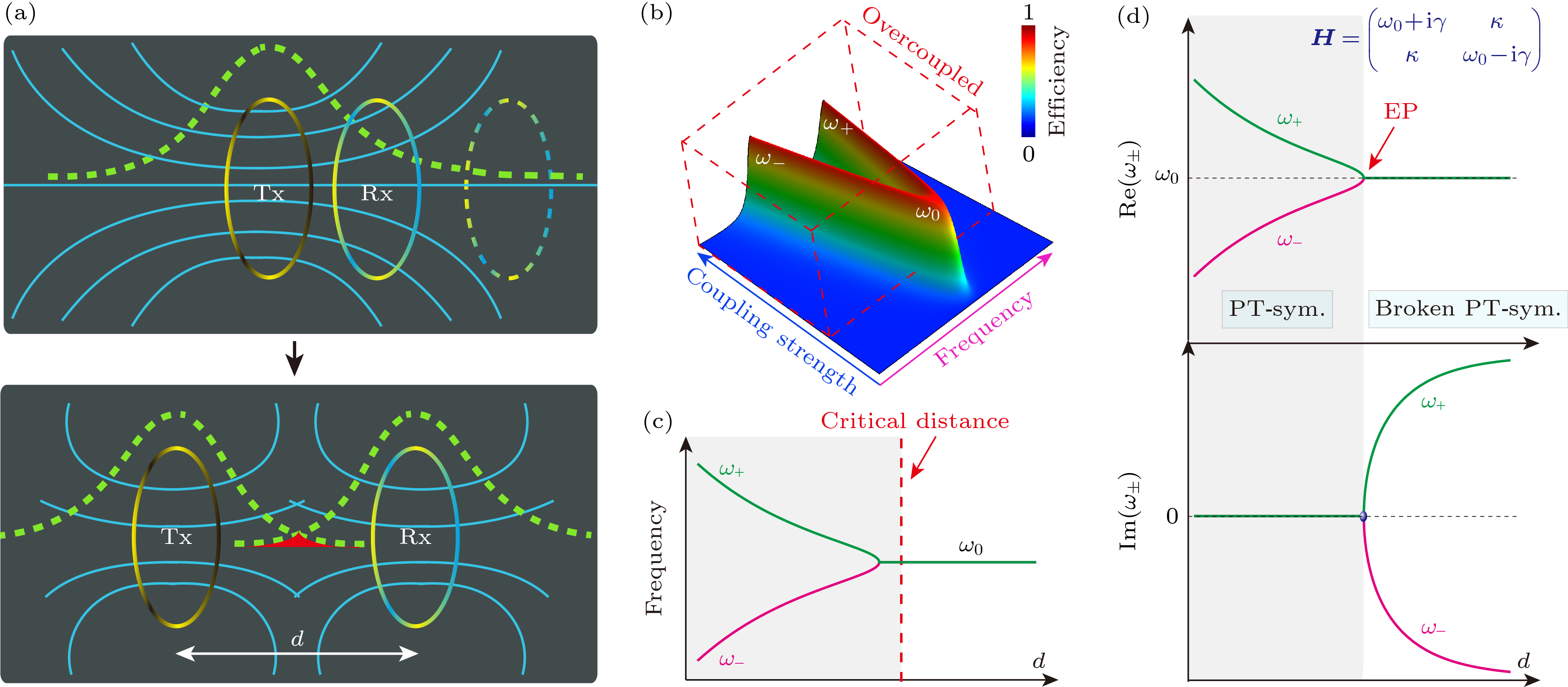
图 1 (a) 感应式和谐振式模型及能量分布; (b) 谐振式模型的传输特性; (c) 频率随距离劈裂现象(电路方程解); (d) 非厄密物理PT对称相图(哈密顿量解)
Fig. 1. (a) Inductive and resonant models and energy distribution; (b) the transmission characteristics of resonant model; (c) frequency splitting phenomenon with distance (circuit equation solution); (d) phase diagrams of PT-symmetric non-Hermitian system (Hamiltonian solution).
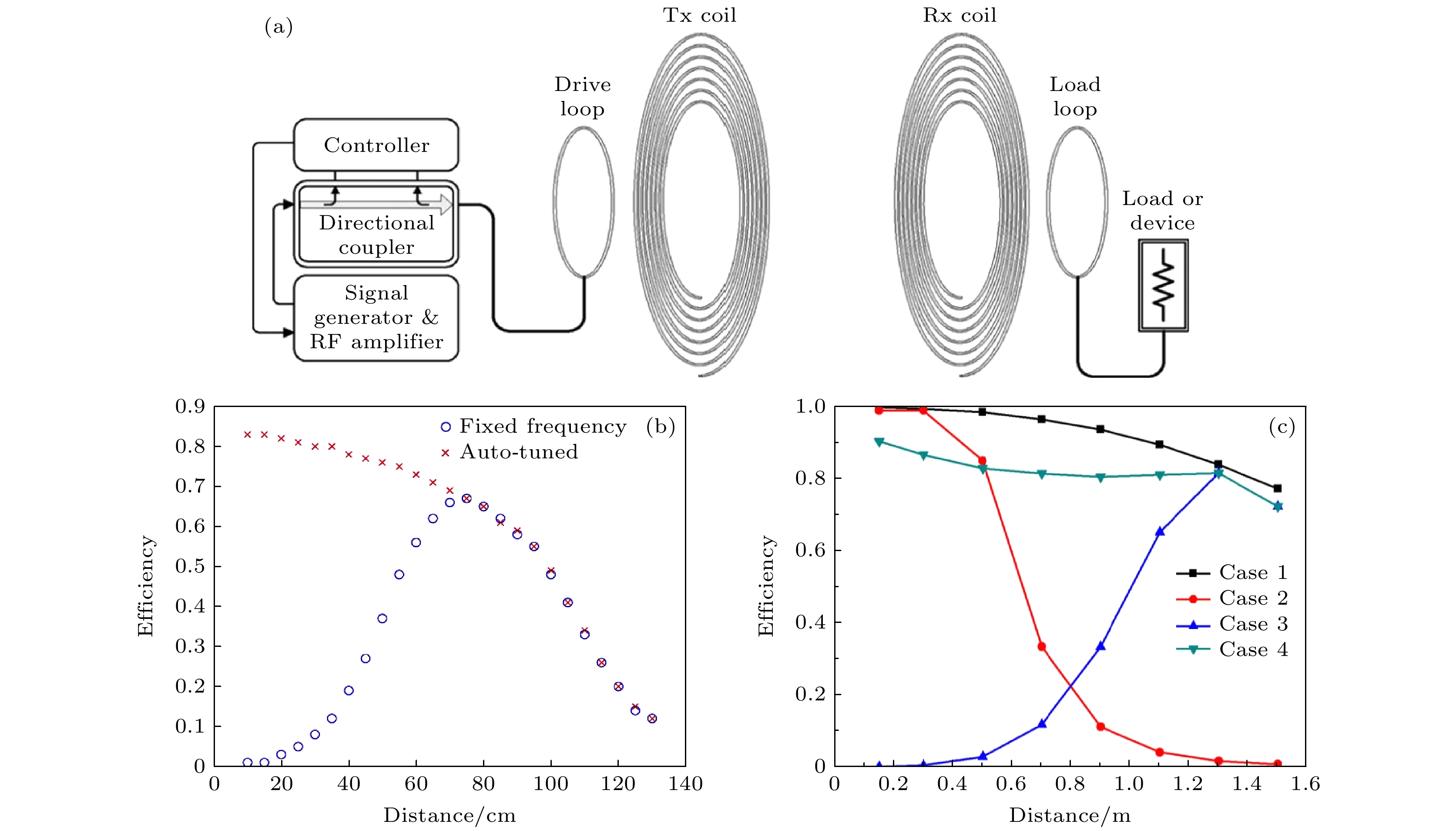
图 2 (a) 由射频放大器组成的频率追踪式磁耦合谐振式WPT的示意图[27]; (b) 固定驱动频率系统与自适应频率调谐系统随距离变化的传输效率对比图[27]; (c) 4种不同情形下的实验传输效率对比[28]
Fig. 2. (a) Schematic diagram of frequency tracking magnetic coupling resonant WPT composed of RF amplifiers[27]; (b) comparison of transmission efficiency between fixed frequency system and auto-tuned system with distance[27]; (c) comparison of experimental transmission efficiency in four cases[28].
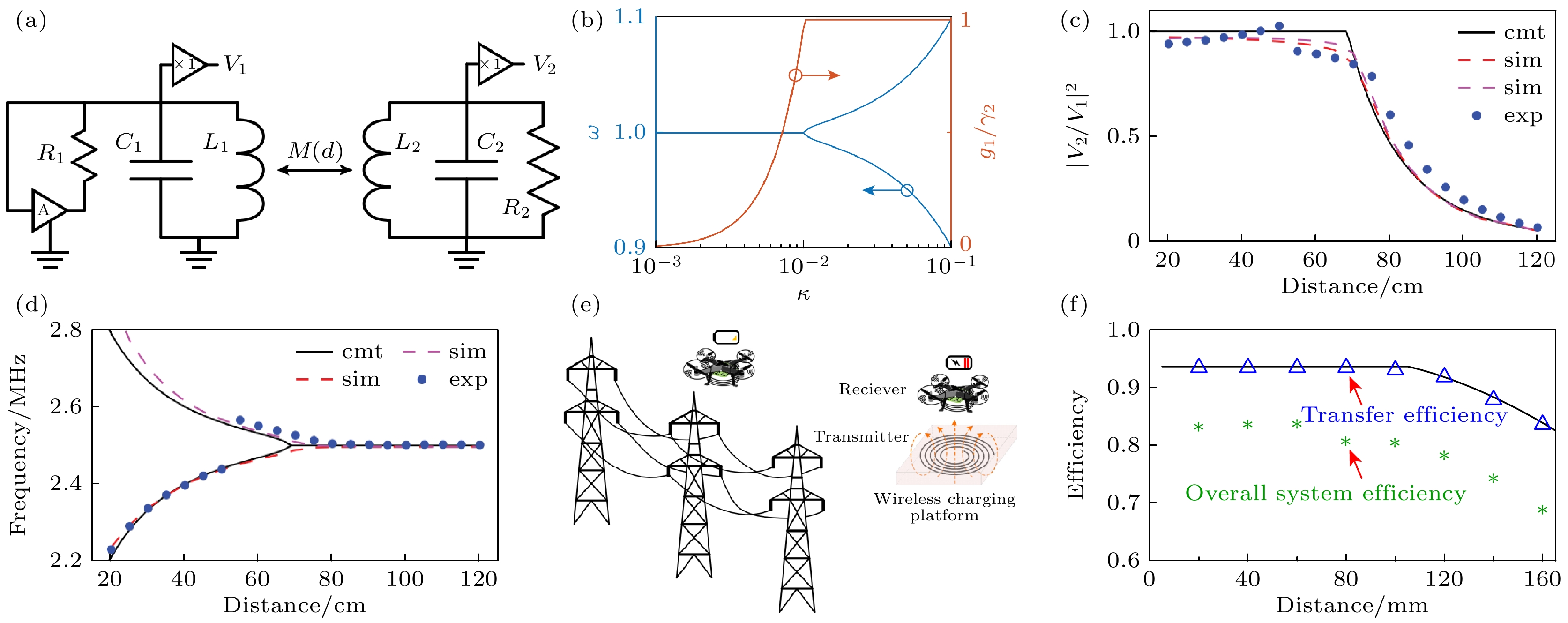
图 3 (a) PT对称WPT的电路模型[32]; (b) 频率及稳态增益随耦合强度(距离)的变化[32]; (c) PT对称WPT的电压比[32]; (d) 理论(黑线)、电路仿真(品红虚线)和实验结果(蓝色圆点)对比[32]; (e) 无人机WPT传输示意图[35]; (f) 无人机平台原边副边传输效率及总体效率[35]
Fig. 3. (a) The Circuit model of PT symmetric WPT[32]; (b) frequency and steady-state gain as a function of coupling strength (distance)[32]; (c) voltage ratio of PT symmetric WPT[32]; (d) comparison of theoretical (black line), circuit simulation (magenta dashed line), and experimental results (blue dots)[32]; (e) schematic of UAV WPT transmission[35]; (f) UAV platform primary-side secondary-side transmission efficiency and overall efficiency[35].
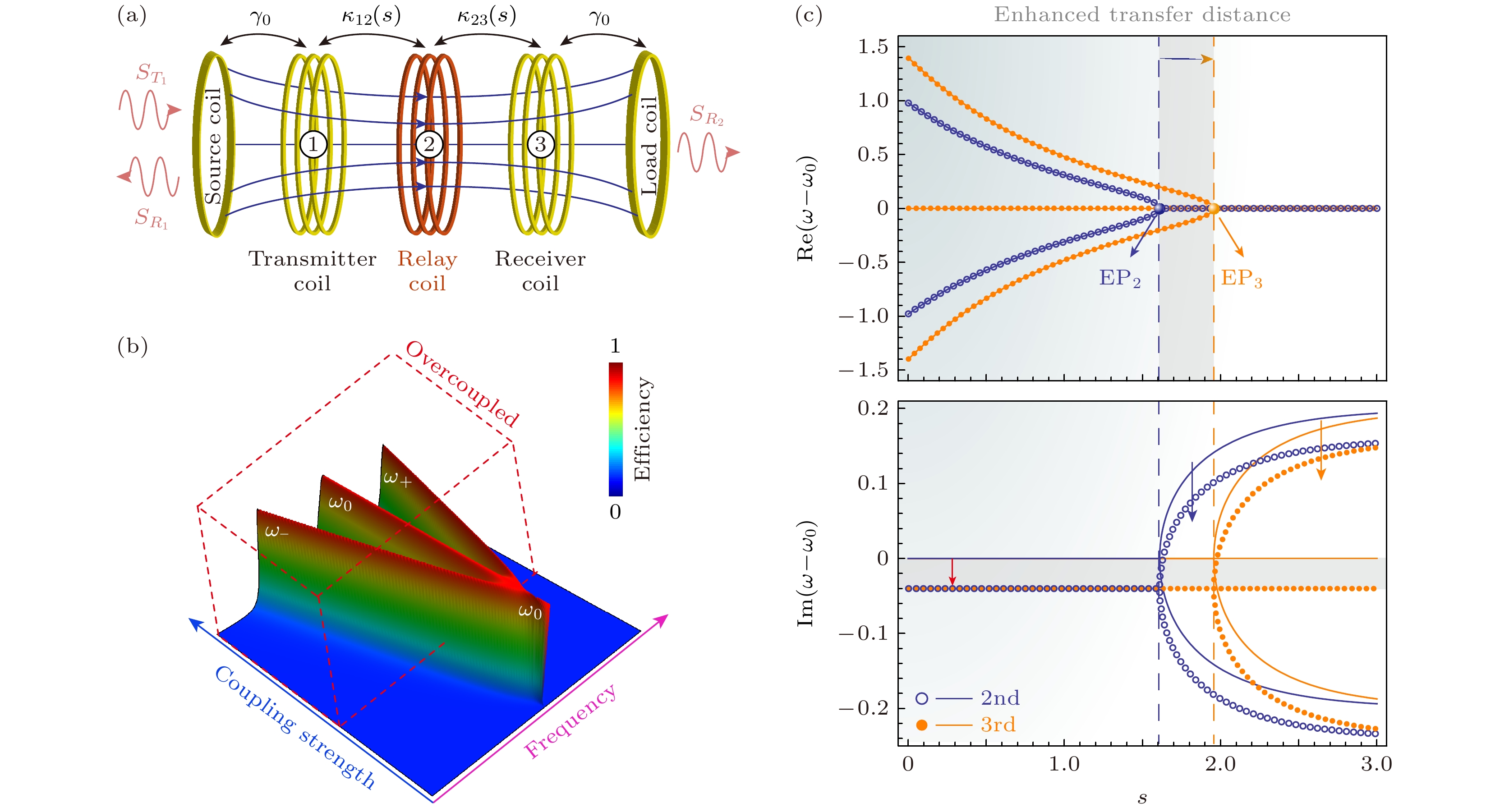
图 4 三阶PT对称WPT系统[38] (a) 三阶PT对称模型图; (b) 三阶PT对称系统效率随频率和耦合强度变化关系; (c) 二阶和三阶PT对称系统传输实部虚部相图对比
Fig. 4. Third-order PT-symmetric WPT system[38]: (a) Diagram of the third-order PT-symmetric model; (b) variation of the efficiency of the third-order PT-symmetric system with frequency and coupling strength; (c) comparison of the phase diagrams of the real and imaginary parts of the transmission of the second- and third-order PT-symmetric systems.
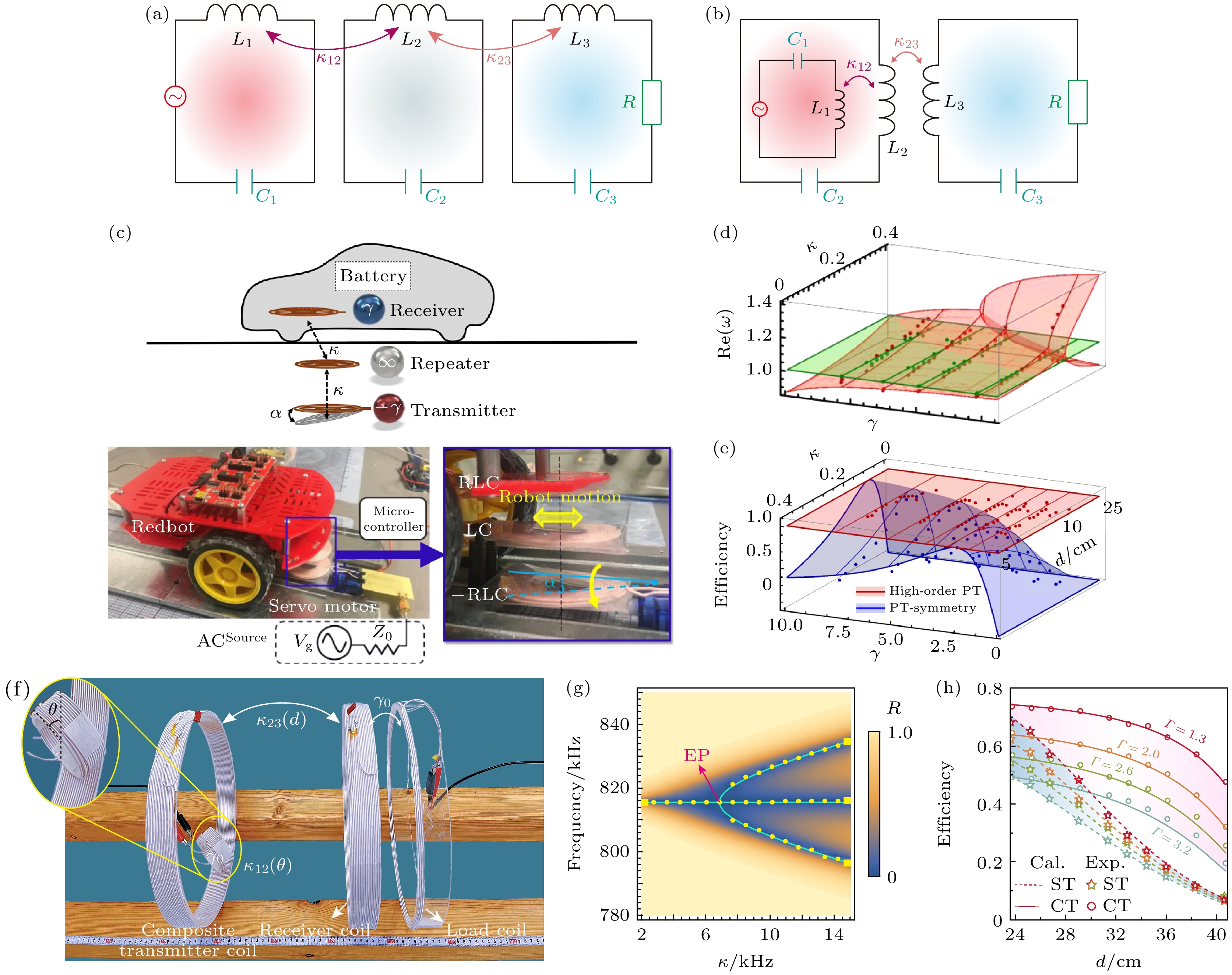
图 5 三阶PT对称WPT系统的实现 (a) 分离型三阶系统电路图; (b) 合成型三阶系统电路; (c) 小车三阶WPT演示图[23]; (d) 三阶系统实部随耦合和损耗的演化轨迹[23]; (e) 理想情况下三阶和二阶系统效率对比图[23]; (f) (b)图对应实验图[38]; (g) 三阶系统反射率随频率和耦合强度的变化关系[38]; (h) 不同本征损耗下效率与传输距离变化图[38]
Fig. 5. Realization of the third-order PT symmetric WPT system: (a) Circuit diagram of the separated third-order system; (b) circuit of the synthesized third-order system; (c) demonstration diagram of the third-order WPT of the cart[23]; (d) evolution trajectory of the real part of the third-order system with coupling and loss[23]; (e) comparison of the efficiencies of the third-order and the second-order systems in the ideal case[23]; (f) experimental plots corresponding to the diagrams in (b)[38]; (g) variation of the reflectivity of the third-order system with frequency and coupling strength[38]; (h) different intrinsic losses in the efficiency versus transmission distance plots[38].
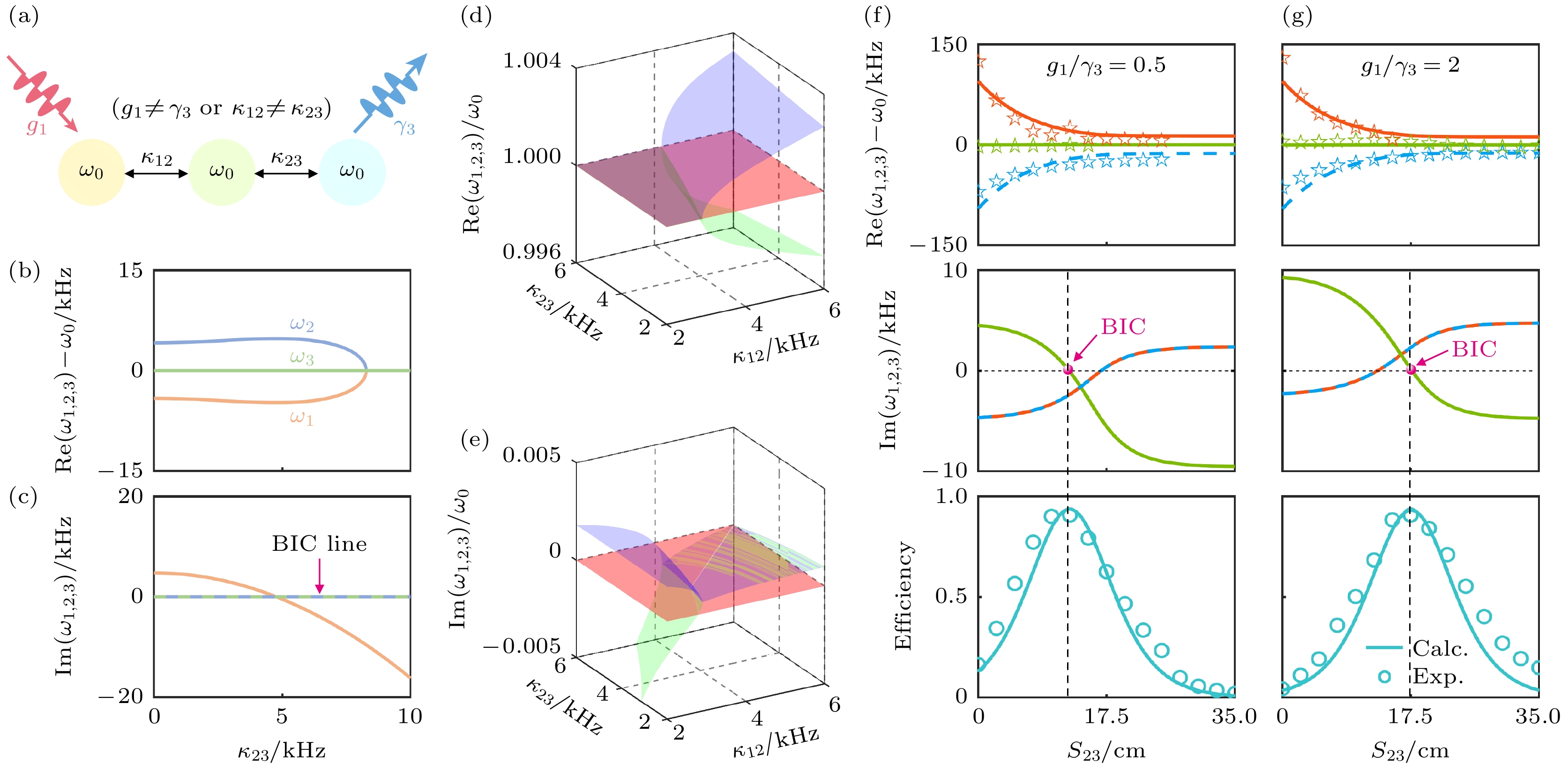
图 6 (a) 三阶PT非对称结构图; (b) 三阶PT非对称系统实部随${\kappa _{23}}$变化相图; (c) 三阶PT非对称系统虚部随${\kappa _{23}}$变化相图; (d) 同(b)但关于耦合${\kappa _{12}}$${\kappa _{23}}$三维实部相图演化; (e) 同(c)但关于耦合${\kappa _{12}}$${\kappa _{23}}$三维虚部相图演化; 三阶非厄密WPT系统本征频率实部, 虚部和系统效率在不同增益损耗比下的演化: (f) 增益损耗比例为0.5; (g) 增益损耗比例为2[40]
Fig. 6. (a) Third-order PT asymmetric structure; (b) phase diagram of the real part of the third-order PT asymmetric system as a function of the variation; (c) phase diagram of the imaginary part of the third-order PT asymmetric system as a function of the variation; (d) same as in figure (b) but with respect to the coupling three-dimensional real phase diagram evolution; (e) same as in figure (c) but with respect to the coupling Three-dimensional imaginary phase diagram evolution; evolution of the real and imaginary parts and the system efficiency of the characteristic frequencies of the third-order non-Hermitian WPT system for different gain-loss ratios: (f) gain-loss ratio of 0.5; (g) gain-loss ratio of 2[40].
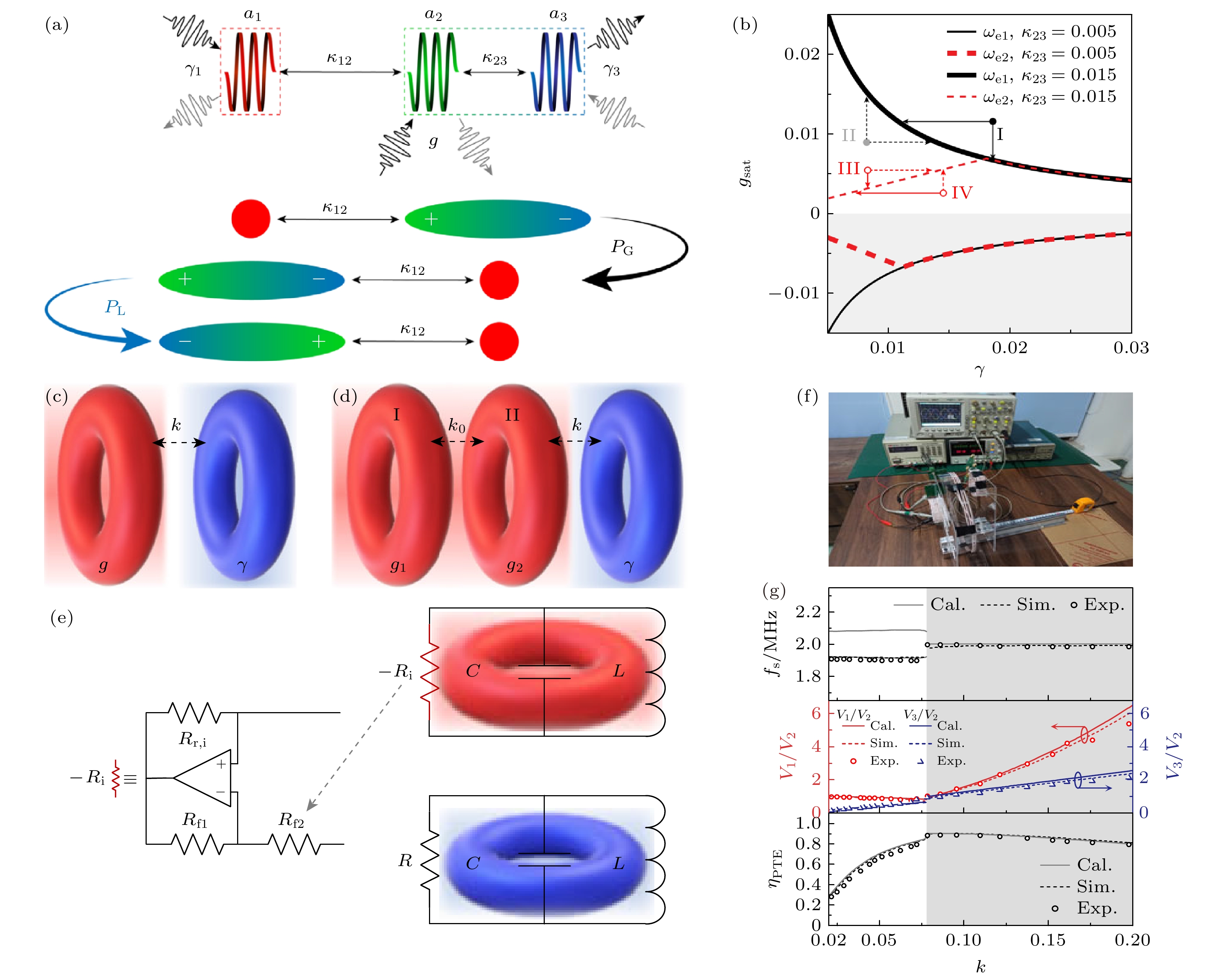
图 7 (a) 基于偶极-单极类比的广义奇偶性的局部和全局奇偶性分解[41]; (b) 高维参数空间$(g, \gamma , {\kappa _{12}}, {\kappa _{23}})$中WPT 系统的能带理论解释[41]; (c) 标准PT对称电子二聚体的示意图[42]; (d) 由两个增益(红色)单元和一个损耗(蓝色)单元组成的三阶赝厄密系统[42]; (e) 增益单元和损耗单元对应的等效电路[42]; (f) 图(d)模型的实验装置示意图[42]; (g) 稳态频率${f_{\text{s}}}$(上图), 电压比$ {V_1}/{V_2} $(左侧红色y轴)和$ {V_3}/{V_2} $(右侧蓝色y轴)(中间图), 以及传输效率${\eta _{{\text{PTE}}}}$(下图), 作为耦合系数$\kappa $的函数. 理论, 模拟和实验结果分别用实线、虚线和空心圆表示. 阴影区域表示$\kappa \geqslant \gamma =0.078$[42]
Fig. 7. (a) Local and global parity decomposition based on the generalized parity of the dipole-monopole analogy[41]; (b) band theory explanation of the WPT system in high-dimensional parameter space $(g, \gamma , {\kappa _{12}}, {\kappa _{23}})$[41]; (c) schematic diagram of a standard PT-symmetric electronic dimer[42]; (d) third-order pseudo-Hermitian system composed of two gain (red) units and one loss (blue) unit[42]; (e) equivalent circuit corresponding to the gain and loss units[42]; (f) schematic diagram of the experimental setup for the model in Figure (d)[42]; (g) steady-state frequency ${f_{\text{s}}}$(upper panel), voltage ratios $ {V_1}/{V_2} $ (left red y-axis) and $ {V_3}/{V_2} $ (right blue y-axis) (middle panel), and transmission efficiency ${\eta _{{\text{PTE}}}}$ (lower panel), as functions of the coupling coefficient $\kappa $. Theoretical, simulated, and experimental results are represented by solid lines, dashed lines, and hollow circles, respectively. The shaded area represents $\kappa \geqslant \gamma =0.078$[42].
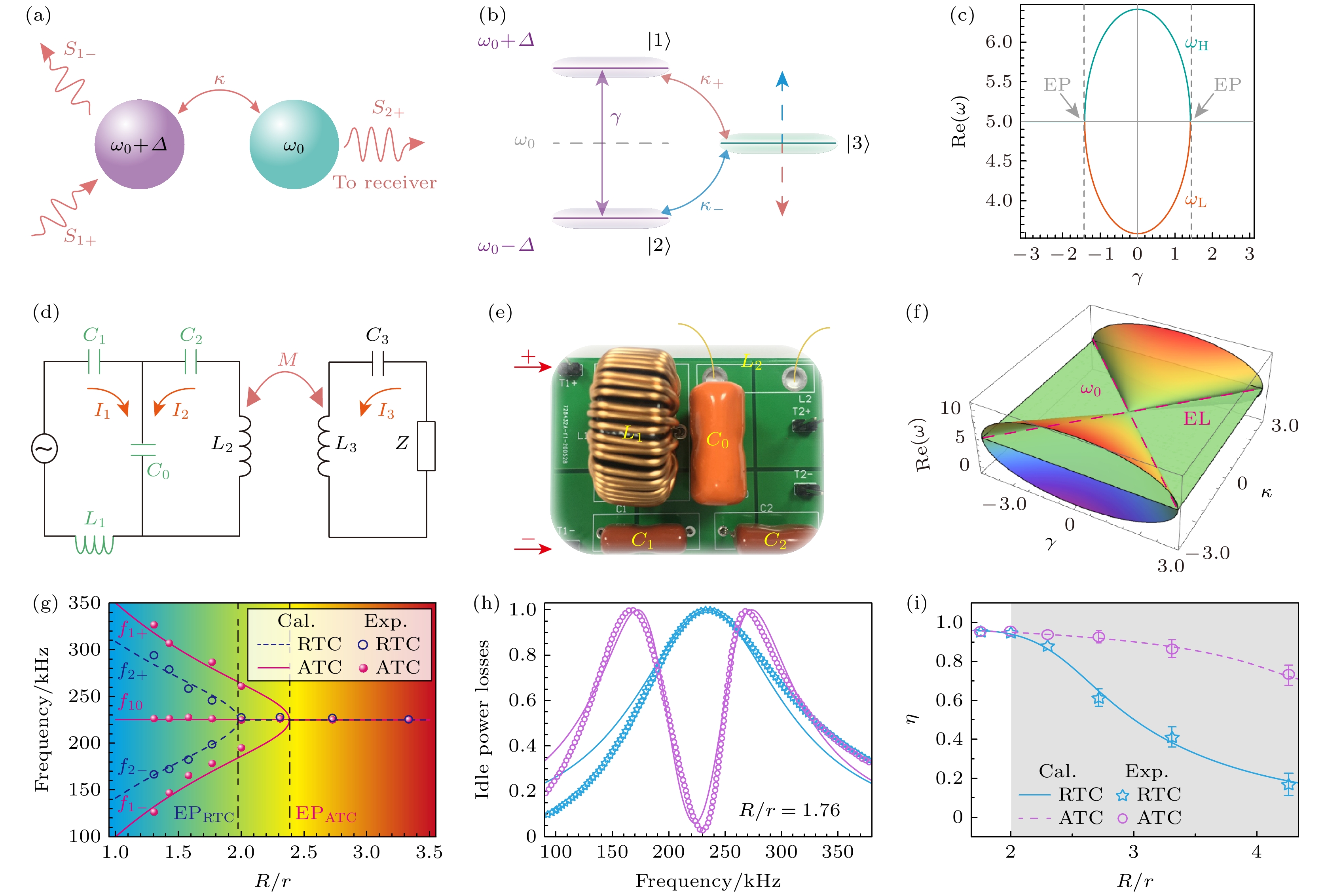
图 8 (a) 由3个耦合谐振器构成的Anti-PT对称模型[48]; (b) “能级钉扎”原理图[48]; (c) 反共振系统中本征频率实部的演化[48]; (d) 等效电路图[48]; (e) 实物图[48]; (f) 系统中本征频率实部随耗散耦合($\gamma $)和相干耦合($\kappa $)的演化[48]; (g) 合成三阶Anti-PT对称中本征频率计算(测量)的实部[48]; (h) WPT系统待机功率损耗[48]; (i) 具有RTC(ATC)的匹配WPT系统在追踪工作频率下的传输效率[48]
Fig. 8. (a) Anti-PT symmetry model consisting of three coupled resonators[48]; (b) “energy level pinning” schematic[48]; (c) evolution of the real part of the eigenfrequency in the anti-resonant system[48]; (d) equivalent circuit diagram[48]; (e) physical diagram[48]; (f) evolution of the real part of the eigenfrequency in the system with dissipative coupling $\gamma $ and coherent coupling $\kappa $[48]; (g) real part of the computed (measured) eigenfrequency in the synthesized third-order inverse PT symmetry[48]; (h) standby power loss of the WPT system[48]; (i) transmission efficiency of the matched WPT system with RTC (ATC) at the tracking operating frequency[48].
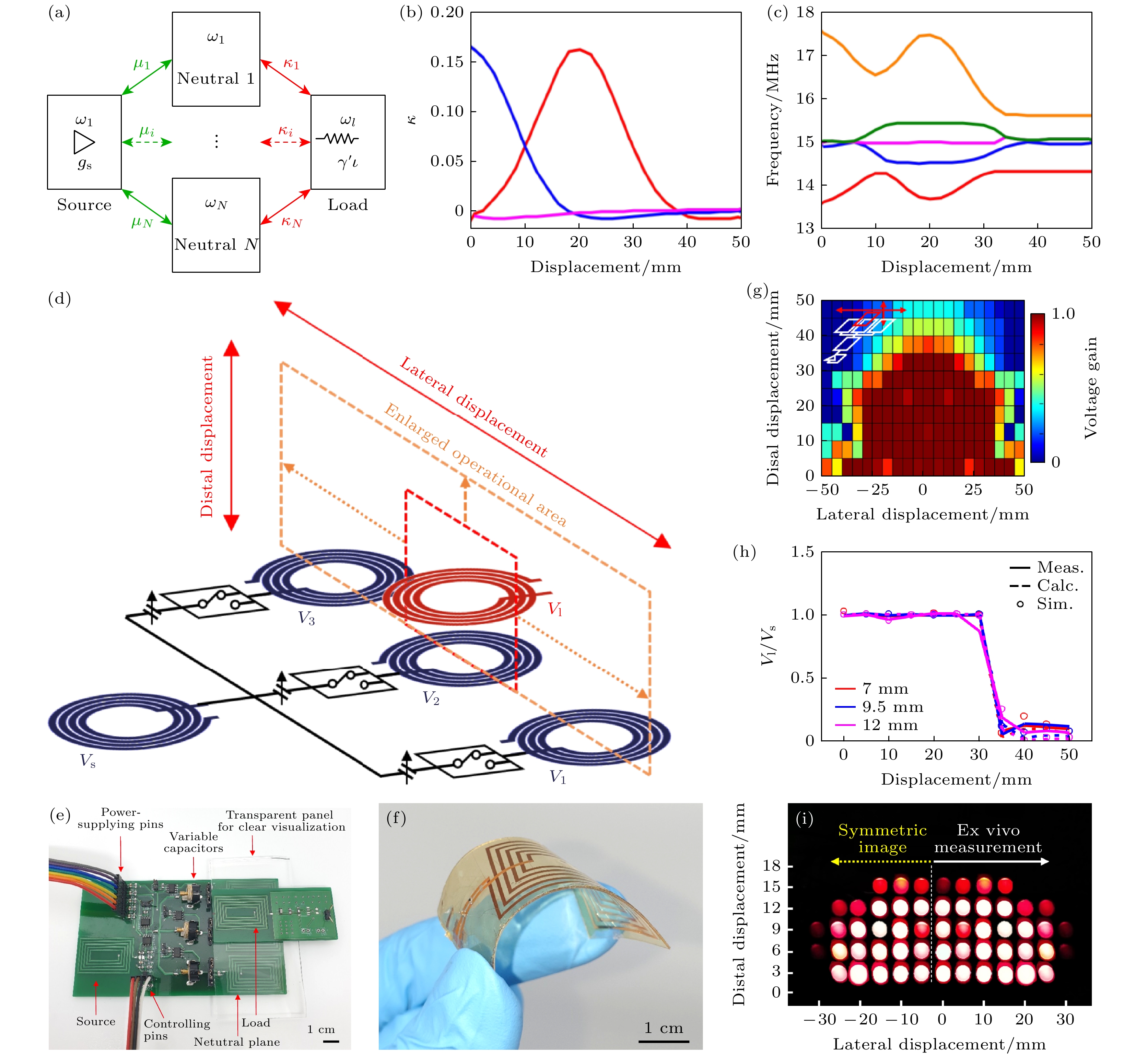
图 9 (a) 高阶PT对称系统机制演示[50]; (b) 当负载线圈移动时, 不同位置中性原子耦合强度变化[50]; (c) 系统本征频率随位移的变化[50]; (d) 异质结型电路示意图[50]; (e) 实验PCB元件图[50]; (f) 柔性负载谐振器实物图[50]; (g) 高阶系统高效区域的可视化[50]; (h) 系统从远端位移获得的恒定电压增益[50]; (i) 二极管在远端和横向位移下通过组织对负载谐振器进行可靠的WPT演示[50]
Fig. 9. (a) Demonstration of the higher-order PT symmetric system mechanism[50]; (b) variation of the neutral atom coupling strength at different locations when the load coil is moved[50]; (c) variation of the system intrinsic frequency with displacement[50]; (d) schematic diagram of a heterogeneous junction-type circuit[50]; (e) diagram of the experimental PCB components[50]; (f) physical diagram of a flexible loaded resonator[50]; (g) visualization of the efficient region of the higher-order system[50]; (h) the system’s gain from distal displacements with a constant voltage gain[50]; (i) reliable WPT demonstration of the loaded resonator by organization of the diode under far-end and lateral displacements[50].
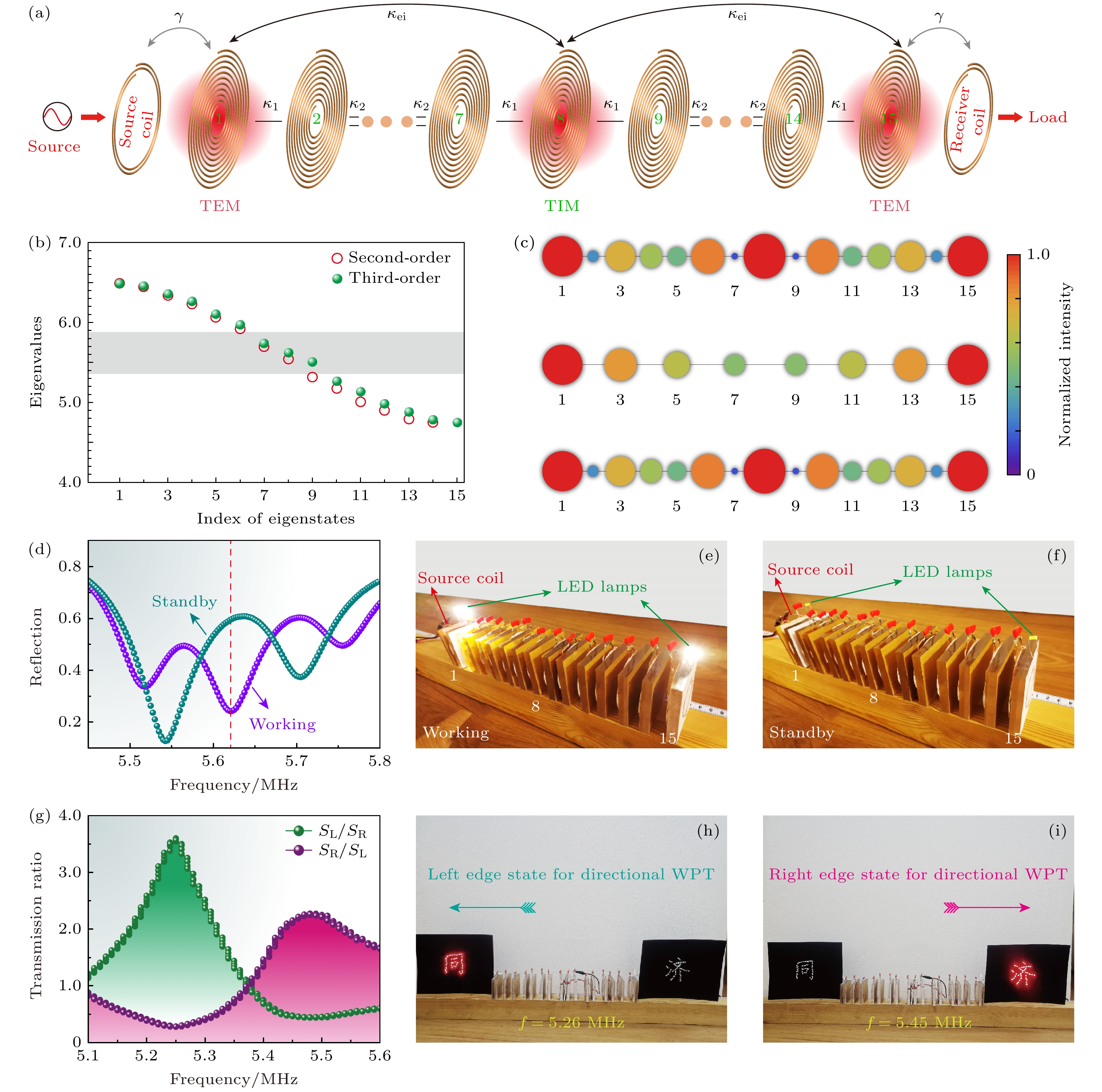
图 10 (a) PT对称的多线圈复合二聚链WPT系统示意图[59]; (b) 等效三阶 PT 对称(绿色)和等效二阶 PT 对称(橙色)拓扑二聚体链的特征值谱[59]; (c) 等效三阶 PT 对称的复合拓扑二聚体链中的三种拓扑模式的归一化强度分布[59]; (d) 拓扑二聚体链在工作和待机状态下的反射谱[59]; (e) 图(d)在工作状态下实验演示[59]; (f) 图(d)在待机状态下实验演示[59]; (g) 一维 Harper 链左右两端的传输比[60]; LED 灯组成汉字的“同”和“济”的定向 WPT 的演示实验 (h) 左向演示[60]; (i) 右向演示[60]
Fig. 10. (a) Schematic diagram of the PT-symmetric multi-coil WPT system[59]; (b) eigenvalue spectra of the equivalent third-order PT-symmetric (green) and equivalent second-order PT-symmetric (orange) topological dimer chains[59]; (c) normalized intensity distributions of the three topological modes in the equivalent third-order PT-symmetric composite topological dimer chain[59]; (d) reflection spectra of the topological dimer chain in the operating and standby states[59]; (e) demonstration of experiment in working condition in figure (d) [59]; (f) demonstration of experiment in standby condition in figure (d) [59]; (g) transmission ratio between left and right ends of one-dimensional Harper chain[60]; demonstration of directional WPT with LEDs forming Chinese characters “Tong” and “Ji”; (h) left-oriented demonstration[60]; (i) right-oriented demonstration[60].
-
[1] Tesla N 1914 U. S. Patent 1 119 732 [1914-12-1]
[2] Hui S Y R, Zhong W X, Lee C K 2013 IEEE Trans. Power Electron. 29 4500
[3] Wang C S, Covic G A, Stielau O H 2004 IEEE Trans. Ind. Electron. 51 148
 Google Scholar
Google Scholar
[4] Ho S L, Wang J, Fu W N, Sun M 2011 IEEE Trans. Magn. 47 1522
 Google Scholar
Google Scholar
[5] Shen D, Du G P, Zeng W, Yang Z J, Li J J 2020 IEEE Access 8 59648
 Google Scholar
Google Scholar
[6] Kurs A, Karalis A, Moffatt R, Joannopoulos J D, Fisher P, Soljacic M 2007 Science 31 75834
[7] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
 Google Scholar
Google Scholar
[8] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S, Christodoulides D N 2018 Nat. Phys. 14 11
 Google Scholar
Google Scholar
[9] Li A, Wei H, Cotrufo M, Chen W, Mann S, Ni X, Xu B, Chen J, Wang J, Fan S, Qiu C W, Alù A, Chen L 2023 Nat. Nanotechnol. 18 706
 Google Scholar
Google Scholar
[10] Feng L, El-Ganainy R, Ge L 2017 Nat. Photonics 11 752
 Google Scholar
Google Scholar
[11] Özdemir K, Rotter S, Nori F, Yang L 2019 Nat. Mater. 18 783
 Google Scholar
Google Scholar
[12] Zhang S M, Jin L, Song Z 2022 Chin. Phys. B 31 010312
 Google Scholar
Google Scholar
[13] 唐原江, 梁超, 刘永椿 2022 71 171101
 Google Scholar
Google Scholar
Tang Y J, Liang C, Liu Y C 2022 Acta Phys. Sin. 71 171101
 Google Scholar
Google Scholar
[14] 祝可嘉, 郭志伟, 陈鸿 2022 71 131101
 Google Scholar
Google Scholar
Zhu K J, Guo Z W, Chen H 2022 Acta Phys. Sin. 71 131101
 Google Scholar
Google Scholar
[15] Cao W, Wang C, Chen W, Hu S, Wang H, Yang L, Zhang X 2022 Nat Nanotechnol. 17 262
 Google Scholar
Google Scholar
[16] Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101(R
[17] Li H, Yin S, Galiffi E, Alù A 2021 Phys. Rev. Lett. 127 153903
 Google Scholar
Google Scholar
[18] Yang X, Li J, Ding Y, Xu M, Zhu X F, Zhu J 2022 Phys. Rev. Lett. 128 065701
 Google Scholar
Google Scholar
[19] Chen P Y, Sakhdari M, Hajizadegan M, Cui Q, Cheng M M C, El-Ganainy R, Alù A 2018 Nat. Electron. 1 297
 Google Scholar
Google Scholar
[20] Zeng C, Guo Z W, Zhu K J, Fan C F, Li G, Jiang J, Li Y H, Jiang H T, Yang Y P, Sun Y, Chen H 2022 Chin. Phys. B 31 010307
 Google Scholar
Google Scholar
[21] Song M, Jayathurathnage P, Zanganeh E, Krasikova M, Smirnov P, Belov P, Kapitanova P, Simovski C, Tretyakov S, Krasnok, A 2021 Nat. Electron. 4 707
 Google Scholar
Google Scholar
[22] Song M, Belov P, Kapitanova P 2017 Appl. Phys. Rev. 4 021102
 Google Scholar
Google Scholar
[23] Sakhdari M, Hajizadegan M, Chen P Y 2020 Phys. Rev. Res. 2 013152
 Google Scholar
Google Scholar
[24] Guo Z W, Chen H 2024 Physics 53 33 [郭志伟, 陈鸿 2024 物理 53 33]
 Google Scholar
Google Scholar
Guo Z W, Chen H 2024 Physics 53 33
 Google Scholar
Google Scholar
[25] Miri M A, Alù A 2019 Science 363 7709
 Google Scholar
Google Scholar
[26] Ding K, Fang C, Ma G 2022 Nat. Rev. Phys. 4 745
 Google Scholar
Google Scholar
[27] Sample A P, Meyer D T, Smith J R 2010 IEEE Trans. Ind. Electron. 58 544
[28] Park J, Tak Y, Kim Y, Kim Y, Nam S 2011 IEEE Trans. Antennas Propag. 59 1769
 Google Scholar
Google Scholar
[29] Li Y, Wang M, Zhang W, Zhao M, Liu J 2019 Energies 12 2626
 Google Scholar
Google Scholar
[30] Song M, Baryshnikova K, Markvart A, Belov P, Nenasheva E, Simovski C, Kapitanova P 2019 Phys. Rev. Appl. 11 054046
 Google Scholar
Google Scholar
[31] Lerosey G 2017 Nature 546 354
 Google Scholar
Google Scholar
[32] Assawaworrarit S, Yu X, Fan S 2017 Nature 546 387
 Google Scholar
Google Scholar
[33] Guo Z, Jiang H, Li Y, Chen H, Agarwal G. S 2018 Opt. Express 26 627
 Google Scholar
Google Scholar
[34] Fan S H , Suh W, Joannopoulos J D 2003 J. Opt. Soc. Am. A 20 569
[35] Zhou J, Zhang B, Xiao W, Qiu D, Chen Y 2019 IEEE Trans. Ind. Electron. 66 4097
 Google Scholar
Google Scholar
[36] Assawaworrarit S, Fan S 2020 Nat. Electron. 3 273
 Google Scholar
Google Scholar
[37] Zeng C, Sun Y, Li G, Li Y, Jiang H, Yang Y, Chen H 2020 Phys. Rev. Appl. 13 034054
 Google Scholar
Google Scholar
[38] Guo Z, Jiang J, Wu X, Zhang H, Hu S, Wang Y, Li Y, Yang Y, Chen H 2023 Fundam. Res. 11 2667
[39] Xie Y, Zhang Z, Lin Y, Feng T, Xu Y 2021 Phys. Rev. Appl. 15 044024
 Google Scholar
Google Scholar
[40] Zhang H, Guo Z, Li Y, Yang Y, Chen Y, Chen H 2024 Front. Phys. 19 43209
 Google Scholar
Google Scholar
[41] Wu Y, Kang L, Douglas H. Werner 2022 Phys. Rev. Lett. 129 200201
 Google Scholar
Google Scholar
[42] Hao X, Yin K, Zou J, Wang R, Huang Y, Ma X, Dong T 2023 Phys. Rev. Lett. 130 077202
 Google Scholar
Google Scholar
[43] Zhang G Q, You J Q 2019 Phys. Rev. B 99 054404
 Google Scholar
Google Scholar
[44] Wu H C, Jin L, Song Z 2021 Phys. Rev. B 103 235110
 Google Scholar
Google Scholar
[45] Peng P, Cao W, Shen C, Qu W, Wen J, Jiang L, Xiao Y 2016 Nat. Phys. 12 1139
 Google Scholar
Google Scholar
[46] Zhang H, Huang R, Zhang S D, Li Y, Qiu C W, Nori F, Jing H 2020 Nano Lett. 20 7594
 Google Scholar
Google Scholar
[47] Ke S, Zhao D, Liu J, Liu Q, Liao Q, Wang B, Lu P 2019 Opt. Express 27 13858
 Google Scholar
Google Scholar
[48] Guo Z, Yang F, Zhang H, Wu X, Wu Q, Zhu K, Jiang J, Jiang H, Yang Y, Li Y, Chen H 2024 Natl. Sci. Rev. 11 172
 Google Scholar
Google Scholar
[49] Ozaki T, Ohta N, Jimbo T, Hamaguchi K 2021 Nat. Electron. 4 845
 Google Scholar
Google Scholar
[50] Kim H, Yoo S, Joo H, Lee J. An D, Nam S, Han H, Kim D H, Kim S 2022 Sci. Adv. 8 4610
 Google Scholar
Google Scholar
[51] Shu J C, Cao M S, Zhang M, Wang X X, Cao W Q, Fang X Y, Cao M Q 2020 Adv. Funct. Mater. 30 1908299
 Google Scholar
Google Scholar
[52] Gutruf P, Krishnamurthi V, Vázquez-Guardado A, Xie Z, Banks A, Su C J, Xu Y, Haney C R, Waters E A, Kandela I, Krishnan S R, Ray T, Leshock J P, Huang G Y, Chanda D, Rogers J A 2018 Nat. Electron. 1 652
 Google Scholar
Google Scholar
[53] Gutruf P, Yin R T, Lee K B, Ausra J, Brennan J A, Qiao Y, Xie Z, Peralta R, Talarico O, Murillo A, Chen S W, Leshock J P, Haney C R, Waters E A, Zhang C X, Luan H, Huang Y G, Trachiotis G, Efimov I R, Rogers J A 2019 Nat. Commun. 10 5742
 Google Scholar
Google Scholar
[54] Lyu H, John M, Burkland D, Greet B, Post A, Babakhani A, Razavi M 2020 Sci. Rep. 10 2067
 Google Scholar
Google Scholar
[55] Yoo S, Lee J, Joo H, Sunwoo S H, Kim S, Kim D H 2021 Adv. Healthcare Mater. 10 2100614
 Google Scholar
Google Scholar
[56] Kim J, Banks A, Xie Z, Heo S Y, Gutruf P, Lee J W, Xu S, Jang K I, Liu F, Brown G, Choi J, Kim J H, Feng X, Huang Y, Paik U Rogers, J A 2015 Adv. Funct. Mater. 25 4761
 Google Scholar
Google Scholar
[57] Khan S R, Pavuluri S K, Cummins G, Desmulliez M P 2020 Sensors 20 3487
[58] Zhong W X, Lee C K, Ron Hui S Y 2013 IEEE Trans. Ind. Electron. 60 261
 Google Scholar
Google Scholar
[59] Song J, Yang F, Guo Z, Wu X, Zhu K, Jiang J, Sun Y, Li Y, Jiang H, Chen H 2021 Phys. Rev. Appl. 15 014009
 Google Scholar
Google Scholar
[60] Yang F, Song J, Guo Z, Wu X, Zhu, K, Jiang J, Sun Y, Jiang H, Li Y, Chen H 2021 Opt. Express 29 7844
 Google Scholar
Google Scholar
[61] Zhang L, Yang Y, Jiang Z, Chen Q, Yan Q, Wu Z, Zhang B, Huangfu J, Chen H, 2021 Sci. Bull. 66 974
 Google Scholar
Google Scholar
[62] Lu L, Joannopoulos J D, Soljacic M 2014 Nat. Photonics 8 821
 Google Scholar
Google Scholar
[63] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
[64] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006
 Google Scholar
Google Scholar
[65] Ashida Y, Gong Z, Ueda M 2020 Adv. Phys. 69 249
[66] Guo Z, Wang Y, Ke S, Su X, Ren J, Chen H 2024 Adv. Phys. Res. 3 2300125
 Google Scholar
Google Scholar
[67] Guo Z, Zhang T, Song J, Jiang H, Chen H 2021 Photonics Res. 9 574
 Google Scholar
Google Scholar
[68] Zangeneh‐Nejad F, Fleury R 2020 Adv. Mater. 32 2001034
 Google Scholar
Google Scholar
[69] Feis J, Solymar L, Shamonina E 2023 J. Appl. Phys. 133 22
[70] Puchnin V M, Matvievskaya O V, Slobozhanyuk A P, Shchelokova A V, Olekhno N A 2023 Phys. Rev. Appl. 20 024076
 Google Scholar
Google Scholar
[71] Guo Z, Jiang H, Sun Y, Li Y, Chen H 2018 Opt. Lett. 43 51425
[72] Wu H C, Xu H S, Xie L C, Jin L 2024 Phys. Rev. Lett. 132 083801
 Google Scholar
Google Scholar
[73] Lu C C, Yuan H Y, Zhang H Y, Zhao W, Zhang N E, Zheng Y J, Elshahat S, Liu Y C 2022 Chip 1 100025
 Google Scholar
Google Scholar
[74] Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature 548 187
 Google Scholar
Google Scholar
[75] Maamache M, Kheniche L 2020 Prog. Theor. Exp. Phys. 12 123A01
[76] Li Y, Peng Y G, Han L, Miri M A, Li W, Xiao M, Zhu X F, Zhao J, Alù A, Fan S, Qiu C W 2019 Science 364 170
 Google Scholar
Google Scholar
[77] Yang Y, Wang Y P, Rao J W, Gui Y S, Yao B M, Lu W, Hu C M 2020 Phys. Rev. Lett. 125 147202
 Google Scholar
Google Scholar
[78] Kim D H, Ahn D 2019 IEEE Trans. Power Electron. 35 11391
[79] Ma W, Liu Z, Kudyshev Z A, Boltasseva A, Cai W, Liu Y 2021 Nat. Photonics 15 77
 Google Scholar
Google Scholar
[80] Genty G, Salmela L, Dudley J M, Brunner D, Kokhanovskiy A, Kobtsev S, Turitsyn S K 2021 Nat. Photonics 15 91
 Google Scholar
Google Scholar
[81] Nadell C C, Huang B, Malof J M, Padilla W J 2019 Opt. Express 27 27523
 Google Scholar
Google Scholar
计量
- 文章访问数: 4137
- PDF下载量: 170
- 被引次数: 0













 下载:
下载: