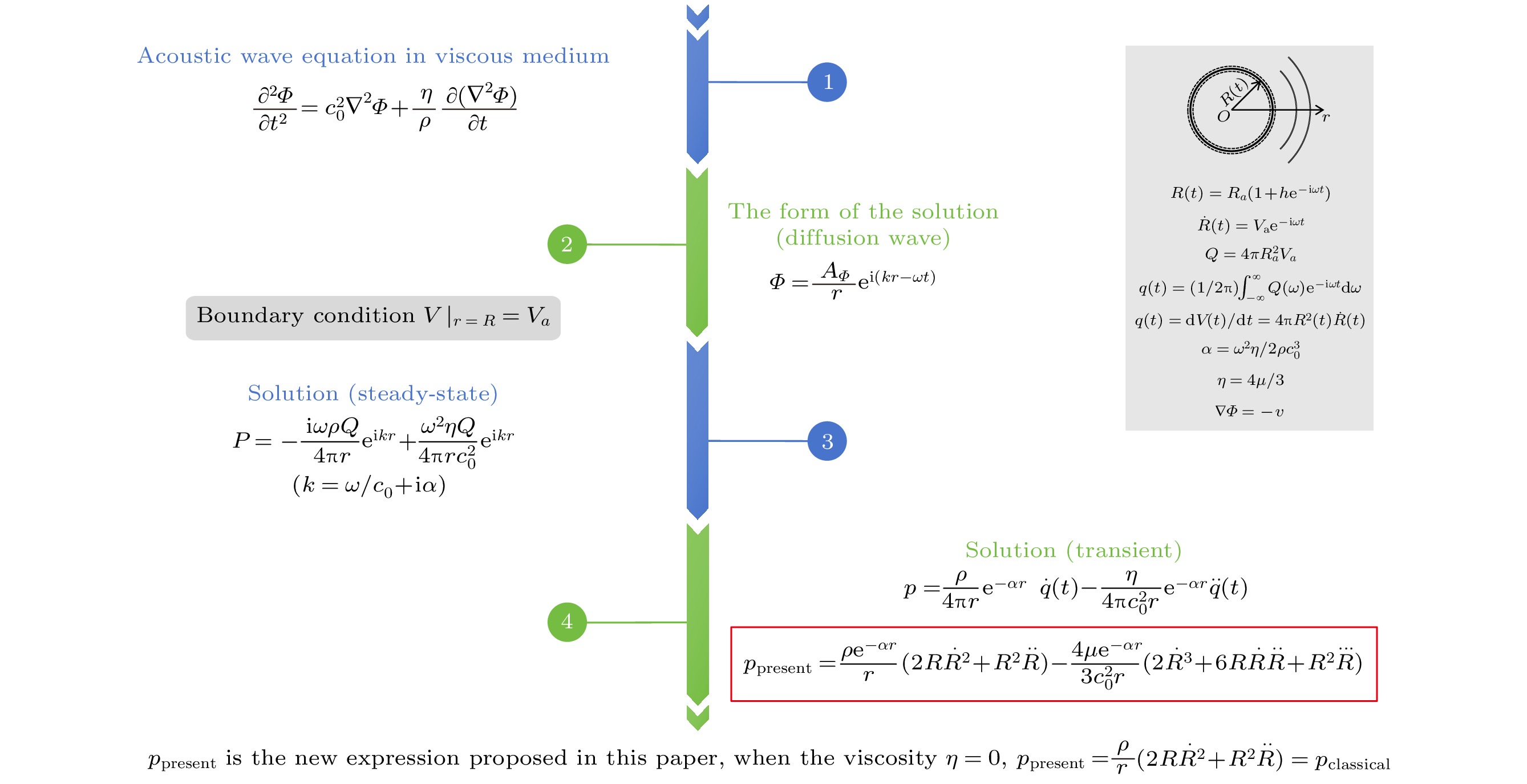
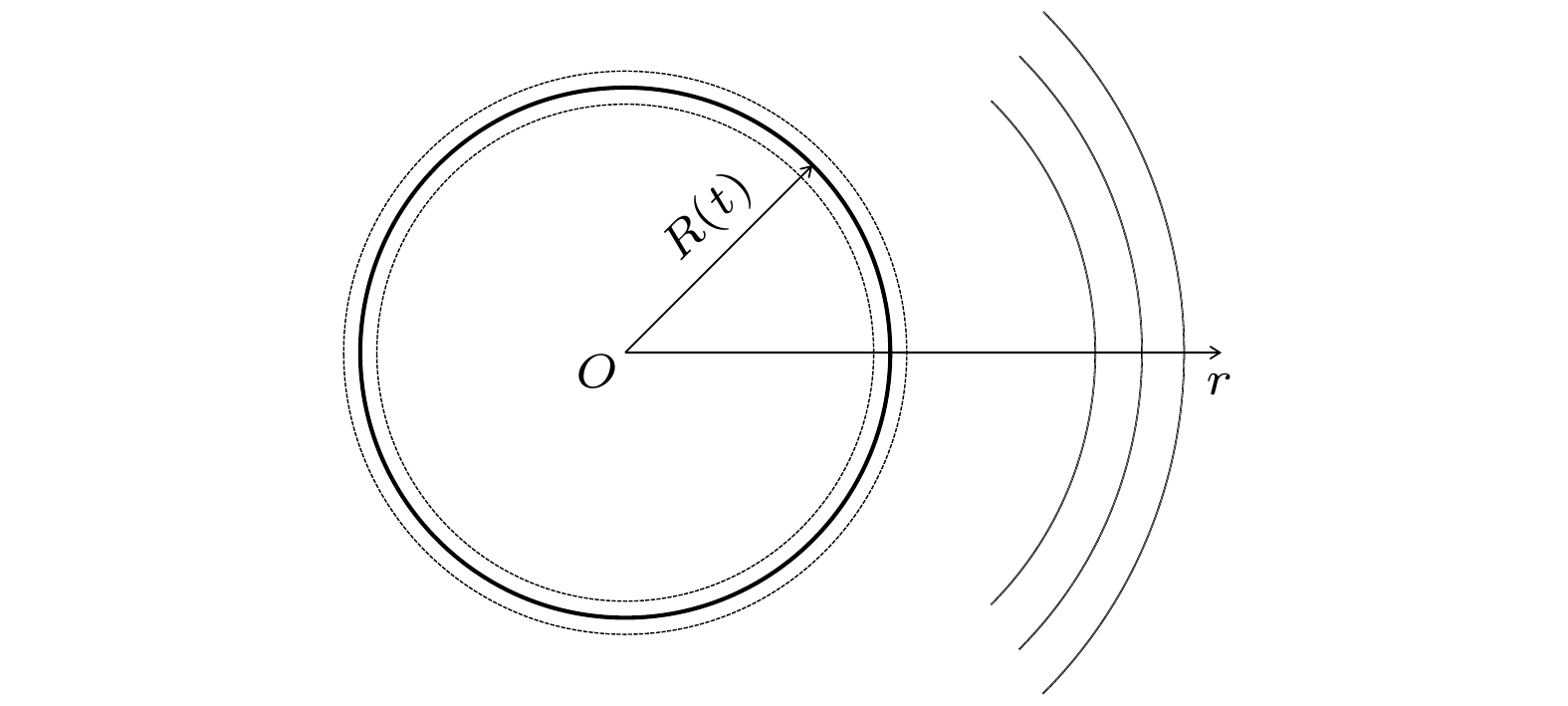
-
The classical single bubble’s acoustic emission equation has been used to describe the sound filed radiated by bubble for a long time. Because this formula does not consider the influence of the medium viscosity in the process of sound wave propagation, it is more reasonable to modify it in some special cases. Based on the boundary condition of the bubbles, i.e. the vibration velocity of the bubble wall is equal to the particle vibration velocity of the external medium at the bubble boundary, the acoustic wave equation in spherical coordinate system in viscous medium is solved, and the modified acoustic emission formula of the bubble in the viscous medium is given. The bubble radius R(t) is obtained numerically from the bubble dynamics equation by using the fourth-fifth order Runge-Kutta method. Then the bubble's radiation sound field is obtained by using the direct substitution method and the finite element (The pressure acoustics module; two-dimensional (2D) axisymmetric geometric model) method, respectively. The modified expression ppresent given in this work is more accurate to describe the bubble’s radiation than the classical expression pclassical in the cases of high-viscosity, high-frequency and long-distance. In these cases, continuing to measure the acoustic emission of bubbles by using the classical expression may have an influence on the characteristics of cavitation, such as the inaccurate descriptions of parameters such as cavitation intensity and cavitation threshold. 
-
Keywords:
- bubble acoustic emission /
- viscous acoustic wave equation /
- bubble dynamics /
- finite element simulation
[1] 柯乃普R T, 达利 J W, 哈米特 F G著(水利水电科学研究所译)1981 空化与空蚀(北京: 水利出版社)第8—11页
Knapp R T, Daily J W, Hammitt F G (translated by China Institute of Water Resources and Hydropower) 1981 Cavitation (Beijing: China Water & Power Press) pp8–11
[2] 汪德昭, 尚尔昌 2013 水声学(北京: 科学出版社)第376, 590页
Wang D Z, Shang E C 2013 Underwater Acoustics (Beijing: Science Press) pp376, 590
[3] Wan M X, Feng Y, Haar G T 2015 Cavitation in Biomedicine: Principles and Techniques (Berlin, Heidelberg: Springer) pp1–5, 47–49
[4] Du G H, Wu J R 1990 J. Acoust. Soc. Am. 87 965
[5] Ye Z 1997 J. Acoust. Soc. Am. 101 809
Google Scholar
[6] Zilonova E, Solovchuk M, Sheu T W 2019 Phys. Rev. E 99 023109
Google Scholar
[7] Kou S Y, Chen W Z, Wu Y R, Zhao G Y 2023 Ultrason Sonochem 94 106352
Google Scholar
[8] Yuan Y, An Y 2021 Int. Commun. Heat Mass 126 105378
Google Scholar
[9] Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701 [秦对, 邹青钦, 李章勇, 王伟, 万明习, 冯怡 2021 70 154701]
Google Scholar
Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701
Google Scholar
[10] Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303 [刘睿, 黄晨阳, 武耀蓉, 胡静, 莫润阳, 王成会 2024 73 084303]
Google Scholar
Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303
Google Scholar
[11] Shen X Z, Wu P F, Lin W J 2024 Ultrason Sonochem 107 106890
Google Scholar
[12] Zhang H L 2012 Theoretical Acoustics (revised version) (Beijing: Higher Education Press pp221–223) [张海澜 2012 理论声学 (修订版) (北京: 高等教育出版社) 第221—223页]
Zhang H L 2012 Theoretical Acoustics (revised version) (Beijing: Higher Education Press pp221–223)
[13] Currie G I 2003 Fundamental Mechanics of Fluids (3rd Ed.) (Boca Raton: CRC Press) pp30-33
[14] Filonets T, Solovchuk M 2022 Ultrason Sonochem 88 106056
Google Scholar
[15] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[16] Lauterborn W, Kurz T 2010 Rep. Prog. Phys. 73 106501
Google Scholar
-
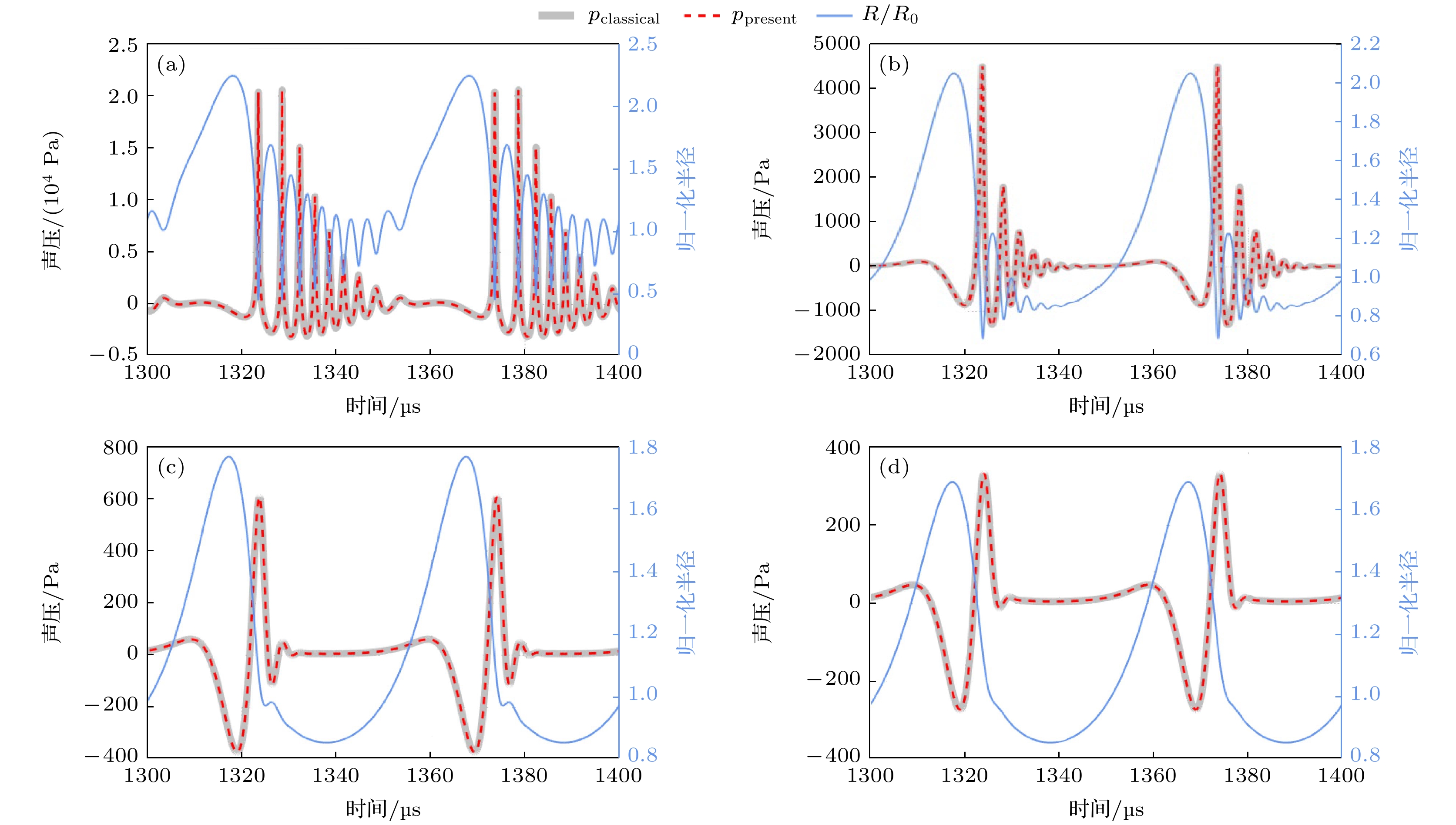
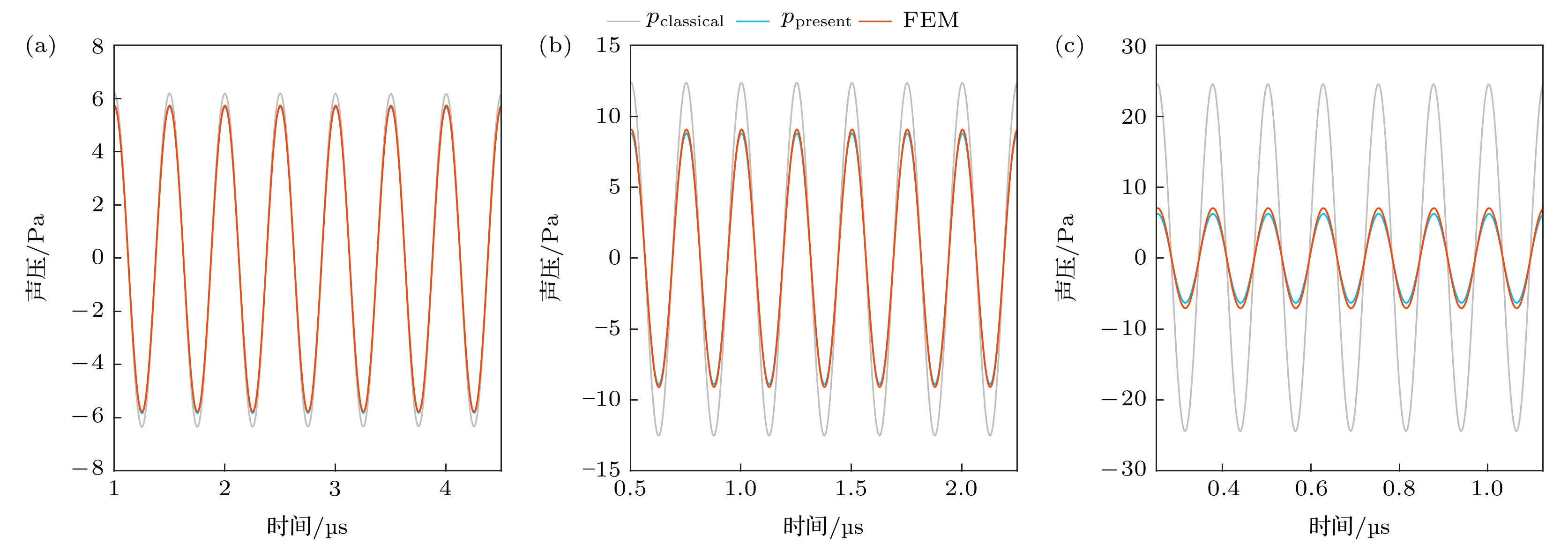
图 2 气泡半径及辐射声压曲线, f = 20 kHz, pa = 100 kPa, R0 = 15 μm, r = 1000 μm (a) μ = 0.005 Pa·s; (b) μ = 0.025 Pa·s; (c) μ = 0.075 Pa·s; (d) μ = 0.1 Pa·s
Fig. 2. Bubble radius and radiation sound pressure curves, f = 20 kHz, pa = 100 kPa, R0 = 15 μm, r = 1000 μm: (a) μ = 0.005 Pa·s; (b) μ = 0.025 Pa·s; (c) μ = 0.075 Pa·s; (d) μ = 0.1 Pa·s.
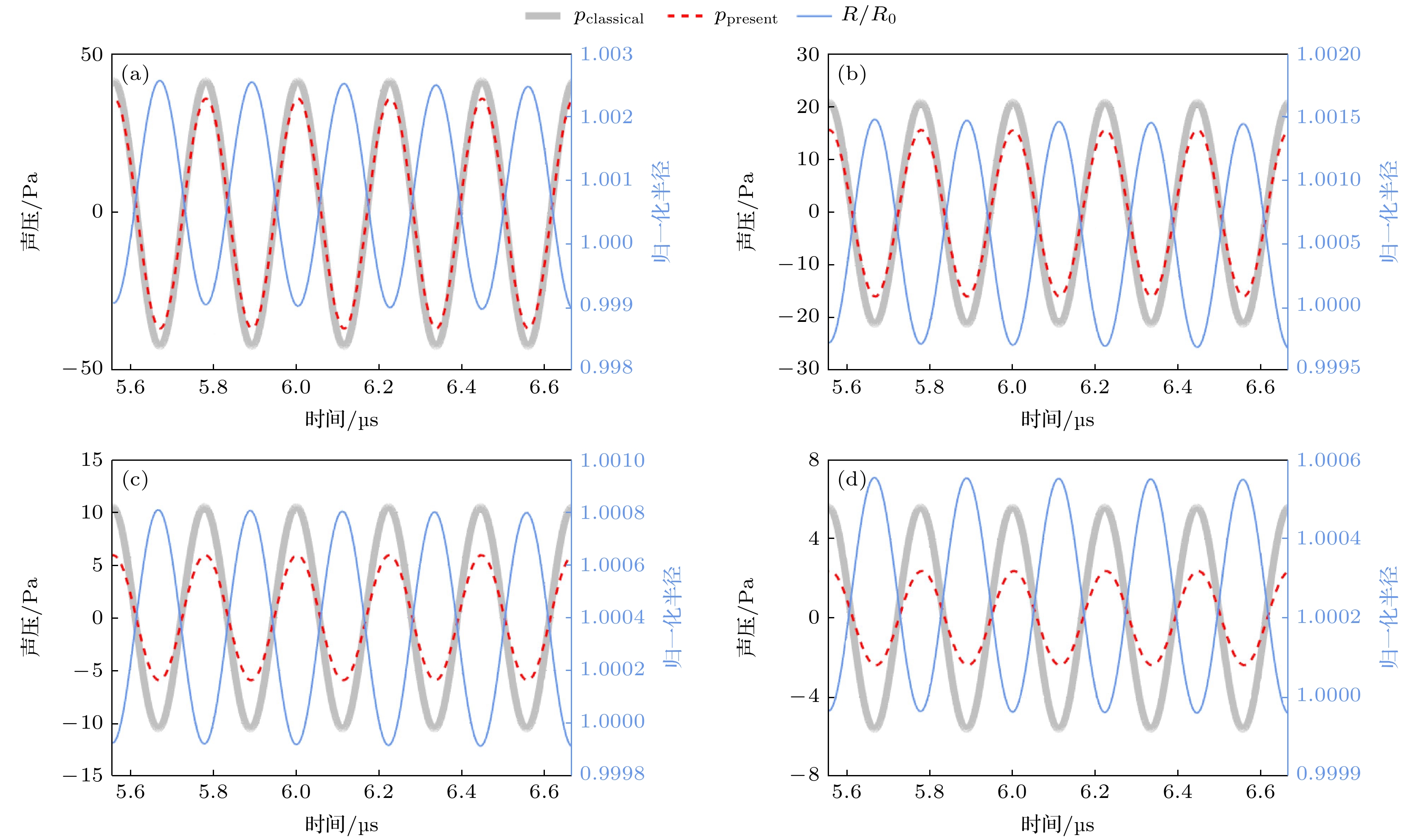
图 3 气泡半径及辐射声压曲线, f = 4500 kHz, pa = 200 kPa, R0 = 3 μm, r = 1000 μm (a) μ = 1 Pa·s; (b) μ = 2 Pa·s; (c) μ = 4 Pa·s; (d) μ = 6 Pa·s
Fig. 3. Bubble radius and radiation sound pressure curves, f = 4500 kHz, pa = 200 kPa, R0 = 3 μm, r = 1000 μm: (a) μ = 1 Pa·s; (b) μ = 2 Pa·s; (c) μ = 4 Pa·s; (d) μ = 6 Pa·s.
图 4 气泡声辐射的有限元计算模型 (a) 二维轴对称几何模型; (b) 局部网格划分1; (c) 局部网格划分2
Fig. 4. Finite element model for calculating bubble acoustic radiation: (a) Two-dimensional axisymmetric geometric model; (b) localised grid division 1; (c) localised grid division 2.
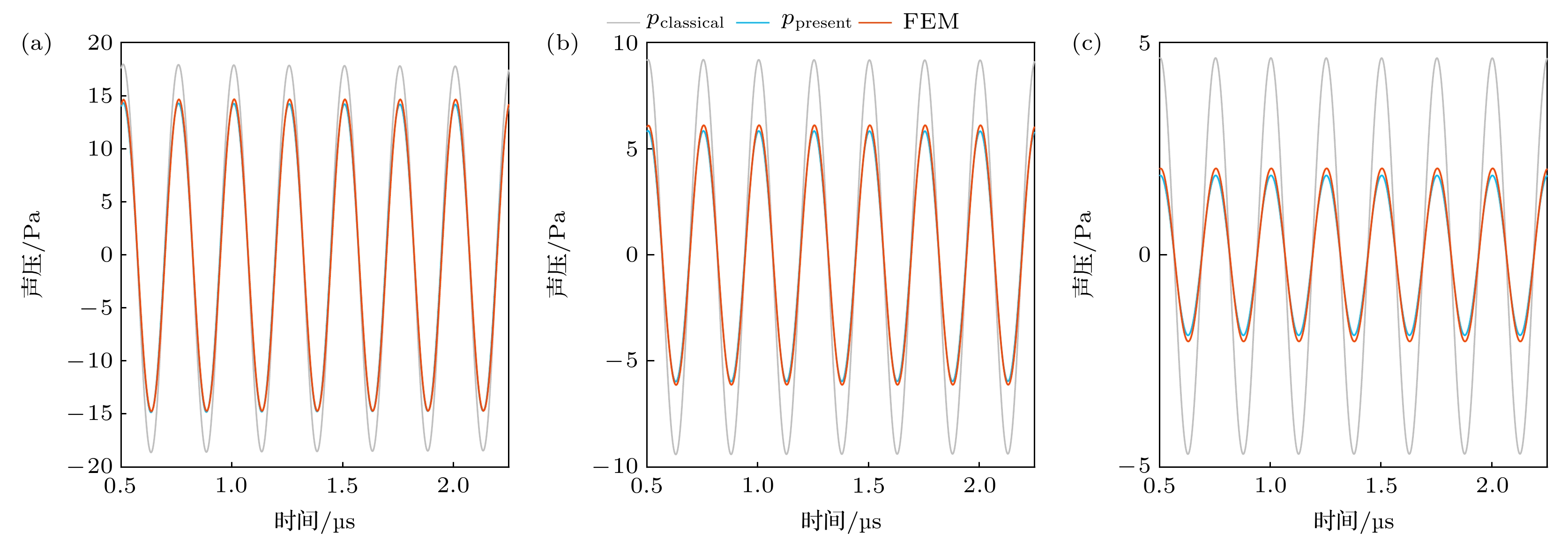
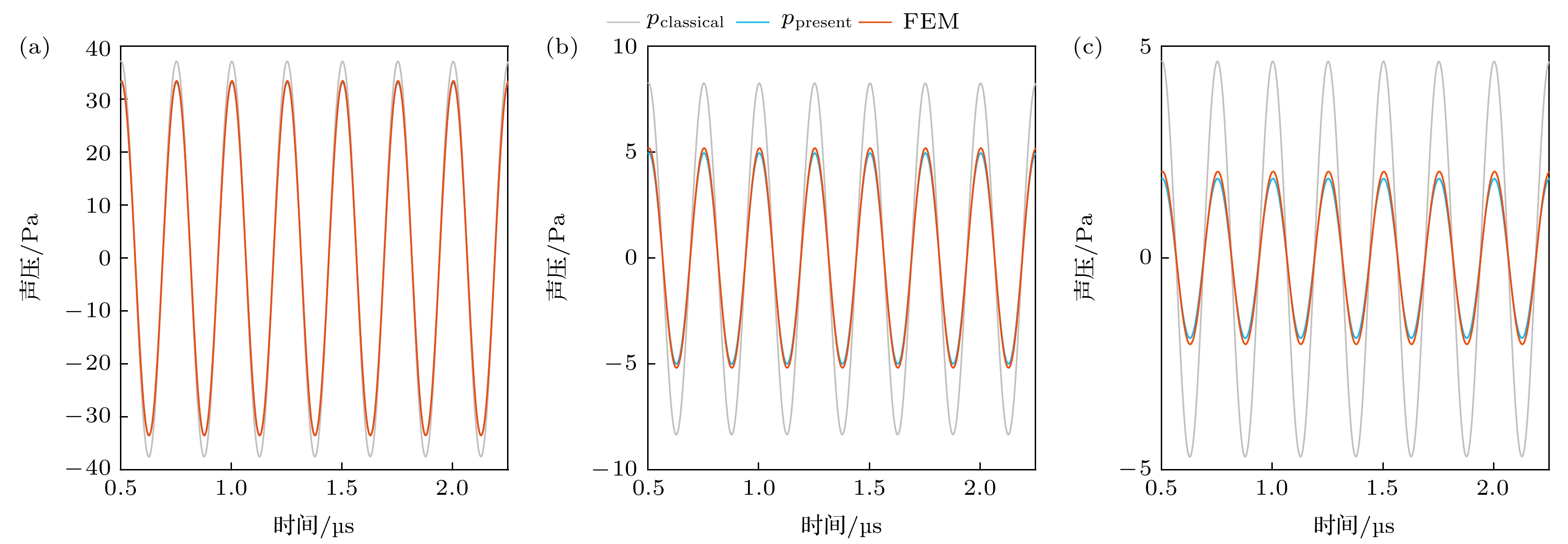
图 5 不同黏度下气泡辐射声压, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, r = 8000 μm (a) μ = 0.25 Pa·s; (b) μ = 0.5 Pa·s; (c) μ = 1 Pa·s
Fig. 5. Sound pressure curves of bubble radiation under different viscosity, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, r = 8000 μm: (a) μ = 0.25 Pa·s; (b) μ = 0.5 Pa·s; (c) μ = 1 Pa·s.
图 6 不同频率下气泡辐射声压, R0 = 3 μm, pa = 200 kPa, r = 3000 μm, μ = 1 Pa·s (a) f = 2000 kHz; (b) f = 4000 kHz; (c) f = 8000 kHz
Fig. 6. Sound pressure curves of bubble radiation under different frequency, R0 = 3 μm, pa = 200 kPa, r = 3000 μm, μ = 1 Pa·s: (a) f = 2000 kHz; (b) f = 4000 kHz; (c) f = 8000 kHz.
图 7 不同距离下气泡辐射声压, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, μ = 1 Pa·s (a) r = 1000 μm; (b) r = 4500 μm; (c) r = 8000 μm
Fig. 7. Sound pressure curves of bubble radiation under different distance, f = 4000 kHz, R0 = 3 μm, pa = 200 kPa, μ = 1 Pa·s: (a) r = 1000 μm; (b) r = 4500 μm; (c) r = 8000 μm.
表 1 数值计算中参数的含义及取值
Table 1. Definition and value of parameters in numerical calculation.
参数 含义 取值 σ/(N·m–1) 表面张力系数 0.056 c/(m·s–1) 声速 1549 c0/(m·s–1) 理想介质中的声速 1500 ρ/(kg·m–3) 密度 1100 p0/kPa 环境静压 101.3 pv/kPa 泡内水蒸气压 2.33 κ 绝热指数 1.4 
下载: 导出CSV
-
[1] 柯乃普R T, 达利 J W, 哈米特 F G著(水利水电科学研究所译)1981 空化与空蚀(北京: 水利出版社)第8—11页
Knapp R T, Daily J W, Hammitt F G (translated by China Institute of Water Resources and Hydropower) 1981 Cavitation (Beijing: China Water & Power Press) pp8–11
[2] 汪德昭, 尚尔昌 2013 水声学(北京: 科学出版社)第376, 590页
Wang D Z, Shang E C 2013 Underwater Acoustics (Beijing: Science Press) pp376, 590
[3] Wan M X, Feng Y, Haar G T 2015 Cavitation in Biomedicine: Principles and Techniques (Berlin, Heidelberg: Springer) pp1–5, 47–49
[4] Du G H, Wu J R 1990 J. Acoust. Soc. Am. 87 965
[5] Ye Z 1997 J. Acoust. Soc. Am. 101 809
Google Scholar
[6] Zilonova E, Solovchuk M, Sheu T W 2019 Phys. Rev. E 99 023109
Google Scholar
[7] Kou S Y, Chen W Z, Wu Y R, Zhao G Y 2023 Ultrason Sonochem 94 106352
Google Scholar
[8] Yuan Y, An Y 2021 Int. Commun. Heat Mass 126 105378
Google Scholar
[9] Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701 [秦对, 邹青钦, 李章勇, 王伟, 万明习, 冯怡 2021 70 154701]
Google Scholar
Qin D, Zou Q Q, Li Z Y, Wang W, Wan M X, Feng Y 2021 Acta Phys. Sin. 70 154701
Google Scholar
[10] Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303 [刘睿, 黄晨阳, 武耀蓉, 胡静, 莫润阳, 王成会 2024 73 084303]
Google Scholar
Liu R, Huang C Y, Wu Y R, Hu J, Mo R Y, Wang C H 2024 Acta Phys. Sin. 73 084303
Google Scholar
[11] Shen X Z, Wu P F, Lin W J 2024 Ultrason Sonochem 107 106890
Google Scholar
[12] Zhang H L 2012 Theoretical Acoustics (revised version) (Beijing: Higher Education Press pp221–223) [张海澜 2012 理论声学 (修订版) (北京: 高等教育出版社) 第221—223页]
Zhang H L 2012 Theoretical Acoustics (revised version) (Beijing: Higher Education Press pp221–223)
[13] Currie G I 2003 Fundamental Mechanics of Fluids (3rd Ed.) (Boca Raton: CRC Press) pp30-33
[14] Filonets T, Solovchuk M 2022 Ultrason Sonochem 88 106056
Google Scholar
[15] Keller J B, Miksis M 1980 J. Acoust. Soc. Am. 68 628
Google Scholar
[16] Lauterborn W, Kurz T 2010 Rep. Prog. Phys. 73 106501
Google Scholar
下载:
计量
- 文章访问数: 569
- PDF下载量: 16
- 被引次数: 0
