-
自然界的许多活性物质都处在复杂的环境中, 例如动物群体穿过丛林、微生物在土壤中迁移、细菌被设计用于感知肿瘤的多孔环境等. 活性物质在复杂环境中的行为是一个值得探究的课题, 在生物物理、医疗工程、工业领域具有可观的应用意义. 本文用活性哑铃代表细菌等具有形状各向异性的活性物质, 采用郎之万动力学模拟, 研究它们渗透有限多孔介质的行为. 研究发现在低温和适当的活性力下, 活性哑铃能在介质内外聚集并形成4种稳定的聚集结构. 4种聚集结构分别是中空巨聚集、介质内中空聚集、密实巨聚集、介质内密实聚集. 定向运动的持久性决定了活性哑铃的聚集程度. 4种聚集结构的密度、极性序参量、热力学温度在介质内外的分布有明显的区别. 本研究结果有助于进一步理解活性物质在复杂环境中的生命活动, 为微流器件的设计、药物的输运等医学操作提供新的思路.Many active substances in nature are in complex environments, such as animal populations passing through the jungles, microorganisms migrating in the soil, and bacteria designed to sense the porous environment of tumors. The behavior of active substances in complex environments is a subject worth exploring, because they have great application significance in biophysics, medical engineering, and industrial fields. In this work, we use active dumbbells to represent bacteria and other active substances with shape anisotropy, and use Langevin dynamics simulation to study their permeation behaviors in finite porous media. We find that under low temperature and appropriate activity, active dumbbells can aggregate inside and outside the medium and form four stable aggregation structures, they being hollow giant aggregation, hollow aggregation in medium, dense giant aggregation, and dense aggregation in medium. The aggregation is caused by the small space of the medium region, and the geometric trap is easily formed when the active dumbbells meet in the medium. Unlike motility-induced phase separation, the formation of such an aggregation relies on the assistance of obstacles. The persistence of directional motion determines the degree of aggregation of active dumbbells. There are significant differences among the four aggregation structures in density distribution, polar order parameter, and thermodynamic temperature inside and outside the medium. Under certain conditions, the disorder of medium arrangement can promote the aggregation behavior of active dumbbells, and the increase of lattice constant makes it easier for active dumbbells to form dense aggregation. Our research findings contribute to a more in-depth understanding of the life activities of active substances in complex environments, thus providing new ideas for designing microfluidic devices, drug delivery and other medical operations.
-
Keywords:
- active matter /
- porous media /
- Langevin dynamics simulation
[1] Ramaswamy S 2010 Annu. Rev. Condens. Matter Phys. 1 323
Google Scholar
[2] Buttinoni I, Bialké J, Kümmel F, Löwen H, Bechinger C, Speck T 2013 Phys. Rev. Lett. 110 238301
Google Scholar
[3] Caporusso C B, Digregorio P, Levis D, Cugliandolo L F, Gonnella G 2020 Phys. Rev. Lett. 125 178004
Google Scholar
[4] Shi X Q, Fausti G, Chaté H, Nardini C, Solon A 2020 Phys. Rev. Lett. 125 168001
Google Scholar
[5] Suma A, Gonnella G, Marenduzzo D, Orlandini E 2014 EPL 108 56004
Google Scholar
[6] Caporusso C B, Negro G, Suma A, Digregorio P, Carenza L N, Gonnella G, Cugliandolo L F 2024 Soft Matter 20 923
Google Scholar
[7] Gonnella G, Lamura A, Suma A 2014 Int. J. Mod. Phys. C 25 1441004
Google Scholar
[8] Suma A, Gonnella G, Laghezza G, Lamura A, Mossa A, Cugliandolo L F 2014 Phys. Rev. E 90 052130
Google Scholar
[9] Henkes S, Fily Y, Marchetti M C 2011 Phys. Rev. E 84 040301
Google Scholar
[10] Reichhardt C, Reichhardt C J O 2015 Phys. Rev. E 91 032313
Google Scholar
[11] Giomi L 2015 Phys. Rev. X 5 031003
Google Scholar
[12] Riedel I H, Kruse K, Howard J 2005 Science 309 300
Google Scholar
[13] Gao W, Wang J 2014 ACS Nano 8 3170
Google Scholar
[14] Tan Z, Yang M, Ripoll M 2019 Phys. Rev. Appl. 11 054004
Google Scholar
[15] Kagan D, Laocharoensuk R, Zimmerman M, Clawson C, Balasubramanian S, Kong D, Bishop D, Sattayasamitsathit S, Zhang L, Wang J 2010 Small 6 2741
Google Scholar
[16] Sanchez S, Solovev A A, Schulze S, Schmidt O G 2011 Chem. Commun. 47 698
Google Scholar
[17] Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006
Google Scholar
[18] Qian B S, Tian W D, Chen K 2021 Phys. Chem. Chem. Phys. 23 20388
Google Scholar
[19] Moore F, Russo J, Liverpool T B, Royall C P 2023 J. Chem. Phys. 158 104907
Google Scholar
[20] Das S, Ghosh S, Chelakkot R 2020 Phys. Rev. E 102 032619
Google Scholar
[21] Nayak S, Das S, Bag P, Debnath T, Ghosh P K 2023 J. Chem. Phys. 159 164109
Google Scholar
[22] Ai B Q, Meng F H, He Y L, Zhang X M 2019 Soft Matter 15 3443
Google Scholar
[23] Das S, Chelakkot R 2020 Soft Matter 16 7250
Google Scholar
[24] Reichhardt C, Reichhardt C J O 2022 J. Chem. Phys. 156 124901
Google Scholar
[25] Zhu W J, Huang X Q, Ai B Q 2018 Chin. Phys. B 27 080504
Google Scholar
[26] Pan J X, Wei H, Qi M J, Wang H F, Zhang J J, Tian W D, Chen K 2020 Soft Matter 16 5545
Google Scholar
[27] Bhattacharjee T, Amchin D B, Ott J A, Kratz F, Datta S S 2021 Biophys. J. 120 3483
Google Scholar
[28] Sosa-Hernandez J, Santillan M, Santana-Solano J 2017 Phys. Rev. E 95 032404
Google Scholar
[29] Kumar P, Theeyancheri L, Chakrabarti R 2022 Soft Matter 18 2663
Google Scholar
[30] Lohrmann C, Holm C 2023 Phys. Rev. E 108 054401
Google Scholar
[31] Irani E, Mokhtari Z, Zippelius A 2022 Phys. Rev. Lett. 128 144501
Google Scholar
[32] Cugliandolo L F, Gonnella G, Suma A 2015 Phys. Rev. E 91 062124
Google Scholar
[33] 王晶, 焦阳, 田文得, 陈康 2023 72 190501
Google Scholar
Wang J, Jiao Y, Tian W D, Chen K 2023 Acta Phys. Sin. 72 190501
Google Scholar
-
图 1 模型示意图 (a)活性哑铃模型; (b)划分区域的模拟盒子
Fig. 1. Schematic diagram of the model: (a) Active dumbbell model; (b) simulation box divided into areas.
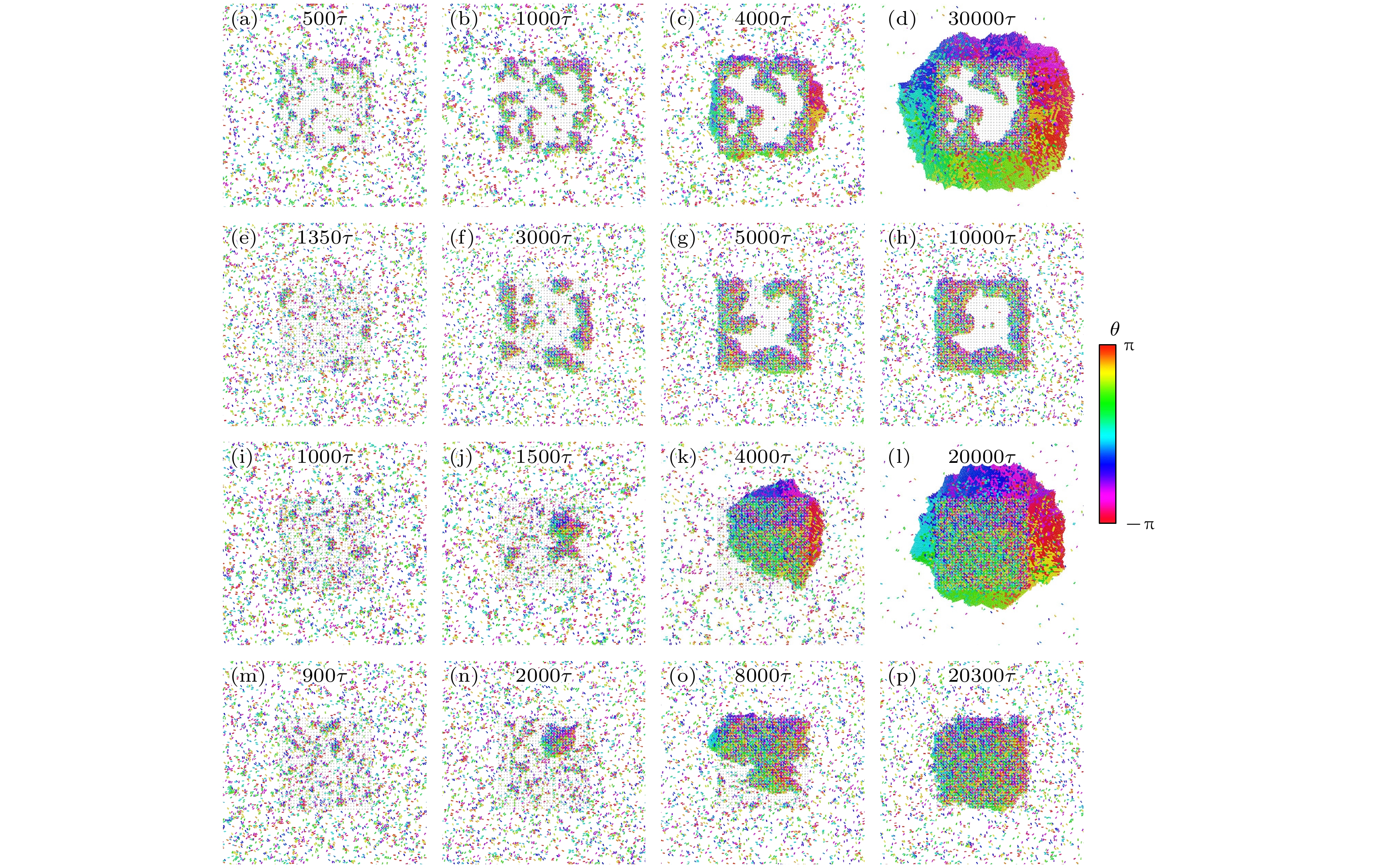
图 2 活性哑铃进入有限多孔介质的4种聚集过程的模拟快照, 颜色表示活性哑铃的取向, 图片上标注了对应的模拟时刻(a)—(d) ${f_{\text{a}}} = 10, {\text{ }}T = 0.02$; (e)—(h) ${f_{\text{a}}} = 10, {\text{ }}T = 0.2$; (i)—(l) ${f_{\text{a}}} = {4}0, {\text{ }}T = 0.2$; (m)—(p) ${f_{\text{a}}} = {3}0, {\text{ }}T = 0.{5}$
Fig. 2. Simulation snapshot of four aggregation processes of active dumbbells entering finite porous media, the color indicates the orientation of the active dumbbell, the corresponding simulation time has been marked on the pictures: (a)–(d) ${f_{\text{a}}} = 10, {\text{ }}T = 0.02$; (e)–(h) ${f_{\text{a}}} = 10, {\text{ }}T = 0.2$; (i)–(l) ${f_{\text{a}}} = {4}0, {\text{ }}T = 0.2$; (m)–(p) ${f_{\text{a}}} = {3}0, {\text{ }}T = 0.{5}$.
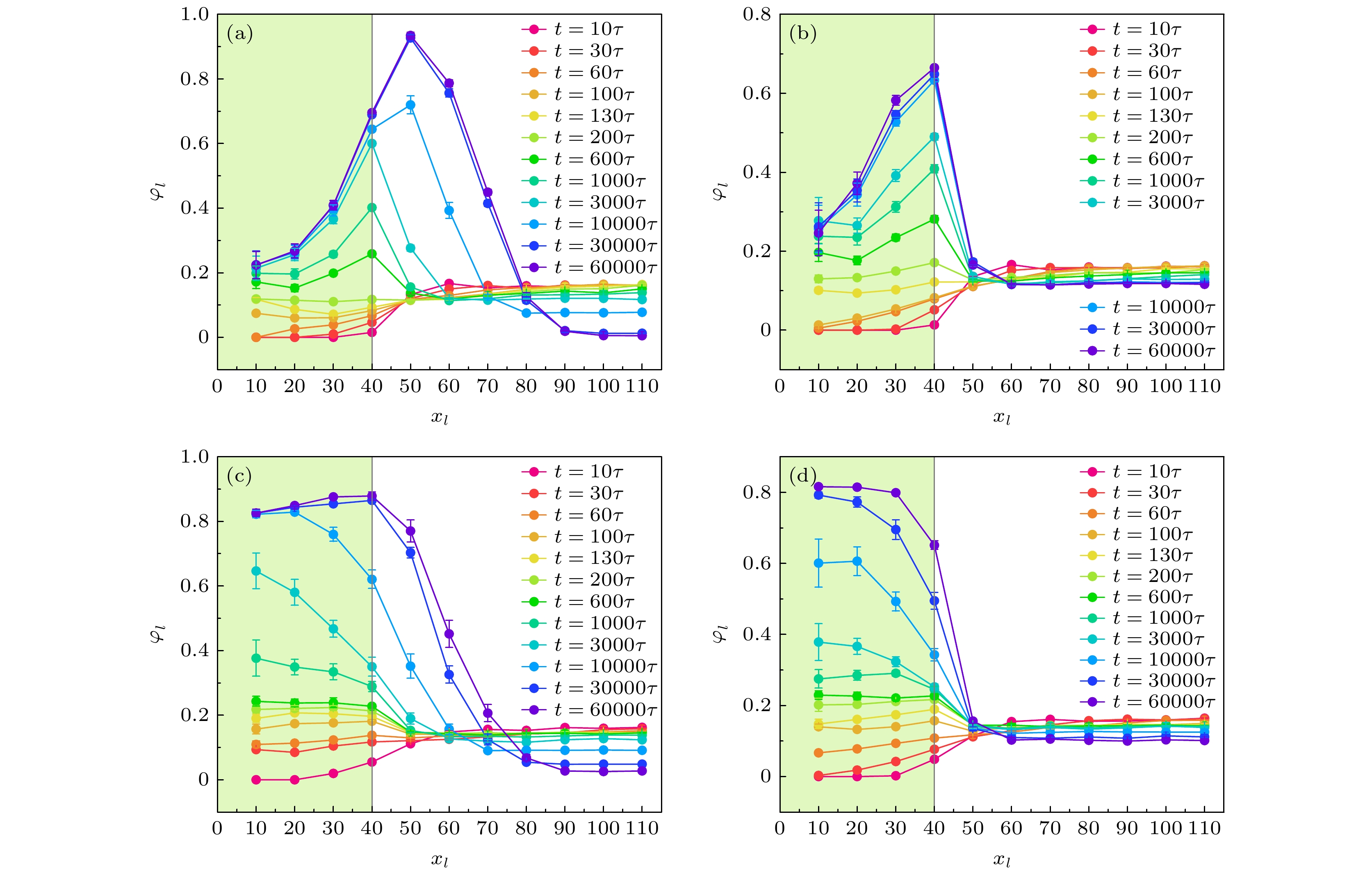
图 3 不同时刻各正方环形区域中活性哑铃的平均密度${\varphi _l}$, 绿色背景表示介质区域 (a) ${f_{\text{a}}} = 10, {\text{ }}T = 0.02$; (b) ${f_{\text{a}}} = $$ 10, {\text{ }}T = 0.2$; (c) ${f_{\text{a}}} = {4}0, {\text{ }}T = 0.2$; (d)${f_{\text{a}}} = {3}0, {\text{ }}T = 0.{5}$
Fig. 3. Average density ${\varphi _l}$ of active dumbbells in each square ring region at different times, and the green background indicates the medium region: (a) ${f_{\text{a}}} = 10, {\text{ }}T = 0.02$; (b) ${f_{\text{a}}} = 10, {\text{ }}T = 0.2$; (c) ${f_{\text{a}}} = {4}0, {\text{ }}T = 0.2$; (d) ${f_{\text{a}}} = {3}0, {\text{ }}T = 0.{5}$.
图 4 形态图, 蓝色空心圆代表中空巨聚集, 蓝色实心圆代表密实巨聚集, 紫色空心正方形代表介质内中空聚集, 紫色实心正方形代表介质内密实聚集, 黑色叉号表示介质内外无聚集, 背景颜色表示活性哑铃的持久长度
Fig. 4. Morphology diagram, the blue hollow circle represents the hollow giant aggregation, the blue solid circle represents the dense giant aggregation, the purple hollow square represents the hollow aggregation in the media, the purple solid square represents the dense aggregation in the media, and the black cross indicates no aggregation inside or outside the medium, the background color indicates the persistence length of the active dumbbell.
图 5 (a)活性哑铃的聚集度$M$; (b)介质中活性哑铃聚集的孔隙度$C$
Fig. 5. (a) Degree of aggregation $M$ of active dumbbells; (b) porosity of media with active dumbbell aggregation.
图 6 四种典型聚集结构中活性哑铃的极性序参量${P_l}$(a)和热力学温度${T_l}$(b)
Fig. 6. Polar order parameter ${P_l}$ (a) and thermodynamic temperature ${T_l}$ (b) of active dumbbells in four typical aggregation structures.
-
[1] Ramaswamy S 2010 Annu. Rev. Condens. Matter Phys. 1 323
Google Scholar
[2] Buttinoni I, Bialké J, Kümmel F, Löwen H, Bechinger C, Speck T 2013 Phys. Rev. Lett. 110 238301
Google Scholar
[3] Caporusso C B, Digregorio P, Levis D, Cugliandolo L F, Gonnella G 2020 Phys. Rev. Lett. 125 178004
Google Scholar
[4] Shi X Q, Fausti G, Chaté H, Nardini C, Solon A 2020 Phys. Rev. Lett. 125 168001
Google Scholar
[5] Suma A, Gonnella G, Marenduzzo D, Orlandini E 2014 EPL 108 56004
Google Scholar
[6] Caporusso C B, Negro G, Suma A, Digregorio P, Carenza L N, Gonnella G, Cugliandolo L F 2024 Soft Matter 20 923
Google Scholar
[7] Gonnella G, Lamura A, Suma A 2014 Int. J. Mod. Phys. C 25 1441004
Google Scholar
[8] Suma A, Gonnella G, Laghezza G, Lamura A, Mossa A, Cugliandolo L F 2014 Phys. Rev. E 90 052130
Google Scholar
[9] Henkes S, Fily Y, Marchetti M C 2011 Phys. Rev. E 84 040301
Google Scholar
[10] Reichhardt C, Reichhardt C J O 2015 Phys. Rev. E 91 032313
Google Scholar
[11] Giomi L 2015 Phys. Rev. X 5 031003
Google Scholar
[12] Riedel I H, Kruse K, Howard J 2005 Science 309 300
Google Scholar
[13] Gao W, Wang J 2014 ACS Nano 8 3170
Google Scholar
[14] Tan Z, Yang M, Ripoll M 2019 Phys. Rev. Appl. 11 054004
Google Scholar
[15] Kagan D, Laocharoensuk R, Zimmerman M, Clawson C, Balasubramanian S, Kong D, Bishop D, Sattayasamitsathit S, Zhang L, Wang J 2010 Small 6 2741
Google Scholar
[16] Sanchez S, Solovev A A, Schulze S, Schmidt O G 2011 Chem. Commun. 47 698
Google Scholar
[17] Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006
Google Scholar
[18] Qian B S, Tian W D, Chen K 2021 Phys. Chem. Chem. Phys. 23 20388
Google Scholar
[19] Moore F, Russo J, Liverpool T B, Royall C P 2023 J. Chem. Phys. 158 104907
Google Scholar
[20] Das S, Ghosh S, Chelakkot R 2020 Phys. Rev. E 102 032619
Google Scholar
[21] Nayak S, Das S, Bag P, Debnath T, Ghosh P K 2023 J. Chem. Phys. 159 164109
Google Scholar
[22] Ai B Q, Meng F H, He Y L, Zhang X M 2019 Soft Matter 15 3443
Google Scholar
[23] Das S, Chelakkot R 2020 Soft Matter 16 7250
Google Scholar
[24] Reichhardt C, Reichhardt C J O 2022 J. Chem. Phys. 156 124901
Google Scholar
[25] Zhu W J, Huang X Q, Ai B Q 2018 Chin. Phys. B 27 080504
Google Scholar
[26] Pan J X, Wei H, Qi M J, Wang H F, Zhang J J, Tian W D, Chen K 2020 Soft Matter 16 5545
Google Scholar
[27] Bhattacharjee T, Amchin D B, Ott J A, Kratz F, Datta S S 2021 Biophys. J. 120 3483
Google Scholar
[28] Sosa-Hernandez J, Santillan M, Santana-Solano J 2017 Phys. Rev. E 95 032404
Google Scholar
[29] Kumar P, Theeyancheri L, Chakrabarti R 2022 Soft Matter 18 2663
Google Scholar
[30] Lohrmann C, Holm C 2023 Phys. Rev. E 108 054401
Google Scholar
[31] Irani E, Mokhtari Z, Zippelius A 2022 Phys. Rev. Lett. 128 144501
Google Scholar
[32] Cugliandolo L F, Gonnella G, Suma A 2015 Phys. Rev. E 91 062124
Google Scholar
[33] 王晶, 焦阳, 田文得, 陈康 2023 72 190501
Google Scholar
Wang J, Jiao Y, Tian W D, Chen K 2023 Acta Phys. Sin. 72 190501
Google Scholar
下载:
计量
- 文章访问数: 703
- PDF下载量: 35
- 被引次数: 0
