-
光晶格中的冷原子系统是实现量子模拟和量子计算的有效平台之一, 其相变特性的研究有助于系统中新奇量子态物理机制的探索和实验观测. 本文利用朗道相变理论和非均匀平均场方法, 研究了人工磁场下光晶格中各向异性偶极玻色气体的相变, 得到了系统不可压缩相(Mott绝缘相、棋盘或条纹密度波相)-可压缩相(超流、棋盘或条纹超固相)的解析相变条件, 给出了系统的完整相图. 有趣的是, 各向异性偶极相互作用会使得系统中的棋盘密度波相和棋盘超固相变为条纹密度波相和条纹超固相, 人工磁场会稳定绝缘相和超固相, 使得绝缘相和超固相在相图中的存在区域变大. 此外, 引入外加谐振势后发现系统中的不同量子相可以共存.
-
关键词:
- 光晶格 /
- 各向异性偶极相互作用 /
- 人工磁场 /
- 超固相
The quantum system composed of optical lattice and ultracold atomic gas is an ideal platform for realizing quantum simulation and quantum computing. Especially for dipolar bosons in optical lattices with artificial gauge fields, the interplay between anisotropic dipolar interactions and artificial gauge fields leads to many novel phases. Exploring the phase transition characteristics of the system is beneficial to understanding the physics of quantum many-body systems and observing quantum states of dipolar system in experiments. In this work, we investigate the quantum phase transitions of anisotropic dipolar bosons in a two-dimensional optical lattice with an artificial magnetic field. Using an inhomogeneous mean-field method and a Landau phase transition theory, we obtain complete phase diagrams and analytical expressions for phase boundaries between an incompressible phase and a compressible phase. Our results show that both the artificial magnetic field and the anisotropic dipolar interaction have a significant effect on the phase diagram. When the polar angle increases, the system undergoes the phase transition from a checkerboard supersolid to a striped supersolid. For small polar angle ($V_x/U= 0.2, V_y/U=0.1$ , Fig.(a)), artificial magnetic field induces both checkerboard solid phase and supersolid phase to extend to a large hopping region. For a larger polar angle ($V_x/U=0.2, $ $ V_y/U=-0.1$ , Fig.(b)), artificial magnetic field induces both striped solid and striped supersolid to extend to a large hopping region. Thus, the artificial magnetic field stabilizes the density wave and supersolid phases. In addition, we reveal the coexistence of different quantum phases in the presence of an external trapping potential. The research results provide a theoretical basis for manipulating the quantum phase in experiments on anisotropic dipolar atoms by using an artificial magnetic field.
-
Keywords:
- optical lattice /
- anisotropic dipolar interaction /
- artificial magnetic field /
- supersolid phase
[1] Gross C, Bloch I 2017 Science 357 995
Google Scholar
[2] 谭辉, 曹睿, 李永强 2023 72 183701
Google Scholar
Tan H, Cao R, Li Y Q 2023 Acta Phys. Sin. 72 183701
Google Scholar
[3] Liu J Y, Wang X Q, Xu Z F 2023 Chin. Phys. Lett. 40 086701
Google Scholar
[4] Sukachev D, Sokolov A, Chebakov K, Akimov A, Kanorsky S, Kolachevsky N, Sorokin V 2010 Phys. Rev. A 82 011405
Google Scholar
[5] Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39
Google Scholar
[6] Dash J G, Wettlaufer J S 2005 Phys. Rev. Lett. 94 235301
Google Scholar
[7] Recati A, Stringari S 2023 Nat. Rev. Phys. 5 735
Google Scholar
[8] 王欢, 贺夏瑶, 李帅, 刘博 2023 72 100309
Google Scholar
Wang H, He X Y, Li S, Liu B 2023 Acta Phys. Sin. 72 100309
Google Scholar
[9] Bernardet K, Batrouni G G, Troyer M 2002 Phys. Rev. B 66 054520
Google Scholar
[10] Iskin M 2011 Phys. Rev. A 83 051606(R
Google Scholar
[11] Baranov M A, Dalmonte M, Pupillo G, Zoller P 2012 Chem. Rev. 112 5012
Google Scholar
[12] Gao J M, Tang R A, Xue J K 2017 EPL 117 60007
Google Scholar
[13] Masella G, Angelone A, Mezzacapo F, Pupillo G, Prokof'ev N V 2019 Phys. Rev. Lett. 123 045301
Google Scholar
[14] Wu H K, Tu W L 2020 Phys. Rev. A 102 053306
Google Scholar
[15] Bandyopadhyay S, Bai R, Pal S, Suthar K, Nath R, Angom D 2019 Phys. Rev. A 100 053623
Google Scholar
[16] Zhang J, Zhang C, Yang J, Capogrosso-Sansone B 2022 Phys. Rev. A 105 063302
Google Scholar
[17] Griesmaier A, Werner J, Hensler S, Stuhler J, Pfau T 2005 Phys. Rev. Lett. 94 160401
Google Scholar
[18] Yi S, You L 2000 Phys. Rev. A 61 041604
Google Scholar
[19] Ospelkaus C, Ospelkaus S, Humbert L, Ernst P, Sengstock K, Bongs K 2006 Phys. Rev. Lett. 97 120402
Google Scholar
[20] Léonard J, Morales A, Zupancic P, Esslinger T, Donner T 2017 Nature 543 87
Google Scholar
[21] Li J R, Lee J, Huang W, Burchesky S, Shteynas B, Top F Ç, Jamison A O, Ketterle W 2017 Nature 543 91
Google Scholar
[22] Tanzi L, Lucioni E, Famà F, Catani J, Fioretti A, Gabbanini C, Bisset R N, Santos L, Modugno G 2019 Phys. Rev. Lett. 122 130405
Google Scholar
[23] Guo M, Böttcher F, Hertkorn J, Schmidt J N, Wenzel M, Büchler H P, Langen T, Pfau T 2019 Nature 574 386
Google Scholar
[24] Norcia M A, Politi C, Klaus L, Poli E, Sohmen M, Mark M J, Bisset R N, Santos L, Ferlaino F 2021 Nature 596 357
Google Scholar
[25] Williams R A, Al-Assam S, Foot C J 2010 Phys. Rev. Lett. 104 050404
Google Scholar
[26] Aidelsburger M, Atala M, Nascimbène S, Trotzky S, Chen Y A, Bloch I 2011 Phys. Rev. Lett. 107 255301
Google Scholar
[27] Hügel D, Paredes B 2014 Phys. Rev. A 89 023619
Google Scholar
[28] Grusdt F, Letscher F, Hafezi M, Fleischhauer M 2014 Phys. Rev. Lett. 113 155301
Google Scholar
[29] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[30] Piraud M, Heidrich-Meisner F, McCulloch I P, Greschner S, Vekua T, Schollwöck U 2015 Phys. Rev. B 91 140406
Google Scholar
[31] Orignac E, Giamarchi T 2001 Phys. Rev. B 64 144515
Google Scholar
[32] Kolley F, Piraud M, McCulloch I P, Schollwöck U, Heidrich-Meisner F 2015 New J. Phys. 17 092001
Google Scholar
[33] Song Y F, Yang S J 2020 New J.Phys. 22 073001
Google Scholar
[34] Zhang X R, Yang S J 2023 Results Phys. 53 106998
Google Scholar
[35] Oktel M Ö, Nită M, Tanatar B 2007 Phys. Rev. B 75 045133
Google Scholar
[36] Pal S, Bai R, Bandyopadhyay S, Suthar K, Angom D 2019 Phys. Rev. A 99 053610
Google Scholar
[37] Suthar K, Sable H, Bai R, Bandyopadhyay S, Pal S, Angom D 2020 Phys. Rev. A 102 013320
Google Scholar
[38] Su L, Douglas A, Szurek M, Groth R, Ozturk S, Krahn A, Hébert A, Phelps G, Ebadi S, Dickerson S, Ferlaino F, Marković O, Greiner M 2023 Nature 622 724
Google Scholar
[39] Ohgoe T, Suzuki T, Kawashima N 2012 Phys. Rev. B 86 054520
Google Scholar
[40] Bai R, Bandyopadhyay S, Pal S, Suthar K, Angom D 2018 Phys. Rev. A 98 023606
Google Scholar
[41] Scarola V W, Pollet L, Oitmaa J, Troyer M 2009 Phys. Rev. Lett. 102 135302
Google Scholar
[42] Iskin M, Freericks J K 2009 Phys. Rev. A 79 053634
Google Scholar
[43] Sant’Ana F T, Pelster A, dos Santos F E A 2019 Phys. Rev. A 100 043609
Google Scholar
[44] Iskin M 2012 Eur. Phys. J. B 85 76
Google Scholar
[45] Sachdeva R, Singh M, Busch T 2017 Phys. Rev. A 95 063601
Google Scholar
-
图 1 二维正方光晶格中偶极量子气体示意图. 晶格中的偶极原子具有相同极化方向, 极化方向与z轴的夹角为θ, 与位置矢量${\boldsymbol{r}}_{ij}={\boldsymbol{r}}_{i}-{\boldsymbol{r}}_{j}$$(i=(p, q), j=(p^{\prime}, q^{\prime}))$的夹角为$\alpha_{ij}$
Fig. 1. Schematic representation of the dipoles in a two-dimensional optical lattice. Dipoles are aligned parallel to each other along the direction of polarization, θ is the polar angle between z axis and polarization direction, $\alpha_{ij}$ is the angle between the polarization axis and ${\boldsymbol{r}}_{ij}$, $ {\boldsymbol{r}}_{ij}={\boldsymbol{r}}_{i}- $$ {\boldsymbol{r}}_{j}$$(i=(p, q), j=(p^{\prime}, q^{\prime}))$.
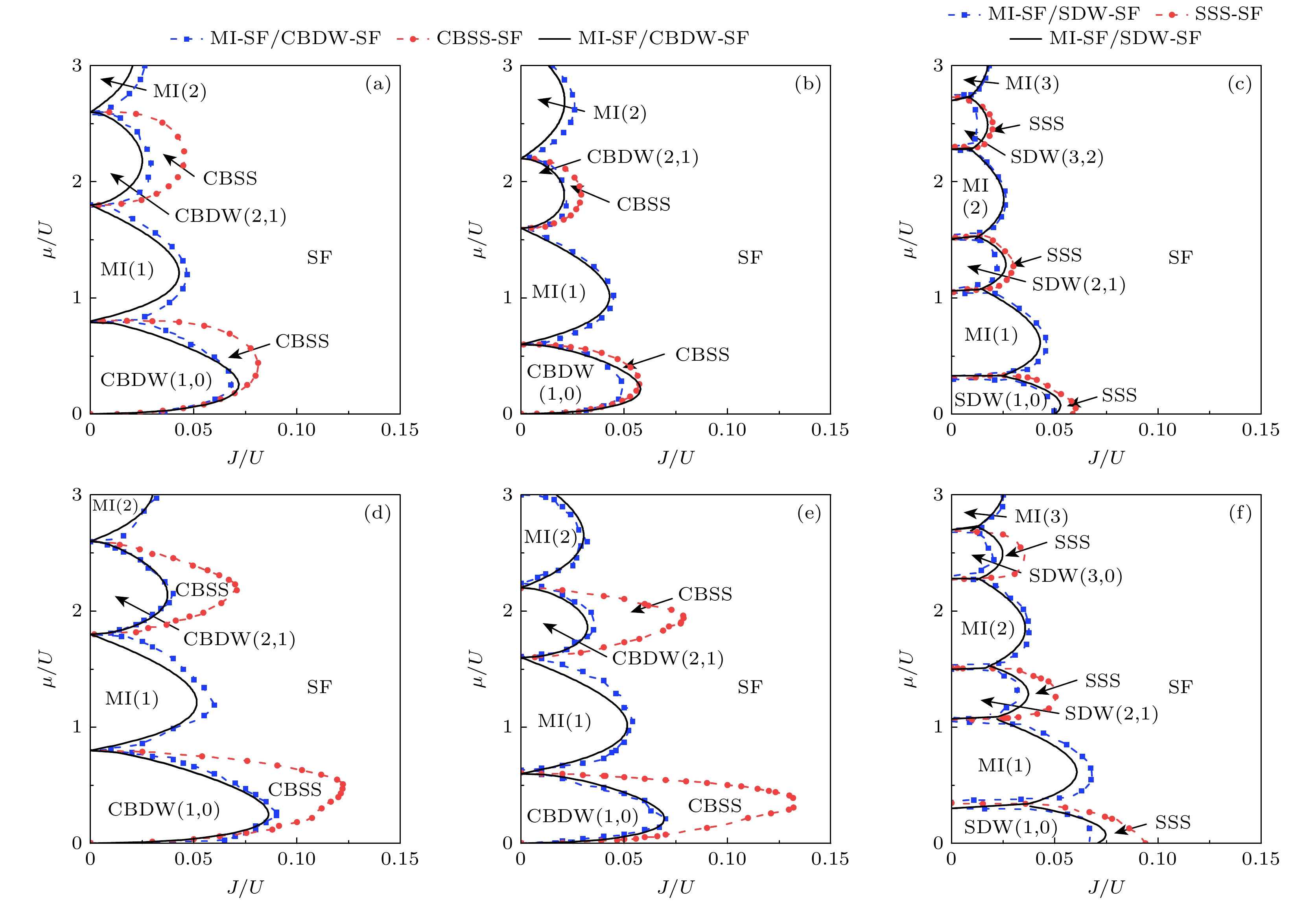
图 2 $V_x/U=0.2$时, EBHM的相图 (a)—(c) $\alpha=0$, $V_y/U$分别为$0.2, \;0.1, \;-0.1$; (d)—(f) $\alpha=1/2$, $V_y/U$分别为$0.2, \;0.1, $$ -0.1$. 蓝色方形点线为不可压缩相-可压缩相的相变边界的数值结果, 黑色实线为解析结果. 红色圆形点线为超固相-超流相的相变边界
Fig. 2. Phase diagram of EBHM with $V_x/U=0.2$: (a)–(c) $\alpha=0$, $V_y/U=0.2, \;0.1, \;-0.1$; (d)–(f) $\alpha=1/2$, $V_y/U=0.2,\; 0.1, $$ -0.1$. Blue square dot line is the numerical result of phase transition boundary between incompressible phase and compressible phase, and the solid black line is the analytical result. Red dot line is the phase transition boundary between the supersolid phase and the superfluid phase.
图 3 序参量ϕ(上图)和粒子数密度n(下图)在$N=50\times50$晶格中的分布, $\mu/U=0.3$, $\alpha=0$ (a) CBDW相, $J/U=0.02$, $V_x/U=V_y/U=0.4$; (b) CBSS相, $J/U=0.12$, $V_x/U=V_y/U=0.4$; (c) SDW相, $J/U=0.02$, $V_x/U= 0.4$, $V_y/U=-0.4$; (d) SSS相, $J/U=0.12$, $V_x/U=0.4$, $V_y/U=-0.4$
Fig. 3. Order parameter ϕ (upper panel) and boson densities n (lower panel) in a $N =50\times50$ lattice with different phases at $\mu/U=0.3$ and $\alpha=0$: (a) CBDW phase, $J/U=0.02$, $V_x/U=V_y/U=0.4$; (b) CBSS phase, $J/U=0.12$, $V_x/U= $$ V_y/U=0.4$; (c) SDW phase, $J/U=0.02$, $V_x/U=0.4$, $V_y/U=-0.4$; (d) SSS phase, $J/U=0.12$, $V_x/U=0.4$, $V_y/U=-0.4$.
图 4 $\alpha=0$时序参量$\bar{\phi}$, 粒子数密度$\bar{n}$, 结构因子$S(\pi, \pi)$和$S(\pi, 0)$随$J/U$和$\mu/U$的变化 (a) $\mu/U=0.5,\; V_x/U= V_y/U= $$ 0.2$; (b) $J/U=0.0125, \;V_x/U=V_y/U=0.2$; (c) $\mu/U=0.1,\; V_x/U=0.2$, $V_y/U=-0.1$; (d) $J/U=0.0125, \;V_x/U=0.2$, $V_y/U=-0.1$
Fig. 4. Order parameter $\bar{\phi}$, density $\bar{n}$, structural factor $S(\pi, \pi)$ and $S(\pi, 0)$ as a function of J/U and $\mu/U$ with $\alpha=0$: (a) $\mu/U=0.5$, $V_x/U=V_y/U=0.2$; (b) $J/U=0.0125$, $V_x/U=V_y/U=0.2$; (c) $\mu/U=0.1$, $V_x/U=0.2$, $V_y/U=-0.1$; (d) $J/U=0.0125$, $V_x/U=0.2$, $V_y/U=-0.1$.
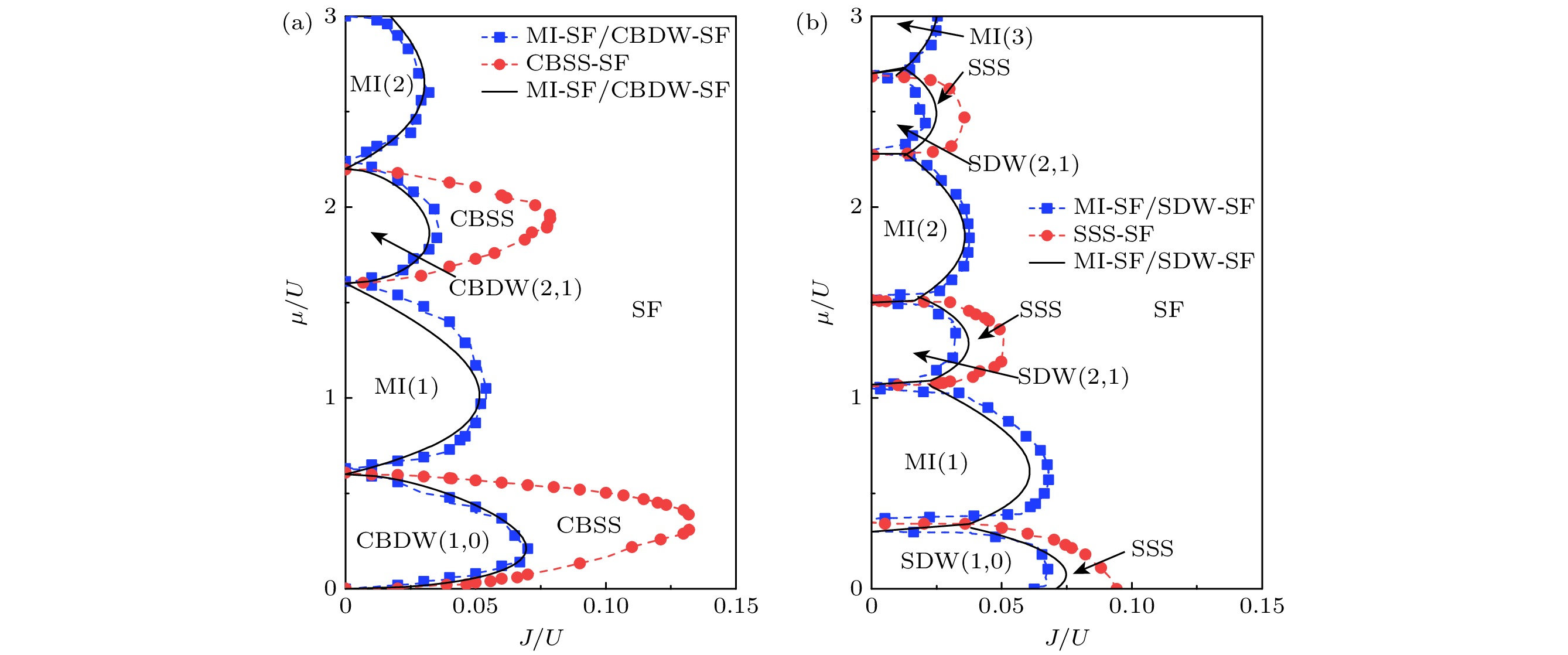
图 5 $V_x/U = 0.8$时, EBHM的相图 (a)—(c) $\alpha = 0$, $V_y/U$分别为$0.8, 0.4, -0.1$; (d)—(f) $\alpha = 1/2$, $V_y/U$分别为$0.8, 0.4, -0.1$. 蓝色正方形点线为不可压缩相-可压缩相相变边界的数值结果, 黑色实线为解析结果. 红色圆点线为超固相-超流相的相变边界
Fig. 5. Phase diagram of EBHM with $V_x/U=0.8$: (a)–(c) $\alpha=0$, $V_y/U=0.8, 0.4, -0.1$, (d)–(f) $\alpha=1/2$, $V_y/U=0.8, 0.4, $$ -0.1$. Blue square dot line is the numerical result of phase transition boundary between incompressible phase and compressible phase, and the solid black line is the analytical result. Red dot line is the phase transition boundary between the supersolid phase and the superfluid phase.
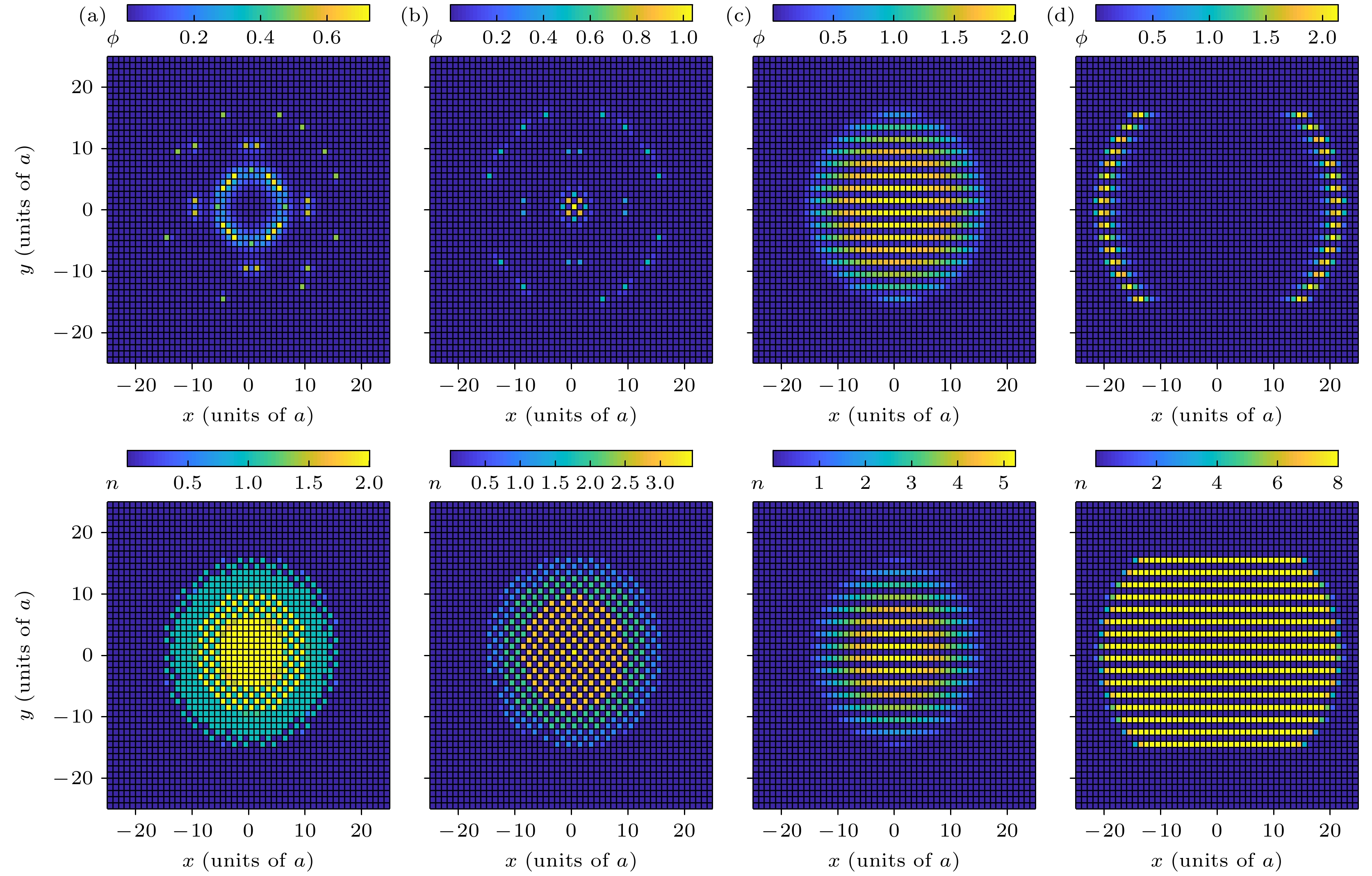
图 6 $\varOmega/U=0.012,\; \alpha=0$时序参量ϕ (上图)和粒子数密度n (下图)在$N=50\times50$晶格中的分布 (a) $V_x/U=0.2$, $V_y/U= $$ 0.2,\; J/U=0.0155$; (b) $V_x/U=0.8$, $V_y/U=0.8,\; J/U=0.08$; (c) $V_x/U=0.8$, $V_y/U=-0.2, \; J/U=0.125$; (d) $V_x/U=0.8$, $V_y/U=-0.8,\; J/U=0.125$
Fig. 6. Order parameter ϕ (upper panel) and boson densities n (lower panel) in a $N=50\times50$ lattice with $\varOmega/U=0.012$ and $\alpha=0$: (a) $V_x/U=0.2$, $V_y/U=0.2, \; J/U=0.0155$; (b) $V_x/U=0.8$, $V_y/U=0.8,\; J/U=0.08$; (c) $V_x/U=0.8$, $V_y/U= $$ -0.2,\; J/U=0.125$; (d) $V_x/U=0.8$, $V_y/U=-0.8,\; J/U=0.125$.
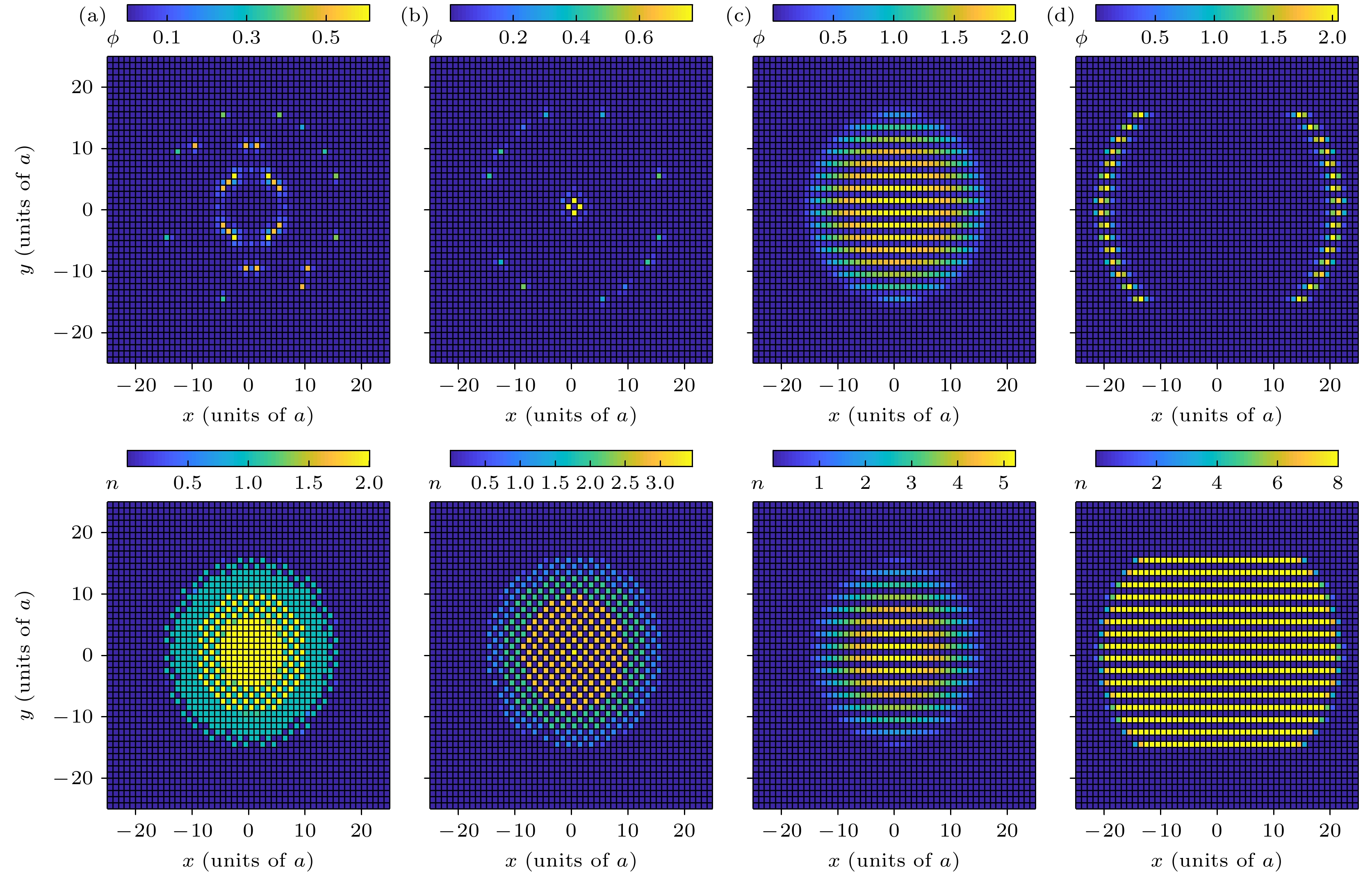
图 7 $\varOmega/U=0.012$, $\alpha=1/2$时序参量ϕ (上图)和粒子数密度n (下图)在$N=50\times50$晶格中的分布 (a) $V_x/U=0.2$, $V_y/U=0.2$; (b) $V_x/U=0.8$, $V_y/U=0.8$; (c) $V_x/U=0.8$, $V_y/U=-0.2$; (d) $V_x/U=0.8$, $V_y/U=-0.8$
Fig. 7. Order parameter ϕ (upper panel) and boson densities n (lower panel) in a $N =50\times50$ lattice with $\varOmega/U=0.012$ and $\alpha=1/2$: (a) $V_x/U=0.2$, $V_y/U=0.2$; (b) $V_x/U=0.8$, $V_y/U=0.8$; (c) $V_x/U=0.8$, $V_y/U=-0.2$; (d) $V_x/U= 0.8$, $V_y/U=-0.8$.
表 1 不同量子相的序参量
Table 1. Order parameters of each quantum phases.
量子相 简写 $\bar{n}$ $\bar{\phi}$ $S(\pi, \pi)$ $S(\pi, 0)$ 莫特绝缘相(Mott insulator) MI 整数 0 0 0 超流体(superfluid) SF 实数 $\neq0$ 0 0 棋盘密度波(checkerboard density wave) CBDW 整数 0 $\neq0$ 0 棋盘超固相(checkerboard supersolid) CBSS 实数 $\neq0 $ $\neq0$ 0 条纹密度波(striped density wave) SDW 整数 0 0 $\neq0$ 条纹超固相(striped supersolid) SSS 实数 $\neq0$ 0 $\neq0$ 
下载: 导出CSV
-
[1] Gross C, Bloch I 2017 Science 357 995
Google Scholar
[2] 谭辉, 曹睿, 李永强 2023 72 183701
Google Scholar
Tan H, Cao R, Li Y Q 2023 Acta Phys. Sin. 72 183701
Google Scholar
[3] Liu J Y, Wang X Q, Xu Z F 2023 Chin. Phys. Lett. 40 086701
Google Scholar
[4] Sukachev D, Sokolov A, Chebakov K, Akimov A, Kanorsky S, Kolachevsky N, Sorokin V 2010 Phys. Rev. A 82 011405
Google Scholar
[5] Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39
Google Scholar
[6] Dash J G, Wettlaufer J S 2005 Phys. Rev. Lett. 94 235301
Google Scholar
[7] Recati A, Stringari S 2023 Nat. Rev. Phys. 5 735
Google Scholar
[8] 王欢, 贺夏瑶, 李帅, 刘博 2023 72 100309
Google Scholar
Wang H, He X Y, Li S, Liu B 2023 Acta Phys. Sin. 72 100309
Google Scholar
[9] Bernardet K, Batrouni G G, Troyer M 2002 Phys. Rev. B 66 054520
Google Scholar
[10] Iskin M 2011 Phys. Rev. A 83 051606(R
Google Scholar
[11] Baranov M A, Dalmonte M, Pupillo G, Zoller P 2012 Chem. Rev. 112 5012
Google Scholar
[12] Gao J M, Tang R A, Xue J K 2017 EPL 117 60007
Google Scholar
[13] Masella G, Angelone A, Mezzacapo F, Pupillo G, Prokof'ev N V 2019 Phys. Rev. Lett. 123 045301
Google Scholar
[14] Wu H K, Tu W L 2020 Phys. Rev. A 102 053306
Google Scholar
[15] Bandyopadhyay S, Bai R, Pal S, Suthar K, Nath R, Angom D 2019 Phys. Rev. A 100 053623
Google Scholar
[16] Zhang J, Zhang C, Yang J, Capogrosso-Sansone B 2022 Phys. Rev. A 105 063302
Google Scholar
[17] Griesmaier A, Werner J, Hensler S, Stuhler J, Pfau T 2005 Phys. Rev. Lett. 94 160401
Google Scholar
[18] Yi S, You L 2000 Phys. Rev. A 61 041604
Google Scholar
[19] Ospelkaus C, Ospelkaus S, Humbert L, Ernst P, Sengstock K, Bongs K 2006 Phys. Rev. Lett. 97 120402
Google Scholar
[20] Léonard J, Morales A, Zupancic P, Esslinger T, Donner T 2017 Nature 543 87
Google Scholar
[21] Li J R, Lee J, Huang W, Burchesky S, Shteynas B, Top F Ç, Jamison A O, Ketterle W 2017 Nature 543 91
Google Scholar
[22] Tanzi L, Lucioni E, Famà F, Catani J, Fioretti A, Gabbanini C, Bisset R N, Santos L, Modugno G 2019 Phys. Rev. Lett. 122 130405
Google Scholar
[23] Guo M, Böttcher F, Hertkorn J, Schmidt J N, Wenzel M, Büchler H P, Langen T, Pfau T 2019 Nature 574 386
Google Scholar
[24] Norcia M A, Politi C, Klaus L, Poli E, Sohmen M, Mark M J, Bisset R N, Santos L, Ferlaino F 2021 Nature 596 357
Google Scholar
[25] Williams R A, Al-Assam S, Foot C J 2010 Phys. Rev. Lett. 104 050404
Google Scholar
[26] Aidelsburger M, Atala M, Nascimbène S, Trotzky S, Chen Y A, Bloch I 2011 Phys. Rev. Lett. 107 255301
Google Scholar
[27] Hügel D, Paredes B 2014 Phys. Rev. A 89 023619
Google Scholar
[28] Grusdt F, Letscher F, Hafezi M, Fleischhauer M 2014 Phys. Rev. Lett. 113 155301
Google Scholar
[29] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045
Google Scholar
[30] Piraud M, Heidrich-Meisner F, McCulloch I P, Greschner S, Vekua T, Schollwöck U 2015 Phys. Rev. B 91 140406
Google Scholar
[31] Orignac E, Giamarchi T 2001 Phys. Rev. B 64 144515
Google Scholar
[32] Kolley F, Piraud M, McCulloch I P, Schollwöck U, Heidrich-Meisner F 2015 New J. Phys. 17 092001
Google Scholar
[33] Song Y F, Yang S J 2020 New J.Phys. 22 073001
Google Scholar
[34] Zhang X R, Yang S J 2023 Results Phys. 53 106998
Google Scholar
[35] Oktel M Ö, Nită M, Tanatar B 2007 Phys. Rev. B 75 045133
Google Scholar
[36] Pal S, Bai R, Bandyopadhyay S, Suthar K, Angom D 2019 Phys. Rev. A 99 053610
Google Scholar
[37] Suthar K, Sable H, Bai R, Bandyopadhyay S, Pal S, Angom D 2020 Phys. Rev. A 102 013320
Google Scholar
[38] Su L, Douglas A, Szurek M, Groth R, Ozturk S, Krahn A, Hébert A, Phelps G, Ebadi S, Dickerson S, Ferlaino F, Marković O, Greiner M 2023 Nature 622 724
Google Scholar
[39] Ohgoe T, Suzuki T, Kawashima N 2012 Phys. Rev. B 86 054520
Google Scholar
[40] Bai R, Bandyopadhyay S, Pal S, Suthar K, Angom D 2018 Phys. Rev. A 98 023606
Google Scholar
[41] Scarola V W, Pollet L, Oitmaa J, Troyer M 2009 Phys. Rev. Lett. 102 135302
Google Scholar
[42] Iskin M, Freericks J K 2009 Phys. Rev. A 79 053634
Google Scholar
[43] Sant’Ana F T, Pelster A, dos Santos F E A 2019 Phys. Rev. A 100 043609
Google Scholar
[44] Iskin M 2012 Eur. Phys. J. B 85 76
Google Scholar
[45] Sachdeva R, Singh M, Busch T 2017 Phys. Rev. A 95 063601
Google Scholar
下载:
计量
- 文章访问数: 1429
- PDF下载量: 43
- 被引次数: 0
