-
In a two-dimensional boron structure, the ordered high-concentration vacancy distribution can enhance structural stability and significantly modulates material properties. Based on recent experimental progress, herein we particularly focus on the two-dimensional boron structures with a striped distribution of hexagonal vacancies, in order to explore the formation of long-period boron structures. Utilizing the structures of alloy generation and recognition (SAGAR) program developed by our group, we eliminate duplicate structures according to the structural symmetry to reduce computational cost. An effective model system is proposed to investigate the effect of vacancy distribution on the stability of the system, where the interactions between vacancies are utilized for estimating the total energy. By selecting structures with appropriate concentrations and combining first-principles calculations, the parameters in the model are fitted for different vacancy neighbor interactions, which can be further used to predict stable structures at various vacancy concentrations. The feasibility of model analysis is emphasized for structural screening, showing the good agreement between the parameterized model and the first-principles calculations. Interestingly, under the same vacancy concentration, stable boron structures with different cell sizes exhibit distinct vacancy distributions, indicating a trend of long-period distribution for ground state structures. To address this phenomenon, when the stable candidate structures from the 1/6 series are dominant in number within the computable range and the changes in neighbor statistics can be clearly seen, we select the structures from this concentration series for detailed calculations. The calculation results indicate that the convergence of the average energy is primarily influenced by the interaction between the fourth nearest neighbor and the sixth nearest neighbor. When considering only these two neighbors, the system energy changes with the increase of cell size as follows: the average energy of structures with a cell size being an even multiple of the minimum cell size keeps unchanged, while the average energy of structure with a cell size being an odd multiple of the minimum cell size gradually decreases, eventually converging to a stable value. When including the interactions between the ninth nearest neighbor and the tenth nearest neighbor, the average energy of structures with a cell size being an even times the minimum cell size also decreases gradually. The average energy decreases with oscillations, with the magnitude gradually diminishing and eventually stabilizing. This discovery reveals that the enhanced stability of long-period structures is attributed to the competitive interactions among different neighboring vacancies. 
-
Keywords:
- two-dimensional boron structure /
- long-period structure /
- vacancy distribution /
- first-principles calculation
[1] Zhao L, Schwarz W E, Frenking G 2019 Nat. Rev. Chem. 3 35
Google Scholar
[2] Jhi S H, Louie S G, Cohen M L, Ihm J 2001 Phys. Rev. Lett. 86 3348
Google Scholar
[3] Hart G L, Zunger A 2001 Phys. Rev. Lett. 87 275508
Google Scholar
[4] Kaneti Y V, Benu D P, Xu X, Yuliarto B, Yamauchi Y, Golberg D 2021 Chem. Rev. 122 1000
Google Scholar
[5] Tang H, Ismail-Beigi S 2007 Phys. Rev. Lett. 99 115501
Google Scholar
[6] Yang X B, Ding Y, Ni J 2008 Phys. Rev. B 77 041402(R
Google Scholar
[7] Wu X J, Dai J, Zhao Y, Zhuo Z W, Yang J L, Zeng X C 2012 ACS Nano 6 7443
Google Scholar
[8] Mannix A J, Zhou X F, Kiraly B, Wood J D, Alducin D, Myers B D, Liu X, Fisher B L, Santiago U, Guest J R 2015 Science 350 1513
Google Scholar
[9] Zhang L Z, Yan Q B, Du S X, Su G, Gao H J 2012 J. Phys. Chem. C 116 18202
Google Scholar
[10] Liu Y, Penev E S, Yakobson B I 2013 Angew. Chem. Int. Ed. 52 3156
Google Scholar
[11] Liu H S, Gao J F, Zhao J J 2013 Sci. Rep. 3 3238
Google Scholar
[12] Zhang Z H, Yang Y, Gao G Y, Yakobson B I 2015 Angew. Chem. 54 13022
Google Scholar
[13] Feng B J, Zhang J, Zhong Q, Li W B, Li S, Li H, Cheng P, Meng S, Chen L, Wu K H 2016 Nat. Chem. 8 563
Google Scholar
[14] Zhong Q, Kong L J, Gou J, Li W B, Sheng S X, Yang S, Cheng P, Li H, Wu K H, Chen L 2017 Phys. Rev. Mater. 1 021001
Google Scholar
[15] Wang Y, Kong L, Chen C, Cheng P, Feng B, Wu K H, Chen L 2020 Adv. Mater. 32 2005128
Google Scholar
[16] Li W B, Kong L J, Chen C Y, Gou J, Sheng S X, Zhang W F, Li H, Chen L, Cheng P, Wu K H 2018 Sci. Bull. 63 282
Google Scholar
[17] Wu R, Drozdov I K, Eltinge S, Zahl P, Ismail-Beigi S, Božović I, Gozar A 2019 Nat. Nanotechnol. 14 44
Google Scholar
[18] Vinogradov N A, Lyalin A, Taketsugu T, Vinogradov A S, Preobrajenski A 2019 ACS Nano 13 14511
Google Scholar
[19] Kiraly B, Liu X, Wang L, Zhang Z, Mannix A J, Fisher B L, Yakobson B I, Hersam M C, Guisinger N P 2019 ACS Nano 13 3816
Google Scholar
[20] Xu S G, He C C, Zhao Y J, Xu H, Yang X B 2021 Phys. Rev. Mater. 5 044003
Google Scholar
[21] Floría L M, Mazo J J 1996 Adv. Phys. 45 505
Google Scholar
[22] He C C, Liao J H, Qiu S B, Zhao Y J, Yang X B 2021 Comput. Mater. Sci. 193 110386
Google Scholar
-
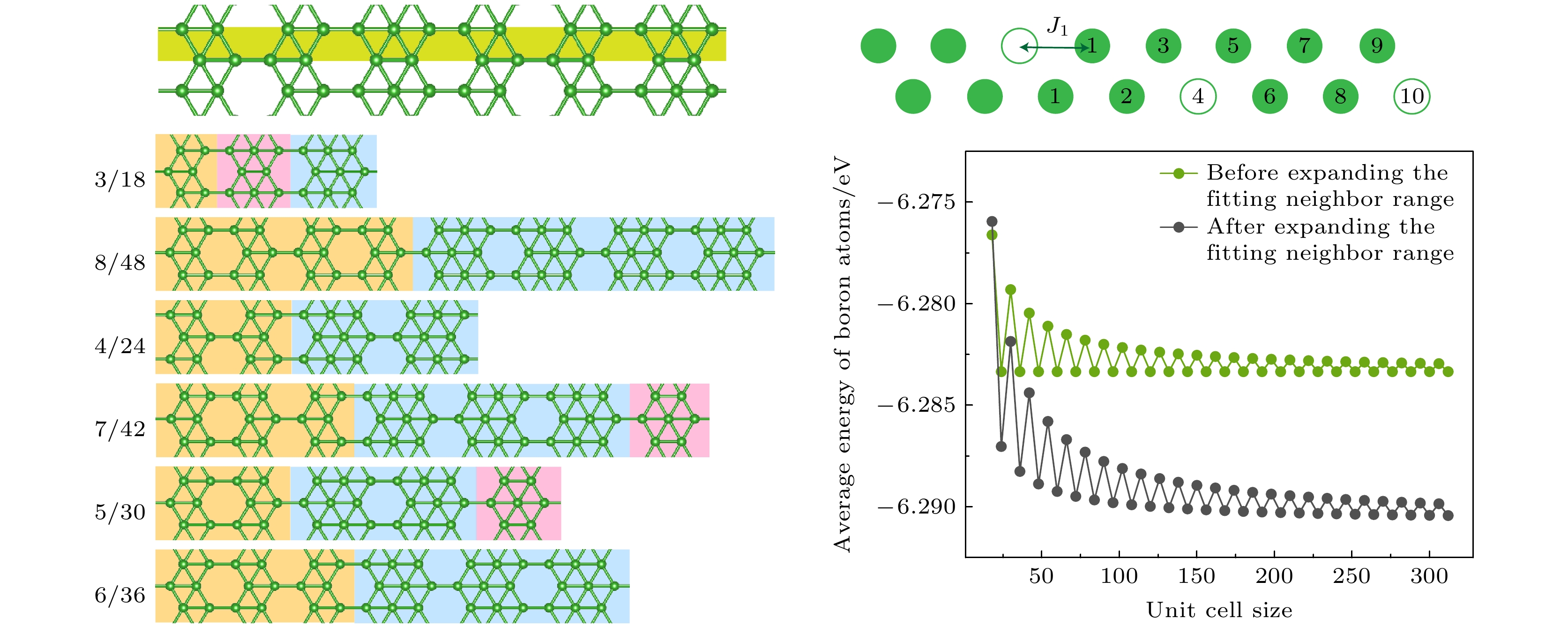
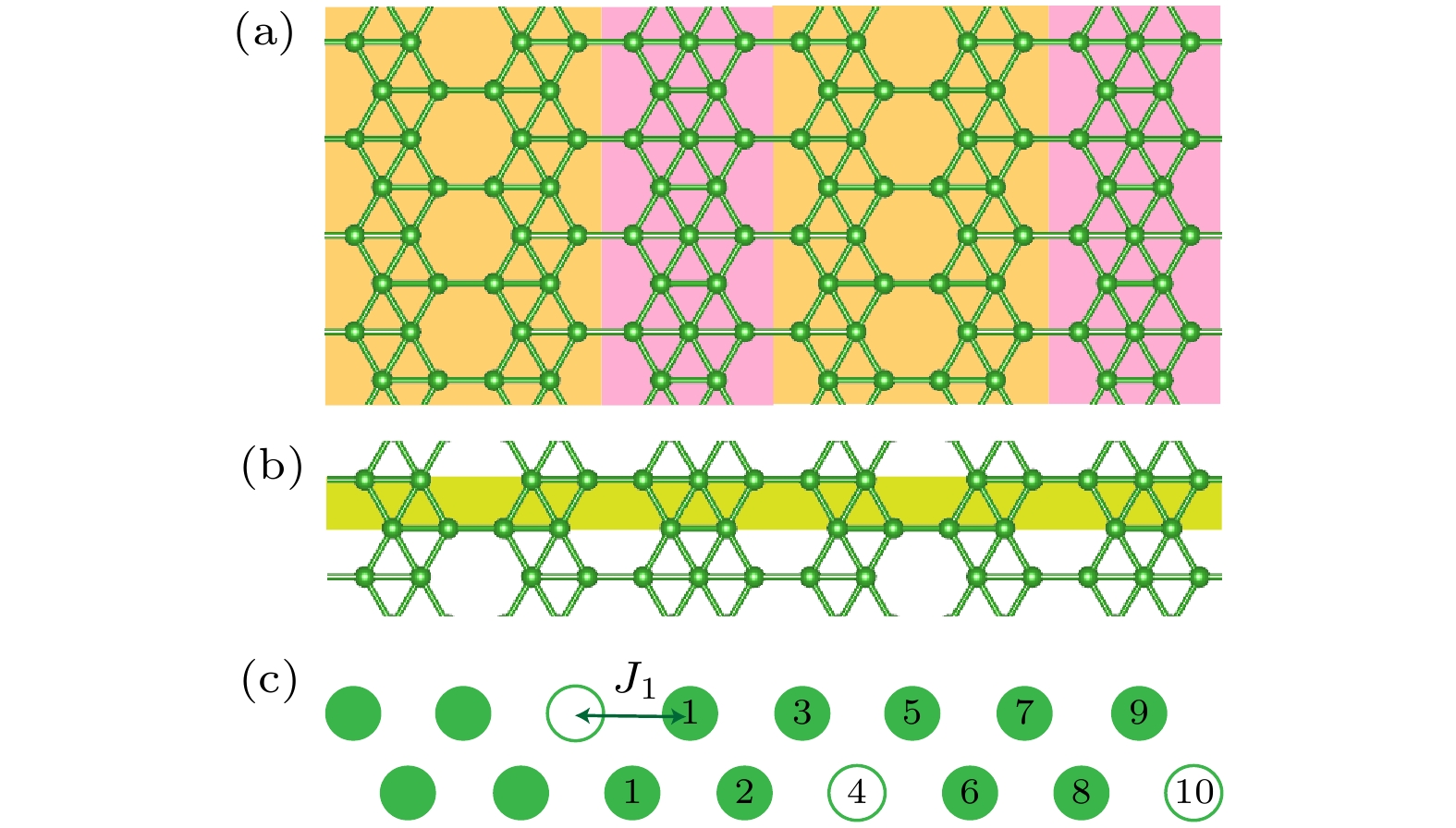
图 1 (a)在Ag(100)表面生长出的A相的理论模型结构; (b)将该结构从横向看作是一个包含点空位分布的条带硼链; (c)上述条带硼链的模型示意图, 其原胞为包含3个空位的16个原子位点的结构, 其中空点圆代表空位, 实心圆代表硼原子, 对于最左边的空位, 用数字标出其不同近邻的位置
Fig. 1. (a) Theoretical model structure of phase A grown on the Ag(100) surface; (b) a lateral view of the structure as a strip boron chain containing a distribution of point vacancies; (c) a schematic representation of the strip boron chain model, with a unit cell consisting of 16 atomic sites, including 3 vacancies. The point vacancies are denoted by open circles, while the boron atoms are represented by solid circles. For the vacancy on the far left, the diagram has been annotated with numbers to indicate its various neighboring positions.
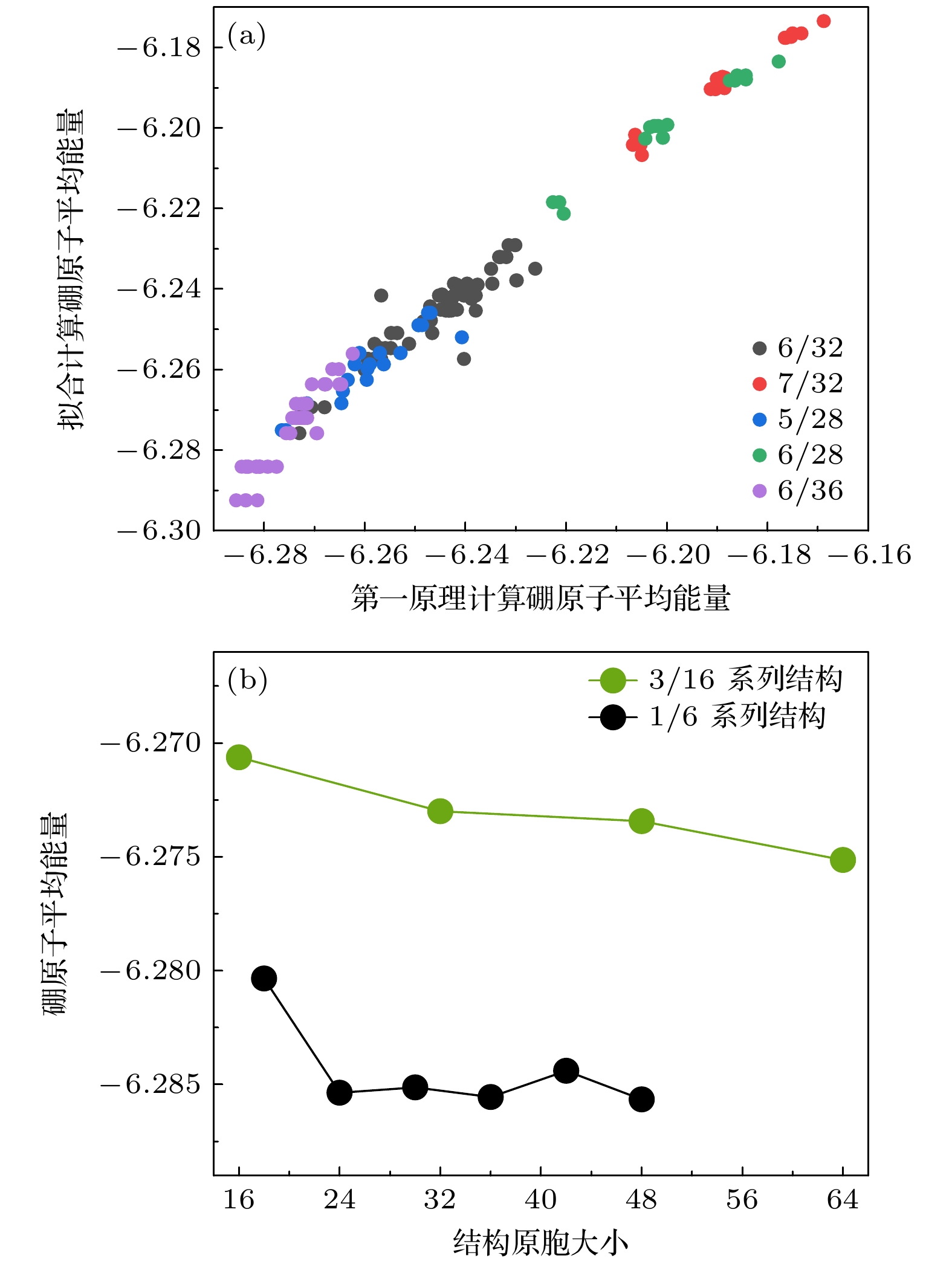
图 2 (a)参数拟合计算和第一性原理计算的相关性图像, 其中不同颜色的点代表不同空位浓度的候选结构; (b)第一性原理计算下3/16和1/6系列结构随着原胞大小变化的硼原子平均能量趋势图
Fig. 2. (a) Correlation plot between parameter fitting calculations and first-principles calculations; (b) trend graphs of average energy of boron atoms in structures of 3/16 and 1/6 under different cell sizes, as calculated by first-principles methods.
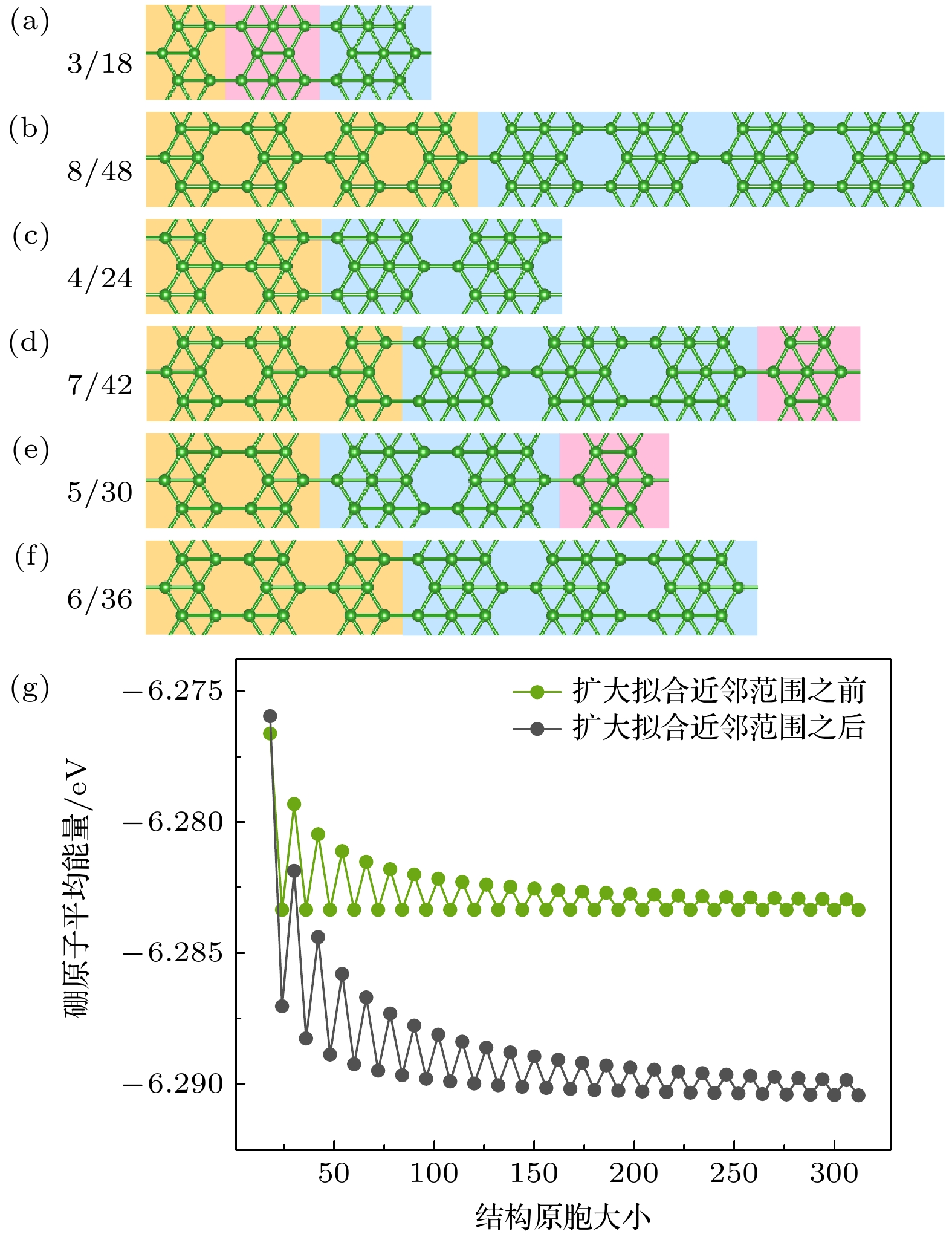
图 3 (a)—(c)分别为在第一原理计算下3/16系列结构不同原胞大小下的稳定结构, 同时也是参数拟合计算所指向的稳定结构; (d)构造原胞大小为64的3/16系列结构
Fig. 3. (a)–(c) Stable structures of the 3/16 series under different cell sizes obtained through first-principles calculations, which are also the stable structures indicated by parameter fitting calculations; (d) artificially constructed structures of 3/16 with a cell size of 64.
图 4 (a)—(f)分别为1/6系列结构不同原胞的稳定结构. 每个结构的原胞大小分别表示在每个结构图的左上角; (g) 1/6结构随着原胞大小变化的硼原子平均能变化图, 绿线代表拟合计算过程中只选取第4, 5, 6近邻结果, 黑线代表拟合计算过程近邻范围截取到第10近邻结果
Fig. 4. (a)–(f) Depict stable structures of the 1/6 series with different cell sizes. The cell size for each structure is indicated in the top left corner of each respective structure diagram. (g) Average energy variation of boron atoms in the 1/6 structure as a function of cell size. The green line represents the fitting calculation process with only the 4th, 5th, and 6th nearest neighbors considered, while the black line represents the fitting calculation process with the neighbor range truncated to the 10th nearest neighbor.
表 1 4个相同浓度结构的近邻统计数目
Table 1. Neighbor count for four structures at the same concentration.
Si ni n2 n3 n4 n5 n6 n7 n8 n9 n10 S1 0 0 2 1 0 0 0 1 2 S2 0 0 5 0 1 0 0 4 0 S3 0 0 7 1 1 0 0 6 1 S4 0 0 10 0 2 0 0 9 0 注: Si 代表空位浓度为3/16、原胞大小为16i的结构 Note: Si represents structures with a vacancy concentration of 3/16 and a cell size of 16i. 
下载: 导出CSV
表 2 不同原胞大小、浓度相等的稳定结构近邻统计数目
Table 2. Neighbor count for stable structures with equivalent concentrations at different cell sizes.
Si ni n4 n5 n6 n7 n8 n9 n10 S1 1 1 1 0 0 0 1 S2 2 0 2 0 0 1 0 S3 2 1 2 0 0 1 1 S4 3 0 3 0 0 2 0 S5 3 1 3 0 0 2 1 S6 4 0 4 0 0 3 0 S7 4 1 4 0 0 3 1 S8 5 0 5 0 0 4 0 注: Si 代表空位浓度为1/6、原胞大小为6(i+2)的结构 Note: Si represents structures with a vacancy concentration of 1/6 and a cell size of 6(i+2).
下载: 导出CSV
-
[1] Zhao L, Schwarz W E, Frenking G 2019 Nat. Rev. Chem. 3 35
Google Scholar
[2] Jhi S H, Louie S G, Cohen M L, Ihm J 2001 Phys. Rev. Lett. 86 3348
Google Scholar
[3] Hart G L, Zunger A 2001 Phys. Rev. Lett. 87 275508
Google Scholar
[4] Kaneti Y V, Benu D P, Xu X, Yuliarto B, Yamauchi Y, Golberg D 2021 Chem. Rev. 122 1000
Google Scholar
[5] Tang H, Ismail-Beigi S 2007 Phys. Rev. Lett. 99 115501
Google Scholar
[6] Yang X B, Ding Y, Ni J 2008 Phys. Rev. B 77 041402(R
Google Scholar
[7] Wu X J, Dai J, Zhao Y, Zhuo Z W, Yang J L, Zeng X C 2012 ACS Nano 6 7443
Google Scholar
[8] Mannix A J, Zhou X F, Kiraly B, Wood J D, Alducin D, Myers B D, Liu X, Fisher B L, Santiago U, Guest J R 2015 Science 350 1513
Google Scholar
[9] Zhang L Z, Yan Q B, Du S X, Su G, Gao H J 2012 J. Phys. Chem. C 116 18202
Google Scholar
[10] Liu Y, Penev E S, Yakobson B I 2013 Angew. Chem. Int. Ed. 52 3156
Google Scholar
[11] Liu H S, Gao J F, Zhao J J 2013 Sci. Rep. 3 3238
Google Scholar
[12] Zhang Z H, Yang Y, Gao G Y, Yakobson B I 2015 Angew. Chem. 54 13022
Google Scholar
[13] Feng B J, Zhang J, Zhong Q, Li W B, Li S, Li H, Cheng P, Meng S, Chen L, Wu K H 2016 Nat. Chem. 8 563
Google Scholar
[14] Zhong Q, Kong L J, Gou J, Li W B, Sheng S X, Yang S, Cheng P, Li H, Wu K H, Chen L 2017 Phys. Rev. Mater. 1 021001
Google Scholar
[15] Wang Y, Kong L, Chen C, Cheng P, Feng B, Wu K H, Chen L 2020 Adv. Mater. 32 2005128
Google Scholar
[16] Li W B, Kong L J, Chen C Y, Gou J, Sheng S X, Zhang W F, Li H, Chen L, Cheng P, Wu K H 2018 Sci. Bull. 63 282
Google Scholar
[17] Wu R, Drozdov I K, Eltinge S, Zahl P, Ismail-Beigi S, Božović I, Gozar A 2019 Nat. Nanotechnol. 14 44
Google Scholar
[18] Vinogradov N A, Lyalin A, Taketsugu T, Vinogradov A S, Preobrajenski A 2019 ACS Nano 13 14511
Google Scholar
[19] Kiraly B, Liu X, Wang L, Zhang Z, Mannix A J, Fisher B L, Yakobson B I, Hersam M C, Guisinger N P 2019 ACS Nano 13 3816
Google Scholar
[20] Xu S G, He C C, Zhao Y J, Xu H, Yang X B 2021 Phys. Rev. Mater. 5 044003
Google Scholar
[21] Floría L M, Mazo J J 1996 Adv. Phys. 45 505
Google Scholar
[22] He C C, Liao J H, Qiu S B, Zhao Y J, Yang X B 2021 Comput. Mater. Sci. 193 110386
Google Scholar
下载:
计量
- 文章访问数: 1478
- PDF下载量: 45
- 被引次数: 0
