太阳高能粒子强度与日冕物质抛射及其II型射电暴的关系

严豪; 丁留贯; 封莉; 顾斌

doi:10.7498/aps.73.20231855

摘要

本文选取了第24太阳活动周2010年1月至2014年9月期间的快速、大角宽日冕物质抛射(CME)事件, 结合不同约束条件下Richardson (2014) 太阳高能粒子(SEP)强度经验模型输出结果, 分析了CME属性、先行CME (pre-CME)、II型射电暴等观测特征对SEP强度的影响, 探讨了SEP事件的产生及其强度与这些特征的关系. 主要结论如下: 1) 快速CME前13 h内是否存在pre-CME对模型预测效果和快速CME是否产生SEP事件有明显影响, 但pre-CME的数量对模型输出结果没有明显改善. 2) 相比于无II型射电暴伴随的快速CME而言, 伴随II型射电暴的CME爆发产生SEP事件的误报占比明显更低(42%), 以此为约束条件, 可更加突显大SEP事件(如峰值≥0.01 pfu/MeV)的模型预测值与观测值的关联; 如果考虑射电增强, 则SEP事件的误报占比可进一步下降至29.4%, 模型预测效果显著提升. 3) II型射电暴的起始频率和结束频率对误报占比的影响不大, 以此作为条件约束对模型预测效果提升不明显. 4) 如考虑II型射电暴的细分类型作为模型约束条件, 伴随多波段II型射电暴的CME比单一波段事件具有更好的模型预测效果, 如m-DH-km II型射电暴事件, 具有较低的误报占比(35.4%), 准确率较高. 研究结果显示, 除了CME的速度和角宽参数外, pre-CME、II型射电暴及其增强、多波段类型等特征作为CME产生SEP事件的约束条件, SEP预测强度与观测强度具有较好的一致性, 可以获得较优的模型预测效果. 这也进一步表明了伴随有pre-CME、多波段II型射电暴及其增强的快速大角宽CME更容易产生SEP事件, 这些特征可作为SEP-rich类CME的辨别信号.

关键词:

Abstract

Based on the multiple-vantage observations of STEREO, SOHO, wind and other spacecraft, the fast and wide coronal mass ejections (CME) during the 24th solar cycle from January 2010 to September 2014 are selected in this paper. Using the outputs of Richardson’s (2014) empirical model of solar energetic particle (SEP) intensity under different conditions, the effects of its associations such as CME, pre-CME, and type II radio bursts, on SEP intensity are analyzed, and the relationship between SEP event and these characteristics is also discussed. The main conclusions are as follows. 1) The presence or absence of pre-CME within 13 h before fast CME significantly improves the model prediction effect and has a significant influence on whether fast CME produces SEP event. Compared with the events without pre-CMEs, the events with pre-CMEs have a low proportion of false alarms (FR: 47.7% vs. 70%). However, the number of pre-CMEs does not improve the model output. 2) CMEs with type-II radio bursts have significantly lower FR to generate SEP events than fast CMEs without type-II radio bursts (42% vs. 68%). And selecting type-II radio bursts as a constraint will filter out some small/weak SEP events, the relationship between model predictions and observations especially for large SEP events (e.g. I_p ≥ 0.01 pfu/MeV) will stand out. Moreover, if the type-II radio enhancement is taken into account, FR can be further reduced to 29.4%, and the proportion of hits can be further increased (HR: 48.5%), and the model prediction is significantly improved. 3) The larger the start frequency of type II radio bursts, the smaller the end frequency is, and FR decreases slightly, but at the same time, a large number of SEP events are excluded by this condition, and the results show that the constraints on the start/end frequency of type-II radio bursts do not improve the model predictions distinctly. 4) If the sub-classification of type-II radio bursts is considered as the model constraint, the CMEs associated with multi-band type-II radio bursts have better model predictions than those with single-band events. For example, m-DH-km type-II radio bursts have lower FR (35.4%) and higher HR (48%), and the accuracy of empirical model is higher. In summary, we find that in addition to the velocity and angular width of CME, the associations of pre-CME, type II radio bursts and their enhancement, and multi-band sub-classification are the favorable conditions for CME to generate SEP events. The SEP intensities obtained by the empirical model have better consistency with the observations, and better predictions can be obtained. This investigation indicates that SEP events are more likely generated by fast and wide CMEs accompanied by pre-CMEs, multi-band type II radio bursts and their enhancements, which seem to serve as discriminative signal for SEP-rich and SEP-poor CMEs.

Keywords:

作者及机构信息

1.
南京信息工程大学大气物理学院, 南京　210044

2.
无锡学院大气与遥感学院, 无锡　214105

3.
中国科学院紫金山天文台, 南京　210008

4.
南京信息工程大学物理与光电工程学院, 南京　210044

通信作者: 丁留贯, dlg@nuist.edu.cn

基金项目: 国家自然科学基金 (批准号: 42274215)、江苏省高校“青蓝工程”和江苏省“333”高层次人才培养工程资助的课题.

Authors and contacts

1.
School of Atmospheric Physics, Nanjing University of Information Science & Technology, Nanjing 210044, China

2.
College of Atmosphere and Remote Sensing, Wuxi University, Wuxi 214105, China

3.
Purple Mountain Observatory, Chinese Academy of Sciences, Nanjing 210008, China

4.
School of Physics and Optoelectronic Engineering, Nanjing University of Information Science & Technology, Nanjing 210044, China

Corresponding author: Ding Liu-Guan, dlg@nuist.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 42274215), the “Qing Lan” Program of Jiangsu Province, China, and the “333” High-Level Talent Cultivation Project of Jiangsu Province, China.

文章全文 : translate this paragraph

参考文献

[1]	王劲松, 吕建永 2010 空间天气学第1版 (北京: 气象出版社) 第16—31页 Wang J S, Lü J Y 2010 Space Weather Science (1st Ed.) (Beijing: Meteorological Press) pp16–31
[2]	Kahler S W 2001 J. Geophys. Res. 106 20947 Google Scholar
[3]	Reams D V 1999 Space. Sci. Rev. 90 413 Google Scholar
[4]	Cliver E W, Kahler S W 2004 Astrophys. J. 605 902 Google Scholar
[5]	Kahler S W 1992 Annu. Rev. Astron. Astrophys. 30 113 Google Scholar
[6]	Gopalswamy N, Yashiro S, Krucker S, Stenborg G, Howard R A 2004 J. Geophys. Res. 109 12 Google Scholar
[7]	Ding L G, Jiang Y, Zhao L, Li G 2013 Astrophys. J. 763 30 Google Scholar
[8]	Cane H V, Von Rosenvinge T T, Cohen C M S, Mewaldt R A 2003 Geophys. Res. Lett. 30 12 Google Scholar
[9]	Cane H V, Mewaldt R A, Cohen C M S, Von Rosenvinge T T 2006 J. Geophys. Res. 111 90 Google Scholar
[10]	Le G M, Zhang X F 2017 Rev. Astron. Astrophys. 17 123 Google Scholar
[11]	Le G M, Li C, Zhang X F 2017 Rev. Astron. Astrophys. 17 73 Google Scholar
[12]	Wang Y, Lyu D, Wu X H, Qin G 2022 Astrophys. J. 940 67 Google Scholar
[13]	Stewart R T, McCabe M K, Koomen M J, Hansen R T, Dulk G A 1974 Sol. Phys. 36 203 Google Scholar
[14]	Hundhausen A J, Holzer T E, Low B C 1987 J. Geophys. Res. 92 0148 Google Scholar
[15]	Vršnak B, Lulić S 2000 Sol. Phys. 196 181 Google Scholar
[16]	Vršnak B, Cliver E 2008 Sol. Phys. 253 215 Google Scholar
[17]	Kahler S W 1982 J. Geophys. Res. 87 2439 Google Scholar
[18]	Cane H V, Erickson W C, Prestage N P 2002 J. Geophys. Res. 107 1315 Google Scholar
[19]	Wild J, McCready L 1950 Aust. J. Sci. Res. Ser. A: Phys. Sci. 3 387
[20]	Cane H V, Stone R G, Fainberg J, Stewart R T, Steinberg J L, Hoang S 1981 Geophys. Res. Lett. 8 1285 Google Scholar
[21]	Prakash O, Umapathy S, Shanmugaraju A, Vršnak B 2009 Sol. Phys. 258 105 Google Scholar
[22]	Kahler S W 1996 Amer. Inst. Phys. 374 61
[23]	Gopalswamy N, Aguilar-Rodriguez E, Yashiro S, Nunes S, Kaiser M L, Howard R A 2005 J. Geophys. Res. 110 07 Google Scholar
[24]	Winter L M, Ledbetter K 2015 Astrophys. J. 809 105 Google Scholar
[25]	Kahler S W, Ling A G, Gopalswamy N 2019 Sol. Phys. 294 13 Google Scholar
[26]	朱聪, 丁留贯, 周坤论, 钱天麒 2021 70 099601 Google Scholar Zhu C, Ding L G, Zhou K L, Qian T Q 2021 Acta Phys. Sin. 70 099601 Google Scholar
[27]	Marqué C, Posner A, Klein K L 2006 Astrophys. J. 642 1222 Google Scholar
[28]	Gopalswamy N, Yashiro S, Akiyama S, Mäkelä P, Xie H, Kaiser M, Howard R, Bougeret J 2008 Ann. Geophys. 26 3033 Google Scholar
[29]	Kahler S W, Reames D V, Burkepile J T 2000 High Energy Solar Physics- Anticipating Hessi 206 468
[30]	Shen C, Li G, Kong X, Hu J, Sun X D, Ding L, Chen Y, Wang Y M, Xia L 2013 Astrophys. J. 763 2 Google Scholar
[31]	Ding L G, Li G, Dong L H, Jiang Y, Jian Y, Gu B 2014 J. Geophys. Res. 119 1463 Google Scholar
[32]	Gopalswamy N, Yashiro S, Kaiser M L, Howard R A, Bougeret J L 2001 Astrophys. J. 548 L91 Google Scholar
[33]	Ding L G, Wang Z W, Feng L, Li G, Jiang Y 2019 Res. Astron. Astrophys. 19 001 Google Scholar
[34]	周坤论, 丁留贯, 钱天麒, 朱聪, 王智伟, 封莉 2020 69 169601 Google Scholar Zhou K L, Ding L G, Qian T Q, Zhu C, Wang Z W, Feng L 2020 Acta Phys. Sin. 69 169601 Google Scholar
[35]	Posner A 2007 Space Weather 5 05001 Google Scholar
[36]	Richardson I G, Mays M L, Thompson B J 2018 Space Weather 16 1862 Google Scholar
[37]	Falconer D, Barghouty A F, Khazanov I, Moore R 2011 Space Weather 9 04003 Google Scholar
[38]	Papaioannou A, Anastasiadis A, Kouloumvakos A, Paassilta M, Vainio R, Valtonen E, Belov A V, Eroshenko E, Abunina M, Abunin A 2018 Sol. Phys. 293 1 Google Scholar
[39]	Laurenza M, Cliver E W, Hewitt J, Storini M, Ling A G, Balch C C, Kaiser M L 2009 Space Weather 7 4 Google Scholar
[40]	Balch C C 1999 Radiat. Meas. 30 231 Google Scholar
[41]	Bruno A, Richardson I G 2021 Sol. Phys. 296 36 Google Scholar
[42]	Garcia H A 2004 Space Weather 2 02002 Google Scholar
[43]	Huang X, Wang H N, Li L P 2012 Res. Astron. Astrophys. 12 313 Google Scholar
[44]	Núñez M 2011 Space Weather 9 07003 Google Scholar
[45]	Núñez M 2015 Space Weather 13 727 Google Scholar
[46]	Núñez M, Santiago P, Malandraki O 2017 Space Weather 15 861 Google Scholar
[47]	Núñez M 2018 J. Space Weather Space Clim. 8 A36 Google Scholar
[48]	Richardson L G, von Rosenvinge T T, Cane H V, Christian E R, Cohen C M S, Labrador A W, Leske R A, Mewaldt R A, Wiedenbeck M E, Stone E C 2014 Sol. Phys. 289 3059 Google Scholar
[49]	Torres J, Zhao L, Chan P K, Zhang M 2022 Space Weather 20 002797 Google Scholar
[50]	王智伟, 丁留贯, 周坤论, 乐贵明 2018 地球 61 3515 Google Scholar Wang Z W, Ding L G, Zhou K L, Le G M 2018 Chin. J. Geophys. 61 3515 Google Scholar
[51]	Hanssen A W, Kuipers W J A 1965 Koninklijk Ned. Meteor. Instit. 81 2

施引文献

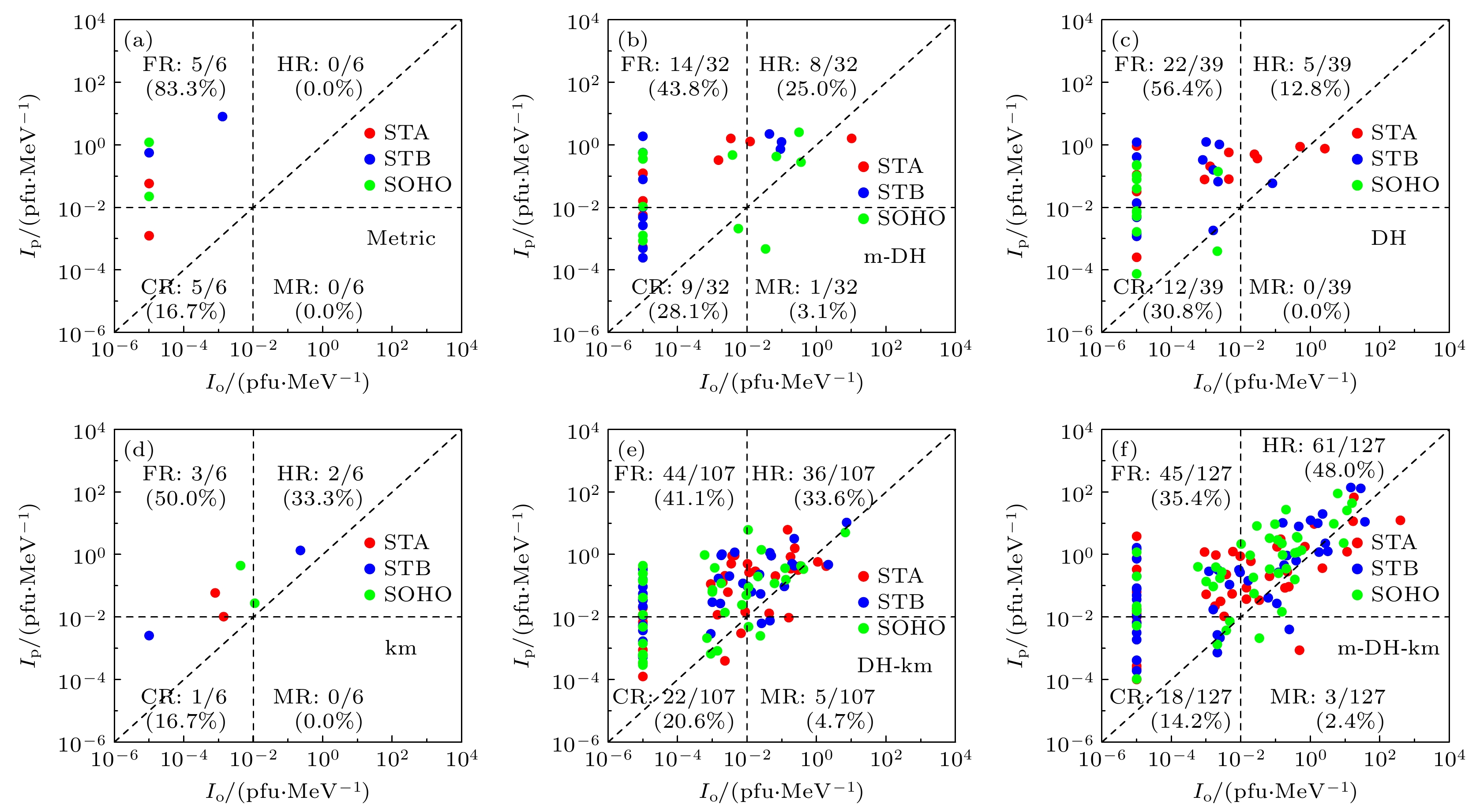
图 1 SEP强度预测值(I_p)与观测值(I_o)对比, SEP事件阈值准线将事件样本分为四类

Fig. 1. Predicted versus observed SEP peak intensities at SOHO or STEREO-A/B (STA/STB) spacecraft for the fast and wide CMEs with speed greater than 900 km/s and width greater than 60º in the study period. The quadrants defined by crosshairs set at equal predicted and observed intensity thresholds divide the events into hits, false alarms, correct rejections, and misses.

下载: 全尺寸图片幻灯片

图 2 (a)不存在pre-CME时, SEP强度预测值与观测值关系; (b)存在pre-CME时, SEP强度预测值与观测值关系; (c)样本事件数量随pre-CME事件数量的变化(黑), HR, FR, CR和MR随pre-CME事件数量的变化(蓝、红、橙、紫)

Fig. 2. Predicted versus observed SEP intensities for the fast and wide CMEs without (a) or with (b) pre-CMEs, and (c) the number of selected events (black) and percentages of HR (blue), FR (red), CR (yellow), and MR (purple) versus the number of pre-CMEs.

下载: 全尺寸图片幻灯片

图 3 不伴随II型射电暴(a)和伴随II型射电暴(b)时, SEP强度预测值与观测值关系

Fig. 3. Predicted versus observed proton intensities for the fast and wide CMEs without (a) and with (b) type II radio bursts, respectively.

下载: 全尺寸图片幻灯片

图 4 II型射电暴无射电增强(a)和II型射电暴有射电增强(b)时, SEP强度预测值与观测值关系

Fig. 4. Predicted versus observed proton intensities for the fast and wide CMEs without (a) and with (b) radio enhancements during the period of type II radio bursts.

下载: 全尺寸图片幻灯片

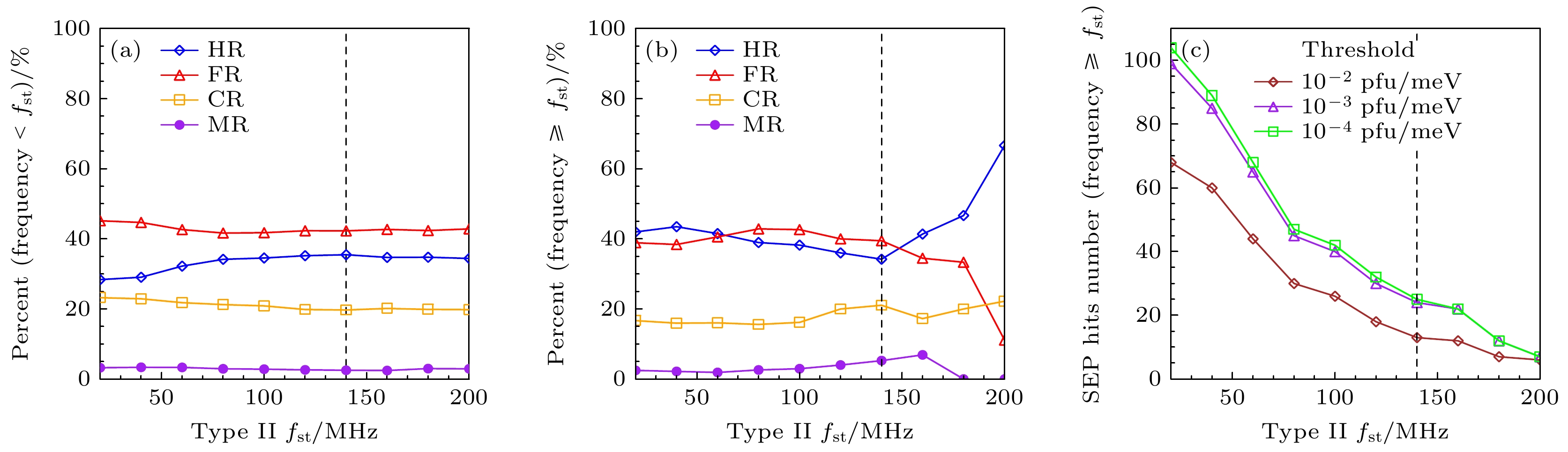
图 5 (a) 击中、误报、正确拒绝和漏报占比随II型射电暴起始频率上限阈值($ {f}_{{\mathrm{s}}{\mathrm{t}}} $)的变化; (b) HR, FR, CR, MR随起始频率下限阈值($ {f}_{{\mathrm{s}}{\mathrm{t}}} $)的变化; (c) 不同SEP事件强度阈值情况下, 击中事件数量随II型射电暴起始频率阈值条件的变化

Fig. 5. (a) Fraction of hits, false alarms, correct rejections, and misses in all predictions versus the upper limit threshold ($ {f}_{{\mathrm{s}}{\mathrm{t}}} $) of the starting frequency of type II radio bursts; (b) similar to panel (a) but for the lower limit threshold $ {(f}_{{\mathrm{s}}{\mathrm{t}}}) $; (c) number of hit events among all the predictions in different thresholds of SEP intensity using the lower limit starting frequency threshold for type II radio bursts.

下载: 全尺寸图片幻灯片

图 6 (a) 击中、误报、正确拒绝和漏报占比随II型射电暴结束频率上限阈值($ {f}_{{\mathrm{e}}{\mathrm{d}}} $)的变化; (b) HR, FR, CR, MR随下限阈值$ ({f}_{{\mathrm{e}}{\mathrm{d}}} $)的变化; (c) 不同SEP事件强度阈值情况下, 击中事件数量随II型射电暴结束频率阈值条件的变化

Fig. 6. (a) Fraction of hits, false alarms, correct rejections, and misses in all predictions versus the upper limit threshold ($ {f}_{{\mathrm{e}}{\mathrm{d}}} $) of the ending frequency of type II radio bursts; (b) similar to panel (a) but for the lower limit threshold $ {(f}_{{\mathrm{e}}{\mathrm{d}}}) $; (c) number of hit events among all the predictions in different thresholds of SEP intensity using the lower limit ending frequency threshold for type II radio bursts.

下载: 全尺寸图片幻灯片

图 7 不同类型的II型射电暴对模型输出结果的影响　(a) metric; (b) m-DH; (c) DH; (d) km; (e) DH-km; (f) m-DH-km

Fig. 7. Predictions versus observations of SEP intensities for different classes of type II radio bursts: (a) metric; (b) m-DH; (c) DH; (d) km; (e) DH-km; (f) m-DH-km.

下载: 全尺寸图片幻灯片

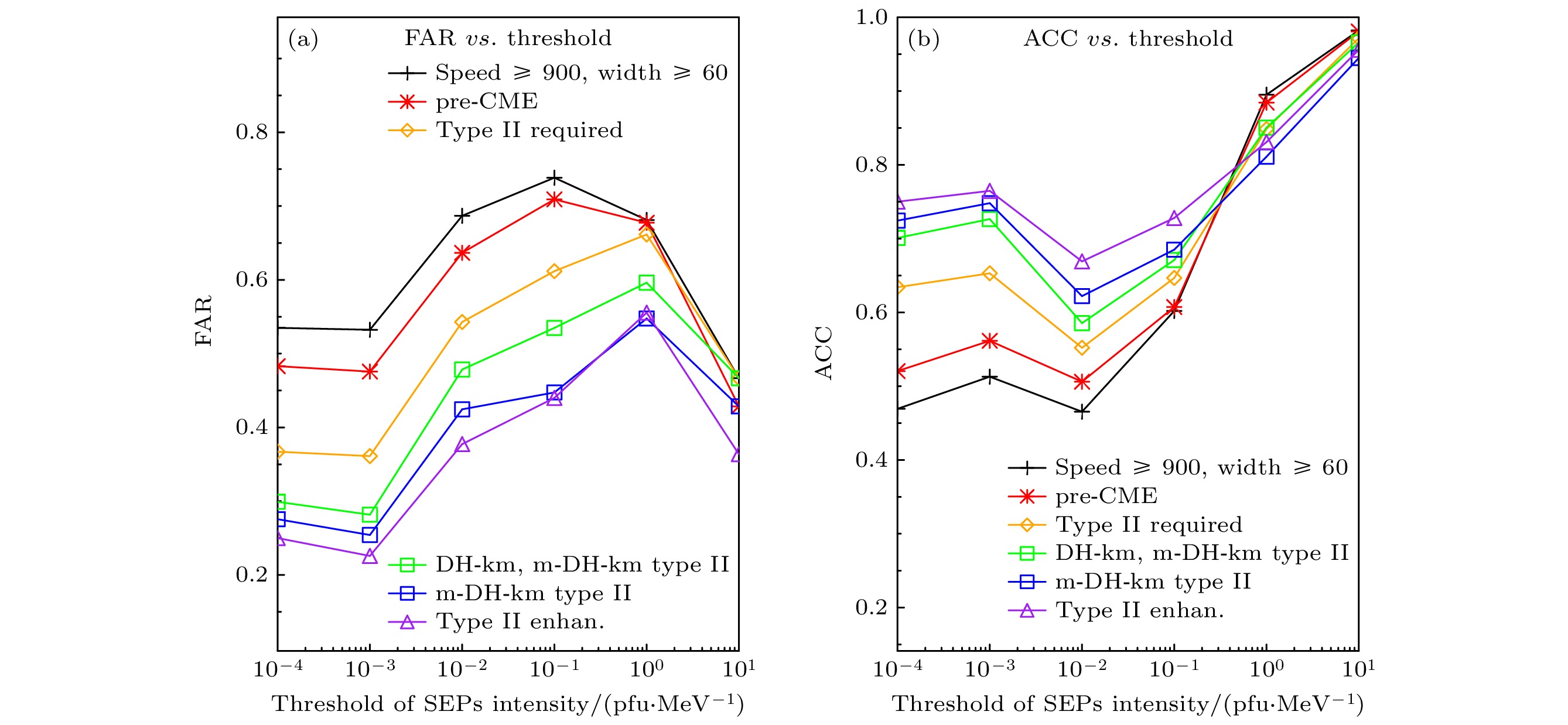
图 8 (a)误报率FAR和(b)准确率ACC随SEP事件峰值强度阈值设定值的变化. 黑色“+”表示CME速度≥900 km/s且角宽≥60°; 红色“*”表示存在pre-CME; 橙色菱形表示存在II型射电暴; 绿色正方形表示伴随DH-km或m-DH-km波段的II型射电暴, 即IP II型射电暴; 蓝色正方形表示伴随m-DH-km波段的II型射电暴; 紫色三角形表示伴随的II型射电暴存在射电增强

Fig. 8. (a) False alarm ratio versus threshold of SEP peak intensity (0 is a perfect score), for different CME selections based on their associations. The curves are for CME with speed ≥ 900 km/s and angular width ≥ 60° (black crosses), pre-CME required (red asterisks), type II radio bursts required (orange diamonds), IP type II radio bursts (DH-km or m-DH-km) required (green squares), m-DH-km type II radio bursts required (blue squares); radio enhancement in type II radio bursts (purple triangles). (b) The accuracy (fraction of correct predictions) versus threshold (perfect score = 1).

下载: 全尺寸图片幻灯片

图 9 (a)偏差BIAS和(b)命中率POD随SEP强度阈值变化

Fig. 9. (a) Frequency bias (BIAS) and (b) probability of detection (POD) versus threshold of solar energetic particle peak intensity (Bias: perfect score = 1, POD: perfect score = 1).

下载: 全尺寸图片幻灯片

图 10 (a)报空率POFD和(b) HK评分随SEP峰值强度阈值变化

Fig. 10. (a) Probability of false detection (POFD) and (b) Hanssen-Kuipers Discriminant (HK) versus threshold of solar energetic particle peak intensity (POFD: perfect score = 0, HK: perfect score = 1).

下载: 全尺寸图片幻灯片

表 1 不同SEP事件强度阈值情况下有/无II型射电暴伴随的SEP事件误报对比

Table 1. False alarms fraction of SEP predictions for CMEs with/without type II radio bursts at different SEP intensity thresholds.

强度阈值/ (pfu⋅MeV^–1)	无II型射电暴(188)	有II型射电暴(317)
$ {10}^{-2} $	68.1%	42.0%
$ {10}^{-3} $	71.8%	32.8%
$ {10}^{-4} $	80.9%	36.6%

下载: 导出CSV

表 2 不同类型II型射电暴条件下的模型输出结果

Table 2. Predicted results of SEPs associated with different classes of type II radio bursts.

II型射电暴类型	事件数量	数量占比/%	误报占比/%	击中占比/%
metric	6	1.9	83.3	0
DH	39	12.3	56.4	12.8
km	6	1.9	50	33.3
m-DH	32	10.1	43.8	25.0
DH-km	107	33.8	41.1	33.6
m-DH-km	127	40.1	35.4	48.0

下载: 导出CSV

表 3 当SEP阈值强度选为0.01 pfu/MeV时的模型输出结果和评价指标

Table 3. Example of skill scores for SEP intensity threshold = 0.01 pfu/MeV.

条件	total	Hits	FA	Cr	Misses	FAR	POD	BIAS	POFD	HK	ACC
完美得分						0	1	1	0	1	1
CME速度≥900 km/s, 角宽≥60°(对照组)	505	119	261	116	9	0.69	0.93	2.97	0.69	0.24	0.47
无pre-CME	90	6	63	19	2	0.91	0.75	8.63	0.77	-0.02	0.28
有pre-CME	415	113	198	97	7	0.64	0.94	2.59	0.67	0.27	0.51
无II型射电暴	188	7	128	53	0	0.95	1.00	19.29	0.71	0.29	0.32
有II型射电暴	317	112	133	63	9	0.54	0.93	2.02	0.68	0.25	0.55
无射电增强	181	46	93	38	4	0.67	0.92	2.78	0.71	0.21	0.46
有射电增强	136	66	40	25	5	0.38	0.93	1.49	0.62	0.31	0.67
$ {f}_{{\mathrm{s}}{\mathrm{t}}} $<140 MHz	279	99	118	55	7	0.54	0.93	2.05	0.68	0.25	0.55
$ {f}_{{\mathrm{s}}{\mathrm{t}}} $≥140 MHz	38	13	15	8	2	0.54	0.87	1.87	0.65	0.21	0.55
$ {f}_{{\mathrm{e}}{\mathrm{d}}} $ < 0.1 MHz	45	22	17	4	2	0.44	0.92	1.63	0.81	0.11	0.58
$ {f}_{{\mathrm{e}}{\mathrm{d}}} $ ≥ 0.1 MHz	272	90	116	59	7	0.56	0.93	2.08	0.66	0.27	0.55
m-DH-km II型射电暴	127	61	45	18	3	0.42	0.95	1.66	0.71	0.24	0.62
DH-km II型射电暴	107	36	44	22	5	0.55	0.88	1.95	0.66	0.22	0.54
m-DH-km + DH-km (行星际II型射电暴)	234	97	89	40	8	0.48	0.92	1.77	0.69	0.23	0.59

下载: 导出CSV

map

[1]	王劲松, 吕建永 2010 空间天气学第1版 (北京: 气象出版社) 第16—31页 Wang J S, Lü J Y 2010 Space Weather Science (1st Ed.) (Beijing: Meteorological Press) pp16–31
[2]	Kahler S W 2001 J. Geophys. Res. 106 20947 Google Scholar
[3]	Reams D V 1999 Space. Sci. Rev. 90 413 Google Scholar
[4]	Cliver E W, Kahler S W 2004 Astrophys. J. 605 902 Google Scholar
[5]	Kahler S W 1992 Annu. Rev. Astron. Astrophys. 30 113 Google Scholar
[6]	Gopalswamy N, Yashiro S, Krucker S, Stenborg G, Howard R A 2004 J. Geophys. Res. 109 12 Google Scholar
[7]	Ding L G, Jiang Y, Zhao L, Li G 2013 Astrophys. J. 763 30 Google Scholar
[8]	Cane H V, Von Rosenvinge T T, Cohen C M S, Mewaldt R A 2003 Geophys. Res. Lett. 30 12 Google Scholar
[9]	Cane H V, Mewaldt R A, Cohen C M S, Von Rosenvinge T T 2006 J. Geophys. Res. 111 90 Google Scholar
[10]	Le G M, Zhang X F 2017 Rev. Astron. Astrophys. 17 123 Google Scholar
[11]	Le G M, Li C, Zhang X F 2017 Rev. Astron. Astrophys. 17 73 Google Scholar
[12]	Wang Y, Lyu D, Wu X H, Qin G 2022 Astrophys. J. 940 67 Google Scholar
[13]	Stewart R T, McCabe M K, Koomen M J, Hansen R T, Dulk G A 1974 Sol. Phys. 36 203 Google Scholar
[14]	Hundhausen A J, Holzer T E, Low B C 1987 J. Geophys. Res. 92 0148 Google Scholar
[15]	Vršnak B, Lulić S 2000 Sol. Phys. 196 181 Google Scholar
[16]	Vršnak B, Cliver E 2008 Sol. Phys. 253 215 Google Scholar
[17]	Kahler S W 1982 J. Geophys. Res. 87 2439 Google Scholar
[18]	Cane H V, Erickson W C, Prestage N P 2002 J. Geophys. Res. 107 1315 Google Scholar
[19]	Wild J, McCready L 1950 Aust. J. Sci. Res. Ser. A: Phys. Sci. 3 387
[20]	Cane H V, Stone R G, Fainberg J, Stewart R T, Steinberg J L, Hoang S 1981 Geophys. Res. Lett. 8 1285 Google Scholar
[21]	Prakash O, Umapathy S, Shanmugaraju A, Vršnak B 2009 Sol. Phys. 258 105 Google Scholar
[22]	Kahler S W 1996 Amer. Inst. Phys. 374 61
[23]	Gopalswamy N, Aguilar-Rodriguez E, Yashiro S, Nunes S, Kaiser M L, Howard R A 2005 J. Geophys. Res. 110 07 Google Scholar
[24]	Winter L M, Ledbetter K 2015 Astrophys. J. 809 105 Google Scholar
[25]	Kahler S W, Ling A G, Gopalswamy N 2019 Sol. Phys. 294 13 Google Scholar
[26]	朱聪, 丁留贯, 周坤论, 钱天麒 2021 70 099601 Google Scholar Zhu C, Ding L G, Zhou K L, Qian T Q 2021 Acta Phys. Sin. 70 099601 Google Scholar
[27]	Marqué C, Posner A, Klein K L 2006 Astrophys. J. 642 1222 Google Scholar
[28]	Gopalswamy N, Yashiro S, Akiyama S, Mäkelä P, Xie H, Kaiser M, Howard R, Bougeret J 2008 Ann. Geophys. 26 3033 Google Scholar
[29]	Kahler S W, Reames D V, Burkepile J T 2000 High Energy Solar Physics- Anticipating Hessi 206 468
[30]	Shen C, Li G, Kong X, Hu J, Sun X D, Ding L, Chen Y, Wang Y M, Xia L 2013 Astrophys. J. 763 2 Google Scholar
[31]	Ding L G, Li G, Dong L H, Jiang Y, Jian Y, Gu B 2014 J. Geophys. Res. 119 1463 Google Scholar
[32]	Gopalswamy N, Yashiro S, Kaiser M L, Howard R A, Bougeret J L 2001 Astrophys. J. 548 L91 Google Scholar
[33]	Ding L G, Wang Z W, Feng L, Li G, Jiang Y 2019 Res. Astron. Astrophys. 19 001 Google Scholar
[34]	周坤论, 丁留贯, 钱天麒, 朱聪, 王智伟, 封莉 2020 69 169601 Google Scholar Zhou K L, Ding L G, Qian T Q, Zhu C, Wang Z W, Feng L 2020 Acta Phys. Sin. 69 169601 Google Scholar
[35]	Posner A 2007 Space Weather 5 05001 Google Scholar
[36]	Richardson I G, Mays M L, Thompson B J 2018 Space Weather 16 1862 Google Scholar
[37]	Falconer D, Barghouty A F, Khazanov I, Moore R 2011 Space Weather 9 04003 Google Scholar
[38]	Papaioannou A, Anastasiadis A, Kouloumvakos A, Paassilta M, Vainio R, Valtonen E, Belov A V, Eroshenko E, Abunina M, Abunin A 2018 Sol. Phys. 293 1 Google Scholar
[39]	Laurenza M, Cliver E W, Hewitt J, Storini M, Ling A G, Balch C C, Kaiser M L 2009 Space Weather 7 4 Google Scholar
[40]	Balch C C 1999 Radiat. Meas. 30 231 Google Scholar
[41]	Bruno A, Richardson I G 2021 Sol. Phys. 296 36 Google Scholar
[42]	Garcia H A 2004 Space Weather 2 02002 Google Scholar
[43]	Huang X, Wang H N, Li L P 2012 Res. Astron. Astrophys. 12 313 Google Scholar
[44]	Núñez M 2011 Space Weather 9 07003 Google Scholar
[45]	Núñez M 2015 Space Weather 13 727 Google Scholar
[46]	Núñez M, Santiago P, Malandraki O 2017 Space Weather 15 861 Google Scholar
[47]	Núñez M 2018 J. Space Weather Space Clim. 8 A36 Google Scholar
[48]	Richardson L G, von Rosenvinge T T, Cane H V, Christian E R, Cohen C M S, Labrador A W, Leske R A, Mewaldt R A, Wiedenbeck M E, Stone E C 2014 Sol. Phys. 289 3059 Google Scholar
[49]	Torres J, Zhao L, Chan P K, Zhang M 2022 Space Weather 20 002797 Google Scholar
[50]	王智伟, 丁留贯, 周坤论, 乐贵明 2018 地球 61 3515 Google Scholar Wang Z W, Ding L G, Zhou K L, Le G M 2018 Chin. J. Geophys. 61 3515 Google Scholar
[51]	Hanssen A W, Kuipers W J A 1965 Koninklijk Ned. Meteor. Instit. 81 2

[1]	邢阳光, 彭吉龙, 段紫雯, 闫雷, 李林, 刘越. 太阳极紫外He II 30.4 nm谱线层析成像及其光谱数据反演. , 2022, 71(15): 159501. doi: 10.7498/aps.71.20220084
[2]	朱聪, 丁留贯, 周坤论, 钱天麒. II型射电暴分类及其与太阳高能粒子事件的关系. , 2021, 70(9): 099601. doi: 10.7498/aps.70.20201800
[3]	周坤论, 丁留贯, 钱天麒, 朱聪, 王智伟, 封莉. II型射电暴射电增强与太阳高能粒子事件关系的统计. , 2020, 69(16): 169601. doi: 10.7498/aps.69.20200041
[4]	霍志胜, 蒲红斌, 李维勤. 高能透射电子束照射聚合物薄膜的带电效应. , 2019, 68(23): 230201. doi: 10.7498/aps.68.20191112
[5]	周坤论, 丁留贯, 王智伟, 封莉. 基于射电观测的日冕物质抛射驱动激波的统计特征研究. , 2019, 68(13): 139601. doi: 10.7498/aps.68.20190223
[6]	倪素兰, 顾斌, 韩智伊. 行星际日冕物质抛射引起福布斯下降的一维随机微分模拟. , 2017, 66(13): 139601. doi: 10.7498/aps.66.139601
[7]	胡帅, 高太长, 李浩, 程天际, 刘磊, 黄威, 江诗阳. 低太阳高度角条件下的天空偏振模式模拟及大气折射影响研究. , 2016, 65(1): 014203. doi: 10.7498/aps.65.014203
[8]	周双, 冯勇, 吴文渊. 太阳高纬和低纬活动现象的混沌与分形特征. , 2015, 64(24): 249601. doi: 10.7498/aps.64.249601
[9]	陈海军, 张耀文. 空间调制作用下Bessel型光晶格中物质波孤立子的稳定性. , 2014, 63(22): 220303. doi: 10.7498/aps.63.220303
[10]	陆文, 严卫, 艾未华, 施健康. 星载极化相关型全极化微波辐射计天线交叉极化校正技术 (II) : 校正试验. , 2013, 62(7): 078403. doi: 10.7498/aps.62.078403
[11]	郝大鹏, 唐刚, 夏辉, 韩奎, 寻之朋. 遮蔽效应对抛射沉积模型标度性质的影响. , 2012, 61(2): 028102. doi: 10.7498/aps.61.028102
[12]	欧阳建明, 马燕云, 邵福球, 邹德滨. 高能电子碰撞电离对高空核爆炸辐射电离的影响. , 2012, 61(21): 212802. doi: 10.7498/aps.61.212802
[13]	郝大鹏, 唐刚, 夏辉, 韩奎, 寻之朋. 含遮蔽抛射沉积模型的有限尺寸效应. , 2011, 60(3): 038102. doi: 10.7498/aps.60.038102
[14]	杨天丽, 杨朝文, 迮仁德, 熊宗华, 郝樊华. 高能α粒子轰击Yb箔制备178Hfm2核素的初步研究. , 2010, 59(12): 8465-8470. doi: 10.7498/aps.59.8465
[15]	肖中银, 王廷云, 罗文芸, 王子华. 高能粒子辐照二氧化硅玻璃E′色心形成机理研究. , 2008, 57(4): 2273-2277. doi: 10.7498/aps.57.2273
[16]	王晶, 冯学尚. 日冕物质抛射引起地磁扰动的分类预报. , 2007, 56(4): 2466-2474. doi: 10.7498/aps.56.2466
[17]	陈雁萍, R. J. HASTIE, 柯孚久, 蔡诗东, 陈骝. 高能俘获粒子对内扭曲模的稳定效应. , 1988, 37(4): 546-556. doi: 10.7498/aps.37.546
[18]	罗辽复, 陆埮. 高能正负电子对的湮没与超窄共振ψ粒子的作用. , 1975, 24(2): 145-150. doi: 10.7498/aps.24.145
[19]	李正武. 磁镜系统内高能粒子的注入和积聚. , 1962, 18(11): 586-593. doi: 10.7498/aps.18.586
[20]	王璈, 李鹤年, 简而智, 萧健. 高能带电粒子直接产生电子对. , 1961, 17(6): 263-272. doi: 10.7498/aps.17.263

计量

文章访问数: 1599
PDF下载量: 43
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板