-
由区域选择性生长方法(即分子在预图案表面的自组装技术)制备的有机微纳米图案有望在光电和全彩显示方面发挥巨大作用. 而制备多色图案薄膜的有机器件依赖于两种及多种有机分子的成核分配, 特别是混合沉积方法的应用有效提高了多色薄膜成核的效率. 本文利用动力学蒙特卡罗方法研究了两种分子间的结合能强弱对混合沉积两种分子以实现相分离式生长的影响. 结果表明: 当分子间结合能较弱时, 两种分子表现出完全不同的相分离生长行为, 绝大部分的非平面和平面分子分别沉积在电极顶部和侧面; 当分子间结合能较强时, 电极顶部及侧面都出现了两类分子的掺杂生长, 导致了分子相分离生长的失效. 研究证明了分子间的结合能会影响多种有机分子选区生长分离的效果, 因此混合沉积两种有机分子时, 通过适当调整分子间的结合能, 在电极顶部和侧面可分别获得较纯结晶的单色薄膜, 从而促进了多色有机微纳米图案在微显示等领域的进一步应用.The selective area growth approach (namely the self-assembly of molecules on pre-patterned surfaces) that takes into account the properties of organic molecular materials and traditional lithography techniques, is expected to play a significant role in manufacturing organic micro-nano patterns for photoelectric and full-color display. The manufacture of organic devices with tunable multicolor patterned films depends on the control of nucleation distribution of two or more organic molecules by using a selective area growth approach, particularly through the application of mixed deposition growth that can enhance the nucleation efficiency of multicolor thin films. However, till now the issue of mixed deposition growth of two kinds of organic molecules has been rarely reported, owing to the complexity in experimental operation. In this work, the selective area growth of mixed deposition of two kinds of molecules is studied by molecular kinetic Monte Carlo approach in order to find the experimental conditions for separating two kinds of molecular growth. In the simulation, the interaction energy between the two molecules is adjusted and controlled to study its influence on the separately selective area growth of the two molecules. The results show that when the intermolecular interaction energy is weak, the planar molecules and the non-planar molecules exhibit completely different growth behaviors. The most of non-planar molecules gather at the top of the electrode in an island mode, while planar molecules mainly accumulate in a layer-by-layer mode on the sides of the electrode. On the contrary, when the intermolecular interaction energy is strong, the number of non-planar particles on the tops decreases and a large number of planar particles appear. Moreover, on the sides of the electrode, the doping nucleation of planar molecules and non-planar molecules also exists, resulting in the failure of molecular phase separation growth. It proves that the intermolecular interaction energy can affect separately area-selective growth of various organic molecules. Therefore, when several different kinds of molecules are mixed and deposited, relatively pure crystalline monochromatic films can be obtained at the top and on the sides of the electrode, respectively, by appropriately adjusting the intermolecular interaction energy, which can further facilitate the application of multi-color organic micro-nano pattern in display and other fields.
-
Keywords:
- area selective growth /
- kinetic Monte Carlo /
- organic molecules /
- phase separation
[1] Shaw J M, Seidler P F 2001 IBM J. Res. Dev. 45 3
Google Scholar
[2] Kippelen B, Brédas J L 2009 Energy Enviro. Sci. 2 251
Google Scholar
[3] Baek S, Kim K, Sung Y, Jung P, Ju S, Kim W, Kim S J, Hong S H, Lee H 2020 Nanotechnology 31 125301
Google Scholar
[4] Tian P F, Bulovic V, Burrows P E, Gu G, Forrest S R, Zhou T X 1999 J. Vac. Sci. Technol. A 17 2975
Google Scholar
[5] Saba M H, Mukherjee S, Dutta S, Mallisetty P K, Murmu N C 2021 Mater. Today: Proc. 46 1749
Google Scholar
[6] Spiegel I A, Sammons P, Barton K 2020 IEEE Trans. Control Syst. Technol. 28 2322
Google Scholar
[7] Wang W C, Chi L F 2012 Acc. Chem. Res. 45 1646
Google Scholar
[8] Bardotti L, Prevel B, Jensen P, Treilleux M, Mélinon P, Perez A, Mailly D 2002 Appl. Surf. Sci. 191 205
Google Scholar
[9] Wang W C, Zhong D Y, Zhu J, Kalischewski F, Dou R F, Wedeking K, Chi L F 2007 Phys. Rev. Lett. 98 225504
Google Scholar
[10] Speth R L, Lauga E 2009 New J. Phys. 11 075024
Google Scholar
[11] Hopp S F, Heuer A 2010 J. Chem. Phys. 133 204101
Google Scholar
[12] Lied F, Mues T, Wang W C, Chi L F, Heuer A 2012 J. Chem. Phys. 136 024704
Google Scholar
[13] Zhang H, Liu G, Wang W C, Chi L F, Yuan S L 2014 RSC Adv. 4 25005
Google Scholar
[14] Kotelyanskii M, Theodorou D N 2004 Simulation Methods for Polymers (Boca Raton: CRC Press
[15] Neurock M, Hansen E W 1998 Comput. Chem. Eng. 22 S1045
Google Scholar
[16] Liu G, Zhang H, Liu G K, Yuan S L 2016 Colloids Surf. A Physicochem. Eng. Asp. 494 186
Google Scholar
[17] Liu G, Zhang H, Liu G K, Yuan S L, Zhu Q Z 2016 Colloids Surf. A Physicochem. Eng. Asp. 509 401
Google Scholar
[18] Blel S, Hamouda A B H 2019 Results Phys. 12 1475
Google Scholar
[19] Jiang Y, Shi L, Chen N B, Hu L G, Wang W C, Nie Q M, Yan B 2023 Results Phys. 44 106145
Google Scholar
[20] Wang W C, Du C, Zhong D Y, Hirtz M, Wang Y, Lu N, Wu L X, Ebeling D, Li L Q, Fuchs H, Chi L F 2009 Adv. Mater. 21 4721
Google Scholar
[21] Kalischewski F, Heuer A 2009 Phys. Rev. B 80 155421
Google Scholar
[22] Kalischewski F, Zhu J, Heuer A 2008 Phys. Rev. B 78 155401
Google Scholar
[23] Klawtanong M, Srinitiwarawong C, Chatraphorn P 2018 Thin Solid Films 645 431
Google Scholar
[24] Huitema H E A, van der Eerden J P 1999 J. Chem. Phys. 110 3267
Google Scholar
[25] Larsson M I 2001 Phys. Rev. B 64 115428
Google Scholar
[26] Michely T, Krug J 2004 Islands, Mounds and Atoms (Vol. 42) (Berlin: Springer
[27] Liu G, Zhang H, Wang W, Yuan S L 2015 Chem. Phys. Lett. 628 54
Google Scholar
-
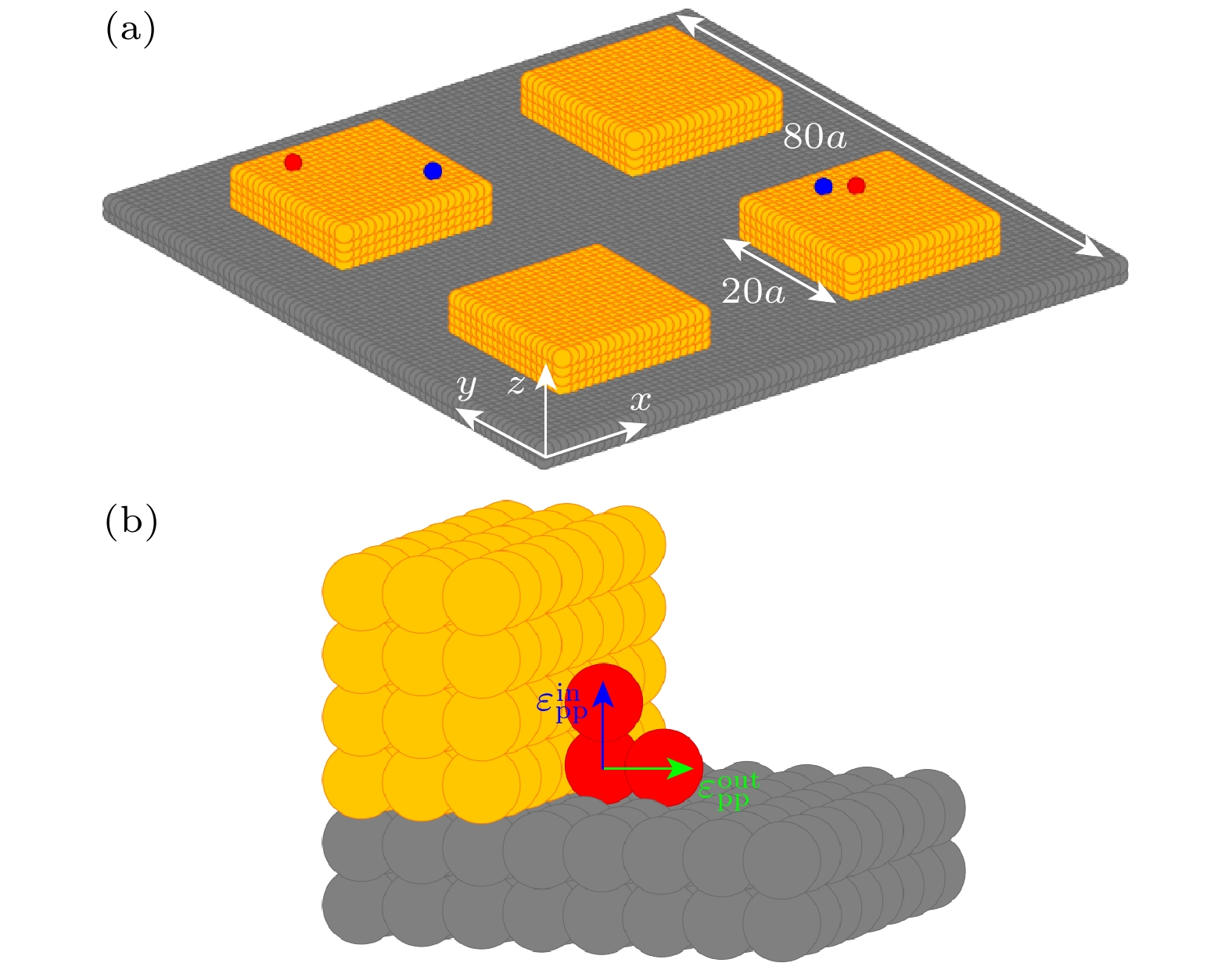
图 1 (a)模拟系统结构图, 其中大的灰色和小的黄色方块分别代表二氧化硅基底和金电极, 沉积的非平面(平面)粒子用蓝色(红色)的球表示, 衬底的尺寸为80a×80a×2a, 方形电极(20a×20a×4a)以40a的周期布置在基板上, a是晶格常数, 设为1; (b)平面分子的各向异性分子间相互作用的示意图
Fig. 1. (a) Set-up of the simulation system. The large gray and small yellow squares represent the SiO2 substrate and the gold electrode, respectively. The deposited non-planar (planar) particles are represented by blue (red) balls. The size of the substrate is 80a×80a×2a. Square electrodes (20a×20a×4a) are arranged on the substrate with a 40a period. Here a is the lattice constant and set to 1. (b) Schematic diagram of anisotropic intermolecular interactions of planar molecules.
图 2 当非平面分子(蓝色)和平面分子(红色)垂直面间(沿着面内方向)结合能为0.4kBT (0.2kBT )时, 预图案表面沉积粒子形貌的截面快照随粒子数的演化 (a) 5000; (b) 15000; (c) 30000; (d) 50000
Fig. 2. Evolution of the section snapshots of the morphology after (a) 5000, (b) 15000, (c) 30000 and (d) 50000 particles deposited on the surface of the pre-pattern. Here the out-plane (in-plane) interaction energy between the molecules of non-planar (blue) and planar (red) is 0.4kBT (0.2kBT ).
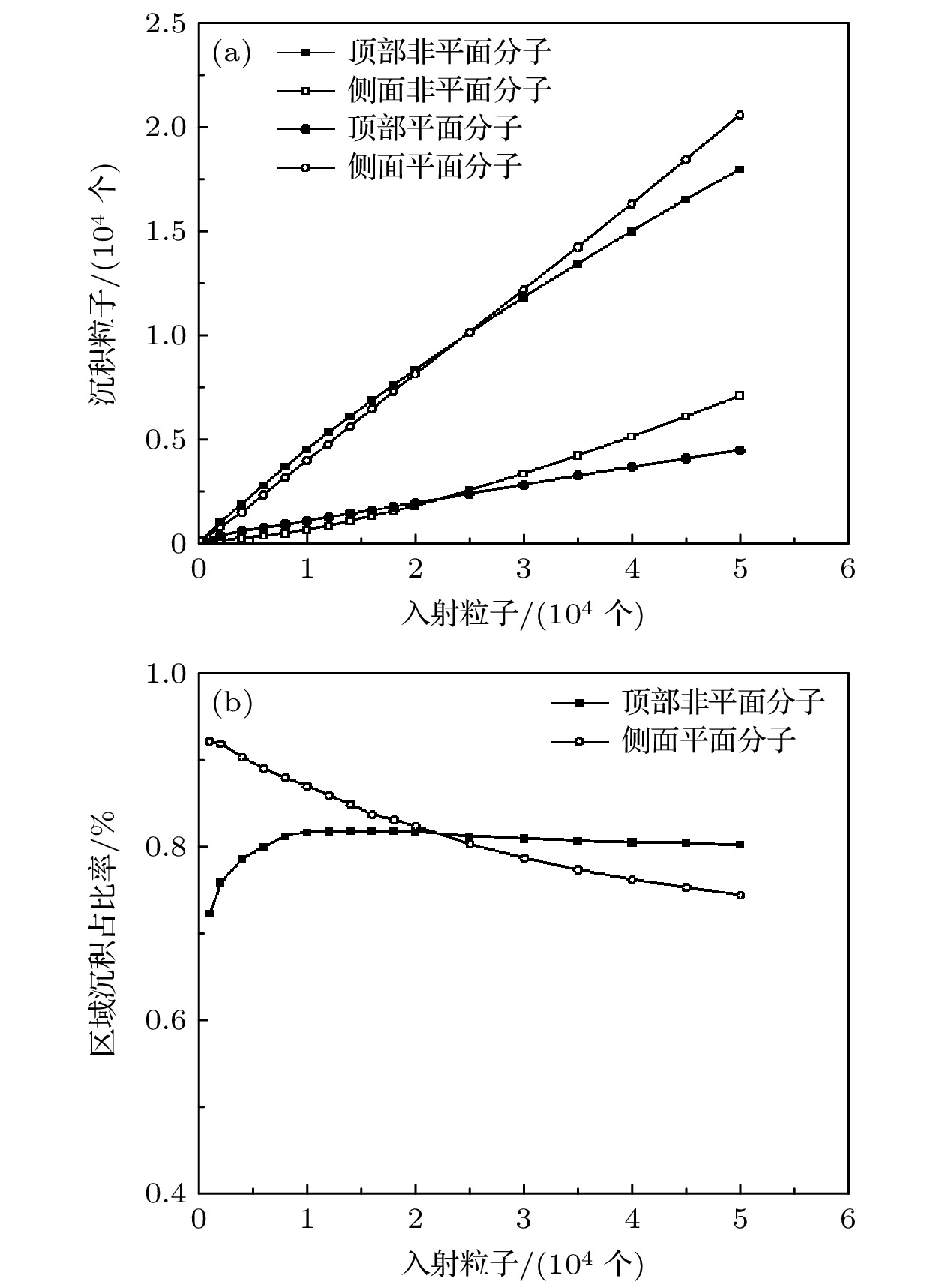
图 3 当非平面分子和平面分子垂直面间(沿着面内方向)结合能为0.4kBT (0.2kBT )时 (a)非平面分子(平面分子)在电极顶部、侧面的沉积粒子数随入射总粒子数的变化; (b)沉积在电极顶部(侧面)非平面分子(平面分子)的粒子数占顶部(侧面)总粒子数的比率随入射总粒子数的变化
Fig. 3. (a) Variation of the number of deposited non-planar (planar) particles on (at) the tops (sides) of the electrodes with the number of incident particles; (b) the variation of the ratio of the number of deposited non-planar (planar) particles on (at) the tops (sides) of the electrodes to the total number of particles with the number of incident particles. Here the out-plane (in-plane) interaction energy between the molecules of non-planar and planar is 0.4kBT (0.2kBT ).
图 4 当非平面分子(蓝色)和平面分子(红色)垂直面间(沿着面内方向)结合能分别为(a) 0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), (b) 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), (c) 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $)以及(d) 2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $)时, 预图案表面沉积50000个粒子(非平面分子和平面分子各25000个)的最终形貌的截面快照
Fig. 4. Section snapshots of the final morphology after 50000 particles deposited on the pre-patterned surface (25000 each for the molecule of non-planar and planar) by varying the out-plane (in-plane) interaction energies between the molecules of non-planar (blue) and planar (red) from (a) 0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), (b) 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), (c) 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $) to (d) 2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $).
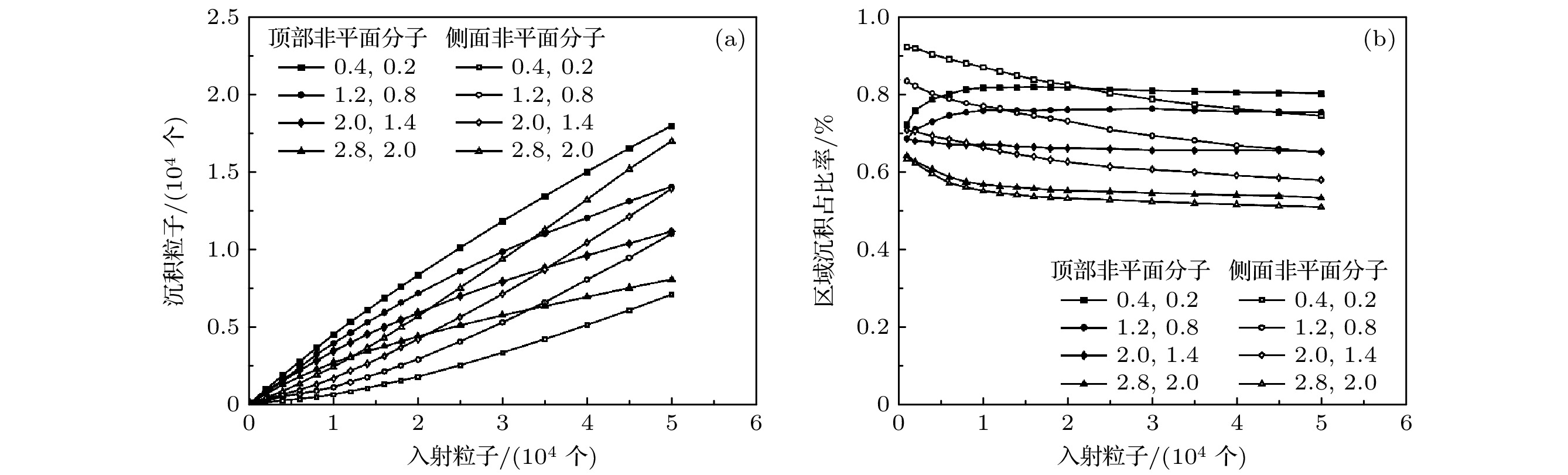
图 5 当非平面分子和平面分子垂直面间(沿着面内方向)结合能分别为0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $)以及2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $)时, (a)非平面分子在电极顶部、侧面的沉积粒子数随入射粒子总数的变化; (b)沉积在电极顶部(侧面)非平面分子(平面分子)的粒子数占顶部(侧面)总粒子数的比率随入射总粒子数的变化
Fig. 5. (a) Variation of the number of deposited particles of non-planar on (at) the tops (sides) of the electrodes with the number of incident particles; (b) the variation of the ratio of the number of deposited particles of non-planar (planar) on (at) the tops (sides) of the electrodes to the total number of particles with the number of incident particles. Here the out-plane (in-plane) interaction energy between the molecules of non-planar and planar is 0.4$ {k}_{{\mathrm{B}}}T $(0.2$ {k}_{{\mathrm{B}}}T $), 1.2$ {k}_{{\mathrm{B}}}T $(0.8$ {k}_{{\mathrm{B}}}T $), 2$ {k}_{{\mathrm{B}}}T $(1.4$ {k}_{{\mathrm{B}}}T $) and 2.8$ {k}_{{\mathrm{B}}}T $(2$ {k}_{{\mathrm{B}}}T $), respectively.
-
[1] Shaw J M, Seidler P F 2001 IBM J. Res. Dev. 45 3
Google Scholar
[2] Kippelen B, Brédas J L 2009 Energy Enviro. Sci. 2 251
Google Scholar
[3] Baek S, Kim K, Sung Y, Jung P, Ju S, Kim W, Kim S J, Hong S H, Lee H 2020 Nanotechnology 31 125301
Google Scholar
[4] Tian P F, Bulovic V, Burrows P E, Gu G, Forrest S R, Zhou T X 1999 J. Vac. Sci. Technol. A 17 2975
Google Scholar
[5] Saba M H, Mukherjee S, Dutta S, Mallisetty P K, Murmu N C 2021 Mater. Today: Proc. 46 1749
Google Scholar
[6] Spiegel I A, Sammons P, Barton K 2020 IEEE Trans. Control Syst. Technol. 28 2322
Google Scholar
[7] Wang W C, Chi L F 2012 Acc. Chem. Res. 45 1646
Google Scholar
[8] Bardotti L, Prevel B, Jensen P, Treilleux M, Mélinon P, Perez A, Mailly D 2002 Appl. Surf. Sci. 191 205
Google Scholar
[9] Wang W C, Zhong D Y, Zhu J, Kalischewski F, Dou R F, Wedeking K, Chi L F 2007 Phys. Rev. Lett. 98 225504
Google Scholar
[10] Speth R L, Lauga E 2009 New J. Phys. 11 075024
Google Scholar
[11] Hopp S F, Heuer A 2010 J. Chem. Phys. 133 204101
Google Scholar
[12] Lied F, Mues T, Wang W C, Chi L F, Heuer A 2012 J. Chem. Phys. 136 024704
Google Scholar
[13] Zhang H, Liu G, Wang W C, Chi L F, Yuan S L 2014 RSC Adv. 4 25005
Google Scholar
[14] Kotelyanskii M, Theodorou D N 2004 Simulation Methods for Polymers (Boca Raton: CRC Press
[15] Neurock M, Hansen E W 1998 Comput. Chem. Eng. 22 S1045
Google Scholar
[16] Liu G, Zhang H, Liu G K, Yuan S L 2016 Colloids Surf. A Physicochem. Eng. Asp. 494 186
Google Scholar
[17] Liu G, Zhang H, Liu G K, Yuan S L, Zhu Q Z 2016 Colloids Surf. A Physicochem. Eng. Asp. 509 401
Google Scholar
[18] Blel S, Hamouda A B H 2019 Results Phys. 12 1475
Google Scholar
[19] Jiang Y, Shi L, Chen N B, Hu L G, Wang W C, Nie Q M, Yan B 2023 Results Phys. 44 106145
Google Scholar
[20] Wang W C, Du C, Zhong D Y, Hirtz M, Wang Y, Lu N, Wu L X, Ebeling D, Li L Q, Fuchs H, Chi L F 2009 Adv. Mater. 21 4721
Google Scholar
[21] Kalischewski F, Heuer A 2009 Phys. Rev. B 80 155421
Google Scholar
[22] Kalischewski F, Zhu J, Heuer A 2008 Phys. Rev. B 78 155401
Google Scholar
[23] Klawtanong M, Srinitiwarawong C, Chatraphorn P 2018 Thin Solid Films 645 431
Google Scholar
[24] Huitema H E A, van der Eerden J P 1999 J. Chem. Phys. 110 3267
Google Scholar
[25] Larsson M I 2001 Phys. Rev. B 64 115428
Google Scholar
[26] Michely T, Krug J 2004 Islands, Mounds and Atoms (Vol. 42) (Berlin: Springer
[27] Liu G, Zhang H, Wang W, Yuan S L 2015 Chem. Phys. Lett. 628 54
Google Scholar
下载:
计量
- 文章访问数: 1183
- PDF下载量: 32
- 被引次数: 0
