-
为预测大晶粒UO2燃料中裂变气体的释放行为, 从而为事故容错燃料的发展提供支持, 本文采用相场模型, 对裂变气体在UO2多晶微观结构中的释放行为进行了模拟. 该模型采用一组耦合的Cahn-Hilliard方程与Allen-Cahn方程, 用守恒场变量表示裂变气体与空位的分布, 以及用序参量区分气泡相与基质相. 该模型重点考察了不同晶粒尺寸、不同温度条件与扩散系数对裂变气体释放行为产生的影响, 展现了气泡的形核、生长、融合等行为, 得到了一定程度燃耗深度下燃料的孔隙度、晶界处气泡覆盖率、气泡平均半径等模拟结果. 结果表明, 温度与扩散系数对孔隙度、晶界处气泡覆盖率的影响较为显著, 在扩散系数较大时, 晶粒尺寸也会对裂变气体释放行为产生较大影响, 扩散系数较小时, 晶粒尺寸的影响则不明显. 此外, 通过该模型得出的高燃耗深度下裂变气体气泡分布状况与实验结果也较为符合, 该模型能较好地预测大晶粒UO2裂变气体释放行为.In order to predict the release behavior of fission gas in large grain UO2 fuel and provide support for the development of accident tolerant fuel, a phase-field model is used to simulate the release behavior of fission gas in the microstructure of UO2 polycrystalline in this work. This model adopts a set of coupled Cahn-Hilliard equations and Allen-Cahn equations, using conserved field variables to represent the distribution of fission gas and vacancies, and distinguishing bubble phase from matrix phase by using order parameters. This model focuses on investigating the effects of different grain sizes, temperature conditions, and diffusion coefficients on the release behavior of fission gas, demonstrating the nucleation, growth, and fusion behavior of bubbles. Simulation results are obtained for fuel porosity, bubble coverage on grain boundaries, and average bubble radius at a certain degree of burnup. The results show that temperature and diffusion coefficient have a significant influence on porosity and bubble coverage on grain boundaries. When the diffusion coefficient is high, grain size also has a significant influence on fission gas release behavior. And when the diffusion coefficient is low, the influence of grain size is not significant. In addition, the distribution of fission gas bubbles under high burnup obtained through this model is also in good agreement with experimental result. The model can predict the behavior of fission gas release in large grain UO2 fuel.
-
Keywords:
- phase field model /
- large grain UO2 fuel /
- release of fission gas
[1] Rest J 2010 J. Nucl. Mater. 402 179
Google Scholar
[2] Trinkaus H, Singh B N 2003 J. Nucl. Mater. 323 229
Google Scholar
[3] Rest J, Hofman G L 1999 Nucl. Technol. 126 88
Google Scholar
[4] Pastore G, Luzzi L, Di Marcello V, van Uffelen P 2013 Nucl. Eng. Des. 256 75
Google Scholar
[5] Piro M H, Sunderland D, Livingstone S, Sercombe J, Revie R W, Quastel A, Terrani K A, Judge C 2020 Comprehensive Nuclear Materials (2nd Ed.) (Amsterdam: Elsevier) p248
[6] 何文, 伍晓勇, 吴璐, 温榜, 朱伟, 张伟, 潘荣剑, 王桢, 黄伟杰 2017 核动力工程 38 170
Google Scholar
He W, Wu X Y, Wu L, Wen B, Zhu W, Zhang W, Pan R J, Wang Z, Huang W J 2017 Nucl. Power Eng. 38 170
Google Scholar
[7] Killeen J C 1980 J. Nucl. Mater. 88 177
Google Scholar
[8] Cooper M W D, Pastore G, Che Y, Matthews C, Forslund A, Stanek C R, Shirvan K, Tverberg T, Gamble K A, Mays B, Andersson D A 2021 J. Nucl. Mater. 545 152590
Google Scholar
[9] Aagesen L K, Schwen D, Tonks M R, Zhang Y 2019 Comput. Mater. Sci. 161 35
Google Scholar
[10] Yuda R, Harada H, Hirai M, Hosokawa T, Une K, Kashibe S, Shimizu S, Kubo T 1997 J. Nucl. Mater. 248 262
Google Scholar
[11] 庞华, 辛勇, 岳慧芳, 彭航, 蒲曾坪, 邱玺, 孙志鹏, 刘仕超 2022 材料导报 36 5
Google Scholar
Pang H, Xin Y, Yue H F, Peng H, Pu Z P, Qiu X, Sun Z P, Liu S C 2022 Mater. Rev. 36 5
Google Scholar
[12] Delafoy C, Dewes P, Miles T 2007 Proceedings of the 2007 LWR Fuel Performance Meeting/TopFuel 2007 San Francisco, CA, United States, September 30–October 3, 2007 p1
[13] Kashibe S, Une K 1998 J. Nucl. Mater. 254 234
Google Scholar
[14] Che Y, Pastore G, Hales J, Shirvan K 2018 Nucl. Eng. Des. 337 271
Google Scholar
[15] Moelans N, Blanpain B, Wollants P 2008 Comput. Coupling Phase Diagrams Thermochem 32 268
Google Scholar
[16] 郭灿, 康晨瑞, 高莹, 张一弛, 邓英远, 马超, 徐春杰, 梁淑华 2022 71 096401
Google Scholar
Guo C, Kang C R, Gao Y, Zhang Y C, Deng Y Y, Ma C, Xu C J, Liang S H 2022 Acta Phys. Sin. 71 096401
Google Scholar
[17] Hu S, Henager Jr C H 2009 J. Nucl. Mater. 394 155
Google Scholar
[18] Millett P C, El-Azab A, Rokkam S, Tonks M, Wolf D 2011 Comput. Mater. Sci. 50 949
Google Scholar
[19] Jiang Y B, Liu W B, Li W J, Sun Z Y, Xin Y, Chen P H, Yun D 2021 Comput. Mater. Sci. 188 110176.
Google Scholar
[20] Zhao J J, Sun D, Xi L, Chen P, Zhao J J, Wang Y Y 2023 Phys. Chem. Chem. Phys. 25 14928
Google Scholar
[21] Cahn J W, Hilliard J E 1958 J. Chem. Phys. 28 258
Google Scholar
[22] Li Y, Hu S, Montgomery R, Gao F, Sun X 2013 Nucl. Instrum. Methods Phys. Res. , Sect. B 303 62
Google Scholar
[23] Kittel C, Kroemer H 1980 Thermal Physics (New York: WH Freeman and Company) pp287–306
[24] Moelans N 2011 Acta Mater. 59 1077
Google Scholar
[25] Moelans N, Blanpain B, Wollants P 2008 Phys. Rev. B 78 024113
Google Scholar
[26] Cahn J W 1961 Acta Metall. 9 795
Google Scholar
[27] Allen S M, Cahn J W 1972 Acta Metall. 20 423
Google Scholar
[28] Allen S M, Cahn J W 1973 Scr. Metall. 7 1261
Google Scholar
[29] Turnbull J A, Friskney C A, Findlay J R, Johnson F A, Walter A J 1982 J. Nucl. Mater. 107 168
Google Scholar
[30] Turnbull J A, White R J, Wise C 1989 Technical Committee on Water Reactor Fuel Element Computer Modelling in Steady State, Transient and Accident Conditions Preston, United Kingdom, September 18–22, 1988 p174
[31] INTRODUCTION TO COMSOL Multiphysics, COMSOL Co Ltd. https://cdn.comsol.com/doc/5.2/IntroductionToCOMSOLMultiphysics.zh_CN.pdf [2023-11-1]
[32] Millett P C, El-Azab A, Wolf D 2011 Comput. Mater. Sci. 50 960
Google Scholar
[33] Sagui C, Grant M 1999 Phys. Rev. E 59 4175.
Google Scholar
[34] Bullough R, Nelson R S 1974 Phys. Technol. 5 29
Google Scholar
[35] Zacharie I, Lansiart S, Combette P, Trotabas M, Coster M, Groos M 1998 J. Nucl. Mater. 255 85
Google Scholar
[36] Sheng J, Wang Y C, Liu Y, Wu S, Xu K, Chen Z H, Bo S, Liu H F, Song H F 2022 Comput. Mater. Sci. 213 111663
Google Scholar
[37] Wu S, Sheng J, Yang C, Shi X, Huang H, Liu Y, Song H 2022 Front. Mater. 9 916593
Google Scholar
[38] 姜彦博, 柳文波, 孙志鹏, 喇永孝, 恽迪 2022 71 026103
Google Scholar
Jiang Y B, Liu W B, Sun Z P, La Y X, Yun D 2022 Acta Phys. Sin. 71 026103
Google Scholar
-
图 1 序参量η与ϕi的取值在相场模型中的表现
Fig. 1. Representation of the values of order parameters η and ϕi in the phase-field model.
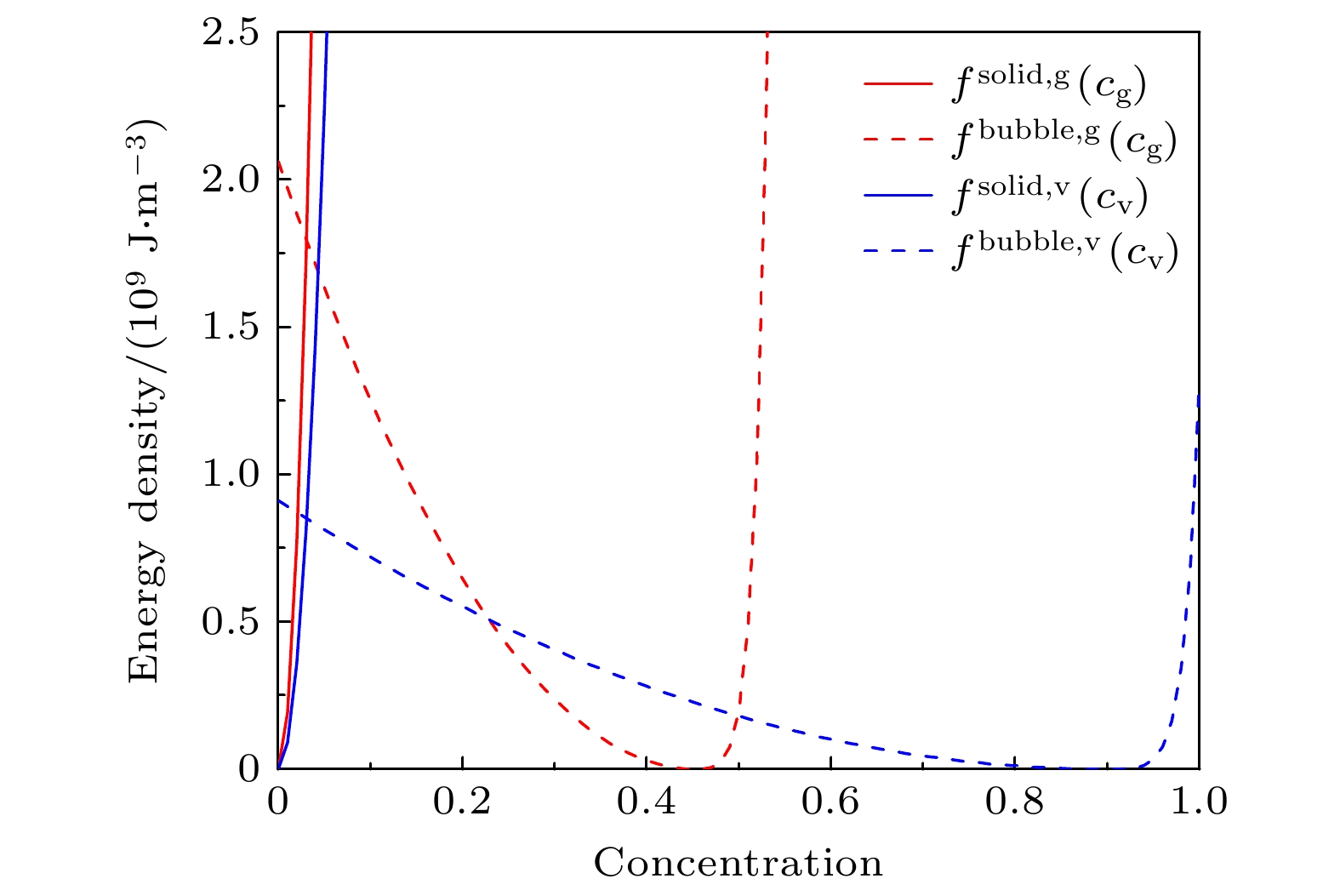
图 2 自由能密度随浓度(cv, cg)分布的变化, 曲线最低点的横坐标为平衡浓度, 随着cg增加, $ c_{\text{v}}^{{\text{b, eq}}} $逐渐减小, f bubble,v的图像(蓝色虚线)将向左平移
Fig. 2. Variation of free energy density with concentration (cv, cg) distribution, the abscissa of the lowest point of the curve is the equilibrium concentration. As cg increases, $ c_{\text{v}}^{{\text{b, eq}}} $ gradually decreases, and the image of f bubble,v (blue dashed line) will shift to the left.
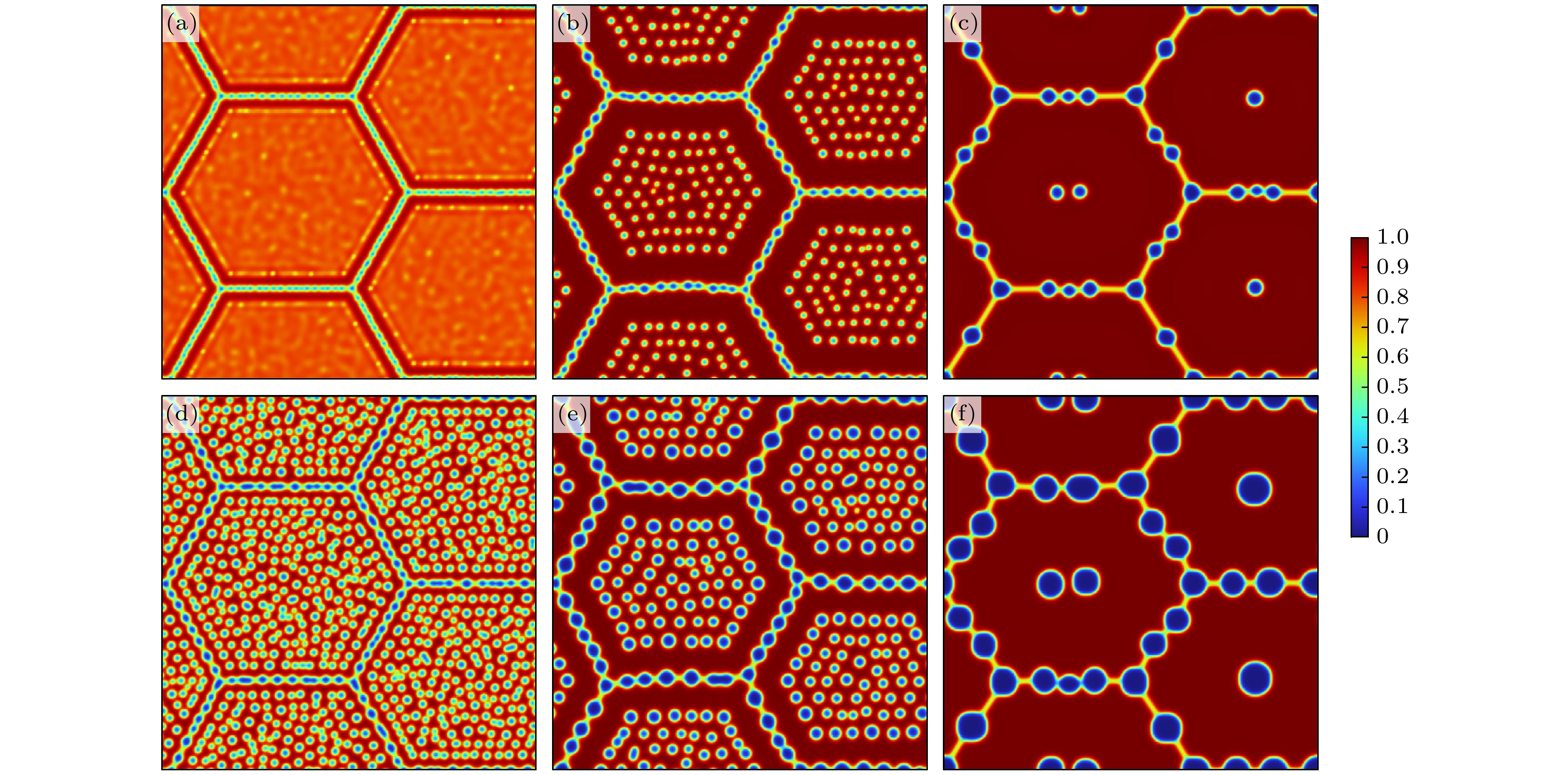
图 3 T = 1276 K条件下直径5 μm晶粒与气泡随时间演化分布 (a) τ = 0 s; (b) τ = 140 s; (c) τ = 160 s; (d) τ = 200 s; (e) τ = 300 s; (f) τ = 550 s
Fig. 3. Distribution of grain with a diameter of 5 μm and bubble evolution over time at T = 1276 K: (a) τ = 0 s; (b) τ = 140 s; (c) τ = 160 s; (d) τ = 200 s; (e) τ = 300 s; (f) τ = 550 s.
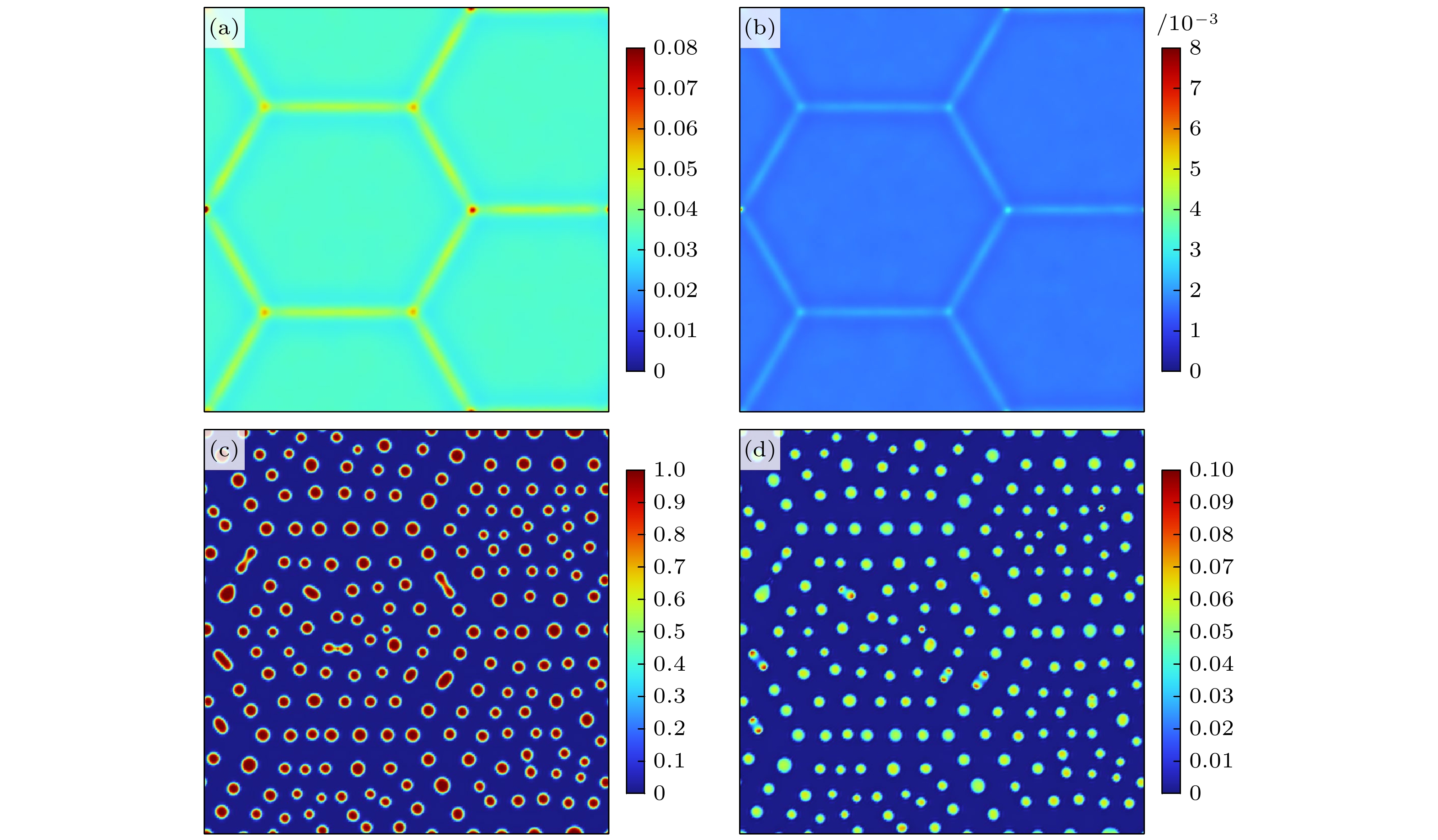
图 4 空位(cv, (a), (c))与裂变气体(cg, (b), (d))在τ = 140 s与τ = 550 s的浓度分布(不同的颜色代表浓度的取值) (a), (b) τ = 140 s; (c), (d) τ = 550 s
Fig. 4. Concentration distribution of vacancies (cv, (a) and (c)) and fission gases (cg, (b) and (d)) at τ = 140 s and τ = 550 s, different color represent the value of concentration: (a), (b) τ = 140 s; (c), (d) τ = 550 s.
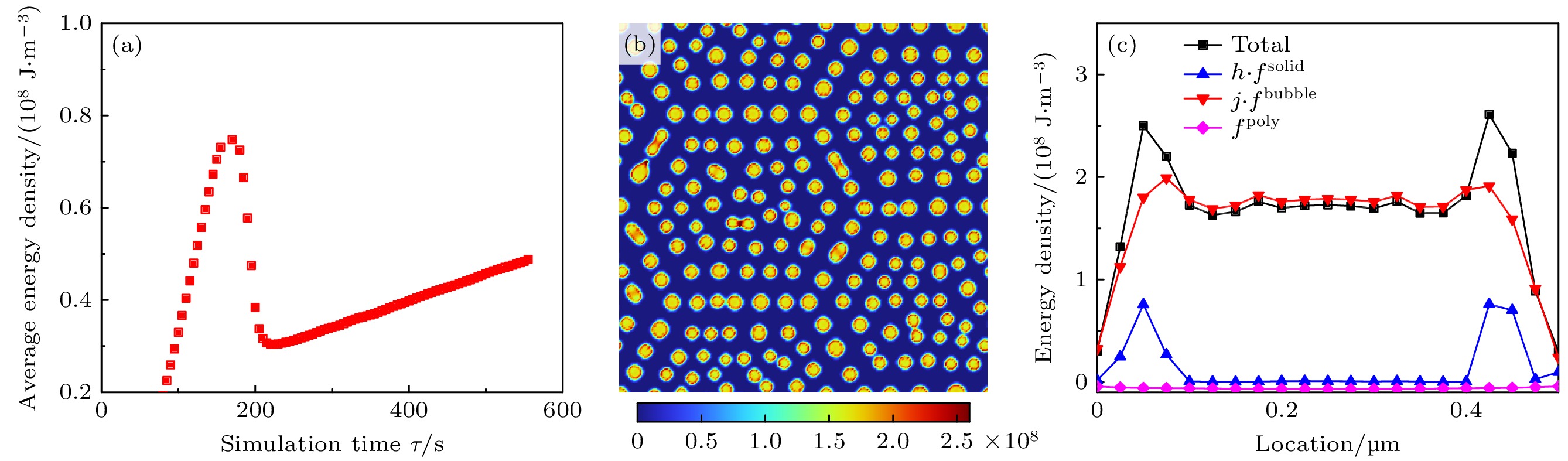
图 5 (a) 整个模拟区域内的平均自由能密度随时间的变化; (b) 总自由能密度在整个模拟区域分布, 颜色栏为取值范围; (c)某一气泡径向自由能密度分布
Fig. 5. (a) Variation of average free energy density over time in simulation area; (b) distribution of the total free energy density in simulation area, the color bar represents the range of values; (c) radial free energy density distribution of a certain bubble.
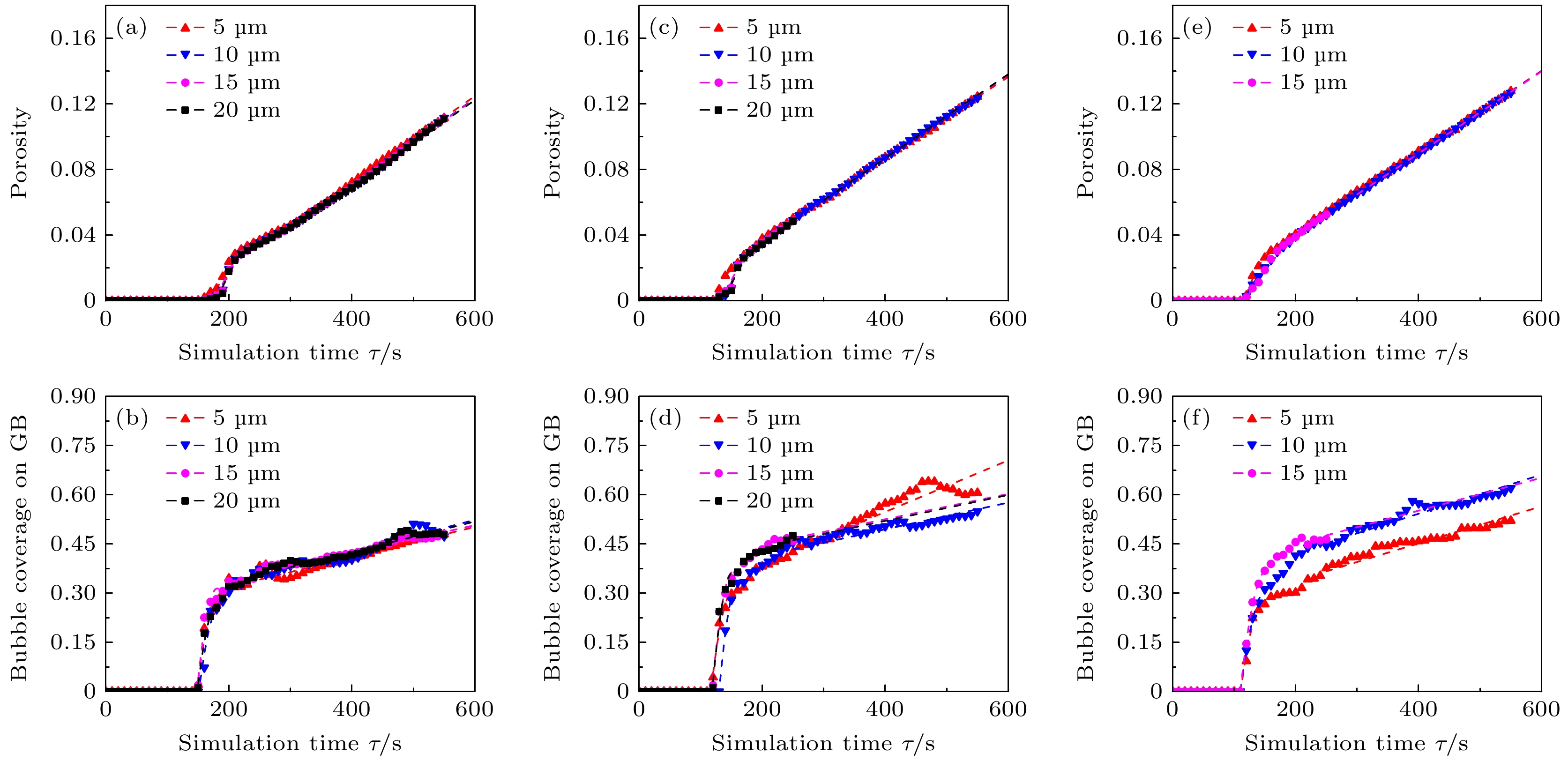
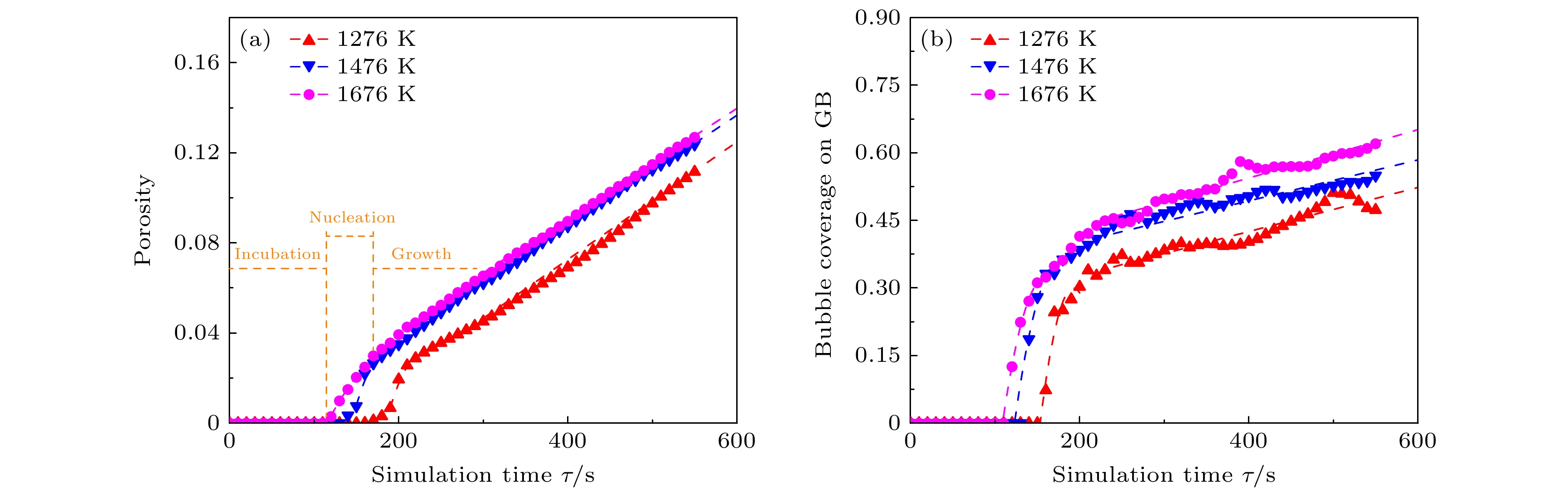
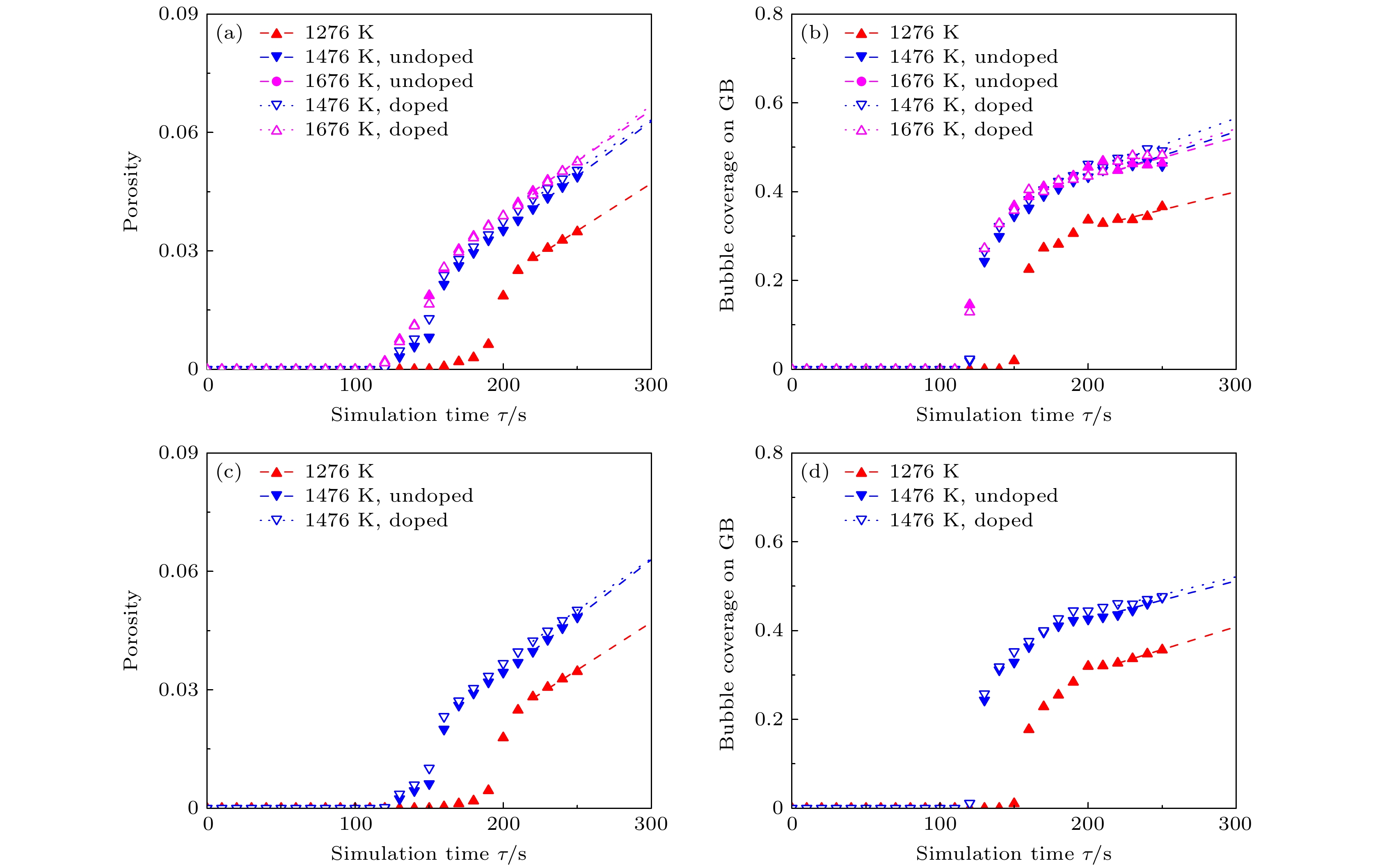
图 9 相同温度不同晶粒尺寸, (a), (c), (e)孔隙度与(b), (d), (f)晶界气泡覆盖率随时间演化 (a), (b) T = 1276 K; (c), (d) T = 1476 K; (e), (f) T = 1676 K
Fig. 9. Evolution of (a), (c), (e) porosity and (b), (d), (f) bubble coverage on GB over time for the same temperature but different grain sizes: (a), (b) T = 1276 K; (c), (d) T = 1476 K; (e), (f) T = 1676 K.
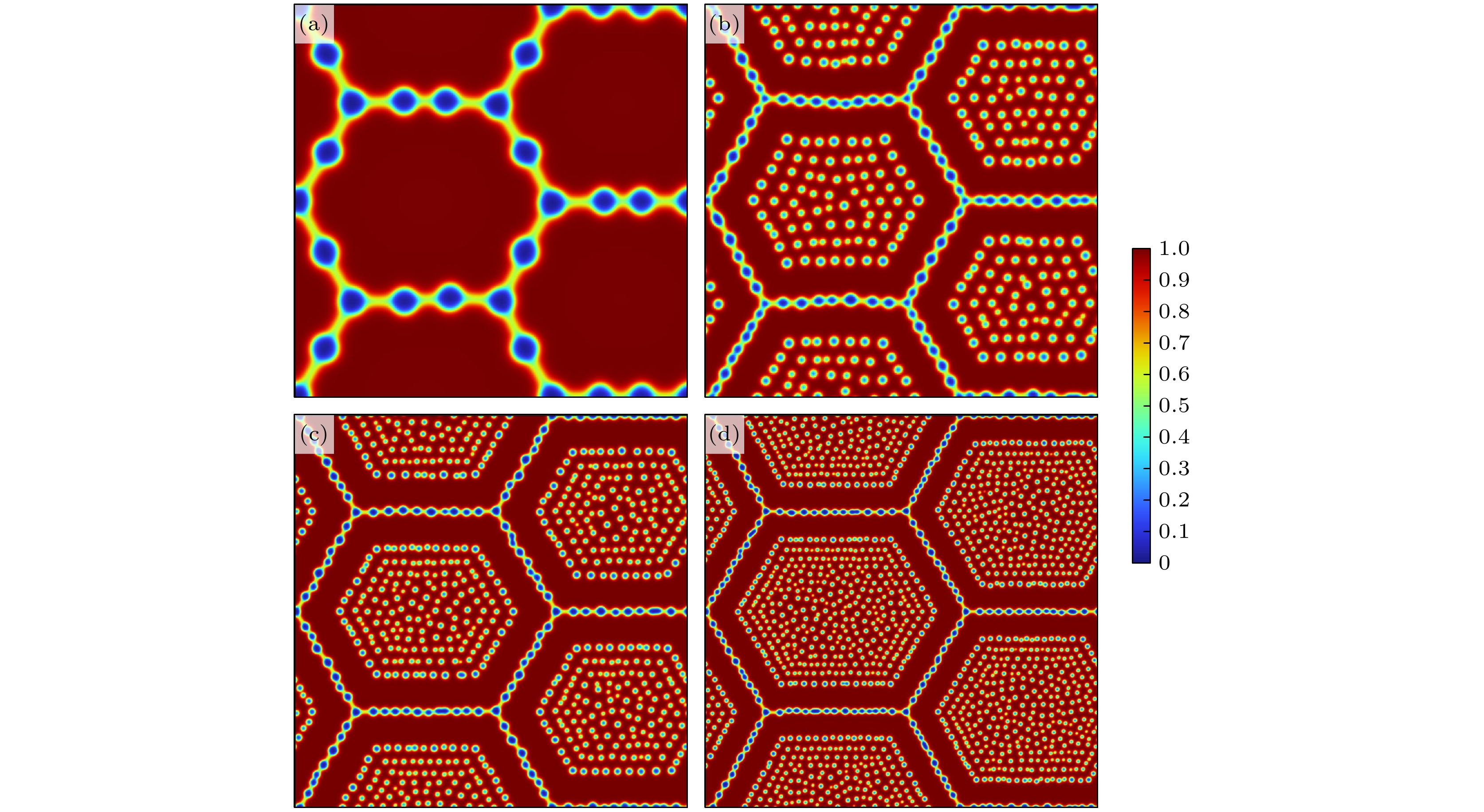
图 6 T = 1276, 1476, 1676 K条件下直径10 μm晶粒与气泡分布图 (a) T = 1276 K, τ = 180 s; (b) T = 1476 K, τ = 180 s; (c) T = 1676 K, τ = 180 s; (d) T = 1276 K, τ = 500 s; (e) T = 1476 K, τ = 500 s; (f) T = 1676 K, τ = 500 s
Fig. 6. Distribution of grains with a diameter of 10 μm and bubbles under T = 1276, 1476, 1676 K: (a) T = 1276 K, τ = 180 s; (b) T = 1476 K, τ = 180 s; (c) T = 1676 K, τ = 180 s; (d) T = 1276 K, τ = 500 s; (e) T = 1476 K, τ = 500 s; (f) T = 1676 K, τ = 500 s.
图 7 直径10 μm晶粒3种温度条件下(a)孔隙度与(b)晶界气泡覆盖率随时间演化
Fig. 7. Evolution of (a) porosity and (b) bubble coverage on grain boundaries over time under three temperature conditions for grains with a diameter of 10 μm.
图 8 T = 1476 K, τ = 250 s时晶粒与气泡分布 (a) 5 μm; (b) 10 μm; (c) 15 μm; (d) 20 μm
Fig. 8. Distribution of grains and bubbles at τ = 250 s, T = 1476 K: (a) 5 μm; (b) 10 μm; (c) 15 μm; (d) 20 μm.
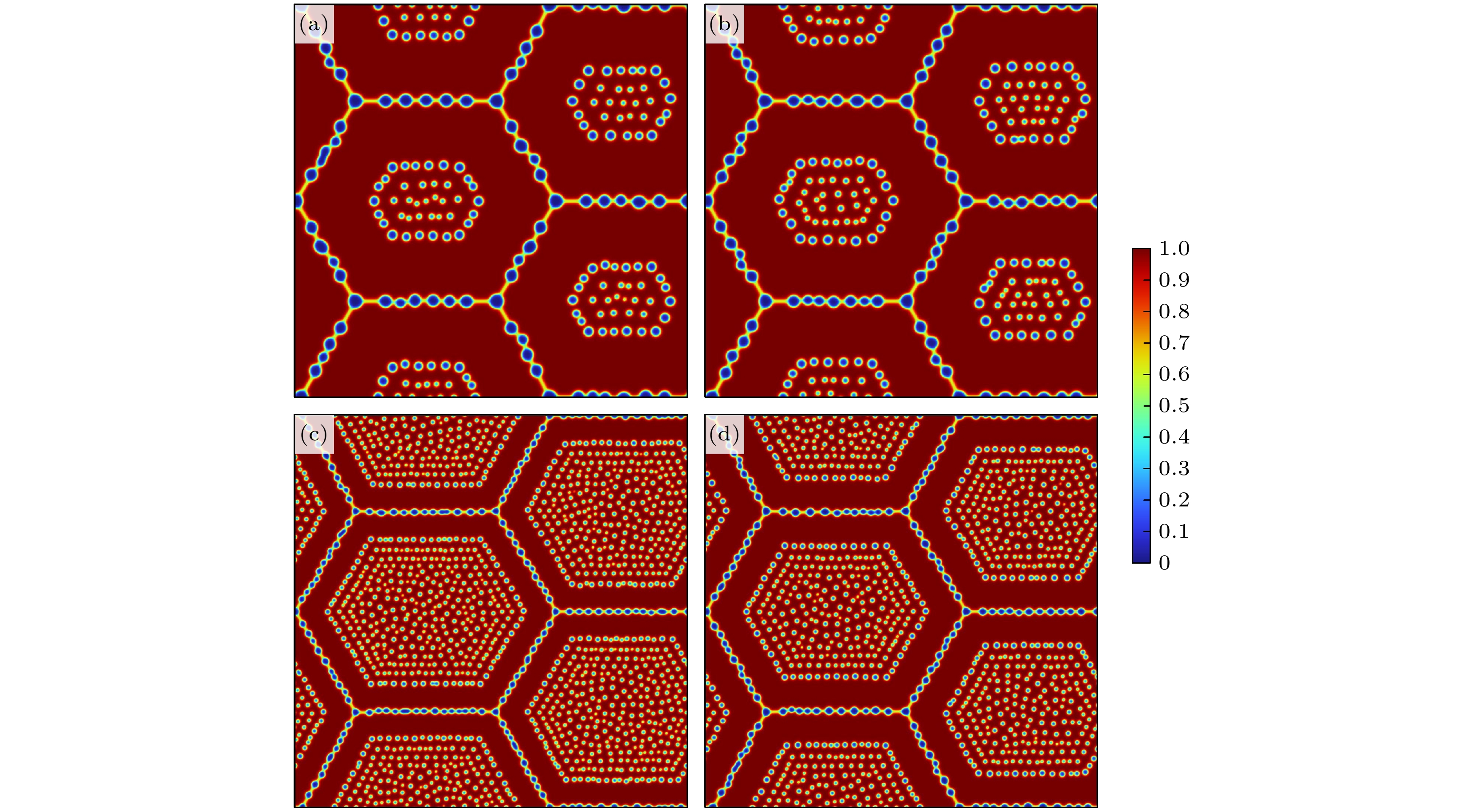
图 10 采用$ {D^{{\text{undoped}}}} $与$ {D^{{\text{doped}}}} $晶粒与气泡分布对比 (a) T = 1676 K, 15 μm, $ {D^{{\text{undoped}}}} $; (b) T = 1676 K, 15 μm, $ {D^{{\text{doped}}}} $; (c) T = 1476 K, 20 μm, $ {D^{{\text{undoped}}}} $; (d) T = 1476 K, 20 μm, $ {D^{{\text{doped}}}} $
Fig. 10. Comparison of the distribution of grains and bubbles using $ {D^{{\text{undoped}}}} $ and $ {D^{{\text{doped}}}} $: (a) T = 1676 K, 15 μm, $ {D^{{\text{undoped}}}} $; (b) T = 1676 K, 15 μm, $ {D^{{\text{doped}}}} $; (c) T = 1476 K, 20 μm, $ {D^{{\text{undoped}}}} $; (d) T = 1476 K, 20 μm, $ {D^{{\text{doped}}}} $.
图 11 对于直径15 μm与20 μm晶粒, (a), (c) 孔隙度与(b), (d)晶界气泡覆盖率随时间演化 (a), (b) 直径15 μm; (c), (d) 直径20 μm
Fig. 11. Evolution of (a), (c) porosity and (b), (d) bubble coverage on grain boundary with time for grains with a diameter of 15 μm and 20 μm: (a), (b) Diameter 15 μm; (c), (d) diameter 20 μm.
表 1 模拟采用的部分参数
Table 1. Parameters used in simulation.
参数 符号 值 玻尔兹曼常量/(J·K–1) kB 1.3806 × 10–23 理想气体常数/(J·mol–1·K–1) R 8.3145 UO2晶胞U原子体积/ nm–³ Va 0.0409 空位形成能/eV $ E_{\text{v}}^{\text{f}} $ 5.1 气体原子缺陷形成能/eV $ E_{\text{g}}^{\text{f}} $ 10.31 扩散界面系数 aGB 1.2 as 0.8 自由能势垒系数/(J·m–3) m 3.0 × 107 梯度项系数/(J·m–3) κϕ 3.38 × 10–7 κv, κg, κη 1.69 × 10–6 迁移率/(m3·J–1·s–1) Lη, Lϕ 1.56 × 10–11 裂变率密度/(次裂变·m3·s–1) $ \dot F $ 1.09 × 1019 Xe产额 Y 0.27 
下载: 导出CSV
表 2 不同温度下采用的扩散系数
Table 2. Diffusion coefficients used at different temperatures.
温度T/K $ {D^{{\text{undoped}}}} $/(m2·s–1) $ {D^{{\text{doped}}}} $/(m2·s–1) 1276 8.72 × 10–21 8.72 × 10–21 1476 1.583 × 10–19 2.4593 × 10–19 1676 5.7461 × 10–19 5.0906 × 10–19
下载: 导出CSV
-
[1] Rest J 2010 J. Nucl. Mater. 402 179
Google Scholar
[2] Trinkaus H, Singh B N 2003 J. Nucl. Mater. 323 229
Google Scholar
[3] Rest J, Hofman G L 1999 Nucl. Technol. 126 88
Google Scholar
[4] Pastore G, Luzzi L, Di Marcello V, van Uffelen P 2013 Nucl. Eng. Des. 256 75
Google Scholar
[5] Piro M H, Sunderland D, Livingstone S, Sercombe J, Revie R W, Quastel A, Terrani K A, Judge C 2020 Comprehensive Nuclear Materials (2nd Ed.) (Amsterdam: Elsevier) p248
[6] 何文, 伍晓勇, 吴璐, 温榜, 朱伟, 张伟, 潘荣剑, 王桢, 黄伟杰 2017 核动力工程 38 170
Google Scholar
He W, Wu X Y, Wu L, Wen B, Zhu W, Zhang W, Pan R J, Wang Z, Huang W J 2017 Nucl. Power Eng. 38 170
Google Scholar
[7] Killeen J C 1980 J. Nucl. Mater. 88 177
Google Scholar
[8] Cooper M W D, Pastore G, Che Y, Matthews C, Forslund A, Stanek C R, Shirvan K, Tverberg T, Gamble K A, Mays B, Andersson D A 2021 J. Nucl. Mater. 545 152590
Google Scholar
[9] Aagesen L K, Schwen D, Tonks M R, Zhang Y 2019 Comput. Mater. Sci. 161 35
Google Scholar
[10] Yuda R, Harada H, Hirai M, Hosokawa T, Une K, Kashibe S, Shimizu S, Kubo T 1997 J. Nucl. Mater. 248 262
Google Scholar
[11] 庞华, 辛勇, 岳慧芳, 彭航, 蒲曾坪, 邱玺, 孙志鹏, 刘仕超 2022 材料导报 36 5
Google Scholar
Pang H, Xin Y, Yue H F, Peng H, Pu Z P, Qiu X, Sun Z P, Liu S C 2022 Mater. Rev. 36 5
Google Scholar
[12] Delafoy C, Dewes P, Miles T 2007 Proceedings of the 2007 LWR Fuel Performance Meeting/TopFuel 2007 San Francisco, CA, United States, September 30–October 3, 2007 p1
[13] Kashibe S, Une K 1998 J. Nucl. Mater. 254 234
Google Scholar
[14] Che Y, Pastore G, Hales J, Shirvan K 2018 Nucl. Eng. Des. 337 271
Google Scholar
[15] Moelans N, Blanpain B, Wollants P 2008 Comput. Coupling Phase Diagrams Thermochem 32 268
Google Scholar
[16] 郭灿, 康晨瑞, 高莹, 张一弛, 邓英远, 马超, 徐春杰, 梁淑华 2022 71 096401
Google Scholar
Guo C, Kang C R, Gao Y, Zhang Y C, Deng Y Y, Ma C, Xu C J, Liang S H 2022 Acta Phys. Sin. 71 096401
Google Scholar
[17] Hu S, Henager Jr C H 2009 J. Nucl. Mater. 394 155
Google Scholar
[18] Millett P C, El-Azab A, Rokkam S, Tonks M, Wolf D 2011 Comput. Mater. Sci. 50 949
Google Scholar
[19] Jiang Y B, Liu W B, Li W J, Sun Z Y, Xin Y, Chen P H, Yun D 2021 Comput. Mater. Sci. 188 110176.
Google Scholar
[20] Zhao J J, Sun D, Xi L, Chen P, Zhao J J, Wang Y Y 2023 Phys. Chem. Chem. Phys. 25 14928
Google Scholar
[21] Cahn J W, Hilliard J E 1958 J. Chem. Phys. 28 258
Google Scholar
[22] Li Y, Hu S, Montgomery R, Gao F, Sun X 2013 Nucl. Instrum. Methods Phys. Res. , Sect. B 303 62
Google Scholar
[23] Kittel C, Kroemer H 1980 Thermal Physics (New York: WH Freeman and Company) pp287–306
[24] Moelans N 2011 Acta Mater. 59 1077
Google Scholar
[25] Moelans N, Blanpain B, Wollants P 2008 Phys. Rev. B 78 024113
Google Scholar
[26] Cahn J W 1961 Acta Metall. 9 795
Google Scholar
[27] Allen S M, Cahn J W 1972 Acta Metall. 20 423
Google Scholar
[28] Allen S M, Cahn J W 1973 Scr. Metall. 7 1261
Google Scholar
[29] Turnbull J A, Friskney C A, Findlay J R, Johnson F A, Walter A J 1982 J. Nucl. Mater. 107 168
Google Scholar
[30] Turnbull J A, White R J, Wise C 1989 Technical Committee on Water Reactor Fuel Element Computer Modelling in Steady State, Transient and Accident Conditions Preston, United Kingdom, September 18–22, 1988 p174
[31] INTRODUCTION TO COMSOL Multiphysics, COMSOL Co Ltd. https://cdn.comsol.com/doc/5.2/IntroductionToCOMSOLMultiphysics.zh_CN.pdf [2023-11-1]
[32] Millett P C, El-Azab A, Wolf D 2011 Comput. Mater. Sci. 50 960
Google Scholar
[33] Sagui C, Grant M 1999 Phys. Rev. E 59 4175.
Google Scholar
[34] Bullough R, Nelson R S 1974 Phys. Technol. 5 29
Google Scholar
[35] Zacharie I, Lansiart S, Combette P, Trotabas M, Coster M, Groos M 1998 J. Nucl. Mater. 255 85
Google Scholar
[36] Sheng J, Wang Y C, Liu Y, Wu S, Xu K, Chen Z H, Bo S, Liu H F, Song H F 2022 Comput. Mater. Sci. 213 111663
Google Scholar
[37] Wu S, Sheng J, Yang C, Shi X, Huang H, Liu Y, Song H 2022 Front. Mater. 9 916593
Google Scholar
[38] 姜彦博, 柳文波, 孙志鹏, 喇永孝, 恽迪 2022 71 026103
Google Scholar
Jiang Y B, Liu W B, Sun Z P, La Y X, Yun D 2022 Acta Phys. Sin. 71 026103
Google Scholar
下载:
计量
- 文章访问数: 2217
- PDF下载量: 64
- 被引次数: 0
