-
量子Fisher信息给出参数估计的最优精度极限, 在量子度量学中有重要的应用. 近年来, 在量子系统中实现非厄米哈密顿量的理论与实验研究受到广泛关注. 本文研究基于非厄米哈密顿量本征态的参数估计, 给出其中单参数与两参数估计的量子Fisher信息及其量子Cramér-Rao下界, 计算与分析非互易、具有增益-耗散的Su-Schrieffer-Heeger模型, 非厄米量子Ising链、拓扑陈绝缘体模型和二能级系统中动量及外场参数估计的量子Fisher信息. 结果表明: 在这几个非厄米模型中, 对于单参数估计, 量子Fisher信息在能隙闭合区域和例外点附近显著增大, 从而提高参数估计的精度极限; 对于两参数估计, 量子Fisher信息矩阵的行列式在能隙闭合和例外点附近同样明显增大, 拓扑区域比平庸区域的整体评估精度更高, 且由陈数确定两参数估计误差的拓扑下界.
-
关键词:
- 量子Fisher信息 /
- 参数估计 /
- 非厄米系统 /
- 拓扑态
Quantum Fisher information bounds the ultimate precision limit in the parameter estimation and has important applications in quantum metrology. In recent years, the theoretical and experimental studies of non-Hermitian Hamiltonians realized in quantum systems have attracted wide attention. Here, the parameter estimation based on eigenstates of non-Hermitian Hamiltonians is investigated, and the corresponding quantum Fisher information and quantum Cramér-Rao bound for the single-parameter and two-parameter estimations are given. In particular, the quantum Fisher information about estimating intrinsic momentum and external parameters in the non-reciprocal and gain-and-loss Su-Schrieffer-Heeger models, and non-Hermitian versions of the quantum Ising chain, Chern-insulator model and two-level system are calculated and analyzed. For these non-Hermitian models, the results show that in the case of single-parameter estimation in these non-Hermitian models, the quantum Fisher information increases significantly in the gapless regime and near the exceptional points, which can improve the accuracy limit of parameter estimation. For the two-parameter estimation, the determinant of the quantum Fisher information matrix also increases obviously near the gapless and exceptional points. In addition, a higher overall accuracy can be achieved in the topological regime than in the trivial regime, and the topological bound in two-parameter estimation can be determined by the Chern number.-
Keywords:
- quantum Fisher information /
- parameter estimation /
- non-Hermitian systems /
- topological states
[1] Helstrom C W 1969 J. Stat. Phys. 1 231
Google Scholar
[2] Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439
Google Scholar
[3] Liu J, Yuan H D, Lu X M, Wang X G 2020 J. Phys. A: Math. Theor. 53 023001
Google Scholar
[4] Sidhu J S, Kok P 2020 AVS Quantum Sci. 2 014701
Google Scholar
[5] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[6] Provost J P, Vallee G 1980 Commun. Math. Phys. 76 289
Google Scholar
[7] Mera B, Zhang A W, Goldman N 2022 SciPost Phys. 12 018
Google Scholar
[8] Guo W, Zhong W, Jing X X, Fu L B, Wang X G 2016 Phys. Rev. A 93 042115
Google Scholar
[9] Tan X S, Zhang D W, Yang Z, Chu J, Zhu Y Q, Li D Y, Yang X P, Song S Q, Han Z K, Li Z Y, Dong Y Q, Yu H F, Yan H, Zhu S L, Yu Y 2019 Phys. Rev. Lett. 122 210401
Google Scholar
[10] Tan X S, Zhang D W, Zheng W, Yang X P, Song S Q, Han Z K, Dong Y Q, Wang Z M, Lan D, Yan H, Zhu S L, Yu Y 2021 Phys. Rev. Lett. 126 017702
Google Scholar
[11] Ding H T, Zhu Y Q, He P, Liu Y G, Wang J T, Zhang D W, Zhu S L 2022 Phys. Rev. A 105 012210
Google Scholar
[12] Yu M, Liu Y, Yang P C, Gong M S, Cao Q Y, Zhang S L, Liu H B, Heyl M, Ozawa T, Goldman N, Cai J M 2022 npj Quantum Inf. 8 56
Google Scholar
[13] Yu M, Li X B, Chu Y M, Mera B, Ünal F N, Yang P C, Liu Y, Goldman N, Cai J M 2022 arXiv: 2206.00546[quant-ph
[14] Li C H, Chen M, Cappellaro P 2022 arXiv: 2204.13777[quant-ph
[15] Zhang X Y, Lu X M, Liu J, Ding W K, Wang X G 2023 Phys. Rev. A 107 012414
Google Scholar
[16] Boixo S, Flammia S T, Caves C M, Geremia J M 2007 Phys. Rev. Lett. 98 090401
Google Scholar
[17] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222
Google Scholar
[18] 刘然, 吴泽, 李宇晨, 陈昱全, 彭新华 2023 72 110305
Google Scholar
Liu R, Wu Z, Li Y C, Chen Y Q, Peng X H 2023 Acta Phys. Sin. 72 110305
Google Scholar
[19] Di Candia R, Minganti F, Petrovnin K V, Paraoanu G S, Felicetti S 2023 npj Quantum Inf. 9 23
Google Scholar
[20] Liang H B, Su Y G, Xiao X, Che Y M, Sanders B C, Wang X G 2020 Phys. Rev. A 102 013722
Google Scholar
[21] He W T, Lu C W, Yao Y X, Zhu H Y, Ai Q 2023 Front. Phys. 18 31304
Google Scholar
[22] 牛明丽, 王月明, 李志坚 2022 71 090601
Google Scholar
Niu M L, Wang Y M, Li Z J 2022 Acta Phys. Sin. 71 090601
Google Scholar
[23] Lu X M, Wang X G 2021 Phys. Rev. Lett. 126 120503
Google Scholar
[24] Lin Q, Li T Y, Xiao L, Wang K K, Yi W, Xue P 2022 Nat. Commun. 13 3229
Google Scholar
[25] Xiao L, Deng T S, Wang K K, Zhu G Y, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761
Google Scholar
[26] Li J M, Harter A K, Liu J, Leonardo D M, Joglekar Y N, Luo L 2019 Nat. Commun. 10 855
Google Scholar
[27] Wu Y, Liu W Q, Geng J P, Song X R, Ye X Y, Duan C K, Rong X, Du J F 2019 Science 364 878
Google Scholar
[28] Naghiloo M, Abbasi M, Joglekar Y N, Murch K W 2019 Nat. Phys. 15 1232
Google Scholar
[29] 高雪儿, 李代莉, 刘志航, 郑超 2022 71 240303
Google Scholar
Gao X E, Li D L, Liu Z H, Zheng C 2022 Acta Phys. Sin. 71 240303
Google Scholar
[30] 张禧征, 王鹏, 张坤亮, 杨学敏, 宋智 2022 71 174501
Google Scholar
Zhang X Z, Wang P, Zhang K L, Yang X M, Song Z 2022 Acta Phys. Sin. 71 174501
Google Scholar
[31] Solnyshkov D D, Leblanc C, Bessonart L, Nalitov A, Ren J H, Liao Q, Li F, Malpuech G 2021 Phys. Rev. B 103 125302
Google Scholar
[32] Liao Q, Leblanc C, Ren J H, Li F, Li Y M, Solnyshkov D, Malpuech G, Yao J N, Fu H B 2021 Phys. Rev. Lett. 127 107402
Google Scholar
[33] Wiersig J 2020 Photonics Res. 8 1457
Google Scholar
[34] Zhang D W, Zhu Y Q, Zhao Y X, Yan H, Zhu S L 2018 Adv. Phys. 67 253
Google Scholar
[35] Lang L J, Zhu S L, Chong Y D 2021 Phys. Rev. B 104 L020303
Google Scholar
[36] Zhang D W, Chen Y L, Zhang G Q, Lang L J, Li Z, Zhu S L 2020 Phys. Rev. B 101 235150
Google Scholar
[37] Xu Z C, Zhou Z Y, Cheng E H, Lang L J, Zhu S L 2022 Sci. China: Phys., Mech. Astron. 65 283011
Google Scholar
[38] Shen H T, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402
Google Scholar
[39] Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[40] Zhang D W, Tang L Z, Lang L J, Yan H, Zhu S L 2020 Sci. China: Phys., Mech. Astron. 63 267062
Google Scholar
[41] Tang L Z, Zhang L F, Zhang G Q, Zhang D W 2020 Phys. Rev. A 101 063612
Google Scholar
[42] Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301
Google Scholar
[43] Budich J C, Bergholtz E J 2020 Phys. Rev. Lett. 125 180403
Google Scholar
[44] Koch F, Budich J C 2022 Phys. Rev. Res. 4 013113
Google Scholar
[45] Pati A K, Singh U, Sinha U 2015 Phys. Rev. A 92 052120
Google Scholar
[46] Heeger A J, Kivelson S, Schrieffer J R, Su W P 1988 Rev. Mod. Phys. 60 781
Google Scholar
[47] Yin C H, Jiang H, Li L H, Lü R, Chen S 2018 Phys. Rev. A 97 052115
Google Scholar
[48] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[49] Yuce C 2018 Phys. Rev. A 97 042118
Google Scholar
[50] Li C, Zhang G, Zhang X Z, Song Z 2014 Phys. Rev. A 90 012103
Google Scholar
[51] Guo Z X, Yu X J, Hu X D, Li Z 2022 Phys. Rev. A 105 053311
Google Scholar
[52] Jordan P, Wigner E 1928 Z. Physik 47 631
Google Scholar
[53] Qi X L, Wu Y S, Zhang S C 2006 Phys. Rev. B 74 085308
Google Scholar
[54] Kawabata K, Shiozaki K, Ueda M 2018 Phys. Rev. B 98 165148
Google Scholar
-
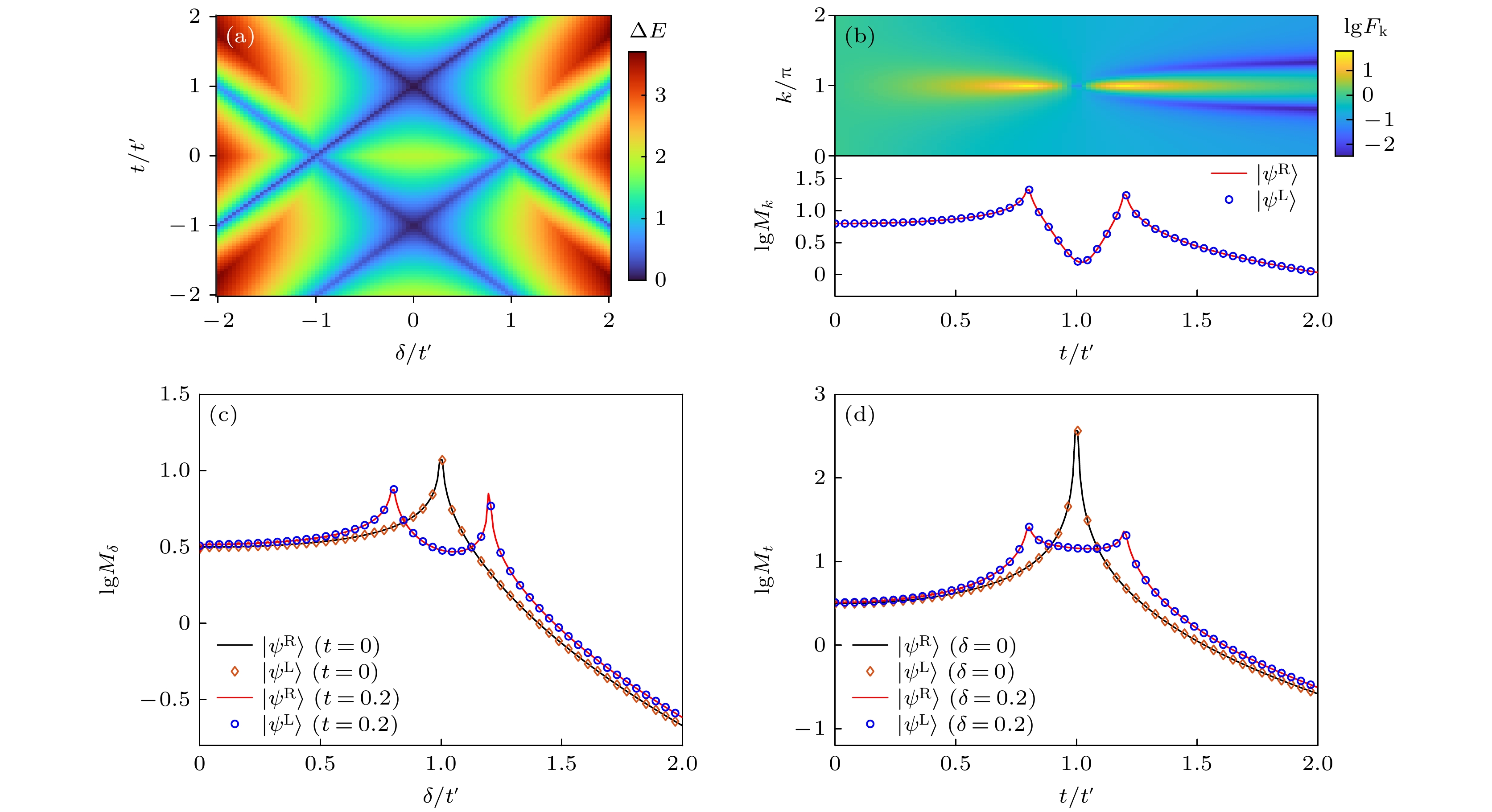
图 1 基于非互易SSH模型的单参数估计 (a)能隙
$ \Delta E $ 随t和δ的变化; (b)$ \delta=0.2 $ 时利用右本征矢$ |\psi^{{\rm{R}}}\rangle $ 评估k的量子Fisher信息$ F_k $ 随k和t的变化(上图)及其积分$ M_k $ 随t的变化(下图实线); (c)利用$ |\psi^{{\rm{R}}}\rangle $ 评估δ时$ M_\delta $ 随δ的变化(实线); (d)利用$ |\psi^{{\rm{R}}}\rangle $ 评估t时$ M_t $ 随t的变化(实线). 图(b)—(d)中的数据点表示利用左本征矢$ |\psi^{{\rm{L}}}\rangle $ 评估k, t或δ时相应的数值结果. 图中$ t^\prime=1 $ ,$ F_k $ 和$ M_\mu $ 做对数处理Fig. 1. Single-parameter estimation based on the non-reciprocal SSH model: (a) Energy gap
$ \Delta E $ as functions of t and δ; (b)$ F_k $ by the right eigenstate$ |\psi^{{\rm{R}}}\rangle $ as functions of k and t for estimating k (top) and the integration$ M_k $ by$ |\psi^{{\rm{R}}}\rangle $ as a function of t (solid line in the bottom)with$ \delta=0.2 $ ; (c) the integration$ M_\delta $ by using$ |\psi^{{\rm{R}}}\rangle $ (solid line) as a function of δ for estimating δ; (d) the integration$ M_t $ by using$ |\psi^{{\rm{R}}}\rangle $ (solid line) as a function of t for estimating t. The data points in panels (b)–(d) denote the corresponding numerical results for estimating k, t or δ by using the left eigenstate$ |\psi^{{\rm{L}}}\rangle $ .$ t^\prime=1 $ is set and$ F_k $ and$ M_\mu $ are logarithmically plotted in the picture.
图 2 原胞数
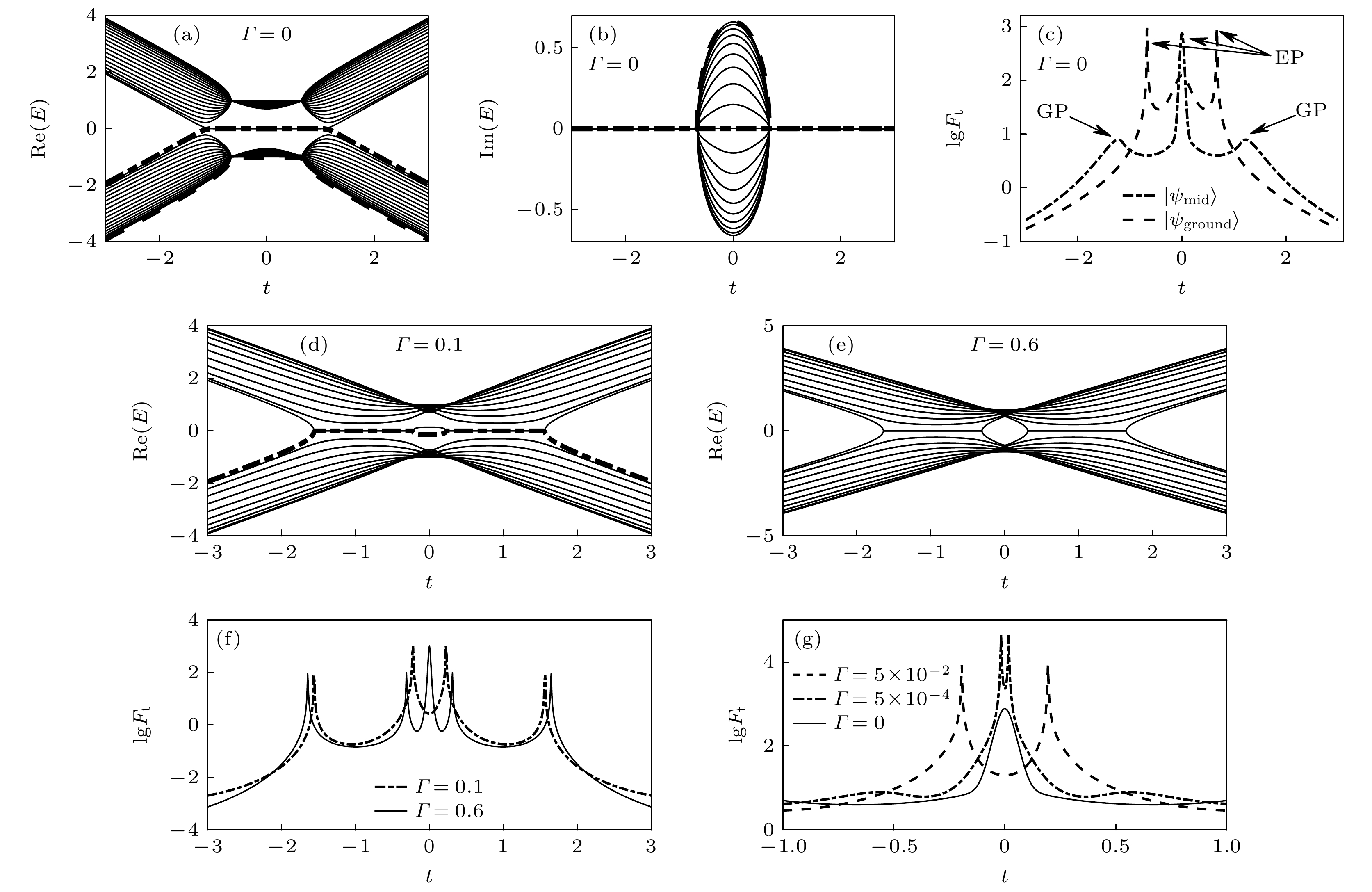
$ N=20 $ 的非互易SSH模型在不同边界耦合常数Γ下的单参数估计 (a)和(b)分别是开边界情况$ \varGamma = 0 $ 时本征能量的实部与虚部随参数t的变化; (c)为开边界条件下利用中间能态$ |\psi_{{\rm{mid}}}\rangle $ 和基态$ |\psi_{{\rm{ground}}}\rangle $ 评估参数t的量子Fisher信息$ F_{t} $ 随t的变化, 图中EP表示例外点, GP表示能隙闭合点; (d)和(e)分别是$ \varGamma = 0.1, 0.6 $ 时本征能量实部随t的变化; (f)和(g)为不同边界耦合常数Γ下$ F_{t} $ 随t的变化. 图中$ t^\prime=1,\; \delta=2/3 $ ,$ F_{t} $ 做对数处理Fig. 2. Single-parameter estimation based on the non-reciprocal SSH model with different boundary coupling coefficients Γ and the unit cell of
$ N=20 $ : (a) The real part and (b) the imaginary part of the eigen-spectrum as functions of t under open boundary condition with$ \varGamma = 0 $ ; (c)$ F_t $ as a function of t by the mid-spectrum eigenstate$ |\psi_{{\rm{mid}}}\rangle $ and the ground state$ |\psi_{{\rm{ground}}}\rangle $ for estimating t with$ \varGamma = 0 $ . Here EP and GP denote exceptional point and gapless point, respectively; (d) and (e) the real part of energy as a function of t with$ \varGamma = 0.1, 0.6 $ , respectively; (f) and (g)$ F_t $ as a function of t different values of Γ. In the figure,$ t^\prime=1,\; \delta=2/3 $ , and$ F_{t} $ is logarithmically plotted.
图 3 基于具有增益-耗散的SSH模型((a), (b))和非厄米量子Ising链((c), (d))的单参数估计 (a)能隙
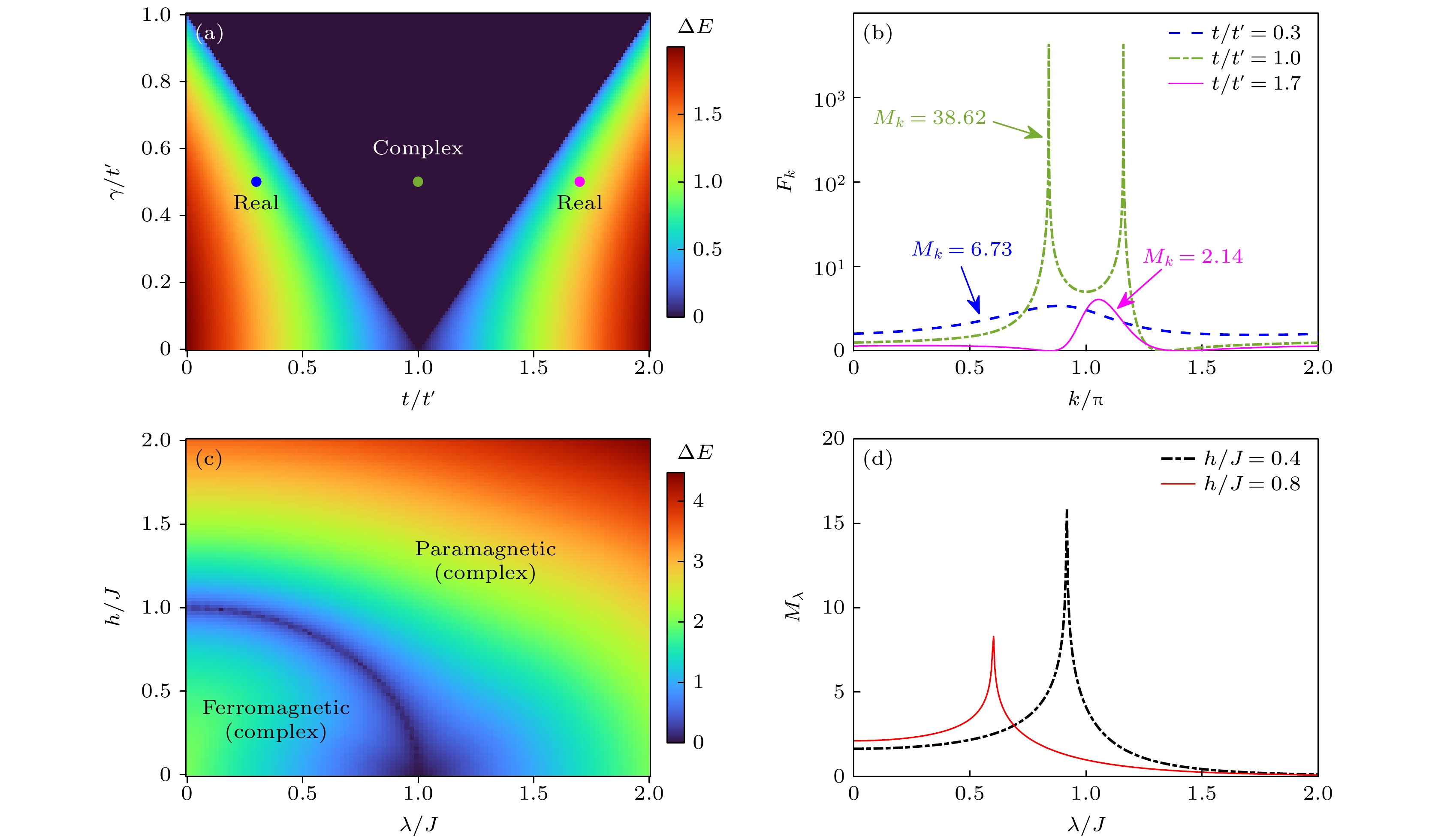
$ \Delta E $ 随t和γ的变化, 有能隙区域能谱为实, 无能隙区域能谱为复且存在EP点; (b)$ \gamma=0.5 $ 和$ t=\{0.3, 1, 1.7\} $ 时评估k的量子Fisher信息$ F_k $ 随k的变化; (c)能隙$ \Delta E $ 随λ和h的变化, 能隙关闭处为复能量的铁磁态和顺磁态的相边界; (d)评估λ时的$ M_\lambda $ 随λ的变化. 图中$ t^\prime=1 $ 和$ J=1 $ Fig. 3. Single-parameter estimation based on the gain-and-loss SSH model ((a), (b)) and the non-Hermtian quantum Ising chain ((c), (d)): (a) Energy gap
$ \Delta E $ as functions of t and γ, and the gapped (gapless) region contains real (complex) eigen-spectrum (with exceptional points); (b)$ F_k $ as a function of k for estimating k with$ \gamma=0.5 $ and$ t=\{0.3, 1, 1.7\} $ ; (c) energy gap$ \Delta E $ as functions of λ and h, and the gapless line denotes the phase boundary between the ferromagnetic and paramagnetic states with complex energies; (d)$ M_\lambda $ as a function of λ for estimating λ.$ t^\prime=1 $ and$ J=1 $ are set.
图 4 基于非厄米陈绝缘体模型的两参数估计 (a)拓扑相图, 包括有能隙的拓扑和平庸区域, 分别对应陈数
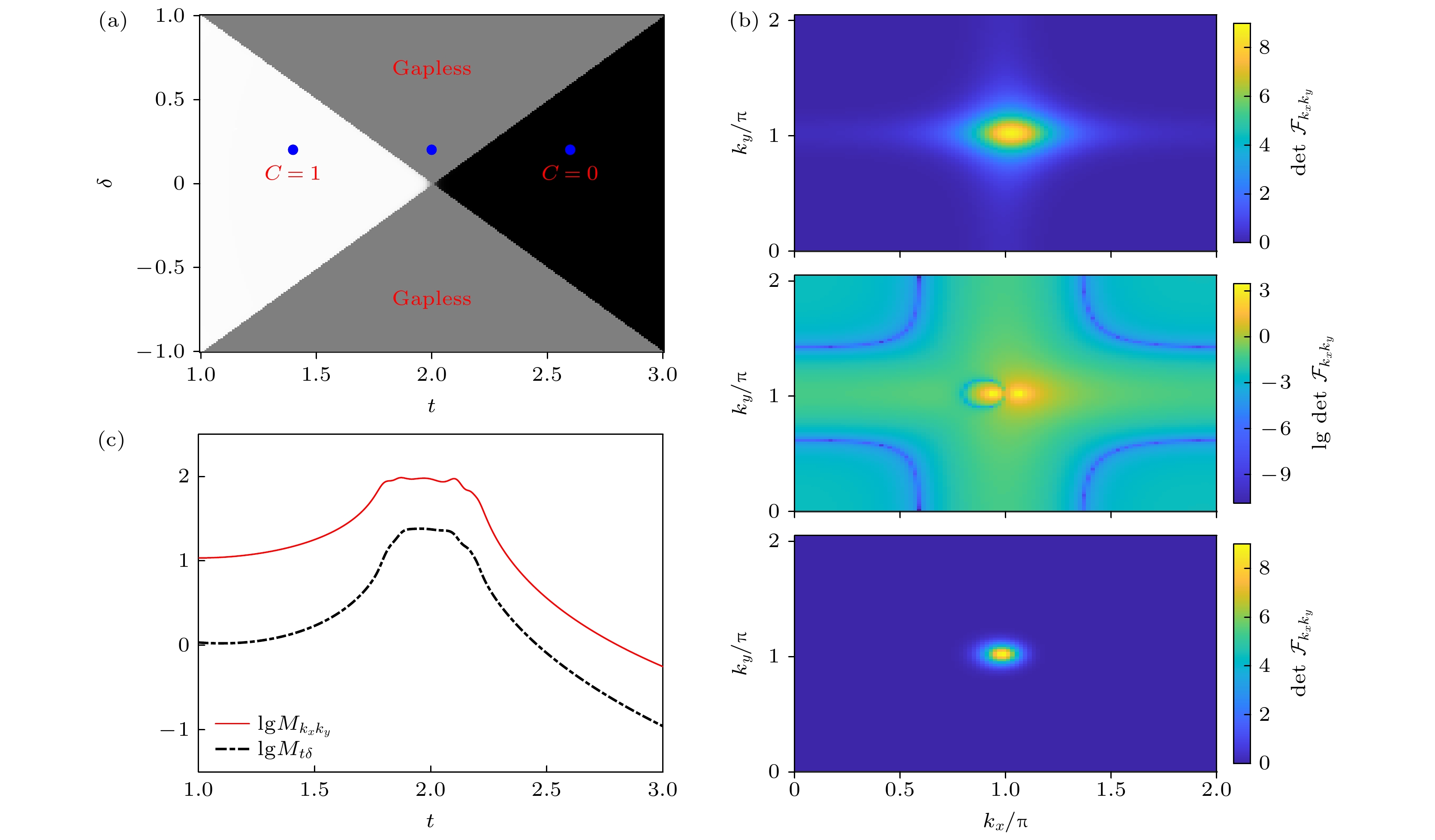
$ C=1 $ 和$ C=0 $ , 以及无能隙区域; (b)$ \delta=0.2 $ 和$ t=\{1.4, 2, 2.6\} $ (依次从上到下)时评估$ \{k_x, k_y\} $ 的量子Fisher信息矩阵行列式$ {\rm{det}}{\cal{F}}{_{k_xk_y}} $ 随$ k_x, k_y $ 的变化; (c)$ \delta=0.2 $ 时评估$ \{k_x, k_y\} $ 的$ M_{k_xk_y} $ 和评估$ \{t, \delta\} $ 的$ M_{t\delta} $ 随t的变化. 图(c)中$ M_{\mu\nu} $ 和图(b)中间图$ {\rm{det}}{\cal{F}}{_{k_xk_y}} $ 做对数处理Fig. 4. Two-parameter estimation based on the non-Hermtian Chern-insulator model: (a) Topological phase diagram with gapped topological (
$ C=1 $ ), trivial ($ C=0 $ ), and gapless regions; (b) determinant of quantum Fisher information matrix$ {\rm{det}}{\cal{F}}{_{k_xk_y}} $ as functions of$ k_x $ and$ k_y $ for estimating$ \{k_x, k_y\} $ with$ \delta=0.2 $ and$ t=\{1.4, 2, 2.6\} $ (from top to bottom); (c) the integration$ M_{k_xk_y} $ for estimating$ \{k_x, k_y\} $ and$ M_{t\delta} $ for estimating$ \{t, \delta\} $ as a function of t with$ \delta=0.2 $ .$ M_{\mu\nu} $ in panel (c) and$ {\rm{det}}{\cal{F}}{_{k_xk_y}} $ in the middle of panels (b) are logarithmically plotted.
图 5 基于非厄米二能级系统的两参数估计评估
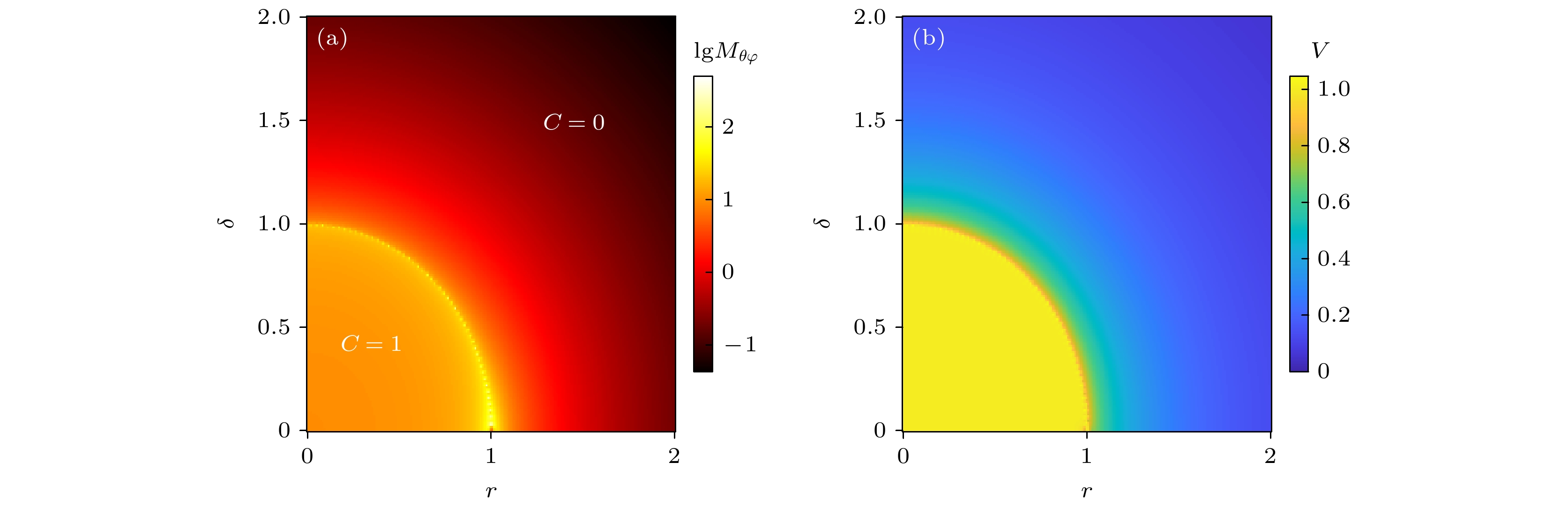
$ \{k_x, k_y\} $ 时, (a)$ M_{k_xk_y} $ 和(b)V随r和δ的变化. 图(a)中$ M_{k_xk_y} $ 做对数处理Fig. 5. Two-parameter estimation based on the non-Hermitian two-level system. (a)
$ M_{k_xk_y} $ and (b) V as functions of r and δ for estimating$ \{k_x, k_y\} $ .$ M_{k_xk_y} $ in panel (a) is logarithmically plotted. -
[1] Helstrom C W 1969 J. Stat. Phys. 1 231
Google Scholar
[2] Braunstein S L, Caves C M 1994 Phys. Rev. Lett. 72 3439
Google Scholar
[3] Liu J, Yuan H D, Lu X M, Wang X G 2020 J. Phys. A: Math. Theor. 53 023001
Google Scholar
[4] Sidhu J S, Kok P 2020 AVS Quantum Sci. 2 014701
Google Scholar
[5] 任志红, 李岩, 李艳娜, 李卫东 2019 68 040601
Google Scholar
Ren Z H, Li Y, Li Y N, Li W D 2019 Acta Phys. Sin. 68 040601
Google Scholar
[6] Provost J P, Vallee G 1980 Commun. Math. Phys. 76 289
Google Scholar
[7] Mera B, Zhang A W, Goldman N 2022 SciPost Phys. 12 018
Google Scholar
[8] Guo W, Zhong W, Jing X X, Fu L B, Wang X G 2016 Phys. Rev. A 93 042115
Google Scholar
[9] Tan X S, Zhang D W, Yang Z, Chu J, Zhu Y Q, Li D Y, Yang X P, Song S Q, Han Z K, Li Z Y, Dong Y Q, Yu H F, Yan H, Zhu S L, Yu Y 2019 Phys. Rev. Lett. 122 210401
Google Scholar
[10] Tan X S, Zhang D W, Zheng W, Yang X P, Song S Q, Han Z K, Dong Y Q, Wang Z M, Lan D, Yan H, Zhu S L, Yu Y 2021 Phys. Rev. Lett. 126 017702
Google Scholar
[11] Ding H T, Zhu Y Q, He P, Liu Y G, Wang J T, Zhang D W, Zhu S L 2022 Phys. Rev. A 105 012210
Google Scholar
[12] Yu M, Liu Y, Yang P C, Gong M S, Cao Q Y, Zhang S L, Liu H B, Heyl M, Ozawa T, Goldman N, Cai J M 2022 npj Quantum Inf. 8 56
Google Scholar
[13] Yu M, Li X B, Chu Y M, Mera B, Ünal F N, Yang P C, Liu Y, Goldman N, Cai J M 2022 arXiv: 2206.00546[quant-ph
[14] Li C H, Chen M, Cappellaro P 2022 arXiv: 2204.13777[quant-ph
[15] Zhang X Y, Lu X M, Liu J, Ding W K, Wang X G 2023 Phys. Rev. A 107 012414
Google Scholar
[16] Boixo S, Flammia S T, Caves C M, Geremia J M 2007 Phys. Rev. Lett. 98 090401
Google Scholar
[17] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222
Google Scholar
[18] 刘然, 吴泽, 李宇晨, 陈昱全, 彭新华 2023 72 110305
Google Scholar
Liu R, Wu Z, Li Y C, Chen Y Q, Peng X H 2023 Acta Phys. Sin. 72 110305
Google Scholar
[19] Di Candia R, Minganti F, Petrovnin K V, Paraoanu G S, Felicetti S 2023 npj Quantum Inf. 9 23
Google Scholar
[20] Liang H B, Su Y G, Xiao X, Che Y M, Sanders B C, Wang X G 2020 Phys. Rev. A 102 013722
Google Scholar
[21] He W T, Lu C W, Yao Y X, Zhu H Y, Ai Q 2023 Front. Phys. 18 31304
Google Scholar
[22] 牛明丽, 王月明, 李志坚 2022 71 090601
Google Scholar
Niu M L, Wang Y M, Li Z J 2022 Acta Phys. Sin. 71 090601
Google Scholar
[23] Lu X M, Wang X G 2021 Phys. Rev. Lett. 126 120503
Google Scholar
[24] Lin Q, Li T Y, Xiao L, Wang K K, Yi W, Xue P 2022 Nat. Commun. 13 3229
Google Scholar
[25] Xiao L, Deng T S, Wang K K, Zhu G Y, Wang Z, Yi W, Xue P 2020 Nat. Phys. 16 761
Google Scholar
[26] Li J M, Harter A K, Liu J, Leonardo D M, Joglekar Y N, Luo L 2019 Nat. Commun. 10 855
Google Scholar
[27] Wu Y, Liu W Q, Geng J P, Song X R, Ye X Y, Duan C K, Rong X, Du J F 2019 Science 364 878
Google Scholar
[28] Naghiloo M, Abbasi M, Joglekar Y N, Murch K W 2019 Nat. Phys. 15 1232
Google Scholar
[29] 高雪儿, 李代莉, 刘志航, 郑超 2022 71 240303
Google Scholar
Gao X E, Li D L, Liu Z H, Zheng C 2022 Acta Phys. Sin. 71 240303
Google Scholar
[30] 张禧征, 王鹏, 张坤亮, 杨学敏, 宋智 2022 71 174501
Google Scholar
Zhang X Z, Wang P, Zhang K L, Yang X M, Song Z 2022 Acta Phys. Sin. 71 174501
Google Scholar
[31] Solnyshkov D D, Leblanc C, Bessonart L, Nalitov A, Ren J H, Liao Q, Li F, Malpuech G 2021 Phys. Rev. B 103 125302
Google Scholar
[32] Liao Q, Leblanc C, Ren J H, Li F, Li Y M, Solnyshkov D, Malpuech G, Yao J N, Fu H B 2021 Phys. Rev. Lett. 127 107402
Google Scholar
[33] Wiersig J 2020 Photonics Res. 8 1457
Google Scholar
[34] Zhang D W, Zhu Y Q, Zhao Y X, Yan H, Zhu S L 2018 Adv. Phys. 67 253
Google Scholar
[35] Lang L J, Zhu S L, Chong Y D 2021 Phys. Rev. B 104 L020303
Google Scholar
[36] Zhang D W, Chen Y L, Zhang G Q, Lang L J, Li Z, Zhu S L 2020 Phys. Rev. B 101 235150
Google Scholar
[37] Xu Z C, Zhou Z Y, Cheng E H, Lang L J, Zhu S L 2022 Sci. China: Phys., Mech. Astron. 65 283011
Google Scholar
[38] Shen H T, Zhen B, Fu L 2018 Phys. Rev. Lett. 120 146402
Google Scholar
[39] Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803
Google Scholar
[40] Zhang D W, Tang L Z, Lang L J, Yan H, Zhu S L 2020 Sci. China: Phys., Mech. Astron. 63 267062
Google Scholar
[41] Tang L Z, Zhang L F, Zhang G Q, Zhang D W 2020 Phys. Rev. A 101 063612
Google Scholar
[42] Jiang H, Lang L J, Yang C, Zhu S L, Chen S 2019 Phys. Rev. B 100 054301
Google Scholar
[43] Budich J C, Bergholtz E J 2020 Phys. Rev. Lett. 125 180403
Google Scholar
[44] Koch F, Budich J C 2022 Phys. Rev. Res. 4 013113
Google Scholar
[45] Pati A K, Singh U, Sinha U 2015 Phys. Rev. A 92 052120
Google Scholar
[46] Heeger A J, Kivelson S, Schrieffer J R, Su W P 1988 Rev. Mod. Phys. 60 781
Google Scholar
[47] Yin C H, Jiang H, Li L H, Lü R, Chen S 2018 Phys. Rev. A 97 052115
Google Scholar
[48] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[49] Yuce C 2018 Phys. Rev. A 97 042118
Google Scholar
[50] Li C, Zhang G, Zhang X Z, Song Z 2014 Phys. Rev. A 90 012103
Google Scholar
[51] Guo Z X, Yu X J, Hu X D, Li Z 2022 Phys. Rev. A 105 053311
Google Scholar
[52] Jordan P, Wigner E 1928 Z. Physik 47 631
Google Scholar
[53] Qi X L, Wu Y S, Zhang S C 2006 Phys. Rev. B 74 085308
Google Scholar
[54] Kawabata K, Shiozaki K, Ueda M 2018 Phys. Rev. B 98 165148
Google Scholar
下载:
计量
- 文章访问数: 3613
- PDF下载量: 206
- 被引次数: 0
