-
锡(Sn)是13.5 nm光刻光源的材料, Sn等离子体辐射性质对光源设计意义重大. 基于细致能级模型, 在局域热平衡假设条件下计算得到了Sn等离子体辐射不透明度和发射谱. 使用多组态Dirac-Fock方法获得了
${\rm{Sn}}^{6+}\text{-}{\rm{Sn}}^{14+}$ 离子的能级和辐射跃迁振子强度等基本原子参数. 针对波长在13.5 nm附近的4d-4f和4p-4d跃迁系, 重点考虑了4dm-4f m(m = 1, 2, 3, 4)和4pn-4dn(n = 1, 2, 3)的电子关联效应. 在大规模组态相互作用计算中, 每种电荷态离子的精细能级数目约为20万. 对较强的吸收谱线(振子强度大于0.01), 其长度和速度表示的相对差异为20%—30%. 基于精密原子参数, 计算了Sn等离子体在30 eV, 0.01 g/cm3条件下的透射谱, 与实验结果基本符合. 系统计算了温度16—30 eV, 密度0.0001—0.1 g/cm3条件下的Sn等离子体辐射不透明度和发射光谱, 分析了极紫外(extreme ultraviolet, EUV)光谱随温度和密度的变化规律. 研究表明温度一定时, 密度增大会使得13.5 nm附近的辐射不透明度和发射谱包络增宽. 而密度一定时, 随着温度的增加, 辐射不透明度和发射谱在13.5 nm附近存在明显的窄化效应. 本文工作有助于EUV光刻光源的设计和研究.Sn is the material for an extreme ultraviolet (EUV) light source working at 13.5 nm, therefore the radiative properties of Sn plasma are of great importance in designing light source. The radiative opacity and emissivity of Sn plasma at local thermodynamic equilibrium are investigated by using a detailed-level-accounting model. In order to obtain precise atomic data, a multi-configuration Dirac-Fock method is used to calculate energy levels and oscillator strengths of${\rm{Sn}}^{6+}$ -${\rm{Sn}}^{14+}$ . The electronic correlation effects of$4{\rm d}^m\text{-}4{\rm f}^m$ ($m=1, 2, 3, 4$ ) and$ 4\mathrm{p}^n\text{-}4\mathrm{d}^n $ ($n=1, 2, 3$ ) are mainly considered, which dominate the radiation near 13.5 nm. The number of fine-structure levels reaches about 200000 for each ionization stage in the present large-scale configuration interaction calculations. For the large oscillator strengths (> 0.01), the length form is in accord with the velocity form and their relative difference is about 20%–30%. The calculated transmission spectra of Sn plasma at 30 eV and 0.01 g/cm3 are compared with the experimental result, respectively, showing that they have both good consistency. The radiative opacity and emissivity of Sn plasma at the temperature in a range of 16–30 eV and density in a scope of of 0.0001–0.1 g/cm3 are investigated systematically. The effects of the plasma temperature and plasma density on radiation characteristics are studied. The results show that the radiative properties near 13.5 nm are broadened with the increase of density at a specific temperature, while it is narrowed with the increase of temperature for a specific density. The present investigation should be helpful in designing and studying EUV light source in the future.-
Keywords:
- extreme ultraviolet light source /
- detailed-level-accounting model /
- configuration interaction
[1] Pirati A, Van Shoot J, Troost K, van Ballegoij R, Krabbendam P, Stoeldraijer J, Loopstra E, Benschop J, Finders J, Meiling H, van Setten E, Mika N, Driedonkx J, Stamm U 2017 Proc. SPIE 10143 101430G
Google Scholar
[2] Hutcheson G D 2018 Proc. SPIE 10583 1058303
[3] David A 2007 Soft x-rays and Extreme Ultraviolet Radiation: Principles and Applications (Cambridge: Cambridge University Press) pp17–20
[4] 宗楠, 胡蔚敏, 王志敏, 王小军, 张申金, 薄勇, 彭钦军, 许祖彦 2020 中国光学 13 28
Google Scholar
Zong N, Hu W M, Wang Z M, Wang X J, Zhang S J, Bo Y, Peng Q J, Xu Z Y 2020 Chin. Opt. 13 28
Google Scholar
[5] Versolato O O 2019 Plasma Sources Sci. Technol. 28 083001
Google Scholar
[6] Kieft E R, Garloff K, van der Mullen J J A M, Banine V 2005 Phys. Rev. E 71 036402
Google Scholar
[7] Ueno Y, Soumagne G, Sumitani A, Endo A, Higashiguchi T 2007 Appl. Phys. Lett. 91 231501
Google Scholar
[8] Svendsen W, O’Sullivan G 1994 Phys. Rev. A 50 3710
Google Scholar
[9] Churilov S S, Ryabtsev A N 2006 Opt. Spectrosc. 101 169
Google Scholar
[10] D'Arcy R, Ohashi H, Suda S, Tanuma H, Fujioka S, Nishimura H, Nishihara K, Suzuki C, Kato T, Koike F, White J, O’Sullivan G 2009 Phys. Rev. A 79 042509
Google Scholar
[11] Ohashi H, Suda S, Tanuma H, Fujioka S, Nishimura H, Sasaki A, Nishihara K 2010 J. Phys. B: At. Mol. Opt. Phys. 43 065204
Google Scholar
[12] O'Sullivan G, Li B, D’Arcy R, Dunne P, Hayden P, Kilbane D, McCormack T, Ohashi H, O'Reilly F, Sheridan P, Sokell E, Suzuki C, Higashiguchi T 2015 J. Phys. B: At. Mol. Opt. Phys. 48 144025
Google Scholar
[13] Windberger A, Torretti F, Borschevsky A, Ryabtsev A, Dobrodey S, Bekker H, Eliav E, Kaldor U, Ubachs W, Hoekstra R, Crespo López-Urrutia J R, Versolato O O 2016 Phys. Rev. A 94 012506
Google Scholar
[14] Torretti F, Windberger A, Ryabtsev A, Dobrodey S, Bekker H, Ubachs W, Hoekstra R, Kahl E V, Berengut J C, Crespo López-Urrutia J R, Versolato O O 2017 Phys. Rev. A 95 042503
Google Scholar
[15] Torretti F, Schupp R, Kurilovich D, Bayerle A, Scheers J, Ubachs W, Hoekstra R, Versolato O O 2018 J. Phys. B: At. Mol. Opt. Phys. 51 045005
Google Scholar
[16] de Gaufridy de Dortan F 2007 J. Phys. B: At. Mol. Opt. Phys. 40 599
Google Scholar
[17] Koike F, Fritzsche S 2007 Radiat. Phys. Chem. 76 404
Google Scholar
[18] Kagawa T, Tanuma H, Ohashi H, Nishihara K 2007 J. Phys.: Conf. Ser. 58 149
Google Scholar
[19] Eliav E, Kaldor U, Ishikawa Y 1994 Phys. Rev. A 49 1724
Google Scholar
[20] Berengut J C, Flambaum V V, Kozlov M G 2006 Phys. Rev. A 73 012504
Google Scholar
[21] Lysaght M, Kilbane D, Murphy N, Cummings A, Dunne P, O’Sullivan G 2005 Phys. Rev. A 72 014502
Google Scholar
[22] Fujioka S, Nishimura H, Nishihara K, Sasaki A, Sunahara A, Okuno T, Ueda N, Ando T, Tao Y, Shimada Y, Hashimoto K, Yamaura M, Shigemori K, Nakai M, Nagai K, Norimatsu T, Nishikawa T, Miyanaga N, Izawa Y, Mima K 2005 Phys. Rev. Lett. 95 235004
Google Scholar
[23] 蔡懿, 王文涛, 杨明, 刘建胜, 陆培祥, 李儒新, 徐至展 2008 57 5100
Google Scholar
Cai Y, Wang W T, Yang M, Liu J S, Lu P X, Li R X, Xu Z Z 2008 Acta Phys. Sin. 57 5100
Google Scholar
[24] 陈鸿, 兰慧, 陈子琪, 刘璐宁, 吴涛, 左都罗, 陆培祥, 王新兵 2015 64 075202
Google Scholar
Chen H, Lan H, Chen Z Q, Liu L N, Wu T, Zuo D L, Lu P X, Wang X B 2015 Acta Phys. Sin. 64 075202
Google Scholar
[25] Su M G, Min Q, Cao S Q, Sun D X, Hayden P, O’Sullivan G, Dong C Z 2017 Sci. Rep. 7 45212
Google Scholar
[26] Schupp R, Torretti F, Meijer R A, Bayraktar M, Sheil J, Scheers J, Kurilovich D, Bayerle A, Schafgans A A, Purvis M, Eikema K S E, Witte S, Ubachs W, Hoekstra R, Versolato O O 2019 Appl. Phys. Lett. 115 124101
Google Scholar
[27] Zeng J, Gao C, Yuan J 2010 Phys. Rev. E 82 026409
Google Scholar
[28] Colgan J, Kilcrease D P, Jr. Abdallah J, Sherrill M E, Fontes C J, Hakel P, Armstrong G S J 2017 High Energy Density Phys. 23 133
Google Scholar
[29] Torretti F, Sheil J, Schupp R, Basko M M, Bayraktar M, Meijer R A, Witte S, Ubachs W, Hoekstra R, Versolato O O, Neukirch A J, Colgan J 2020 Nat. Commun. 11 2334
Google Scholar
[30] Sheil J, Versolato O O, Neukirch A J, Colgan J 2021 J. Phys. B: At. Mol. Opt. Phys. 54 035002
Google Scholar
[31] Cowan R D 1981 The Theory of Atomic Structure and Spectra (Berkeley: University of California Press
[32] Jönson P, Gaigalas G, Bieroń, Froese Fischer C, Grant I P 2013 Comput. Phys. Commun. 184 2197
Google Scholar
[33] Zeng J L, Yuan J M 2006 Phys. Rev. E 74 025401(R
Google Scholar
[34] Gao C, Zeng J, Jin F, Yuan J 2013 High Energy Density Phys. 9 419
Google Scholar
[35] Zeng J L, Gao C, Liu P F, Li Y J, Meng C S, Hou Y, Kang D D, Yuan J M 2022 Sci. China-Phys. Mech. Astron. 65 233011
Google Scholar
[36] Stewart J C, Pyatt K D Jr. 1966 Astrophys. J. 144 1203
Google Scholar
[37] 李世昌 1992 高温辐射物理与量子辐射理论 (北京: 国防工业出版社) 第6页
Li S C 1992 High Temperature Radiation Physics and Quantum Radaition Theory (Beijing: National Defense Industry Press) p6
[38] Zeng J L, Zhao G, Yuan J M 2006 J. Quant. Spectrosc. Radiat. Transfer 102 172
Google Scholar
[39] Wu Z W, Tian Z Q, An Y H, Dong C Z 2021 Astrophys. J. 910 142
Google Scholar
[40] Kühn S, Cheung C, Oreshkina N S, Steinbrügge, Togawa M, Bernitt S, Berger L, Buck J, Hoesch M, Seltmann J, Trinter F, Keitel C H, Kozlov M G, Porsev S G, Gu M F, Porter F S, Pfeifer T, Leutenegger M A, Harman Z, Safronova M S, López-Urrutia J R C, Shah C 2022 Phys. Rev. Lett. 129 245001
Google Scholar
[41] Colgan J, Kilcrease D P, Magee N H, Sherrill M E, Abdallah Jr. J, Hakel P, Fontes C J, Guzik J A, Mussack K A 2016 Astrophys. J. 817 116
Google Scholar
[42] 兰慧 2016 博士学位论文 (武汉: 华中科技大学)
Lan H 2016 Ph. D. Dissertation (Wuhan: Huazhong University of Science and Technology
[43] Hansen S B, Chung H K, Fontes C J, Ralchenko Yu, Scott H A, Stambulchik E 2020 High Energy Density Phys. 35 100693
Google Scholar
[44] Gao C, Zeng J, Li Y, Jin F, Yuan J 2013 High Energy Density Phys. 9 583
Google Scholar
-
图 1 (a)
${\rm{Sn}}^{5+}$ , (b)${\rm{Sn}}^{8+}$ , (c)${\rm{Sn}}^{10+}$ 和(d)${\rm{Sn}}^{13+}$ 离子的4s, 4p, 4d和4f轨道波函数Fig. 1. Radial wavefunctions of 4s, 4p, 4d and 4f belonging to (a)
${\rm{Sn}}^{5+}$ , (b)${\rm{Sn}}^{8+}$ , (c)${\rm{Sn}}^{10+}$ and (d)${\rm{Sn}}^{13+}$ .
图 2
${\rm{Sn}}^{10+}$ 束缚组态, 其中长条表示相应组态分裂而成的精细能级的能量范围, 虚线表示电离阈值Fig. 2. Bound configurations of
${\rm{Sn}}^{10+}$ . Each bar represents the energy range of fine-structure levels belonging to the corresponding configuration. The dashed line represents ionization threshold.
图 3
${\rm{Sn}}^{10+}$ 振子强度 (a) 振子强度的长度和速度表示, 红色虚线斜率为1; (b) 波长11—20 nm的振子强度长度和速度表示的比值, 上下两条红色虚线分别表示比值为1和0.8Fig. 3. Oscillator strengths of
${\rm{Sn}}^{10+}$ : (a) Length and velocity forms of oscillator strengths; the slope of the red dashed line is 1; (b) ratio of length form to velocity form. The upper and lower red dashed lines represent 1 and 0.8, respectively.
图 4 温度30 eV, 密度0.01 g/cm3条件下Sn等离子体中不同电荷态对辐射不透明度的贡献 (a)
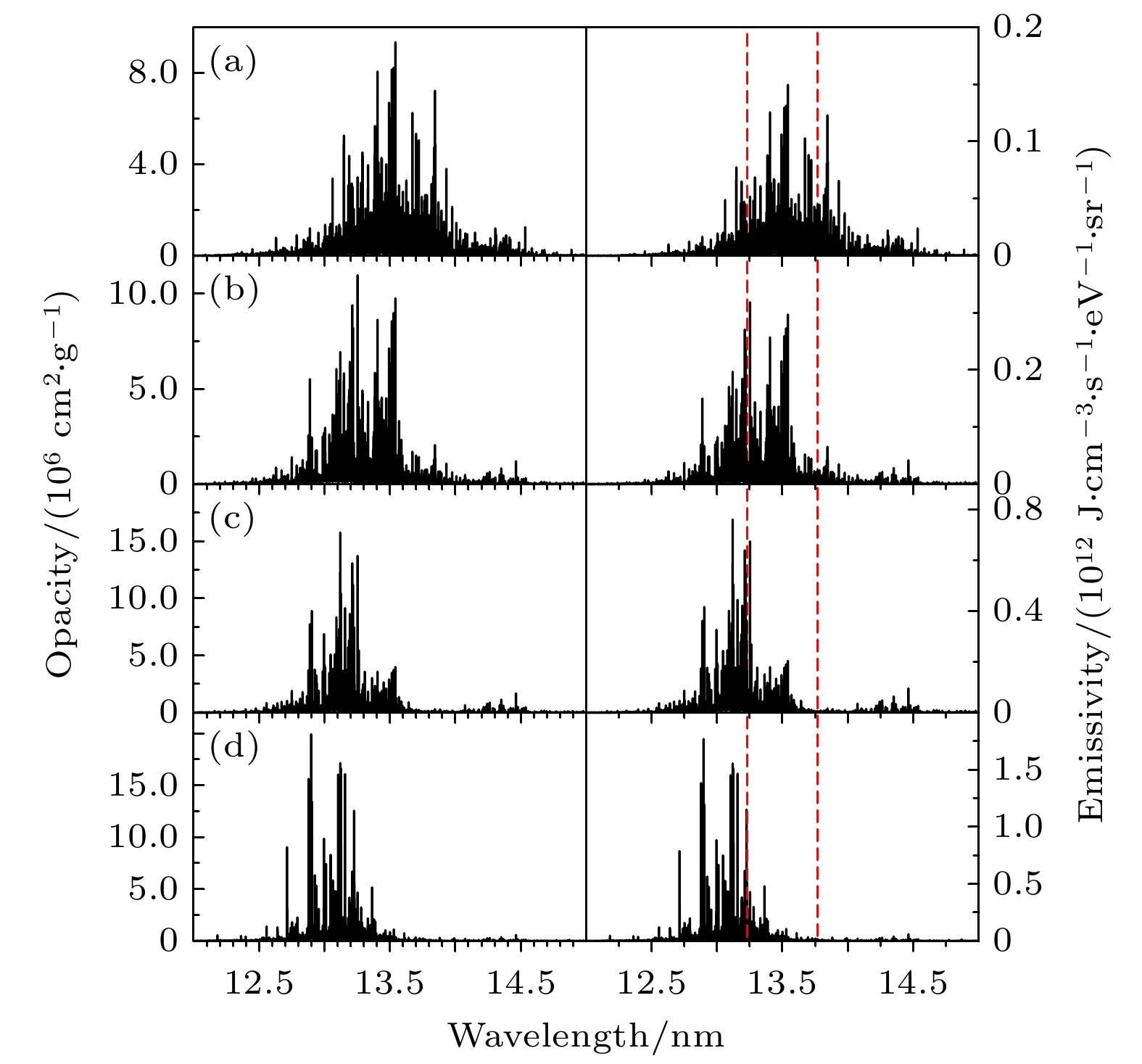
${\rm{Sn}}^{9+}$ ; (b)${\rm{Sn}}^{10+}$ ; (c)${\rm{Sn}}^{11+}$ ; (d)${\rm{Sn}}^{12+}$ ; (e)总不透明度, 红线为只包含基组态和单电子激发组态的结果, 绿线为包括了基组态、单电子和双电子激发组态的结果Fig. 4. Radiative opacity of Sn at a temperature of 30 eV and a density of 0.01 g/cm3 contributed by different ionization stages: (a)
${\rm{Sn}}^{9+}$ ; (b)${\rm{Sn}}^{10+}$ ; (c)${\rm{Sn}}^{11+}$ ; (d)${\rm{Sn}}^{12+}$ ; (e) total opacity. The red line represents the result including only ground and singly excited configurations. The green line represents the result including ground, singly and doubly excited configurations
图 5 Sn等离子体透射谱 (a)温度30 eV, 密度0.01 g/cm3时本文计算、ATOMIC[28]与实验[22]结果; (b) 本文计算的密度0.01 g/cm3, 温度为25, 27, 30和32 eV的Sn等离子体透射谱. 本文计算取仪器展宽为0.5 eV
Fig. 5. Transmission spectra of Sn plasmas: (a) Present calculation, ATOMIC[28] and experimental results[22] of Sn at a temperature of 30 eV and a density of 0.01 g/cm3; (b) present calculated transmission spectra of Sn at a density of 0.01 g/cm3 and temperatures of 25, 27, 30 and 32 eV. The instrumental broadening in the present calculation is set to be 0.5 eV
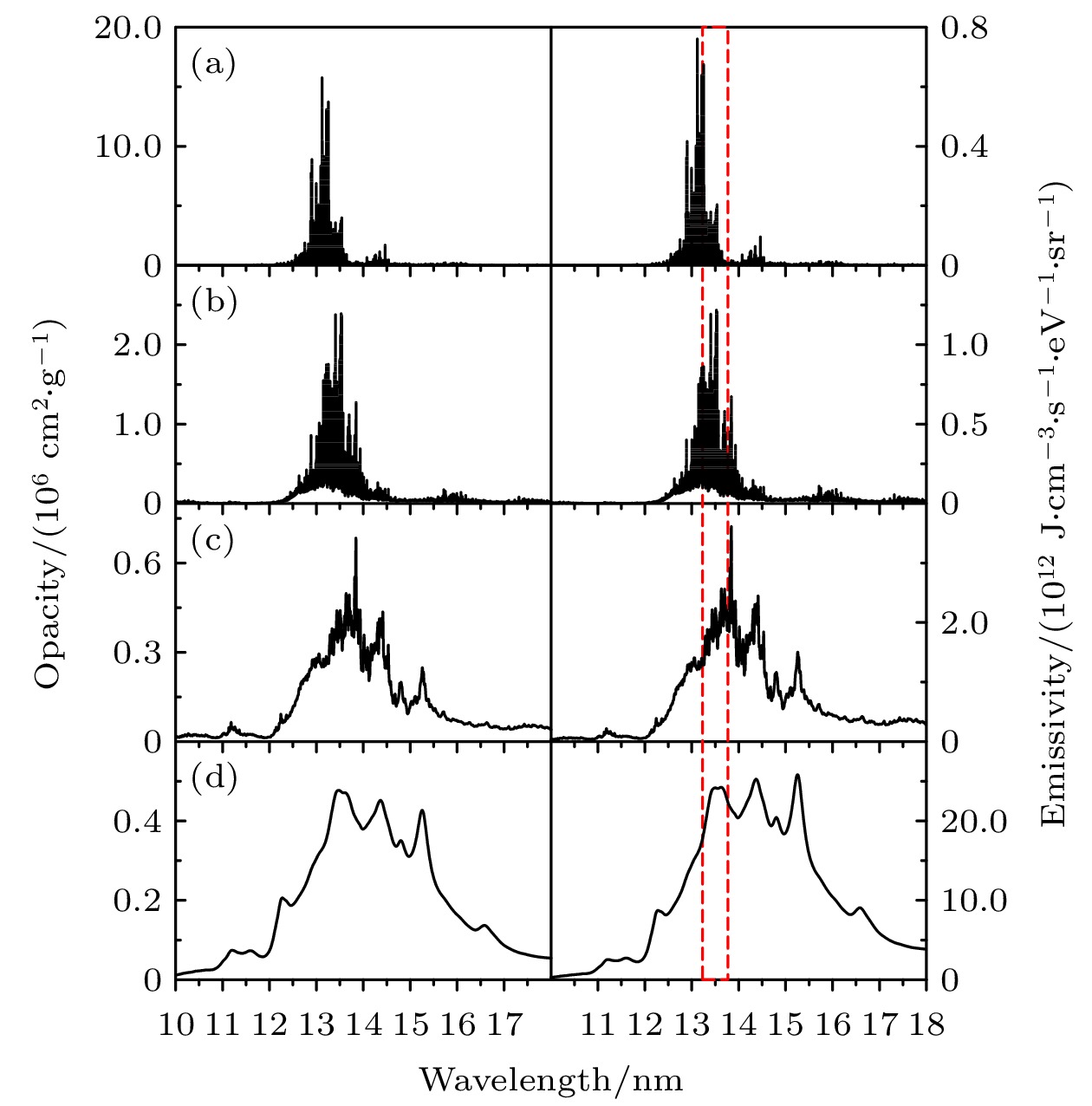
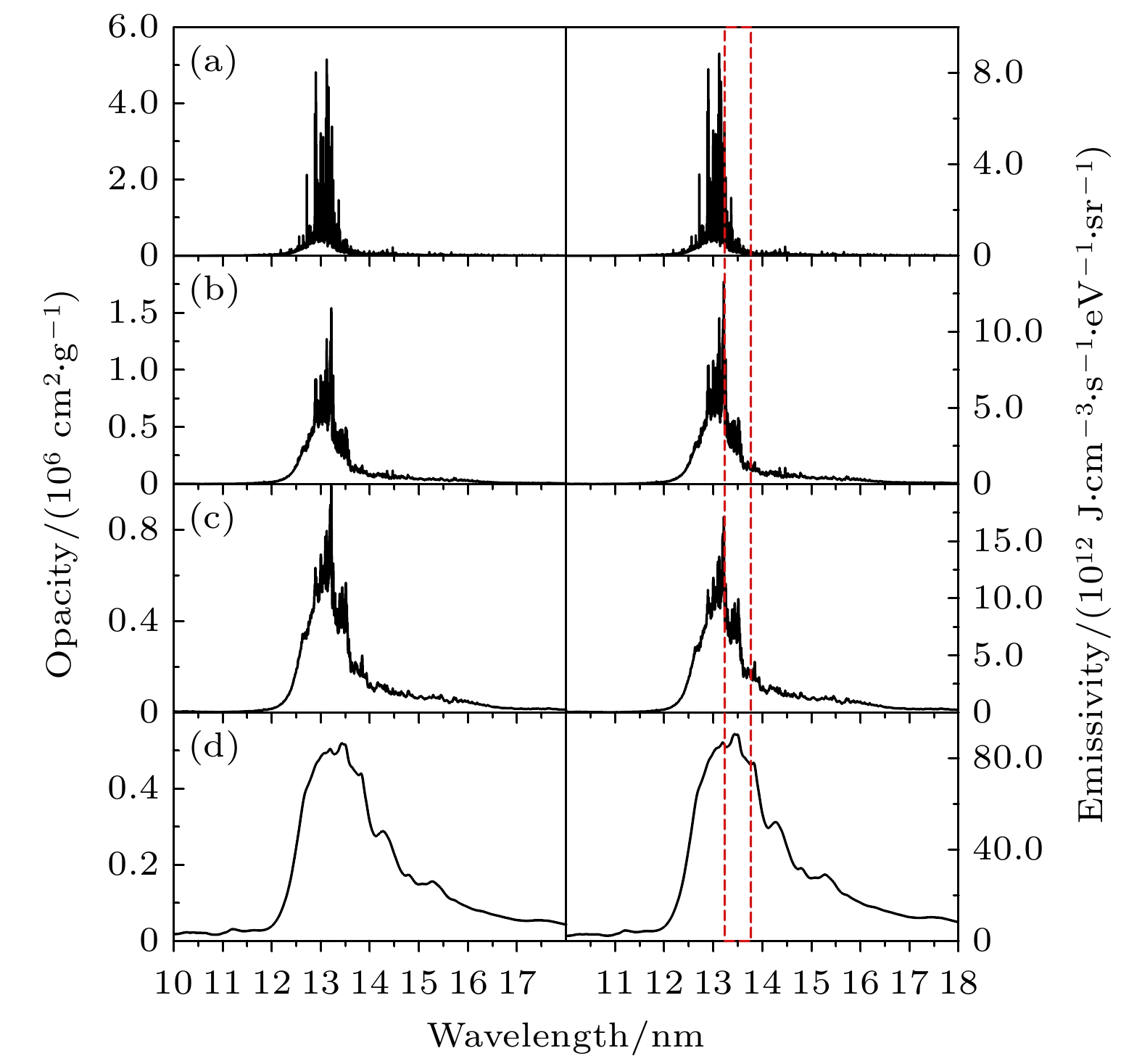
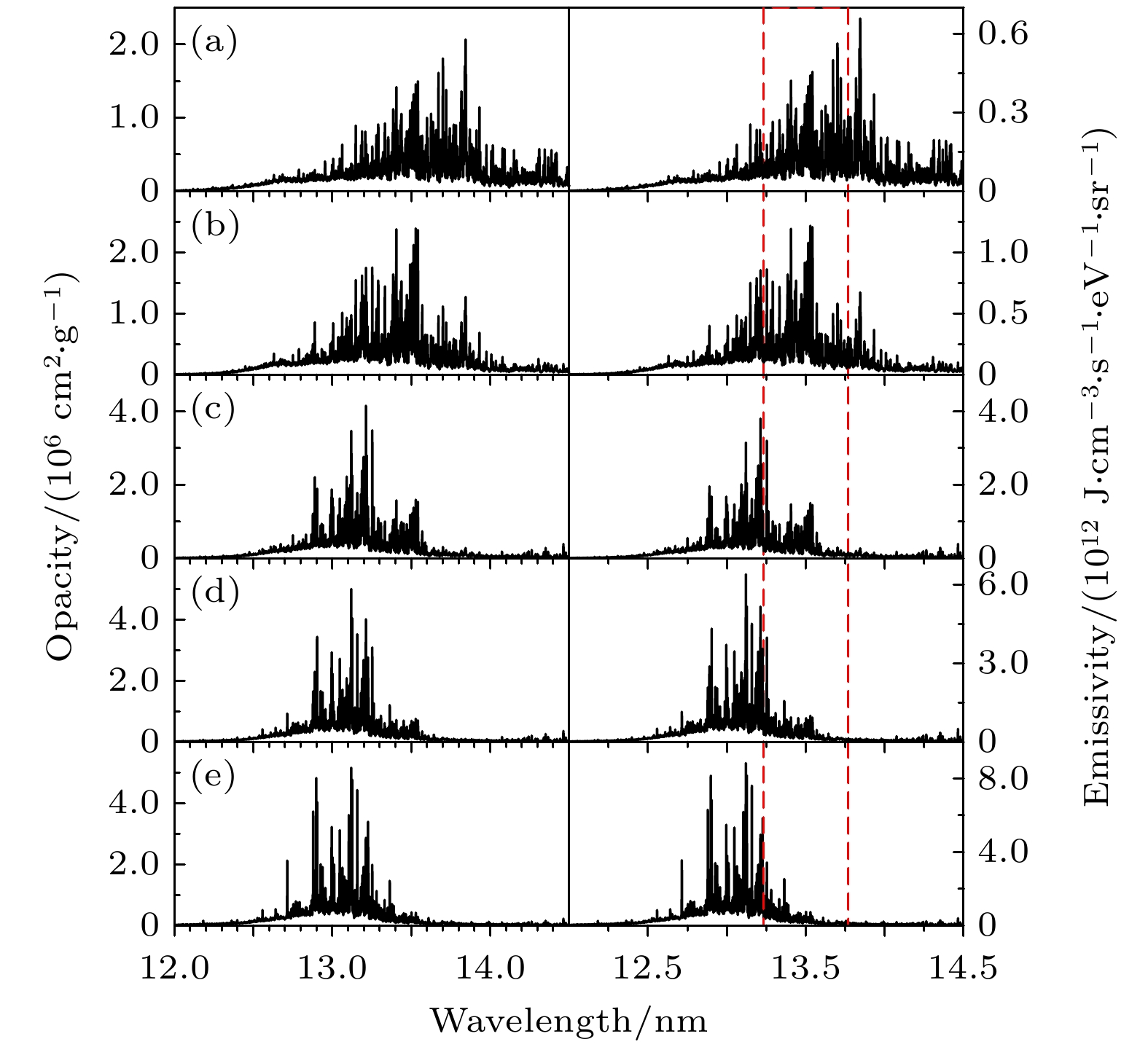
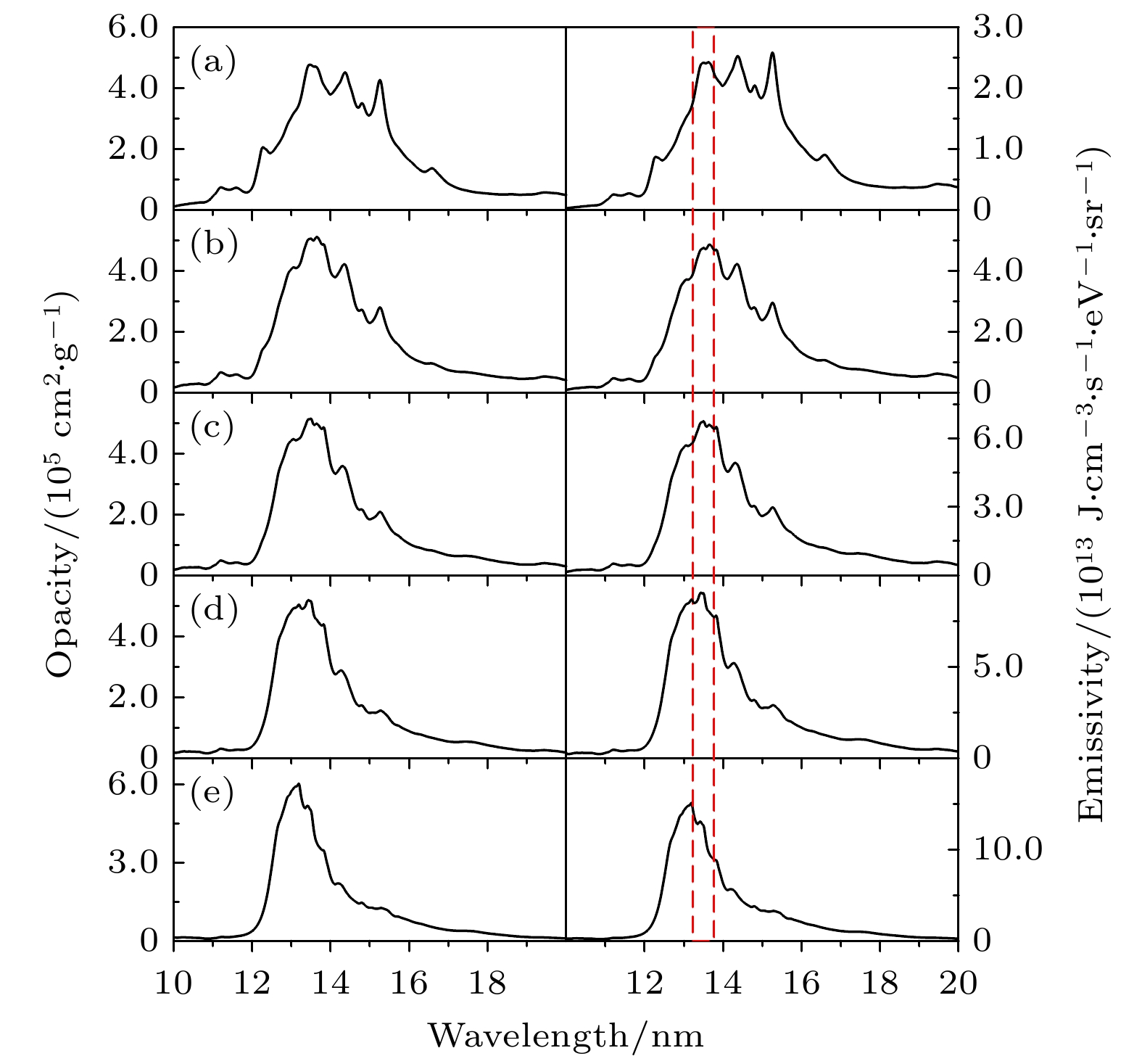
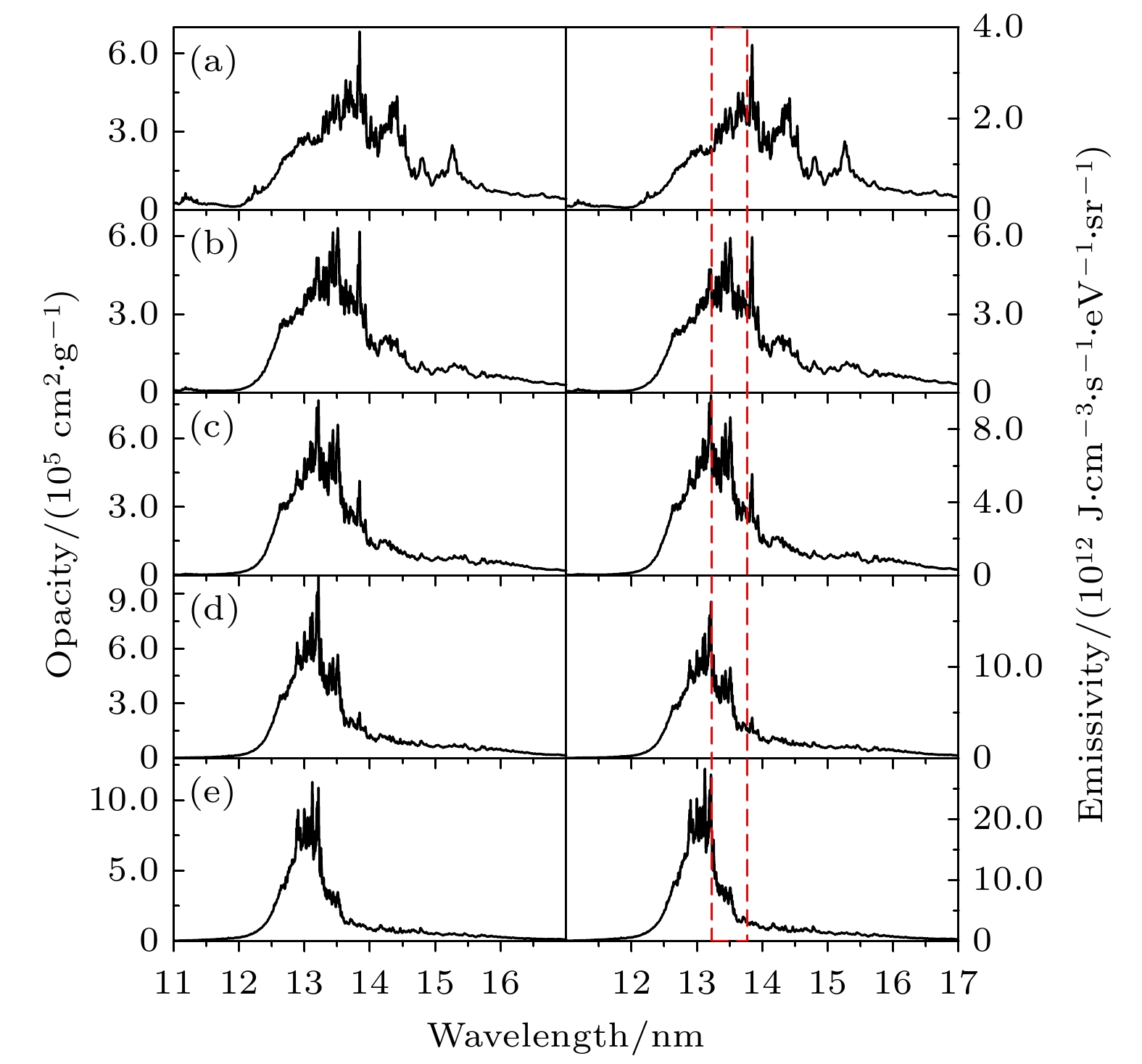
图 6 温度为20 eV, 密度为(a) 0.0001, (b) 0.001, (c) 0.01和(d) 0.1 g/cm3的Sn等离子体EUV辐射不透明度(左图)和发射系数(右图). 平均电离度分别为10.96, 9.63, 8.36和7.16, 自由电子密度分别为5.56 × 1018, 4.89 × 1019, 4.24 × 1020和3.63 × 1021 cm–3. 红色虚线表示中心波长13.5 nm, 带宽2%的波长范围
Fig. 6. EUV Radiative opacity (left) and emissivity (right) of Sn plasmas at a temperature of 20 eV and densities of (a) 0.0001, (b) 0.001, (c) 0.01 and (d) 0.1 g/cm3. The average ionization is 10.96, 9.63, 8.36 and 7.16, respectively. The free electron density is 5.56 × 1018, 4.89 × 1019, 4.24 × 1020 and 3.63 × 1021 cm–3, respectively. The red-dashed lines represent the 2% wavelength region centered at 13.5 nm
图 7 温度为23 eV, 密度为(a) 0.001, (b) 0.005, (c) 0.01和(d) 0.1 g/cm3的Sn等离子体EUV辐射不透明度(左图)和发射系数(右图)
Fig. 7. EUV Radiative opacity (left panel) and emissivity (right panel) of Sn plasmas at a temperature of 23 eV and densities of (a) 0.001, (b) 0.005, (c) 0.01 and (d) 0.1 g/cm3
图 8 温度为27 eV, 密度为(a) 0.001, (b) 0.005, (c) 0.01和(d) 0.1 g/cm3的Sn等离子体EUV辐射不透明度(左图)和发射系数(右图)
Fig. 8. EUV Radiative opacity (left panel) and emissivity (right panel) of Sn plasmas at a temperature of 27 eV and densities of (a) 0.001, (b) 0.005, (c) 0.01 and (d) 0.1 g/cm3
图 9 密度为0.0001 g/cm3, 温度为(a) 16, (b) 18, (c) 20和(d) 23 eV的Sn等离子体EUV辐射不透明度(左图)和发射系数(右图)
Fig. 9. EUV radiative opacity (left panel) and emissivity (right panel) of Sn plasmas at a density of 0.0001 g/cm3 and temperatures of (a) 16, (b) 18, (c) 20 and (d) 23 eV
图 10 密度为0.001 g/cm3, 温度为(a) 18, (b) 20, (c) 23, (d) 25和(e) 27 eV的Sn等离子体EUV辐射不透明度(左图)和发射系数(右图)
Fig. 10. EUV radiative opacity (left panel) and emissivity (right panel) of Sn plasmas at a density of 0.001 g/cm3 and temperatures of (a) 18, (b) 20, (c) 23, (d) 25 and (e) 27 eV
图 12 密度为0.1 g/cm3, 温度为(a) 20, (b) 23, (c) 25, (d) 27和(e) 30 eV的Sn等离子体EUV辐射不透明度(左图)和发射系数(右图)
Fig. 12. EUV radiative opacity (left panel) and emissivity (right panel) of Sn plasmas at a density of 0.1 g/cm3 and temperatures of (a) 20, (b) 23, (c) 25, (d) 27 and (e) 30 eV
图 11 密度为0.01 g/cm3, 温度为(a) 20, (b) 23, (c) 25, (d) 27和(e) 30 eV的Sn等离子体EUV辐射不透明度(左图)和发射系数(右图)
Fig. 11. EUV radiative opacity (left panel) and emissivity (right panel) of Sn plasmas at a density of 0.01 g/cm3 and temperatures of (a) 20, (b) 23, (c) 25, (d) 27 and (e) 30 eV
表 1
${\rm{Sn}}^{10+}$ 基组态4s24p64d4的精细能级(单位: eV), 能级符号中省略了满壳层的4s和4p轨道.Table 1. Fine-structure levels belonging to the ground configuration 4s24p64d4 of
${\rm{Sn}}^{10+}$ (Unit: eV), where the fully occupied 4s and 4p orbitals are omitted.能级 J 本文(MCDF) 实验[14] CI+MBPT [14] 1 ${\rm{4d}}_{3/2}^4$ 0 0.00 0.00 0.00 2 $(\text{4d}_{3/2}^3)_{3/2}\text{4d}_{5/2}$ 1 0.36 0.38 0.39 3 $(\text{4d}_{3/2}^2)_{2}(\text{4d}_{5/2}^2)_4$ 2 0.79 0.82 0.83 4 $(\text{4d}_{3/2}^2)_{2}(\text{4d}_{5/2}^2)_4$ 3 1.22 1.25 1.27 5 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{9/2}$ 4 1.64 1.65 1.68 6 $(\text{4d}_{3/2}^2)_{2}(\text{4d}_{5/2}^2)_2$ 0 3.48 3.32 3.28 7 $(\text{4d}_{3/2}^3)_{3/2}\text{4d}_{5/2}$ 4 3.98 3.67 3.60 8 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_2$ 3 4.58 4.33 4.29 9 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{9/2}$ 5 4.61 4.36 4.30 10 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_2$ 1 4.68 4.39 4.39 11 $(\text{4d}_{3/2}^3)_{3/2}\text{4d}_{5/2}$ 2 4.80 4.55 4.54 12 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_4$ 6 5.09 4.74 4.67 13 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{9/2}$ 4 5.29 5.02 4.99 14 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_2$ 2 5.61 5.38 5.40 15 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_2$ 4 5.72 5.43 5.40 16 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{3/2}$ 3 5.87 5.60 5.60 17 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_2$ 3 6.27 5.99 5.99 18 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_4$ 5 6.36 6.06 6.03 19 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{3/2}$ 2 6.69 6.42 6.43 20 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{3/2}$ 1 6.81 6.55 6.56 21 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{9/2}$ 6 7.15 6.68 6.60 22 $\text{4d}_{5/2}^4$ 4 7.72 7.40 7.38 23 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{3/2}$ 0 7.77 7.55 7.57 24 $\text{4d}_{5/2}^4$ 2 8.41 8.01 8.00 25 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{3/2}$ 3 8.89 8.43 8.42 26 $(\text{4d}_{3/2}^2)_0(\text{4d}_{5/2}^2)_2$ 2 9.86 — 9.40 27 $(\text{4d}_{3/2}^2)_0(\text{4d}_{5/2}^2)_4$ 4 10.27 9.77 9.78 28 $(\text{4d}_{3/2}^2)_2(\text{4d}_{5/2}^2)_0$ 2 10.48 9.97 9.98 29 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{5/2}$ 3 10.66 10.15 10.16 30 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{5/2}$ 1 10.77 — 10.30 31 $\text{4d}_{5/2}^4$ 0 11.23 — 10.77 32 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{5/2}$ 4 11.79 — 11.11 33 $\text{4d}_{3/2}(\text{4d}_{5/2}^3)_{5/2}$ 2 14.70 — 13.95 34 $(\text{4d}_{3/2}^2)_0(\text{4d}_{5/2}^2)_0$ 0 18.87 — 17.98 
下载: 导出CSV
表 2 不同温度和密度条件下, Sn等离子体在(13.5 ± 2%) nm波长范围的总发射功率. a(b)表示a ×
$10^{b}$ Table 2. Total emissivity of Sn plasmas in (13.5 ± 2%) nm wavelength region at a variety of temperature and density. a(b) represents a ×
$10^{b}$ $T_{\rm{e}}$/eV ρ/(g·cm–3) $j_{{\rm{tot}}}$/(W·cm–3) 20 0.0001 4.52(10) 0.001 7.86(11) 0.01 6.68(12) 0.1 8.36(13) 23 0.0001 5.50(10) 0.001 1.01(12) 0.01 1.42(13) 0.1 1.69(14) 27 0.001 1.13(12) 0.005 9.07(12) 0.01 2.24(13) 0.1 3.11(14)
下载: 导出CSV
-
[1] Pirati A, Van Shoot J, Troost K, van Ballegoij R, Krabbendam P, Stoeldraijer J, Loopstra E, Benschop J, Finders J, Meiling H, van Setten E, Mika N, Driedonkx J, Stamm U 2017 Proc. SPIE 10143 101430G
Google Scholar
[2] Hutcheson G D 2018 Proc. SPIE 10583 1058303
[3] David A 2007 Soft x-rays and Extreme Ultraviolet Radiation: Principles and Applications (Cambridge: Cambridge University Press) pp17–20
[4] 宗楠, 胡蔚敏, 王志敏, 王小军, 张申金, 薄勇, 彭钦军, 许祖彦 2020 中国光学 13 28
Google Scholar
Zong N, Hu W M, Wang Z M, Wang X J, Zhang S J, Bo Y, Peng Q J, Xu Z Y 2020 Chin. Opt. 13 28
Google Scholar
[5] Versolato O O 2019 Plasma Sources Sci. Technol. 28 083001
Google Scholar
[6] Kieft E R, Garloff K, van der Mullen J J A M, Banine V 2005 Phys. Rev. E 71 036402
Google Scholar
[7] Ueno Y, Soumagne G, Sumitani A, Endo A, Higashiguchi T 2007 Appl. Phys. Lett. 91 231501
Google Scholar
[8] Svendsen W, O’Sullivan G 1994 Phys. Rev. A 50 3710
Google Scholar
[9] Churilov S S, Ryabtsev A N 2006 Opt. Spectrosc. 101 169
Google Scholar
[10] D'Arcy R, Ohashi H, Suda S, Tanuma H, Fujioka S, Nishimura H, Nishihara K, Suzuki C, Kato T, Koike F, White J, O’Sullivan G 2009 Phys. Rev. A 79 042509
Google Scholar
[11] Ohashi H, Suda S, Tanuma H, Fujioka S, Nishimura H, Sasaki A, Nishihara K 2010 J. Phys. B: At. Mol. Opt. Phys. 43 065204
Google Scholar
[12] O'Sullivan G, Li B, D’Arcy R, Dunne P, Hayden P, Kilbane D, McCormack T, Ohashi H, O'Reilly F, Sheridan P, Sokell E, Suzuki C, Higashiguchi T 2015 J. Phys. B: At. Mol. Opt. Phys. 48 144025
Google Scholar
[13] Windberger A, Torretti F, Borschevsky A, Ryabtsev A, Dobrodey S, Bekker H, Eliav E, Kaldor U, Ubachs W, Hoekstra R, Crespo López-Urrutia J R, Versolato O O 2016 Phys. Rev. A 94 012506
Google Scholar
[14] Torretti F, Windberger A, Ryabtsev A, Dobrodey S, Bekker H, Ubachs W, Hoekstra R, Kahl E V, Berengut J C, Crespo López-Urrutia J R, Versolato O O 2017 Phys. Rev. A 95 042503
Google Scholar
[15] Torretti F, Schupp R, Kurilovich D, Bayerle A, Scheers J, Ubachs W, Hoekstra R, Versolato O O 2018 J. Phys. B: At. Mol. Opt. Phys. 51 045005
Google Scholar
[16] de Gaufridy de Dortan F 2007 J. Phys. B: At. Mol. Opt. Phys. 40 599
Google Scholar
[17] Koike F, Fritzsche S 2007 Radiat. Phys. Chem. 76 404
Google Scholar
[18] Kagawa T, Tanuma H, Ohashi H, Nishihara K 2007 J. Phys.: Conf. Ser. 58 149
Google Scholar
[19] Eliav E, Kaldor U, Ishikawa Y 1994 Phys. Rev. A 49 1724
Google Scholar
[20] Berengut J C, Flambaum V V, Kozlov M G 2006 Phys. Rev. A 73 012504
Google Scholar
[21] Lysaght M, Kilbane D, Murphy N, Cummings A, Dunne P, O’Sullivan G 2005 Phys. Rev. A 72 014502
Google Scholar
[22] Fujioka S, Nishimura H, Nishihara K, Sasaki A, Sunahara A, Okuno T, Ueda N, Ando T, Tao Y, Shimada Y, Hashimoto K, Yamaura M, Shigemori K, Nakai M, Nagai K, Norimatsu T, Nishikawa T, Miyanaga N, Izawa Y, Mima K 2005 Phys. Rev. Lett. 95 235004
Google Scholar
[23] 蔡懿, 王文涛, 杨明, 刘建胜, 陆培祥, 李儒新, 徐至展 2008 57 5100
Google Scholar
Cai Y, Wang W T, Yang M, Liu J S, Lu P X, Li R X, Xu Z Z 2008 Acta Phys. Sin. 57 5100
Google Scholar
[24] 陈鸿, 兰慧, 陈子琪, 刘璐宁, 吴涛, 左都罗, 陆培祥, 王新兵 2015 64 075202
Google Scholar
Chen H, Lan H, Chen Z Q, Liu L N, Wu T, Zuo D L, Lu P X, Wang X B 2015 Acta Phys. Sin. 64 075202
Google Scholar
[25] Su M G, Min Q, Cao S Q, Sun D X, Hayden P, O’Sullivan G, Dong C Z 2017 Sci. Rep. 7 45212
Google Scholar
[26] Schupp R, Torretti F, Meijer R A, Bayraktar M, Sheil J, Scheers J, Kurilovich D, Bayerle A, Schafgans A A, Purvis M, Eikema K S E, Witte S, Ubachs W, Hoekstra R, Versolato O O 2019 Appl. Phys. Lett. 115 124101
Google Scholar
[27] Zeng J, Gao C, Yuan J 2010 Phys. Rev. E 82 026409
Google Scholar
[28] Colgan J, Kilcrease D P, Jr. Abdallah J, Sherrill M E, Fontes C J, Hakel P, Armstrong G S J 2017 High Energy Density Phys. 23 133
Google Scholar
[29] Torretti F, Sheil J, Schupp R, Basko M M, Bayraktar M, Meijer R A, Witte S, Ubachs W, Hoekstra R, Versolato O O, Neukirch A J, Colgan J 2020 Nat. Commun. 11 2334
Google Scholar
[30] Sheil J, Versolato O O, Neukirch A J, Colgan J 2021 J. Phys. B: At. Mol. Opt. Phys. 54 035002
Google Scholar
[31] Cowan R D 1981 The Theory of Atomic Structure and Spectra (Berkeley: University of California Press
[32] Jönson P, Gaigalas G, Bieroń, Froese Fischer C, Grant I P 2013 Comput. Phys. Commun. 184 2197
Google Scholar
[33] Zeng J L, Yuan J M 2006 Phys. Rev. E 74 025401(R
Google Scholar
[34] Gao C, Zeng J, Jin F, Yuan J 2013 High Energy Density Phys. 9 419
Google Scholar
[35] Zeng J L, Gao C, Liu P F, Li Y J, Meng C S, Hou Y, Kang D D, Yuan J M 2022 Sci. China-Phys. Mech. Astron. 65 233011
Google Scholar
[36] Stewart J C, Pyatt K D Jr. 1966 Astrophys. J. 144 1203
Google Scholar
[37] 李世昌 1992 高温辐射物理与量子辐射理论 (北京: 国防工业出版社) 第6页
Li S C 1992 High Temperature Radiation Physics and Quantum Radaition Theory (Beijing: National Defense Industry Press) p6
[38] Zeng J L, Zhao G, Yuan J M 2006 J. Quant. Spectrosc. Radiat. Transfer 102 172
Google Scholar
[39] Wu Z W, Tian Z Q, An Y H, Dong C Z 2021 Astrophys. J. 910 142
Google Scholar
[40] Kühn S, Cheung C, Oreshkina N S, Steinbrügge, Togawa M, Bernitt S, Berger L, Buck J, Hoesch M, Seltmann J, Trinter F, Keitel C H, Kozlov M G, Porsev S G, Gu M F, Porter F S, Pfeifer T, Leutenegger M A, Harman Z, Safronova M S, López-Urrutia J R C, Shah C 2022 Phys. Rev. Lett. 129 245001
Google Scholar
[41] Colgan J, Kilcrease D P, Magee N H, Sherrill M E, Abdallah Jr. J, Hakel P, Fontes C J, Guzik J A, Mussack K A 2016 Astrophys. J. 817 116
Google Scholar
[42] 兰慧 2016 博士学位论文 (武汉: 华中科技大学)
Lan H 2016 Ph. D. Dissertation (Wuhan: Huazhong University of Science and Technology
[43] Hansen S B, Chung H K, Fontes C J, Ralchenko Yu, Scott H A, Stambulchik E 2020 High Energy Density Phys. 35 100693
Google Scholar
[44] Gao C, Zeng J, Li Y, Jin F, Yuan J 2013 High Energy Density Phys. 9 583
Google Scholar
下载:
计量
- 文章访问数: 3718
- PDF下载量: 128
- 被引次数: 0
