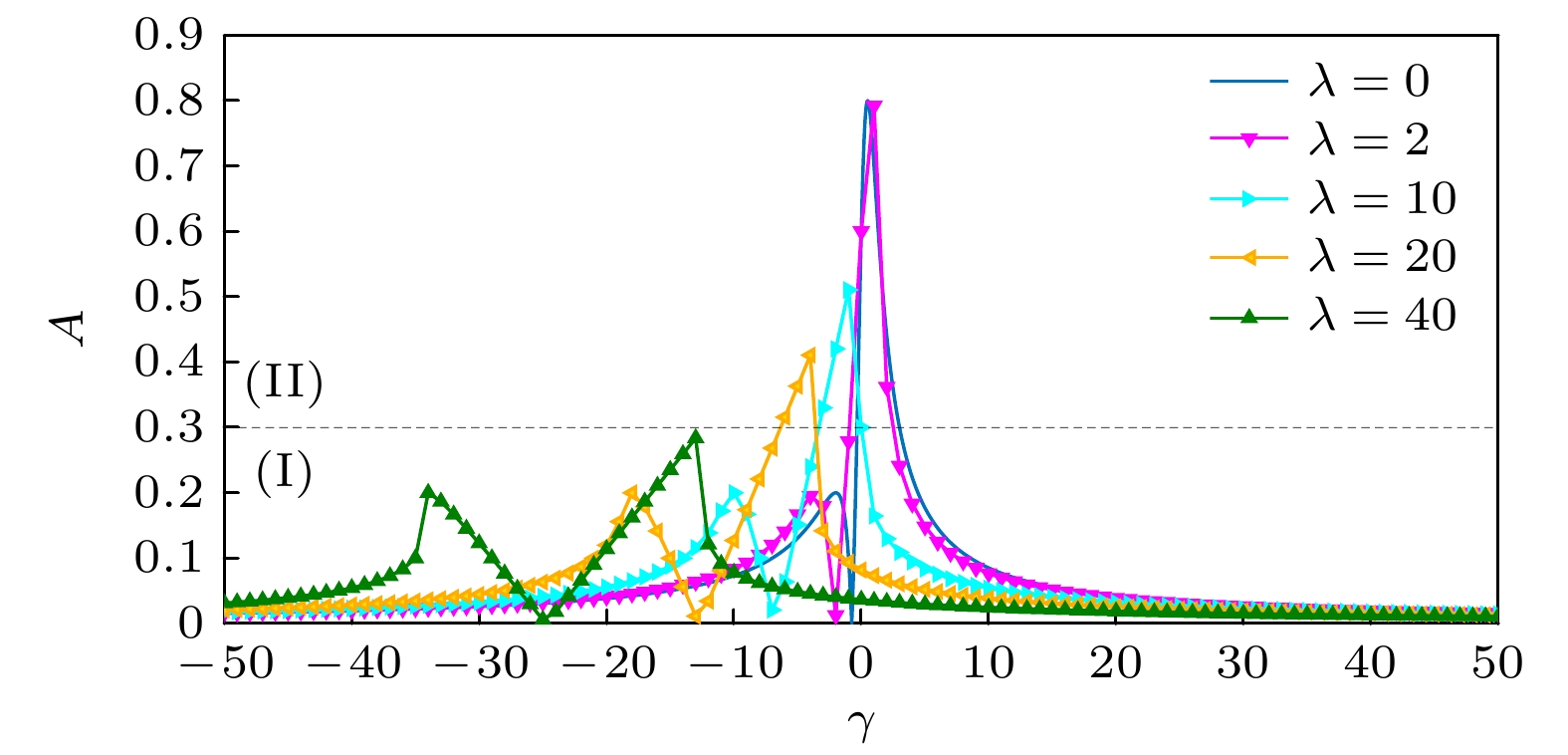
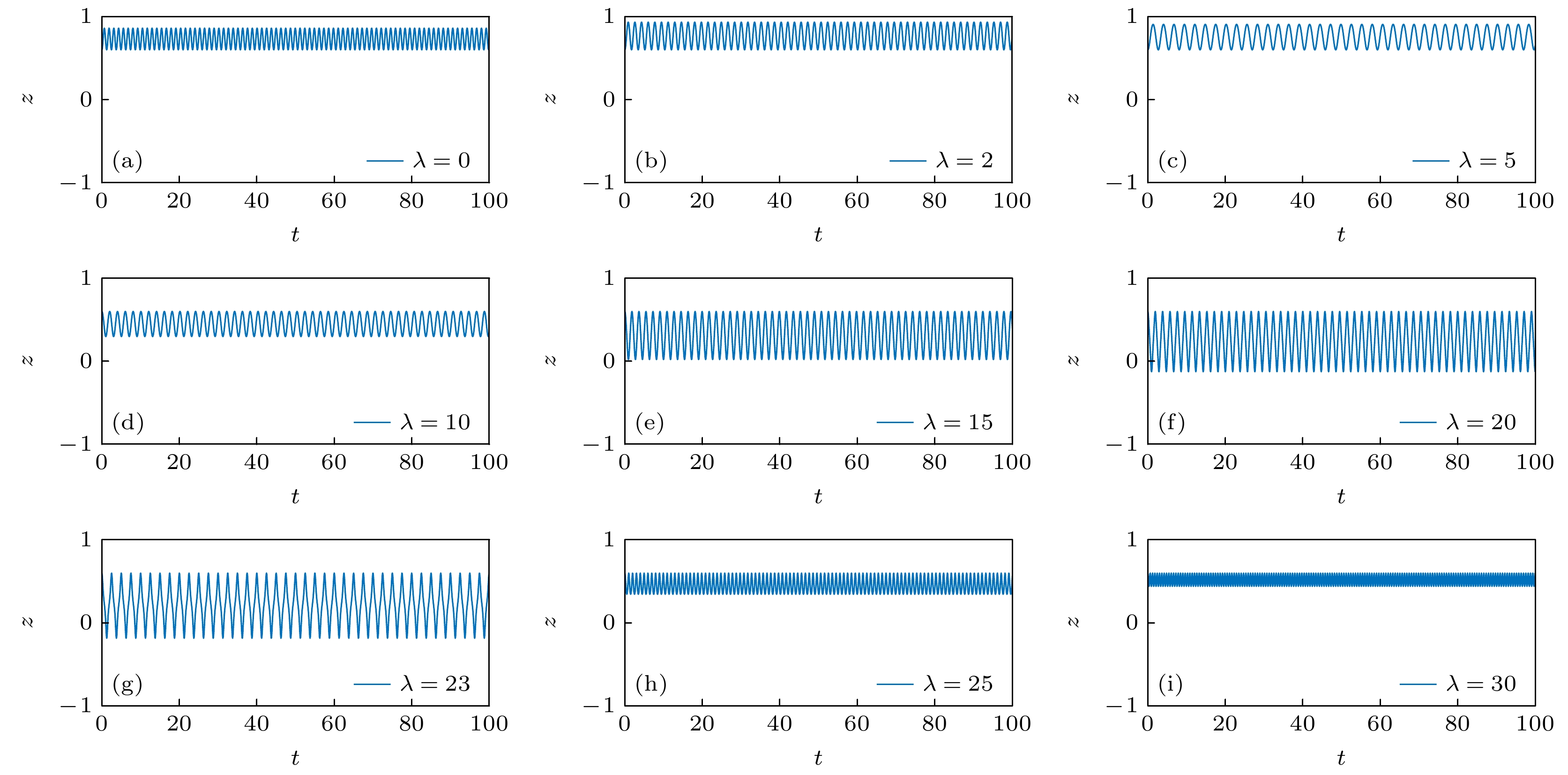
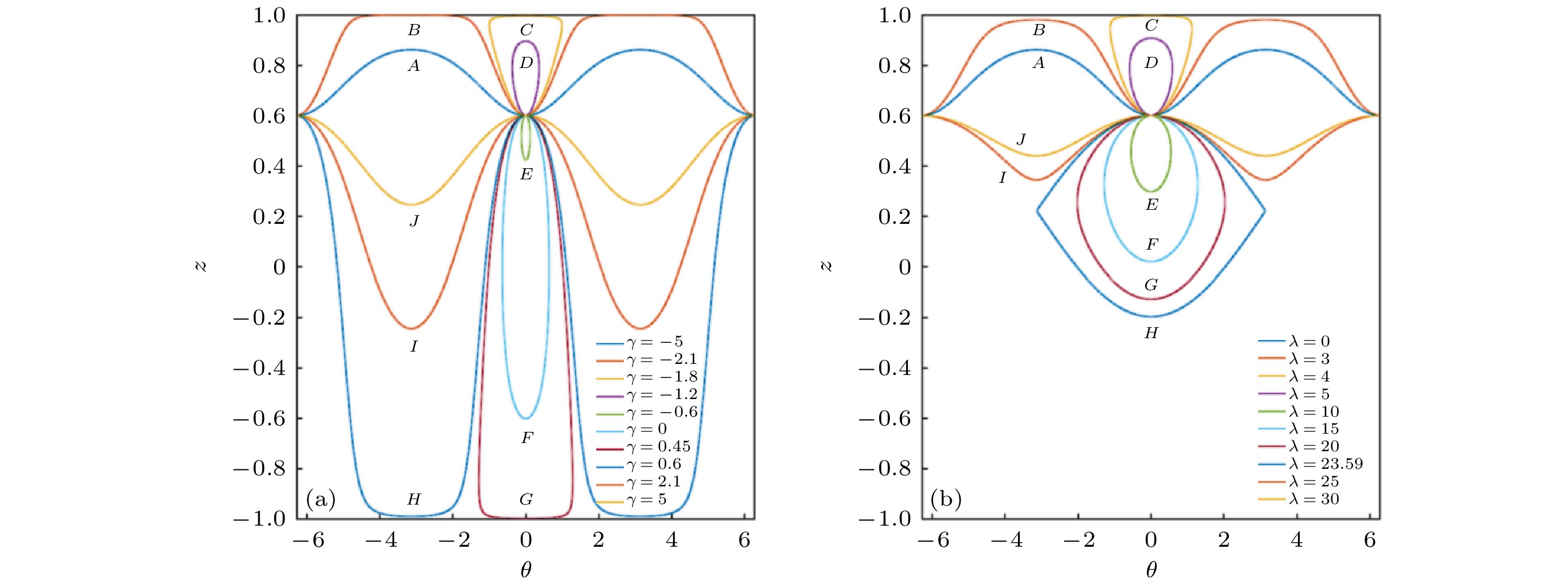
-
研究了玻色-爱因斯坦凝聚体在不对称双势阱中, 随着两势阱局域基态能量差和非线性相互作用的变化而表现出的动力学特性. 对双模理论的解析分析可以发现, 在无相互作用情况下, 当双势阱能量差比较大时, 凝聚体会主要聚集在初始分布较多的势阱中, 而和高低势阱的位置无关. 数值计算表明, 当相互作用存在且逐渐增大时, 凝聚体的分布呈现出不同的变化. 当初始分布聚集在一个势阱时, 会呈现出先加强聚集, 然后促进隧穿, 最后又重新导致聚集的现象. 同时, 通过对相图的分析, 利用等效势概念为这些现象的出现给出了合理的解释. 为了验证上述现象, 还对Gross-Pitaevskii方程进行了直接数值模拟, 结果和上述采用双模理论得到的结论一致.Josephson effect of Bose-Einstein condensate in double-well potential is an obvious manifestation of macroscopic quantum coherence. Most of researches focus on the symmetric double-well potential. In this work, we investigate the dynamic of Bose-Einstein condensates in an asymmetric double-well potential by using two-mode theory and computer simulation. In the absence of the interaction between atoms, the dynamic equation of condensate can be solved analytically. The amplitude as a function of energy difference of two wells is obtained. We can find that the change of energy difference will lead to the different dynamic behaviors of condensate. If the energy difference is relatively large, the condensate will primarily occupy the well that is occupied more than the other well at the beginning time. It is interesting that such a trap phenomenon is not dependent on the position of the high energy potential well nor the position of low energy potential well. If the energy difference becomes small, the tunneling and oscillation of condensate will be enhanced. When the interaction between atoms is present, our numerical calculations show that as the nonlinear interaction increases, the dynamic behavior of condensate exhibits different characteristics, such as trapping in a well, enhancing the tunneling and oscillation between two wells, and enhancing the trapping in a well at large nonlinear interaction, which is similar to the dynamic change caused by the energy difference in the case of ideal condensate. That is to say, on the one hand, the nonlinear interaction can lead to the trap of condensate as well as the dynamic trap to happen in symmetric double-well potential. On the other hand, the nonlinearity can promote the tunneling of condensate, counteracting the effect of the asymmetry of potential. And, this counteracting effect is related to the difference in energy between asymmetric potential wells. To understand the underlying mechanism, the full dynamic behavior of two-mode model is illustrated and the dynamic transition can be seen clearly. Combining the results obtained with and without interaction, regarding nonlinear interaction as effective potential provides a clear way to explain dynamic transition of condensate in an asymmetric double-well potential. In addition, we also perform the numerical simulations of the Gross-Pitaevskii equation, and the results are consistent with the conclusions obtained by using the two-mode theory.
-
Keywords:
- Bose-Einstein condensate /
- asymmetric double-well potential /
- dynamics
[1] Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198
Google Scholar
[2] Davis K B, Mewes M O, Andrews M R, Vandruten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969
Google Scholar
[3] Bradley C C, Sackett C A, Tollett J J, Hulet R G 1995 Phys. Rev. Lett. 75 1687
Google Scholar
[4] Andrews M R, Townsend C G, Miesner H J, Durfee D S, Kurn D M, Ketterle W 1997 Science 275 637
Google Scholar
[5] Gross E P 1961 Il Nuovo Cimento 20 454
Google Scholar
[6] Pitaevskii L P 1961 Sov. Phys. JETP 13 451
[7] Dalfovo F, Giorgini S, Pitaevskii L P, Stringari S 1999 Rev. Mod. Phys. 71 463
Google Scholar
[8] Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885
Google Scholar
[9] Josephson B D 1962 Phys. Lett. 1 251
Google Scholar
[10] Milburn G J, Corney J, Wright E M, Walls D F 1997 Phys. Rev. A 55 4318
Google Scholar
[11] Smerzi A, Fantoni S, Giovanazzi S, Shenoy S R 1997 Phys. Rev. Lett. 79 4950
Google Scholar
[12] Raghavan S, Smerzi A, Fantoni S, Shenoy S R 1999 Phys. Rev. A 59 620
Google Scholar
[13] Cataliotti F S, Burger S, Fort C, Maddaloni P, Minardi F, Trombettoni A, Smerzi A, Inguscio M 2001 Science 293 843
Google Scholar
[14] Albiez M, Gati R, Folling J, Hunsmann S, Cristiani M, Oberthaler M K 2005 Phys. Rev. Lett. 95 010402
Google Scholar
[15] Giovanazzi S, Smerzi A, Fantoni S 2000 Phys. Rev. Lett. 84 4521
Google Scholar
[16] Zhang Y B, Muller-Kirsten H J W 2001 Phys. Rev. A 64 023608
Google Scholar
[17] Ananikian D, Bergeman T 2006 Phys. Rev. A 73 013604
Google Scholar
[18] Giovanazzi S, Esteve J, Oberthaler M K 2008 New J. Phys. 10 045009
Google Scholar
[19] Julia-Diaz B, Martorell J, Mele-Messeguer M, Polls A 2010 Phys. Rev. A 82 063626
Google Scholar
[20] Jezek D M, Capuzzi P, Cataldo H M 2013 Phys. Rev. A 87 053625
Google Scholar
[21] Burchianti A, Fort C, Modugno M 2017 Phys. Rev. A 95 023627
Google Scholar
[22] Fu L, Liu J 2006 Phys. Rev. A 74 063614
Google Scholar
[23] Spagnolli G, Semeghini G, Masi L, Ferioli G, Trenkwalder A, Coop S, Landini M, Pezze L, Modugno G, Inguscio M, Smerzi A, Fattori M 2017 Phys. Rev. Lett. 118 230403
Google Scholar
[24] Zhang D W, Fu L B, Wang Z D, Zhu S L 2012 Phys. Rev. A 85 043609
Google Scholar
[25] Wang W Y, Dou F Q, Duan W S 2018 J. Phys. B: At. Mol. Opt. Phys. 51 035002
Google Scholar
[26] Hou J, Luo X W, Sun K, Bersano T, Gokhroo V, Mossman S, Engels P, Zhang C 2018 Phys. Rev. Lett. 120 120401
Google Scholar
[27] 王冠芳, 傅立斌, 赵鸿, 刘杰 2005 54 5003
Google Scholar
Wang G F, Fu L B, Zhao H, Liu J 2005 Acta Phys. Sin. 54 5003
Google Scholar
[28] 刘泽专, 杨志安 2007 56 1245
Google Scholar
Liu Z Z, Yang Z A 2007 Acta Phys. Sin. 56 1245
Google Scholar
[29] 房永翠, 杨志安, 杨丽云 2008 57 661
Google Scholar
Fang Y C, Yang Z A, Yang L Y 2008 Acta Phys. Sin. 57 661
Google Scholar
[30] 黄芳, 李海彬 2011 60 020303
Google Scholar
Huang F, Li H B 2011 Acta Phys. Sin. 60 020303
Google Scholar
[31] 马云, 傅立斌, 杨志安, 刘杰 2006 55 5623
Google Scholar
Ma Y, Fu L B, Yang Z A, Liu J 2006 Acta Phys. Sin. 55 5623
Google Scholar
[32] 臧小飞, 李菊萍, 谭磊 2007 56 4348
Google Scholar
Zang X F, Li J P, Tan L 2007 Acta Phys. Sin. 56 4348
Google Scholar
[33] 李菊萍, 谭磊, 臧小飞, 杨科 2008 57 7467
Google Scholar
Li J P, Tan L, Zang X F, Yang K 2008 Acta Phys. Sin. 57 7467
Google Scholar
[34] 张恒, 段文山 2013 62 160303
Google Scholar
Zhang H, Duan W S 2013 Acta Phys. Sin. 62 160303
Google Scholar
[35] Levy S, Lahoud E, Shomroni I, Steinhauer J 2007 Nature 449 579
Google Scholar
[36] LeBlanc L J, Bardon A B, McKeever J, Extavour M H T, Jervis D, Thywissen J H, Piazza F, Smerzi A 2011 Phys. Rev. Lett. 106 025302
Google Scholar
[37] Trenkwalder A, Spagnolli G, Semeghini G, Coop S, Landini M, Castilho P, Pezze L, Modugno G, Inguscio M, Smerzi A, Fattori M 2016 Nat. Phys. 12 826
Google Scholar
[38] 肖宇飞, 王登龙, 王凤姣, 颜晓红 2006 55 547
Google Scholar
Xiao Y F, Wang D L, Wang F J, Yan X H 2006 Acta Phys. Sin. 55 547
Google Scholar
[39] Julia-Diaz B, Martorell J, Polls A 2010 Phys. Rev. A 81 063625
Google Scholar
[40] Hunn S, Zimmermann K, Hiller M, Buchleitner A 2013 Phys. Rev. A 87 043626
Google Scholar
[41] Cataldo H M, Jezek D M 2014 Phys. Rev. A 90 043610
Google Scholar
[42] Cosme J G, Andersen M F, Brand J 2017 Phys. Rev. A 96 013616
Google Scholar
[43] Haldar S K, Alon O E 2019 New J. Phys. 21 103037
Google Scholar
-
图 1
$ z\left(0\right)=0.6 $ 时, 无相互作用下当$ \gamma $ 变化时占据数差随时间的演化Fig. 1. Population imbalance versus time at different
$ \gamma $ without interactions at$ z\left(0\right)=0.6$ .
图 2
$ z\left(0\right)=0.6 $ 时, 当非线性相互作用取不同值时, 振幅对能量差的依赖关系Fig. 2. Amplitude versus energy difference when the nonlinear interaction parameter is different at
$ z\left(0\right)=0.6 $ .
图 3
$ z\left(0\right)=0.6 $ ,$ \gamma =-5 $ , 当$ \lambda $ 变化时, 占据数差随时间的演化Fig. 3. Population imbalance versus time at different
$ \lambda $ at$ z\left(0\right)=0.6 $ ,$ \gamma =-5 $ .
图 4
$ z\left(0\right)=0.6 $ , 势阱能量差取不同值时, 振幅随$ \lambda $ 的变化Fig. 4. Amplitude versus
$ \lambda $ when energy difference is different at$ z\left(0\right)=0.6 $ .
图 5
$ z\left(0\right)=0.6 $ , 相空间中的等能量线Fig. 5. Constant energy line in phase-space at
$ z\left(0\right)=0.6 $ .
图 6
$ \beta =20 $ ,$ z\left(0\right)=0.6 $ , 不同$ g $ 条件下粒子占据数差随时间的变化Fig. 6. Population imbalance versus time at different
$ g $ ,$\beta =20 \;{\rm{and}} \;z\left(0\right)=0.6$ . -
[1] Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198
Google Scholar
[2] Davis K B, Mewes M O, Andrews M R, Vandruten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969
Google Scholar
[3] Bradley C C, Sackett C A, Tollett J J, Hulet R G 1995 Phys. Rev. Lett. 75 1687
Google Scholar
[4] Andrews M R, Townsend C G, Miesner H J, Durfee D S, Kurn D M, Ketterle W 1997 Science 275 637
Google Scholar
[5] Gross E P 1961 Il Nuovo Cimento 20 454
Google Scholar
[6] Pitaevskii L P 1961 Sov. Phys. JETP 13 451
[7] Dalfovo F, Giorgini S, Pitaevskii L P, Stringari S 1999 Rev. Mod. Phys. 71 463
Google Scholar
[8] Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885
Google Scholar
[9] Josephson B D 1962 Phys. Lett. 1 251
Google Scholar
[10] Milburn G J, Corney J, Wright E M, Walls D F 1997 Phys. Rev. A 55 4318
Google Scholar
[11] Smerzi A, Fantoni S, Giovanazzi S, Shenoy S R 1997 Phys. Rev. Lett. 79 4950
Google Scholar
[12] Raghavan S, Smerzi A, Fantoni S, Shenoy S R 1999 Phys. Rev. A 59 620
Google Scholar
[13] Cataliotti F S, Burger S, Fort C, Maddaloni P, Minardi F, Trombettoni A, Smerzi A, Inguscio M 2001 Science 293 843
Google Scholar
[14] Albiez M, Gati R, Folling J, Hunsmann S, Cristiani M, Oberthaler M K 2005 Phys. Rev. Lett. 95 010402
Google Scholar
[15] Giovanazzi S, Smerzi A, Fantoni S 2000 Phys. Rev. Lett. 84 4521
Google Scholar
[16] Zhang Y B, Muller-Kirsten H J W 2001 Phys. Rev. A 64 023608
Google Scholar
[17] Ananikian D, Bergeman T 2006 Phys. Rev. A 73 013604
Google Scholar
[18] Giovanazzi S, Esteve J, Oberthaler M K 2008 New J. Phys. 10 045009
Google Scholar
[19] Julia-Diaz B, Martorell J, Mele-Messeguer M, Polls A 2010 Phys. Rev. A 82 063626
Google Scholar
[20] Jezek D M, Capuzzi P, Cataldo H M 2013 Phys. Rev. A 87 053625
Google Scholar
[21] Burchianti A, Fort C, Modugno M 2017 Phys. Rev. A 95 023627
Google Scholar
[22] Fu L, Liu J 2006 Phys. Rev. A 74 063614
Google Scholar
[23] Spagnolli G, Semeghini G, Masi L, Ferioli G, Trenkwalder A, Coop S, Landini M, Pezze L, Modugno G, Inguscio M, Smerzi A, Fattori M 2017 Phys. Rev. Lett. 118 230403
Google Scholar
[24] Zhang D W, Fu L B, Wang Z D, Zhu S L 2012 Phys. Rev. A 85 043609
Google Scholar
[25] Wang W Y, Dou F Q, Duan W S 2018 J. Phys. B: At. Mol. Opt. Phys. 51 035002
Google Scholar
[26] Hou J, Luo X W, Sun K, Bersano T, Gokhroo V, Mossman S, Engels P, Zhang C 2018 Phys. Rev. Lett. 120 120401
Google Scholar
[27] 王冠芳, 傅立斌, 赵鸿, 刘杰 2005 54 5003
Google Scholar
Wang G F, Fu L B, Zhao H, Liu J 2005 Acta Phys. Sin. 54 5003
Google Scholar
[28] 刘泽专, 杨志安 2007 56 1245
Google Scholar
Liu Z Z, Yang Z A 2007 Acta Phys. Sin. 56 1245
Google Scholar
[29] 房永翠, 杨志安, 杨丽云 2008 57 661
Google Scholar
Fang Y C, Yang Z A, Yang L Y 2008 Acta Phys. Sin. 57 661
Google Scholar
[30] 黄芳, 李海彬 2011 60 020303
Google Scholar
Huang F, Li H B 2011 Acta Phys. Sin. 60 020303
Google Scholar
[31] 马云, 傅立斌, 杨志安, 刘杰 2006 55 5623
Google Scholar
Ma Y, Fu L B, Yang Z A, Liu J 2006 Acta Phys. Sin. 55 5623
Google Scholar
[32] 臧小飞, 李菊萍, 谭磊 2007 56 4348
Google Scholar
Zang X F, Li J P, Tan L 2007 Acta Phys. Sin. 56 4348
Google Scholar
[33] 李菊萍, 谭磊, 臧小飞, 杨科 2008 57 7467
Google Scholar
Li J P, Tan L, Zang X F, Yang K 2008 Acta Phys. Sin. 57 7467
Google Scholar
[34] 张恒, 段文山 2013 62 160303
Google Scholar
Zhang H, Duan W S 2013 Acta Phys. Sin. 62 160303
Google Scholar
[35] Levy S, Lahoud E, Shomroni I, Steinhauer J 2007 Nature 449 579
Google Scholar
[36] LeBlanc L J, Bardon A B, McKeever J, Extavour M H T, Jervis D, Thywissen J H, Piazza F, Smerzi A 2011 Phys. Rev. Lett. 106 025302
Google Scholar
[37] Trenkwalder A, Spagnolli G, Semeghini G, Coop S, Landini M, Castilho P, Pezze L, Modugno G, Inguscio M, Smerzi A, Fattori M 2016 Nat. Phys. 12 826
Google Scholar
[38] 肖宇飞, 王登龙, 王凤姣, 颜晓红 2006 55 547
Google Scholar
Xiao Y F, Wang D L, Wang F J, Yan X H 2006 Acta Phys. Sin. 55 547
Google Scholar
[39] Julia-Diaz B, Martorell J, Polls A 2010 Phys. Rev. A 81 063625
Google Scholar
[40] Hunn S, Zimmermann K, Hiller M, Buchleitner A 2013 Phys. Rev. A 87 043626
Google Scholar
[41] Cataldo H M, Jezek D M 2014 Phys. Rev. A 90 043610
Google Scholar
[42] Cosme J G, Andersen M F, Brand J 2017 Phys. Rev. A 96 013616
Google Scholar
[43] Haldar S K, Alon O E 2019 New J. Phys. 21 103037
Google Scholar
下载:
计量
- 文章访问数: 2711
- PDF下载量: 107
- 被引次数: 0
