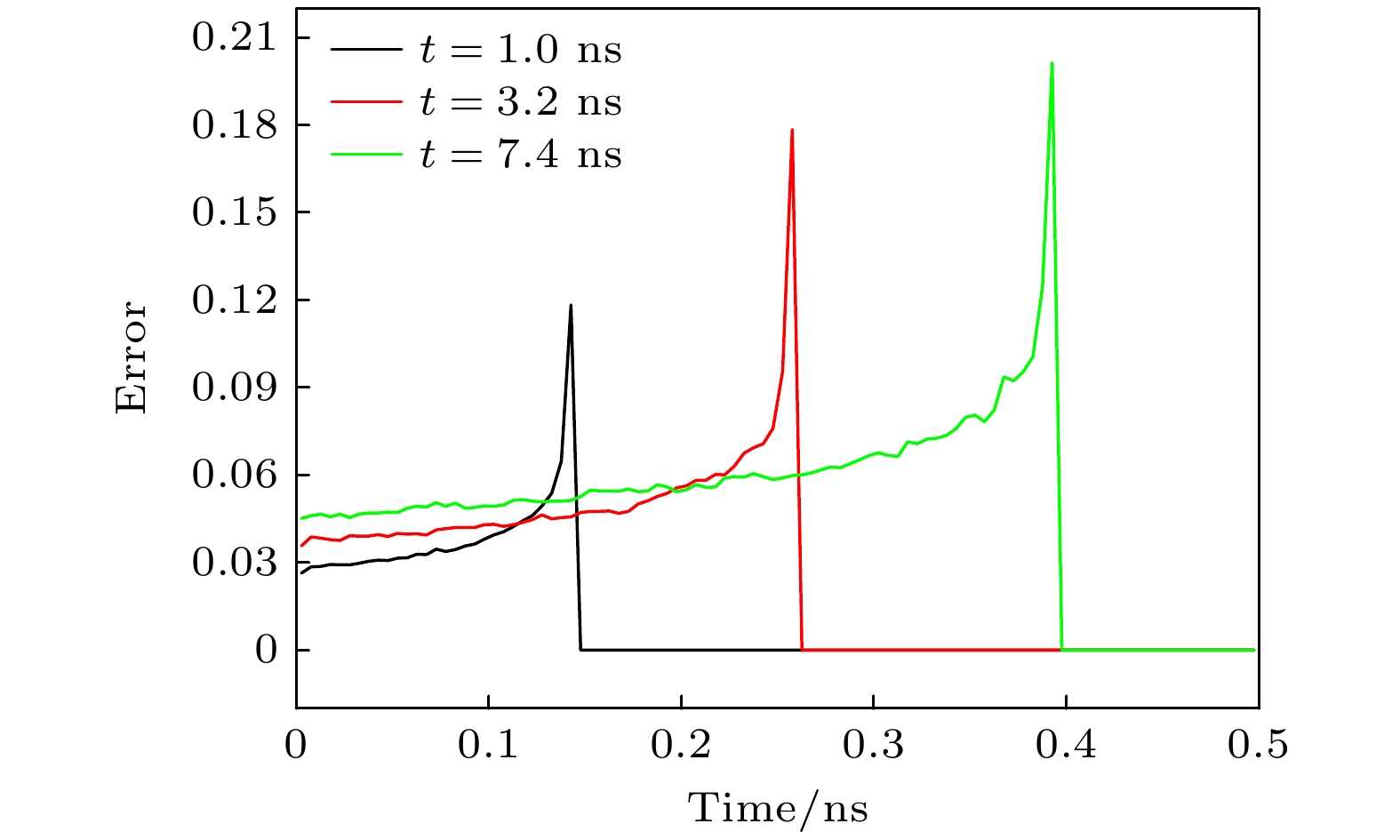
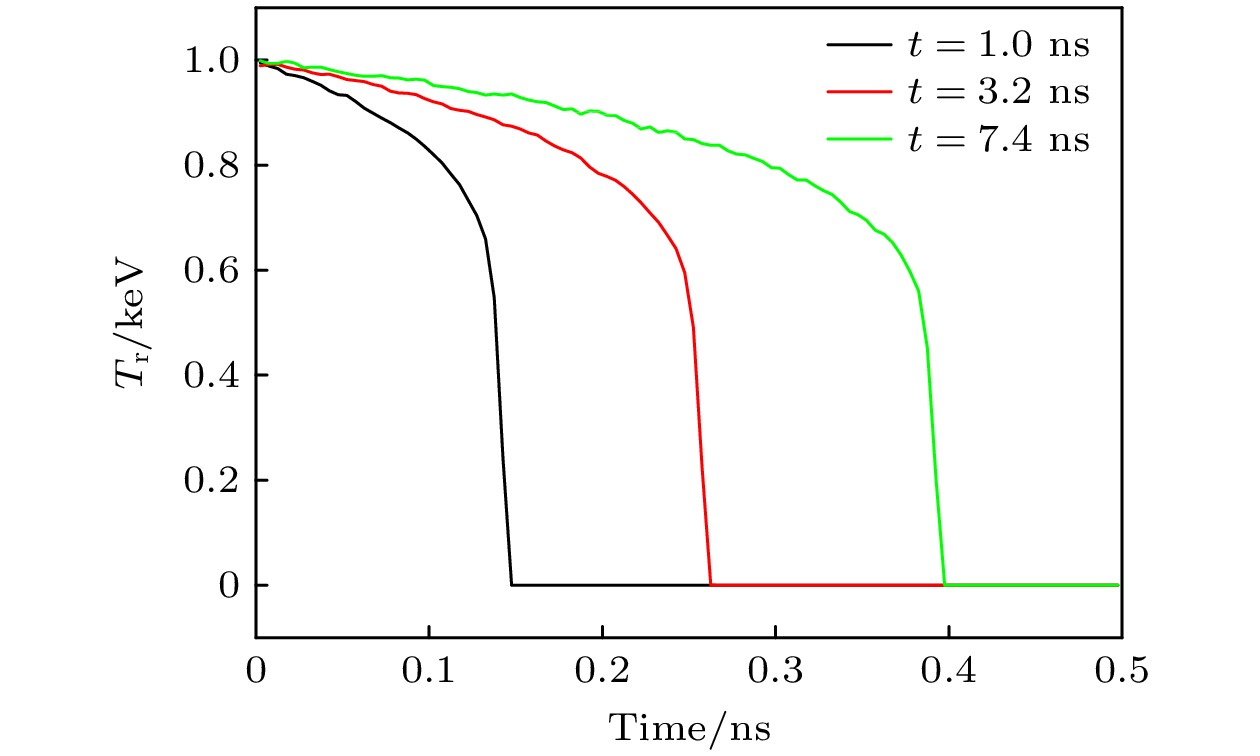
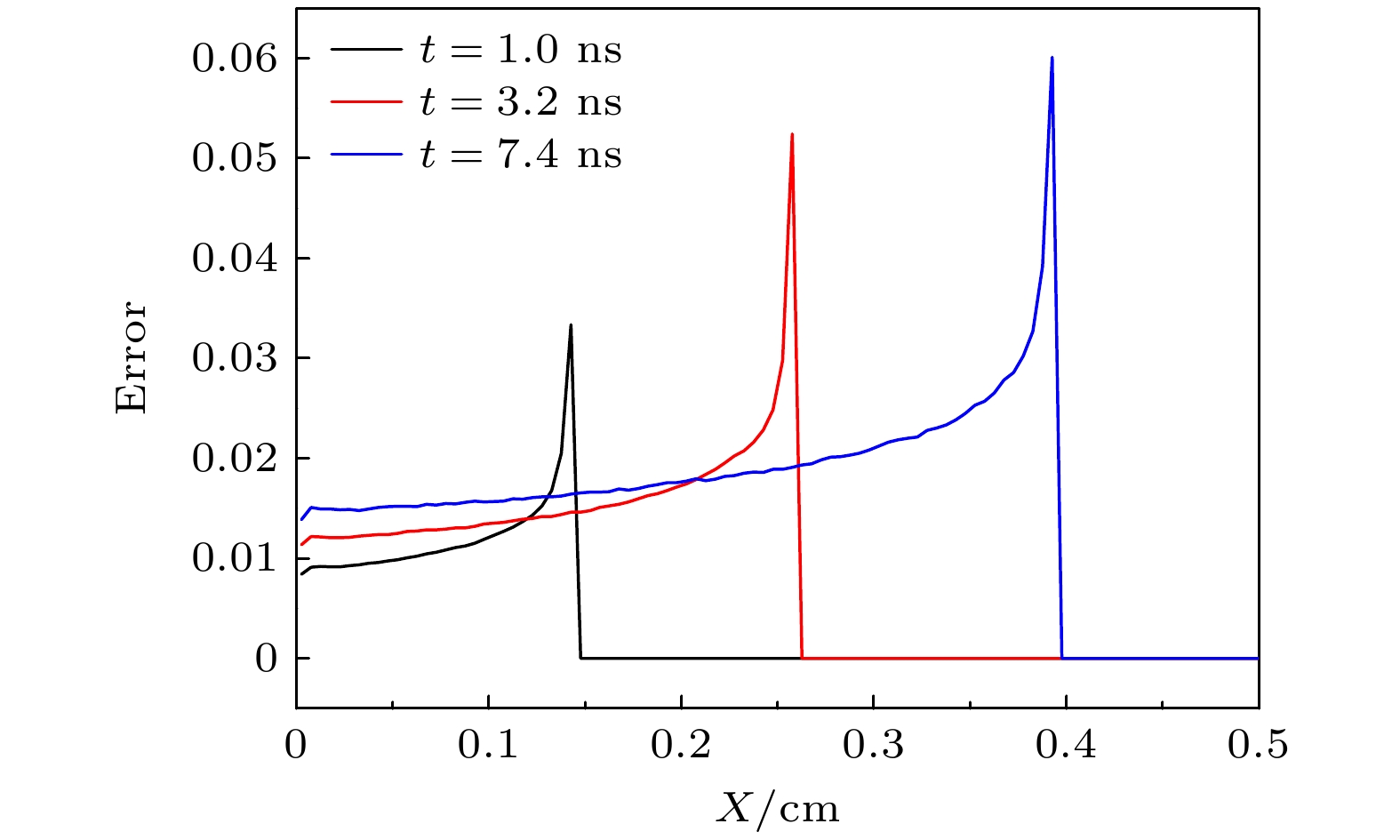
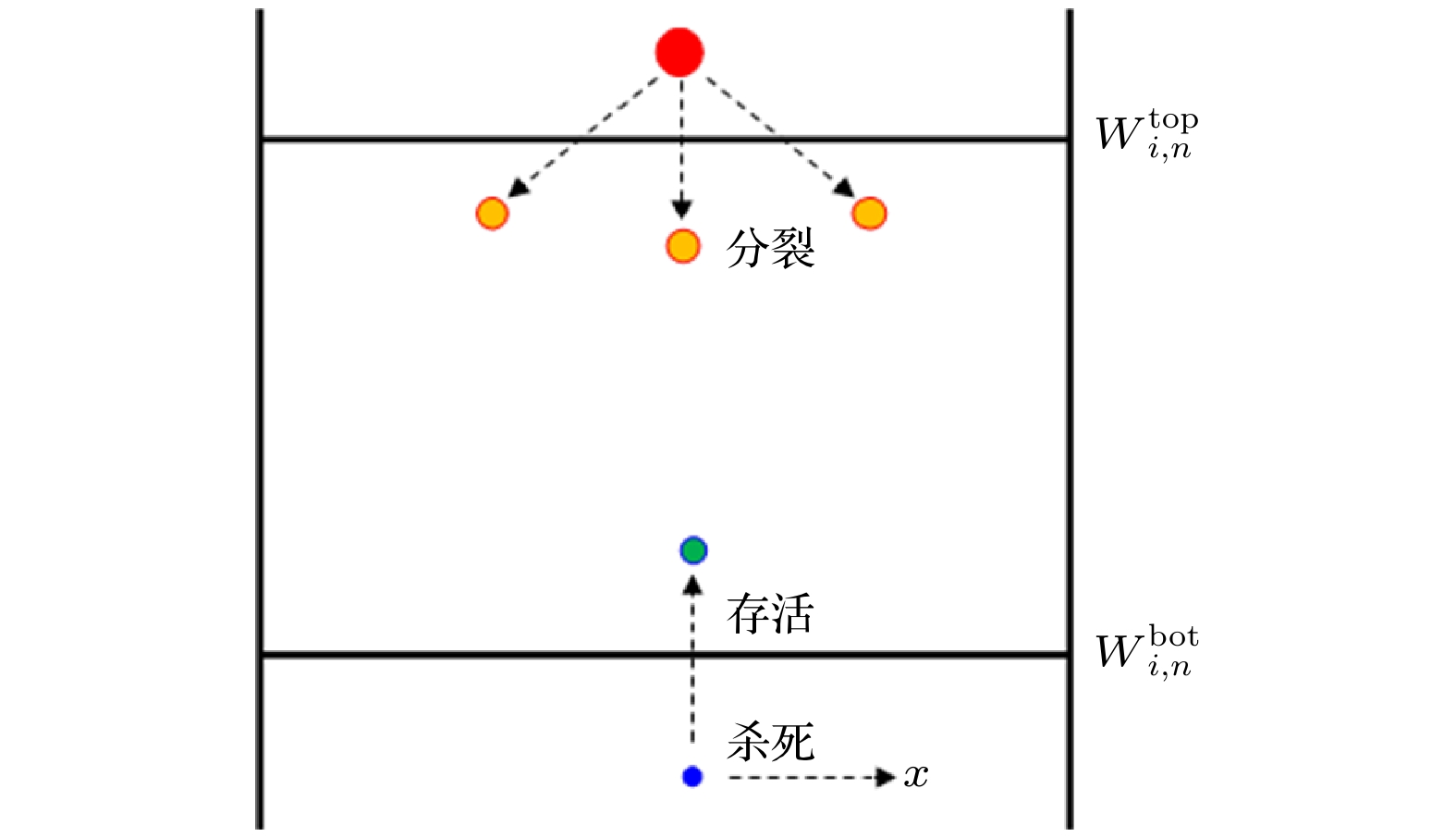
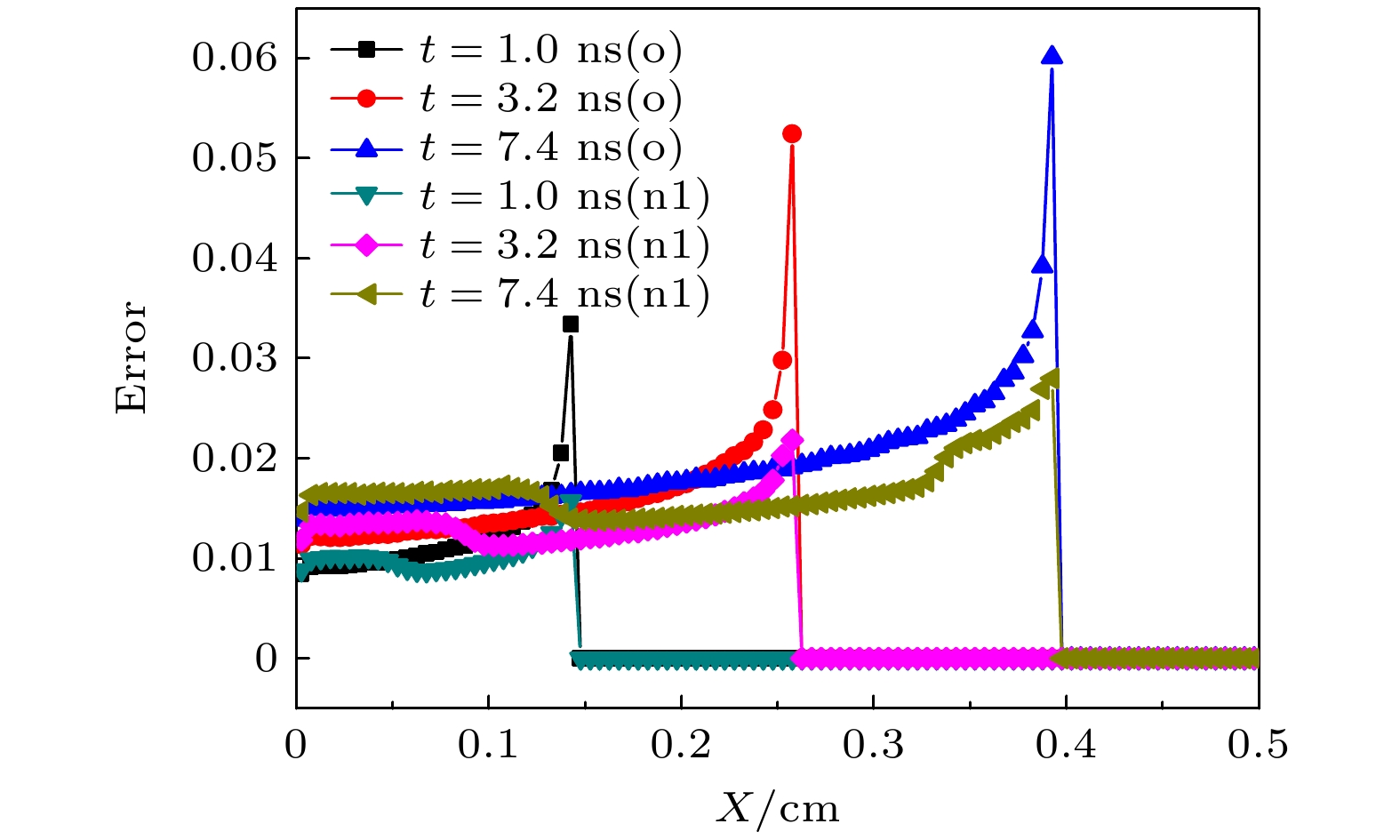
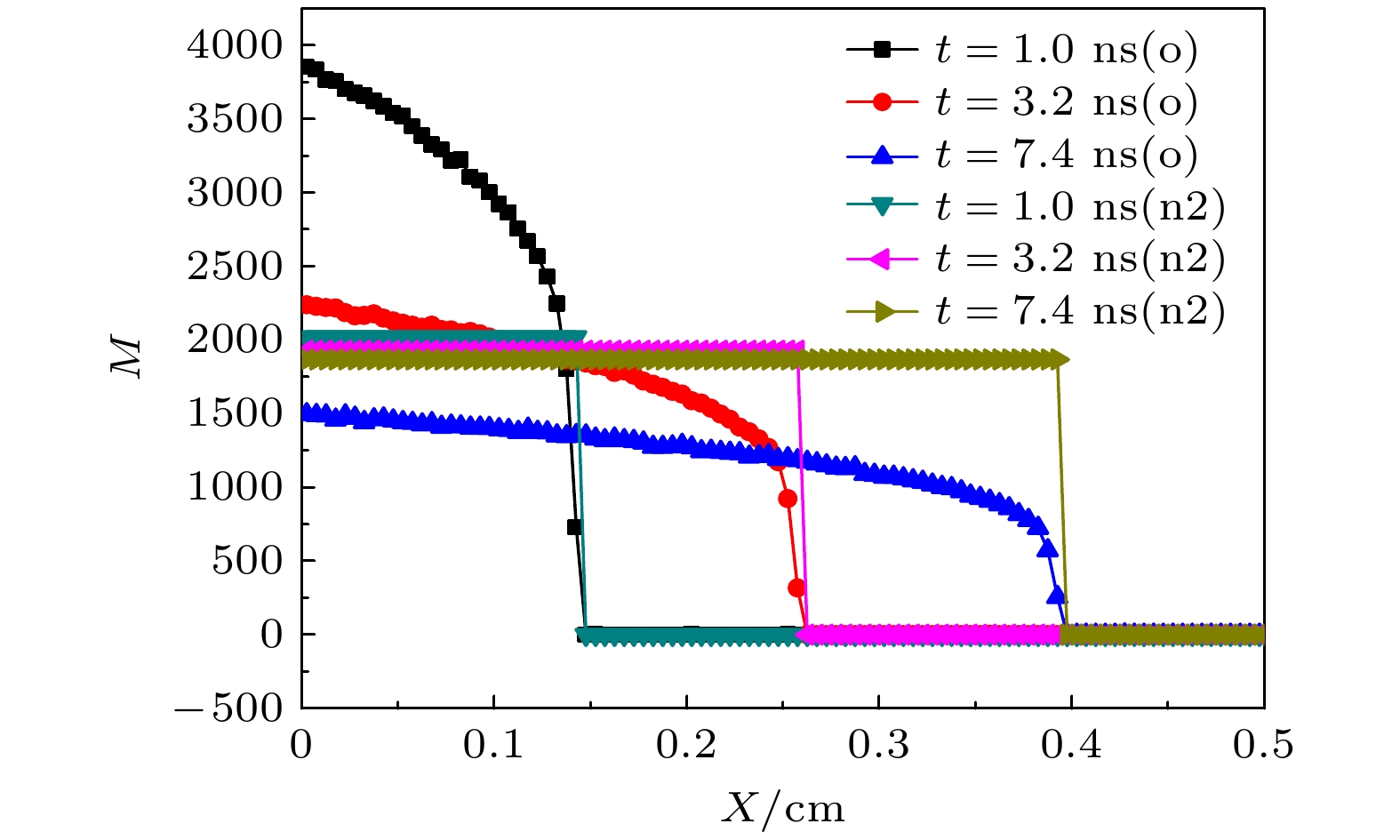
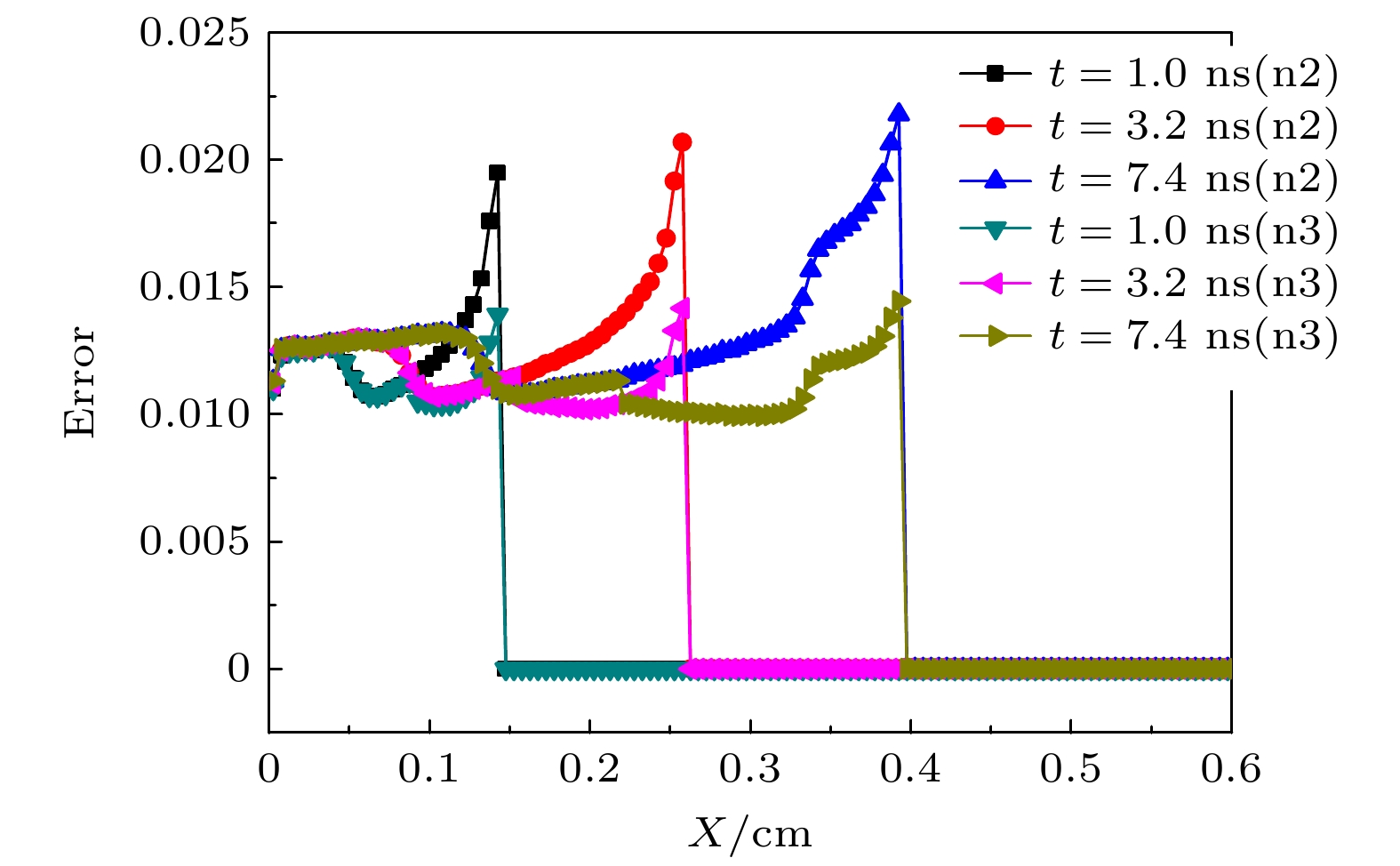
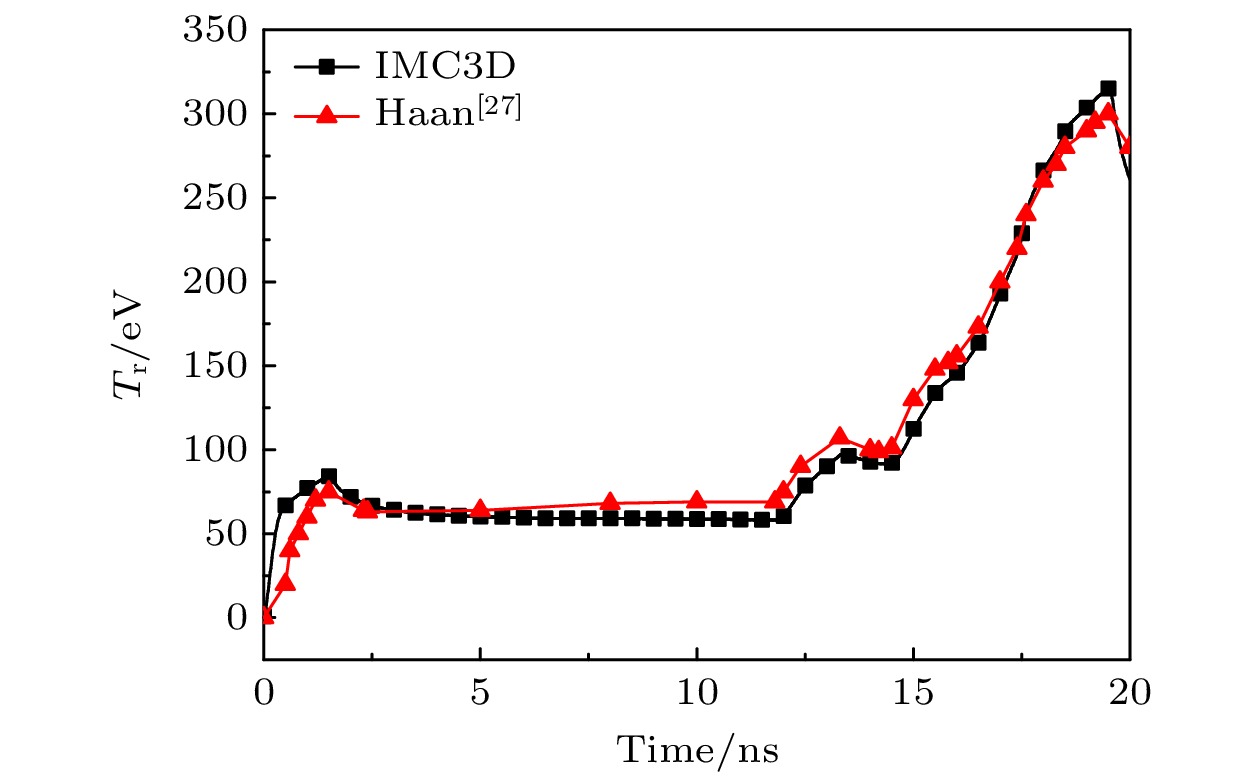
-
针对隐式蒙特卡罗方法模拟高温热辐射输运问题时存在的“辐射强度计算误差时间空间分布严重不均匀”现象, 通过理论分析和数值模拟手段, 找到决定误差大小的主要因素为“网格内的辐射径迹长度记录数”. 据此提出“隐式蒙特卡罗全局降方差方法”并推导相应的计算公式. 该方法主要包含如下3个关键技术: 1)针对辐射输运蒙特卡罗模拟的自适应动态分配源粒子方法; 2)与自适应动态分配源粒子相匹配的动态权窗设计技术及粒子权无偏估计算法; 3)辐射强度的解析估计降方差方法. 针对这3个关键技术, 设计蒙特卡罗数值模拟方案, 编写相应的数值模拟程序模块. 典型辐射输运问题模拟结果显示: 隐式蒙特卡罗全局降方差方法能够使网格辐射强度计算误差在整个时空范围内分布相对比较均匀, 最大误差可控, 计算效率提升10倍左右. 新方法在激光惯性约束聚变的黑腔辐射输运模拟应用中取得了显著效果.The implicit Monte Carlo (IMC) method is an important numerical approximation method of simulating the thermal radiative transfer problems under high temperature condition. However, one problem plaguing the IMC method is that the calculation error distributions of the radiation specific intensities are highly asymmetric in space and time. By theoretical analysis and numerical simulations, we find that the error is affected by the records of track in the tallying mesh. Accordingly, a global variance reduction method for implicit Monte Carlo simulation is developed and the corresponding formulas are derived. This method includes three key techniques: 1) the automated dynamic distribution method for the Monte Carlo simulation source particles; 2) the dynamic weight-window technique and the none-bias weight revise algorithm that is suited to the particle distribution method; 3) the analytical estimation variance reduction method of the radiation specific intensity. In view of the above, a three-dimensional simulation code, named IMC3D, is developed to simulate the thermal radiative transfer phenomena. The typical thermal radiative transport problem, known as Marshak wave, is simulated. The simulation results indicate that the global variance reduction method for implicit Monte Carlo makes the statistical errors much more symmetric in space and time and the maximum of error is controllable, thereby increasing the calculation speed approximately 10 times. The new IMC method and code are used for simulating the radiative transportation in hohlraum of ICF successfully.
-
Keywords:
- implicit Monte Carlo method /
- thermal radiative transfer /
- global variance reduction method /
- inertial confinement fusion
[1] 彭惠民 2008 等离子体中辐射输运和辐射流体力学 (北京: 国防工业出版社) 第39, 232页
Peng H M 2008 Radiation Transport and Radiation Hydrodynamics in Plasmas (Beijing: National Defense Industry Press) pp39, 232
[2] Lindl J D 1995 Phys. Plasmas 2 3933
Google Scholar
[3] 张均, 常铁强 2004 激光核聚变靶物理基础 (北京: 国防工业出版社) 第1—9页
Zhang J, Chang T Q 2004 Fundaments of the Target Physics for Laser Fusion (Beijing: National Defense Industry Press) pp1–9 (in Chinese)
[4] 阿采尼, 迈尔·特尔·费恩 著 (沈百飞译) 2008 惯性聚变物理 (北京: 科学出版社) 第23, 254页
Stefano Atzeni, Jurgen Meyer-ter-Vehn (translated by Shen B F) 2008 The Physics of Inertial Fusion (Beijing: Science Press) pp23, 254 (in Chinese)
[5] 裴鹿成, 张孝泽 1980 蒙特卡罗方法及其在粒子输运问题中的应用 (北京: 科学出版社) 第1—20页
Pei L C, Zhang X Z 1980 Monte Carlo Method and Application in Particle Transportation (Beijing: Science Press) pp1–20 (in Chinese)
[6] Kalos M H, Whitlock P A 2022 Monte Carlo Methods (Weinheim: WILEY-VCH Verlag GmbH & Co KGaA) pp1–34
[7] Fleck J A, Cummings J D 1971 J. Comput. Phys. 8 313
Google Scholar
[8] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2005 American Nuclear Society Topical Meeting in Mathematics and Computations Avignon, France, September 12–15, 2005 LA-UR-05-3781
[9] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2007 J. Comput. Phys. 222 485
Google Scholar
[10] Cleveland M A, Gentile N, Palmer T S 2010 J. Comput. Phys. 229 5707
Google Scholar
[11] Densmore J D, Thompson K G, Urbatsch T J 2012 J. Comput. Phys. 231 6924
Google Scholar
[12] Cleveland M A, Wollaber A B 2018 J. Comput. Phys. 359 20
Google Scholar
[13] Marinak M M, Remington B A, Weber S V, Tipton R E, Haan S W, Budil K S, Landen O L, Kilkenny J D, Wallace R 1995 Phys. Rev. Lett. 75 3677
Google Scholar
[14] Rathkopf J A, Miller D S, Owen J M, et al. 2000 KULL: LLNL's ASCI Inertial Confinement Fusion Simulation Code (Livermore: Lawrence Livermore National Laboratory) UCRL-JC-137053
[15] 李树, 李刚, 田东风, 邓力 2013 62 249501
Google Scholar
Li S, Li G, Tian D F, Deng L 2013 Acta Phys. Sin. 62 249501
Google Scholar
[16] 李树, 邓力, 田东风, 李刚 2014 63 239501
Google Scholar
Li S, Deng L, Tian D F, Li G 2014 Acta Phys. Sin. 63 239501
Google Scholar
[17] 李树, 蓝可, 赖东显, 刘杰 2015 64 145203
Google Scholar
Li S, Lan K, Lai D X Liu J 2015 Acta Phys. Sin. 64 145203
Google Scholar
[18] Li S, Lan K, Liu J 2015 Laser Part. Beams 33 731
Google Scholar
[19] 李树, 陈耀华, 姬志成, 章明宇, 任国利, 霍文义, 闫威华, 韩小英, 李志超, 刘杰, 蓝可 2018 67 025202
Google Scholar
Li S, Chen Y H, Ji Z C, Zhang M Y, Ren G L, Huo W Y, Yan W H, Han X Y, Li Z C, Liu J, Lan K 2018 Acta Phys. Sin. 67 025202
Google Scholar
[20] Marshak R E 1958 Phys. Fluids 1 24
Google Scholar
[21] Pomraning G C 1979 J. Quant. Spectrosc. Radiat. Transfer 21 249
Google Scholar
[22] Hurricane O A, Hammer J H 2006 Phys. Plasmas 13 113303
Google Scholar
[23] Cooper M A 1999 Ph. D. Dissertation (Ann Arbor: University of Michigan)
[24] Lan K, Liu J, Lai D X, Zheng W D, He X T 2014 Phys. Plasmas 21 010704
Google Scholar
[25] Huo W Y, Liu J, Zhao Y Q, Zheng W D, Lan K 2014 Phys. Plasmas 21 114503
Google Scholar
[26] Lan K, Liu J, Li Z, et al. 2016 Matter and Radiation at Extremes 1 8
Google Scholar
[27] Haan S W, Lindl J D, Callahan D A, et al. 2011 Phys. Plasmas 18 051001
Google Scholar
[28] Cao H, Chen Y H, Zhai C L, Zheng C Y, Lan K 2017 Phys. Plasmas 24 082701
Google Scholar
-
图 1 Marshak波辐射温度分布(104粒子/步)
Fig. 1. Radiation temperature for the Marshak wave (104 particles/step).
图 2 Marshak波辐射温度误差分布(105粒子/步)
Fig. 2. Statistical error of radiation temperature for the Marshak wave (105 particles/step).
图 3 Marshak波辐射温度分布(105粒子/步)
Fig. 3. Radiation temperature for the Marshak wave (105 particles/step).
图 4 Marshak波辐射温度误差分布(105粒子/步)
Fig. 4. Statistical error of radiation temperature for the Marshak wave (105 particles/step).
图 6 3个时刻的辐射强度误差分布
Fig. 6. Statistical error of radiation intensity for different time step.
图 9 源粒子分配数比较(old vs. new 1)
Fig. 9. Comparison of the source particles (old vs. new 1).
图 11 源粒子分配数比较(old vs. new 2)
Fig. 11. Comparison of the source particles (old vs. new 2).
图 13 误差分布比较(new 2 vs. new 3)
Fig. 13. Comparison of statistical error (new 2 vs. new 3)
表 1 计算时间及计算效率比较
Table 1. Comparison of calculated CPU time and efficiency.
原方法 情况I 情况II 情况III 实际计算时间/min 606 852 863 971 时间比值(情况x/原方法) 1.0 1.4 1.4 1.6 7.4 ns时刻波头误差 0.06011 0.02799 0.02179 0.01445 等效计算时间/min 606 185 113 56 效率提升(情况x/原方法) 1.0 3.27 5.36 10.82 注: 等效时间折算方法. 根据“误差与源粒子数的1/2次方呈反比”、“源粒子数与计算时间呈正比”原则, 在误差相等条件下, 等效 时间 = 情况 x 实际计算时间×(情况 x 误差的2次方/原方法误差的2次方). 
下载: 导出CSV
-
[1] 彭惠民 2008 等离子体中辐射输运和辐射流体力学 (北京: 国防工业出版社) 第39, 232页
Peng H M 2008 Radiation Transport and Radiation Hydrodynamics in Plasmas (Beijing: National Defense Industry Press) pp39, 232
[2] Lindl J D 1995 Phys. Plasmas 2 3933
Google Scholar
[3] 张均, 常铁强 2004 激光核聚变靶物理基础 (北京: 国防工业出版社) 第1—9页
Zhang J, Chang T Q 2004 Fundaments of the Target Physics for Laser Fusion (Beijing: National Defense Industry Press) pp1–9 (in Chinese)
[4] 阿采尼, 迈尔·特尔·费恩 著 (沈百飞译) 2008 惯性聚变物理 (北京: 科学出版社) 第23, 254页
Stefano Atzeni, Jurgen Meyer-ter-Vehn (translated by Shen B F) 2008 The Physics of Inertial Fusion (Beijing: Science Press) pp23, 254 (in Chinese)
[5] 裴鹿成, 张孝泽 1980 蒙特卡罗方法及其在粒子输运问题中的应用 (北京: 科学出版社) 第1—20页
Pei L C, Zhang X Z 1980 Monte Carlo Method and Application in Particle Transportation (Beijing: Science Press) pp1–20 (in Chinese)
[6] Kalos M H, Whitlock P A 2022 Monte Carlo Methods (Weinheim: WILEY-VCH Verlag GmbH & Co KGaA) pp1–34
[7] Fleck J A, Cummings J D 1971 J. Comput. Phys. 8 313
Google Scholar
[8] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2005 American Nuclear Society Topical Meeting in Mathematics and Computations Avignon, France, September 12–15, 2005 LA-UR-05-3781
[9] Densmore J D, Urbatsch T J, Evans T M, Buksas M W 2007 J. Comput. Phys. 222 485
Google Scholar
[10] Cleveland M A, Gentile N, Palmer T S 2010 J. Comput. Phys. 229 5707
Google Scholar
[11] Densmore J D, Thompson K G, Urbatsch T J 2012 J. Comput. Phys. 231 6924
Google Scholar
[12] Cleveland M A, Wollaber A B 2018 J. Comput. Phys. 359 20
Google Scholar
[13] Marinak M M, Remington B A, Weber S V, Tipton R E, Haan S W, Budil K S, Landen O L, Kilkenny J D, Wallace R 1995 Phys. Rev. Lett. 75 3677
Google Scholar
[14] Rathkopf J A, Miller D S, Owen J M, et al. 2000 KULL: LLNL's ASCI Inertial Confinement Fusion Simulation Code (Livermore: Lawrence Livermore National Laboratory) UCRL-JC-137053
[15] 李树, 李刚, 田东风, 邓力 2013 62 249501
Google Scholar
Li S, Li G, Tian D F, Deng L 2013 Acta Phys. Sin. 62 249501
Google Scholar
[16] 李树, 邓力, 田东风, 李刚 2014 63 239501
Google Scholar
Li S, Deng L, Tian D F, Li G 2014 Acta Phys. Sin. 63 239501
Google Scholar
[17] 李树, 蓝可, 赖东显, 刘杰 2015 64 145203
Google Scholar
Li S, Lan K, Lai D X Liu J 2015 Acta Phys. Sin. 64 145203
Google Scholar
[18] Li S, Lan K, Liu J 2015 Laser Part. Beams 33 731
Google Scholar
[19] 李树, 陈耀华, 姬志成, 章明宇, 任国利, 霍文义, 闫威华, 韩小英, 李志超, 刘杰, 蓝可 2018 67 025202
Google Scholar
Li S, Chen Y H, Ji Z C, Zhang M Y, Ren G L, Huo W Y, Yan W H, Han X Y, Li Z C, Liu J, Lan K 2018 Acta Phys. Sin. 67 025202
Google Scholar
[20] Marshak R E 1958 Phys. Fluids 1 24
Google Scholar
[21] Pomraning G C 1979 J. Quant. Spectrosc. Radiat. Transfer 21 249
Google Scholar
[22] Hurricane O A, Hammer J H 2006 Phys. Plasmas 13 113303
Google Scholar
[23] Cooper M A 1999 Ph. D. Dissertation (Ann Arbor: University of Michigan)
[24] Lan K, Liu J, Lai D X, Zheng W D, He X T 2014 Phys. Plasmas 21 010704
Google Scholar
[25] Huo W Y, Liu J, Zhao Y Q, Zheng W D, Lan K 2014 Phys. Plasmas 21 114503
Google Scholar
[26] Lan K, Liu J, Li Z, et al. 2016 Matter and Radiation at Extremes 1 8
Google Scholar
[27] Haan S W, Lindl J D, Callahan D A, et al. 2011 Phys. Plasmas 18 051001
Google Scholar
[28] Cao H, Chen Y H, Zhai C L, Zheng C Y, Lan K 2017 Phys. Plasmas 24 082701
Google Scholar
下载:
计量
- 文章访问数: 2751
- PDF下载量: 90
- 被引次数: 0
