基于空间光调制器构建二维任意形状的<sup>87</sup>Rb原子阵列

王良伟; 刘方德; 李云达; 韩伟; 孟增明; 张靖

doi:10.7498/aps.72.20222096

摘要

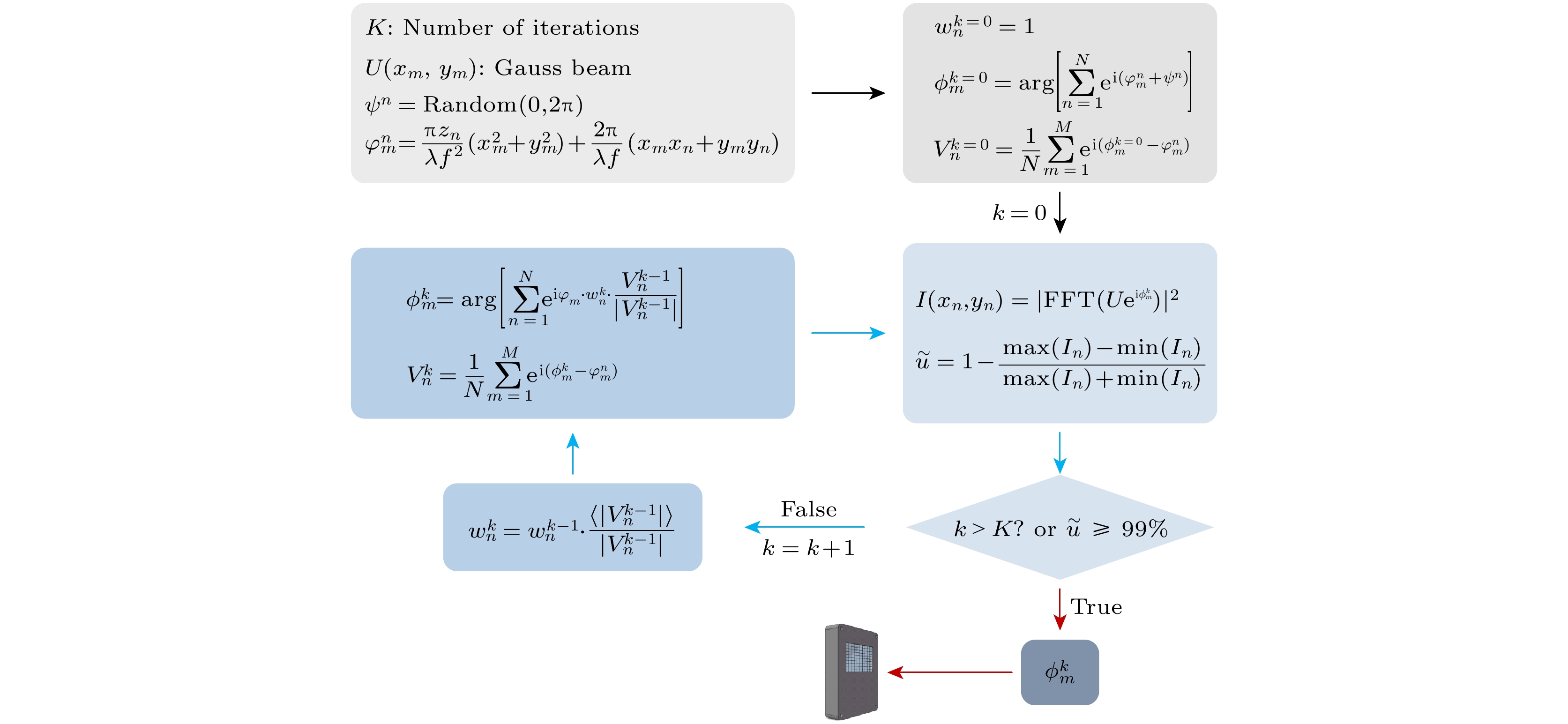
超冷原子系统是一个纯净的、高度可控的量子体系, 可对凝聚态物理、高能物理、天体物理和化学反应等领域的重要物理问题进行量子模拟. 构造不同构型的光晶格是模拟多样化的复杂量子系统的一个重要前提. 本文采用权重Gerchberg-Saxton算法生成多种形状的光晶格全息图, 利用液晶型空间光调制器和高分辨率光学系统, 把全息图(动量空间)变换到实空间构造出多种形状的二维晶格阵列, 包括简单的三角、六角、正方晶格和更为复杂的蜂巢晶格等, 并实现对⁸⁷Rb超冷原子二维晶格阵列的装载, 晶格的最小间距为3 μm. 这种方法具有通用性强、操控灵活的优势, 将有助于拓展光晶格中超冷原子量子模拟的应用.

关键词:

Abstract

The ultra-cold atomic system is a clean and highly controllable quantum system, which can be used for quantum simulation of important physical problems in many fields such as condensed matter physics, high-energy physics, astrophysics, and chemical reactions. The constructions of optical lattices with different configurations are an important prerequisite for simulating diverse complex quantum systems, especially solid materials. In this work, we use weighted Gerchberg-Saxton algorithm to generate holograms. By using liquid crystal spatial light modulator and high-resolution imaging system, holograms (in momentum space) are transformed into images in real space for constructing various two-dimensional (2D) optical trap arrays, such as simple triangular, hexagonal, square lattice and more complex honeycomb lattice. We load ⁸⁷Rb ultra-cold atoms into the 2D optical trap arrays with a minimal spacing of 3 μm in between. This method is versatile and flexible, which is helpful in expanding the application scope of quantum simulation with optical lattices.

Keywords:

作者及机构信息

1.
山西大学光电研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

2.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 孟增明, zmmeng01@sxu.edu.cn ; 张靖, jzhang74@sxu.edu.cn

基金项目: 科技创新2030重大专项(批准号: 2021ZD0302003)、国家重点研发计划(批准号: 2018YFA0307601, 2021YFA1401700, 2022YFA1404101)和国家自然科学基金(批准号: 12034011, 92065108, 11974224, 12022406, 12004229) 资助的课题.

Authors and contacts

1.
State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China

2.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Meng Zeng-Ming, zmmeng01@sxu.edu.cn ; Zhang Jing, jzhang74@sxu.edu.cn

Funds: Project supported by the Science and Technology Innovation of 2030-Major Project, China (Grant No. 2021ZD0302003), the National Key Research and Development Program of China (Grant Nos. 2018YFA0307601, 2021YFA1401700, 2022YFA1404101), and the National Natural Science Foundation of China (Grant Nos. 12034011, 92065108, 11974224, 12022406, 12004229).

文章全文 : translate this paragraph

参考文献

[1]	Georgescu I M, Ashhab S, Nori F 2014 Rev. Mod. Phys. 86 153 Google Scholar
[2]	Gross C, Bloch I 2017 Science 357 995 Google Scholar
[3]	Das A, Chakrabarti B K 2008 Rev. Mod. Phys. 80 1061 Google Scholar
[4]	Hofstetter W, Cirac J I, Zoller P, Demler E, Lukin M D 2002 Phys. Rev. Lett. 89 220407 Google Scholar
[5]	Lee P A, Nagaosa N, Wen X G 2006 Rev. Mod. Phys. 78 17 Google Scholar
[6]	Le Hur K, Rice T M 2009 Annals of Physics 324 1452 Google Scholar
[7]	Polkovnikov A, Sengupta K, Silva A, Vengalattore M 2011 Rev. Mod. Phys. 83 863 Google Scholar
[8]	Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39 Google Scholar
[9]	Sherson J F, Weitenberg C, Endres M, Cheneau M, Bloch I, Kuhr S 2010 Nature 467 68 Google Scholar
[10]	Bakr W S, Peng A, Tai M E, Ma R, Simon J, Gillen J I, Fölling S, Pollet L, Greiner M 2010 Science 329 547 Google Scholar
[11]	Jördens R, Strohmaier N, Günter K, Moritz H, Esslinger T 2008 Nature 455 204 Google Scholar
[12]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[13]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[14]	Semeghini G, Levine H, Keesling A, Ebadi S, Wang T T, Bluvstein D, Verresen R, Pichler H, Kalinowski M, Samajdar R, Omran A, Sachdev S, Vishwanath A, Greiner M, Vuletić V, Lukin M D 2021 Science 374 1242 Google Scholar
[15]	Li C H, Yan Y, Feng S W, Choudhury S, Blasing D B, Zhou Q, Chen Y P 2022 PRX Quantum 3 010316 Google Scholar
[16]	Struck J, Ölschläger C, Le Targat R, Soltan-Panahi P, Eckardt A, Lewenstein M, Windpassinger P, Sengstock K 2011 Science 333 996 Google Scholar
[17]	Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, Esslinger T 2014 Nature 515 237 Google Scholar
[18]	Uehlinger T, Jotzu G, Messer M, Greif D, Hofstetter W, Bissbort U, Esslinger T 2013 Phys. Rev. Lett. 111 185307 Google Scholar
[19]	González-Tudela A, Cirac J I 2019 Phys. Rev. A 100 053604 Google Scholar
[20]	Meng Z M, Wang L W, Han W, Liu F D, Wen K, Gao C, Wang P J, Chin C, Zhang J 2023 Nature 615 231
[21]	Dai H N, Yang B, Reingruber A, Xu X F, Jiang X, Chen Y A, Yuan Z S, Pan J W 2016 Nat. Phys. 12 783 Google Scholar
[22]	Mandel O, Greiner M, Widera A, Rom T, Hänsch T W, Bloch I 2003 Phys. Rev. Lett. 91 010407 Google Scholar
[23]	Choi J Y, Hild S, Zeiher J, Schauß P, Rubio-Abadal A, Yefsah T, Khemani V, Huse D A, Bloch I, Gross C 2016 Science 352 1547 Google Scholar
[24]	White D H, Haase T A, Brown D J, Hoogerland M D, Najafabadi M S, Helm J L, Gies C, Schumayer D, Hutchinson D A W 2020 Nat. Commun. 11 4942 Google Scholar
[25]	Zhang Z D, Chen L C, Yao K X, Chin C 2021 Nature 592 708 Google Scholar
[26]	Mazurenko A, Chiu C S, Ji G, Parsons M F, Kanász-Nagy M, Schmidt R, Grusdt F, Demler E, Greif D, Greiner M 2017 Nature 545 462 Google Scholar
[27]	Endres M, Bernien H, Keesling A, Levine H, Anschuetz E R, Krajenbrink A, Senko C, Vuletic V, Greiner M, Lukin M D 2016 Science 354 1024 Google Scholar
[28]	Henderson K, Ryu C, MacCormick C, Boshier M G 2009 New J. Phys. 11 043030 Google Scholar
[29]	Fatemi F K, Bashkansky M, Dutton Z 2007 Opt. Express 15 3589 Google Scholar
[30]	Zhang D F, Gao T Y, Zou P, Kong L R, Li R Z, Shen X, Chen X L, Peng S G, Zhan M S, Pu H, Jiang K J 2019 Phys. Rev. Lett. 122 110402 Google Scholar
[31]	Chen P K, Liu L R, Tsai M J, Chiu N C, Kawaguchi Y, Yip S K, Chang M S, Lin Y J 2018 Phys. Rev. Lett. 121 250401 Google Scholar
[32]	Goodman J W 2005 Introduction to Fourier Optics (Greenwood Village: Roberts and Company Publishers) p63
[33]	Di Leonardo R, Ianni F, Ruocco G 2007 Opt. Express 15 1913 Google Scholar
[34]	Bengtsson J 1994 Appl. Opt. 33 6879 Google Scholar
[35]	Turtaev S, Leite I T, Mitchell K J, Padgett M J, Phillips D B, Čižmár T 2017 Opt. Express 25 29874 Google Scholar

施引文献

图 1 SLM的标量衍射理论图

Fig. 1. Foundations of scalar diffraction theory of SLM.

下载: 全尺寸图片幻灯片

图 2 迭代GSW算法的流程图

Fig. 2. Flow chart of iterative GSW algorithm.

下载: 全尺寸图片幻灯片

图 3 实验装置图　(a) SLM光路图; (b) 成像光路图; (c) 手风琴光晶格光路图(CCD, 电荷耦合器件; PBS, 偏振分束器, BD, 光挡; FM, 翻转镜片; DM, 双色分束器; PD, 光电二极管; AOD, 声光偏转器)

Fig. 3. Experimental configuration: (a) SLM setup; (b) imaging setup; (c) accordion lattice setup (CCD, charge coupled device; PBS, polarizing beam splitter, BD, beam dump; FM, flip mirror; DM, dichroic mirror; PD, photodiode detectors; AOD, acousto-optic deflector).

下载: 全尺寸图片幻灯片

图 4 相图合成(上)和实验结果(下)　(a) GSW算法获得的光晶格相图, 零级光和目标晶格混合在一起; (b) 闪耀光栅相图; (c) 合成相图

Fig. 4. Composition of the phase pattern (up) and the optical intensity distribution (bottom): (a) Optical lattice phase diagram obtained by GSW algorithm, zero-order light and target lattice mixed together; (b) blaze grating pattern; (c) final phase pattern.

下载: 全尺寸图片幻灯片

图 5 算法的性能比较(第一行为相图, 第二行为实验结果)　(a) SPL算法; (b) SR算法; (c) RM算法; (d) GSW算法

Fig. 5. Performance comparison of different theoretical algorithms (Row 1, phase patterns; Row 2, optical intensity distribution): (a) SPL algorithm; (b) SR algorithm; (c) RM algorithm; (d) GSW algorithm.

下载: 全尺寸图片幻灯片

图 6 双层扭转类石墨烯光晶格

Fig. 6. Twisted-bilayer graphene-like optical lattice.

下载: 全尺寸图片幻灯片

图 7 强度调控　(a) 非均匀光晶格; (b) 沿虚线路径的光强分布

Fig. 7. Intensity control: (a) Inhomogeneous optical lattice; (b) optical intensity profiles along the dashed lines on panel (a)

下载: 全尺寸图片幻灯片

图 8 具有不同相位模式的原子阵列　(a1), (a2)相图; (b1), (b2)原子阵列

Fig. 8. Atomic arrays with different phase patterns: (a1), (a2) Phase patterns; (b1), (b2) atomic arrays.

下载: 全尺寸图片幻灯片

map

[1]	Georgescu I M, Ashhab S, Nori F 2014 Rev. Mod. Phys. 86 153 Google Scholar
[2]	Gross C, Bloch I 2017 Science 357 995 Google Scholar
[3]	Das A, Chakrabarti B K 2008 Rev. Mod. Phys. 80 1061 Google Scholar
[4]	Hofstetter W, Cirac J I, Zoller P, Demler E, Lukin M D 2002 Phys. Rev. Lett. 89 220407 Google Scholar
[5]	Lee P A, Nagaosa N, Wen X G 2006 Rev. Mod. Phys. 78 17 Google Scholar
[6]	Le Hur K, Rice T M 2009 Annals of Physics 324 1452 Google Scholar
[7]	Polkovnikov A, Sengupta K, Silva A, Vengalattore M 2011 Rev. Mod. Phys. 83 863 Google Scholar
[8]	Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39 Google Scholar
[9]	Sherson J F, Weitenberg C, Endres M, Cheneau M, Bloch I, Kuhr S 2010 Nature 467 68 Google Scholar
[10]	Bakr W S, Peng A, Tai M E, Ma R, Simon J, Gillen J I, Fölling S, Pollet L, Greiner M 2010 Science 329 547 Google Scholar
[11]	Jördens R, Strohmaier N, Günter K, Moritz H, Esslinger T 2008 Nature 455 204 Google Scholar
[12]	Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 Google Scholar
[13]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[14]	Semeghini G, Levine H, Keesling A, Ebadi S, Wang T T, Bluvstein D, Verresen R, Pichler H, Kalinowski M, Samajdar R, Omran A, Sachdev S, Vishwanath A, Greiner M, Vuletić V, Lukin M D 2021 Science 374 1242 Google Scholar
[15]	Li C H, Yan Y, Feng S W, Choudhury S, Blasing D B, Zhou Q, Chen Y P 2022 PRX Quantum 3 010316 Google Scholar
[16]	Struck J, Ölschläger C, Le Targat R, Soltan-Panahi P, Eckardt A, Lewenstein M, Windpassinger P, Sengstock K 2011 Science 333 996 Google Scholar
[17]	Jotzu G, Messer M, Desbuquois R, Lebrat M, Uehlinger T, Greif D, Esslinger T 2014 Nature 515 237 Google Scholar
[18]	Uehlinger T, Jotzu G, Messer M, Greif D, Hofstetter W, Bissbort U, Esslinger T 2013 Phys. Rev. Lett. 111 185307 Google Scholar
[19]	González-Tudela A, Cirac J I 2019 Phys. Rev. A 100 053604 Google Scholar
[20]	Meng Z M, Wang L W, Han W, Liu F D, Wen K, Gao C, Wang P J, Chin C, Zhang J 2023 Nature 615 231
[21]	Dai H N, Yang B, Reingruber A, Xu X F, Jiang X, Chen Y A, Yuan Z S, Pan J W 2016 Nat. Phys. 12 783 Google Scholar
[22]	Mandel O, Greiner M, Widera A, Rom T, Hänsch T W, Bloch I 2003 Phys. Rev. Lett. 91 010407 Google Scholar
[23]	Choi J Y, Hild S, Zeiher J, Schauß P, Rubio-Abadal A, Yefsah T, Khemani V, Huse D A, Bloch I, Gross C 2016 Science 352 1547 Google Scholar
[24]	White D H, Haase T A, Brown D J, Hoogerland M D, Najafabadi M S, Helm J L, Gies C, Schumayer D, Hutchinson D A W 2020 Nat. Commun. 11 4942 Google Scholar
[25]	Zhang Z D, Chen L C, Yao K X, Chin C 2021 Nature 592 708 Google Scholar
[26]	Mazurenko A, Chiu C S, Ji G, Parsons M F, Kanász-Nagy M, Schmidt R, Grusdt F, Demler E, Greif D, Greiner M 2017 Nature 545 462 Google Scholar
[27]	Endres M, Bernien H, Keesling A, Levine H, Anschuetz E R, Krajenbrink A, Senko C, Vuletic V, Greiner M, Lukin M D 2016 Science 354 1024 Google Scholar
[28]	Henderson K, Ryu C, MacCormick C, Boshier M G 2009 New J. Phys. 11 043030 Google Scholar
[29]	Fatemi F K, Bashkansky M, Dutton Z 2007 Opt. Express 15 3589 Google Scholar
[30]	Zhang D F, Gao T Y, Zou P, Kong L R, Li R Z, Shen X, Chen X L, Peng S G, Zhan M S, Pu H, Jiang K J 2019 Phys. Rev. Lett. 122 110402 Google Scholar
[31]	Chen P K, Liu L R, Tsai M J, Chiu N C, Kawaguchi Y, Yip S K, Chang M S, Lin Y J 2018 Phys. Rev. Lett. 121 250401 Google Scholar
[32]	Goodman J W 2005 Introduction to Fourier Optics (Greenwood Village: Roberts and Company Publishers) p63
[33]	Di Leonardo R, Ianni F, Ruocco G 2007 Opt. Express 15 1913 Google Scholar
[34]	Bengtsson J 1994 Appl. Opt. 33 6879 Google Scholar
[35]	Turtaev S, Leite I T, Mitchell K J, Padgett M J, Phillips D B, Čižmár T 2017 Opt. Express 25 29874 Google Scholar

[1]	李婷, 汪涛, 王叶兵, 卢本全, 卢晓同, 尹默娟, 常宏. 浅光晶格中量子隧穿现象的实验观测. , 2022, 71(7): 073701. doi: 10.7498/aps.71.20212038
[2]	张爱霞, 姜艳芳, 薛具奎. 光晶格中自旋轨道耦合玻色-爱因斯坦凝聚体的非线性能谱特性. , 2021, 70(20): 200302. doi: 10.7498/aps.70.20210705
[3]	喻欢欢, 张晨爽, 林丹樱, 于斌, 屈军乐. 基于高速相位型空间光调制器的双光子多焦点结构光显微技术. , 2021, 70(9): 098701. doi: 10.7498/aps.70.20201797
[4]	文凯, 王良伟, 周方, 陈良超, 王鹏军, 孟增明, 张靖. 超冷⁸⁷Rb原子在二维光晶格中Mott绝缘态的实验实现. , 2020, 69(19): 193201. doi: 10.7498/aps.69.20200513
[5]	卢晓同, 李婷, 孔德欢, 王叶兵, 常宏. 锶原子光晶格钟碰撞频移的测量. , 2019, 68(23): 233401. doi: 10.7498/aps.68.20191147
[6]	赵兴东, 张莹莹, 刘伍明. 光晶格中超冷原子系统的磁激发. , 2019, 68(4): 043703. doi: 10.7498/aps.68.20190153
[7]	李晓云, 孙博文, 许正倩, 陈静, 尹亚玲, 印建平. 基于调制光晶格的中性分子束光学Stark减速与囚禁的理论研究. , 2018, 67(20): 203702. doi: 10.7498/aps.67.20181348
[8]	林弋戈, 方占军. 锶原子光晶格钟. , 2018, 67(16): 160604. doi: 10.7498/aps.67.20181097
[9]	白云鹤, 臧瑞环, 汪盼, 荣腾达, 马凤英, 杜艳丽, 段智勇, 弓巧侠. 基于空间光调制器的非相干数字全息单次曝光研究. , 2018, 67(6): 064202. doi: 10.7498/aps.67.20172127
[10]	解万财, 黄素娟, 邵蔚, 朱福全, 陈木生. 基于混合光模式阵列的自由空间编码通信. , 2017, 66(14): 144102. doi: 10.7498/aps.66.144102
[11]	席思星, 王晓雷, 黄帅, 常胜江, 林列. 基于光学全息的任意矢量光的生成方法. , 2015, 64(12): 124202. doi: 10.7498/aps.64.124202
[12]	田晓, 王叶兵, 卢本全, 刘辉, 徐琴芳, 任洁, 尹默娟, 孔德欢, 常宏, 张首刚. 锶玻色子的“魔术”波长光晶格装载实验研究. , 2015, 64(13): 130601. doi: 10.7498/aps.64.130601
[13]	藤斐, 谢征微. 光晶格中双组分玻色-爱因斯坦凝聚系统的调制不稳定性. , 2013, 62(2): 026701. doi: 10.7498/aps.62.026701
[14]	周巧巧, 徐淑武, 陆俊发, 周琦, 纪宪明, 印建平. 液晶空间光调制器产生可调三光学势阱. , 2013, 62(15): 153701. doi: 10.7498/aps.62.153701
[15]	顾宋博, 徐淑武, 陆俊发, 纪宪明, 印建平. 用液晶空间光调制器产生光阱阵列. , 2012, 61(15): 153701. doi: 10.7498/aps.61.153701
[16]	徐淑武, 周巧巧, 顾宋博, 纪宪明, 印建平. 用空间光调制器产生三维光阱阵列. , 2012, 61(22): 223702. doi: 10.7498/aps.61.223702
[17]	张科智, 王建军, 刘国荣, 薛具奎. 两组分BECs在光晶格中的隧穿动力学及其周期调制效应. , 2010, 59(5): 2952-2961. doi: 10.7498/aps.59.2952
[18]	周骏, 任海东, 冯亚萍. 强非局域光晶格中空间孤子的脉动传播. , 2010, 59(6): 3992-4000. doi: 10.7498/aps.59.3992
[19]	黄劲松, 陈海峰, 谢征微. 光晶格中双组分偶极玻色-爱因斯坦凝聚体的调制不稳定性. , 2008, 57(6): 3435-3439. doi: 10.7498/aps.57.3435
[20]	徐志君, 程　成, 杨欢耸, 武　强, 熊宏伟. 三维光晶格中玻色凝聚气体基态波函数及干涉演化. , 2004, 53(9): 2835-2842. doi: 10.7498/aps.53.2835

计量

文章访问数: 3890
PDF下载量: 151
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于空间光调制器构建二维任意形状的⁸⁷Rb原子阵列