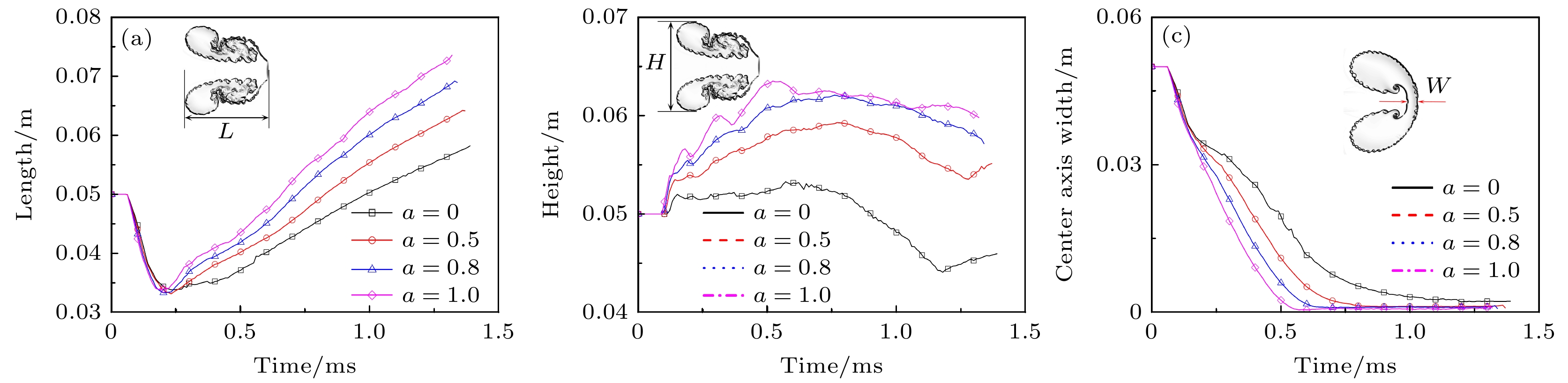
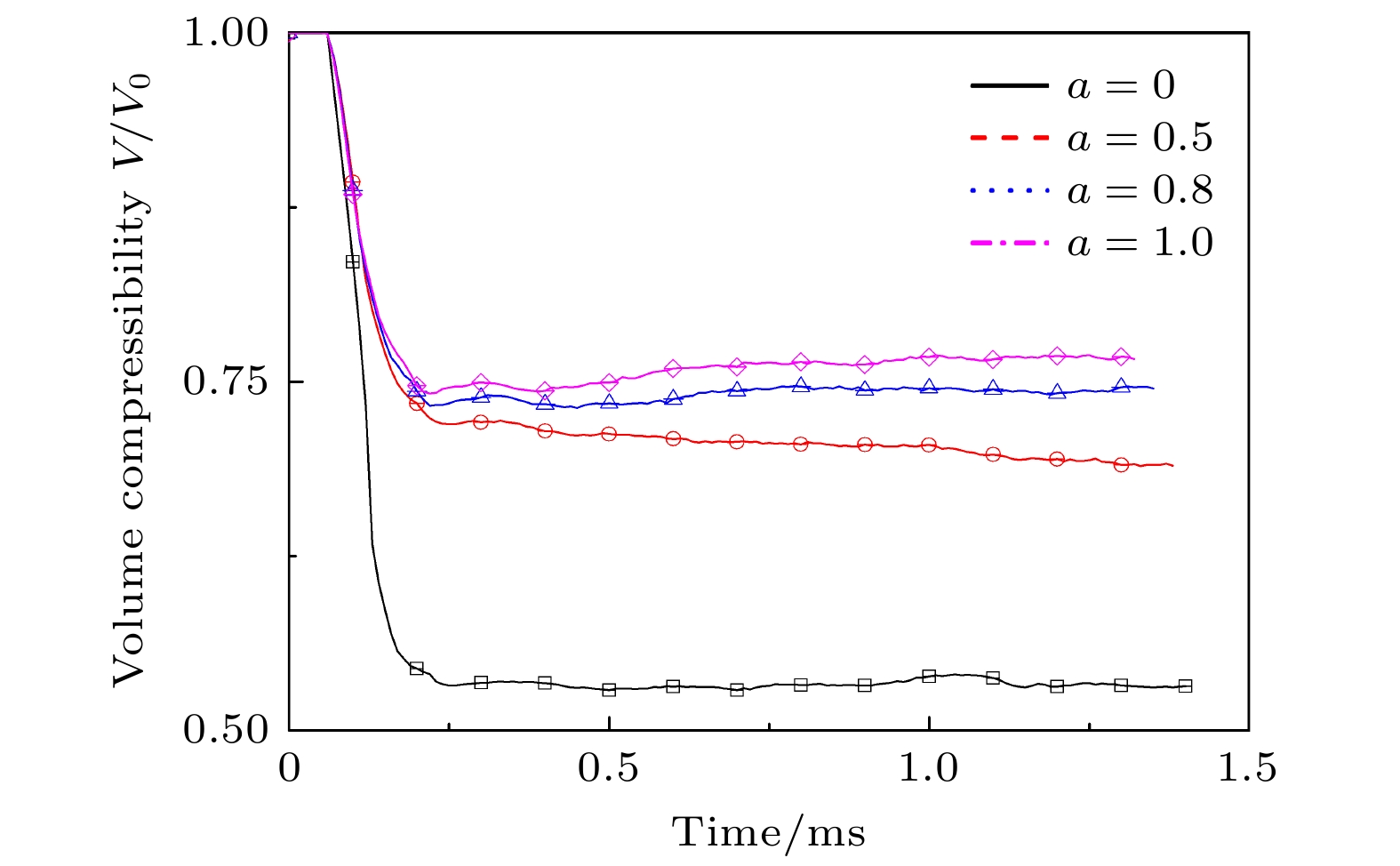
-
基于二维非定常Euler方程, 对平面激波与不同界面组分分布下氦气气柱作用过程所引起的Richtmyer-Meshkov不稳定性现象进行了数值模拟, 探讨了激波冲击轻质气柱后气柱界面形态的演变及流场波系结构, 定量分析了气柱特征尺度(气柱长度、高度和中轴宽度)和气柱体积压缩率随时间变化. 此外, 结合流场压强、速度、环量和气体混合率, 多角度分析了激波驱动界面气体混合的流动机制, 获得了不同界面组分分布对界面不稳定性的影响. 结果表明, 随着气柱界面从完全扩散界面向间断界面的过渡, 界面两侧的声反射系数随之增大, 使入射激波与气柱界面的作用由常规透射转变为非常规透射, 反射激波逐渐加强, 透射激波逐渐减弱, 使得Richtmyer-Meshkov不稳定性随之增强; 同时, 界面两侧阿特伍德数的增大, 加强了Rayleigh-Taylor不稳定性和Kelvin-Helmholtz不稳定性的发展. 此外, 界面不稳定性的加强使得流场环量增大, 导致气体混合率的增长速率随之升高.
-
关键词:
- Richtmyer-Meshkov不稳定性 /
- 间断界面 /
- 扩散界面 /
- 氦气柱 /
- 激波
In this paper, the Richtmyer-Meshkov instability is studied numerically by using the high-resolution Roe scheme based on the two-dimensional unsteady Euler equation, which is caused by the interaction between shock wave and the helium circular light gas cylinder with different component distributions. The numerical results are used to further discuss the deformation process of the gas cylinder and the wave structure of the flow field, and also to quantitatively analyze the characteristic dimensions (length, height and central axial width) of the gas cylinder, the time-dependent volume compression ratio of the cylinder. In addition, the flow mechanism of shock-driven interface gas mixing is analyzed from multiple perspectives by combining the flow field pressure, velocity, circulation and gas mixing rate. Then the effects of different initial component distribution conditions on interface instability are investigated. The results show that when the diffusion interface transforms into the sharp interface, the reflection coefficient gradually increases on both sides of interface. When the incident shock wave interacts with the cylinder, the transmission of the shock wave will transform from conventional transmission into unconventional transmission. At the same time, the reflected shock wave is gradually strengthened and the transmitted shock wave is gradually weakened, which leads the Richtmyer-Meshkov instability to be strengthened. Moreover, the Atwood numbers on both sides of the interface also increase as the diffusion interface transforms into the sharp interface, which leads the Rayleigh-Taylor instability and the Kelvin-Helmholtz instability to be strengthened. Therefore, the increase of instability will cause the circulation to increase, resulting in the increase of the growth rate of gas mixing rate.-
Keywords:
- Richtmyer-Meshkov instability /
- sharp interface /
- diffusive interface /
- Helium cylinder /
- shock wave
[1] 林震亚, 张焕好, 陈志华, 刘迎 2017 爆炸与冲击 37 748
Google Scholar
Lin Z Y, Zhang H H, Chen Z H, Liu Y 2017 Explosion and Shock Waves 37 748
Google Scholar
[2] Markstein G H 1957 J Aero Sci. 24 238
[3] Richtmyer R D 1960 Commun. Pure. Appl. Math. 13 297
Google Scholar
[4] Meshkov E E 1969 Fluid Dyn. 4 101
Google Scholar
[5] Kelvin L 1871 Philos Mag. 150 405
[6] Helmholtz H V 1868 Monthly Reports of the Royal Prussian Academy of Philosophy in Berlin 23 pp215–288
[7] Rayleigh L 1882 Proc. R. Math. Soc. s1-14 170
[8] Taylor S G 1950 Proc. R Soc. London Ser. A 201 192
Google Scholar
[9] Lindl J D, Mccrory R L, Campbell E M 1992 Phys. Today 45 32
Google Scholar
[10] Balakrishnan K, Menon S 2011 Flow Turbul. Combust. 87 639
Google Scholar
[11] Ji S Q, Peng Oh S, Ruszkowski M, Markevitch M 2016 Mon. Not. R Astron. Soc. 463.4 3989
[12] Rudinger G, Somers L M 1960 J. Fluid Mech. 7 161
Google Scholar
[13] Haas J F, Sturtevant B 1987 J. Fluid Mech. 181 41
Google Scholar
[14] Zhai Z G, Si T, Luo X S, Yang J M 2011 Phys. Fluids. 23 084104
Google Scholar
[15] Zhai Z G, Wang M H, Si T, Luo X S 2014 J. Fluid Mech. 757 800
Google Scholar
[16] Layes G, Jourdan G, Houas L 2003 Phys. Rev. Lett. 91 174502
Google Scholar
[17] Layes G, Jourdan G, Houas L 2005 Phys. Fluids. 17 028103
Google Scholar
[18] Layes G, Métayer O Le 2007 Phys. Fluids. 19 042105
Google Scholar
[19] Layes G, Jourdan G, Houas L 2009 Phys. Fluids. 21 074102
Google Scholar
[20] Wang M H, Si T, Luo X S 2013 Exp Fluids. 54 1427
Google Scholar
[21] Luo X S, Wang M H, Si T, Zhai Z G 2015 J. Fluid Mech. 773 366
Google Scholar
[22] 范美如, 翟志刚, 司廷, 罗喜盛, 杨基名 2011 中国科学: 物理学 力学 天文学 41 7
Google Scholar
Fan M R, Zhai Z G, Si T, Luo X S, Yang J M 2011 Sci. Sin. Phys. Mech Astron. 41 7
Google Scholar
[23] 王显圣, 司廷, 罗喜盛, 杨基明 2012 力学学报 4 664
Google Scholar
Wang X S, Si T, Luo X S, Yang J M 2012 Acta Mech Sin. 4 664
Google Scholar
[24] 沙莎, 陈志华, 薛大文 2013 62 144701
Google Scholar
Sha S, Chen Z H, Xue D W 2013 Acta Phys. Sin. 62 144701
Google Scholar
[25] 沙莎, 陈志华, 张庆兵 2015 64 15201
Google Scholar
Sha S, Chen Z H, Zhang Q B 2015 Acta Phys. Sin. 64 15201
Google Scholar
[26] Ding J C, Si T, Chen M J, Zhai Z G, Lu X Y, Luo X S 2017 J. Fluid Mech. 828 289
Google Scholar
[27] 李冬冬, 王革, 张斌 2018 67 184702
Google Scholar
Li D D, Wang G, Zhang B 2018 Acta Phys. Sin. 67 184702
Google Scholar
[28] Jacobs J W 1993 Phys. Fluids A 5 2239
Google Scholar
[29] Tomkins C, Kumar S, Orlicz G, Prestridge K 2008 J. Fluid Mech. 611 131
Google Scholar
[30] Shankar S K, Kawai S, Lele S K 2011 Phys. Fluids. 23 024102
Google Scholar
[31] Zou L Y, Liu C L, Tan D W, Huang W B, Luo X S 2010 J. Vis. 13 347
Google Scholar
[32] Zhai Z G, Zhang F, Si T, Luo X S 2014 J. Vis. 17 123
Google Scholar
[33] Bai J S, Zou L Y, Wang T, Liu K, Huang W B, Liu J H, Li P, Tan D W, Liu C L 2010 Phys. Rev E. 82 056318
Google Scholar
[34] Li D, Wang G, Guan B 2019 Acta Mech. Sin. 35 750
Google Scholar
[35] Wan W C, Malamud G, Shimony A, Di Stefano C A, Trantham M R, Klein S R, Shvarts D, Kuranz C C, Drake R P 2015 Phys. Rev. Lett. 115 145001
Google Scholar
[36] Giordano J, Burtschell Y 2006 Phys. Fluids. 18 036102
Google Scholar
-
图 1 (a)计算模型; (b)氦气沿轴对称的组分分布
Fig. 1. (a) Schematic of the computational model; (b) the distribution of He mole fraction along the symmetry axis of cylinder.
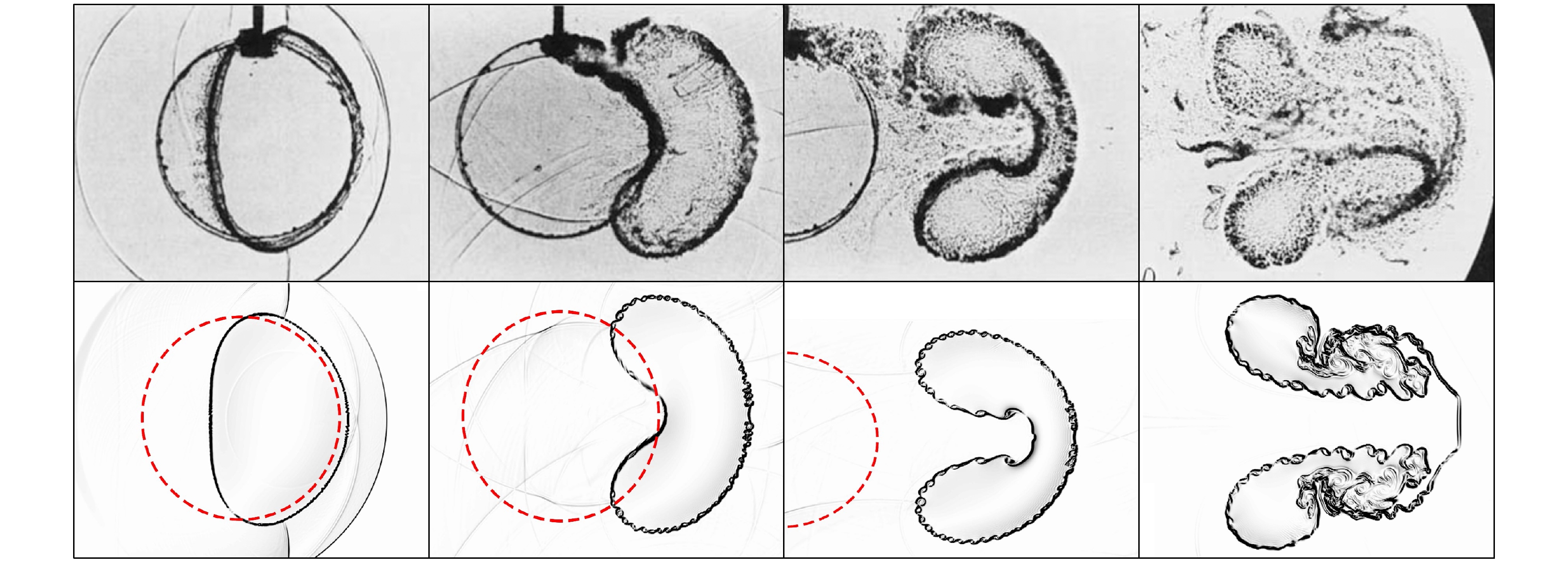
图 2 激波(Ma = 1.22)与有膜He气柱作用过程的流场结果(下)与Haas和Sturtevant[13]的实验结果(上)对比
Fig. 2. Comparison of Haas and Sturtevant[13] related experimental results (up) with our numerical results (down) for the flow field structure during the interaction of the shock wave (Ma = 1.22) with a cylinder of He gas with a film.
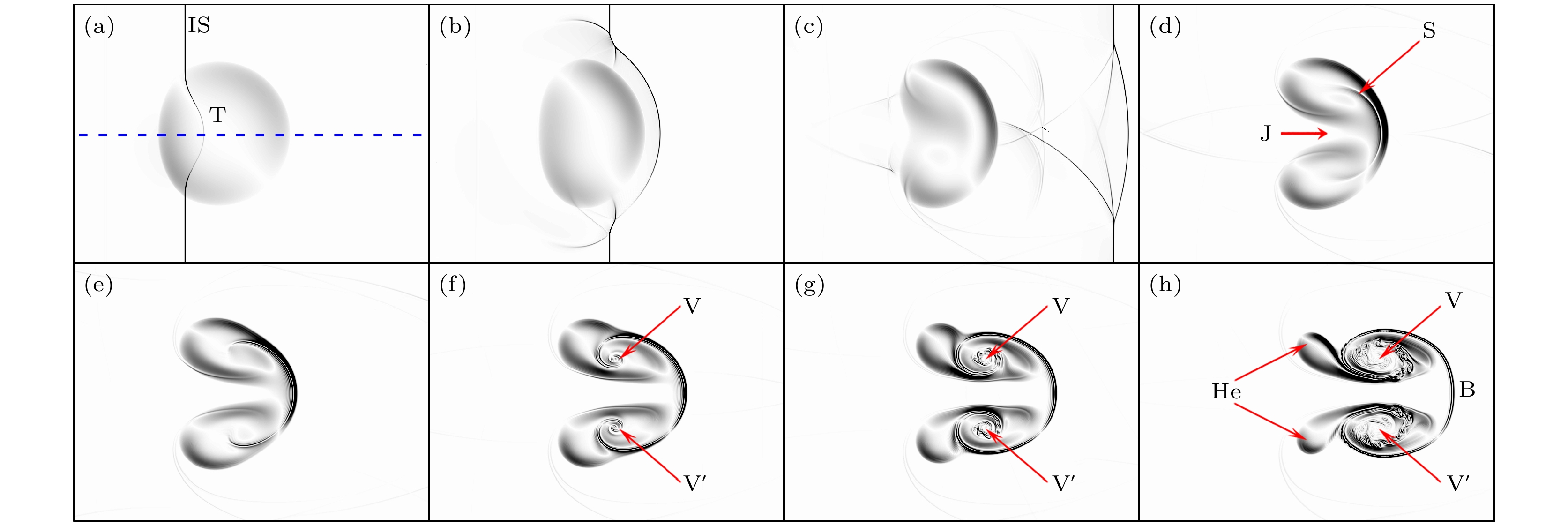
图 4 a = 0.8时, 激波与He气柱作用过程的计算纹影图 (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms
Fig. 4. Numerical schlieren image of the interaction between the shock wave and the He cylinder at a = 0.8: (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms.
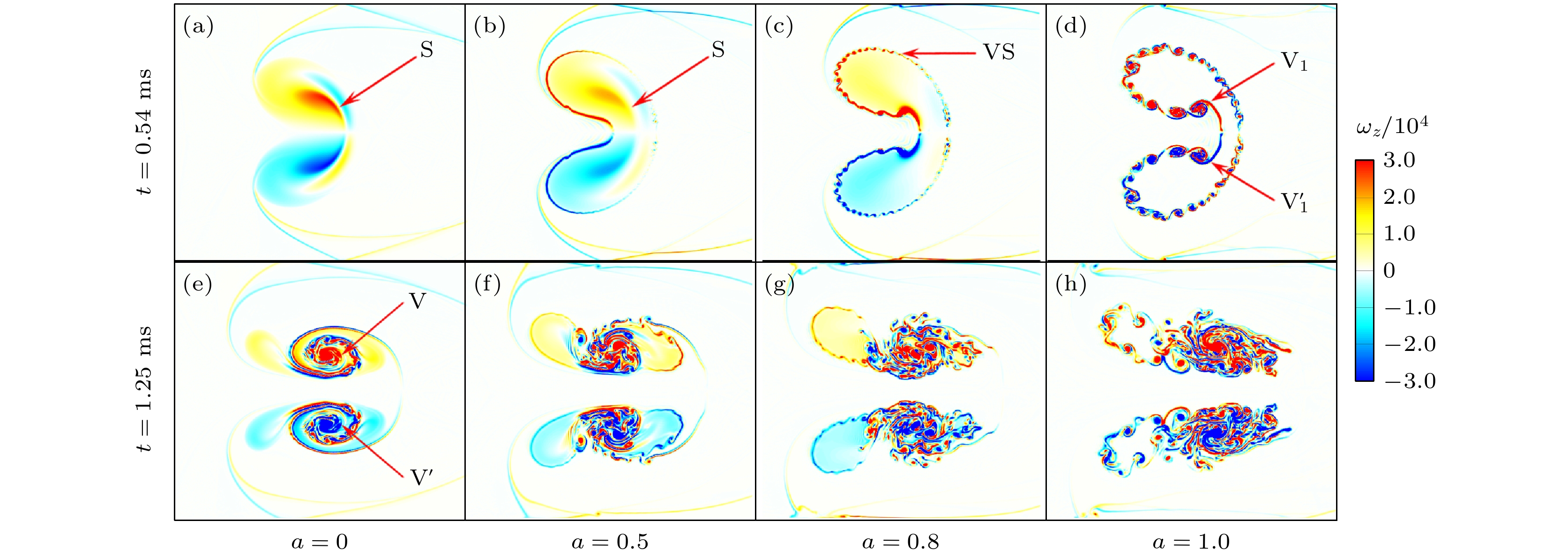
图 8 t = 0.54 ms (上)和1.25 ms (下)时, 流场涡量分布图 (a) a = 0; (b) a = 0.5; (c) a = 0.8; (d) a = 1.0; (e) a = 0, (f) a = 0.5;(g) a = 0.8; (h) a = 1.0
Fig. 8. Vorticity distribution at t = 0.54 ms (up) and 1.25 ms (down): (a) a = 0; (b) a = 0.5; (c) a = 0.8; (d) a = 1.0; (e) a = 0; (f) a = 0.5; (g) a = 0.8; (h) a = 1.0.
图 5 a = 1时, 激波(Ma = 1.22)与He气柱作用过程的计算纹影图 (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms
Fig. 5. Numerical schlieren image of the interaction between the shock wave (Ma = 1.22) and the He cylinder at a = 1: (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms.
图 6 a = 0.5时, 激波与气柱作用过程的计算纹影图 (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms
Fig. 6. Numerical schlieren image of the interaction between the shock wave and the cylinder at a = 0.5: (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms.
图 7 a = 0时, 激波与气柱作用过程的计算数值纹影图 (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms
Fig. 7. Numerical schlieren image of the interaction between the shock wave and the cylinder at a = 0: (a) t = 0.09 ms; (b) t = 0.15 ms; (c) t = 0.31 ms; (d) t = 0.54 ms; (e) t = 0.65 ms; (f) t = 0.80 ms; (g) t = 0.96 ms; (h) t = 1.25 ms.
图 9 t = 0.09 ms时, 气柱中轴线上流向速度u (a)与压强p (b)的分布
Fig. 9. Distribution of streamwise velocity u (a) and pressure p (b) along the axis of the cylinder at t = 0.09 ms.
图 10 不同界面组分下, 密度梯度(上)与压强梯度(下)在不同方向的分量
Fig. 10. Different directional components of the density gradient (up) and pressure gradient (down) for the different component distributions.
图 11 流场能量随时间的变化 (a)总能量E和内能Ep; (b)横向总动能Ekx; (c)纵向总动能Eky
Fig. 11. Change of flow energy with time: (a) Total energy E and internal energy Ep; (b) transverse total kinetic energy Ekx; (c) longitudinal total kinetic energy Eky.
图 12 a = 1(上)和0(下)时, 流场纵向动能Eky分布图 (a) t = 0.14 ms; (b) t = 0.25 ms; (c) t = 0.46 ms; (d) t = 1.25 ms; (e) t = 0.14 ms; (f) t = 0.25 ms; (g) t = 0.46 ms; (h) t = 1.25 ms
Fig. 12. When a = 1 (up) and 0 (down), cloud plot of the longitudinal kinetic energy Eky of the flow field: (a) t = 0.14 ms; (b) t = 0.25 ms; (c) t = 0.46 ms; (d) t = 1.25 ms; (e) t = 0.14 ms; (f) t = 0.25 ms; (g) t = 0.46 ms; (h) t = 1.25 ms.
图 13 同一阶段, 流场密度分布及速度矢量图 (a) a = 0, t = 0.6 ms; (b) a = 0.5, t = 0.59 ms; (c) a = 0.8, t = 0.51 ms; (d) a = 1.0, t = 0.46 ms
Fig. 13. At the same development stage, flow field density distribution and velocity vector diagram: (a) a = 0, t = 0.6 ms; (b) a = 0.5, t = 0.59 ms; (c) a = 0.8, t = 0.51 ms; (d) a = 1.0, t = 0.46 ms.
图 14 上半部分流场环量随时间的变化 (a) 正环量Γ+; (b) 负环量Γ–; (c) 总环量Γ
Fig. 14. Variation of circulation versus time in the upper half of the flow field: (a) Positive circulation Γ+; (b) negative circulation Γ–; (c) total circulation Γ
图 15 不同时刻, 氦气质量分数f_He分布 (a1) a = 0, t = 0.6 ms; (b1) a = 0.5, t = 0.59 ms; (c1) a = 0.8, t = 0.51 ms; (d1) a = 1, t = 0.46 ms; (a2) a = 0, t = 1.25 ms; (b2) a = 0.5, t = 1.25 ms; (c2) a = 0.8, t = 1.25 ms; (d2) a = 1, t = 1.25 ms
Fig. 15. Cloud plot of the distribution of helium mass fraction f_He in the flow field at different moments under different initial conditions: (a1) a = 0, t = 0.6 ms; (b1) a = 0.5, t = 0.59 ms; (c1) a = 0.8, t = 0.51 ms; (d1) a = 1, t = 0.46 ms; (a2) a = 0, t = 1.25 ms; (b2) a = 0.5, t = 1.25 ms; (c2) a = 0.8, t = 1.25 ms; (d2) a = 1, t = 1.25 ms.
图 17 激波与He气柱作用过程中气柱特征尺寸随时间的变化 (a) 气柱长度L; (b) 气柱高度H; (c) 中轴宽度W
Fig. 17. The development of gas cylinder characteristic during the shock wave impacting on the cylinder: (a) Length L; (b) height H; (c) width of the center axis W
图 18 不同组分分布下, 氦气柱体积压缩率变化
Fig. 18. Volume compressibility of He cylinder for different component distributions.
表 1 气体参数
Table 1. Gas parameters.
气体 密度ρ/(kg·m–3) 比热比
$ \gamma $摩尔质量/(g·mol–1) 当地声速${c}_{ {\rm{A} } }/({\rm{m} }{\cdot}{ {\rm{s} } }^{-2})$ Air 1.176 1.40 28.96 347 He 0.162 1.67 4.00 1021 
下载: 导出CSV
-
[1] 林震亚, 张焕好, 陈志华, 刘迎 2017 爆炸与冲击 37 748
Google Scholar
Lin Z Y, Zhang H H, Chen Z H, Liu Y 2017 Explosion and Shock Waves 37 748
Google Scholar
[2] Markstein G H 1957 J Aero Sci. 24 238
[3] Richtmyer R D 1960 Commun. Pure. Appl. Math. 13 297
Google Scholar
[4] Meshkov E E 1969 Fluid Dyn. 4 101
Google Scholar
[5] Kelvin L 1871 Philos Mag. 150 405
[6] Helmholtz H V 1868 Monthly Reports of the Royal Prussian Academy of Philosophy in Berlin 23 pp215–288
[7] Rayleigh L 1882 Proc. R. Math. Soc. s1-14 170
[8] Taylor S G 1950 Proc. R Soc. London Ser. A 201 192
Google Scholar
[9] Lindl J D, Mccrory R L, Campbell E M 1992 Phys. Today 45 32
Google Scholar
[10] Balakrishnan K, Menon S 2011 Flow Turbul. Combust. 87 639
Google Scholar
[11] Ji S Q, Peng Oh S, Ruszkowski M, Markevitch M 2016 Mon. Not. R Astron. Soc. 463.4 3989
[12] Rudinger G, Somers L M 1960 J. Fluid Mech. 7 161
Google Scholar
[13] Haas J F, Sturtevant B 1987 J. Fluid Mech. 181 41
Google Scholar
[14] Zhai Z G, Si T, Luo X S, Yang J M 2011 Phys. Fluids. 23 084104
Google Scholar
[15] Zhai Z G, Wang M H, Si T, Luo X S 2014 J. Fluid Mech. 757 800
Google Scholar
[16] Layes G, Jourdan G, Houas L 2003 Phys. Rev. Lett. 91 174502
Google Scholar
[17] Layes G, Jourdan G, Houas L 2005 Phys. Fluids. 17 028103
Google Scholar
[18] Layes G, Métayer O Le 2007 Phys. Fluids. 19 042105
Google Scholar
[19] Layes G, Jourdan G, Houas L 2009 Phys. Fluids. 21 074102
Google Scholar
[20] Wang M H, Si T, Luo X S 2013 Exp Fluids. 54 1427
Google Scholar
[21] Luo X S, Wang M H, Si T, Zhai Z G 2015 J. Fluid Mech. 773 366
Google Scholar
[22] 范美如, 翟志刚, 司廷, 罗喜盛, 杨基名 2011 中国科学: 物理学 力学 天文学 41 7
Google Scholar
Fan M R, Zhai Z G, Si T, Luo X S, Yang J M 2011 Sci. Sin. Phys. Mech Astron. 41 7
Google Scholar
[23] 王显圣, 司廷, 罗喜盛, 杨基明 2012 力学学报 4 664
Google Scholar
Wang X S, Si T, Luo X S, Yang J M 2012 Acta Mech Sin. 4 664
Google Scholar
[24] 沙莎, 陈志华, 薛大文 2013 62 144701
Google Scholar
Sha S, Chen Z H, Xue D W 2013 Acta Phys. Sin. 62 144701
Google Scholar
[25] 沙莎, 陈志华, 张庆兵 2015 64 15201
Google Scholar
Sha S, Chen Z H, Zhang Q B 2015 Acta Phys. Sin. 64 15201
Google Scholar
[26] Ding J C, Si T, Chen M J, Zhai Z G, Lu X Y, Luo X S 2017 J. Fluid Mech. 828 289
Google Scholar
[27] 李冬冬, 王革, 张斌 2018 67 184702
Google Scholar
Li D D, Wang G, Zhang B 2018 Acta Phys. Sin. 67 184702
Google Scholar
[28] Jacobs J W 1993 Phys. Fluids A 5 2239
Google Scholar
[29] Tomkins C, Kumar S, Orlicz G, Prestridge K 2008 J. Fluid Mech. 611 131
Google Scholar
[30] Shankar S K, Kawai S, Lele S K 2011 Phys. Fluids. 23 024102
Google Scholar
[31] Zou L Y, Liu C L, Tan D W, Huang W B, Luo X S 2010 J. Vis. 13 347
Google Scholar
[32] Zhai Z G, Zhang F, Si T, Luo X S 2014 J. Vis. 17 123
Google Scholar
[33] Bai J S, Zou L Y, Wang T, Liu K, Huang W B, Liu J H, Li P, Tan D W, Liu C L 2010 Phys. Rev E. 82 056318
Google Scholar
[34] Li D, Wang G, Guan B 2019 Acta Mech. Sin. 35 750
Google Scholar
[35] Wan W C, Malamud G, Shimony A, Di Stefano C A, Trantham M R, Klein S R, Shvarts D, Kuranz C C, Drake R P 2015 Phys. Rev. Lett. 115 145001
Google Scholar
[36] Giordano J, Burtschell Y 2006 Phys. Fluids. 18 036102
Google Scholar
下载:
计量
- 文章访问数: 3366
- PDF下载量: 70
- 被引次数: 0
