-
理论上分析了受自旋指标调控并施以增益和损耗复势能的一维非厄米自旋轨道耦合Su-Schrieffer-Heeger (SSH)模型的拓扑性质和能谱特性. 发现虚势能导致体系的拓扑非平庸区出现能谱虚化, 而在拓扑平庸区发生
${\cal {PT}}$ 相变. 此外, 虚势能和自旋轨道耦合共同作用使得拓扑平庸区中发生拓扑相变, 并且拓扑非平庸区变宽. 能谱结果显示, 虚势能和自旋轨道耦合对于体系的零能态有明显的调控作用, 主要在于出现了4种局域性、数目均不同的零能态. 这说明虚势能和自旋轨道耦合对体系的能带结构的特殊调节效果. 本文有助于理解${\cal {PT}}$ 对称非厄米系统的拓扑相变行为.-
关键词:
- ${\cal{PT}}$对称 /
- 拓扑相变 /
- Su-Schrieffer-Heeger晶格 /
- 自旋轨道耦合
The topological property and the energy property of one-dimensional non-Hermitian spin-orbit-coupled Su-Schrieffer-Heeger (SSH) model are investigated theoretically, by introducing spin-dependent imaginary potentials with gain and loss effects. It is found that the imaginary potential leads the imaginary energy spectra to appera in the topologically nontrivial region of this system, and the${\cal {PT}}$ phase transition to happen in the topologically trivial region. In addition, the imaginary potential energy and spin-orbit coupling work together to make the topological phase transition occur in the topologically trivial region, and the topological non-trivial region becomes wider. The energy spectrum results show that the imaginary potential energy and the spin-orbit coupling can obviously control the zero-energy states of the system, which mainly lies in the presence of four zero-energy states with four different localities and numbers. This shows the special adjustment effect of imaginary potential energy and spin-orbit coupling on the energy band structure of the system. It is believed that these results are helpful in understanding the topological phase transition behavior of${\cal {PT}}$ -symmetric non-Hermitian system.-
Keywords:
- $\cal{PT}$ symmetry /
- topological phase transition /
- Su-Schrieffer-Heeger lattice /
- spin-orbit coupling
[1] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[2] Liang G Q, Chong Y D 2013 Phys. Rev. Lett. 110 203904
Google Scholar
[3] Zeuner J M, Rechtsman M C, Plotnik Y, Lumer Y, Nolte S, Rudner M S, Segev M, Szameit A 2015 Phys. Rev. Lett. 115 040402
Google Scholar
[4] Malzard S, Poli C, Schomerus H 2015 Phys. Rev. Lett. 115 200402
Google Scholar
[5] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S, Christodoulides D N 2018 Nat. Phys. 14 11
Google Scholar
[6] Rudner M S, Levitov L S 2009 Phys. Rev. Lett. 102 065703
Google Scholar
[7] Li L H, Xu Z H, Chen S 2014 Phys. Rev. B 89 085111
Google Scholar
[8] Li C, Lin S, Zhang G, Song Z 2017 Phys. Rev. B 96 125418
Google Scholar
[9] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[10] Wang L, Troyer M, Dai X 2013 Phys. Rev. Lett. 111 026802
Google Scholar
[11] Leder M, Grossert C, Sitta L, Genske M, Rosch A, Weitz M 2016 Nat. Comm. 7 13112
Google Scholar
[12] Lohse M, Schweizer C, Zilberberg O, Aidelsburger M, Bloch I 2016 Nat. Phys. 12 350
Google Scholar
[13] Shen S Q 2012 Topological Insulators-Dirac Equation in Condensed Matters (New York: Springer) pp83–84
[14] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[15] Xing Y, Qi L, Cao J, Wang D Y, Bai C H, Wang H F, Zhu A D, Zhang S 2017 Phys. Rev. A 96 043810
Google Scholar
[16] Yuce C 2018 Phys. Rev. A 97 042118
Google Scholar
[17] Dangel F, Wagner M, Cartarius H, Main J, Wunner G 2018 Phys. Rev. A 98 013628
Google Scholar
[18] Zhang K L, Wang P, Zhang G, Song Z 2018 Phys. Rev. A 98 022128
Google Scholar
[19] Lieu S 2018 Phys. Rev. B 97 045106
Google Scholar
[20] Jin J, Wang P, Song Z 2017 Sci. Rep. 7 5903
Google Scholar
[21] Li X S, Li Z Z, Zhang L L, Gong W J 2020 J. Phys.: Condens. Matter 32 165401
Google Scholar
[22] Kawabata K, Ashida Y, Katsura H, Ueda M 2018 Phys. Rev. B 98 085116
Google Scholar
[23] Klett M, Cartarius H, Dast D, Main J, Wunner G 2017 Phys. Rev. A 95 053626
Google Scholar
[24] Jin L 2017 Phys. Rev. A 96 032103
Google Scholar
[25] Zhang L L, Li J R, Zhang D, Xu T T, C ui, W B, Gong W J 2022 Res. Phys. 34 105274
Google Scholar
[26] Guo A, Salamo G J, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, Siviloglou G A, Christodoulides D N 2009 Phys. Rev. Lett. 103 093902
Google Scholar
[27] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[28] Zhen B, Hsu C W, Igarashi Y C, Lu L, Kaminer I, Pick A, Chua S L, Joannopoulos J D, Soljačić M 2015 Nature 525 354
Google Scholar
[29] Fleury R, Sounas D, Alù A 2015 Nat. Commun. 6 5905
Google Scholar
[30] Schindler L, Li A, Zheng C M, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101
[31] Lin Z, Schindler J, Ellis F M, Kottos T 2012 Phys. Rev. A 85 050101
Google Scholar
[32] Liu Y, Han Y Z, Liu C S 2022 Optik 255 168727
Google Scholar
[33] Han Y Z, Jiang H, Chen S, Liu C S 2019 Phys. E: Low -Dimens. Syst. Nanostruct. 110 68
[34] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽 2021 70 087301
Google Scholar
Xue H B, Duan Z L, Chen B, Chen J B, Xing L L 2021 Acta Phys. Sin. 70 087301
Google Scholar
[35] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
Google Scholar
[36] Altland A, Zirnbauer M R 1997 Phys. Rev. B 55 1142
Google Scholar
[37] Wu H C, Jin L, Song Z 2021 Phys. Rev. B 103 235110
Google Scholar
[38] Takata K, Notomi M 2018 Phys. Rev. Lett. 121 213902
Google Scholar
-
图 1 非厄米自旋轨道SSH模型示意图. A和B表示两种晶格, 紫色上箭头和绿色下箭头分别表示具有增益和损耗的虚势能
${\rm{i}}\gamma$ 和$-{\rm{i}}\gamma$ , 浅绿色线和黑色线分别表示胞内跃迁v和胞间跃迁w, 蓝色线和粉色线表示胞内自旋轨道耦合跃迁$\lambda_v$ 和胞间自旋轨道耦合跃迁$\lambda_w$ Fig. 1. Schematic diagram of the non-Hermitian spin-orbit SSH model. A and B represent two kinds of lattices, and purple-up and green-down arrows represent imaginary potentials
${\rm{i}}\gamma$ and$-{\rm{i}}\gamma$ , respectively. Light-green and black lines denote intracell hopping v and intercell hopping w, and the blue and pink lines describe the intracell spin-orbit coupling$\lambda_v$ and the intercell spin-orbit coupling$\lambda_w$ 
图 2 (a), (b) 厄米情况下, 体系的动量空间能谱图,
$\lambda=0.3$ (a)$\delta=0.4$ ; (b)$\delta=2.5$ . (c) 动量空间相图, 其中黄色对应${\cal{Z}}=2\pi$ , 绿色对应${\cal{Z}}=\pi$ 以及紫色对应${\cal{Z}}=0$ . (d) 体系能谱随着二聚化参量$\delta$ 的变化Fig. 2. (a), (b) The energy spectra of system in the momentum space under the Hermitian condition with
$\lambda=0.3$ : (a)$\delta=0.4$ ; (b)$\delta=2.5$ . (c) Phase diagram in the momentum space, where yellow region corresponds to${\cal{Z}}=2\pi$ , green region corresponds to${\cal{Z}}=\pi$ , and purple corresponds to${\cal{Z}}=0$ . (d) Energy spectrum with the change of dimerization parameter$\delta$ 
图 3 随
$\gamma$ 和$\lambda$ 变化的拓扑相图. 蓝色对应$\cal{Z}=\pi$ 的拓扑非平庸相, 绿色区域表示$\cal{Z}=\text{0}$ 的拓扑平庸相. 相关参数为$\delta=0.4$ 以及$t=1.0$ Fig. 3. Topological phase diagram with changes in
$\gamma$ and$\lambda$ . Blue region corresponds to the topologically non-trivial phase of$\cal{Z}=\pi$ , and green region represents the topologically trivial phase of$\cal{Z}=\text{0}$ . Relevant parameters are taken to be$\delta=0.4$ and$t=1.0$ 
图 4 不同虚势能
$\gamma$ 的能带结构 (a)$\gamma=0.3$ ; (b)$\gamma=\sqrt{7}/5$ ; (c)$\gamma=0.8$ ; (d)$\gamma=1.0$ ; (e)$\gamma\approx1.986$ ; (f)$\gamma= $ $ 2.0$ . 对应于图3中标出的各个位置. 蓝线表示能量的实部, 红线对应于虚部. 其他参数为$\lambda=0.3$ 和$\delta=0.4$ Fig. 4. Band structures for different values of imaginary potential
$\gamma$ : (a)$\gamma=0.3$ ; (b)$\gamma=\sqrt{7}/5$ ; (c)$\gamma= $ $ 0.8$ ; (d)$\gamma=1.0$ ; (e)$\gamma\approx1.986$ ; (f)$\gamma=2$ . Correspond to the respective points in Fig. 3. The blue lines indicate the real part of energy, and the red lines correspond to the imaginary part. Other parameters are$\lambda=0.3$ and$\delta=0.4$ 
图 5 开边界情况下, 不同
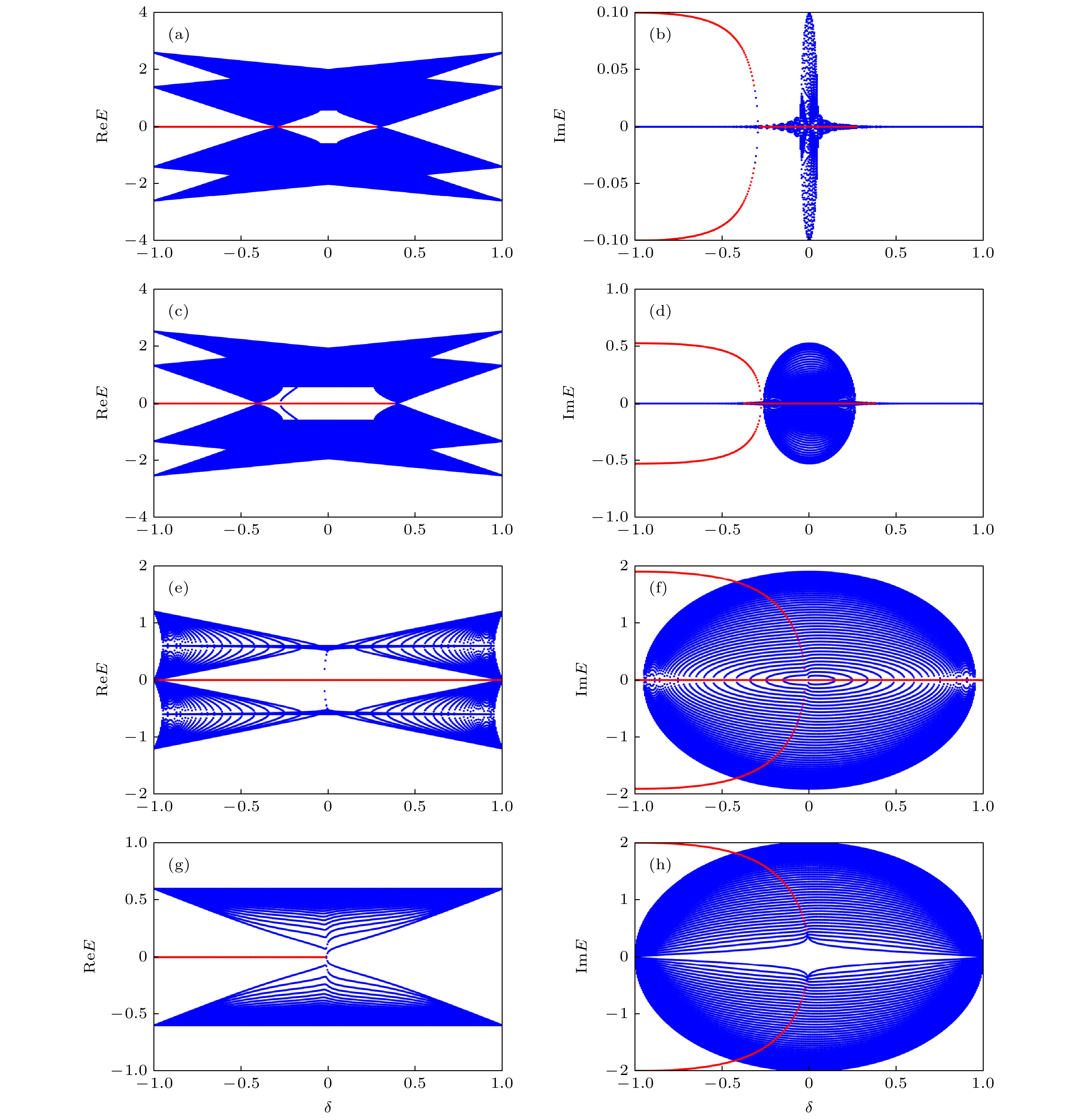
$\delta$ 的能量实部和虚部 (a), (b)$\gamma=0.1$ ; (c), (d)$\gamma=\sqrt{7}/5$ ; (e), (f)$\gamma\approx 1.908$ ; (g), (h)$\gamma=2.0$ . 左侧显示能量的实部, 右侧对应于能量的虚部. 其他参数设为$\lambda=0.3$ . 图中红线代表零能态的实部和虚部Fig. 5. Real and imaginary parts of energy for different
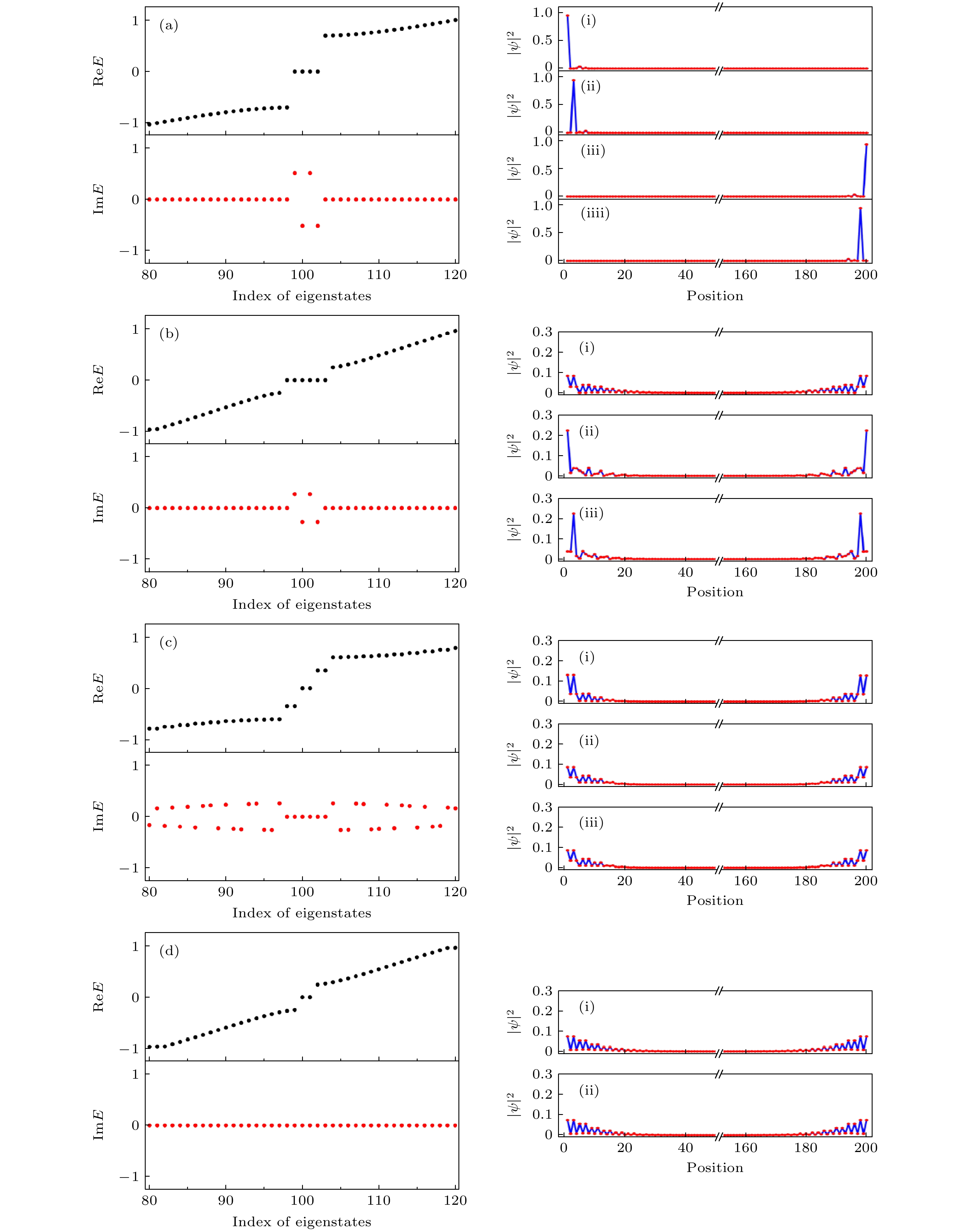
$\delta$ : (a), (b)$\gamma=0.1$ ; (c), (d)$\gamma=\sqrt{7}/5$ ; (e), (f)$\gamma\approx $ $ 1.908$ ; (g), (h)$\gamma= $ $ 2.0$ . Left panel shows the real part of energy, and the right corresponds to the imaginary part of energy. Other parameters are$\lambda=0.3$ . The red lines denote the real and imaginary parts of zero energy states
图 6 开边界条件下的能谱和概率密度谱 (a)
$\delta=-0.7$ ; (b)$\delta=-0.32$ ; (c)$\delta=-0.23$ ; (d)$\delta=0.32$ . 其他参数设为$\lambda=0.3$ 以及$\gamma=\sqrt{7}/5$ Fig. 6. Energy and probability density spectra with open boundary conditions: (a)
$\delta=-0.7$ ; (b)$\delta=-0.32$ ; (c)$\delta=-0.23$ ; (d)$\delta= $ $ 0.32$ . The other parameters are$\lambda=0.3$ and$\gamma=\sqrt{7}/5$ 
图 7
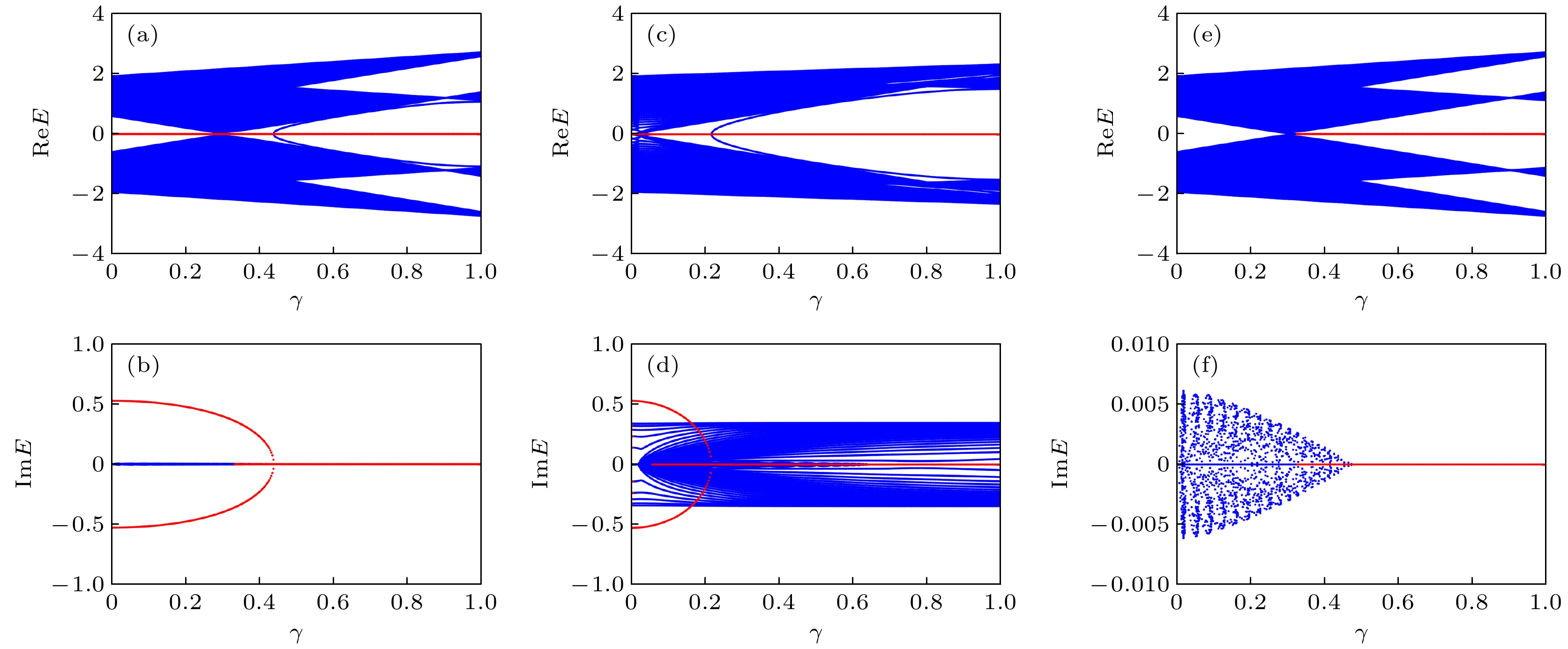
$\gamma$ 变化对能量实部和虚部的影响 (a), (b)$\delta=-0.4$ ; (c), (d)$\delta=-0.2$ ; (e), (f)$\delta=0.4$ . 左侧显示能量的实部, 右侧对应于能量的虚部. 其他参数为$\lambda=0.3$ . 图中红线代表零能态的实部和虚部Fig. 7. Real and imaginary parts of energy for different
$\gamma$ : (a), (b)$\delta=-0.4$ ; (c), (d)$\delta=-0.2$ ; (e), (f)$\delta= $ $ 0.4$ . Left panel shows the real part of energy, and the right corresponds to the imaginary part. Other parameters are$\lambda=0.3$ . The red lines describe the real and imaginary parts of zero energy states, respectively.
图 8 不同
$\lambda$ 导致的能量实部和虚部 (a), (b)$\delta=-0.4$ ; (c), (d)$\delta=-0.2$ ; (e), (f)$\delta=0.4$ . 左侧显示能量的实部, 右侧对应于能量的虚部. 参数设置为$\gamma=\sqrt{7}/5$ . 图中红线代表零能态的实部和虚部Fig. 8. Real and imaginary parts of energy for different
$\lambda$ : (a), (b)$\delta=-0.4$ ; (c), (d)$\delta=-0.2$ ; (e), (f)$\delta= $ $ 0.4$ . Left panel shows the real part of energy, and the right corresponds to the imaginary part. Other parameters are$\gamma=\sqrt{7}/5$ . The red lines describe the real and imaginary parts of zero energy states, respectively表 1 厄米和非厄米情况的
$\mathrm{BDI}$ 和$\mathrm{BDI}^{\dagger}$ 类Table 1. The
$\mathrm{BDI}$ and$\mathrm{BDI}^{\dagger}$ classes for Hermitian and non-Hermitian HamiltoniansSymmetry TRS PHS $\mathrm{TRS}^\dagger$ $\mathrm{PHS}^\dagger$ CS Class ${\boldsymbol{{\cal{T} }}}({\boldsymbol{{\cal{T} }}}_{+})$ ${\boldsymbol{{\varGamma}}}({\boldsymbol{{\cal{C} }}}_{-})$ $~{\boldsymbol{{\cal{C}}}}_{+}$ ${\boldsymbol{{\cal{T}}}}_{-}$ ${\boldsymbol{{\cal {C} }}}$ ${\mathrm{BDI}}$ +1 +1 0 0 1 ${\mathrm{BDI}}^{\dagger}$ 0 0 +1 +1 1 
下载: 导出CSV
-
[1] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[2] Liang G Q, Chong Y D 2013 Phys. Rev. Lett. 110 203904
Google Scholar
[3] Zeuner J M, Rechtsman M C, Plotnik Y, Lumer Y, Nolte S, Rudner M S, Segev M, Szameit A 2015 Phys. Rev. Lett. 115 040402
Google Scholar
[4] Malzard S, Poli C, Schomerus H 2015 Phys. Rev. Lett. 115 200402
Google Scholar
[5] El-Ganainy R, Makris K G, Khajavikhan M, Musslimani Z H, Rotter S, Christodoulides D N 2018 Nat. Phys. 14 11
Google Scholar
[6] Rudner M S, Levitov L S 2009 Phys. Rev. Lett. 102 065703
Google Scholar
[7] Li L H, Xu Z H, Chen S 2014 Phys. Rev. B 89 085111
Google Scholar
[8] Li C, Lin S, Zhang G, Song Z 2017 Phys. Rev. B 96 125418
Google Scholar
[9] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698
Google Scholar
[10] Wang L, Troyer M, Dai X 2013 Phys. Rev. Lett. 111 026802
Google Scholar
[11] Leder M, Grossert C, Sitta L, Genske M, Rosch A, Weitz M 2016 Nat. Comm. 7 13112
Google Scholar
[12] Lohse M, Schweizer C, Zilberberg O, Aidelsburger M, Bloch I 2016 Nat. Phys. 12 350
Google Scholar
[13] Shen S Q 2012 Topological Insulators-Dirac Equation in Condensed Matters (New York: Springer) pp83–84
[14] Zhu B G, Lü R, Chen S 2014 Phys. Rev. A 89 062102
Google Scholar
[15] Xing Y, Qi L, Cao J, Wang D Y, Bai C H, Wang H F, Zhu A D, Zhang S 2017 Phys. Rev. A 96 043810
Google Scholar
[16] Yuce C 2018 Phys. Rev. A 97 042118
Google Scholar
[17] Dangel F, Wagner M, Cartarius H, Main J, Wunner G 2018 Phys. Rev. A 98 013628
Google Scholar
[18] Zhang K L, Wang P, Zhang G, Song Z 2018 Phys. Rev. A 98 022128
Google Scholar
[19] Lieu S 2018 Phys. Rev. B 97 045106
Google Scholar
[20] Jin J, Wang P, Song Z 2017 Sci. Rep. 7 5903
Google Scholar
[21] Li X S, Li Z Z, Zhang L L, Gong W J 2020 J. Phys.: Condens. Matter 32 165401
Google Scholar
[22] Kawabata K, Ashida Y, Katsura H, Ueda M 2018 Phys. Rev. B 98 085116
Google Scholar
[23] Klett M, Cartarius H, Dast D, Main J, Wunner G 2017 Phys. Rev. A 95 053626
Google Scholar
[24] Jin L 2017 Phys. Rev. A 96 032103
Google Scholar
[25] Zhang L L, Li J R, Zhang D, Xu T T, C ui, W B, Gong W J 2022 Res. Phys. 34 105274
Google Scholar
[26] Guo A, Salamo G J, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, Siviloglou G A, Christodoulides D N 2009 Phys. Rev. Lett. 103 093902
Google Scholar
[27] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[28] Zhen B, Hsu C W, Igarashi Y C, Lu L, Kaminer I, Pick A, Chua S L, Joannopoulos J D, Soljačić M 2015 Nature 525 354
Google Scholar
[29] Fleury R, Sounas D, Alù A 2015 Nat. Commun. 6 5905
Google Scholar
[30] Schindler L, Li A, Zheng C M, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101
[31] Lin Z, Schindler J, Ellis F M, Kottos T 2012 Phys. Rev. A 85 050101
Google Scholar
[32] Liu Y, Han Y Z, Liu C S 2022 Optik 255 168727
Google Scholar
[33] Han Y Z, Jiang H, Chen S, Liu C S 2019 Phys. E: Low -Dimens. Syst. Nanostruct. 110 68
[34] 薛海斌, 段志磊, 陈彬, 陈建宾, 邢丽丽 2021 70 087301
Google Scholar
Xue H B, Duan Z L, Chen B, Chen J B, Xing L L 2021 Acta Phys. Sin. 70 087301
Google Scholar
[35] Kawabata K, Shiozaki K, Ueda M, Sato M 2019 Phys. Rev. X 9 041015
Google Scholar
[36] Altland A, Zirnbauer M R 1997 Phys. Rev. B 55 1142
Google Scholar
[37] Wu H C, Jin L, Song Z 2021 Phys. Rev. B 103 235110
Google Scholar
[38] Takata K, Notomi M 2018 Phys. Rev. Lett. 121 213902
Google Scholar
下载:
计量
- 文章访问数: 4774
- PDF下载量: 403
- 被引次数: 0
