-
随着高功率激光技术的进步, 激光等离子体加速因其优异的加速结构获得迅速发展, 现已获得近百MeV质子以及数GeV电子输出. 激光驱动质子束具有μm量级尺寸、ps量级脉冲长度的优异品质. 由于强激光场的存在, 原位直接应用存在一定困难, 因而更多应用场景需要通过束线把质子束传输到应用端. 激光加速离子束由于具有宽能谱和大散角的特点, 通过束线传输具有一定困难. 常梯度磁场中的弱聚焦作用具有特别的优势: 在水平和竖直方向可同时聚焦, 在水平方向可进行能量分析, 在水平和竖直方向的聚焦力可以通过磁场降落指数n进行分配, 色差效应影响较小. 通过对质子束在弱聚焦磁场中运动的束流动力学的研究, 探索了弱聚焦作用在大能散、大散角质子束聚焦和能量分析中的要求、特点和优势. 在合适的束流光学设计中, 可以实现聚焦、选能的同时, 压缩脉冲长度, 有效缩减束线尺寸, 优势显著.
With the development of high-power laser technology, laser plasma acceleration has developed rapidly due to its excellent acceleration structure. Nearly one-hundred-MeV proton beams and several GeV electron outputs are obtained. The laser-driven proton beams have excellent quality of μm-scale sizes and ps-scale pulse lengths. Owing to the existence of the accelerating laser field, direct application is difficult, so the proton beams need to be transmitted to the application terminal through the beamline. However, the wide energy spectrum and large divergence angle bring difficulties in transmitting the beam. The weak focusing in the constant gradient magnetic field is neglected in the transmission of laser-driven particle beams because of the relatively weak focusing force. But weak focusing has special advantages: simultaneous focusing in the horizontal direction and the vertical direction, energy analysis in the horizontal direction, focusing force in the horizontal and vertical direction distributed by the field index n, and smaller influence of chromatic aberration effect. In this paper, we propose the beam transmission with weak-focusing magnet. The requirements for the focusing of proton beams with the same energy and different divergence angles in the X direction and Y direction in the weak-focusing magnetic field are explored by studying the linear beam dynamics of the beams. Then the conditions of precise energy analysis for particle beams with large divergence angle can be determined. For beams with 2% energy spread, the lengths of the drift space before and after the weak-focusing magnet and deflection radius are scanned to find out the minimum beam size and the shortest pulse length after transmission. It is found that a certain combination of drift space and deflection radius can minimize the beam size or the pulse length. Focusing and energy selection can be achieved while compressing the pulse length and effectively reducing the size of the beamline, which has significant advantages. When the deflection radius is 0.65 m, the proton beam with 20 MeV energy, 2% energy spread, and an initial divergence angle of ±50 mrad has the root-mean-square size of 108 μm in both the X direction and the Y direction, and a pulse length of 154 ps at the application terminal. Comparing with common beam transmission elements such as quadrupole lenses and deflection magnets, the laser-accelerated ion beam benefits from the integration of focusing and energy analysis of weak-focusing magnetic fields (focusing and energy analysis exist at the same time and continuously change with deflection angle), as well as the horizontal and vertical focusing forces can be distributed by the magnetic field index n (the larger the n, the stronger the focusing force in the vertical direction is and the weaker the focusing force in the horizontal direction). When the proton beam is transmitted in a weak-focusing magnetic field, the advantages of the focusing element and the energy selection element are combined, so the influence of the chromatic aberration effect can be reduced, the pulse length can be compressed, and the beamline size can be effectively reduced. -
Keywords:
- laser acceleration /
- particle beam delivery /
- particle beam applications /
- ultrafast
[1] Tajima T, Dawson J M 1979 Phys. Rev. Lett. 43 267
[2] Kim I J, Pae K H, Choi I W, Lee C L, Kim H T, Singhal H, Sung J H, Lee S K, Lee H W, Nickles P V, Jeong T M, Kim C M, Nam C H 2016 Phys. Plasmas 23 070701
Google Scholar
[3] Higginson A, Gray R J, King M, Dance R J, Williamson S D R, Butler N M H, Wilson R, Capdessus R, Armstrong C, Green J S, Hawkes S J, Martin P, Wei W Q, Mirfayzi S R, Yuan X H, Kar S, Borghesi M, Clarke R J, Neely D, McKenna P 2018 Nat. Commun. 9 724
Google Scholar
[4] Wilks S C, Langdon A B, Cowan T E, Roth M, Singh M, Hatchett S, Key M H, Pennington D, MacKinnon A, Snavely RA 2001 Phys. Plasmas 8 542
Google Scholar
[5] Esirkepov T, Borghesi M, Bulanov S V, Mourou G, Tajima T 2004 Phys. Rev. Lett. 92 175003
Google Scholar
[6] Yin L, Albright B J, Hegelich B M, Bowers K J, Flippo K A, Kwan T J, Fernández J C 2007 Phys. Plasmas 14 056706
Google Scholar
[7] Dromey B, Coughlan M, Senje L, Taylor M, Kuschel S, Villagomez-Bernabe B, Stefanuik R, Nersisyan G, Stella L, Kohanoff J, Borghesi M, Currell F, Riley D, Jung D, Wahlström C G, Lewis C L S, Zepf M 2016 Nat. Commun. 7 10642
Google Scholar
[8] Romagnani L, Fuchs J, Borghesi M, Antici P, Audebert P, Ceccherini F, Cowan T, Grismayer T, Kar S, MacChi A, Mora P, Pretzler G, Schiavi A, Toncian T, Willi O 2005 Phys. Rev. Lett. 95 195001
Google Scholar
[9] Nakamura T, Sakagami H, Johzaki T, Nagatomo H, Mima K, Koga J 2007 Phys. Plasmas 14 103105
Google Scholar
[10] Faure J, Rechatin C, Norlin A, Lifschitz A, Glinec Y, Malka V 2006 Nature 444 737
Google Scholar
[11] Morrison J T, Feister S, Frische K D, Austin D R, Ngirmang G K, Murphy N R, Orban C, Chowdhury E A, Roquemore W M 2018 New J. Phys. 20 022001
Google Scholar
[12] Nishiuchi M, Daito I, Ikegami M, Daido H, Mori M, Orimo S, Ogura K, Sagisaka A, Yogo A, Pirozhkov A S, Sugiyama H, Kiriyama H, Okada H, Kanazawa S, Kondo S, Shimomura T, Tanoue M, Nakai Y, Sasao H, Wakai D, Sakaki H, Bolton P, Choi I W, Sung J H, Lee J, Oishi Y, Fujii T, Nemoto K, Souda H, Noda A, Iseki Y, Yoshiyuki T 2009 Appl. Phys. Lett. 94 61107
Google Scholar
[13] Schollmeier M, Becker S, Geißel M, Flippo K A, Blažević A, Gaillard S A, Gautier D C, Grüner F, Harres K, Kimmel M, others 2008 Phys. Rev. Lett. 101 55004
Google Scholar
[14] Pommarel L, Vauzour B, Mégnin-Chanet F, Bayart E, Delmas O, Goudjil F, Nauraye C, Letellier V, Pouzoulet F, Schillaci F, Romano F, Scuderi V, Cirrone G A P, Deutsch E, Flacco A, Malka V 2017 Phys. Rev. Accel. Beams 20 032801
Google Scholar
[15] Zhu J G, Wu M J, Zhu K, Geng Y X, Liao Q, Li D Y, Yang T, Easton M J, Li C C, Xu X H, Shou Y R, Yu J Q, Gong Z, Zhao Y Y, Wang P J, Wang D H, Tao L, Chen C E, Ma W J, Lu H Y, Tajima T, Mourou G, Lin C, Yan X Q 2020 Phys. Rev. Accel. Beams 23 121304
Google Scholar
[16] Zhu J G, Wu M J, Liao Q, Geng Y X, Zhu K, Li C C, Xu X H, Li D Y, Shou Y R, Yang T, Wang P J, Wang D H, Wang J J, Chen C E, He X T, Zhao Y Y, Ma W J, Lu H Y, Tajima T, Lin C, Yan X Q 2019 Phys. Rev. Accel. Beams 22 061302
Google Scholar
[17] Hofmann I, Meyer-ter-Vehn J, Yan X, Orzhekhovskaya A, Yaramyshev S 2011 Phys. Rev. Spec. Top. Accel. Beams 14 31304
Google Scholar
[18] Harres K, Alber I, Tauschwitz A, Bagnoud V, Daido H, Günther M, Nürnberg F, Otten A, Schollmeier M, Schütrumpf J, Tampo M, Roth M 2010 Phys. Plasmas 17 23107
Google Scholar
[19] Agosteo S, Anania M P, Caresana M, Cirrone G A P, Martinis C De, Side D D, Fazzi A, Gatti G, Giove D, Giulietti D, Gizzi L A, Labate L, Londrillo P, Maggiore M, Nassisi V, Sinigardi S, Tramontana A, Schillaci F, Scuderi V, Turchetti G, Varoli V, Velardi L 2014 Nucl. Inst. Methods Phys. Res. B 331 15
Google Scholar
[20] Burris-Mog T, Harres K, Nürnberg F, Busold S, Bussmann M, Deppert O, Hoffmeister G, Joost M, Sobiella M, Tauschwitz A, Zielbauer B, Bagnoud V, Herrmannsdoerfer T, Roth M, Cowan T E 2011 Phys. Rev. Spec. Top. Accel. Beams 14 121301
Google Scholar
[21] Roth M, Alber I, Bagnoud V, Brown C R D, Clarke R, Daido H, Fernandez J, Flippo K, Gaillard S, Gauthier C, et al. 2009 Plasma Phys. Controlled Fusion 51 124039
Google Scholar
[22] Hofmann I, Meyer-Ter-Vehn J, Yan X, Al-Omari H 2012 Nucl. Instrum. Methods Phys. Res. , Sect. A 681 44
Google Scholar
[23] Milluzzo G, Pipek J, Amico A G, Cirrone G A P, Cuttone G, Korn G, Larosa G, Leanza R, Margarone D, Petringa G, Russo A, Schillaci F, Scuderi V, Romano F 2018 Nucl. Instrum. Methods Phys. Res. , Sect. A 909 298
Google Scholar
[24] Qi F F, Ma Z R, Zhao L R, Cheng Y, Jiang W X, Lu C, Jiang T, Qian D, Wang Z, Zhang W T, Zhu P F, Zou X, Wan W S, Xiang D, Zhang J 2020 Phys. Rev. Lett. 124 134803
Google Scholar
[25] Scisciò M, Lancia L, Migliorati M, Mostacci A, Palumbo L, Papaphilippou Y, Antici P 2016 J. Appl. Phys. 119 535
[26] 陈佳洱 2012 加速器物理基础 (北京: 北京大学出版社) 第136页
Chen J E 2012 Fundamentals of Accelerator Physics (Beijing: Peking University Press) p136 (in Chinese)
-
图 1 质子束满足水平或竖直方向成像传输条件时
$\theta $ 随$n$ 的变化曲线Fig. 1. Variation curves of θ with n when the proton beams satisfies the imaging transmission conditions in the horizontal or vertical direction.
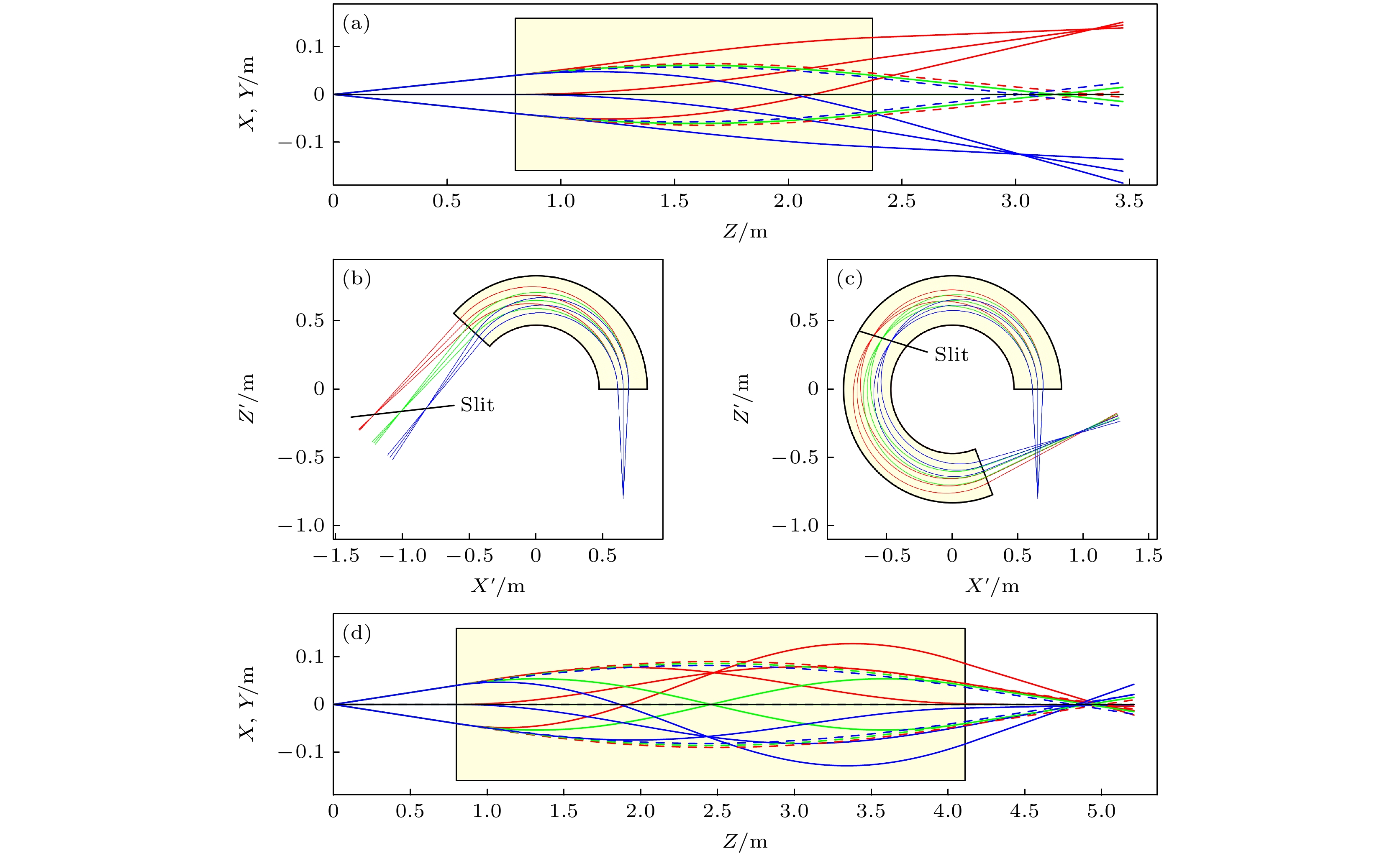
图 2 质子束水平和竖直方向的像点位置相同时的传输. 浅黄色背景区域代表弱聚焦磁铁 (a) 交点1对应的质子束的传输包络; (b) 交点1对应的质子束在
$X'Z'$ 平面的传输包络; (c) 交点2对应的质子束在$X'Z'$ 平面的传输包络; (d) 交点2对应的质子束的传输包络Fig. 2. Transmission of the proton beams when the positions of the image points in the horizontal and vertical directions are the same. The light yellow background area represents the weak-focusing magnet: (a) The transmission envelope of the proton beam corresponding to crossing point 1; (b) the transmission envelope of the proton beam corresponding to crossing point 1 in the
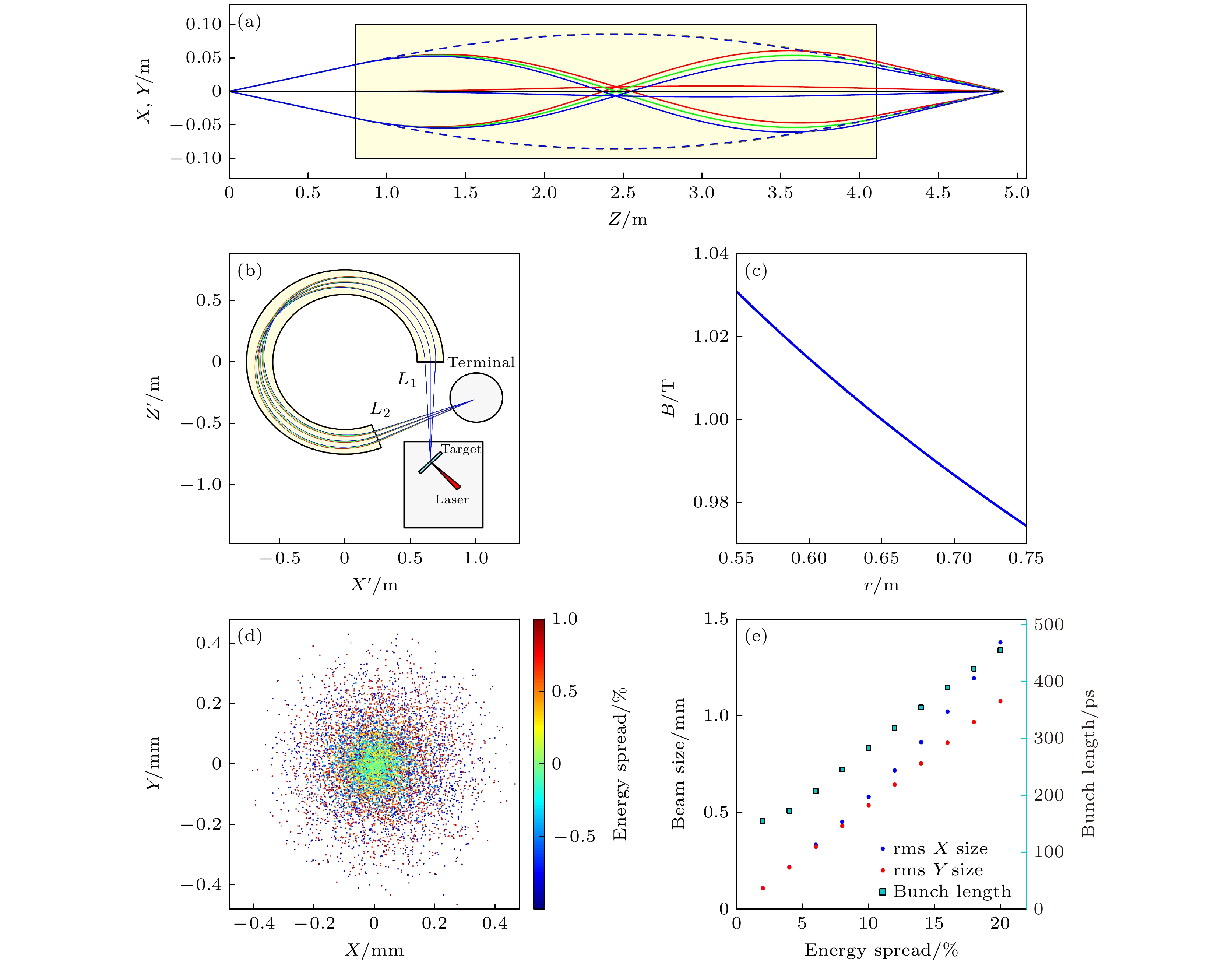
$X'Z'$ plane; (c) the transmission envelope of the proton beam corresponding to crossing point 2 in the$X'Z'$ plane; (d) the transmission envelope of the proton beam corresponding to crossing point 2.
图 3 L1分别等于0.3 m(上)、0.7 m(中)和 L2(下)时, X方向质子束rms尺寸(左)、脉冲长度(中)和偏转角度(右)随L2和rc的变化
Fig. 3. Variations of proton beam size (left), pulse length (middle) and deflection angle (right) with L2 and rc when L1 equals to 0.3 m (upper), 0.7 m (middle) and L2 (lower) respectively.
图 4 质子束的传输束线设计 (a) 2%能散质子束的传输包络; (b) 2%能散质子束在
$X'Z'$ 平面的传输包络与束线布局示意图; (c) Y方向磁场强度随半径的变化; (d) 2%能散质子束在束线出口的分布; (e) 不同能散质子束在束线出口的尺寸和脉冲长度Fig. 4. Transmission beamline design for proton beams: (a) The transmission envelope of the proton beam with 2% energy spread; (b) the transmission envelope of the proton beam with 2% energy spread in the
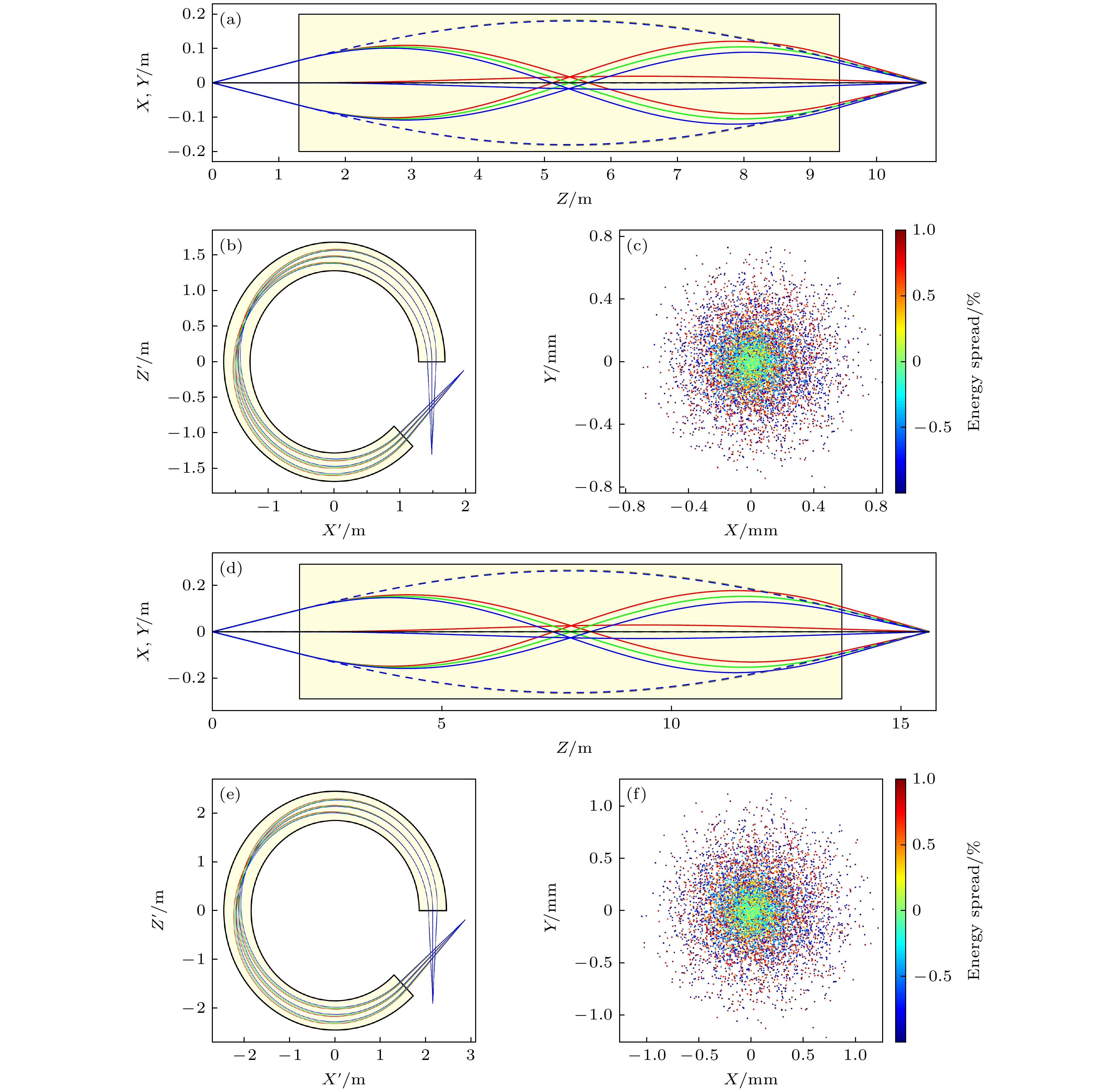
$X'Z'$ plane and the schematic diagram of beamline layout; (c) Y-direction magnetic field strength as a function of radius; (d) distribution of proton beam with 2% energy spread at the beamline exit; (e) the sizes and pulse lengths of proton beams with different energy spread at the beamline exit.
图 5 100和200 MeV质子束的传输束线设计 (a) 100 MeV质子束的传输包络; (b) 100 MeV质子束在
$X'Z'$ 平面的传输包络; (c) 100 MeV质子束在束线出口的分布; (d) 200 MeV质子束的传输包络; (e) 200 MeV质子束在$X'Z'$ 平面的传输包络; (f) 200 MeV质子束在束线出口的分布Fig. 5. Transmission beamline design for 100 and 200 MeV proton beams: (a) Transmission envelope of 100 MeV proton beams; (b) the transmission envelope of 100 MeV proton beams in the
$X'Z'$ plane; (c) distribution of 100 MeV proton beams at the beamline exit; (d) transmission envelope of 200 MeV proton beams; (e) the transmission envelope of 200 MeV proton beams in the$X'Z'$ plane; (f) distribution of 200 MeV proton beams at the beamline exit. -
[1] Tajima T, Dawson J M 1979 Phys. Rev. Lett. 43 267
[2] Kim I J, Pae K H, Choi I W, Lee C L, Kim H T, Singhal H, Sung J H, Lee S K, Lee H W, Nickles P V, Jeong T M, Kim C M, Nam C H 2016 Phys. Plasmas 23 070701
Google Scholar
[3] Higginson A, Gray R J, King M, Dance R J, Williamson S D R, Butler N M H, Wilson R, Capdessus R, Armstrong C, Green J S, Hawkes S J, Martin P, Wei W Q, Mirfayzi S R, Yuan X H, Kar S, Borghesi M, Clarke R J, Neely D, McKenna P 2018 Nat. Commun. 9 724
Google Scholar
[4] Wilks S C, Langdon A B, Cowan T E, Roth M, Singh M, Hatchett S, Key M H, Pennington D, MacKinnon A, Snavely RA 2001 Phys. Plasmas 8 542
Google Scholar
[5] Esirkepov T, Borghesi M, Bulanov S V, Mourou G, Tajima T 2004 Phys. Rev. Lett. 92 175003
Google Scholar
[6] Yin L, Albright B J, Hegelich B M, Bowers K J, Flippo K A, Kwan T J, Fernández J C 2007 Phys. Plasmas 14 056706
Google Scholar
[7] Dromey B, Coughlan M, Senje L, Taylor M, Kuschel S, Villagomez-Bernabe B, Stefanuik R, Nersisyan G, Stella L, Kohanoff J, Borghesi M, Currell F, Riley D, Jung D, Wahlström C G, Lewis C L S, Zepf M 2016 Nat. Commun. 7 10642
Google Scholar
[8] Romagnani L, Fuchs J, Borghesi M, Antici P, Audebert P, Ceccherini F, Cowan T, Grismayer T, Kar S, MacChi A, Mora P, Pretzler G, Schiavi A, Toncian T, Willi O 2005 Phys. Rev. Lett. 95 195001
Google Scholar
[9] Nakamura T, Sakagami H, Johzaki T, Nagatomo H, Mima K, Koga J 2007 Phys. Plasmas 14 103105
Google Scholar
[10] Faure J, Rechatin C, Norlin A, Lifschitz A, Glinec Y, Malka V 2006 Nature 444 737
Google Scholar
[11] Morrison J T, Feister S, Frische K D, Austin D R, Ngirmang G K, Murphy N R, Orban C, Chowdhury E A, Roquemore W M 2018 New J. Phys. 20 022001
Google Scholar
[12] Nishiuchi M, Daito I, Ikegami M, Daido H, Mori M, Orimo S, Ogura K, Sagisaka A, Yogo A, Pirozhkov A S, Sugiyama H, Kiriyama H, Okada H, Kanazawa S, Kondo S, Shimomura T, Tanoue M, Nakai Y, Sasao H, Wakai D, Sakaki H, Bolton P, Choi I W, Sung J H, Lee J, Oishi Y, Fujii T, Nemoto K, Souda H, Noda A, Iseki Y, Yoshiyuki T 2009 Appl. Phys. Lett. 94 61107
Google Scholar
[13] Schollmeier M, Becker S, Geißel M, Flippo K A, Blažević A, Gaillard S A, Gautier D C, Grüner F, Harres K, Kimmel M, others 2008 Phys. Rev. Lett. 101 55004
Google Scholar
[14] Pommarel L, Vauzour B, Mégnin-Chanet F, Bayart E, Delmas O, Goudjil F, Nauraye C, Letellier V, Pouzoulet F, Schillaci F, Romano F, Scuderi V, Cirrone G A P, Deutsch E, Flacco A, Malka V 2017 Phys. Rev. Accel. Beams 20 032801
Google Scholar
[15] Zhu J G, Wu M J, Zhu K, Geng Y X, Liao Q, Li D Y, Yang T, Easton M J, Li C C, Xu X H, Shou Y R, Yu J Q, Gong Z, Zhao Y Y, Wang P J, Wang D H, Tao L, Chen C E, Ma W J, Lu H Y, Tajima T, Mourou G, Lin C, Yan X Q 2020 Phys. Rev. Accel. Beams 23 121304
Google Scholar
[16] Zhu J G, Wu M J, Liao Q, Geng Y X, Zhu K, Li C C, Xu X H, Li D Y, Shou Y R, Yang T, Wang P J, Wang D H, Wang J J, Chen C E, He X T, Zhao Y Y, Ma W J, Lu H Y, Tajima T, Lin C, Yan X Q 2019 Phys. Rev. Accel. Beams 22 061302
Google Scholar
[17] Hofmann I, Meyer-ter-Vehn J, Yan X, Orzhekhovskaya A, Yaramyshev S 2011 Phys. Rev. Spec. Top. Accel. Beams 14 31304
Google Scholar
[18] Harres K, Alber I, Tauschwitz A, Bagnoud V, Daido H, Günther M, Nürnberg F, Otten A, Schollmeier M, Schütrumpf J, Tampo M, Roth M 2010 Phys. Plasmas 17 23107
Google Scholar
[19] Agosteo S, Anania M P, Caresana M, Cirrone G A P, Martinis C De, Side D D, Fazzi A, Gatti G, Giove D, Giulietti D, Gizzi L A, Labate L, Londrillo P, Maggiore M, Nassisi V, Sinigardi S, Tramontana A, Schillaci F, Scuderi V, Turchetti G, Varoli V, Velardi L 2014 Nucl. Inst. Methods Phys. Res. B 331 15
Google Scholar
[20] Burris-Mog T, Harres K, Nürnberg F, Busold S, Bussmann M, Deppert O, Hoffmeister G, Joost M, Sobiella M, Tauschwitz A, Zielbauer B, Bagnoud V, Herrmannsdoerfer T, Roth M, Cowan T E 2011 Phys. Rev. Spec. Top. Accel. Beams 14 121301
Google Scholar
[21] Roth M, Alber I, Bagnoud V, Brown C R D, Clarke R, Daido H, Fernandez J, Flippo K, Gaillard S, Gauthier C, et al. 2009 Plasma Phys. Controlled Fusion 51 124039
Google Scholar
[22] Hofmann I, Meyer-Ter-Vehn J, Yan X, Al-Omari H 2012 Nucl. Instrum. Methods Phys. Res. , Sect. A 681 44
Google Scholar
[23] Milluzzo G, Pipek J, Amico A G, Cirrone G A P, Cuttone G, Korn G, Larosa G, Leanza R, Margarone D, Petringa G, Russo A, Schillaci F, Scuderi V, Romano F 2018 Nucl. Instrum. Methods Phys. Res. , Sect. A 909 298
Google Scholar
[24] Qi F F, Ma Z R, Zhao L R, Cheng Y, Jiang W X, Lu C, Jiang T, Qian D, Wang Z, Zhang W T, Zhu P F, Zou X, Wan W S, Xiang D, Zhang J 2020 Phys. Rev. Lett. 124 134803
Google Scholar
[25] Scisciò M, Lancia L, Migliorati M, Mostacci A, Palumbo L, Papaphilippou Y, Antici P 2016 J. Appl. Phys. 119 535
[26] 陈佳洱 2012 加速器物理基础 (北京: 北京大学出版社) 第136页
Chen J E 2012 Fundamentals of Accelerator Physics (Beijing: Peking University Press) p136 (in Chinese)
下载:
计量
- 文章访问数: 3828
- PDF下载量: 63
- 被引次数: 0
