剪切光束成像技术稀疏重构算法

陈明徕; 刘辉; 张羽; 罗秀娟; 马彩文; 岳泽霖; 赵晶

doi:10.7498/aps.71.20220494

摘要

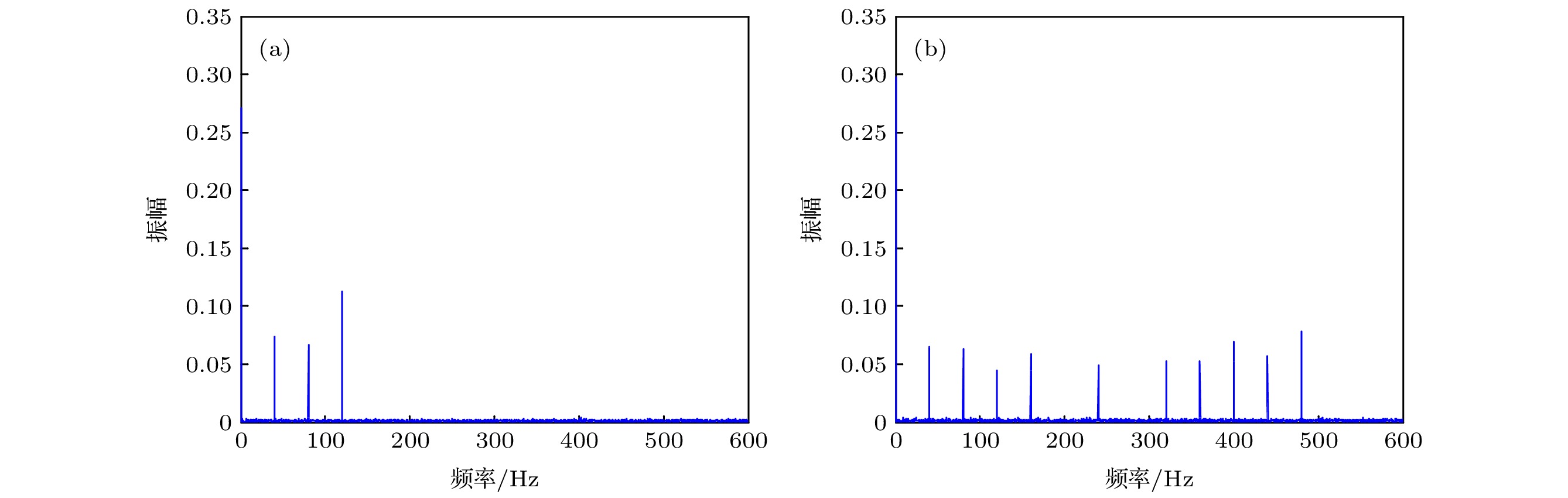
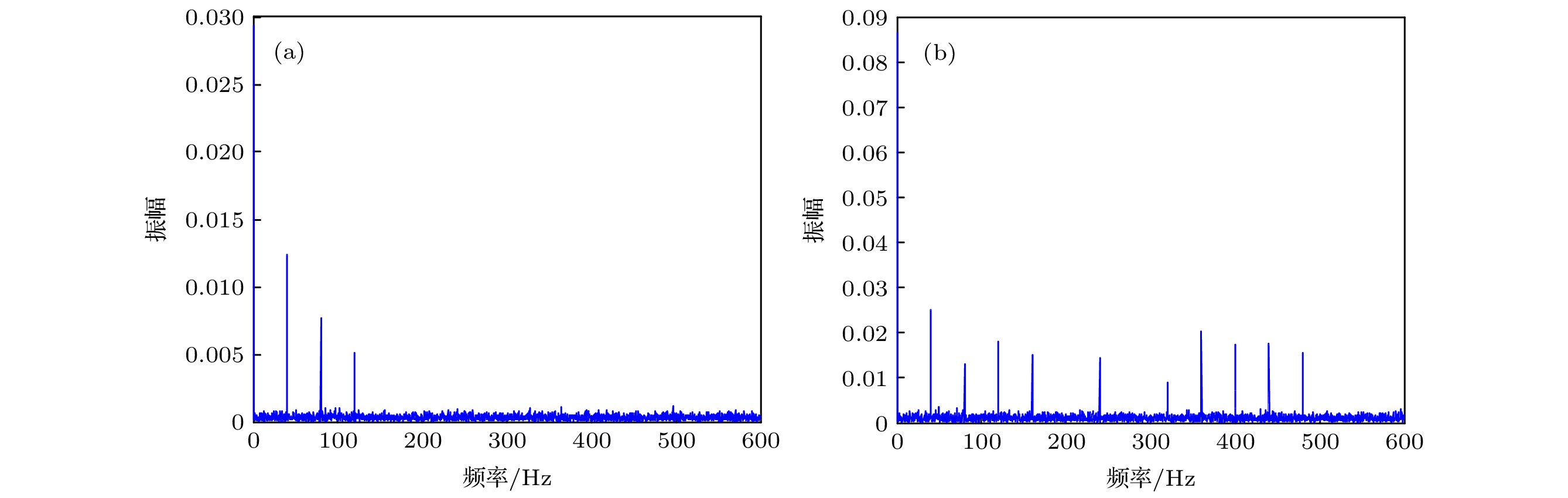
在对低轨道运动目标成像时, 剪切光束成像接收系统所需的探测器阵元数目非常庞大, 探测器接收阵列的研制难度大, 成本高. 本文提出剪切光束成像系统空域稀疏采样技术, 同时发射五束激光照射目标携带更多的频谱信息, 研究稀疏重构算法, 在经稀疏采样的回波信号中提取目标的相位差和振幅信息, 通过波前恢复重构目标图像. 理论上, 在不影响分辨率的前提下, 探测器阵列阵元数目可稀疏为传统三光束方法的1/2, 突破了探测器阵元间距与发射剪切量相等的限制. 仿真结果表明, 与传统三光束方法相比, 所提稀疏重构算法在探测器阵元数目稀疏一倍的情况下, 重构图像质量几乎相同.

关键词:

Abstract

Sheared beam imaging (SBI) is considered a computational imaging technique that transmits three sheared coherent laser beamlets for illumination, and a sensor array to receive the intensity of the speckle pattern reflected from the target. The SBI can be used to image remote objects through a turbulent medium with no need of any adaptive optics. However, while imaging low-orbit moving targets, the number of detectors of sensor array required by the receiving system of SBI is very large, and the development of sensor array is difficult and costly. In this work, a spatial domain sparse sampling technique is proposed for the SBI system through transmitting five laser beamlets to illuminate the target carrying more of its spectral information, which can reduce the number of detectors of the sensor array. Firstly, the principle of the sparse imaging technique is deduced. Then, a sparse reconstruction algorithm is studied. The phase difference and amplitude information of the target in the echo signal after sparse sampling can be extracted accurately by searching for the accurate positions of the beat frequency components. The wavefront phases can be demodulated by the least-squares method, and wavefront amplitude can be obtained by the algebraic operation of speckle amplitude. The reconstructed wavefront is used to formulate the two-dimension image of the target. Theoretically, without affecting the resolution, the number of detectors of the sensor array can be reduced to half of the traditional three-beam method, which breaks through the limitation that the detector spacing of sensor array is equal to the shear length of beamlet. From the simulation results, when the number of detectors of the sensor array is reduced by 50%, the proposed sparse reconstruction algorithm has almost the same quality as the reconstructed image with the traditional three-beam method.

Keywords:

作者及机构信息

1.
中国科学院西安光学精密机械研究所, 西安　710119

2.
中国科学院大学, 北京　100049

3.
中国科学院空间精密测量技术重点实验室, 西安　710119

通信作者: 陈明徕, chenminglai@opt.ac.cn ; 马彩文, cwma@opt.ac.cn ;

基金项目: 陕西省自然科学基础研究计划(批准号: 2020JQ-438)资助的课题.

Authors and contacts

1.
Xi’an Institute of Optics and Precision Mechanics, Chinese Academy of Sciences, Xi’an 710119, China

2.
University of Chinese Academy of Sciences, Beijing 100049, China

3.
Key Laboratory of Space Precision Measurement Technology, Chinese Academy of Sciences, Xi’an 710119, China

Corresponding author: Chen Ming-Lai, chenminglai@opt.ac.cn ; Ma Cai-Wen, cwma@opt.ac.cn ;

Funds: Project supported by the Natural Science Basic Research Program of Shaanxi Province, China (Grant No. 2020JQ-438).

文章全文 : translate this paragraph

参考文献

[1]	Hutchin R A 1993 Proc. SPIE 2029 161 Google Scholar
[2]	Voelz D G, Gonglewski J D, Idell P S 1993 Proc. SPIE 2029 169 Google Scholar
[3]	Hutchin R A 2012 US Patent 20120162631 [2012-6-28]
[4]	Hutchin R A 2012 US Patent 20120292481 [2012-11-22]
[5]	Voelz D G 1995 Proc. SPIE 2566 74 Google Scholar
[6]	Voelz D G, Belsher J F, Ulibarri A L, Gamiz V 2002 Proc. SPIE 4489 35 Google Scholar
[7]	兰富洋, 罗秀娟, 陈明徕, 张羽, 刘辉 2017 66 204202 Google Scholar Lan F Y, Luo X J, Chen M L, Zhang Y, Liu H 2017 Acta Phys. Sin. 66 204202 Google Scholar
[8]	罗秀娟, 刘辉, 张羽, 陈明徕, 兰富洋 2019 中国光学 12 753 Luo X J, Liu H, Zhang Y, Chen M L, Lan F Y 2019 Chin. Opt. 12 753 (in Chinese)
[9]	兰富洋 2019 博士学位论文 (北京: 中国科学院大学) Lan F Y 2019 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[10]	陈明徕, 罗秀娟, 张羽, 兰富洋, 刘辉, 曹蓓, 夏爱利 2017 66 024203 Google Scholar Chen M L, Luo X J, Zhang Y, Lan F Y, Liu H, Cao B, Xia A L 2017 Acta Phys. Sin. 66 024203 Google Scholar
[11]	Fairchild P, Payne I 2013 IEEE Aerospace Conference Big Sky Montana, USA, March 2–9, 2013 p1
[12]	Rider D B, Voelz D G, Bush K A, Magee E 1993 Proc. SPIE 2029 150 Google Scholar
[13]	Bush K A, Barnard C C, Voelz D G 1996 Proc. SPIE 2828 362 Google Scholar
[14]	Sica L 1996 Appl. Opt. 35 264 Google Scholar
[15]	Landesman B T, Olson D F 1994 Proc. SPIE 2302 14 Google Scholar
[16]	兰富洋, 罗秀娟, 樊学武, 张羽, 陈明徕, 刘辉, 贾辉 2018 67 204201 Google Scholar Lan F Y, Luo X J, Fan X W, Zhang Y, Chen M L, Liu H, Jia H 2018 Acta Phys. Sin. 67 204201 Google Scholar
[17]	Gamiz V L 1994 Proc. SPIE 2302 2 Google Scholar
[18]	Stahl S M, Kremer R, Fairchild P, Hughes K, Spivey B 1996 Proc. SPIE 2847 150 Google Scholar
[19]	Olson D F, Long S M, Ulibarri L J 2000 Proc. SPIE 4091 323 Google Scholar
[20]	陆长明, 陈明徕, 罗秀娟, 张羽, 刘辉, 兰富洋, 曹蓓 2017 66 114201 Google Scholar Lu C M, Chen M L, Luo X J, Zhang Y, Liu L, Lan F Y, Cao B 2017 Acta Phys. Sin. 66 114201 Google Scholar
[21]	Fienup J R US Patent 006597304 B2 [2003-7-22]
[22]	Speckle-Based Imaging, Optical Physics Companyhttp://www.opci.com/technologies/ speckle-based-imaging [2017-1-9]
[23]	董磊, 卢振武, 刘欣悦 2019 中国光学 12 138 Google Scholar Dong L, Lu Z W, Liu X Y 2019 Chin. Opt. 12 138 Google Scholar
[24]	Takajo H, Takahashi T 1988 J. Opt. Soc. Am. A 5 416 Google Scholar
[25]	Idell P S, Gonglewski J D 1990 Opt. Lett. 15 1309 Google Scholar
[26]	张羽, 李治国, 刘辉, 陈明徕, 罗秀娟, 马彩文, 张怀利 2021 光子学报 50 1201004 Google Scholar Zhang Y, Li Z G, Liu H, Chen M L, Luo X J, Ma C W, Zhang H L 2021 Acta Photonica Sin. 50 1201004 Google Scholar
[27]	Xiang M, Pan A, Zhao Y Y, Fan X W, Zhao H, Li C, Yao B L 2021 Opt. Lett. 46 29 Google Scholar

施引文献

图 1 SBI技术稀疏采样原理示意图

Fig. 1. Schematic diagram of sparse sampling principle of SBI technique.

下载: 全尺寸图片幻灯片

图 2 四光束成像系统的激光发射排布方式

Fig. 2. Laser emission arrangement of four-beam imaging system.

下载: 全尺寸图片幻灯片

图 3 四光束成像相位复原算法示意图

Fig. 3. Schematic diagram of phase retrieval algorithm for four-beam imaging method.

下载: 全尺寸图片幻灯片

图 4 五光束稀疏采样成像相位复原算法示意图

Fig. 4. Schematic diagram of phase retrieval algorithm for five-beam sparse sampling imaging method.

下载: 全尺寸图片幻灯片

图 5 重构图像及其Strehl比(SNR: 10 dB)　(a), (d), (g) 原始图像, SR = 1; (b) 传统三光束算法, SR = 0.8033; (e) 传统三光束算法, SR = 0.8444; (h) 传统三光束算法, SR = 0.8314; (c) 稀疏重构算法, SR = 0.7935; (f) 稀疏重构算法, SR = 0.8482; (i) 稀疏重构算法, SR = 0.8367

Fig. 5. The reconstructed image and Strehl ratios (SNR: 10 dB): (a), (d), (g) Origin target image, SR = 1; (b) traditional method, SR = 0.8033; (e) traditional method, SR = 0.8444; (h) traditional method, SR = 0.8314; (c) sparse reconstruction method, SR = 0.7935; (f) sparse reconstruction method, SR = 0.8482; (i) sparse reconstruction method, SR = 0.8367.

下载: 全尺寸图片幻灯片

图 6 回波信号振幅频谱(SNR: 10 dB)　(a) 传统三光束方法; (b) 稀疏采样方法

Fig. 6. Amplitude spectrum of echo signals (SNR: 10 dB): (a) Traditional method; (b) sparse sampling method.

下载: 全尺寸图片幻灯片

图 7 重构图像及其Strehl比(SNR: 1 dB)　(a), (d), (g) 原始图像, SR = 1; (b) 传统三光束算法, SR = 0.7554; (e) 传统三光束算法, SR = 0.8309; (h) 传统三光束算法, SR = 0.7954; (c) 稀疏重构算法, SR = 0.7589; (f) 稀疏重构算法, SR = 0.8250; (i) 稀疏重构算法, SR = 0.8092

Fig. 7. The reconstructed image and Strehl ratios (SNR: 1 dB): (a), (d), (g) Origin target image, SR = 1; (b) traditional method, SR = 0.7935; (e) traditional method, SR = 0.8309; (h) traditional method, SR = 0.7954; (c) sparse reconstruction method, SR = 0.7589; (f) sparse reconstruction method, SR = 0.8250; (i) sparse reconstruction method, SR = 0.8092.

下载: 全尺寸图片幻灯片

图 8 回波信号振幅频谱(SNR: 1 dB)　(a) 传统三光束方法; (b) 稀疏采样方法

Fig. 8. Amplitude spectrum of echo signals (SNR: 1 dB): (a) Traditional method; (b) sparse sampling method.

下载: 全尺寸图片幻灯片

map

[1]	Hutchin R A 1993 Proc. SPIE 2029 161 Google Scholar
[2]	Voelz D G, Gonglewski J D, Idell P S 1993 Proc. SPIE 2029 169 Google Scholar
[3]	Hutchin R A 2012 US Patent 20120162631 [2012-6-28]
[4]	Hutchin R A 2012 US Patent 20120292481 [2012-11-22]
[5]	Voelz D G 1995 Proc. SPIE 2566 74 Google Scholar
[6]	Voelz D G, Belsher J F, Ulibarri A L, Gamiz V 2002 Proc. SPIE 4489 35 Google Scholar
[7]	兰富洋, 罗秀娟, 陈明徕, 张羽, 刘辉 2017 66 204202 Google Scholar Lan F Y, Luo X J, Chen M L, Zhang Y, Liu H 2017 Acta Phys. Sin. 66 204202 Google Scholar
[8]	罗秀娟, 刘辉, 张羽, 陈明徕, 兰富洋 2019 中国光学 12 753 Luo X J, Liu H, Zhang Y, Chen M L, Lan F Y 2019 Chin. Opt. 12 753 (in Chinese)
[9]	兰富洋 2019 博士学位论文 (北京: 中国科学院大学) Lan F Y 2019 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences) (in Chinese)
[10]	陈明徕, 罗秀娟, 张羽, 兰富洋, 刘辉, 曹蓓, 夏爱利 2017 66 024203 Google Scholar Chen M L, Luo X J, Zhang Y, Lan F Y, Liu H, Cao B, Xia A L 2017 Acta Phys. Sin. 66 024203 Google Scholar
[11]	Fairchild P, Payne I 2013 IEEE Aerospace Conference Big Sky Montana, USA, March 2–9, 2013 p1
[12]	Rider D B, Voelz D G, Bush K A, Magee E 1993 Proc. SPIE 2029 150 Google Scholar
[13]	Bush K A, Barnard C C, Voelz D G 1996 Proc. SPIE 2828 362 Google Scholar
[14]	Sica L 1996 Appl. Opt. 35 264 Google Scholar
[15]	Landesman B T, Olson D F 1994 Proc. SPIE 2302 14 Google Scholar
[16]	兰富洋, 罗秀娟, 樊学武, 张羽, 陈明徕, 刘辉, 贾辉 2018 67 204201 Google Scholar Lan F Y, Luo X J, Fan X W, Zhang Y, Chen M L, Liu H, Jia H 2018 Acta Phys. Sin. 67 204201 Google Scholar
[17]	Gamiz V L 1994 Proc. SPIE 2302 2 Google Scholar
[18]	Stahl S M, Kremer R, Fairchild P, Hughes K, Spivey B 1996 Proc. SPIE 2847 150 Google Scholar
[19]	Olson D F, Long S M, Ulibarri L J 2000 Proc. SPIE 4091 323 Google Scholar
[20]	陆长明, 陈明徕, 罗秀娟, 张羽, 刘辉, 兰富洋, 曹蓓 2017 66 114201 Google Scholar Lu C M, Chen M L, Luo X J, Zhang Y, Liu L, Lan F Y, Cao B 2017 Acta Phys. Sin. 66 114201 Google Scholar
[21]	Fienup J R US Patent 006597304 B2 [2003-7-22]
[22]	Speckle-Based Imaging, Optical Physics Companyhttp://www.opci.com/technologies/ speckle-based-imaging [2017-1-9]
[23]	董磊, 卢振武, 刘欣悦 2019 中国光学 12 138 Google Scholar Dong L, Lu Z W, Liu X Y 2019 Chin. Opt. 12 138 Google Scholar
[24]	Takajo H, Takahashi T 1988 J. Opt. Soc. Am. A 5 416 Google Scholar
[25]	Idell P S, Gonglewski J D 1990 Opt. Lett. 15 1309 Google Scholar
[26]	张羽, 李治国, 刘辉, 陈明徕, 罗秀娟, 马彩文, 张怀利 2021 光子学报 50 1201004 Google Scholar Zhang Y, Li Z G, Liu H, Chen M L, Luo X J, Ma C W, Zhang H L 2021 Acta Photonica Sin. 50 1201004 Google Scholar
[27]	Xiang M, Pan A, Zhao Y Y, Fan X W, Zhao H, Li C, Yao B L 2021 Opt. Lett. 46 29 Google Scholar

[1]	陈明徕, 马彩文, 刘辉, 罗秀娟, 冯旭斌, 岳泽霖, 赵晶. 基于快速采样的剪切光束成像图像重构算法. , 2024, 73(2): 024202. doi: 10.7498/aps.73.20231254
[2]	崔岸婧, 李道京, 吴疆, 周凯, 高敬涵. 频域稀疏采样和激光成像方法. , 2022, 71(5): 058705. doi: 10.7498/aps.71.20211408
[3]	李明飞, 袁梓豪, 刘院省, 邓意成, 王学锋. 光纤相控阵稀疏排布优化算法对比. , 2021, 70(8): 084205. doi: 10.7498/aps.70.20201768
[4]	谢前朋, 潘小义, 陈吉源, 肖顺平. 基于稀疏阵列的电磁矢量传感器多输入多输出雷达高分辨角度和极化参数联合估计. , 2020, 69(7): 074302. doi: 10.7498/aps.69.20191895
[5]	童莹, 沈越泓, 魏以民. 基于旋转主方向梯度直方图特征的判别稀疏图映射算法. , 2019, 68(19): 194202. doi: 10.7498/aps.68.20190224
[6]	郝未倩, 梁忠诚, 刘肖尧, 赵瑞, 孔梅梅, 关建飞, 张月. 分形结构稀疏孔径阵列的成像性能. , 2019, 68(19): 199501. doi: 10.7498/aps.68.20190818
[7]	张涛, 侯宏, 鲍明. 基于稀疏重构的尾波干涉成像方法. , 2019, 68(19): 199101. doi: 10.7498/aps.68.20190831
[8]	兰富洋, 罗秀娟, 樊学武, 张羽, 陈明徕, 刘辉, 贾辉. 上行链路大气波前畸变对剪切光束成像技术的影响. , 2018, 67(20): 204201. doi: 10.7498/aps.67.20181144
[9]	陆长明, 陈明徕, 罗秀娟, 张羽, 刘辉, 兰富洋, 曹蓓. 四光束剪切相干成像目标重构算法研究. , 2017, 66(11): 114201. doi: 10.7498/aps.66.114201
[10]	兰富洋, 罗秀娟, 陈明徕, 张羽, 刘辉. 剪切光束成像技术对纵深目标的成像. , 2017, 66(20): 204202. doi: 10.7498/aps.66.204202
[11]	陈明徕, 罗秀娟, 张羽, 兰富洋, 刘辉, 曹蓓, 夏爱利. 基于全相位谱分析的剪切光束成像目标重构. , 2017, 66(2): 024203. doi: 10.7498/aps.66.024203
[12]	陈典兵, 朱明, 高文, 王慧利, 杨航. 基于残差矩阵估计的稀疏表示目标跟踪算法. , 2016, 65(19): 194201. doi: 10.7498/aps.65.194201
[13]	刘敬, 金伟其, 王霞, 鲁啸天, 温仁杰. 考虑探测器特性的光电偏振成像系统偏振信息重构方法. , 2016, 65(9): 094201. doi: 10.7498/aps.65.094201
[14]	冷雪冬, 巴斌, 逯志宇, 王大鸣. 基于回溯筛选的稀疏重构时延估计算法. , 2016, 65(21): 210701. doi: 10.7498/aps.65.210701
[15]	陈秋菊, 姜秋喜, 曾芳玲, 宋长宝. 基于时间反演电磁波的稀疏阵列单频信号空间功率合成. , 2015, 64(20): 204101. doi: 10.7498/aps.64.204101
[16]	文方青, 张弓, 贲德. 基于块稀疏贝叶斯学习的多任务压缩感知重构算法. , 2015, 64(7): 070201. doi: 10.7498/aps.64.070201
[17]	常松涛, 孙志远, 张尧禹, 朱玮. 制冷型红外成像系统内部杂散辐射测量方法. , 2015, 64(5): 050702. doi: 10.7498/aps.64.050702
[18]	郑仕链, 杨小牛, 赵知劲. 用于随机解调器压缩采样的重构判定方法. , 2014, 63(22): 228401. doi: 10.7498/aps.63.228401
[19]	王保宪, 赵保军, 唐林波, 王水根, 吴京辉. 基于双向稀疏表示的鲁棒目标跟踪算法. , 2014, 63(23): 234201. doi: 10.7498/aps.63.234201
[20]	邴璐, 王伟远, 王永良, 蒋式勤. 基于贪婪稀疏方法的心脏磁场源重构. , 2013, 62(11): 118703. doi: 10.7498/aps.62.118703

计量

文章访问数: 3436
PDF下载量: 45
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

剪切光束成像技术稀疏重构算法