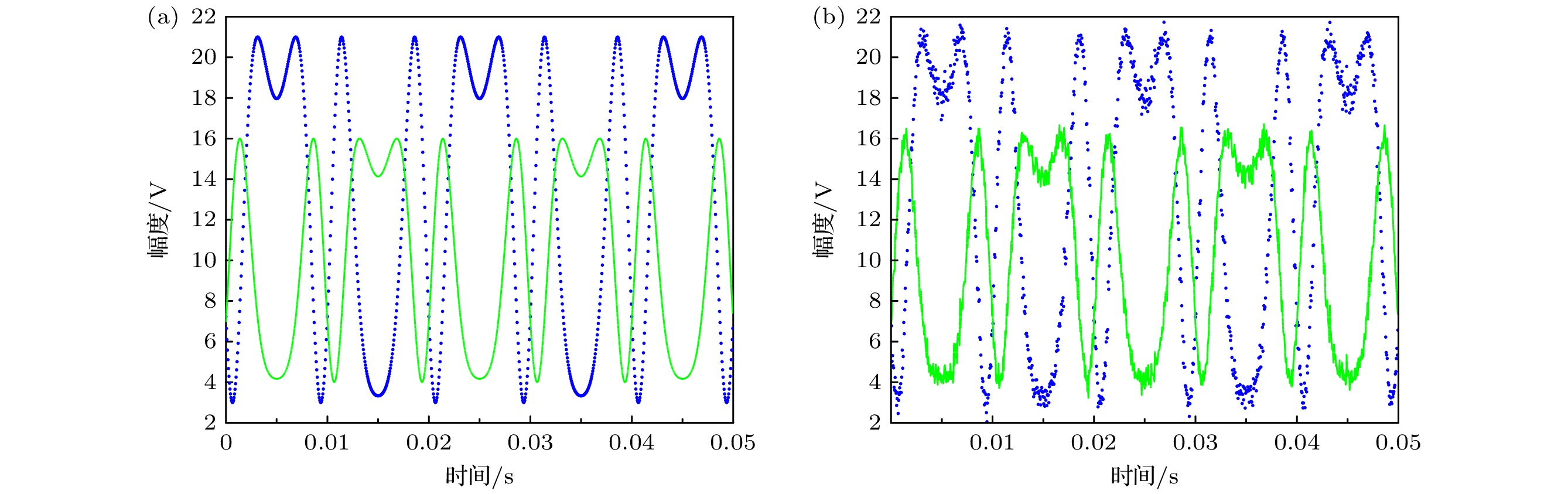
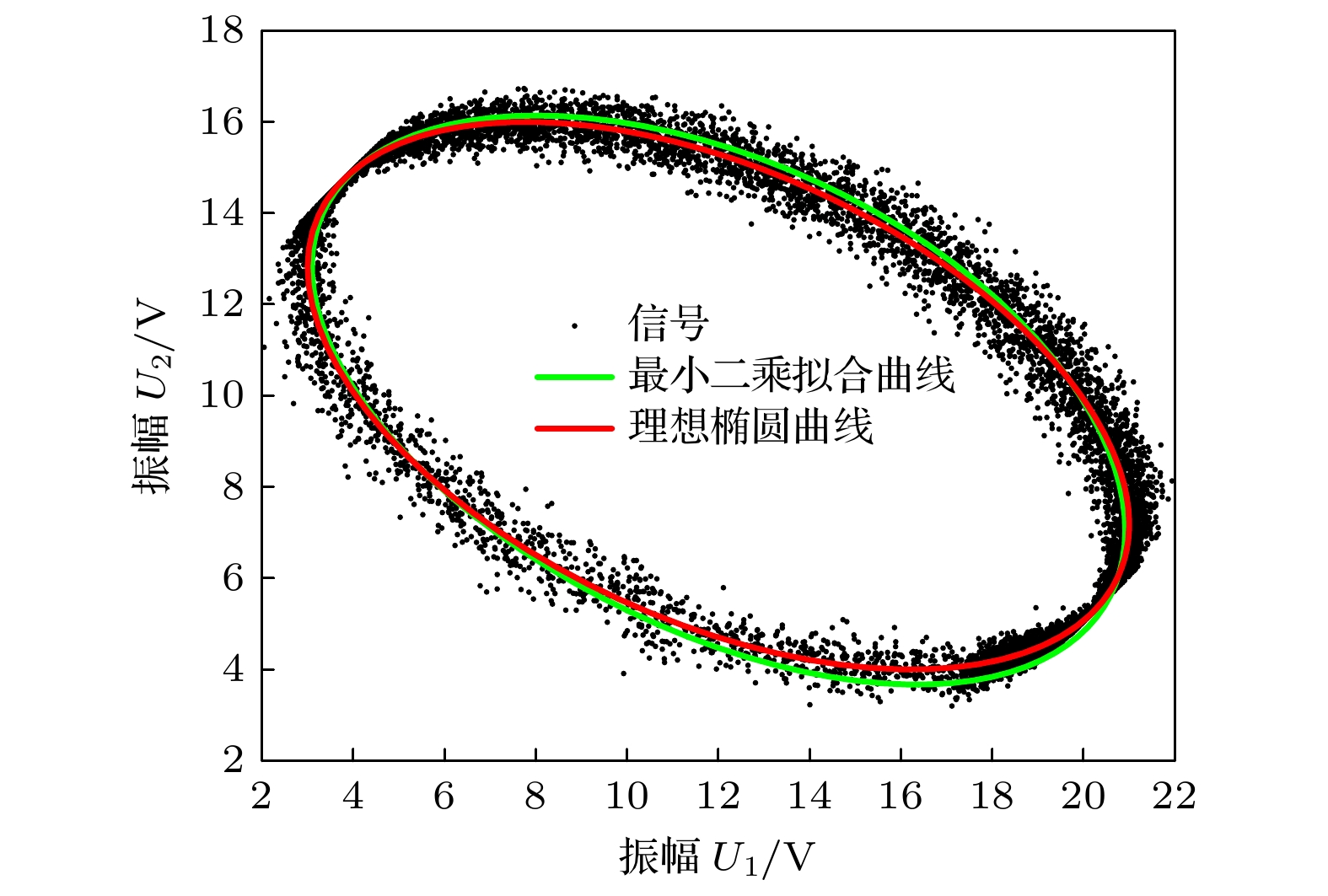
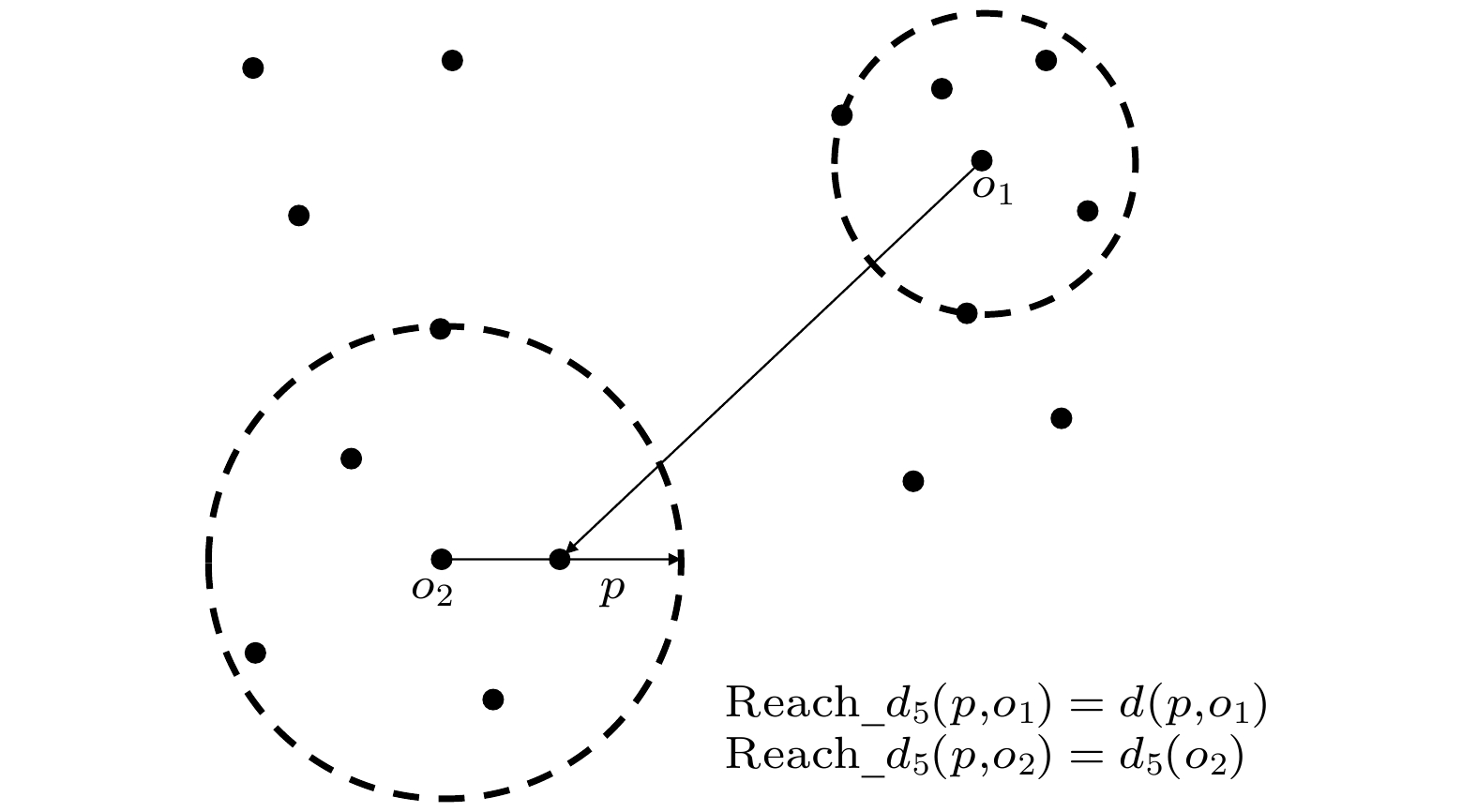
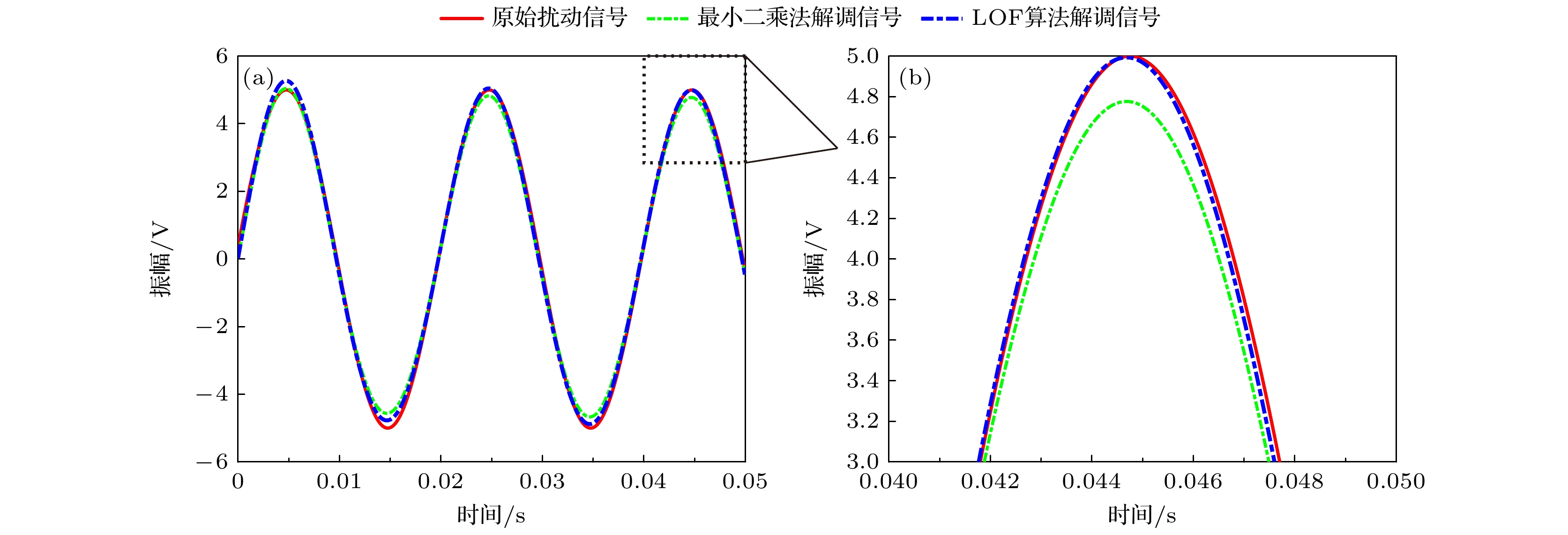
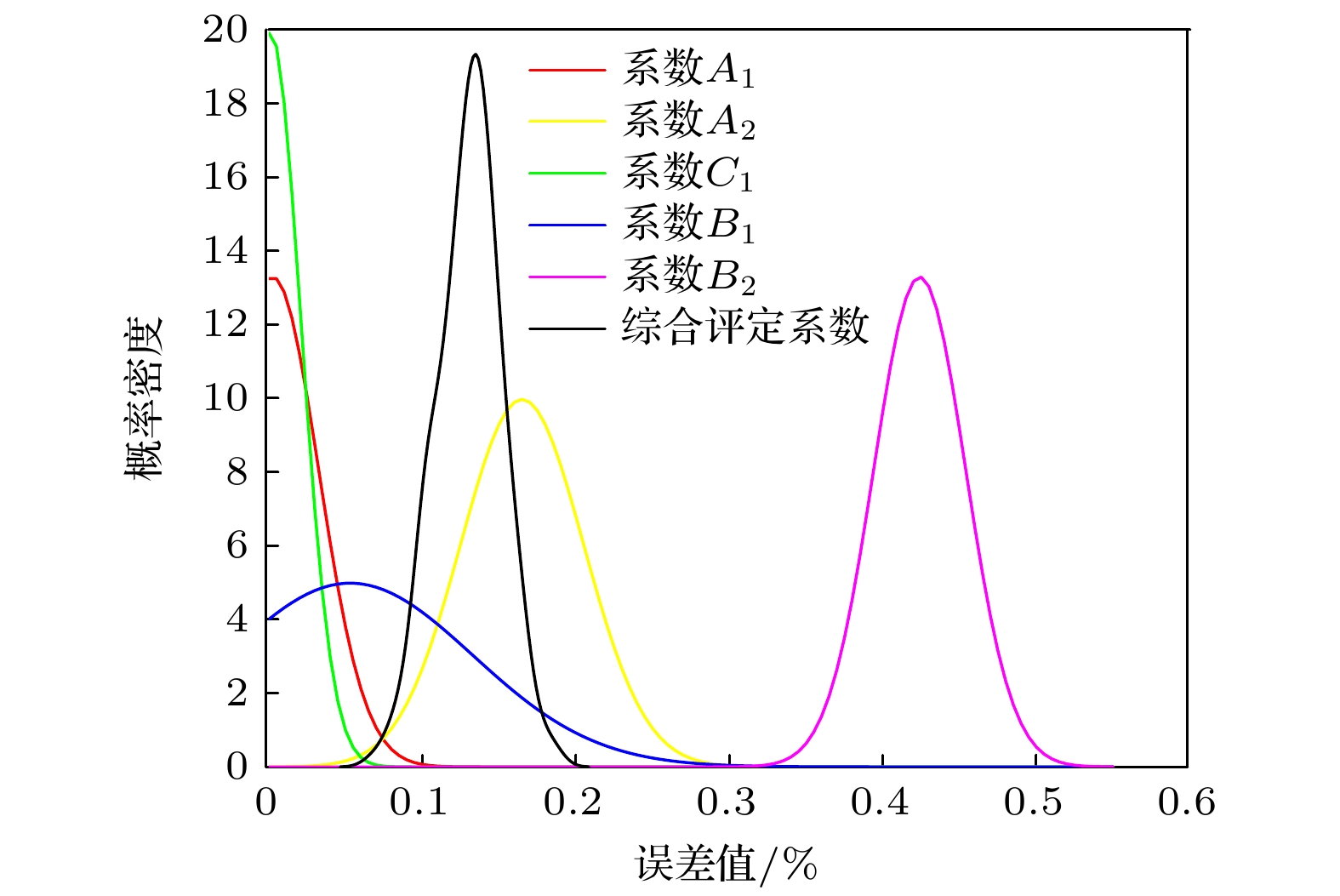
-
In the existing ellipse fitting algorithms, the Lissajous figure is used to solve the demodulation error caused by the non-ideal 3×3 couplers. However, the influence of circuit noise and phase noise on Lissajous figure are not fully considered in the studies. In this work, an ellipse fitting demodulation method based on local outlier factor (LOF) algorithm is proposed, which can effectively eliminate the outlier points in Lissajous figure caused by noises. The proposed method proves to achieve the accurate demodulation of the signals by numerical simulations. In addition, the Monte Carlo analysis is used to obtain the comprehensive error rate of about 0.13%, which verifies the stability of the proposed method. Compared with the traditional least square fitting method, this method improves the stability and accuracy of demodulated signals.
-
Keywords:
- local outlier factor algorithm /
- elliptic fitting /
- noise elimination /
- Monte Carlo analysis
[1] Shi F, Bai X K, Wang F, Pang F F, Pu S L, Zeng X L 2017 IEEE Sens. J. 17 619
Google Scholar
[2] Zhang Y C, Wang J F, Chen M, Wang M Y, Liang Y, Meng Z 2020 Sensors 20 6180
Google Scholar
[3] Fan P J, Yan W, Lu P, Zhang W J, Zhang W, Fu X, Zhang J S 2020 Opt. Express 17 25238
[4] 赵丽娟, 赵海英, 徐志钮 2022 71 074206
Google Scholar
Zhao L J, Zhao H Y, Xu Z N 2022 Acta Phys. Sin. 71 074206
Google Scholar
[5] 于永森, 朱永钦, 赵阳, 潘学鹏 2019 光子学报 48 1148009
Google Scholar
Yu Y S, Zhu Y Q, Zhao Y, Pan X P 2019 Acta Photonica Sin. 48 1148009
Google Scholar
[6] 余有龙, 刘盛春, 谭华耀, Luenfu Lui 2005 光学学报 25 865
Google Scholar
Yu Y L, Liu S C, Tan H Y, Lui L F 2005 Acta Optica. Sinica. 25 865
Google Scholar
[7] 韩国庆, 刘显明, 雷小华, 章鹏, 周峰 2022 仪器仪表学报 43 145
Han G Q, Liu X M, Lei X H, Zhang P, Zhou F 2022 Chinese J. Sci. Instrum. 43 145
[8] Yang T T, Xiao Y B, Ran Z L, He X, Shao T Q, Wang W Y 2021 IEEE Sens. J. 21 22703
Google Scholar
[9] 梁敏富 2019 博士学位论文(江苏: 中国矿业大学)
Liang M F 2019 Ph. D. Dissertation (JiangSu: China University of Mining and Technology) (in Chinese)
[10] 张晓峻, 康崇, 孙晶华 2013 发光学报 34 665
Google Scholar
Zhang X J, Kang C, Sun J H 2013 Chin. J. Lumin. 34 665
Google Scholar
[11] 肖倩 2013 博士学位论文 (上海: 复旦大学)
Xiao Q 2013 Ph. D. Dissertation (ShangHai: Fudan University) (in Chinese)
[12] 郎金鹏, 常天英, 陈建冬, 刘野, 崔洪亮, 于淼 2016 光子学报 45 1207004
Google Scholar
Lang J P, Chang T Y, Chen J D, Liu Y, Cui H L, Yu M 2016 Acta Photonica Sin. 45 1207004
Google Scholar
[13] 孙琪真 2008 博士学位论文 (武汉: 华中科技大学)
Sun Q Z 2008 Ph. D. Dissertation (WuHan: Huazhong University of Science and Technology) (in Chinese)
[14] Liu T T, Cui J, Chen D S, Xiao L, Sun D X 2008 Chin. Opt. Lett. 6 12
Google Scholar
[15] 王伟, 唐瑛, 张雄星, 陈海滨, 郭子龙, 王可宁 2019 光学学报 39 0606001
Google Scholar
Wang W, Tang Y, Zhang X X, Chen H B, Guo Z L, Wang K N 2019 Acta Opt. Sin. 39 0606001
Google Scholar
[16] 梅泽, 吕海飞, 文晓艳, 黎敏 2021 光学学报 41 2412001
Mei Z, Lü H F, Wen H F, Wen X Y, Li M 2021 Acta Opt. Sin. 41 2412001
[17] 高晓文, 张自丽, 叶博, 葛辉良 2019 声学与电子工程 3 15
Gao X W, Zhang X W, Zhang Z L, Ye B 2019 Acoust Electr. Eng. 3 15
[18] Zhao Z Q, Demokan M S, Macalpinem M 1997 J. Lightwave Technol. 15 2059
Google Scholar
[19] 刘俊承, 张自超, 余波, 高峰 2019 光子学报 48 0106002
Google Scholar
Liu J C. Zhang Z C. Yu B. Gao F 2019 Acta Photonica Sin. 48 0106002
Google Scholar
[20] 曾周末, 刘芳, 封皓, 冯欣 2014 光学精密工程 22 1410
Google Scholar
Zeng Z M, Liu F, Feng H, Feng X 2014 Opt. Precis. Eng. 22 1410
Google Scholar
[21] Breunig M M, Kriegel H P, Raymond T N, Sander J 2000 Principles and Practice of Knowledge Discovery in Databases (Prague: Proceedings of the 3rd European Conference) p93
[22] 吴琼, 王博, 王涛, 朱仁江, 张鹏, 汪丽杰 2021 光子学报 50 0406002
Wu Q, Wang B, Wang T, Zhu R J, Zhang P, Wang L J 2021 Acta Photonica Sin. 50 0406002
[23] 赵宁宁, 肖新宇, 凡凤仙, 苏明旭 2022 71 074303
Google Scholar
Zhao N N, Xiao X Y, Fan F X, Su M X 2022 Acta Phys. Sin. 71 074303
Google Scholar
-
图 1 基于3×3耦合器解调的迈克尔逊干涉仪结构
Fig. 1. The structure of Michelson interferometer based on 3×3 coupler.
图 2 两路仿真信号 (a) 无噪声干扰信号; (b) 有噪声干扰信号
Fig. 2. Two simulated signals: (a) Without noise interference; (b) with noise interference.
图 4
$ k=5 $ 时, 对象$ p, {o}_{1} $ 的可达距离和对象$ p, {o}_{2} $ 的可达距离的示意图Fig. 4. The schematic diagram of the reach-distances of
$ p, {o}_{1} $ and$ p, {o}_{2} $ when k = 5.
图 6 LOF算法处理前后的李萨如图像 (a) 处理前的李萨如图像; (b)处理后的李萨如图像
Fig. 6. Lissajous figures with/without LOF processing: (a) Before processing; (b) after processing.
图 7 解调信号 (a) 完整解调信号; (b) 解调信号局部
Fig. 7. The demodulated signals: (a) Full signals; (b) partially-amplified signals.
图 8 综合评定系数误差概率密度
Fig. 8. Error probability density of comprehensive evaluation coefficient.
-
[1] Shi F, Bai X K, Wang F, Pang F F, Pu S L, Zeng X L 2017 IEEE Sens. J. 17 619
Google Scholar
[2] Zhang Y C, Wang J F, Chen M, Wang M Y, Liang Y, Meng Z 2020 Sensors 20 6180
Google Scholar
[3] Fan P J, Yan W, Lu P, Zhang W J, Zhang W, Fu X, Zhang J S 2020 Opt. Express 17 25238
[4] 赵丽娟, 赵海英, 徐志钮 2022 71 074206
Google Scholar
Zhao L J, Zhao H Y, Xu Z N 2022 Acta Phys. Sin. 71 074206
Google Scholar
[5] 于永森, 朱永钦, 赵阳, 潘学鹏 2019 光子学报 48 1148009
Google Scholar
Yu Y S, Zhu Y Q, Zhao Y, Pan X P 2019 Acta Photonica Sin. 48 1148009
Google Scholar
[6] 余有龙, 刘盛春, 谭华耀, Luenfu Lui 2005 光学学报 25 865
Google Scholar
Yu Y L, Liu S C, Tan H Y, Lui L F 2005 Acta Optica. Sinica. 25 865
Google Scholar
[7] 韩国庆, 刘显明, 雷小华, 章鹏, 周峰 2022 仪器仪表学报 43 145
Han G Q, Liu X M, Lei X H, Zhang P, Zhou F 2022 Chinese J. Sci. Instrum. 43 145
[8] Yang T T, Xiao Y B, Ran Z L, He X, Shao T Q, Wang W Y 2021 IEEE Sens. J. 21 22703
Google Scholar
[9] 梁敏富 2019 博士学位论文(江苏: 中国矿业大学)
Liang M F 2019 Ph. D. Dissertation (JiangSu: China University of Mining and Technology) (in Chinese)
[10] 张晓峻, 康崇, 孙晶华 2013 发光学报 34 665
Google Scholar
Zhang X J, Kang C, Sun J H 2013 Chin. J. Lumin. 34 665
Google Scholar
[11] 肖倩 2013 博士学位论文 (上海: 复旦大学)
Xiao Q 2013 Ph. D. Dissertation (ShangHai: Fudan University) (in Chinese)
[12] 郎金鹏, 常天英, 陈建冬, 刘野, 崔洪亮, 于淼 2016 光子学报 45 1207004
Google Scholar
Lang J P, Chang T Y, Chen J D, Liu Y, Cui H L, Yu M 2016 Acta Photonica Sin. 45 1207004
Google Scholar
[13] 孙琪真 2008 博士学位论文 (武汉: 华中科技大学)
Sun Q Z 2008 Ph. D. Dissertation (WuHan: Huazhong University of Science and Technology) (in Chinese)
[14] Liu T T, Cui J, Chen D S, Xiao L, Sun D X 2008 Chin. Opt. Lett. 6 12
Google Scholar
[15] 王伟, 唐瑛, 张雄星, 陈海滨, 郭子龙, 王可宁 2019 光学学报 39 0606001
Google Scholar
Wang W, Tang Y, Zhang X X, Chen H B, Guo Z L, Wang K N 2019 Acta Opt. Sin. 39 0606001
Google Scholar
[16] 梅泽, 吕海飞, 文晓艳, 黎敏 2021 光学学报 41 2412001
Mei Z, Lü H F, Wen H F, Wen X Y, Li M 2021 Acta Opt. Sin. 41 2412001
[17] 高晓文, 张自丽, 叶博, 葛辉良 2019 声学与电子工程 3 15
Gao X W, Zhang X W, Zhang Z L, Ye B 2019 Acoust Electr. Eng. 3 15
[18] Zhao Z Q, Demokan M S, Macalpinem M 1997 J. Lightwave Technol. 15 2059
Google Scholar
[19] 刘俊承, 张自超, 余波, 高峰 2019 光子学报 48 0106002
Google Scholar
Liu J C. Zhang Z C. Yu B. Gao F 2019 Acta Photonica Sin. 48 0106002
Google Scholar
[20] 曾周末, 刘芳, 封皓, 冯欣 2014 光学精密工程 22 1410
Google Scholar
Zeng Z M, Liu F, Feng H, Feng X 2014 Opt. Precis. Eng. 22 1410
Google Scholar
[21] Breunig M M, Kriegel H P, Raymond T N, Sander J 2000 Principles and Practice of Knowledge Discovery in Databases (Prague: Proceedings of the 3rd European Conference) p93
[22] 吴琼, 王博, 王涛, 朱仁江, 张鹏, 汪丽杰 2021 光子学报 50 0406002
Wu Q, Wang B, Wang T, Zhu R J, Zhang P, Wang L J 2021 Acta Photonica Sin. 50 0406002
[23] 赵宁宁, 肖新宇, 凡凤仙, 苏明旭 2022 71 074303
Google Scholar
Zhao N N, Xiao X Y, Fan F X, Su M X 2022 Acta Phys. Sin. 71 074303
Google Scholar
下载:
计量
- 文章访问数: 3733
- PDF下载量: 73
- 被引次数: 0
