-
可视图(visibility graph, VG)算法已被证明是将时间序列转换为复杂网络的简单且高效的方法, 其构成的复杂网络在拓扑结构中继承了原始时间序列的动力学特性. 目前, 单维时间序列的可视图分析已趋于成熟, 但应用于复杂系统时, 单变量往往无法描述系统的全局特征. 本文提出一种新的多元时间序列分析方法, 将心梗和健康人的12导联心电图(electrocardiograph, ECG)信号转换为多路可视图, 以每个导联为一个节点, 两个导联构成可视图的层间互信息为连边权重, 将其映射到复杂网络. 由于不同人群的全连通网络表现为完全相同的拓扑结构, 无法唯一表征不同个体的动力学特征, 根据层间互信息大小重构网络, 提取权重度和加权聚类系数, 实现对不同人群12导联ECG信号的识别. 为判断序列长度对识别效果的影响, 引入多尺度权重度分布熵. 由于健康受试者拥有更高的平均权重度和平均加权聚类系数, 其映射网络表现为更加规则的结构、更高的复杂性和连接性, 可以与心梗患者进行区分, 两个参数的识别准确率均达到93.3%.The visibility graph algorithm proves to be a simple and efficient method to transform time series into complex network and has been widely used in time series analysis because it can inherit the dynamic characteristics of original time series in topological structure. Now, visibility graph analysis of univariate time series has become mature gradually. However, most of complex systems in real world are multi-dimensional, so the univariate analysis is difficult to describe the global characteristics when applied to multi-dimensional series. In this paper, a novel method of analyzing the multivariate time series is proposed. For patients with myocardial infarction and healthy subjects, the 12-lead electrocardiogram signals of each individual are considered as a multivariate time series, which is transformed into a multiplex visibility graph through visibility graph algorithm and then mapped to fully connected complex network. Each node of the network corresponds to a lead, and the inter-layer mutual information between visibility graphs of two leads represents the weight of edges. Owing to the fully connected network of different groups showing an identical topological structure, the dynamic characteristics of different individuals cannot be uniquely represented. Therefore, we reconstruct the fully connected network according to inter-layer mutual information, and when the value of inter-layer mutual information is less than the threshold we set, the edge corresponding to the inter-layer mutual information is deleted. We extract average weighted degree and average weighted clustering coefficient of reconstructed networks for recognizing the 12-lead ECG signals of healthy subjects and myocardial infarction patients. Moreover, multiscale weighted distribution entropy is also introduced to analyze the relation between the length of original time series and final recognition result. Owing to higher average weighted degree and average weighted clustering coefficient of healthy subjects, their reconstructed networks show a more regular structure, higher complexity and connectivity, and the healthy subjects can be distinguished from patients with myocardial infarction, whose reconstructed networks are sparser. Experimental results show that the identification accuracy of both parameters, average weighted degree and average weighted clustering coefficient, reaches 93.3%, which can distinguish between the 12-lead electrocardiograph signals of healthy people and patients with myocardial infarction, and realize the automatic detection of myocardial infarction.
-
Keywords:
- myocardial infarction /
- multivariate time series /
- multiplex visibility graph /
- complex network
[1] Zhang J, Small M 2006 Phys. Rev. Lett. 96 238701
Google Scholar
[2] Zou Y, Donner R V, Marwan N, Donges J F, Kurths J 2019 Phys. Rep. 787 1
Google Scholar
[3] Lacasa L, Luque B, Ballesteros F, Luque J, Nuno J C 2008 Proc. Natl. Acad. Sci. 105 4972
Google Scholar
[4] Luque B, Lacasa L, Ballesteros F, Luque J 2009 Phys. Rev. E 80 046103
Google Scholar
[5] Donner R V, Zou Y, Donges J F, Marwan N, Kurths J 2010 New J. Phys. 12 033025
Google Scholar
[6] Marwan N, Donges J F, Zou Y, Donner R V, Kurths J 2009 Phys. Lett. A 373 4246
Google Scholar
[7] Xu X, Zhang J, Small M 2008 Proc. Natl. Acad. Sci. 105 19601
Google Scholar
[8] Donges J F, Donner R V, Trauth M H, Marwan N, Schellnhuber H J 2011 Proc. Natl. Acad. Sci. 108 20422
Google Scholar
[9] 周婷婷, 金宁德, 高忠科, 罗跃斌 2012 61 030506
Google Scholar
Zhou T T, Jin N D, Gao Z K, Luo Y B 2012 Acta Phys. Sin. 61 030506
Google Scholar
[10] Sun X R, Small M, Zhao Y, Xue X P 2013 Chaos 24 1054
Google Scholar
[11] Zhang J Y, Zhou J, Tang M, Guo H, Small M, Zou Y 2017 Sci. Rep. 7 7795
Google Scholar
[12] Kulp C W, Chobot J M, Freitas H R, Sprechini G D 2016 Chaos 26 073114
Google Scholar
[13] Zou Y, Small M, Liu Z, Kurths J 2014 New J. Phys. 16 013051
Google Scholar
[14] Donner R V, Donges J F 2012 Acta Geophys. 60 589
Google Scholar
[15] Bajestani G S, Behrooz M, Khani A G, Nouri-Baygi M, Mollaei A 2019 Comput. Methods Programs Biomed. 177 277
Google Scholar
[16] Tang X Y, Xia L, Liao Y Z, Liu W F, Peng Y H, Gao T X, Zeng Y J 2013 Clin. EEG Neurosci. 44 150
Google Scholar
[17] Supriya S, Siuly S, Wang H, Cao J L, Zhang Y C 2016 IEEE Access 4 6554
Google Scholar
[18] Bhaduri S, Ghosh D 2015 Clin. EEG Neurosci. 46 218
Google Scholar
[19] Wang L, Long X, Arends J B, Aarts R M 2017 J. Neurosci. Method 290 85
Google Scholar
[20] Kong T J, Shao J, Hu J Y, Yang X, Yang S Y, Malekian R 2021 Sensors 21 1870
Google Scholar
[21] 易娜 2014 硕士学位论文 (广州: 暨南大学)
Yi N 2014 M. S. Thesis (Guangzhou: Jinan University) (in Chinese)
[22] Shi W B, Shang P J, Wang J, Lin A J 2014 Physica A 403 35
[23] Jiang W, Wei B Y, Zhan J, Xie C H, Zhou D Y 2016 Comput. Ind. Eng. 101 260
Google Scholar
[24] Azami H, Escudero J 2017 Physica A 465 261
Google Scholar
[25] Han Y F, Jin N D, Zhai L S, Ren Y Y, He Y S 2019 Physica A 518 131
Google Scholar
[26] Gao Z K, Liu M X, Dang W D, Ma C, Hou L H, Hong X L 2021 Chem. Eng. J. 407 127229
Google Scholar
[27] Tanizawa T, Nakamura T, Taya F, Small M 2018 Physica A 512 437
Google Scholar
[28] Gao Z K, Fang P C, Ding M S, Jin N D 2015 Exp. Therm Fluid Sci. 60 157
Google Scholar
[29] Bianconi G 2013 Phys. Rev. E 87 062806
Google Scholar
[30] Nicosia V, Bianconi G, Latora V, Barthelemy M 2013 Phys. Rev. Lett. 111 058701
Google Scholar
[31] Battiston F, Nicosia V, Latora V 2014 Phys. Rev. E 89 032804
Google Scholar
[32] Quesada D, Valverde G, Larrañaga P, Bielza C 2021 Eng. Appl. Artif. Intell. 103 104301
Google Scholar
[33] Lacasa L, Nicosia V, Latora V 2015 Sci. Rep. 5 15508
Google Scholar
[34] Carmona-Cabezas R, Gómez-Gómez J, Ariza-Villaverde A B, de Ravé E G, Jiménez-Hornero F J 2020 Atmos. Pollut. Res. 11 205
Google Scholar
[35] Gao Z K, Guo W, Cai Q, Ma C, Zhang Y B, Kurths J 2019 Chaos 29 073119
Google Scholar
[36] Cai Q, An J, Gao Z 2021 Brain Sci. Adv. 6 355
Google Scholar
[37] Samanta K, Chatterjee S, Bose R 2020 IEEE Sensors Lett. 4 1
Google Scholar
[38] Thygesen K, Alpert J S, White H D 2007 J. Am. Coll. Cardiol. 50 2173
Google Scholar
[39] Dohare A K, Kumar V, Kumar R 2018 Appl. Soft Comput. 64 138
Google Scholar
[40] Sharma M, San Tan R, Acharya U R 2018 Comput. Biol. Med. 102 341
Google Scholar
[41] Tripathy R K, Bhattacharyya A, Pachori R B 2019 IEEE Sensors J. 19 11437
Google Scholar
[42] Acharya U R, Fujita H, Oh S L, Hagiwara Y, Tan J H, Adam M 2017 Inf. Sci. 415 190
Google Scholar
[43] 熊鹏, 薛彦平, 刘明, 杜海曼, 王洪瑞, 刘秀玲 2020 生物医学工程学杂志 37 142
Google Scholar
Xiong P, Xue Y P, Liu M, Du H M, Wang H R, Liu X L 2020 J. Biomed. Eng. 37 142
Google Scholar
[44] Liu W H, Huang Q J, Chang S, Wang H, He J 2018 Biomed. Signal Process. Control 45 22
Google Scholar
[45] 张汉勇, 孟庆芳, 杜蕾, 刘明敏 2019 中国生物医学工程学报 38 273
Google Scholar
Zhang H Y, Meng Q F, Du L, Liu M M 2019 Chin. J. Biomed. Eng. 38 273
Google Scholar
[46] Goldberger A L, Amaral L, Glass L, Hausdorff J M, Ivanov P C, Mark R G, Mietus J E, Moody G B, Peng C K, Stanley H E 2000 Circulation 101 e215
Google Scholar
[47] Costa M, Goldberger A L, Peng C K 2002 Phys. Rev. Lett. 89 068102
Google Scholar
[48] Chang P C, Lin J J, Hsieh J C, Weng J 2012 Appl. Soft Comput. 12 3165
Google Scholar
[49] Sun L, Lu Y P, Yang K T, Li S Z 2012 IEEE Trans. Biomed. Eng. 59 3348
Google Scholar
[50] 王丹俐 2020 硕士学位论文 (杭州: 杭州电子科技大学)
Wang D L 2020 M. S. Thesis (Hangzhou: Hangzhou Danzi University) (in Chinese)
-
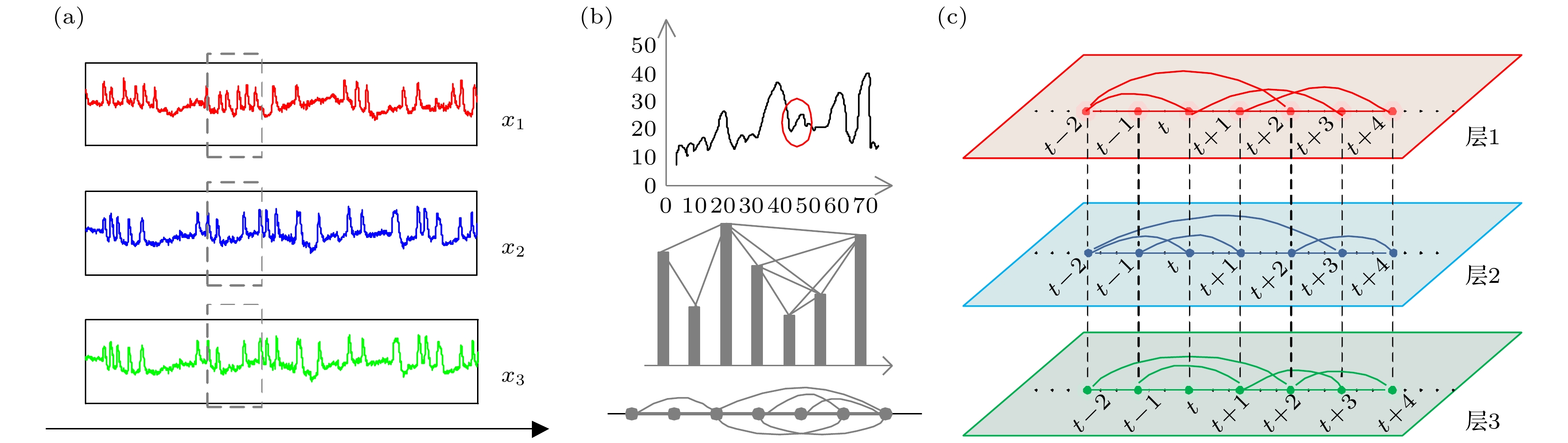
图 1 VG算法构造多路可视图示意图 (a)一个多维时间序列; (b) VG算法示意图, 从上至下依次为原始时间序列、红色圆圈包含片段的VG算法过程及其构造后的网络; (c)图(a)虚线框所含序列通过VG算法构造的多路可视图, 其中层1, 2, 3分别对应时间序列x1, x2, x3
Fig. 1. Schematic diagram of constructing multiplex visibility graph using VG algorithm: (a) a multivariate time series; (b) schematic diagram of VG algorithm. From top to bottom are original time series, VG algorithm procedure for fragment contained in the red circle and the constructed network; (c) multiplex visibility graph of series in dotted box in figure (a) constructed by VG algorithm, where layers 1, 2 and 3 correspond to time series x1, x2 and x3, respectively.
图 2 多路可视图映射后的网络. 节点1, 2, 3对应多路可视图的第1层、第2层和第3层. I1,2, I1,3, I2,3分别为层1和层2、层1和层3、层2和层3之间的互信息, 同时为对应两点连边的权重
Fig. 2. Network mapped by multiplex visibility graph. Nodes 1, 2 and 3 correspond to the 1st, 2nd and 3rd layers of multiplex visibility graph. I1,2, I1,3, I2,3 are the mutual information between layer 1 and layer 2, layer 1 and layer 3, layer 2 and layer 3 respectively, meanwhile, they are the weight of edges of corresponding two points.
图 3 不同年龄的健康人和MI患者在不同尺度因子s下平均权重度分布熵 (a) 60—69岁; (b) 50—59岁; (c) 40—49岁; (d) 30—39岁. 绿色实线为两类人群平均权重度分布熵按比例缩放后的差值, 星号表示差值最大处
Fig. 3. Average weighted distribution entropy of healthy people and patients with MI under different scale factor s: (a) 60–69 years old; (b) 50–59 years old; (c) 40–49 years old; (d) 30–39 years old. The solid green line is the difference of average weighted distribution entropy of two groups after scaling, and asterisk represents the maximum difference.
图 4 不同年龄组健康受试者与MI患者在常数c不同取值时的平均权重度 (a) 60—69岁; (b) 50—59岁; (c) 40—49岁; (d) 30—39岁. 绿色实线为两类人群平均权重度的差值, 星号表示差值最大处, 其值见表2
Fig. 4. Average weighted degree of healthy subjects and myocardial infarction patients at different values of constant c: (a) 60–69 years old; (b) 50–59 years old; (c) 40–49 years old; (d) 30–39 years old. The solid green line is the difference of the average weighted degree of two groups, and the asterisk represents the maximum difference, see Table 2 for specific values.
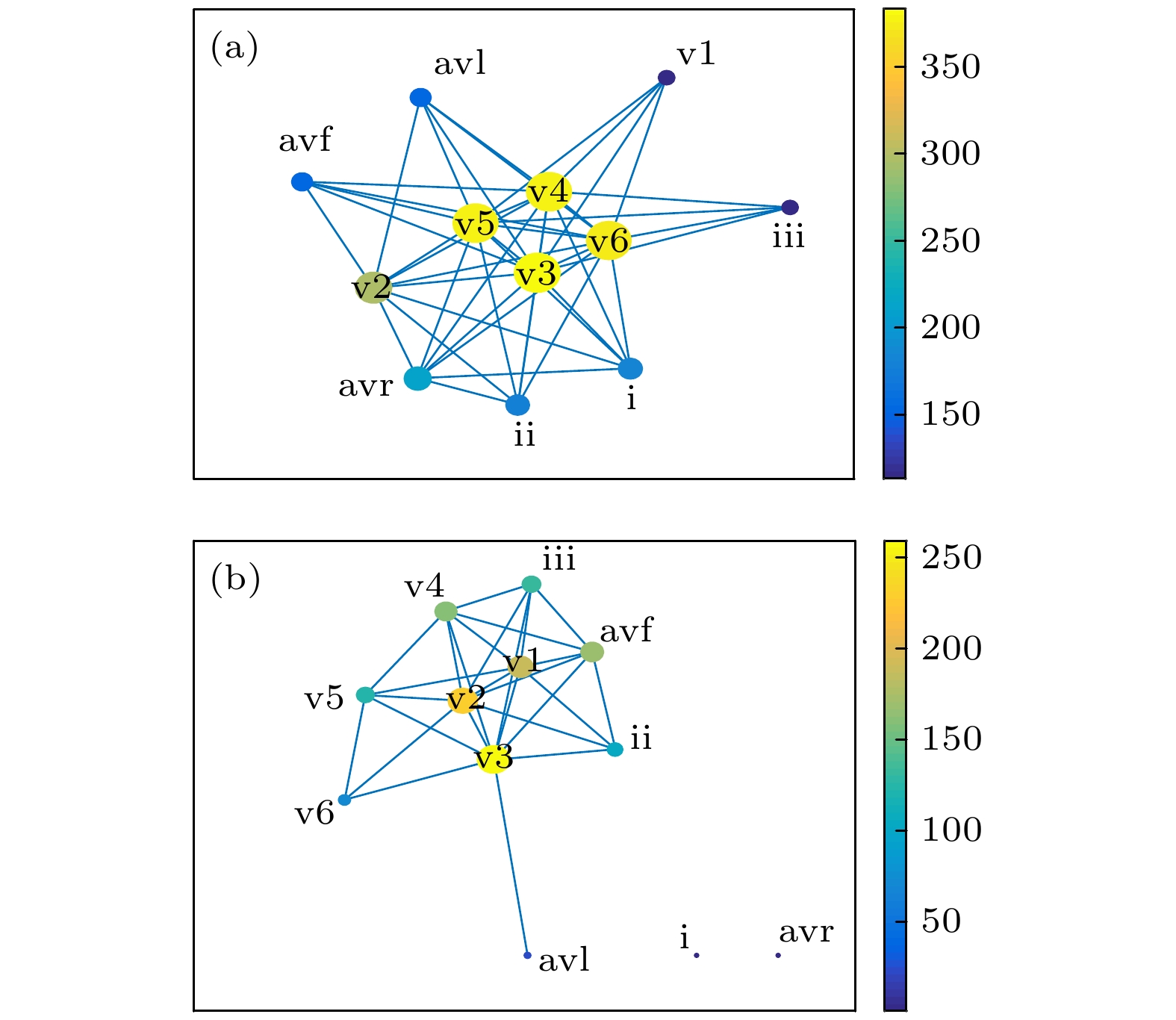
图 5 常数c = 0.43时重构网络的拓扑图 (a)健康受试者; (b) MI患者. 各节点对应的导联已在图中标明. 节点大小和颜色对应该节点的权重度. 图右侧颜色柱表示节点权重度
Fig. 5. Topology of the reconstructed network of (a) healthy subjects and (b) patients with MI at c = 0.43. The corresponding leads of each node have been indicated in the figure. Size and color are relative to the weighted degree of the node. The color bar on the right of the figure indicates the value of weighted degree.
图 6 健康人和MI患者在最佳阈值下的(a)平均权重度和(b)平均加权聚类系数. 第1组—第4组受试者的年龄范围分别为60—69岁、50—59岁、40—49岁以及30—39岁
Fig. 6. (a) Average weighted degree and (b) average weighted clustering coefficients of healthy and myocardial infarction patients under optimal thresholds. Subjects in groups 1–4 correspond to ages of 60–69 years old, 50–59 years old, 40–49 years old and 30 to 39 years old respectively.
表 1 12导联名称及其对应的心脏位置
Table 1. Name of the 12-lead and their corresponding cardiac location
导联名称 心脏部位 I, avl 心脏左室前侧壁 Ⅱ, Ⅲ, avf 心脏后壁、下面 avr 心室内腔 v1, v2 右室 v3, v4 室间隔 v5, v6 左室 
下载: 导出CSV
表 2 4组健康人-MI患者对应重构网络的平均权重度差值最大时的常数c
Table 2. Constant c of four groups when difference of average weighted degree of reconstructed network being maximum.
变量 60—69岁 50—59岁 40—49岁 30—39岁 倍数c 0.67 0.67 0.59 0.43 差值 2.2895 1.8389 2.3592 1.9015
下载: 导出CSV
表 3 本方法与其他现有方法的比较
Table 3. The comparison between proposed method and other existing methods
下载: 导出CSV
-
[1] Zhang J, Small M 2006 Phys. Rev. Lett. 96 238701
Google Scholar
[2] Zou Y, Donner R V, Marwan N, Donges J F, Kurths J 2019 Phys. Rep. 787 1
Google Scholar
[3] Lacasa L, Luque B, Ballesteros F, Luque J, Nuno J C 2008 Proc. Natl. Acad. Sci. 105 4972
Google Scholar
[4] Luque B, Lacasa L, Ballesteros F, Luque J 2009 Phys. Rev. E 80 046103
Google Scholar
[5] Donner R V, Zou Y, Donges J F, Marwan N, Kurths J 2010 New J. Phys. 12 033025
Google Scholar
[6] Marwan N, Donges J F, Zou Y, Donner R V, Kurths J 2009 Phys. Lett. A 373 4246
Google Scholar
[7] Xu X, Zhang J, Small M 2008 Proc. Natl. Acad. Sci. 105 19601
Google Scholar
[8] Donges J F, Donner R V, Trauth M H, Marwan N, Schellnhuber H J 2011 Proc. Natl. Acad. Sci. 108 20422
Google Scholar
[9] 周婷婷, 金宁德, 高忠科, 罗跃斌 2012 61 030506
Google Scholar
Zhou T T, Jin N D, Gao Z K, Luo Y B 2012 Acta Phys. Sin. 61 030506
Google Scholar
[10] Sun X R, Small M, Zhao Y, Xue X P 2013 Chaos 24 1054
Google Scholar
[11] Zhang J Y, Zhou J, Tang M, Guo H, Small M, Zou Y 2017 Sci. Rep. 7 7795
Google Scholar
[12] Kulp C W, Chobot J M, Freitas H R, Sprechini G D 2016 Chaos 26 073114
Google Scholar
[13] Zou Y, Small M, Liu Z, Kurths J 2014 New J. Phys. 16 013051
Google Scholar
[14] Donner R V, Donges J F 2012 Acta Geophys. 60 589
Google Scholar
[15] Bajestani G S, Behrooz M, Khani A G, Nouri-Baygi M, Mollaei A 2019 Comput. Methods Programs Biomed. 177 277
Google Scholar
[16] Tang X Y, Xia L, Liao Y Z, Liu W F, Peng Y H, Gao T X, Zeng Y J 2013 Clin. EEG Neurosci. 44 150
Google Scholar
[17] Supriya S, Siuly S, Wang H, Cao J L, Zhang Y C 2016 IEEE Access 4 6554
Google Scholar
[18] Bhaduri S, Ghosh D 2015 Clin. EEG Neurosci. 46 218
Google Scholar
[19] Wang L, Long X, Arends J B, Aarts R M 2017 J. Neurosci. Method 290 85
Google Scholar
[20] Kong T J, Shao J, Hu J Y, Yang X, Yang S Y, Malekian R 2021 Sensors 21 1870
Google Scholar
[21] 易娜 2014 硕士学位论文 (广州: 暨南大学)
Yi N 2014 M. S. Thesis (Guangzhou: Jinan University) (in Chinese)
[22] Shi W B, Shang P J, Wang J, Lin A J 2014 Physica A 403 35
[23] Jiang W, Wei B Y, Zhan J, Xie C H, Zhou D Y 2016 Comput. Ind. Eng. 101 260
Google Scholar
[24] Azami H, Escudero J 2017 Physica A 465 261
Google Scholar
[25] Han Y F, Jin N D, Zhai L S, Ren Y Y, He Y S 2019 Physica A 518 131
Google Scholar
[26] Gao Z K, Liu M X, Dang W D, Ma C, Hou L H, Hong X L 2021 Chem. Eng. J. 407 127229
Google Scholar
[27] Tanizawa T, Nakamura T, Taya F, Small M 2018 Physica A 512 437
Google Scholar
[28] Gao Z K, Fang P C, Ding M S, Jin N D 2015 Exp. Therm Fluid Sci. 60 157
Google Scholar
[29] Bianconi G 2013 Phys. Rev. E 87 062806
Google Scholar
[30] Nicosia V, Bianconi G, Latora V, Barthelemy M 2013 Phys. Rev. Lett. 111 058701
Google Scholar
[31] Battiston F, Nicosia V, Latora V 2014 Phys. Rev. E 89 032804
Google Scholar
[32] Quesada D, Valverde G, Larrañaga P, Bielza C 2021 Eng. Appl. Artif. Intell. 103 104301
Google Scholar
[33] Lacasa L, Nicosia V, Latora V 2015 Sci. Rep. 5 15508
Google Scholar
[34] Carmona-Cabezas R, Gómez-Gómez J, Ariza-Villaverde A B, de Ravé E G, Jiménez-Hornero F J 2020 Atmos. Pollut. Res. 11 205
Google Scholar
[35] Gao Z K, Guo W, Cai Q, Ma C, Zhang Y B, Kurths J 2019 Chaos 29 073119
Google Scholar
[36] Cai Q, An J, Gao Z 2021 Brain Sci. Adv. 6 355
Google Scholar
[37] Samanta K, Chatterjee S, Bose R 2020 IEEE Sensors Lett. 4 1
Google Scholar
[38] Thygesen K, Alpert J S, White H D 2007 J. Am. Coll. Cardiol. 50 2173
Google Scholar
[39] Dohare A K, Kumar V, Kumar R 2018 Appl. Soft Comput. 64 138
Google Scholar
[40] Sharma M, San Tan R, Acharya U R 2018 Comput. Biol. Med. 102 341
Google Scholar
[41] Tripathy R K, Bhattacharyya A, Pachori R B 2019 IEEE Sensors J. 19 11437
Google Scholar
[42] Acharya U R, Fujita H, Oh S L, Hagiwara Y, Tan J H, Adam M 2017 Inf. Sci. 415 190
Google Scholar
[43] 熊鹏, 薛彦平, 刘明, 杜海曼, 王洪瑞, 刘秀玲 2020 生物医学工程学杂志 37 142
Google Scholar
Xiong P, Xue Y P, Liu M, Du H M, Wang H R, Liu X L 2020 J. Biomed. Eng. 37 142
Google Scholar
[44] Liu W H, Huang Q J, Chang S, Wang H, He J 2018 Biomed. Signal Process. Control 45 22
Google Scholar
[45] 张汉勇, 孟庆芳, 杜蕾, 刘明敏 2019 中国生物医学工程学报 38 273
Google Scholar
Zhang H Y, Meng Q F, Du L, Liu M M 2019 Chin. J. Biomed. Eng. 38 273
Google Scholar
[46] Goldberger A L, Amaral L, Glass L, Hausdorff J M, Ivanov P C, Mark R G, Mietus J E, Moody G B, Peng C K, Stanley H E 2000 Circulation 101 e215
Google Scholar
[47] Costa M, Goldberger A L, Peng C K 2002 Phys. Rev. Lett. 89 068102
Google Scholar
[48] Chang P C, Lin J J, Hsieh J C, Weng J 2012 Appl. Soft Comput. 12 3165
Google Scholar
[49] Sun L, Lu Y P, Yang K T, Li S Z 2012 IEEE Trans. Biomed. Eng. 59 3348
Google Scholar
[50] 王丹俐 2020 硕士学位论文 (杭州: 杭州电子科技大学)
Wang D L 2020 M. S. Thesis (Hangzhou: Hangzhou Danzi University) (in Chinese)
下载:
计量
- 文章访问数: 5414
- PDF下载量: 123
- 被引次数: 0
