-
量子通信是量子科学技术的一个重要研究领域, 是一种利用量子力学原理, 能够在合法各方之间安全地传输私密信息的通信方式. 基于单光子的确定性安全量子通信通常需要在发送方和接收方之间来回两次传输单光子态, 并利用局域幺正变换加载信息. 本文提出了一种单向传输单光子态的确定性安全量子通信方案. 发送方利用单光子的极化和time-bin两自由度构成的两组共轭基矢量来编码经典逻辑比特. 接收方通过设计合适的测量装置可以在发送方辅助下确定性地获取比特信息并感知窃听, 从而实现信息的确定性安全传输. 另外, 我们的协议使用线性光学元件和单光子探测器, 可以在当前的量子通信装置上实现.Quantum communication is an important branch of quantum technology. It can safely transmit private information between legitimate parties and its unconditional security is guaranteed by quantum physics. So far, deterministic secure quantum communication without entanglement usually transmits single photons in two-way quantum channels. We propose a deterministic secure quantum communication proposal, and it requires a one-way quantum channel and a classical channel. In our protocol, a sender encodes logical bits by using two conjugate bases consisting of the polarization and time-bin degrees of freedom of a photon and transmits it to a receiver over a quantum channel. Upon receiving this photon, the receiver measures it randomly in two bases and can decode the bit deterministically with the help of the sender. Any attack from eavesdroppers will be detected by the legitimate parties. Furthermore, this protocol can be implemented with linear-optic elements and single-photon detectors.
-
Keywords:
- quantum communication /
- deterministic /
- single photon /
- two degrees of freedom
[1] Wehner S, Elkouss D, Hanso R 2018 Science 362 eaam9288
Google Scholar
[2] Bennett C H, Brassard G 1984 Proceedings of the IEEE International Conference on Computers, Systems & Signal Processing Bangalore, India, December 10–12, 1984 p175
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[4] Bennett C H 1992 Phys. Rev. Lett. 68 3121
Google Scholar
[5] Guo P L, Dong C, He Y, Jing F, He W T, Ren B C, Li C Y, Deng F G 2020 Opt. Express 28 4611
Google Scholar
[6] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[7] Long G L, Liu X S 2002 Phys. Rev. A 65 032302
Google Scholar
[8] Deng F G, Long G L, Liu X S 2003 Phys. Rev. A 68 042317
Google Scholar
[9] Deng F G, Long G L 2004 Phys. Rev. A 69 052319
Google Scholar
[10] Wang C, Deng F G, Li Y S, Liu X S, Long G L 2005 Phys. Rev. A 71 044305
Google Scholar
[11] Hu J Y, Yu B, Jing M Y, Xiao L T, Jia S T, Qin G Q, Long G L 2016 Light-Sci. Appl. 5 e16144
Google Scholar
[12] Zhang W, Ding D S, Sheng Y B, Zhou L, Shi B S, Guo G C 2017 Phys. Rev. Lett. 118 220501
Google Scholar
[13] Li T, Gao Z K, Li Z H 2020 EPL 131 60001
Google Scholar
[14] Gao Z K, Li T, Li Z H 2019 EPL 125 40004
Google Scholar
[15] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1829
Google Scholar
[16] Karlsson A, Koashi M, Imoto N 1999 Phys Rev. A 59 162
Google Scholar
[17] 邓富国, 李熙涵, 李涛 2018 67 130301
Google Scholar
Deng F G, Li X H, Li T 2018 Acta Phys. Sin. 67 130301
Google Scholar
[18] Gao Z K, Li T, Li Z H 2020 Sci. Chin. -Phys. Mech. Astron. 63 120311
Google Scholar
[19] Shimizu K, Imoto Y 1999 Phys. Rev. A 60 157
Google Scholar
[20] Boström K, Felbinger T 2002 Phys. Rev. Lett. 89 187902
Google Scholar
[21] Cai Q Y, Li B W 2004 Chin. Phys. Lett. 21 601
Google Scholar
[22] Wójcik A 2003 Phys. Rev. Lett. 90 157901
Google Scholar
[23] Long G L, Deng F G, Wang C, Li X H, Wen K, Wang W Y 2007 Front. Phys. Chin. 2 251
[24] Li T, Long G L 2020 New J. Phys. 22 063017
Google Scholar
[25] 王明宇, 王馨德, 阮东, 龙桂鲁 2021 70 190301
Google Scholar
Wang M Y, Wang X D, Ruan D, Long G L 2021 Acta Phys. Sin. 70 190301
Google Scholar
[26] 窦建鹏, 李航, 庞晓玲, 张超妮, 杨天怀, 金贤敏 2019 68 030307
Google Scholar
Dou J P, Li H, Pang X L, Zhang C N, Yang T H, Jin X M 2019 Acta Phys. Sin. 68 030307
Google Scholar
[27] Lucamarini M, Mancini S 2005 Phys. Rev. Lett. 94 140501
Google Scholar
[28] Cai Q Y, Li B W 2004 Phys. Rev. A 69 054301
Google Scholar
[29] Gao T, Yan F L, Wang Z X 2005 J. Phys. A:Gen. Phys. 38 5761
Google Scholar
[30] Elsayed T A 2020 Phys. Scr. 96 025101
Google Scholar
[31] Jeong Y C, Ji S W, Hong C, Park H S, Jang J 2020 Entropy 22 1268
Google Scholar
[32] Jiang D, Chen Y, Gu X, Xie L, Chen L 2017 Sci. Rep. 7 44934
Google Scholar
[33] Wang J D, Wei Z J, Zhang H, Qin X J, Liu X B, Zhang Z M, Liao C J, Liu S H 2010 J. Phys. B:At. Mol. Opt. Phys. 43 095504
Google Scholar
[34] Lu H, Fung C, Ma X, Cai QY 2011 Phys. Rev. A 84 042344
Google Scholar
[35] Beaudry N J, Lucamarini M, Mancini S, Renner R 2013 Phys. Rev. A 88 062302
Google Scholar
[36] Henao C I, Serra R M 2015 Phys. Rev. A 92 052317
Google Scholar
[37] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[38] Meyer-Scott E, Silberhorn C, Migdall A 2020 Rev. Sci. Instrum. 91 041101
Google Scholar
[39] Kaneda F, Kwiat P G 2019 Sci. Adv. 5 eaaw8586
Google Scholar
[40] Hall M A, Altepeter J B, Kumar P 2011 Phys. Rev. Lett. 106 053901
Google Scholar
[41] Cao Y, Liang H, Yin J, Yong H L, Zhou F, Wu Y P, Ren J G, Li Y H, Pan G S, Yang T, Ma X, Peng C Z, Pan J W 2013 Opt. Express 21 27260
Google Scholar
[42] Wang H, Li W, Jiang X, He Y M, Li Y H, Ding X, Chen M C, Qin J, Peng C Z, Schneider C, Kamp M, Zhang W J, Li H, You L X, Wang Z, Dowling J P, Höfling S, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 230502
Google Scholar
[43] Deng F G, Ren B C, Li X H 2017 Sci. Bull. 62 46
Google Scholar
[44] Erhard M, Krenn M, Zeilinger A 2020 Nat. Rev. Phys. 2 365
Google Scholar
[45] 郭邦红, 杨理, 向憧, 关翀, 吴令安, 刘颂豪 2013 62 130303
Google Scholar
Guo B H, Yang L, Xiang C, Guan C, Wu L A, Liu S H 2013 Acta Phys. Sin. 62 130303
Google Scholar
-
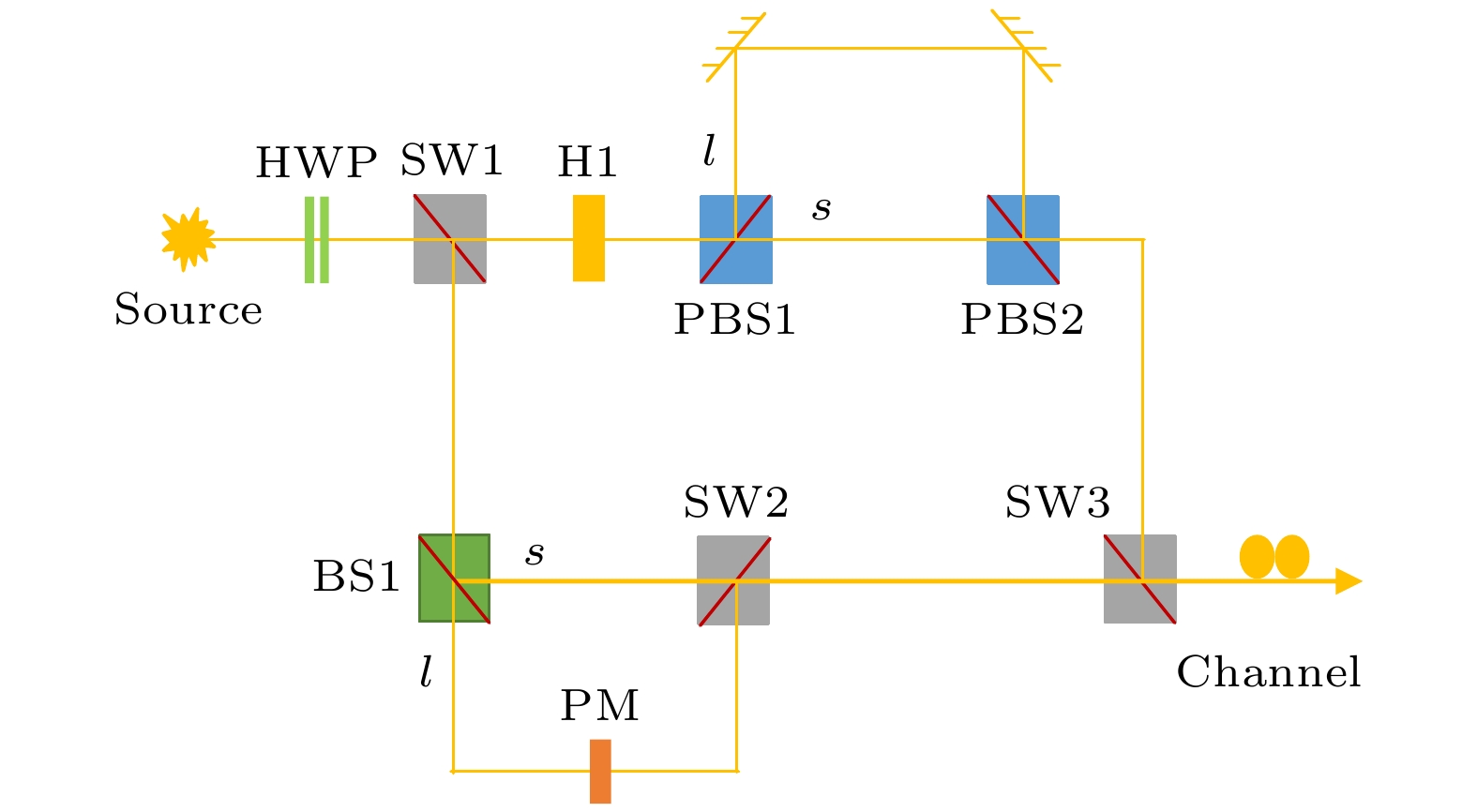
图 1 量子逻辑比特制备示意图. HWP: 半波片, 光轴与水平方向的夹角
$ \theta = 0 $ , 穿过它的光子极化状态保持不变,$ \theta = $ $ {\text{π}}/4 $ , 对穿过它的光子执行以下操作:$\left| H \right\rangle \to \left| V \right\rangle, \;\left| V \right\rangle \to $ $ \left| H \right\rangle$ ;$ {\text{SW}}i \left( {i = 1, \;2, \;3} \right) $ : 开关, 处于T状态时, 光子直接透过器件, 处于R状态时, 光子将被反射; H1: 光轴角度为$ {\text{π}}/8 $ 的半波片, 对经过的光子进行以下操作:$\left| H \right\rangle \to \left| + \right\rangle, \left| V \right\rangle \to $ $ \left| - \right\rangle$ ;$ {{{\rm{PBS1}}, \;{\rm{PBS2}}}} $ : 极化分束器, 将透射$ \left| + \right\rangle $ 光子, 反射$ \left| - \right\rangle $ 光子; PM: 相位调制器, 产生$ \varphi = 0 $ 或$ \varphi = {\text{π}} $ 的相位差; BS1: 50∶50分束器Fig. 1. Schematics of quantum logic qubit preparation. HWP: half wave plate with its axis aligned at
$ \theta = 0 $ ($\theta = $ $ {\text{π}}/4$ ) completes the transformations$ |H\rangle \to |H\rangle, |V\rangle \to |V\rangle $ ($ |H\rangle \to |V\rangle, |V\rangle \to |H\rangle $ );$ {\text{SW}}i \left( {i = 1, \;2, \;3} \right) $ : optical switch transmits (reflects) photons when it is set to modeT(R); H1 with its axis aligned at$ {\text{π}}/8 $ completes the following transmissions:$ |H\rangle \to |+\rangle, |V\rangle \to |-\rangle $ ;$ {\text{PBS1}}\;{\text{and}}\;{\text{PBS2}} $ : polarizing beam splitters that transmit (reflect) photons in state$ \left| + \right\rangle $ ($ \left| - \right\rangle $ ); PM: a phase modulator which introduces a phase$\varphi =0$ or$\varphi ={{ {\text{π}} }}$ ; BS1 : 50∶50 beam splitter.
图 2 量子逻辑比特解码示意图. BS2: 50:50分束器; SW4: 开关, 透射
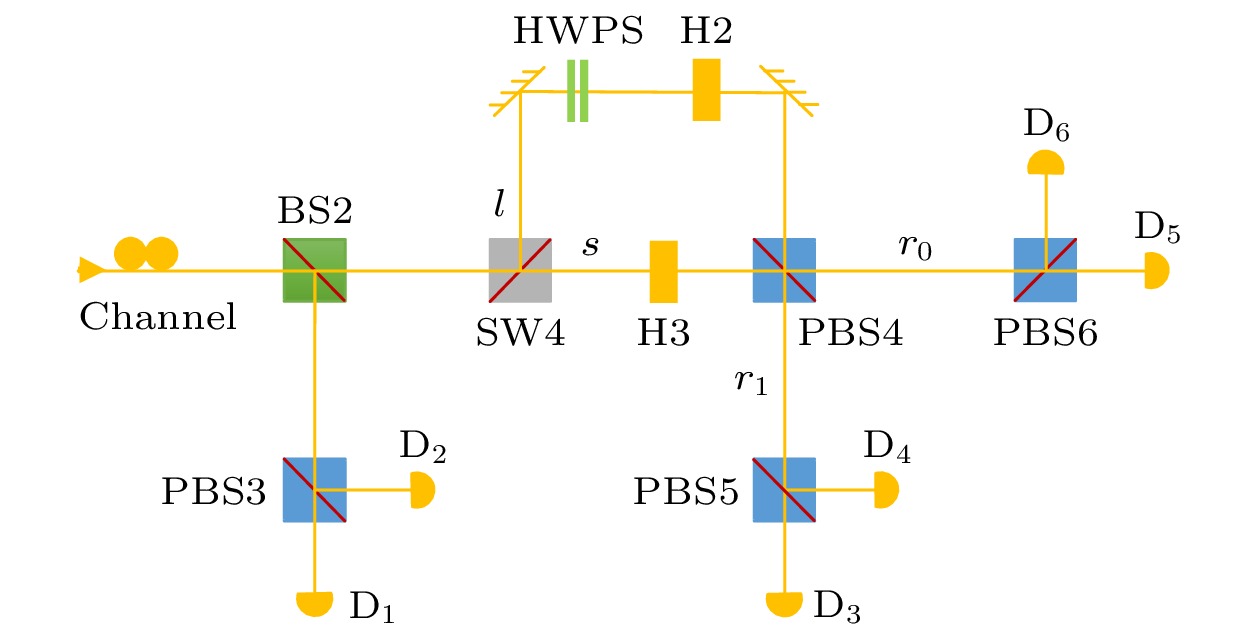
$ {t_1} $ 模式的光子, 反射$ {t_0} $ 模式的光子;${\rm{PBS3}}, \; {\rm{PBS4}}, $ $ \;{\rm{PBS5}}, \;{\rm{PBS6}}$ : 极化分束器($ {{{\rm{PBS3}}, \;{\rm{PBS4}}}} $ 透射$ \left| H \right\rangle $ 光子, 反射$ \left| V \right\rangle $ 光子,$ {{{\rm{PBS5}}, \;{\rm{PBS6}}}} $ 透射$ \left| {{ + }} \right\rangle $ 光子, 反射$ \left| - \right\rangle $ 光子); HWPS: 半波片, 将对光子进行如下操作:$ \left| H \right\rangle \to \left| V \right\rangle $ ,$ \left| V \right\rangle \to - \left| H \right\rangle $ ,$ \left| + \right\rangle \to \left| - \right\rangle $ ,$ \left| - \right\rangle \to - \left| + \right\rangle $ ;$ {\text{H2}}, \;{\rm{H3}} $ : 光轴角度为$ {{{\text{π}} /8}} $ 的半波片, 对经过的光子进行以下操作:$ \left| H \right\rangle \to \left| + \right\rangle, \;\left| V \right\rangle \to \left| - \right\rangle $ ;${{\rm{D}}_i}(i = 1, \cdots, 6)$ : 单光子探测器.Fig. 2. Schematics of quantum logic qubit measurement. BS2: 50:50 beam splitter; SW4: switch transmits photons in
$ {t_1} $ mode and reflects photons in$ {t_0} $ mode;${\text{PBS3}}, \;{\text{PBS4}}, $ $ \; {\text{PBS5}} \;{\text{and}}\;{\text{PBS6}}$ : polarizing beam splitters. PBS3 and PBS4 transmit (reflect) photons in state$ \left| H \right\rangle $ ($ \left| V \right\rangle $ ).$ {\text{PBS5}}\;{\text{and}}\;{\text{PBS6}} $ transmit (reflect) photons in state$ \left| + \right\rangle $ ($ \left| - \right\rangle $ ). HWPS: half wave plate transforms the polarization of a photon passing it as follows:$ |H\rangle \to |V\rangle, |V\rangle \to -|H\rangle$ ,$ |+\rangle \to |-\rangle, |-\rangle \to -|+\rangle $ .$ {\text{H2}}\;{\text{and}}\;{\text{H3}} $ with their axes aligned at$ {\text{π}}/8 $ complete the following transmissions:$ |H\rangle \to |+\rangle, |V\rangle \to |-\rangle $ .${{\rm{D}}_i}\;(i = 1,\cdots, 6)$ : single-photon detectors.表 1 四种单光子态对应的探测器响应情况
Table 1. Clicks of detectors for four different single-photon states.
量子态 下路径 右路径 $ \left| {H{t_{{ + }}}} \right\rangle $ $ {D_1}\left( {{t_0}} \right)/{D_1}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right)/{D_6}\left( {{t_1}} \right) $ $ \left| {V{t_ - }} \right\rangle $ $ {D_2}\left( {{t_0}} \right)/{D_2}\left( {{t_1}} \right) $ $ {D_4}\left( {{t_1}} \right)/{D_5}\left( {{t_1}} \right) $ $ \left| { + {t_0}} \right\rangle $ $ {D_1}\left( {{t_0}} \right)/{D_2}\left( {{t_0}} \right) $ $ {D_5}\left( {{t_1}} \right)/{D_6}\left( {{t_1}} \right) $ $ \left| { - {t_0}} \right\rangle $ $ {D_1}\left( {{t_1}} \right)/{D_2}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right)/{D_4}\left( {{t_1}} \right) $ 
下载: 导出CSV
表 2 Bob探测器响应的可能情况
Table 2. Click probability of Bob’s detectors.
响应 $ {D_1}\left( {{t_0}} \right) $ $ {D_1}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right) $ $ {D_6}\left( {{t_1}} \right) $ 概率 $ {1}/{4} $ $ {1}/{4} $ $ {1}/{4} $ $ {1}/{4} $
下载: 导出CSV
表 3 Eve制备的光子态及概率
Table 3. State and probability of photons prepared by Eve.
光子态 $ \left| {H{t_ + }} \right\rangle $ $ \left| { + {t_0}} \right\rangle $ $ \left| { - {t_1}} \right\rangle $ 概率 $ {1}/{2} $ $ {1}/{4} $ $ {1}/{4} $
下载: 导出CSV
表 4 Eve制备的光子引起的探测器响应的可能情况
Table 4. Click and probability of detectors triggered by Eve’s photon.
探测器响应 $ {D_1}\left( {{t_0}} \right) $ $ {D_1}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right) $ $ {D_6}\left( {{t_1}} \right) $ $ {D_2}\left( {{t_0}} \right) $ $ {D_2}\left( {{t_1}} \right) $ $ {D_4}\left( {{t_1}} \right) $ $ {D_5}\left( {{t_1}} \right) $ 概率 $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $
下载: 导出CSV
表 5 Bob探测器响应的可能情况
Table 5. Click probability of Bob’s detectors.
响应 $ {D_2}\left( {{t_0}} \right) $ $ {D_2}\left( {{t_1}} \right) $ $ {D_4}\left( {{t_1}} \right) $ $ {D_5}\left( {{t_1}} \right) $ 概率 $1/{4}$ $1/{4}$ $1/{4}$ $1/{4}$
下载: 导出CSV
表 6 Eve制备的光子态及概率
Table 6. State and probability of photons prepared by Eve.
光子态 $ \left| {V{t_ - }} \right\rangle $ $ \left| { + {t_0}} \right\rangle $ $ \left| { - {t_1}} \right\rangle $ 概率 $1/{2}$ $1/{4}$ $1/{4}$
下载: 导出CSV
表 7 Eve制备的光子引起的探测器响应的可能情况
Table 7. Click and probability of detectors triggered by Eve’s photon.
探测器响应 $ {D_2}\left( {{t_0}} \right) $ $ {D_2}\left( {{t_1}} \right) $ $ {D_4}\left( {{t_1}} \right) $ $ {D_5}\left( {{t_1}} \right) $ $ {D_1}\left( {{t_0}} \right) $ $ {D_1}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right) $ $ {D_6}\left( {{t_1}} \right) $ 概率 $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $
下载: 导出CSV
表 8 Bob探测器响应的可能情况
Table 8. Click probability of Bob’s detectors.
响应 $ {D_1}\left( {{t_0}} \right) $ $ {D_2}\left( {{t_0}} \right) $ $ {D_5}\left( {{t_1}} \right) $ $ {D_6}\left( {{t_1}} \right) $ 概率 ${1}/{4}$ ${1}/{4}$ ${1}/{4}$ ${1}/{4}$
下载: 导出CSV
表 9 Eve制备的光子态及概率
Table 9. State and probability of photons prepared by Eve.
光子态 $ \left| { + {t_0}} \right\rangle $ $ \left| {H{t_ + }} \right\rangle $ $ \left| {V{t_ - }} \right\rangle $ 概率 ${1}/{2}$ ${1}/{4}$ ${1}/{4}$
下载: 导出CSV
表 10 Eve制备的光子引起的探测器响应的可能情况
Table 10. Click and probability of detectors triggered by Eve’s photon.
探测器响应 $ {D_1}\left( {{t_0}} \right) $ $ {D_2}\left( {{t_0}} \right) $ $ {D_5}\left( {{t_1}} \right) $ $ {D_6}\left( {{t_1}} \right) $ $ {D_1}\left( {{t_1}} \right) $ $ {D_2}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right) $ $ {D_4}\left( {{t_1}} \right) $ 概率 $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $
下载: 导出CSV
表 11 Bob探测器响应的可能情况
Table 11. Click probability of Bob’s detectors.
响应 $ {D_1}\left( {{t_1}} \right) $ $ {D_2}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right) $ $ {D_4}\left( {{t_1}} \right) $ 概率 $1/{4}$ $1/{4}$ $1/{4}$ $1/{4}$
下载: 导出CSV
表 12 Eve制备的光子态及概率
Table 12. State and probability of photons prepared by Eve.
光子态 $ \left| { - {t_1}} \right\rangle $ $ \left| {H{t_ + }} \right\rangle $ $ \left| {V{t_ - }} \right\rangle $ 概率 $1/{2}$ $1/{4}$ $1/{4}$
下载: 导出CSV
表 13 Eve制备的光子引起的探测器响应的可能情况
Table 13. Click and probability of detectors triggered by Eve’s photon.
探测器响应 $ {D_1}\left( {{t_1}} \right) $ $ {D_2}\left( {{t_1}} \right) $ $ {D_3}\left( {{t_1}} \right) $ $ {D_4}\left( {{t_1}} \right) $ $ {D_1}\left( {{t_0}} \right) $ $ {D_2}\left( {{t_0}} \right) $ $ {D_5}\left( {{t_1}} \right) $ $ {D_6}\left( {{t_1}} \right) $ 概率 $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {3}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $ $ {1}/{{16}} $
下载: 导出CSV
-
[1] Wehner S, Elkouss D, Hanso R 2018 Science 362 eaam9288
Google Scholar
[2] Bennett C H, Brassard G 1984 Proceedings of the IEEE International Conference on Computers, Systems & Signal Processing Bangalore, India, December 10–12, 1984 p175
[3] Ekert A K 1991 Phys. Rev. Lett. 67 661
Google Scholar
[4] Bennett C H 1992 Phys. Rev. Lett. 68 3121
Google Scholar
[5] Guo P L, Dong C, He Y, Jing F, He W T, Ren B C, Li C Y, Deng F G 2020 Opt. Express 28 4611
Google Scholar
[6] Gisin N, Ribordy G, Tittel W, Zbinden H 2002 Rev. Mod. Phys. 74 145
Google Scholar
[7] Long G L, Liu X S 2002 Phys. Rev. A 65 032302
Google Scholar
[8] Deng F G, Long G L, Liu X S 2003 Phys. Rev. A 68 042317
Google Scholar
[9] Deng F G, Long G L 2004 Phys. Rev. A 69 052319
Google Scholar
[10] Wang C, Deng F G, Li Y S, Liu X S, Long G L 2005 Phys. Rev. A 71 044305
Google Scholar
[11] Hu J Y, Yu B, Jing M Y, Xiao L T, Jia S T, Qin G Q, Long G L 2016 Light-Sci. Appl. 5 e16144
Google Scholar
[12] Zhang W, Ding D S, Sheng Y B, Zhou L, Shi B S, Guo G C 2017 Phys. Rev. Lett. 118 220501
Google Scholar
[13] Li T, Gao Z K, Li Z H 2020 EPL 131 60001
Google Scholar
[14] Gao Z K, Li T, Li Z H 2019 EPL 125 40004
Google Scholar
[15] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1829
Google Scholar
[16] Karlsson A, Koashi M, Imoto N 1999 Phys Rev. A 59 162
Google Scholar
[17] 邓富国, 李熙涵, 李涛 2018 67 130301
Google Scholar
Deng F G, Li X H, Li T 2018 Acta Phys. Sin. 67 130301
Google Scholar
[18] Gao Z K, Li T, Li Z H 2020 Sci. Chin. -Phys. Mech. Astron. 63 120311
Google Scholar
[19] Shimizu K, Imoto Y 1999 Phys. Rev. A 60 157
Google Scholar
[20] Boström K, Felbinger T 2002 Phys. Rev. Lett. 89 187902
Google Scholar
[21] Cai Q Y, Li B W 2004 Chin. Phys. Lett. 21 601
Google Scholar
[22] Wójcik A 2003 Phys. Rev. Lett. 90 157901
Google Scholar
[23] Long G L, Deng F G, Wang C, Li X H, Wen K, Wang W Y 2007 Front. Phys. Chin. 2 251
[24] Li T, Long G L 2020 New J. Phys. 22 063017
Google Scholar
[25] 王明宇, 王馨德, 阮东, 龙桂鲁 2021 70 190301
Google Scholar
Wang M Y, Wang X D, Ruan D, Long G L 2021 Acta Phys. Sin. 70 190301
Google Scholar
[26] 窦建鹏, 李航, 庞晓玲, 张超妮, 杨天怀, 金贤敏 2019 68 030307
Google Scholar
Dou J P, Li H, Pang X L, Zhang C N, Yang T H, Jin X M 2019 Acta Phys. Sin. 68 030307
Google Scholar
[27] Lucamarini M, Mancini S 2005 Phys. Rev. Lett. 94 140501
Google Scholar
[28] Cai Q Y, Li B W 2004 Phys. Rev. A 69 054301
Google Scholar
[29] Gao T, Yan F L, Wang Z X 2005 J. Phys. A:Gen. Phys. 38 5761
Google Scholar
[30] Elsayed T A 2020 Phys. Scr. 96 025101
Google Scholar
[31] Jeong Y C, Ji S W, Hong C, Park H S, Jang J 2020 Entropy 22 1268
Google Scholar
[32] Jiang D, Chen Y, Gu X, Xie L, Chen L 2017 Sci. Rep. 7 44934
Google Scholar
[33] Wang J D, Wei Z J, Zhang H, Qin X J, Liu X B, Zhang Z M, Liao C J, Liu S H 2010 J. Phys. B:At. Mol. Opt. Phys. 43 095504
Google Scholar
[34] Lu H, Fung C, Ma X, Cai QY 2011 Phys. Rev. A 84 042344
Google Scholar
[35] Beaudry N J, Lucamarini M, Mancini S, Renner R 2013 Phys. Rev. A 88 062302
Google Scholar
[36] Henao C I, Serra R M 2015 Phys. Rev. A 92 052317
Google Scholar
[37] Xu F, Ma X, Zhang Q, Lo H K, Pan J W 2020 Rev. Mod. Phys. 92 025002
Google Scholar
[38] Meyer-Scott E, Silberhorn C, Migdall A 2020 Rev. Sci. Instrum. 91 041101
Google Scholar
[39] Kaneda F, Kwiat P G 2019 Sci. Adv. 5 eaaw8586
Google Scholar
[40] Hall M A, Altepeter J B, Kumar P 2011 Phys. Rev. Lett. 106 053901
Google Scholar
[41] Cao Y, Liang H, Yin J, Yong H L, Zhou F, Wu Y P, Ren J G, Li Y H, Pan G S, Yang T, Ma X, Peng C Z, Pan J W 2013 Opt. Express 21 27260
Google Scholar
[42] Wang H, Li W, Jiang X, He Y M, Li Y H, Ding X, Chen M C, Qin J, Peng C Z, Schneider C, Kamp M, Zhang W J, Li H, You L X, Wang Z, Dowling J P, Höfling S, Lu C Y, Pan J W 2018 Phys. Rev. Lett. 120 230502
Google Scholar
[43] Deng F G, Ren B C, Li X H 2017 Sci. Bull. 62 46
Google Scholar
[44] Erhard M, Krenn M, Zeilinger A 2020 Nat. Rev. Phys. 2 365
Google Scholar
[45] 郭邦红, 杨理, 向憧, 关翀, 吴令安, 刘颂豪 2013 62 130303
Google Scholar
Guo B H, Yang L, Xiang C, Guan C, Wu L A, Liu S H 2013 Acta Phys. Sin. 62 130303
Google Scholar
下载:
计量
- 文章访问数: 5824
- PDF下载量: 171
- 被引次数: 0
