-
本文研究了一个周期驱动的非宇称-时间对称二能级量子系统的非厄米动力学. 通过经典相空间分析方法,解出了该非厄米系统的Floquet态和准能谱, 并解析构造了由该非厄米哈密顿量支配下的量子态的非幺正时间演化算符, 给出了不同参数区域的量子态演化. 本文数值和分析证明, 该非宇称-时间对称二能级Floquet系统, 类似于宇称-时间对称系统, 存在一个准能谱从实数谱到复数谱的相变. 本文还揭示了在量子态的动态演化中存在一种准宇称-时间对称动力学, 即, 该系统的粒子布居概率演化完全满足时间空间对称(宇称-时间对称), 但是由于相位演化违反了宇称-时间对称性的要求, 因此包含相位信息的量子态演化不满足时间空间对称(宇称-时间对称). 这些结果加深了对非厄米物理的理解, 拓展和推广了传统的宇称-时间对称概念.
In recent years, there have been intensive studies of non-Hermitian physics and parity–time (PT) symmetry due to their fundamental importance in theory and outstanding applications. A distinctive character in PT-symmetric system is phase transition (spontaneous PT-symmetry breaking), i.e. an all-real energy spectrum changes into an all-complex one when the non-Hermitian parameter exceeds a certain threshold. However, the conditions for PT-symmetric system with real energy spectrum to occur are rather restrictive. The generalization of PT-symmetric potentials to wider classes of non-PT-symmetric complex potentials with all-real energy spectra is a currently important endeavor. A simple PT-symmetric two-level Floquet quantum system is now being actively explored, because it holds potential for the realization of non-unitary single-qubit quantum gate. However, studies of the evolution dynamics of non-PT-symmetric two-level non-Hermitian Floquet quantum system are still relatively rare. In this paper, we investigate the non-Hermitian physics of a periodically driven non-PT-symmetric two-level quantum system. By phase-space analysis, we find that there exist so-called pseudo fixed points in phase space representing the Floquet solutions with fixed population difference and a time-dependent relative phase between the two levels. According to these pseudo fixed points, we analytically construct a non-unitary evolution operator and then explore the dynamic behaviors of the non-PT-symmetric two-level quantum system in different parameter regions. We confirm both analytically and numerically that the two-level non-Hermitian Floquet quantum system, although it is non-parity-time-symmetric, still features a phase transition with the quasienergy spectrum changing from all-real to all-complex energy spectrum, just like the PT symmetric system. Furthermore, we reveal that a novel phenomenon called quasi-PT symmetric dynamics occurs in the time evolution process. The quasi-PT symmetric dynamics is so named in our paper, in the sense that the time-evolution of population probabilities in the non-PT-symmetric two-level system satisfies fully the time-space symmetry (PT symmetry), while time-evolution of the quantum state (containing the phase) does not meet such a PT symmetry, due to the fact that time-evolution of the phases of the probability amplitudes on the two levels violates the requirement for the PT symmetry. -
Keywords:
- parity-time symmetry /
- periodically driven two-level systems /
- non-Hermitian physics /
- dynamical evolution
[1] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[2] Guo A, Salamo G J, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, Siviloglou G A, Christodoulides D N 2009 Phys. Rev. Lett. 103 093902
Google Scholar
[3] Rüter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192
Google Scholar
[4] Doppler J, Mailybaev A A, Böhm J, Kuhl U, Girschik A, Libisch F, Milburn T J, Rabl P, Moiseyev N, Rotter S 2016 Nature 537 76
Google Scholar
[5] Peng B, Özdemir Ş K, Lei F, Monifi F, Gianfreda M, Long G Lu, Fan S, Nori F, Bender C M, Yang L 2014 Nat. Phys. 10 394
Google Scholar
[6] Chang L, Jiang X, Hua S, Yang C, Wen J, Jiang L, Li G, Wang G, Xiao M 2014 Nat. Photonics 8 524
Google Scholar
[7] Bender C M, Berntson B K, Parker D, Samuel E 2013 Am. J. Phys. 81 173
Google Scholar
[8] Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101(R)
[9] Fleury R, Sounas D, Alù A 2015 Nat. Com. 6 5905
[10] Liu T, Zhu X, Chen F, Liang S, Zhu J 2018 Phys. Rev. Lett. 120 124502
Google Scholar
[11] Tang J S, Wang Y T, Yu S, He D Y, Xu J S, Liu B H, Chen G, Sun Y N, Sun K, Han Y J, Li C F, Guo G C 2016 Nat. Photonics 10 642
Google Scholar
[12] Xiao L, Zhan X, Bian Z H, Wang K K, Zhang X, Wang X P, Li J, Mochizuki K, Kim D, Kawakami N, Yi W, Obuse H, Sanders B C, Xue P 2017 Nat. Phys. 13 1117
Google Scholar
[13] Gao W C, Zheng C, Liu L, Wang T J, Wang C 2021 Optics Express 29 517
Google Scholar
[14] Li J, Harter A K, Liu J, Melo L de, Joglekar Y N, Luo L 2019 Nat. Com. 10 855
Google Scholar
[15] Zhang D K, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Com. 8 1368
Google Scholar
[16] 沈瑞昌, 张国强, 王逸璞, 游建强 2019 68 230305
Google Scholar
Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305
Google Scholar
[17] Wu Y, Liu W, Geng J, Song X, Ye X, Duan C K, Rong X, Dun J 2019 Science 364 878
Google Scholar
[18] Zheng C, Hao L, Long G L 2013 Philos. Trans. R. Soc. A 371 20120053
Google Scholar
[19] Wen J, Zheng C, Kong X, Wei S, Xin T, Long G 2019 Phys. Rev. A 99 062122
Google Scholar
[20] Wang W C, Zhou Y L, Zhang H L, Zhang J, Zhang M C, Xie Y, Wu C W, Chen T, Ou B Q, Wu W, Jing H, Chen P X 2021 Phys. Rev. A 103 L020201
Google Scholar
[21] Ding L, Shi K, Zhang Q, Shen D, Zhang X, Zhang W 2021 Phys. Rev. Lett. 126 083604
Google Scholar
[22] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[23] Regensburger A, Bersch C, Miri M A, Onishchukov G, Christodoulides D N, Peschel U 2012 Nature 488 167
Google Scholar
[24] Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108
Google Scholar
[25] Sun Y, Tan W, Li H Q, Li J, Chen H 2014 Phys. Rev. Lett. 112 143903
Google Scholar
[26] Jin L, Song Z 2018 Phys. Rev. Lett. 121 073901
Google Scholar
[27] Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature 548 187
Google Scholar
[28] Yu S, Meng Y, Tang J, Xu X, Wang Y, Yin P, Ke Z, Liu W, Li Z, Yang Y, Chen G, Han Y, Li C, Guo G 2020 Phys. Rev. Lett. 125 240506
Google Scholar
[29] Feng L, Wong Z J, Ma R M, Wang Y, Zhang X 2014 Science 346 972
Google Scholar
[30] Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975
Google Scholar
[31] Assawaworrarit S, Yu X, Fan S 2017 Nature 546 387
Google Scholar
[32] Xu H, Mason D, Jiang L, Harris J G E 2016 Nature 537 80
Google Scholar
[33] Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401
[34] Bender C M 2007 Rep. Prog. Phys. 70 947
Google Scholar
[35] Mostafazadeh A 2002 J. Math. Phys. 43 205
Google Scholar
[36] Mostafazadeh A 2002 J. Math. Phys. 43 2814
Google Scholar
[37] 黄永峰, 曹怀信, 王文华 2020 69 030301
Google Scholar
Huang Y F, Cao H X, Wang W H 2020 Acta Phys. Sin. 69 030301
Google Scholar
[38] Nixon S, Yang J 2016 Phys. Rev. A 93 031802(R)
[39] Hang C, Gabadadze G, Huang G 2017 Phys. Rev. A 95 023833
Google Scholar
[40] Pan J, Zhou L 2020 Phys. Rev. B 102 094305
Google Scholar
[41] Luo X B, Huang J H, Zhong H H, Qin X Z, Xie Q T, Kivshar Y S, Lee C H 2013 Phys. Rev. Lett. 110 243902
Google Scholar
[42] Chitsazi M, Li H, Ellis F M, Kottos T 2017 Phys. Rev. Lett. 119 093901
Google Scholar
[43] Duan L, Wang Y, Chen Q 2020 Chin. Phys. Lett. 37 081101
Google Scholar
[44] Xie Q, Rong S, Liu X 2018 Phys. Rev. A 98 052122
Google Scholar
[45] Koutserimpas T T, Alù A, Fleury R 2018 Phys. Rev. A 97 013839
Google Scholar
[46] Luo X B, Wu D, Luo S, Guo Y, Yu X, Hu Q 2014 J. Phys. A:Math. Theor 47 345301
Google Scholar
[47] Yang B, Luo X B, Hu Q, Yu X 2016 Phys. Rev. A 94 043828
Google Scholar
[48] Luo X B, Yang B, Zhang X F, Li L, Yu X 2017 Phys. Rev. A 95 052128
Google Scholar
[49] Cui B, Wang L C, Yi X X 2010 Phys. Rev. A 82 062105
[50] Liu Z P, Zhang J, Özdemir Ş K, Peng B, Jing H, Lu X Y, Li C W, Yang L, Nori F, Liu Y 2016 Phys. Rev. Lett. 117 110802
Google Scholar
[51] Bender C M, Brody D C, Jones H F, Meister B K 2007 Phys. Rev. Lett. 98 040403
Google Scholar
-
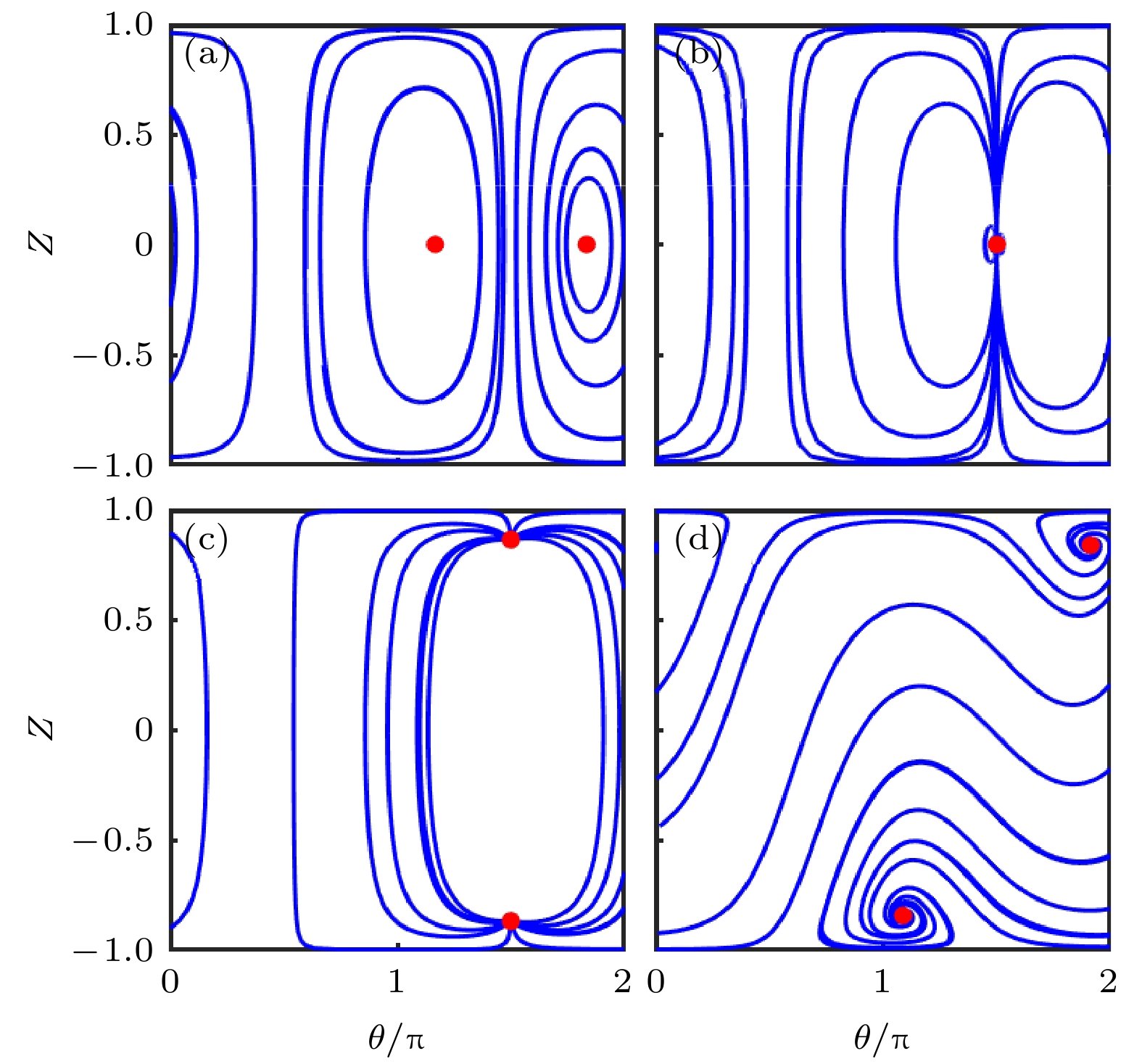
图 1 不同系统参数下的相空间轨道(
$ \omega = 2, \nu = 1 $ ) (a)${\gamma _0} = $ $ 1,\; {\gamma _1} = 0.5$ ; (b)${\gamma _0} = 1,\; {\gamma _1} = 1$ ; (c)${\gamma _0} = 1, \;{\gamma _1} = 2$ ; (d)${\gamma _0} = 2,\; {\gamma _1} = 0.5$ Fig. 1. Phase-space trajectories with different system parameters(
$ \omega = 2, \nu = 1 $ ): (a)${\gamma _0} = 1,\; {\gamma _1} = 0.5$ ; (b)${\gamma _0} = 1, $ $ \;{\gamma _1} = 1$ ; (c)${\gamma _0} = 1, \;{\gamma _1} = 2$ ; (d)${\gamma _0} = 2,\; {\gamma _1} = 0.5$ .
图 2 非厄米系统(1)在周期驱动(7)作用下共振(
$2{\gamma _0} = $ $ \omega$ )情况时的准能谱的实部(a)和虚部(b)随参数${\gamma _1}/\nu $ 的关系. 红线和蓝线代表直接对角化一个驱动周期的时间演化算符的数值结果, 圆圈代表经典相图中赝定点对应的准能量解析结果. 参数取为${\gamma _0} = 1,\; \omega = 2$ Fig. 2. Real (a) and imaginary (b) parts of the quasienergies as a function of
${\gamma _1}/\nu $ for the non-Hermitian system (1) subject to a periodic modulation (7) in the resonant ($2{\gamma _0} = $ $ \omega$ ) case. The red and blue lines denote the numerical results of quasienergies computed through direct diagonalization of the time-evolution operator over one period of the driving, while the circles denote exact analytical results of quasienergies corresponding to the pseudo fixed points in phase space. The system parameters are set as${\gamma _0} = 1, \;\omega = 2$ 
图 3 在共振情况下的系统动力学(
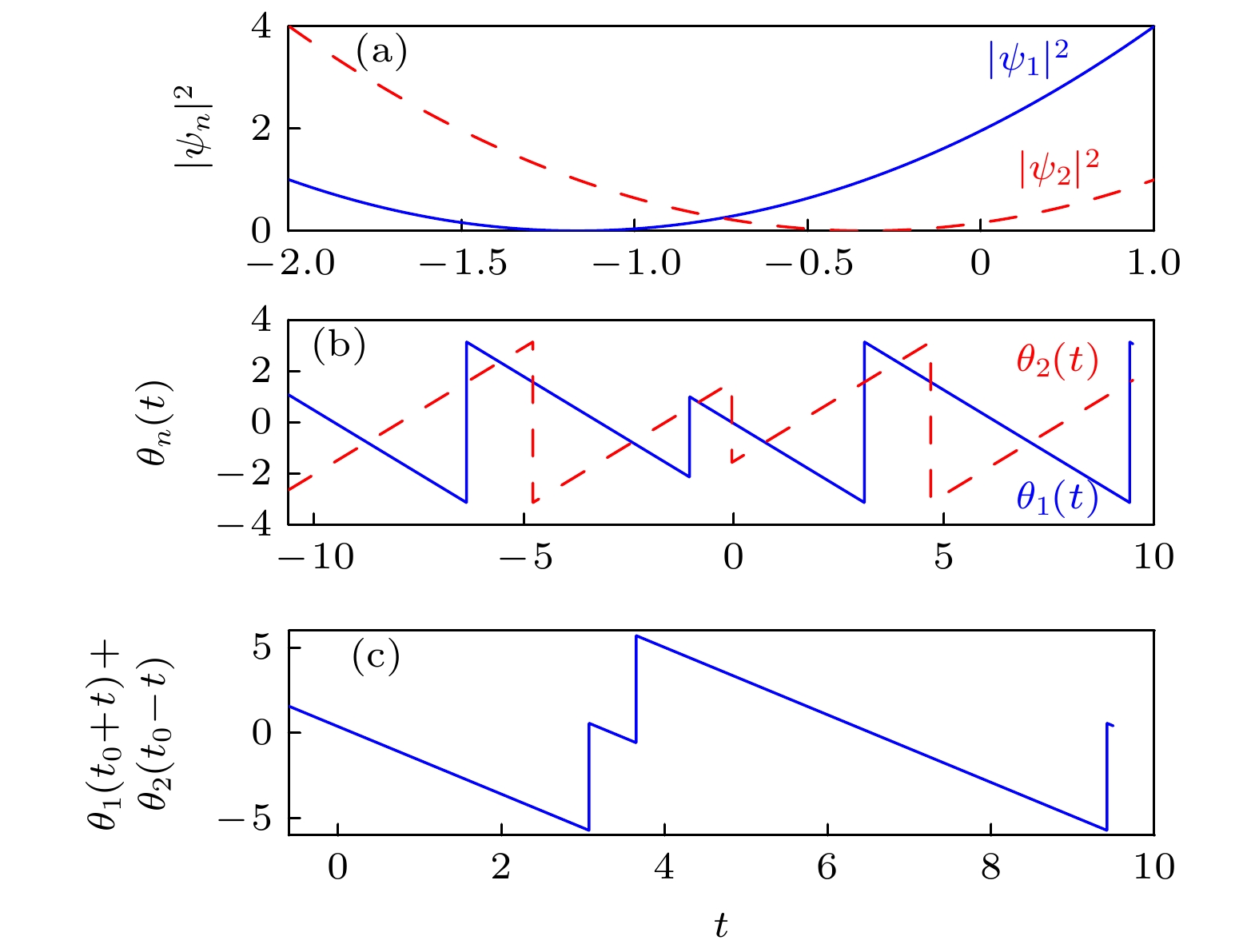
$\tfrac{{{\gamma _1}}}{\nu } < 1$ ) (a) 两能级上的占有概率${\left| {{\psi _n}} \right|^2}$ ($n = 1, 2$ )随时间演化; (b)相位${\theta _n}$ ($n = $ $ 1, 2$ )随时间演化; (c)以$ {t_0} = - 0.605 $ 为时间反演点的$ {\theta _1}({t_0} + t) + {\theta _2}({t_0} - t) $ 演化. 系统参数取为${\gamma _0} = 1, \;{\gamma _1} = 0.5,\; $ $ \omega = 2,\; \nu = 1$ 初态为${\psi _1}(0) = 1, {\psi _2}(0) = 0$ Fig. 3. System dynamics for the resonance case with the non-Hermitian parameters
$\tfrac{{{\gamma _1}}}{\nu } < 1$ , starting the system with the state${\psi _1}(0) = 1,\; {\psi _2}(0) = 0$ : (a) Time evolutions of the occupation probabilities${\left| {{\psi _1}} \right|^2}$ and${\left| {{\psi _2}} \right|^2}$ ; (b) time evolutions of phases${\theta _1}(t)$ and${\theta _2}(t)$ ; (c) time evolution of the sum of phases,$ {\theta _1}({t_0} + t) + {\theta _2}({t_0} - t) $ . Here we choose the time-inversion point$ {t_0} = - 0.605 $ . The system parameters are${\gamma _0} = 1,\; {\gamma _1} = 0.5,\; \omega = 2, \;\nu = 1$ .
图 4 在共振情况下的系统动力学(
${{{\gamma _1}}}/{\nu } = 1$ ) (a) 两能级上的占有概率${\left| {{\psi _n}} \right|^2}$ ($n = 1, 2$ )随时间演化;(b)相位${\theta _n}$ ($n = $ $ 1, 2$ )随时间演化; (c)以$ {t_0} = - 0.5 $ 为时间反演点的$ {\theta _1}({t_0} + t) + {\theta _2}({t_0} - t) $ 演化. 系统参数取为${\gamma _0} = 1,\; {\gamma _1} = 1,\; $ $ \omega = 2,\; \nu = 1$ 初态为${\psi _1}(0) = 1,\; {\psi _2}(0) = 0$ Fig. 4. System dynamics for the resonance case with the non-Hermitian parameters
${{{\gamma _1}}}/{\nu } = 1$ , starting the system with the state${\psi _1}\left( 0 \right) = 1,\; {\psi _2}\left( 0 \right) = 0$ : (a) Time evolutions of the occupation probabilities${\left| {{\psi _1}} \right|^2}$ and${\left| {{\psi _2}} \right|^2}$ ; (b) time evolutions of phases${\theta _1}(t)$ and${\theta _2}(t)$ ; (c) time evolution of the sum of phases,$ {\theta _1}({t_0} + t) + {\theta _2}({t_0} - t) $ . Here the time-inversion point is given by$ {t_0} = - 0.5 $ . The system parameters are${\gamma _0} = 1,\; {\gamma _1} = 1,\; \omega = 2, \;\nu = 1$ .
图 5 在共振情况下的系统动力学.
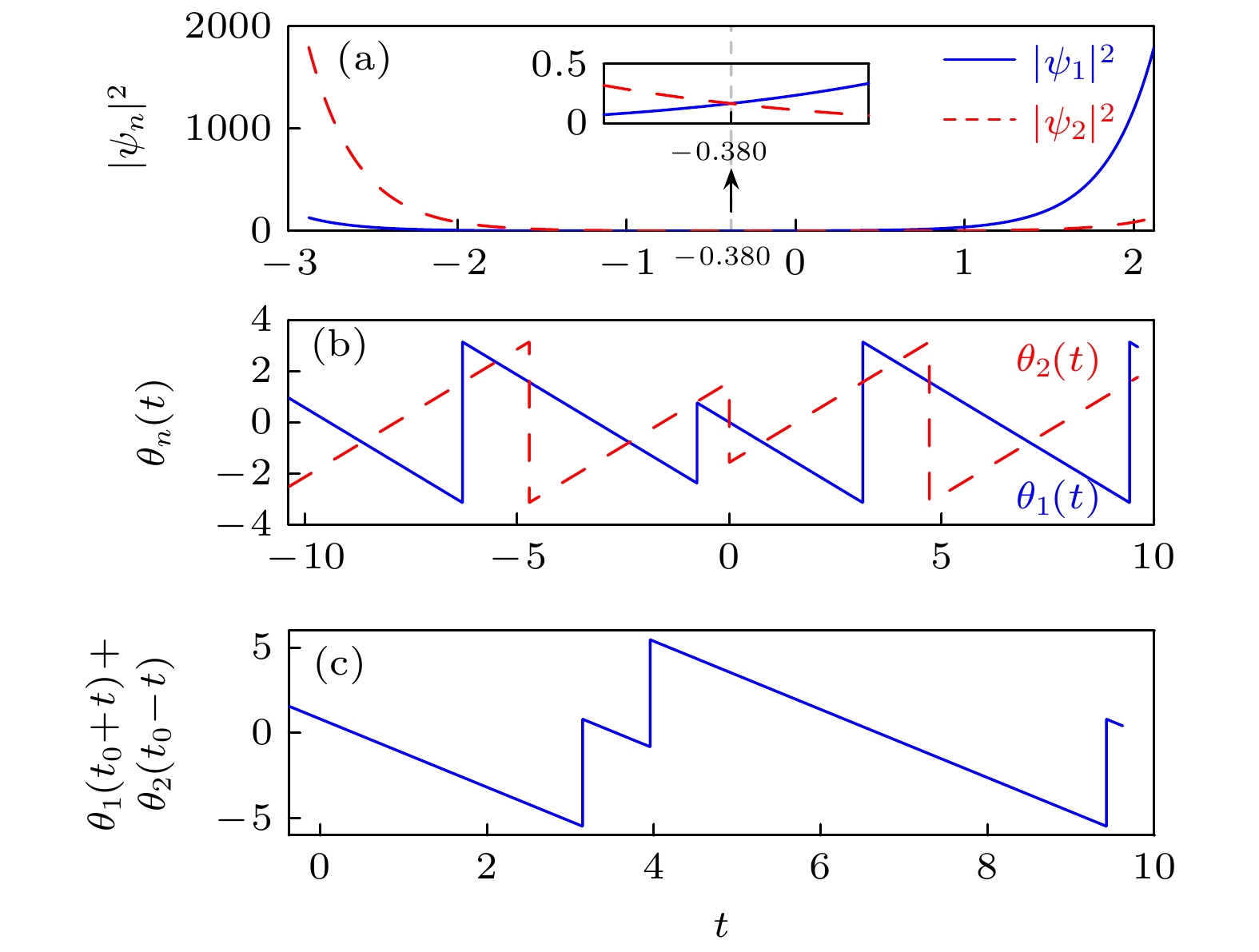
${{{\gamma _1}}}/{\nu } > 1$ . (a) 两能级上的占有概率${\left| {{\psi _n}} \right|^2}$ ($n = 1, 2$ )随时间演化. (b)相位${\theta _n}$ ($n = $ $ 1, 2$ )随时间演化. (c)以$ {t_0} = - 0.380 $ 为时间反演点的$ {\theta _1}({t_0} + t) + {\theta _2}({t_0} - t) $ 演化. 系统参数取为${\gamma _0} = 1,\;{\gamma _1} = 2, \; $ $ \omega = 2,\; \nu = 1$ 初态为${\psi _1}(0) = 1,\; {\psi _2}(0) = 0$ Fig. 5. System dynamics for the resonance case with the non-Hermitian parameters
${{{\gamma _1}}}/{\nu } > 1$ , starting the system with the state${\psi _1}(0) = 1, {\psi _2}(0) = 0$ . (a) Time evolutions of the occupation probabilities${\left| {{\psi _1}} \right|^2}$ and${\left| {{\psi _2}} \right|^2}$ . (b) Time evolutions of phases${\theta _1}(t)$ and${\theta _2}(t)$ . (c) Time evolution of the sum of phases,$ {\theta _1}({t_0} + t) + {\theta _2}({t_0} - t) $ . Here the time-inversion point is given by$ {t_0} = - 0.380 $ . The system parameters are${\gamma _0} = 1,\; {\gamma _1} = 2,\; \omega = 2,\;\nu = 1$ . -
[1] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243
Google Scholar
[2] Guo A, Salamo G J, Duchesne D, Morandotti R, Volatier-Ravat M, Aimez V, Siviloglou G A, Christodoulides D N 2009 Phys. Rev. Lett. 103 093902
Google Scholar
[3] Rüter C E, Makris K G, El-Ganainy R, Christodoulides D N, Segev M, Kip D 2010 Nat. Phys. 6 192
Google Scholar
[4] Doppler J, Mailybaev A A, Böhm J, Kuhl U, Girschik A, Libisch F, Milburn T J, Rabl P, Moiseyev N, Rotter S 2016 Nature 537 76
Google Scholar
[5] Peng B, Özdemir Ş K, Lei F, Monifi F, Gianfreda M, Long G Lu, Fan S, Nori F, Bender C M, Yang L 2014 Nat. Phys. 10 394
Google Scholar
[6] Chang L, Jiang X, Hua S, Yang C, Wen J, Jiang L, Li G, Wang G, Xiao M 2014 Nat. Photonics 8 524
Google Scholar
[7] Bender C M, Berntson B K, Parker D, Samuel E 2013 Am. J. Phys. 81 173
Google Scholar
[8] Schindler J, Li A, Zheng M C, Ellis F M, Kottos T 2011 Phys. Rev. A 84 040101(R)
[9] Fleury R, Sounas D, Alù A 2015 Nat. Com. 6 5905
[10] Liu T, Zhu X, Chen F, Liang S, Zhu J 2018 Phys. Rev. Lett. 120 124502
Google Scholar
[11] Tang J S, Wang Y T, Yu S, He D Y, Xu J S, Liu B H, Chen G, Sun Y N, Sun K, Han Y J, Li C F, Guo G C 2016 Nat. Photonics 10 642
Google Scholar
[12] Xiao L, Zhan X, Bian Z H, Wang K K, Zhang X, Wang X P, Li J, Mochizuki K, Kim D, Kawakami N, Yi W, Obuse H, Sanders B C, Xue P 2017 Nat. Phys. 13 1117
Google Scholar
[13] Gao W C, Zheng C, Liu L, Wang T J, Wang C 2021 Optics Express 29 517
Google Scholar
[14] Li J, Harter A K, Liu J, Melo L de, Joglekar Y N, Luo L 2019 Nat. Com. 10 855
Google Scholar
[15] Zhang D K, Luo X Q, Wang Y P, Li T F, You J Q 2017 Nat. Com. 8 1368
Google Scholar
[16] 沈瑞昌, 张国强, 王逸璞, 游建强 2019 68 230305
Google Scholar
Shen R C, Zhang G Q, Wang Y P, You J Q 2019 Acta Phys. Sin. 68 230305
Google Scholar
[17] Wu Y, Liu W, Geng J, Song X, Ye X, Duan C K, Rong X, Dun J 2019 Science 364 878
Google Scholar
[18] Zheng C, Hao L, Long G L 2013 Philos. Trans. R. Soc. A 371 20120053
Google Scholar
[19] Wen J, Zheng C, Kong X, Wei S, Xin T, Long G 2019 Phys. Rev. A 99 062122
Google Scholar
[20] Wang W C, Zhou Y L, Zhang H L, Zhang J, Zhang M C, Xie Y, Wu C W, Chen T, Ou B Q, Wu W, Jing H, Chen P X 2021 Phys. Rev. A 103 L020201
Google Scholar
[21] Ding L, Shi K, Zhang Q, Shen D, Zhang X, Zhang W 2021 Phys. Rev. Lett. 126 083604
Google Scholar
[22] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901
Google Scholar
[23] Regensburger A, Bersch C, Miri M A, Onishchukov G, Christodoulides D N, Peschel U 2012 Nature 488 167
Google Scholar
[24] Feng L, Xu Y L, Fegadolli W S, Lu M H, Oliveira J E B, Almeida V R, Chen Y F, Scherer A 2013 Nat. Mater. 12 108
Google Scholar
[25] Sun Y, Tan W, Li H Q, Li J, Chen H 2014 Phys. Rev. Lett. 112 143903
Google Scholar
[26] Jin L, Song Z 2018 Phys. Rev. Lett. 121 073901
Google Scholar
[27] Hodaei H, Hassan A U, Wittek S, Garcia-Gracia H, El-Ganainy R, Christodoulides D N, Khajavikhan M 2017 Nature 548 187
Google Scholar
[28] Yu S, Meng Y, Tang J, Xu X, Wang Y, Yin P, Ke Z, Liu W, Li Z, Yang Y, Chen G, Han Y, Li C, Guo G 2020 Phys. Rev. Lett. 125 240506
Google Scholar
[29] Feng L, Wong Z J, Ma R M, Wang Y, Zhang X 2014 Science 346 972
Google Scholar
[30] Hodaei H, Miri M A, Heinrich M, Christodoulides D N, Khajavikhan M 2014 Science 346 975
Google Scholar
[31] Assawaworrarit S, Yu X, Fan S 2017 Nature 546 387
Google Scholar
[32] Xu H, Mason D, Jiang L, Harris J G E 2016 Nature 537 80
Google Scholar
[33] Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401
[34] Bender C M 2007 Rep. Prog. Phys. 70 947
Google Scholar
[35] Mostafazadeh A 2002 J. Math. Phys. 43 205
Google Scholar
[36] Mostafazadeh A 2002 J. Math. Phys. 43 2814
Google Scholar
[37] 黄永峰, 曹怀信, 王文华 2020 69 030301
Google Scholar
Huang Y F, Cao H X, Wang W H 2020 Acta Phys. Sin. 69 030301
Google Scholar
[38] Nixon S, Yang J 2016 Phys. Rev. A 93 031802(R)
[39] Hang C, Gabadadze G, Huang G 2017 Phys. Rev. A 95 023833
Google Scholar
[40] Pan J, Zhou L 2020 Phys. Rev. B 102 094305
Google Scholar
[41] Luo X B, Huang J H, Zhong H H, Qin X Z, Xie Q T, Kivshar Y S, Lee C H 2013 Phys. Rev. Lett. 110 243902
Google Scholar
[42] Chitsazi M, Li H, Ellis F M, Kottos T 2017 Phys. Rev. Lett. 119 093901
Google Scholar
[43] Duan L, Wang Y, Chen Q 2020 Chin. Phys. Lett. 37 081101
Google Scholar
[44] Xie Q, Rong S, Liu X 2018 Phys. Rev. A 98 052122
Google Scholar
[45] Koutserimpas T T, Alù A, Fleury R 2018 Phys. Rev. A 97 013839
Google Scholar
[46] Luo X B, Wu D, Luo S, Guo Y, Yu X, Hu Q 2014 J. Phys. A:Math. Theor 47 345301
Google Scholar
[47] Yang B, Luo X B, Hu Q, Yu X 2016 Phys. Rev. A 94 043828
Google Scholar
[48] Luo X B, Yang B, Zhang X F, Li L, Yu X 2017 Phys. Rev. A 95 052128
Google Scholar
[49] Cui B, Wang L C, Yi X X 2010 Phys. Rev. A 82 062105
[50] Liu Z P, Zhang J, Özdemir Ş K, Peng B, Jing H, Lu X Y, Li C W, Yang L, Nori F, Liu Y 2016 Phys. Rev. Lett. 117 110802
Google Scholar
[51] Bender C M, Brody D C, Jones H F, Meister B K 2007 Phys. Rev. Lett. 98 040403
Google Scholar
下载:
计量
- 文章访问数: 5872
- PDF下载量: 330
- 被引次数: 0
