-
流体动画模拟的真实感与实时性一直是流体模拟研究中的热点. 针对在复杂地形场景中不稳定的流体表面运动现象, 本文提出一种基于地形差异的自适应流体速度控制力, 建立了稳定性光滑粒子流体动力学方法以求解浅水方程数值模型. 首先, 将模拟域从三维降至二维表面来降低计算量, 通过粒子的密度大小表示其水深高度值; 其次, 采用变长光滑搜索半径, 确保搜索邻域内的粒子数目稳定在固定范围内, 提高模拟精度; 最后引入一种基于地形差异的自适应流体速度控制力, 根据粒子密度大小的实时变化来确定计算速度控制力的地形研究范围, 通过插值计算粒子运动前后时间步所处地形位置的差异来修正粒子的速度和位置. 本文使用屏幕空间流体渲染方法对流体表面进行绘制, 避免了表面网格的提取与重建, 流体的运动数值计算和渲染均被加载到GPU上并行化执行, 实验结果表明在达到实时交互级别的同时, 本文方法有效地改善了在复杂地形场景中流体表面的不稳定运动现象, 同时流体模拟过程中密度与压强的分布均匀.The reality and real-time performance have always been the research hot-point of fluid simulation. Aiming at the unstable fluid surface motion in the scenes with complex terrain, in this paper, we propose an adaptive fluid velocity control force calculation model based on terrain difference, and a stable SPH numerical model for solving the shallow water equations is established. In this proposed numerical model, firstly we reduce the simulation domain from three-dimensional space to two-dimensional surface for reducing calculation quantity, and the water depth is represented by the density of particles at the meantime. Secondly, to ensure that the number of neighborhood particles is stable within a fixed range and to improve the accuracy of simulation, we apply a variable smoothing length to our numerical model. Then, an adaptive fluid velocity control force calculation model is introduced based on terrain difference, in which the velocity and position of particles are corrected by calculating the terrain difference caused by particle movement between each time step. The coordinates on terrain used for the calculation of terrain difference are dynamically chosen by the density of the particles. To improve the real-time performance of simulation, a screen space fluid rendering method is used to refrain the extraction and reconstruction of fluid surface. The numerical calculation and fluid surface rendering both load on the GPU for parallel execution. The simulation result shows that the proposed method can effectively improve the unstable fluid surface movement in scenes with complex terrain while reaching a real-time interaction level. The density and pressure are evenly distributed during the simulation.
-
Keywords:
- smoothed particle hydrodynamics /
- shallow water equations /
- parallel computing /
- complex terrain
[1] Harada T, Koshizuka S, Kawaguchi Y 2007 Proceedings of the 23rd Spring Conference on Computer Graphics Budmerice, Slovakia, April 26−28, 2007 p191
[2] Mastin G A, Watterberg P A, Mareda J F 1987 IEEE Comput. Graph. 7 16
Google Scholar
[3] Chentanez N, Müller M, Kim T Y 2015 IEEE T Vis. Comput. Gr. 21 1116
Google Scholar
[4] Monaghan J J 1994 J. Comput. Phys. 110 399
Google Scholar
[5] Brodtkorb A R, Sætra M L, Altinakar M 2012 Comput. Fluids 55 1
Google Scholar
[6] Monaghan J J 1992 Annu. Rev. Astron. Astr. 30 543
Google Scholar
[7] Swegle J W, Hicks D L, Attaway S W 1995 J. Comput. Phys. 116 123
Google Scholar
[8] Ata R, Soulaïmani A 2005 Int. J. Numer. Meth. Fl. 47 139
Google Scholar
[9] Rodriguez-Paz M, Bonet J 2005 Comput. Struct. 83 1396
Google Scholar
[10] Chang T J, Kao H M, Chang K H, Hsu M H 2011 J. Hydrol. 408 78
Google Scholar
[11] Xia X L, Liang Q H, Pastor M, Zou W L, Zhuang Y F 2013 Adv. Water Resour. 59 25
Google Scholar
[12] Chentanez N, Müller M 2010 Symposium on Computer Animation Goslar, Germany, July 2−4, 2010 p197
[13] De Leffe M, Le Touzé D, Alessandrini B 2010 J. Hydraul. Res. 48 118
Google Scholar
[14] Chládek M, Ďurikovič R 2015 Comput. Graph. 53 170
Google Scholar
[15] Solenthaler B, Bucher P, Chentanez N, Müller M 2011 VRIPHYS 11: 8th Workshop on Virtual Reality Interactions and Physical Simulations Lyon, France, December 5−6, 2011 p39
[16] Lee H, Han S 2010 Visual Comput. 26 865
Google Scholar
[17] 张海超, 郑丹晨, 边茂松, 韩敏 2016 65 244701
Google Scholar
Zhang H C, Zheng D C, Bian M S, Han M 2016 Acta Phys. Sin. 65 244701
Google Scholar
[18] Capecelatro J 2018 J. Comput. Phys. 356 174
Google Scholar
[19] van der Laan W J, Green S, Sainz M 2009 Proceedings of the 2009 Symposium on Interactive 3D Graphics and Games Boston, Massachusetts, February 27−March 1, 2009 p91
[20] Müller M, Solenthaler B, Keiser R, Gross M 2005 Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation Los Angeles, California, July 29−31, 2005 p237
[21] Fujisawa M, Nakada T, Mikawa M 2017 J. Inform. Processing. 25 486
Google Scholar
[22] Müller M, Charypar D, Gross M H 2003 Symposium on Computer Animation Goslar, Germany, July 26−27, 2003 p154
[23] Liu M B, Liu G R, Lam K Y 2002 Shock Waves 12 181
Google Scholar
[24] Akinci N, Ihmsen M, Akinci G, Solenthaler B, Teschner M 2012 ACM T. Graphic. 31 1
[25] Müller M, Schirm S, Duthaler S 2007 Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation Goslar, Germany, August 2, 2007 p9
[26] dos Santos Brito C J, Almeida M W S, Vieira-e-Silva A L B, Teixeira J M X N, Teichrieb V 2017 2017 19th Symposium on Virtual and Augmented Reality (SVR). IEEE Curitiba, Brazil, November 1−4, 2017 p309
-
图 1 地形引起粒子堆积、无序飞溅趋势
Fig. 1. The tendency of particle accumulation and disordered splashing caused by terrain.
图 3 地形整体平坦但局部凹陷严重
Fig. 3. A terrain which is flat on the whole but severely depressed locally.
图 4 基于地形差异的自适应流体速度控制力计算模型
Fig. 4. An adaptive fluid velocity control force calculation model based on terrain difference.
图 6 相机与流体表面关系示意图
Fig. 6. Schematic diagram of the relationship between camera and fluid surface.
图 8 施加控制力前后效果对比 (a) 未施加控制力; (b) 施加控制力
Fig. 8. The comparison before and after applying control force: (a) Without adding control force; (b) with control force.
图 9 流体与几何体交互 (a) 流体与长方体交互; (b) 流体与圆柱体交互
Fig. 9. Fluid interacts with geometry: (a) Fluid interacts with the cuboid; (b) fluid interacts with the cylinder.
图 10 爱荷华河场景的四个时刻模拟渲染图 (a) 0 s时刻; (b) 30 s时刻; (c) 90 s时刻; (d) 120 s时刻
Fig. 10. Fluid surface rendering of the Iowa river scene at four moments: (a) 0 s; (b) 30 s; (c) 90 s; (d) 120 s.
图 11 赤水河谷场景的四个时刻模拟渲染图 (a) 15 s时刻; (b) 30 s时刻; (c) 45 s时刻; (d) 60 s时刻
Fig. 11. Fluid surface rendering of the Chishui river valley scene at four moments: (a) 15 s; (b) 30 s; (c) 45 s; (d) 60 s.
图 12 爱荷华场景水淹情况示意图 (a) 依据历年水淹范围统计的淹没概率图; (b) 2008年6月爱荷华雨洪淹没范围图; (c) 水深25 ft, 流量31200 cfs情况下淹没范围图; (d) 本文淹没模拟结果示意图
Fig. 12. The flood inundation maps of iowa scene: (a) The inundation probability map based on the statistics of the flooding range over the years; (b) the flood inundation map of iowa in June, 2008; (c) map of inundation range under the condition of 25 ft water depth and 31200 cfs water flow; (d) the simulated inundation map of our method.
表 1 实验参数取值
Table 1. The values of parameters in experiment.
物理量 值 单位 粒子半径 $ r $ 0.5 m 时间步长 $ \Delta t $ 0.02 s 初始粒子间距 $ {r_0} $ 1 m 初始搜索半径 $ {h_0} $ 2.66 m 静密度 $ {\rho _0} $ 1000 kg/${{\rm{m}}^3}$ 粒子质量 $ m $ 1000 kg 气体常数 $ k $ 10 — 黏度系数 $ \mu $ 0.1 — 
下载: 导出CSV
表 2 实际水深与模拟水深数据对比
Table 2. Comparison between actual and simulated water depth
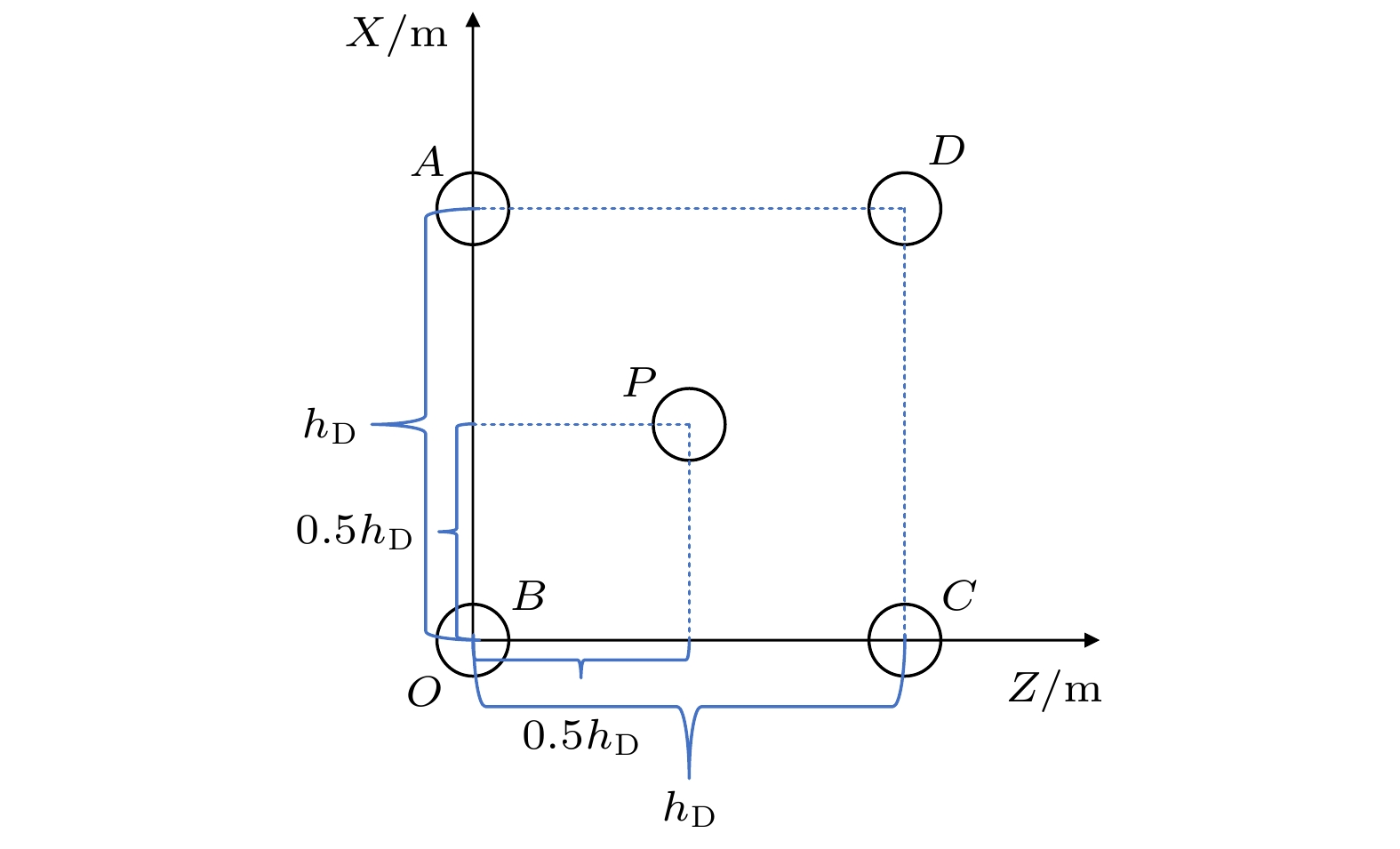
点位 模拟水深/m 实测水深/m 相对误差/% A 1.29 1.43 9.79 B 1.51 1.65 8.48 C 1.97 1.92 2.60 D 1.50 1.40 7.14
下载: 导出CSV
-
[1] Harada T, Koshizuka S, Kawaguchi Y 2007 Proceedings of the 23rd Spring Conference on Computer Graphics Budmerice, Slovakia, April 26−28, 2007 p191
[2] Mastin G A, Watterberg P A, Mareda J F 1987 IEEE Comput. Graph. 7 16
Google Scholar
[3] Chentanez N, Müller M, Kim T Y 2015 IEEE T Vis. Comput. Gr. 21 1116
Google Scholar
[4] Monaghan J J 1994 J. Comput. Phys. 110 399
Google Scholar
[5] Brodtkorb A R, Sætra M L, Altinakar M 2012 Comput. Fluids 55 1
Google Scholar
[6] Monaghan J J 1992 Annu. Rev. Astron. Astr. 30 543
Google Scholar
[7] Swegle J W, Hicks D L, Attaway S W 1995 J. Comput. Phys. 116 123
Google Scholar
[8] Ata R, Soulaïmani A 2005 Int. J. Numer. Meth. Fl. 47 139
Google Scholar
[9] Rodriguez-Paz M, Bonet J 2005 Comput. Struct. 83 1396
Google Scholar
[10] Chang T J, Kao H M, Chang K H, Hsu M H 2011 J. Hydrol. 408 78
Google Scholar
[11] Xia X L, Liang Q H, Pastor M, Zou W L, Zhuang Y F 2013 Adv. Water Resour. 59 25
Google Scholar
[12] Chentanez N, Müller M 2010 Symposium on Computer Animation Goslar, Germany, July 2−4, 2010 p197
[13] De Leffe M, Le Touzé D, Alessandrini B 2010 J. Hydraul. Res. 48 118
Google Scholar
[14] Chládek M, Ďurikovič R 2015 Comput. Graph. 53 170
Google Scholar
[15] Solenthaler B, Bucher P, Chentanez N, Müller M 2011 VRIPHYS 11: 8th Workshop on Virtual Reality Interactions and Physical Simulations Lyon, France, December 5−6, 2011 p39
[16] Lee H, Han S 2010 Visual Comput. 26 865
Google Scholar
[17] 张海超, 郑丹晨, 边茂松, 韩敏 2016 65 244701
Google Scholar
Zhang H C, Zheng D C, Bian M S, Han M 2016 Acta Phys. Sin. 65 244701
Google Scholar
[18] Capecelatro J 2018 J. Comput. Phys. 356 174
Google Scholar
[19] van der Laan W J, Green S, Sainz M 2009 Proceedings of the 2009 Symposium on Interactive 3D Graphics and Games Boston, Massachusetts, February 27−March 1, 2009 p91
[20] Müller M, Solenthaler B, Keiser R, Gross M 2005 Proceedings of the 2005 ACM SIGGRAPH/Eurographics Symposium on Computer Animation Los Angeles, California, July 29−31, 2005 p237
[21] Fujisawa M, Nakada T, Mikawa M 2017 J. Inform. Processing. 25 486
Google Scholar
[22] Müller M, Charypar D, Gross M H 2003 Symposium on Computer Animation Goslar, Germany, July 26−27, 2003 p154
[23] Liu M B, Liu G R, Lam K Y 2002 Shock Waves 12 181
Google Scholar
[24] Akinci N, Ihmsen M, Akinci G, Solenthaler B, Teschner M 2012 ACM T. Graphic. 31 1
[25] Müller M, Schirm S, Duthaler S 2007 Proceedings of the 2007 ACM SIGGRAPH/Eurographics Symposium on Computer Animation Goslar, Germany, August 2, 2007 p9
[26] dos Santos Brito C J, Almeida M W S, Vieira-e-Silva A L B, Teixeira J M X N, Teichrieb V 2017 2017 19th Symposium on Virtual and Augmented Reality (SVR). IEEE Curitiba, Brazil, November 1−4, 2017 p309
下载:
计量
- 文章访问数: 5730
- PDF下载量: 80
- 被引次数: 0
