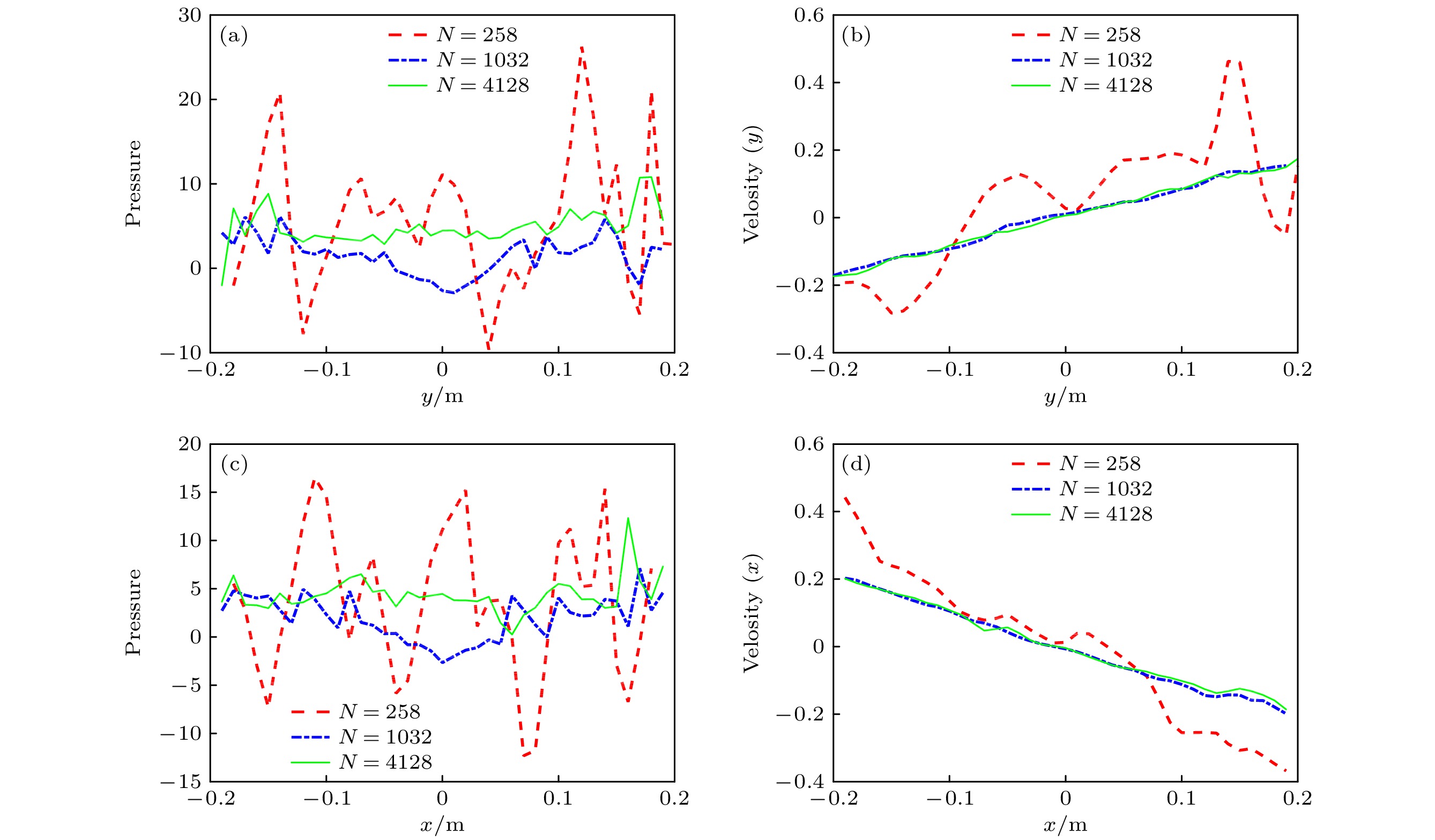
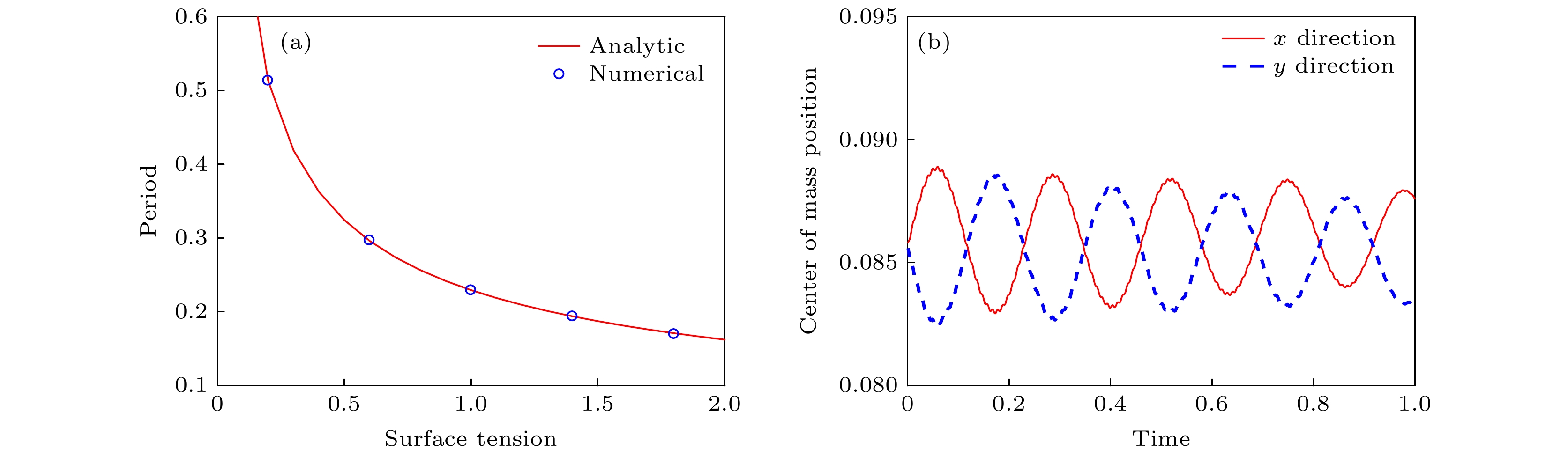
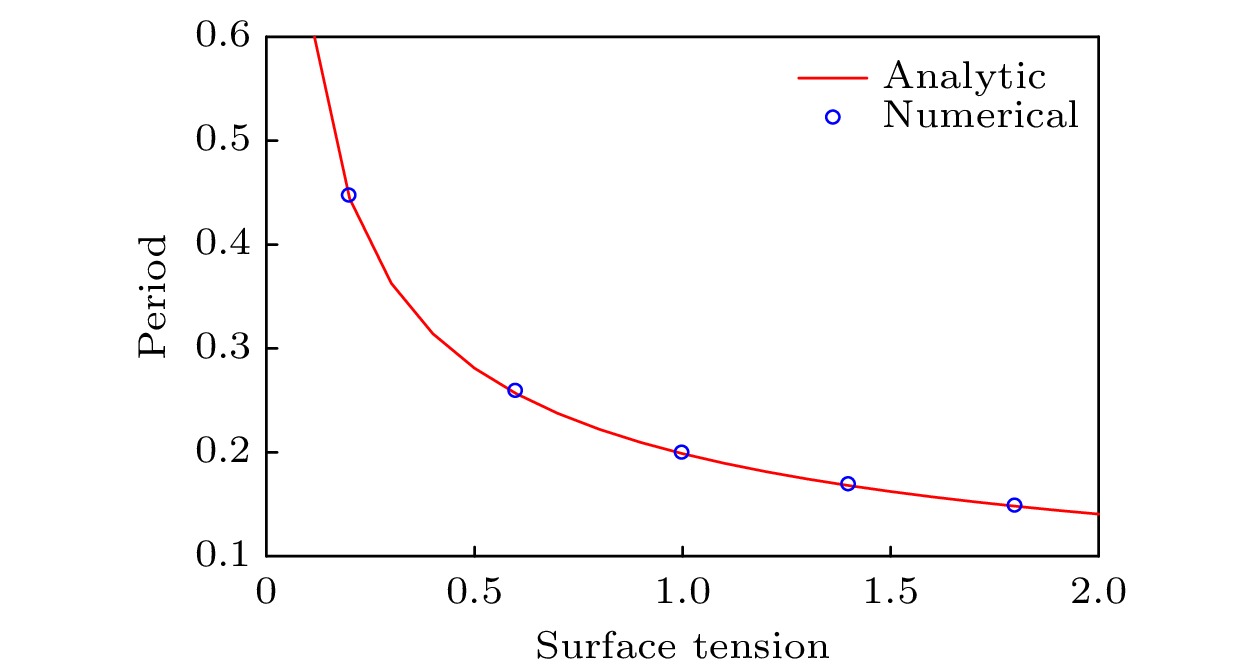
-
基于网格的数值方法(如有限元、有限体积、有限差分等)在大变形、不连续等问题中遇到挑战, 因此人们提出了多种无网格方法. 最优输运无网格方法是一种新型拉格朗日无网格方法, 但是继承了有限元方法在边界表征、边界处理等方面的优势, 在表面张力模拟中具有较大潜力. 基于拉格朗日方程, 通过将表面张力势能加入拉格朗日函数, 得到的表面张力广义力精确地作用在流体表面, 而且表面张力系数是唯一的输入参数. 给出了最优输运无网格方法轴对称离散格式. 通过对二维/三维泊肃叶流、静止和振动的液滴、液滴变形等典型问题的仿真分析, 验证了最优输运无网格方法在表面张力问题模拟中的精度和收敛性.Owing to challenges encountered by mesh-based CFD methods when simulating large material deformation, a number of meshfree methods have been presented. The optimized transportation meshfree method is a newly developed meshfree method, but it inherits the advantage of the finite element method in boundary treatment and thus having great potential applications in surface tension effect simulation. By adding the surface tension potential into the Lagrangian, the resulting generalized force acts on fluid surfaces exactly. The axial symmetry treatment is also discussed. By simulating several benchmark cases such as two- and three-dimensional Poiseuille flow, static and vibrating drop and drop deformation, the advantages like precision and convergence of the optimized transportation meshfree method in simulating surface tension effect are verified.
-
Keywords:
- optimized transportation meshfree method /
- surface tension /
- Lagrangian equations /
- axial symmetry
[1] Wang H, Zhang Z Y, Yang Y M, Zhang H S 2010 Chin. Phys. B 19 026801
Google Scholar
[2] Annaland M, Deen N G, Kuipers J A M 2005 Chem. Eng. Sci. 60 2999
Google Scholar
[3] Croce R, Griebel M, Schweitzer M A 2010 Int. J. Numer. Meth. Fl. 62 963
[4] Liu G R, Liu M B 2003 Smoothed Particle Hydrodynamics: AMeshfree Particle Method (Singapore: World Scientific)
[5] Liu M B, Liu G R, Zong Z 2008 Int. J. Comput. Methods 5 135
Google Scholar
[6] Alexandre M T, Kim F F, Paul M 2009 Comput. Phys. Commun. 18 01874
Google Scholar
[7] Zhou G Z, Ge W, Li J H 2008 Powder Technol. 183 21
Google Scholar
[8] Alexandre T, Paul M 2005 Phys. Rev. E 72 026301
[9] 马理强, 常建忠, 刘汉涛, 刘谋斌 2012 61 054701
Google Scholar
Ma L Q, Chang J Z, Liu H T, Liu M B 2012 Acta Phys. Sin. 61 054701
Google Scholar
[10] 白玲, 李大鸣, 李彦卿, 王志超, 李杨杨 2015 64 114701
Google Scholar
Bai L, Li D M, Li Y Q, Wang Z C, Li Y Y 2015 Acta Phys. Sin. 64 114701
Google Scholar
[11] Brackbill J U, Kothe D B, Zemach C 1992 J. Comput. Phys. 100 354
Google Scholar
[12] 蒋涛, 陆林广, 陆伟刚 2013 62 224701
Google Scholar
Jiang T, Lu L G, Lu W G 2013 Acta Phys. Sin. 62 224701
Google Scholar
[13] Chen J K, Beraun J E 2000 Comp. Meth. Appl. Mech. Eng. 190 225
Google Scholar
[14] Li B, Habbal F, Ortiz M 2010 Powder Technology 83 1541
[15] Sukumar N 2004 Int. J. Numer. Meth. Engineer. 612 159
Google Scholar
[16] Arroyo M, Ortiz M 2006 Int. J. Numer. Meth. Engineer. 652 167
[17] Sukumar N, Wright R W 2007 Int. J. Numer. Meth. Engineer. 70 181
Google Scholar
[18] Li B, Kidane A, Ravichandran G, Ortiz M 2012 Int. J. Impact Eng. 42 25
Google Scholar
[19] Li B, Perotti L, Adams M, Mihaly J, Rosakis A J, Stalzer M, Ortiz M 2013 Procedia Eng. 58 320
Google Scholar
[20] Li B, Stalzer M, Ortiz M 2014 Int. J. Numer. Meth. Eng. 100 40
Google Scholar
[21] 张天龙, 马天宝, 郝莉 2021 兵器装备工程学报 42 144
Google Scholar
Zhang T L, Ma T B, Hao L 2021 J. Ordnance Equip. Eng. 42 144
Google Scholar
[22] Li B, Pandolfi A, Ortiz M 2015 Mechanics of Materials 80 288
Google Scholar
[23] Fedeli L, Pandolfi A, Ortiz M 2017 Int. J. Numer. Meth. Eng. 112 1905
Google Scholar
[24] Morris J P, Fox P J, Zhu Y 1997 J. Comput. Phys. 136 214
Google Scholar
[25] Leonardo D G S, Jaime K, Eloy S, Yasmin M, Anwar H 2003 J. Comput. Phys. 191 622
Google Scholar
[26] Hu X Y, Adams N A 2006 J. Comput. Phys. 213 844
Google Scholar
[27] Tadashi W 2008 WSEAS Transactions on Fluid Mechanics 3 164
-
图 1 利用有限元网格将连续介质离散为粒子和节点 (a)有限元网格; (b)用粒子与节点离散连续介质
Fig. 1. Continuum discretized by particles (red symbols) and nodes (white symbols) in the OTM method by means of finite element mesh: (a) Finite element mesh; (b) continuum discretized by particles and nodes.
图 2 二维条件下的边界节点(白点)
Fig. 2. Boundary nodes (white symbols) in two-dimensional coordinate.
图 3 速度分布的OTM模拟与解析解对比 (a) 二维泊肃叶流; (b) 三维轴对称泊肃叶流
Fig. 3. Comparison of OTM (symbols) and analytic solutions (solid curves) for velocity profile: (a) Two-dimensional Poiseuilleflow; (b) axisymmetric Hagen-Poiseuille flow.
图 4 静止液滴的压力场 (a) 二维液滴; (b) 轴对称三维液滴
Fig. 4. Pressure field: (a) Two-dimensional rod; (b) axisymmetric three dimensional drop.
图 5 t = T/2时刻的压力和速度分布 (a) x = 0上的压力分布; (b) x = 0上的速度分布; (c) y = 0上的压力分布; (d) y = 0上的速度分布
Fig. 5. Pressure and velocity profile at t = T/2: (a) Pressure profile at x = 0; (b) velocity profile at x = 0; (c) pressure profile at y = 0; (d) velocity profile at y = 0.
图 6 二维液滴振荡 (a) 振荡周期理论解和数值解得对比; (b) 表面张力系数为
$ \gamma = 1 $ 时液滴右上部分质心的轨迹Fig. 6. Two-dimensional rod oscillation: (a) Comparison of period between the numerical (symbols) and analytical (solid curve) results; (b) center of mass position history when
$ \gamma = 1 $ .
图 7 轴对称三维液滴振荡周期与理论的对比
Fig. 7. Three-dimensional droplet oscillation, comparing of period between the numerical (symbols) and analytical (solid curve) results.
图 8 压力场 (a) t = 0 s; (b) t = 0.02 s; (c) t = 0.4 s; (d) t = 4 s
Fig. 8. Pressure field at several typical times: (a) t = 0 s; (b) t = 0.02 s; (c) t = 0.4 s; (d) t = 4 s.
图 9 边界位置和压力 (a) 边界位置; (b) 边界压力与Y轴坐标的关系, 压力根据表面曲率和EOS计算
Fig. 9. Boundary position and pressure profile: (a) Boundary position; (b) boundary pressure versus Y coordinate, computed by Young-Laplace equation (circles) and EOS (points).
-
[1] Wang H, Zhang Z Y, Yang Y M, Zhang H S 2010 Chin. Phys. B 19 026801
Google Scholar
[2] Annaland M, Deen N G, Kuipers J A M 2005 Chem. Eng. Sci. 60 2999
Google Scholar
[3] Croce R, Griebel M, Schweitzer M A 2010 Int. J. Numer. Meth. Fl. 62 963
[4] Liu G R, Liu M B 2003 Smoothed Particle Hydrodynamics: AMeshfree Particle Method (Singapore: World Scientific)
[5] Liu M B, Liu G R, Zong Z 2008 Int. J. Comput. Methods 5 135
Google Scholar
[6] Alexandre M T, Kim F F, Paul M 2009 Comput. Phys. Commun. 18 01874
Google Scholar
[7] Zhou G Z, Ge W, Li J H 2008 Powder Technol. 183 21
Google Scholar
[8] Alexandre T, Paul M 2005 Phys. Rev. E 72 026301
[9] 马理强, 常建忠, 刘汉涛, 刘谋斌 2012 61 054701
Google Scholar
Ma L Q, Chang J Z, Liu H T, Liu M B 2012 Acta Phys. Sin. 61 054701
Google Scholar
[10] 白玲, 李大鸣, 李彦卿, 王志超, 李杨杨 2015 64 114701
Google Scholar
Bai L, Li D M, Li Y Q, Wang Z C, Li Y Y 2015 Acta Phys. Sin. 64 114701
Google Scholar
[11] Brackbill J U, Kothe D B, Zemach C 1992 J. Comput. Phys. 100 354
Google Scholar
[12] 蒋涛, 陆林广, 陆伟刚 2013 62 224701
Google Scholar
Jiang T, Lu L G, Lu W G 2013 Acta Phys. Sin. 62 224701
Google Scholar
[13] Chen J K, Beraun J E 2000 Comp. Meth. Appl. Mech. Eng. 190 225
Google Scholar
[14] Li B, Habbal F, Ortiz M 2010 Powder Technology 83 1541
[15] Sukumar N 2004 Int. J. Numer. Meth. Engineer. 612 159
Google Scholar
[16] Arroyo M, Ortiz M 2006 Int. J. Numer. Meth. Engineer. 652 167
[17] Sukumar N, Wright R W 2007 Int. J. Numer. Meth. Engineer. 70 181
Google Scholar
[18] Li B, Kidane A, Ravichandran G, Ortiz M 2012 Int. J. Impact Eng. 42 25
Google Scholar
[19] Li B, Perotti L, Adams M, Mihaly J, Rosakis A J, Stalzer M, Ortiz M 2013 Procedia Eng. 58 320
Google Scholar
[20] Li B, Stalzer M, Ortiz M 2014 Int. J. Numer. Meth. Eng. 100 40
Google Scholar
[21] 张天龙, 马天宝, 郝莉 2021 兵器装备工程学报 42 144
Google Scholar
Zhang T L, Ma T B, Hao L 2021 J. Ordnance Equip. Eng. 42 144
Google Scholar
[22] Li B, Pandolfi A, Ortiz M 2015 Mechanics of Materials 80 288
Google Scholar
[23] Fedeli L, Pandolfi A, Ortiz M 2017 Int. J. Numer. Meth. Eng. 112 1905
Google Scholar
[24] Morris J P, Fox P J, Zhu Y 1997 J. Comput. Phys. 136 214
Google Scholar
[25] Leonardo D G S, Jaime K, Eloy S, Yasmin M, Anwar H 2003 J. Comput. Phys. 191 622
Google Scholar
[26] Hu X Y, Adams N A 2006 J. Comput. Phys. 213 844
Google Scholar
[27] Tadashi W 2008 WSEAS Transactions on Fluid Mechanics 3 164
下载:
计量
- 文章访问数: 5932
- PDF下载量: 83
- 被引次数: 0
