-
Using a state-of-the-art numerical method density-matrix renormalization-group, we study the ground states of one-dimensional spinless Bose-Hubbard model inside a red-detuned cavity. By calculating the superfluid order, density distribution, second and third-order correlation functions, we find that there exist two novel supersolid phases with diagonal, off-diagonal orders beyond mean-field theory. One has package type density modulation along the lattice axis, another exhibits uniform density distribution. Moreover, by calculating the superradiant order parameter and the number of photon inside the cavity, we find that the novel supersolid phases are highly related to cavity-field fluctuation. Our work gives the physics beyond the mean-field theory of the Bose-Hubbard model inside an optical cavity, and provides the complete approach to fully explore the collective state of light and matter inside an optical cavity.
[1] Bloch I, Dalibard J, Nascimbane S 2012 Nat. Phys. 8 267
Google Scholar
[2] Fisher M P A, Weichman P B, Grinstein G, Fisher D S 1989 Phys. Rev. B 40 546
Google Scholar
[3] Jaksch D, Zoller P 2005 Ann. Phys. 315 52
Google Scholar
[4] Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885
Google Scholar
[5] Gross C, Bloch I 2017 Science 357 995
Google Scholar
[6] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
Google Scholar
[7] Nagy D, Konya G, Szirmai G, Domokos P 2010 Phys. Rev. Lett. 104 130401
Google Scholar
[8] Ritsch H, Domokos P, Brennecke F, Esslinger T 2013 Rev. Mod. Phys. 85 553
Google Scholar
[9] Mottl R, Brennecke F, Baumann K, Landig R, Donner T, Esslinger T 2012 Science 336 1570
Google Scholar
[10] Landig R, Hruby L, Dogra N, Landini M, Mottl R, Donner T, Esslinger T 2016 Nature 532 476
Google Scholar
[11] Lang J, Piazza F, Zwerger W 2017 New J. Phys. 19 123027
Google Scholar
[12] Caballero-Benitez S F, Mekhov I B 2015 Phys. Rev. Lett. 115 243604
Google Scholar
[13] Bakhtiari M R, Hemmerich A, Ritsch H, Thorwart M 2015 Phys. Rev. Lett. 114 123601
Google Scholar
[14] Dogra N, Brennecke F, Huber S D, Donner T 2016 Phys. Rev. A 94 023632
Google Scholar
[15] Niederle A E, Morigi G, Rieger H 2016 Phys. Rev. A 94 033607
Google Scholar
[16] Sundar B, Mueller E J 2016 Phys. Rev. A 94 033631
Google Scholar
[17] Chen Y, Yu Z, Zhai H 2016 Phys. Rev. A 93 041601(R
Google Scholar
[18] Panas J, Kauch A, Byczuk K 2017 Phys. Rev. B 95 115105
Google Scholar
[19] Flottat T, de Forges de Parny L, Hebert F, Rousseau V G, Batrouni G G 2017 Phys. Rev. B 95 144501
Google Scholar
[20] Bogner B, Danilo C D, Rieger H 2019 Eur. Phys. J. B 92 111
Google Scholar
[21] Boninsegni M, Prokofev N V 2012 Rev. Mod. Phys. 84 759
Google Scholar
[22] Leggett A J 1970 Phys. Rev. Lett. 25 1543
Google Scholar
[23] Otterlo A V, Wagenblast K H 1994 Phys. Rev. Lett. 72 3598
Google Scholar
[24] Batrouni G G, Scalettar R T, Zimanyi G T, Kampf A P 1995 Phys. Rev. Lett. 74 2527
Google Scholar
[25] Scalettar R T, Batrouni G G, Kampf A P, Zimanyi G T 1995 Phys. Rev. B 51 8467
Google Scholar
[26] Otterlo A V, Wagenblast K H, Baltin R, Bruder C, Fazio R, Schon G 1995 Phys. Rev. B 52 16176
Google Scholar
[27] Rossini D, Fazio R 2011 New J. Phys. 14 065012
[28] White S R 1992 Phys. Rev. Lett. 69 2863
Google Scholar
[29] Schollwok U 2005 Rev. Mod. Phys. 77 259
Google Scholar
[30] Maschler C, Mekhov I B, Ritsch H 2008 Eur. Phys. J. D 46 545
Google Scholar
[31] Hodgman S S, Dall R G, Manning A G, Baldwin K G H, Truscott A G 2011 Science 331 1046
Google Scholar
[32] Liu H C 2016 Phys. Rev. A 94 023827
Google Scholar
[33] Schweigler T, Kasper V, Erne S, Mazets I, Rauer B, Cataldini F, Langen T, Gasenzer T, Berges J, Schmiedmayer J 2017 Nature 545 323
Google Scholar
[34] Hodgman S S, Khakimov R I, Truscott A G, Kheruntsyan K V 2017 Phys. Rev. Lett. 118 240402
Google Scholar
[35] Rispoli M, Lukin A, Schittko R, Kim S, Tai M E, Leonard J, Greiner M 2019 Nature 573 385
Google Scholar
[36] Fan J, Zhou X, Zheng W, Yi W, Chen G, Jia S 2018 Phys. Rev. A 98 043613
Google Scholar
[37] Stenger J, Inouye S, Chikkatur A P, Stamper-Kurn D M, Pritchard D E, Ketterle W 1999 Phys. Rev. Lett. 82 4569
Google Scholar
[38] Steinhauer J, Ozeri R, Katz N, Davidson N 2002 Phys. Rev. Lett. 88 120407
Google Scholar
[39] Greif D, Parsons M F, Mazurenko A, Chiu C S, Blatt S, Huber F, Ji G, Greiner M 2016 Science 351 953
Google Scholar
-
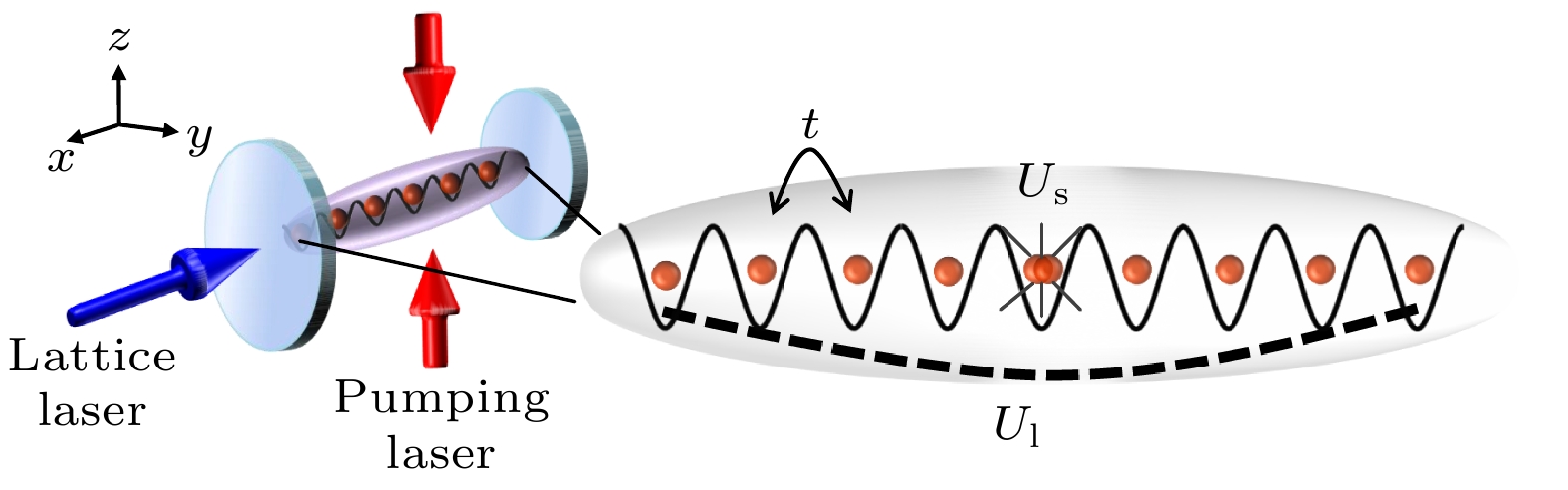
图 1 左图: 玻色原子沿着腔轴方向
$\hat x$ 被俘获在准一维(1D)背景光学晶格中, 费米气被两束圆偏振的横向(沿着$\hat z$ 方向) 抽运激光驱动. 右图: 隧穿系数t, 接触型相互作用${U_{\rm{s}}}$ 和无限长程相互作用${U_{\rm{l}}}$ Fig. 1. Left: Proposed experimental setup that the bosonic atoms trapped in a quasi-1D optical lattice interact with an optical cavity. Right: Illustration of the competing terms among the hopping t, the contact interaction
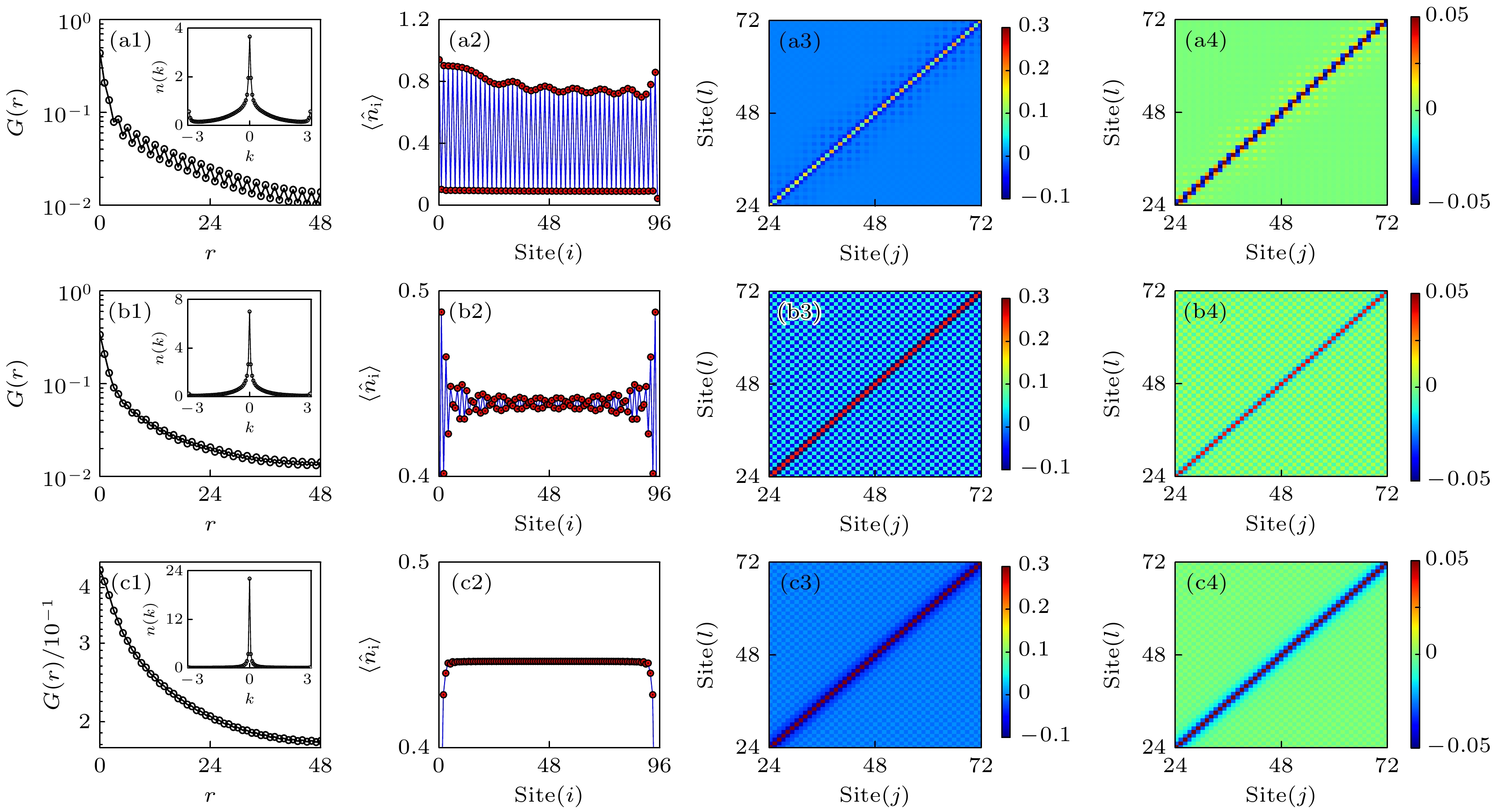
${U_{\rm{s}}}$ and the global-range interaction${U_{\rm{l}}}$ .
图 2 (a1), (b1), (c1)超流序
$G(r)$ 和插图$n(k)$ ; (a2), (b2), (c2)密度分布$\left\langle {{{\hat n}_j}} \right\rangle $ ; (a3), (b3), (c3)二阶关联${D^2}(l, j)$ ; (a4), (b4), (c4)三阶关联${D^3}\left( {i, l, j} \right)$ . (a1)—(a3) 超固0相, 相互作用参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 6$ ; (b1)—(b3) 超固1相, 相互作用参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 4.4$ ; (c1)—(c3) 超固2相, 相互作用参数${U_{\rm{s}}} = 2$ 和${U_{\rm{l}}} = 4.4$ . 所有图中, 共有参数$L = 96$ ,$\rho = 0.4375$ Fig. 2. (a1), (b1), (c1) Superfluid order
$G(r)$ and$n(k)$ ; (a2), (b2), (c2) density profile$\left\langle {{{\hat n}_j}} \right\rangle $ ; (a3), (b3), (c3) two order correlation${D^2}\left( {l, j} \right)$ ; (a4), (b4), (c4) three order correlation${D^3}\left( {i, l, j} \right)$ for$i = j$ of (a1)–(a3) supersolid 0 phase with${U_{\rm{s}}} = 10$ and${U_{\rm{l}}} = 6$ , (b1)–(b3) supersolid 1 phase with${U_{\rm{s}}} = 10$ and${U_{\rm{l}}} = 4.4$ , and (c1)–(c3) supersolid 2 phase with${U_{\rm{s}}} = 2$ and${U_{\rm{l}}} = 4.4$ . In all subfigure, we have$L = 96$ and$\rho = 0.4375$ .
图 3 (a1), (b1)不同尺寸下的超流序
$G(r)$ , 插图为冥率的有限尺寸分析; (a2), (b2)$n(k = 0){{/}}L$ 的有限尺寸分析. (a1), (a2)超固1相, 参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 4.4$ ; (b1), (b2) 超固2相, 参数${U_{\rm{s}}} = 2$ 和${U_{\rm{l}}} = 4.4$ . 所有图中, 共有参数$\rho = 0.4375$ Fig. 3. (a1), (b1) Superfluid order
$G(r)$ of several lattice length. The inset is the finite-size scaling of the decay rate. (a2), (b2) Finite-size scaling of$n(k = 0){{/}}L$ . (a1), (a2) Supersolid 1 phase with${U_{\rm{s}}} = 10$ and${U_{\rm{l}}} = 4.4$ . (b1), (b2) Supersolid 2 phase with${U_{\rm{s}}} = 2$ and${U_{\rm{l}}} = 4.4$ . In all subfigure, we have$\rho = 0.4375$ .
图 4 (a1)—(a3)和(b1)—(b3)密度分布
$\left\langle {{{\hat n}_j}} \right\rangle $ ; (a4), (b4)${\nu _{{\rm{peak}}}}$ 的有限尺寸分析. (a1)—(a4) 超固1相, 参数${U_{\rm{s}}} = 10$ 和${U_{\rm{l}}} = 4.4$ ; (b) 超固2相, 参数${U_{\rm{s}}} = 2$ 和${U_{\rm{l}}} = 4.4$ . (a1), (b1)$L = 80$ ; (a2), (b2)$L = 64$ ; (a3), (b3)$L = 48$ . 所有图中, 共有参数$\rho = 0.4375$ Fig. 4. (a1) –(a3) and (b1) –(b3) the density profile
$\left\langle {{{\hat n}_j}} \right\rangle $ ; (a4), (b4) the finite-size scaling of the${\nu _{{\rm{peak}}}}$ . (a1)–(a4) Supersolid 1 phase with${U_{\rm{s}}} = 10$ and${U_{\rm{l}}} = 4.4$ ; (b1)–(b4) supersolid 2 phase with${U_{\rm{s}}} = 2$ and${U_{\rm{l}}} = 4.4$ . (a1), (b1)$L = 80$ ; (a2), (b2)$L = 64$ ; (a3), (b3)$L = 48$ . In all subfigure, we have$\rho = 0.4375$ .
图 5
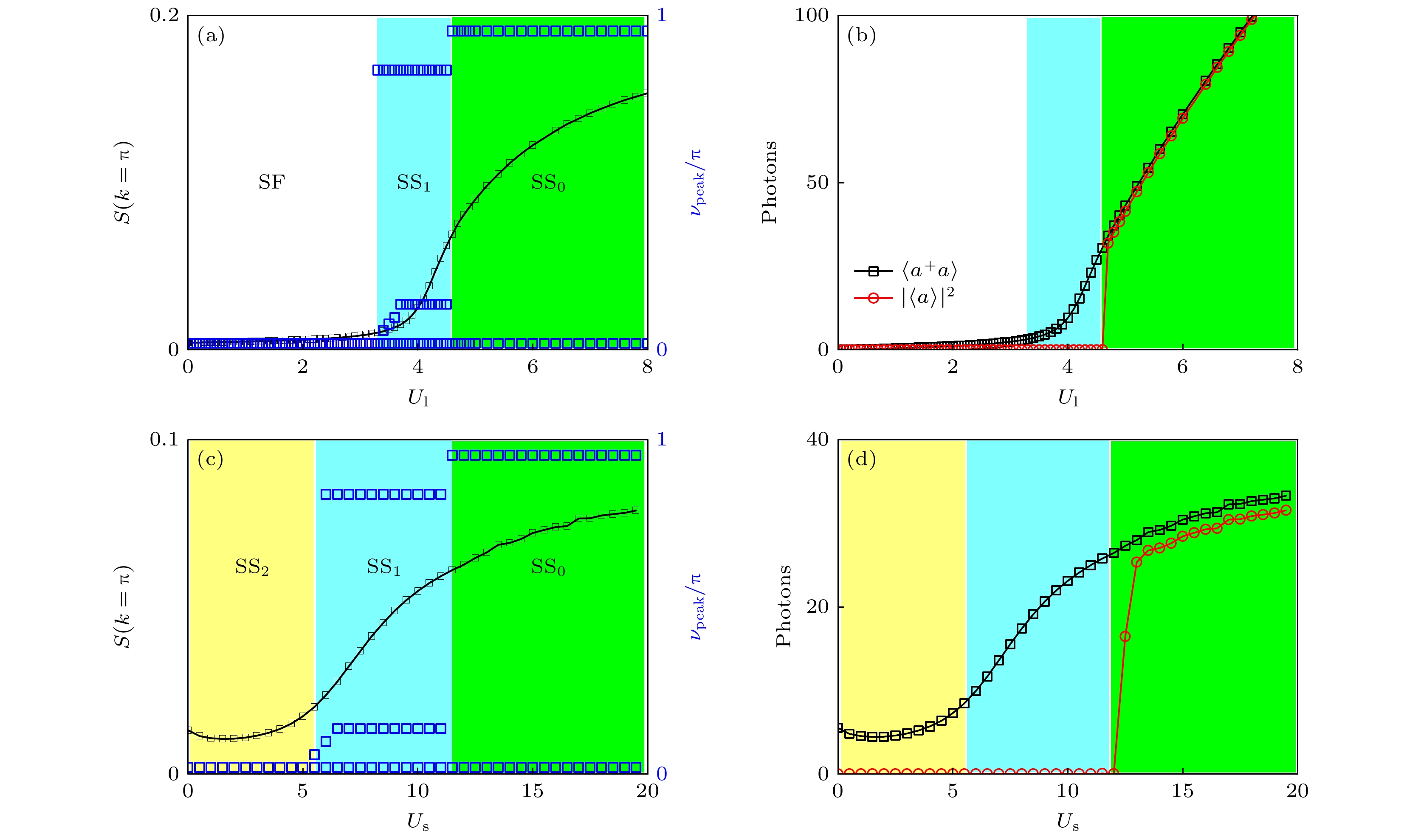
$S(k = {\text{π}})$ (黑色实线)和${\nu _{{\rm{peak}}}}$ (蓝色方块) (a) 关于${U_{\rm{l}}}$ 的变化, 固定${U_{\rm{s}}} = 10$ ; (c) 关于${U_{\rm{s}}}$ 的变化, 固定${U_{\rm{l}}} = 4.4$ . 平均光子数${\left| {\left\langle {\hat a} \right\rangle } \right|^2}$ 和腔中的光子数$\left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle $ 关于 (b) 关于${U_{\rm{l}}}$ 的变化, 固定${U_{\rm{s}}} = 10$ ; (d) 关于${U_{\rm{s}}}$ 的变化, 固定${U_{\rm{l}}} = 4.4$ . 所有图中, 共有参数$L = 96$ 和$\rho = 0.4375$ . SF表示超流, MI表示莫特绝缘体, CDW表示电荷密度波, SS0表示超固0相, SS1表示超固1相, SS2表示超固2相Fig. 5. The
$S(k = {\text{π}})$ (black solid line) and${\nu _{{\rm{peak}}}}$ (blue square) as function of (a)${U_{\rm{l}}}$ with${U_{\rm{s}}} = 10$ , and (c)${U_{\rm{s}}}$ with${U_{\rm{l}}} = 4.4$ . The number of cavity photons$\left\langle {{{\hat a}^{\dagger} }\hat a} \right\rangle $ and mean cavity-field${\left| {\left\langle {\hat a} \right\rangle } \right|^2}$ as a function of (b)${U_{\rm{l}}}$ with${U_{\rm{s}}} = 10$ , (d)${U_{\rm{s}}}$ with${U_{\rm{l}}} = 4.4$ . In all subfigure, we have$L = 96$ and$\rho = 0.4375$ . SF denotes superfluid, MI denotes Mott insulator, CDW denotes charge density wave, SS0 denotes supersolid 0, SS1 denotes supersolid 1, SS2 denotes supersolid 2.
图 6 (a)—(c)
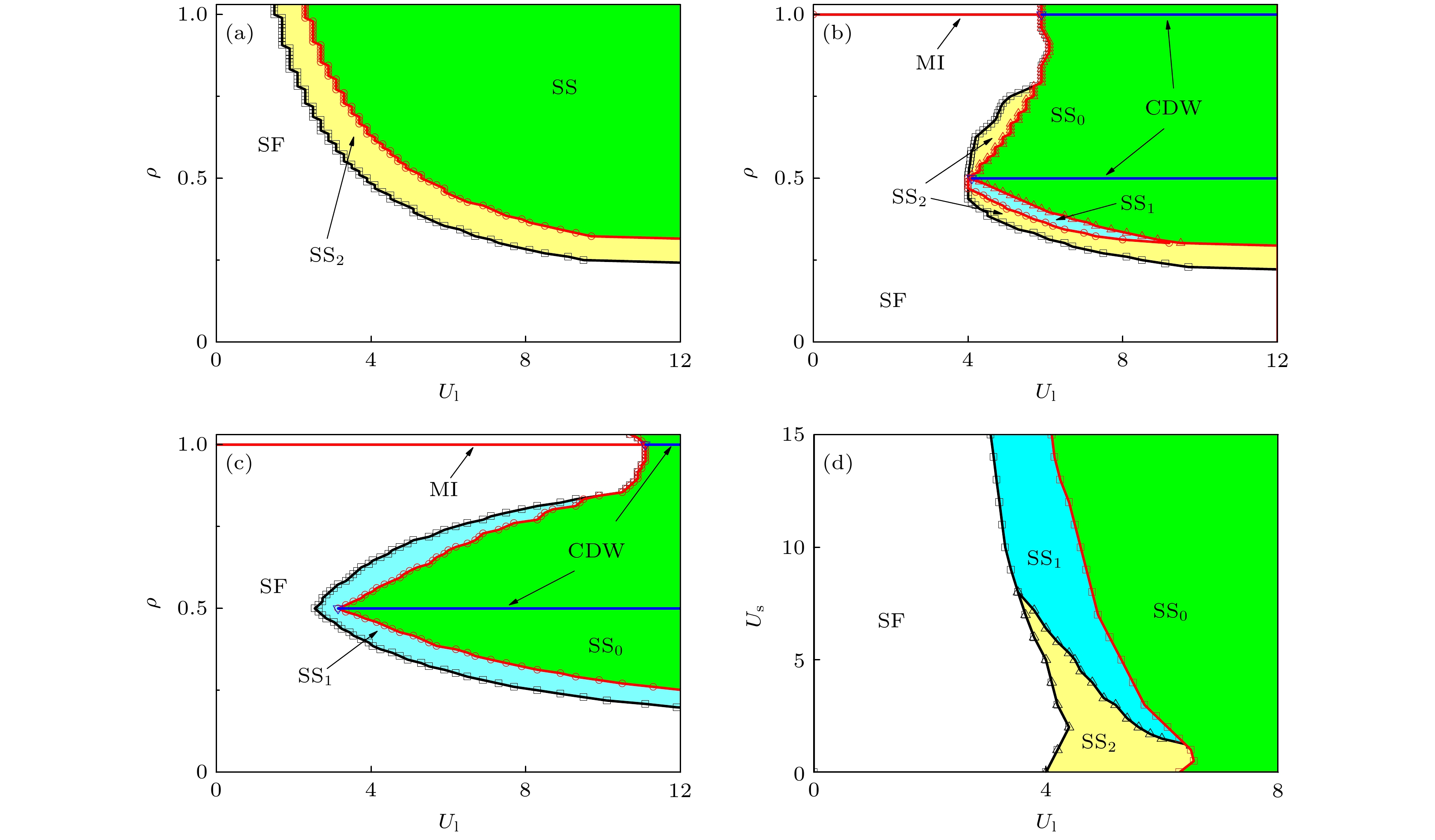
${U_{\rm{l}}}$ -ρ平面的相图 (a)${U_{\rm{s}}} = 0$ ; (b)${U_{\rm{s}}} = 5$ ; (c)${U_{\rm{s}}} = 10$ . (d)${U_{\rm{l}}}$ -${U_{\rm{s}}}$ 平面的相图, 参数$\rho = 0.4375$ . 所有图中, 共有参数$L = 96$ . SF表示超流, MI表示莫特绝缘体, CDW表示电荷密度波, SS0表示超固0相, SS1表示超固1相, SS2表示超固2相Fig. 6. (a)–(c) Phase-diagram between
${U_{\rm{l}}}$ and ρ with (a)${U_{\rm{s}}} = 0$ , (b)${U_{\rm{s}}} = 5$ and (c)${U_{\rm{s}}} = 10$ . (d) Phase-diagram between${U_{\rm{l}}}$ and${U_{\rm{s}}}$ , with filling$\rho = 0.4375$ . In all subfigure, we have$L = 96$ . SF denotes superfluid, MI denotes Mott insulator, CDW denotes charge density wave, SS0 denotes supersolid 0, SS1 denotes supersolid 1, SS2 denotes supersolid 2.表 1 量子相对应的序参量
Table 1. Corresponding orders of the phases.
序/相简写 超流SF 莫特绝缘体MI 电荷密度波CDW 超固0相SS0 超固1相SS1 超固2相SS2 $n~(k = 0)$ > 0 0 0 > 0 > 0 > 0 $S~(k = {\text{π} })$ 0 0 > 0 > 0 > 0 > 0 ${\nu _{{\rm{peak}}}}$ 0 0 π π $(0, {\text{π}})$ 0 
下载: 导出CSV
-
[1] Bloch I, Dalibard J, Nascimbane S 2012 Nat. Phys. 8 267
Google Scholar
[2] Fisher M P A, Weichman P B, Grinstein G, Fisher D S 1989 Phys. Rev. B 40 546
Google Scholar
[3] Jaksch D, Zoller P 2005 Ann. Phys. 315 52
Google Scholar
[4] Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885
Google Scholar
[5] Gross C, Bloch I 2017 Science 357 995
Google Scholar
[6] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301
Google Scholar
[7] Nagy D, Konya G, Szirmai G, Domokos P 2010 Phys. Rev. Lett. 104 130401
Google Scholar
[8] Ritsch H, Domokos P, Brennecke F, Esslinger T 2013 Rev. Mod. Phys. 85 553
Google Scholar
[9] Mottl R, Brennecke F, Baumann K, Landig R, Donner T, Esslinger T 2012 Science 336 1570
Google Scholar
[10] Landig R, Hruby L, Dogra N, Landini M, Mottl R, Donner T, Esslinger T 2016 Nature 532 476
Google Scholar
[11] Lang J, Piazza F, Zwerger W 2017 New J. Phys. 19 123027
Google Scholar
[12] Caballero-Benitez S F, Mekhov I B 2015 Phys. Rev. Lett. 115 243604
Google Scholar
[13] Bakhtiari M R, Hemmerich A, Ritsch H, Thorwart M 2015 Phys. Rev. Lett. 114 123601
Google Scholar
[14] Dogra N, Brennecke F, Huber S D, Donner T 2016 Phys. Rev. A 94 023632
Google Scholar
[15] Niederle A E, Morigi G, Rieger H 2016 Phys. Rev. A 94 033607
Google Scholar
[16] Sundar B, Mueller E J 2016 Phys. Rev. A 94 033631
Google Scholar
[17] Chen Y, Yu Z, Zhai H 2016 Phys. Rev. A 93 041601(R
Google Scholar
[18] Panas J, Kauch A, Byczuk K 2017 Phys. Rev. B 95 115105
Google Scholar
[19] Flottat T, de Forges de Parny L, Hebert F, Rousseau V G, Batrouni G G 2017 Phys. Rev. B 95 144501
Google Scholar
[20] Bogner B, Danilo C D, Rieger H 2019 Eur. Phys. J. B 92 111
Google Scholar
[21] Boninsegni M, Prokofev N V 2012 Rev. Mod. Phys. 84 759
Google Scholar
[22] Leggett A J 1970 Phys. Rev. Lett. 25 1543
Google Scholar
[23] Otterlo A V, Wagenblast K H 1994 Phys. Rev. Lett. 72 3598
Google Scholar
[24] Batrouni G G, Scalettar R T, Zimanyi G T, Kampf A P 1995 Phys. Rev. Lett. 74 2527
Google Scholar
[25] Scalettar R T, Batrouni G G, Kampf A P, Zimanyi G T 1995 Phys. Rev. B 51 8467
Google Scholar
[26] Otterlo A V, Wagenblast K H, Baltin R, Bruder C, Fazio R, Schon G 1995 Phys. Rev. B 52 16176
Google Scholar
[27] Rossini D, Fazio R 2011 New J. Phys. 14 065012
[28] White S R 1992 Phys. Rev. Lett. 69 2863
Google Scholar
[29] Schollwok U 2005 Rev. Mod. Phys. 77 259
Google Scholar
[30] Maschler C, Mekhov I B, Ritsch H 2008 Eur. Phys. J. D 46 545
Google Scholar
[31] Hodgman S S, Dall R G, Manning A G, Baldwin K G H, Truscott A G 2011 Science 331 1046
Google Scholar
[32] Liu H C 2016 Phys. Rev. A 94 023827
Google Scholar
[33] Schweigler T, Kasper V, Erne S, Mazets I, Rauer B, Cataldini F, Langen T, Gasenzer T, Berges J, Schmiedmayer J 2017 Nature 545 323
Google Scholar
[34] Hodgman S S, Khakimov R I, Truscott A G, Kheruntsyan K V 2017 Phys. Rev. Lett. 118 240402
Google Scholar
[35] Rispoli M, Lukin A, Schittko R, Kim S, Tai M E, Leonard J, Greiner M 2019 Nature 573 385
Google Scholar
[36] Fan J, Zhou X, Zheng W, Yi W, Chen G, Jia S 2018 Phys. Rev. A 98 043613
Google Scholar
[37] Stenger J, Inouye S, Chikkatur A P, Stamper-Kurn D M, Pritchard D E, Ketterle W 1999 Phys. Rev. Lett. 82 4569
Google Scholar
[38] Steinhauer J, Ozeri R, Katz N, Davidson N 2002 Phys. Rev. Lett. 88 120407
Google Scholar
[39] Greif D, Parsons M F, Mazurenko A, Chiu C S, Blatt S, Huber F, Ji G, Greiner M 2016 Science 351 953
Google Scholar
下载:
计量
- 文章访问数: 5210
- PDF下载量: 126
- 被引次数: 0
