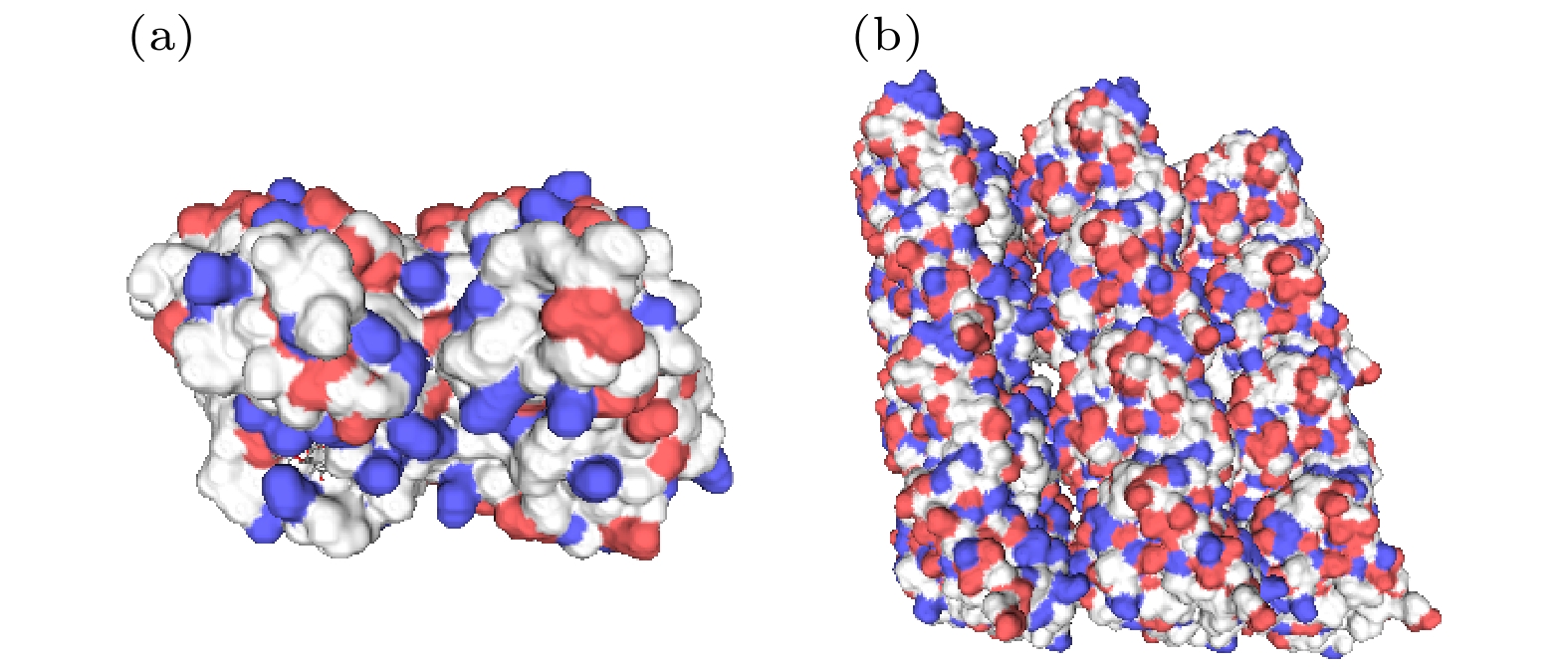
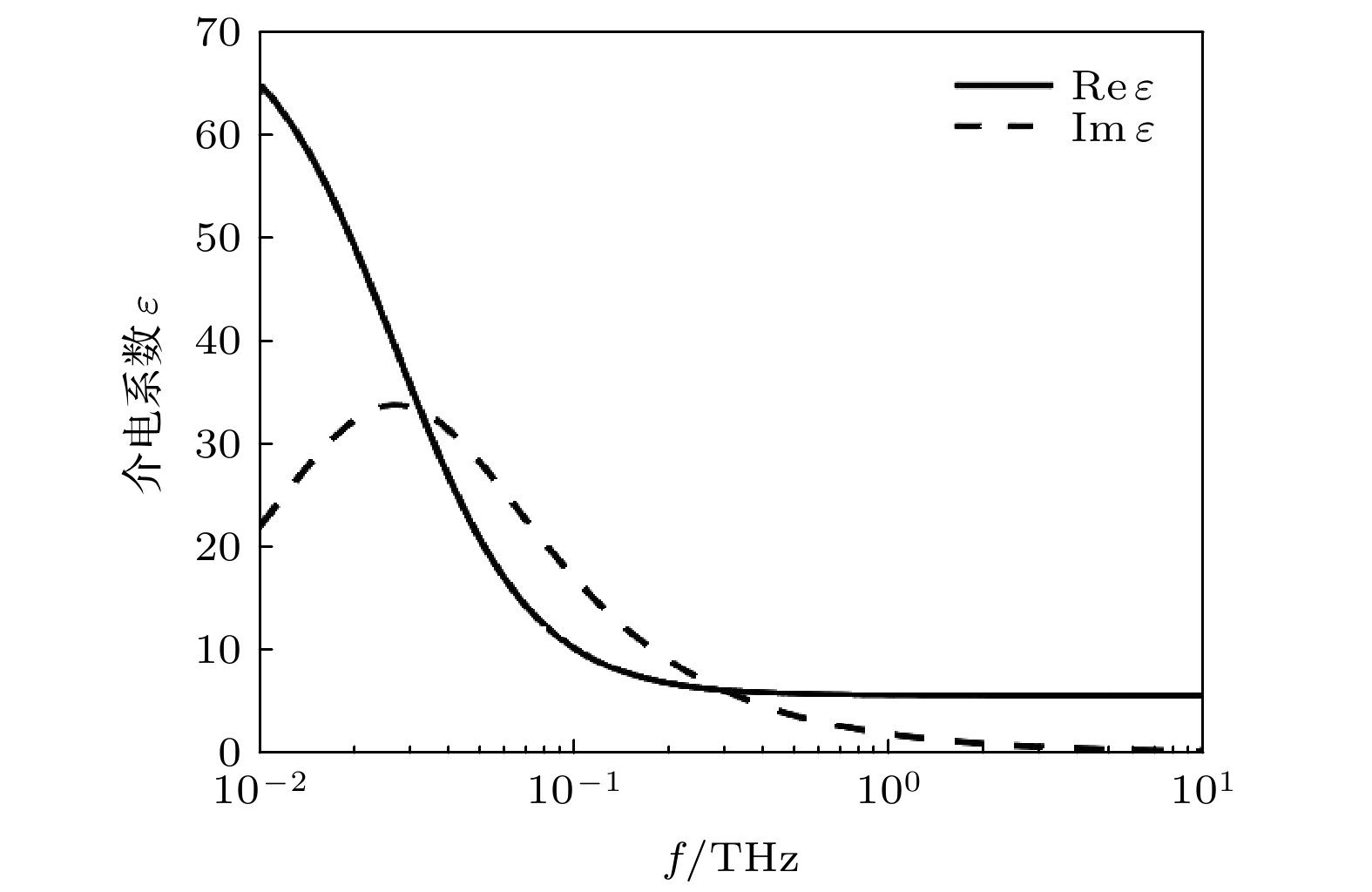
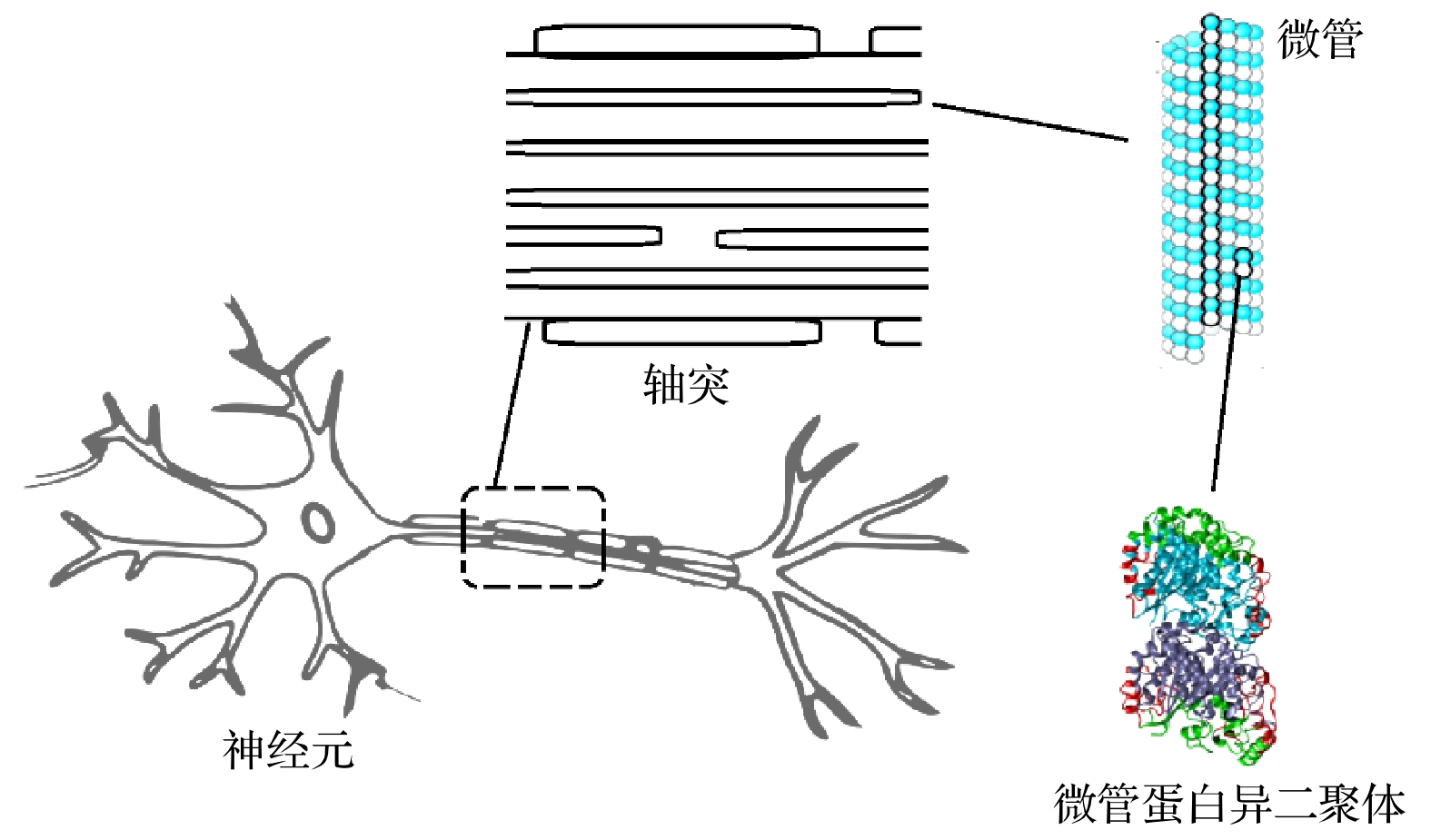
-
Neurons collect information from different parts of the biological body, generate signals and control their functions and activities. There are electromagnetic communication channels between neurons apart from the action potentials. Microtubules are the largest cytoskeletal filaments in neurons, with a diameter of about 25 nm. Microtubule is composed of alpha- and beta-tubulin subunits assembled into hollow cylindrical polymers supporting dynamical growth, and facilitate transport of proteins. In axons, dendrites, growth cones, and migratory neurons, microtubules are generally tightly organized in array and uniformly oriented. Because of the polarity and charge distribution of tubulins, the vibrations of microtubules generate electromagnetic fields. In this paper, electromagnetic fields induced by different vibrational modes of microtubules are studied. The vibrational mode of tubulins calculated using the normal mode analysis shows that there are abundant vibrational modes in the terahertz range. The electric fields of different vibration modes show distinct distribution features. The induced electromagnetic fields of microtubules can be stronger than thermal noise because of reduced permittivity of intracellular fluid for higher frequencies in a nanometric confined region. Since water exhibits layered structuring near all surfaces independent of their hydrophilicity, the permittivity of water surrounding tubulins between microtubules is expected to decrease significantly because of surface-induced alignment of water molecular dipoles. While the permittivity of surrounding medium decreases to 5, the electromagnetic potential energy between two 100-nm-long microtubules can be stronger than the thermal energy within a 30-nm-long distance. As high frequency vibrations are generally localized in the microtubule, terahertz electromagnetic interactions can be present between tubulins and short microtubules. Because the separation between microtubule arrays in neurons is in a range from 20 nm to 100 nm, electromagnetic interactions between microtubules can dominate the thermal motions, and affect the biological functions. Simulation results show that the electromagnetic potential energy increases over one order of magnitude when the vibration amplitude is changed from 0.1 nm to 0.4 nm. The results indicate that the electromagnetic interaction between microtubules is important for a better understanding of neural functions and communication. Terahertz stimulations can be used to detect and modulate the neural signals. The microtubule vibration generated magnetic field can be applied to disease diagnosis and brain-machine interface.
-
Keywords:
- neuron /
- microtubule /
- electromagnetic fields /
- dielectric constant
[1] Hodgkin A L, Huxley A F 1952 Physiol. 117 500
Google Scholar
[2] Hodgkin A L, Huxley A F 1952 Physiol. 116 449
Google Scholar
[3] Hodgkin A L, Huxley A F 1952 Physiol. 116 497
Google Scholar
[4] 刘延生, 吴开杰, 刘春良, 崔刚强, 常超, 刘国志 2020 中国科学: 物理 力学 天文学 63 274211
Google Scholar
Liu Y S, Wu K J, Liu C L, Cui G Q, Chang C, Liu G Z 2020 Sci. China, Ser. G 63 274211
Google Scholar
[5] Kučera O, Havelka D, Cifra M 2017 Wave Motion 72 13
Google Scholar
[6] Cifra M, Fields J Z, Farhadi A 2011 Prog. Biophys. Mol. Biol. 105 223
Google Scholar
[7] 赵月, 詹启民 2012 理论生物学与医学模型 9 26
Google Scholar
Zhao Y, Zhan Q M 2012 Theor. Biol. Med. Modell. 9 26
Google Scholar
[8] De Ninno A, Pregnolato M 2017 Electromagn. Biol. Med. 36 115
Google Scholar
[9] Pokorný J, Jelínek F, Trkal V, Lamprecht I, Hölzel R 1997 J. Biol. Phys. 23 171
Google Scholar
[10] Cifra M, Pokorný J, Havelka D 2010 Biosystems 100 122
Google Scholar
[11] Deriu M A, Soncini M, Orsi M, Patel M, Essex J W, Montevecchi F M, Redaelli A 2010 Biophys. J. 99 2190
Google Scholar
[12] Sirenko Y M, Stroscio M A, Kim K W 1996 Phy. Rev. E 53 1003
Google Scholar
[13] Thackston K, Deheyn D, Sievenpiper D 2019 Phys. Rev. E 100 022410
Google Scholar
[14] Akhmanova A, Steinmetz M O 2015 Nat. Rev. Mol. Cell Biol. 16 711
Google Scholar
[15] Amos L A 1995 Trends Cell Biol. 5 48
Google Scholar
[16] Mershin A, Kolomenski A.A, Schuessler H A, Nanopoulos D V 2004 Biosystems 77 73
Google Scholar
[17] Pohl H A, Braden T, Robinson S, Piclardi J, Pohl D G 1981 J. Biol. Phys. 9 133
Google Scholar
[18] Hölzel R 2001 Electro-Magnetobiol. 20 1
Google Scholar
[19] Pokorný J, Hašek J, Jelínek F, Šaroch J, Palán B 2001 Electro-Magnetobiol. 20 371
Google Scholar
[20] Tuszyński J A, Brown J A, Crawford E, Carpenter E J, Nip M L A, Dixon J M, Satarić M V 2005 Math. Comput. Modell. 41 1055
Google Scholar
[21] van den Heuvel M G L, de Graaff M P, Lemay S G, Dekker C 2007 Proc. Natl. Acad. 104 7770
Google Scholar
-
图 2 (a)微管蛋白异二聚体(PDB:1TUB)电荷分布; (b)微管(PDB:6EW0)电荷分布(swiss model)
Fig. 2. (a) Charge distribution of tubulin alpha-beta dimer; (b) charge distribution of GDP-microtubule (PDB:6EW0).
图 3 微管不同振动模式示意图 (a) 轴向振动; (b) 弯曲振动; (c) 扭转振动; (d) 屈曲振动
Fig. 3. Schematic diagram of microtubule vibrations modes: (a) Axial vibration; (b) bending vibration; (c) twisting vibration; (d) flexing vibration.
图 4 不同长度微管屈曲振动势能的传播特性 (A = 0.1 nm,
${\varepsilon }_{\rm{r}}=80)$ Fig. 4. Vibrating potential transferring performance in different length of microtubule at A = 0.1 nm,
${\varepsilon }_{\rm{r}}=80$ .
图 5 水溶液介电系数的频率响应
Fig. 5. Permittivity of intracellular fluid of neuron as a function of frequency.
图 7 四种振动模态的势能 (L = 100 nm, A = 0.1 nm) (a) 轴向振动; (b) 弯曲振动; (c) 扭转振动; (d) 屈曲振动
Fig. 7. Electromagnetic potential of four modes of microtubule vibration at L = 100 nm, A = 0.1 nm: (a) Axial vibration; (b) bending vibration; (c) twisting vibration; (d) flexing vibration.
图 8 不同振动振幅对势能的影响
$({\varepsilon }_{\rm{r}}=80)$ (a) 轴向振动; (b) 弯曲振动; (c) 扭转振动; (d) 屈曲振动Fig. 8. Potential in various vibration magnitude at
${\varepsilon }_{\rm{r}}=80$ : (a) Axial vibration; (b) flexing vibration; (c) twisting vibration; (d) flexing vibration.
图 9 不同振动模式电场分布
$({\varepsilon }_{\rm{r}}=80,\;A=0.1\;{\rm{nm}})$ (a) 轴向振动; (b) 弯曲振动; (c) 扭转振动; (d) 屈曲振动Fig. 9. Electric field distribution at
${\varepsilon }_{\rm{r}}=80$ and A = 0.1 nm: (a) Axial vibration; (b) bending vibration; (c) twisting vibration; (d) flexing vibration.
图 10 不同振动模式电场分布
$({\varepsilon }_{\rm{r}}=5\;A=0.1\;{\rm{nm}})$ (a) 轴向振动; (b) 弯曲振动; (c) 扭转振动; (d) 屈曲振动Fig. 10. Electric field distribution at
${\varepsilon }_{\rm{r}}=5,$ A = 0.1 nm: (a) Axial vibration; (b) bending vibration; (c) twisting vibration; (d) flexing vibration. -
[1] Hodgkin A L, Huxley A F 1952 Physiol. 117 500
Google Scholar
[2] Hodgkin A L, Huxley A F 1952 Physiol. 116 449
Google Scholar
[3] Hodgkin A L, Huxley A F 1952 Physiol. 116 497
Google Scholar
[4] 刘延生, 吴开杰, 刘春良, 崔刚强, 常超, 刘国志 2020 中国科学: 物理 力学 天文学 63 274211
Google Scholar
Liu Y S, Wu K J, Liu C L, Cui G Q, Chang C, Liu G Z 2020 Sci. China, Ser. G 63 274211
Google Scholar
[5] Kučera O, Havelka D, Cifra M 2017 Wave Motion 72 13
Google Scholar
[6] Cifra M, Fields J Z, Farhadi A 2011 Prog. Biophys. Mol. Biol. 105 223
Google Scholar
[7] 赵月, 詹启民 2012 理论生物学与医学模型 9 26
Google Scholar
Zhao Y, Zhan Q M 2012 Theor. Biol. Med. Modell. 9 26
Google Scholar
[8] De Ninno A, Pregnolato M 2017 Electromagn. Biol. Med. 36 115
Google Scholar
[9] Pokorný J, Jelínek F, Trkal V, Lamprecht I, Hölzel R 1997 J. Biol. Phys. 23 171
Google Scholar
[10] Cifra M, Pokorný J, Havelka D 2010 Biosystems 100 122
Google Scholar
[11] Deriu M A, Soncini M, Orsi M, Patel M, Essex J W, Montevecchi F M, Redaelli A 2010 Biophys. J. 99 2190
Google Scholar
[12] Sirenko Y M, Stroscio M A, Kim K W 1996 Phy. Rev. E 53 1003
Google Scholar
[13] Thackston K, Deheyn D, Sievenpiper D 2019 Phys. Rev. E 100 022410
Google Scholar
[14] Akhmanova A, Steinmetz M O 2015 Nat. Rev. Mol. Cell Biol. 16 711
Google Scholar
[15] Amos L A 1995 Trends Cell Biol. 5 48
Google Scholar
[16] Mershin A, Kolomenski A.A, Schuessler H A, Nanopoulos D V 2004 Biosystems 77 73
Google Scholar
[17] Pohl H A, Braden T, Robinson S, Piclardi J, Pohl D G 1981 J. Biol. Phys. 9 133
Google Scholar
[18] Hölzel R 2001 Electro-Magnetobiol. 20 1
Google Scholar
[19] Pokorný J, Hašek J, Jelínek F, Šaroch J, Palán B 2001 Electro-Magnetobiol. 20 371
Google Scholar
[20] Tuszyński J A, Brown J A, Crawford E, Carpenter E J, Nip M L A, Dixon J M, Satarić M V 2005 Math. Comput. Modell. 41 1055
Google Scholar
[21] van den Heuvel M G L, de Graaff M P, Lemay S G, Dekker C 2007 Proc. Natl. Acad. 104 7770
Google Scholar
下载:
计量
- 文章访问数: 5319
- PDF下载量: 80
- 被引次数: 0
