-
为了提高地声反演算法的计算效率, 探索克服地声反演结果多值性问题, 本文利用宽带、多收发位置的传播损失数据结合传播损失在地声参数先验搜索区间内的随机多项式展开系数矩阵, 反演得到海底纵波声速、吸收率和密度比重. 使用随机多项式展开近似传播损失时, 展开系数的自变量为声波频率、收发位置等参数, 随机多项式的自变量为表示声速、吸收率、比重在各自搜索区间内均匀分布的随机变量. 传播损失的展开系数通过嵌入随机多项式的声学宽角抛物方程结合盖辽金投影、最小角度回归算法计算求得. 在低频、一定声传播水平距离以内和地声参数搜索区间长度适中时, 使用随机多项式展开近似传播损失的相对误差在1%以下. 仿真发现, 在浅海环境中使用低频、一定声传播水平距离以内的传播损失数据, 在接收信号信噪比较高、声源和水听器相对位置误差较小时, 选择合适的随机多项式展开截断幂次可较准确地反演海底声速、吸收率和密度比重, 且计算效率比网格遍历搜索方法提高一个数量级以上.In order to improve the computational efficiency of algorithms while exploring the method to overcome the ambiguity problems in underwater geo-acoustic inversion, we use the data of transmission losses at the broadband sound frequencies and multiple propagating distances with the matrix of polynomial chaos expansion coefficients of transmission losses to invert the speed (c), attenuation (α) of compression sound wave and the density ratio of seabed to seawater (ρ) in their prior searching intervals. When approximating the transmission loss with the polynomial chaos expansion, the expansion coefficients are the functions of parameters including sound frequency, source and hydrophone’s position while the polynomial bases are functions of the above geo-acoustic parameters which are uniformly distributed in their respective intervals. The expansion coefficients are calculated by embedding the orthogonal polynomial bases into the acoustic wide-angle parabolic equation model. After that, the coefficients are deduced using the Galerkin projection and least angel regression. Under the situations of low sound frequency, short or medium sound propagation distance and short or medium length of intervals of geo-acoustic parameters, the polynomial chaos expansion can approximate the transmission losses accurately with the relatively error less than 1%. In the simulation case, with the high signal to noise ratio and the low errors of relative distances between source and receivers, the geo-acoustic parameters can be inverted accurately when the appropriate truncated powers are chosen. And the time cost is reduced by at least an order of magnitude compared with that of traversal grids searching procedure.
-
Keywords:
- geo-acoustic inversion /
- polynomial chaos expansion /
- acoustic wide-angle parabolic equation
[1] 尚尔昌 2019 应用声学 038 468
Google Scholar
Shang E C 2019 J. Appl. Acoust. 038 468
Google Scholar
[2] Gerstoft P 1994 J. Acoust. Soc. Am. 95 770
Google Scholar
[3] Gerstoft P 1998 J. Acoust. Soc. Am. 104 808
[4] Dosso S E 2002 J. Acoust. Soc. Am. 111 129
Google Scholar
[5] Dosso S E, Nielsen P L 2002 J. Acoust. Soc. Am. 111 143
Google Scholar
[6] Sambridge M 1999 Geophys. J. Int. 138 479
Google Scholar
[7] Holland C W, Osler J 2000 J. Acoust. Soc. Am. 107 1263
Google Scholar
[8] 李整林, 鄢锦, 李风华 2002 声学学报 06 487
Google Scholar
Li Z L, Yan J, Li F H 2002 Acta Acoustica 06 487
Google Scholar
[9] 李梦竹, 李整林, 周纪浔, 张仁和 2019 68 094301
Google Scholar
Li M Z, Li Z L, Zhou J X, Zhang R H 2019 Acta Phys. Sin. 68 094301
Google Scholar
[10] Li Z L, Zhang R H, Yan J 2004 IEEE. J. Oceanic. Eng. 29 973
[11] Li Z L, Zhang R H 2004 Chin. Phys. Lett. 21 1100
Google Scholar
[12] Li Z L, Zhang R H 2007 Chin. Phys. Lett. 24 471
Google Scholar
[13] Li Z L, Li F H 2010 Chin. J. Oceanol. Limnol. 28 990
Google Scholar
[14] Xiu D B, Karniadakis G E 2001 SIAM. J. Sci. Comput. 24 619
Google Scholar
[15] Finette S 2005 J. Acoust. Soc. Am. 117 997
Google Scholar
[16] Finette S 2006 J. Acoust. Soc. Am. 120 2567
Google Scholar
[17] Khine Y Y, Creamer D B, Finette S 2011 J. Comput. Acoust. 18 397
Google Scholar
[18] 程广利, 张明敏 2013 声学学报 38 294
Cheng G L, Zhang M M 2013 Acta Acoustica 38 294
[19] 过武宏, 笪良龙, 赵建昕 2013 应用声学 32 464
Guo W H, Da L L, Zhao J X 2013 Appl. Acoust. 32 464
[20] 笪良龙, 过武宏, 赵建昕 2015 声学学报 40 137
Da L L, Guo W H, Zhao J X 2015 Acta Acoustica 40 137
[21] 笪良龙, 崔宝龙, 过武宏 2017 声学学报 42 25
Da L L, Cui B L, Guo W L 2017 Acta Acoustica 42 25
[22] LePage K D 2007 9th International Conference on Information Fusion Florence, Italy, July 10–13, 2007 pp1–5
[23] James K R, Dowling D R, 2011 J. Acoust. Soc. Am. 129 589
Google Scholar
[24] 张鹏, 吴立新 2020 应用声学 40 422
Zhang P, Wu L X 2020 Appl. Acoust. 40 422
[25] Finette S 2009 J. Acoust. Soc. Am. 126 2242
Google Scholar
[26] Gerdes F, Finette S 2012 J. Acoust. Soc. Am. 132 2251
Google Scholar
[27] Collins M D 1993 J. Acoust. Soc. Am. 93 1736
Google Scholar
[28] Creamer D B 2008 Wave Random Complex 18 197
Google Scholar
[29] Choi S K, Canfield R A, Grandhi R V 2004 AIAA J. 42 1191
Google Scholar
[30] Blatman G, Sudret B 2011 J. Comput. Phys. 230 2345
Google Scholar
[31] Creamer D B 2006 J. Acoust. Soc. Am. 119 1919
Google Scholar
[32] Jensen F B, Kuperman W A, Porter M B 2011 Computational Ocean Acoustics (New York: Springer) pp337–455
-
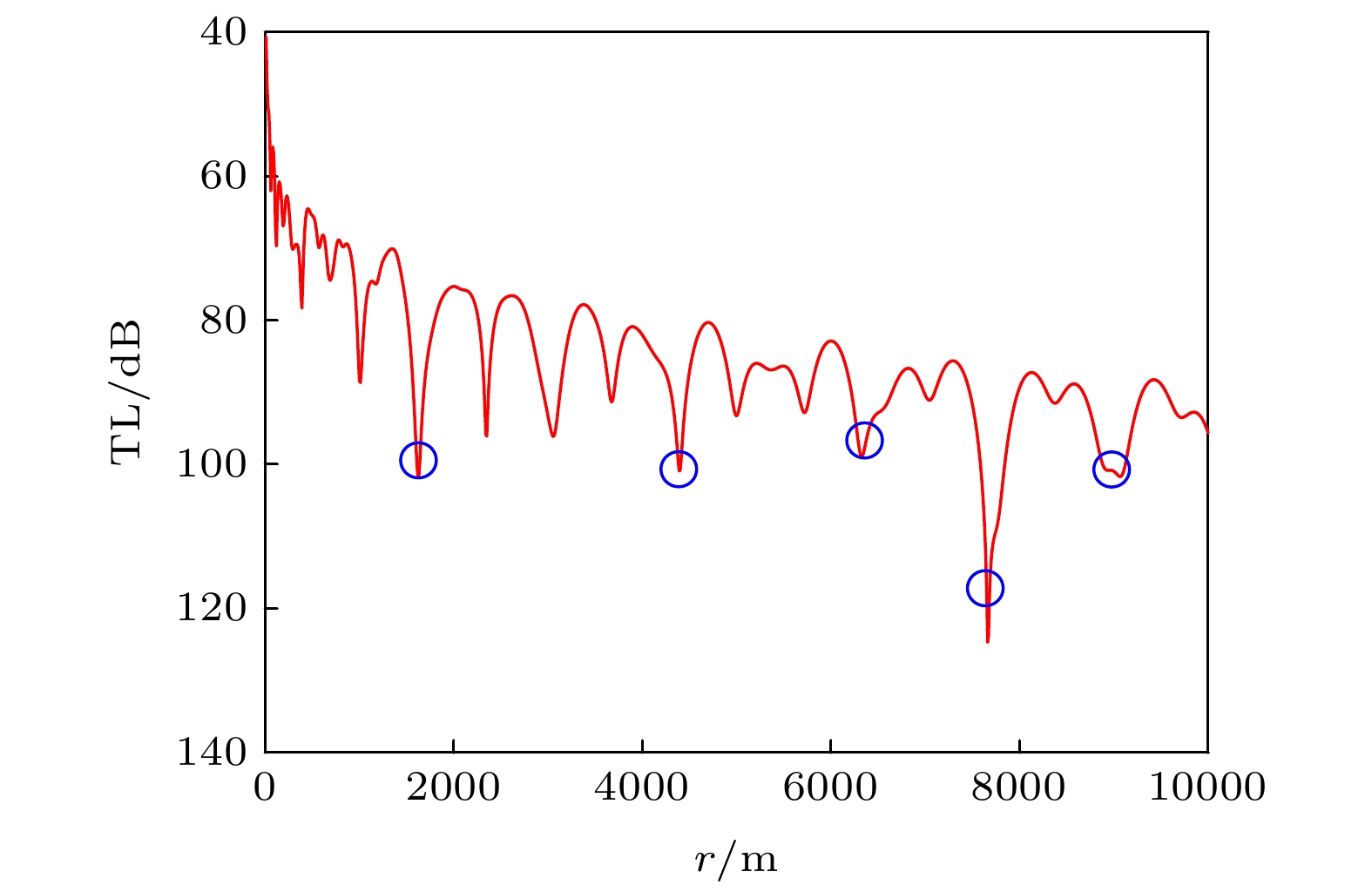
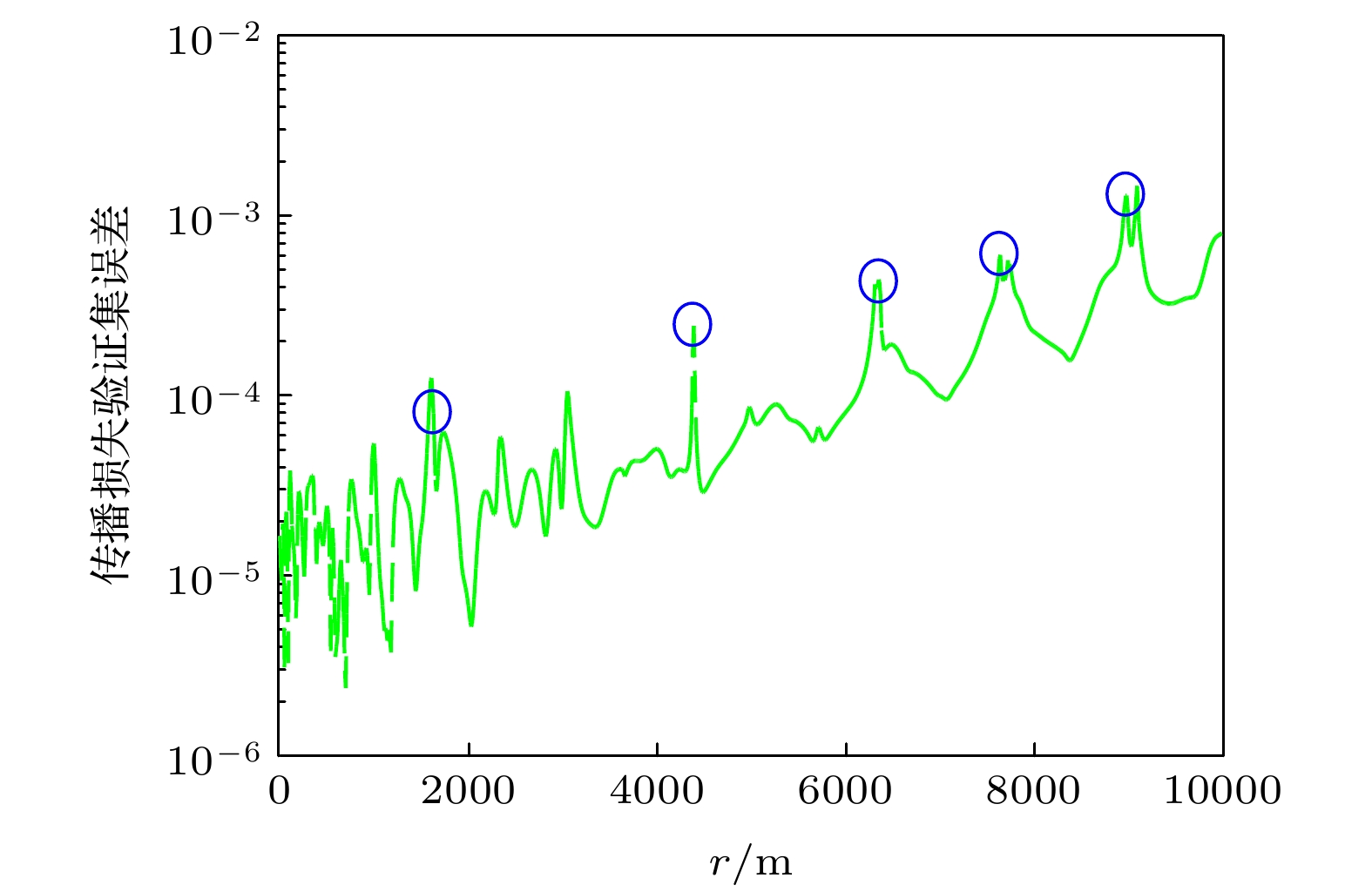
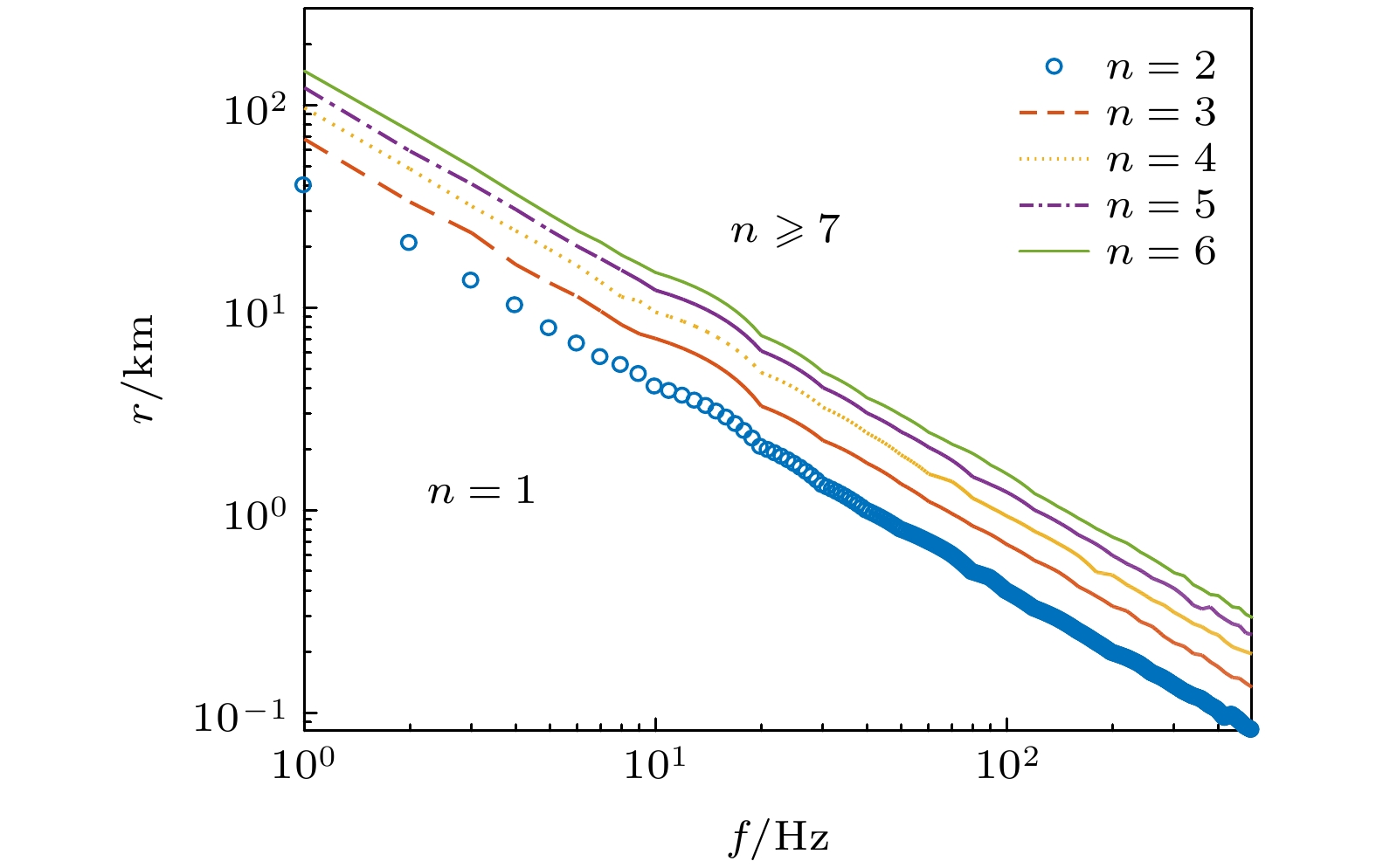
图 1 不同截断幂次下, 在“频率f-距离r”平面上随机多项式展开平面波声压相对误差1%的等值线. 其中声速的范围是1645−1655 m/s, 吸收率的范围是0.55−0.65 dB/λ
Fig. 1. Isolines of 1% relative error about sound pressure for plane wave expanded by the polynomial chaos in frequency-range space. The intervals of sound speed and attenuation are 1645−1655 m/s and 0.55−0.65 dB/λ, respectively.
图 2 Pekeris波导中100 m深度不同水平距离上的声传播损失, 圈点为传播损失的部分极大值点
Fig. 2. Acoustic transmission loss at different horizontal ranges with the depth of 100 m in Pekeris waveguide. Circled points are partial local maximum points.
图 3 Pekeris波导中100 m深度不同水平距离上随机多项式展开近似声传播损失的验证集误差, 圈点为部分误差极大值点
Fig. 3. Validation set errors of acoustic transmission loss expanded by polynomial chaos at different horizontal ranges with the depth of 100 m in Pekeris waveguide. Circled points are partial local maximum points.
图 4 不同随机多项式截断幂次N、不同深度方向差分网格数Z下, 遍历法与随机多项式展开法计算复杂度之比
Fig. 4. Calculation complexity ratio of the ergodic method and the polynomial chaos expansion method under different polynomial truncated power N and difference grid number in depth direction Z.
图 6 不同随机多项式展开截断幂次下, (a)海底声速、(b)吸收率、(c)比重反演结果的误差
Fig. 6. Errors of geo-acoustic inversion results for (a) sound speed, (b) attenuation and (c) ratio of density under different truncated powers of polynomial chaos.
图 7 随机多项式展开截断幂次
$ N=1 $ 时的海底声速的反演结果Fig. 7. Geo-acoustic inversion results of sound speed of seabed when the truncated power of polynomial chaos N =1.
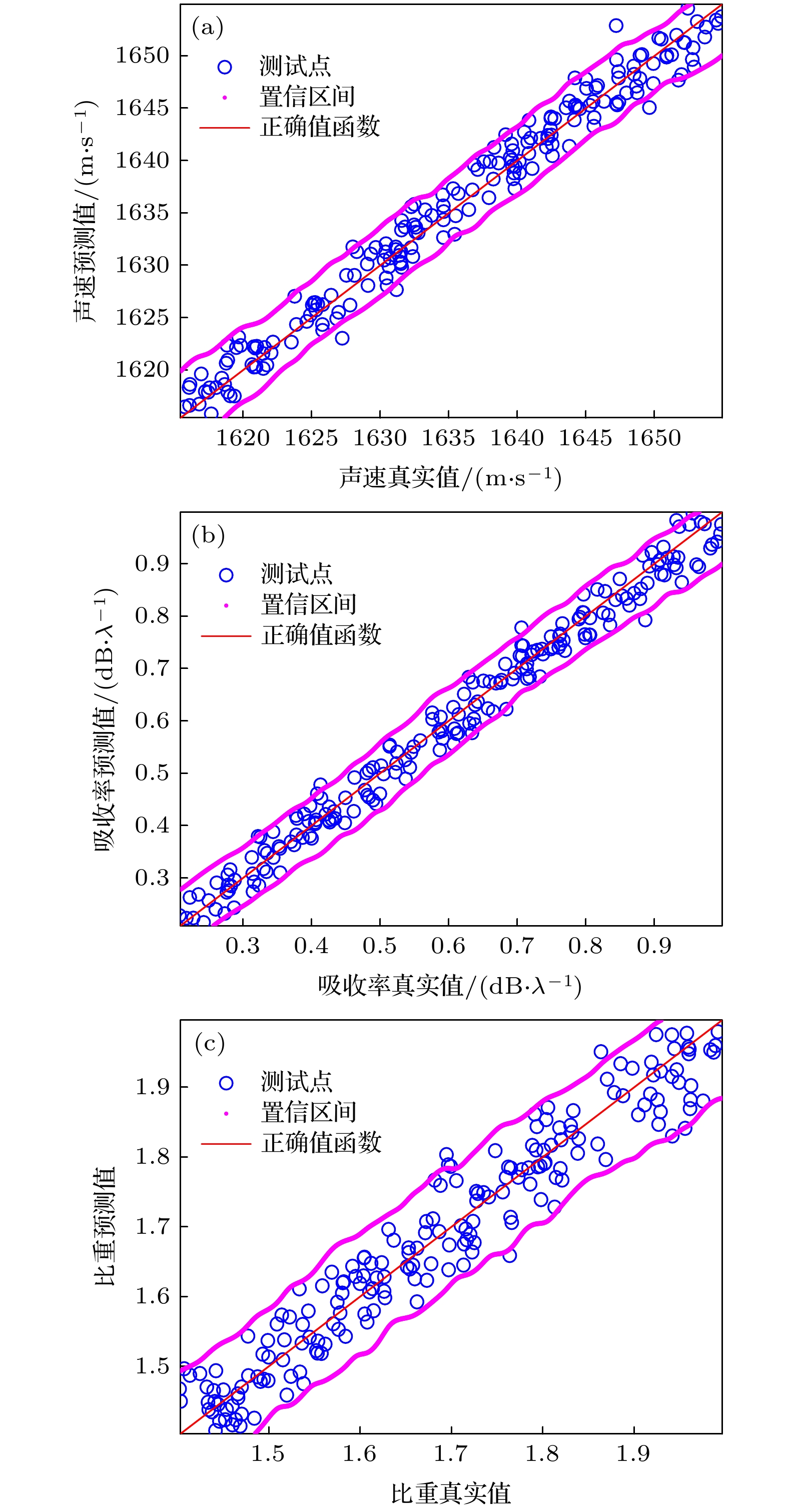
图 8 信噪比为15 dB, 收发水平距离误差为 ± 20 m时, (a)模拟声速、(b)吸收率、(c)比重的反演结果及其置信区间
Fig. 8. Geo-acoustic inversion results and its confidential intervals of (a) sound speed, (b) sound attenuation and (c) ratios of density between seabed and sea water when the signal to noise ratio is 15 dB and error of horizontal distance is ± 20 m.
表 1 Pekeris波导的水文环境和声源参数
Table 1. Hydrological conditions of Pekeris waveguide and acoustic source parameters.
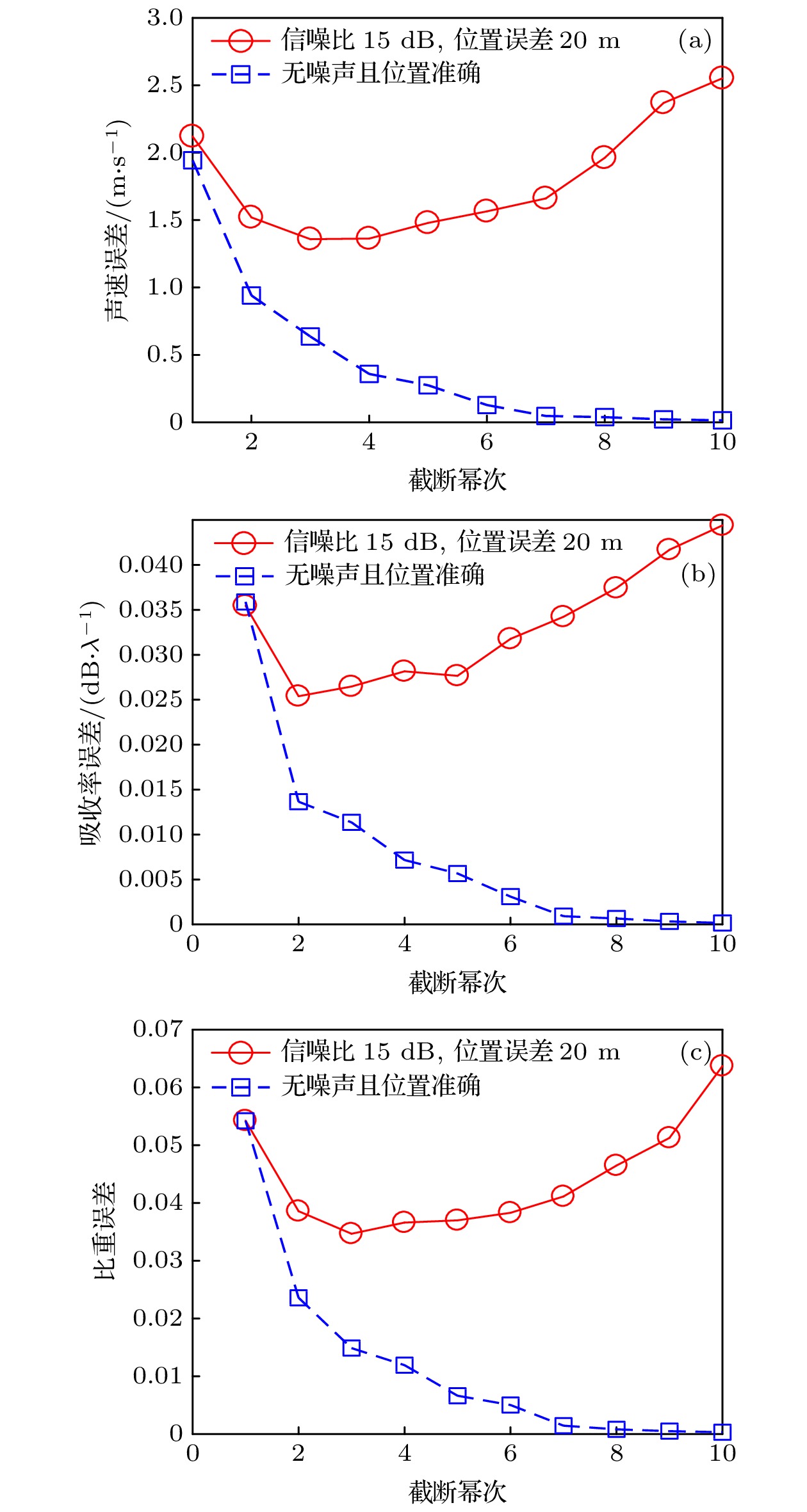
海水深度/m 海水声速/(m·s–1) 声源频率/Hz 发射深度/m 接收深度/m 100 1500 50 100 100 
下载: 导出CSV
表 2 接收信号不同信噪比下反演误差均值
Table 2. Average inversion errors under different signal to noise ratios.
信噪比/dB 0 5 10 15 20 海底声速$ \overline {{\Delta}c}/({\rm{m}}\cdot {\rm{s}}^{-1}) $ 2.63 1.76 1.13 0.71 0.50 海底吸收率$ \overline {{\Delta}\alpha }/({\rm{dB}}\cdot {\lambda }^{-1}) $ 0.09 0.04 0.02 0.02 0.01 海底比重$ \overline {{\Delta}\left(\rho \right)} $ 0.10 0.05 0.03 0.02 0.01
下载: 导出CSV
表 3 收发水平距离不同误差下反演误差均值
Table 3. Average inversion errors under different horizontal distances.
收发水平距离误差$ {\Delta}r/{\rm{m}} $ 50 30 20 10 海底声速$ \overline {{\Delta}c}/({\rm{m}}\cdot {\rm{s}}^{-1}) $ 2.49 1.64 1.21 0.65 海底吸收率$ \overline {{\Delta}\alpha }/({\rm{dB}}\cdot {\lambda }^{-1}) $ 0.04 0.03 0.02 0.01 海底比重$ \overline {{\Delta}\left(\rho \right)} $ 0.06 0.04 0.03 0.01
下载: 导出CSV
表 4 使用遍历法与随机多项式展开法反演海底参数所需计算时间
Table 4. Calculation time of geo-acoustic inversion using method of traversing and polynomial chaos expansion.
遍历法计算时间/min 随机多项式展开法反演计算时间/min 截断幂次N 1 2 3 4 5 6 7 8 9 10 7047 2 9 10 77 199 574 2254 6130 18783 57547
下载: 导出CSV
-
[1] 尚尔昌 2019 应用声学 038 468
Google Scholar
Shang E C 2019 J. Appl. Acoust. 038 468
Google Scholar
[2] Gerstoft P 1994 J. Acoust. Soc. Am. 95 770
Google Scholar
[3] Gerstoft P 1998 J. Acoust. Soc. Am. 104 808
[4] Dosso S E 2002 J. Acoust. Soc. Am. 111 129
Google Scholar
[5] Dosso S E, Nielsen P L 2002 J. Acoust. Soc. Am. 111 143
Google Scholar
[6] Sambridge M 1999 Geophys. J. Int. 138 479
Google Scholar
[7] Holland C W, Osler J 2000 J. Acoust. Soc. Am. 107 1263
Google Scholar
[8] 李整林, 鄢锦, 李风华 2002 声学学报 06 487
Google Scholar
Li Z L, Yan J, Li F H 2002 Acta Acoustica 06 487
Google Scholar
[9] 李梦竹, 李整林, 周纪浔, 张仁和 2019 68 094301
Google Scholar
Li M Z, Li Z L, Zhou J X, Zhang R H 2019 Acta Phys. Sin. 68 094301
Google Scholar
[10] Li Z L, Zhang R H, Yan J 2004 IEEE. J. Oceanic. Eng. 29 973
[11] Li Z L, Zhang R H 2004 Chin. Phys. Lett. 21 1100
Google Scholar
[12] Li Z L, Zhang R H 2007 Chin. Phys. Lett. 24 471
Google Scholar
[13] Li Z L, Li F H 2010 Chin. J. Oceanol. Limnol. 28 990
Google Scholar
[14] Xiu D B, Karniadakis G E 2001 SIAM. J. Sci. Comput. 24 619
Google Scholar
[15] Finette S 2005 J. Acoust. Soc. Am. 117 997
Google Scholar
[16] Finette S 2006 J. Acoust. Soc. Am. 120 2567
Google Scholar
[17] Khine Y Y, Creamer D B, Finette S 2011 J. Comput. Acoust. 18 397
Google Scholar
[18] 程广利, 张明敏 2013 声学学报 38 294
Cheng G L, Zhang M M 2013 Acta Acoustica 38 294
[19] 过武宏, 笪良龙, 赵建昕 2013 应用声学 32 464
Guo W H, Da L L, Zhao J X 2013 Appl. Acoust. 32 464
[20] 笪良龙, 过武宏, 赵建昕 2015 声学学报 40 137
Da L L, Guo W H, Zhao J X 2015 Acta Acoustica 40 137
[21] 笪良龙, 崔宝龙, 过武宏 2017 声学学报 42 25
Da L L, Cui B L, Guo W L 2017 Acta Acoustica 42 25
[22] LePage K D 2007 9th International Conference on Information Fusion Florence, Italy, July 10–13, 2007 pp1–5
[23] James K R, Dowling D R, 2011 J. Acoust. Soc. Am. 129 589
Google Scholar
[24] 张鹏, 吴立新 2020 应用声学 40 422
Zhang P, Wu L X 2020 Appl. Acoust. 40 422
[25] Finette S 2009 J. Acoust. Soc. Am. 126 2242
Google Scholar
[26] Gerdes F, Finette S 2012 J. Acoust. Soc. Am. 132 2251
Google Scholar
[27] Collins M D 1993 J. Acoust. Soc. Am. 93 1736
Google Scholar
[28] Creamer D B 2008 Wave Random Complex 18 197
Google Scholar
[29] Choi S K, Canfield R A, Grandhi R V 2004 AIAA J. 42 1191
Google Scholar
[30] Blatman G, Sudret B 2011 J. Comput. Phys. 230 2345
Google Scholar
[31] Creamer D B 2006 J. Acoust. Soc. Am. 119 1919
Google Scholar
[32] Jensen F B, Kuperman W A, Porter M B 2011 Computational Ocean Acoustics (New York: Springer) pp337–455
下载:
计量
- 文章访问数: 4375
- PDF下载量: 77
- 被引次数: 0
