-
针对雷达、通信系统的正弦中频信号在低信噪比中难以接收的问题, 提出一种经随机共振增强正弦信号的接收方法. 通过分析正弦信号的随机共振机理, 引入判决时刻, 将非自治的福克-普朗克方程(Fokker-Planck Equation, FPE)转化为自治方程求解, 得到FPE的含时间参量的周期定态解; 在得到随机共振输出粒子的概率密度基础上, 通过分析能量接收、匹配滤波接收特点, 提出基于二次多项式的接收结构, 通过使偏移系数最大化, 确定二次多项式系数, 初步确定了检验统计量; 为进一步减小误码率, 结合“N次采样取平均”思想, 根据中心极限定理, 将问题转换为高斯分布下的假设检验问题, 最终提出了随机共振增强正弦信号的二次多项式接收方法和处理流程. 仿真验证了理论的正确性, 并得到: 在最佳匹配随机共振参数的限制下, 当 N = 500时, 二次多项式接收结构在信噪比大于–17 dB时误码率低于2.2 × 10–2.Aiming at the reception of the intermediate frequency signal of sine wave of radio and communication system at extremely low signal-to-noise ratio (SNR), a quadratic polynomial receiving scheme for sine signals enhanced by stochastic resonance (SR) is proposed. Through analyzing the mechanism of sine signals enhanced by SR and introducing the decision time, the analytic periodic stable solution with time parameters of the Fokker-Planck Equation (FPE) is obtained through converting the non-autonomous FPE into an autonomous equation. Based on the probability density function of the particle of SR output, a quadratic polynomial receiving scheme is proposed by analyzing the feature of energy detector and matching filter receiver. By maximizng the deflection coefficient, the binomial coefficients and the test statistic are obtained. For further reducing the bit error, by combining the thought of " the average of N samples”, a quadratic polynomial receiving scheme for sine signals enhanced by SR is proposed through the hypothesis under Gaussian distribution approximation of the law of large N. And the conclusion is obtained as follows. When N is 500 and the SNR is greater than –17 dB, the bit error rate is less than 2.2 × 10–2, under the constraint of the parameters of the optimally matched SR.
-
Keywords:
- stochastic resonance /
- reception of sine signal /
- quadratic polynomial receiving scheme /
- Fokker-Planck equation /
- deflection coefficient
[1] Quan H D, Zhao H, Cui P Z 2015 Wirel. Pers. Commun. 81 1159
Google Scholar
[2] 赵寰, 全厚德, 崔佩璋 2015 系统工程与电子技术 37 671
Zhao H, Quan H D, Cui P Z 2015 Syst. Eng. Electron. 37 671
[3] Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A 14 453
Google Scholar
[4] Gammaitoni L, Hänggi P, Jung P 1998 Rev. Mod. Phys. 70 223
Google Scholar
[5] Chapeau B F, Godivier X 1997 Phys. Rev. E 55 1478
Google Scholar
[6] Tougaard J 2002 Biol. Cybern. 87 79
Google Scholar
[7] Kang Y M 2016 Phys. Lett. A 380 3160
[8] 王珊, 王辅忠 2018 67 160502
Google Scholar
Wang S, Wang F Z 2018 Acta Phys. Sin. 67 160502
Google Scholar
[9] Krauss P, Metzner C, Schilling A 2017 Sci. Rep. 7 2450
Google Scholar
[10] Galdi V, Pierro V, Pinto I M 1998 Phys. Rev. E 57 6470
Google Scholar
[11] Zozor S, Amblard P O 2002 Signal Process. 82 353
Google Scholar
[12] Zozor S, Amblard P O 2003 IEEE Trans. Signal Process. 51 3177
Google Scholar
[13] Chen H, Varshney P K, Kay S M 2007 IEEE Trans. Signal Process. 55 3172
Google Scholar
[14] Chen H, Varshney P K, Kay S M 2008 IEEE Trans. Signal Process. 56 5031
[15] Wang J, Ren X, Zhang S 2014 IEEE Trans. Wireless Commun. 13 4014
Google Scholar
[16] Zhang Z, Kang Y, Xie Y 2014 Commun. Theor. Phys. 61 578
Google Scholar
[17] Zhang L, Song A 2018 Phys. A 503 958
Google Scholar
[18] 胡岗 1994 随机力与非线性系统 (上海: 上海科技教育出版社) 第220−225页
Hu G 1994 Stochastic Force and Nonlinear Systems (Shanghai: Shanghai Scientific and Technological Education) pp220−225 (in Chinese)
[19] 卢志恒, 林建恒, 胡岗 1993 42 1556
Google Scholar
Lu Z H, Lin J H, Hu G 1993 Acta Phys. Sin. 42 1556
Google Scholar
[20] Socha L 2005 Appl. Mech. Rev. 58 178
[21] Askari M, Adibi H 2015 Ain Shams Eng. J. 6 1211
Google Scholar
[22] 胡茑庆 2012 随机共振微弱特征信号检测理论与方法 (北京: 国防工业出版社) 第85, 86页
Hu N Q 2012 The Theory of Detection and Estimation Using Stochastic Resonance (Beijing: National Defence Publishing) pp85, 86 (in Chinese)
[23] 康艳梅, 徐健学, 谢勇 2003 52 2712
Kang Y M, Xu J X, Xie Y 2003 Acta Phys. Sin. 52 2712
[24] 史蒂文 M L 著 (罗鹏飞 译) 2014 统计信号处理基础-估计与检测理论 (北京: 电子工业出版社) 第397−400页
Steven M K (translated by Luo P F) 2014 Fundamentals of Statistical Signal Processing (Beijing: Publishing House of Electronics Industry) pp397−400 (in Chinese)
[25] Picinbono B 1995 IEEE Trans. Aerosp. Electron. Syst. 31 1072
Google Scholar
[26] 盛骤, 谢式千, 潘承毅 2008 概率论与数理统计 (北京: 高等教育出版社) 第147−153页
Sheng Z, Xie S Q, Pan C Y 2008 Probability Theory and Mathematical Statistics (Beijing: Higher Education Press) pp147−153 (in Chinese)
-
图 1 SR系统增强正弦信号的二次多项式接收结构
Fig. 1. Quadratic polynomial receiving structure for sine signals enhanced by SR.
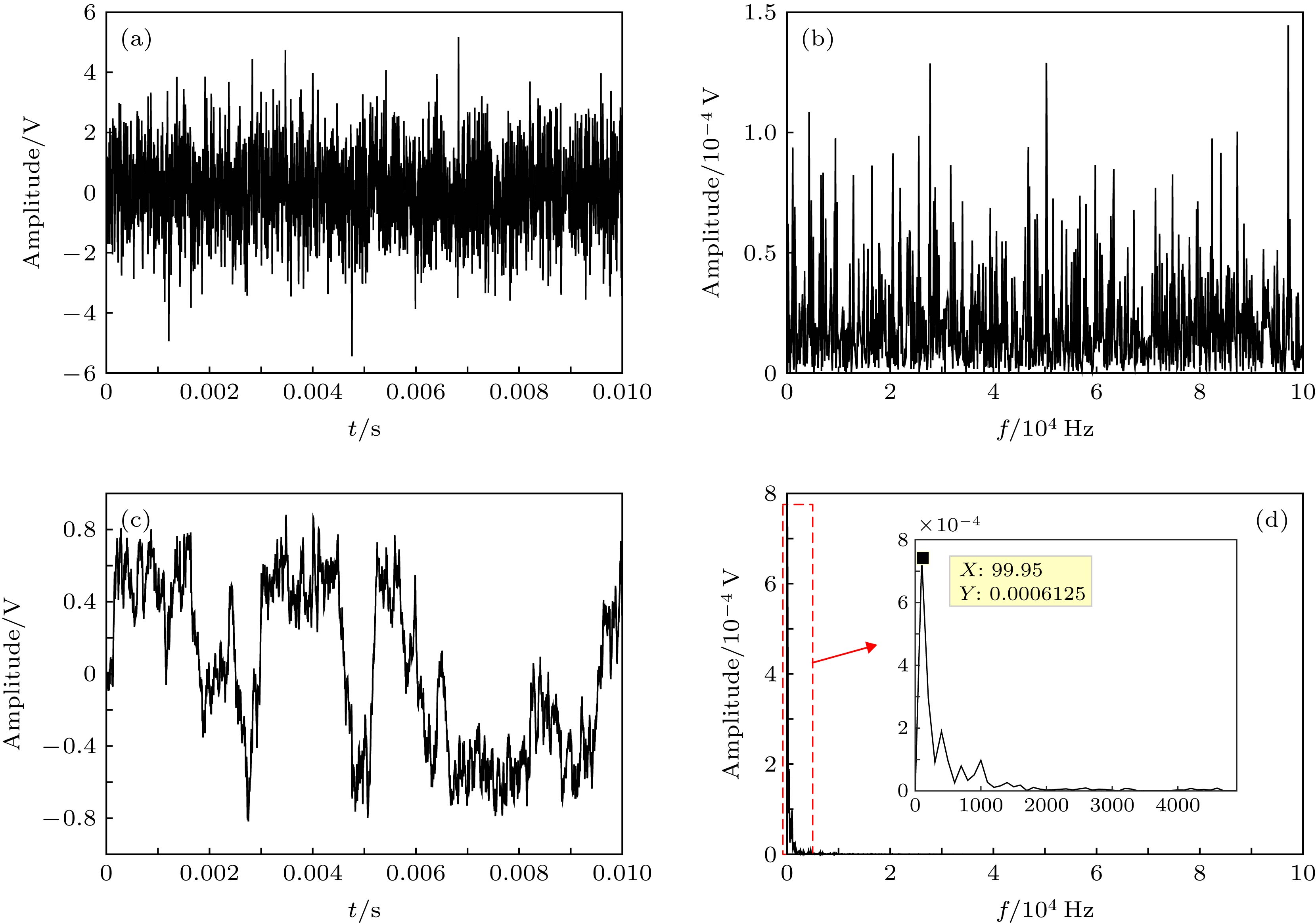
图 2 正弦信号经SR系统增强前后的时频域波形(输入SNR = –18 dB, 噪声功率
${\sigma ^2} = 4$ , 信号幅度$A = 0.25$ , SR系统参数$a = 1 \times {10^4}$ ,$b = 3.3856 \times {10^{12}}$ ) (a) 输入信号时域波形; (b)输入信号频域幅值谱; (c)输出信号时域波形; (d)输出信号频域幅值谱Fig. 2. Waveform of time and frequency zone of sine wave enhanced by SR (input SNR = –18 dB, the noise intensity
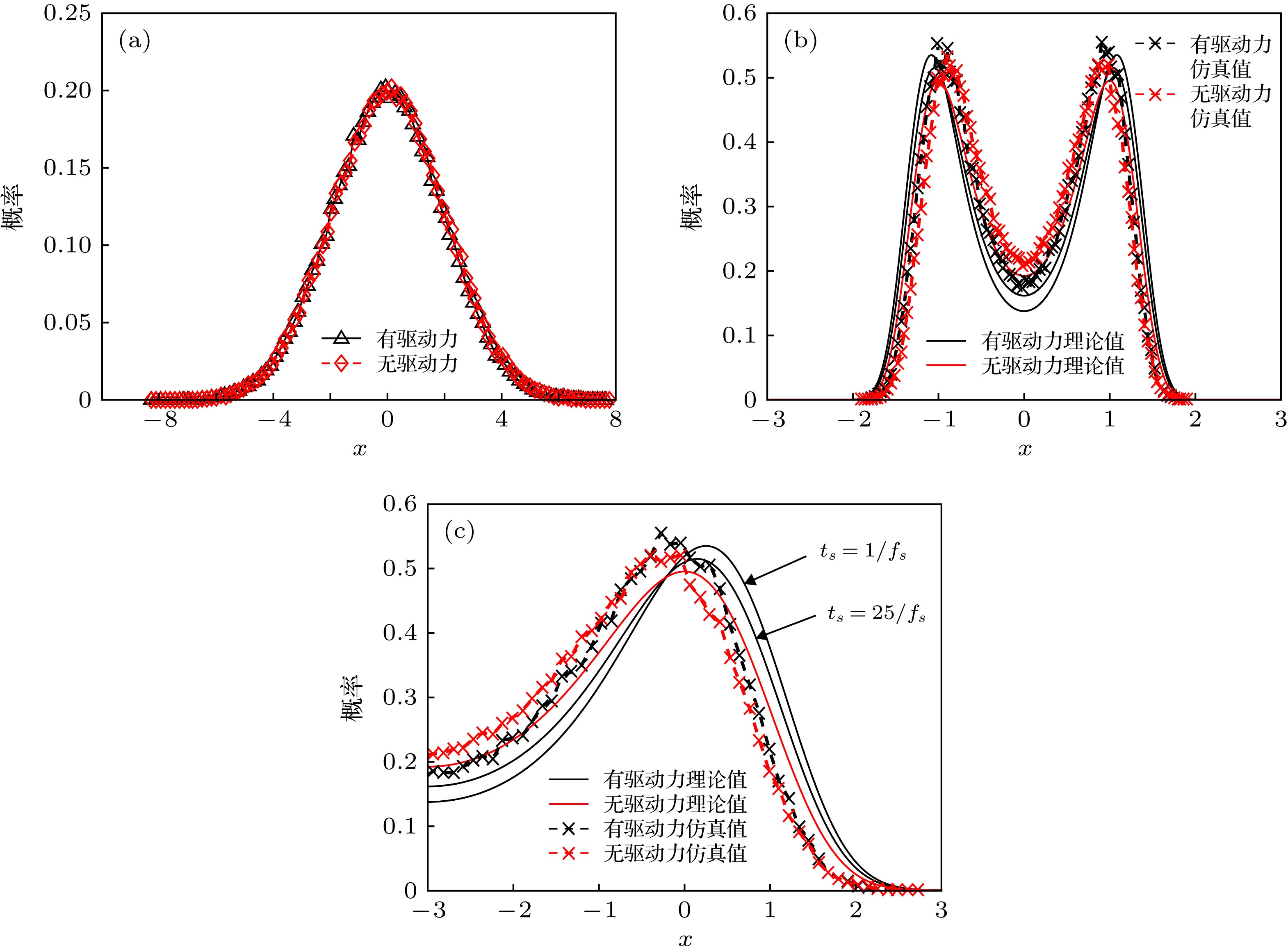
${\sigma ^2} = 4$ , signal amplitude$A = 0.25$ , parameters of system$a = 1 \times {10^4}$ ,$b = 3.3856 \times {10^{12}}$ ): (a) The waveform of input signal in time zone; (b) the amplitude of input signal in frequency zone; (c) the waveform of output signal in time zone; (d) the amplitude of output signal in frequency zone
图 3 粒子处于不同位置时的概率密度(输入SNR = –14 dB dB, 噪声功率
${\sigma ^2} = 4$ , 信号幅度$A = 0.4$ , SR系统参数$a = 1 \times {10^4}$ ,$b = 2.6406 \times {10^{12}}$ ) (a)未经SR处理的粒子的分布概率; (b)经SR处理后粒子的分布概率; (c)经SR处理后粒子的分布概率局部图Fig. 3. Probability density function of particles of SR (input SNR = –14 dB, the noise intensity
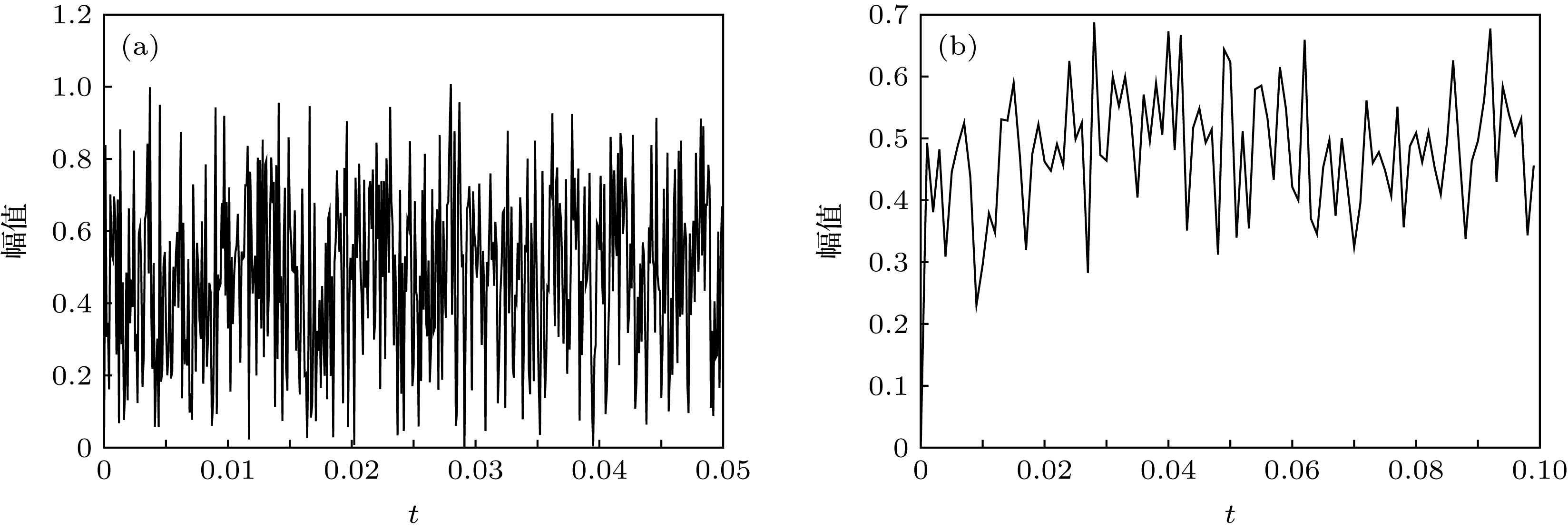
${\sigma ^2} = 4$ , signal amplitude$A = 0.4$ , parameters of system$a = 1 \times {10^4}$ ,$b = 2.6406 \times {10^{12}}$ ): (a) The probability density of particles before SR processed; (b) the probability density of particles after SR processed; (c) the partial of probability density of particles after SR processed
图 4 不同N时
$g\left( {{x_0}} \right)$ 的输出值(输入SNR = –18 dB, 噪声功率${\sigma ^2} = 4$ , 信号幅度$A = 0.25$ , SR系统参数$a = 1 \times {10^4}$ ,$b = 3.3856 \times {10^{12}}$ ) (a) N = 1时检验统计量的时域波形; (b) N = 10时检验统计量的时域波形Fig. 4. Output of
$g\left( {{x_0}} \right)$ at different N (input SNR = –18 dB, the noise intensity${\sigma ^2} = 4$ , signal amplitude$A = 0.25$ , parameters of system$a = 1 \times {10^4}$ ,$b = 3.3856 \times {10^{12}}$ ): (a) The waveform of test statistics when N = 1; (b) the waveform of test statistics when N = 10
图 5 不同N时g(x0)的输出概率密度(输入SNR = –14 dB, 噪声功率
${\sigma ^2} = 4$ , 信号幅度A = 0.4, SR系统参数$a = 1 \;\times $ 104,$b = 2.6406 \times {10^{12}}$ ,$g\left( x \right) = {x^2} + 0.0701x$ ) (a) N = 1时粒子的分布概率; (b) N = 10时粒子的分布概率; (c) N = 50时粒子的分布概率; (d) N = 100时粒子的分布概率Fig. 5. Output probability density function of
$g\left( {{x_0}} \right)$ at different N (input SNR = –14 dB, the noise intensity${\sigma ^2} = 4$ , signal amplitude$A = 0.4$ , parameters of system$a = 1 \times $ 104,$b = 2.6406 \times {10^{12}}$ ,$g\left( x \right) = {x^2} + 0.0701x$ ): (a) The output probability density when N = 1; (b) the output probability density when N = 10; (c) the output probability density when N = 50; (d) the output probability density when N = 100
图 7 不同N时的二次多项式接收结构的误码率
Fig. 7. Output bit error ratio of quadratic polynomial receiving structure at different N
-
[1] Quan H D, Zhao H, Cui P Z 2015 Wirel. Pers. Commun. 81 1159
Google Scholar
[2] 赵寰, 全厚德, 崔佩璋 2015 系统工程与电子技术 37 671
Zhao H, Quan H D, Cui P Z 2015 Syst. Eng. Electron. 37 671
[3] Benzi R, Sutera A, Vulpiani A 1981 J. Phys. A 14 453
Google Scholar
[4] Gammaitoni L, Hänggi P, Jung P 1998 Rev. Mod. Phys. 70 223
Google Scholar
[5] Chapeau B F, Godivier X 1997 Phys. Rev. E 55 1478
Google Scholar
[6] Tougaard J 2002 Biol. Cybern. 87 79
Google Scholar
[7] Kang Y M 2016 Phys. Lett. A 380 3160
[8] 王珊, 王辅忠 2018 67 160502
Google Scholar
Wang S, Wang F Z 2018 Acta Phys. Sin. 67 160502
Google Scholar
[9] Krauss P, Metzner C, Schilling A 2017 Sci. Rep. 7 2450
Google Scholar
[10] Galdi V, Pierro V, Pinto I M 1998 Phys. Rev. E 57 6470
Google Scholar
[11] Zozor S, Amblard P O 2002 Signal Process. 82 353
Google Scholar
[12] Zozor S, Amblard P O 2003 IEEE Trans. Signal Process. 51 3177
Google Scholar
[13] Chen H, Varshney P K, Kay S M 2007 IEEE Trans. Signal Process. 55 3172
Google Scholar
[14] Chen H, Varshney P K, Kay S M 2008 IEEE Trans. Signal Process. 56 5031
[15] Wang J, Ren X, Zhang S 2014 IEEE Trans. Wireless Commun. 13 4014
Google Scholar
[16] Zhang Z, Kang Y, Xie Y 2014 Commun. Theor. Phys. 61 578
Google Scholar
[17] Zhang L, Song A 2018 Phys. A 503 958
Google Scholar
[18] 胡岗 1994 随机力与非线性系统 (上海: 上海科技教育出版社) 第220−225页
Hu G 1994 Stochastic Force and Nonlinear Systems (Shanghai: Shanghai Scientific and Technological Education) pp220−225 (in Chinese)
[19] 卢志恒, 林建恒, 胡岗 1993 42 1556
Google Scholar
Lu Z H, Lin J H, Hu G 1993 Acta Phys. Sin. 42 1556
Google Scholar
[20] Socha L 2005 Appl. Mech. Rev. 58 178
[21] Askari M, Adibi H 2015 Ain Shams Eng. J. 6 1211
Google Scholar
[22] 胡茑庆 2012 随机共振微弱特征信号检测理论与方法 (北京: 国防工业出版社) 第85, 86页
Hu N Q 2012 The Theory of Detection and Estimation Using Stochastic Resonance (Beijing: National Defence Publishing) pp85, 86 (in Chinese)
[23] 康艳梅, 徐健学, 谢勇 2003 52 2712
Kang Y M, Xu J X, Xie Y 2003 Acta Phys. Sin. 52 2712
[24] 史蒂文 M L 著 (罗鹏飞 译) 2014 统计信号处理基础-估计与检测理论 (北京: 电子工业出版社) 第397−400页
Steven M K (translated by Luo P F) 2014 Fundamentals of Statistical Signal Processing (Beijing: Publishing House of Electronics Industry) pp397−400 (in Chinese)
[25] Picinbono B 1995 IEEE Trans. Aerosp. Electron. Syst. 31 1072
Google Scholar
[26] 盛骤, 谢式千, 潘承毅 2008 概率论与数理统计 (北京: 高等教育出版社) 第147−153页
Sheng Z, Xie S Q, Pan C Y 2008 Probability Theory and Mathematical Statistics (Beijing: Higher Education Press) pp147−153 (in Chinese)
下载:
计量
- 文章访问数: 7711
- PDF下载量: 56
- 被引次数: 0
