-
纳米激光器作为未来实现光集成的重要光学元件, 成为了近年来的研究热点之一, 相应的结构工程及输出特性受到了广泛的关注. 然而, 纳米激光的非线性动力学方向上的研究却少有报道. 本文基于纳米激光器的单模速率方程, 应用排列熵复杂度量化工具分析了光反馈及光注入下的混沌纳米光源不可预测程度, 并通过自相关函数进行时延表征. 结果表明: 增加线宽增强因子α、偏置电流Idc、减小增益饱和因子ε、自发辐射增强因子F、自发辐射耦合因子β都有利于提升混沌的不可预测性并抑制时延特征. 而通过光反馈方式产生的混沌光源进一步注入到另一个纳米激光器, 会带来额外的光场非线性作用, 进一步地增强混沌激光的复杂度特性. 此外, 基于绘制频率失谐及注入强度下激光器输出的二维复杂度空间分布, 确定了获取高不可预测度纳米激光混沌信号的参数范围. 这对于实现低成本、小尺寸、高品质混沌光源的研究有重要推动作用.As an important optical element of the optical integration in the future, nanolasers has been a research hotspot in recent years, and the corresponding structural engineering and output characteristics have been widely investigated. However, the nonlinear dynamical performances of nanolasers are rarely reported. Only some preliminary analyses of the dynamic behavior under the optical feedback, optical injection and mutual injection can be found. Some researches pointed out the future prospect of nanolasers, however, some chaos-based applications have not been explored. Therefore, we numerically investigate chaos dynamics in a nanolaser subjected to optical feedback and in another nanolaser subjected to chaotic injection from the former structure by using single mode rate equation, which includes the Purcell cavity-enhanced spontaneous emission factor F and spontaneous emission coupling factor β. The F denotes the ratio of the spontaneous emission rate into the cavity mode to the total spontaneous emission rate in the bulk medium in the absence of a cavity and β represents the fraction of spontaneous emitted photons which are coupled into cavity mode. Specifically, chaos time delay signature (TDS) and unpredictability are evaluated by the peak size of autocorrelation function (ACF) and permutation entropy (PE) respectively. Such kinds of calculations have the advantage of fast operation speed and anti-noise robustness. The results show that the increasing of bias current and the decreasing of gain saturation factor ε, F and β are beneficial to improving the unpredictability and suppressing TDS because the weak damping of the relaxation oscillation leads to strong oscillation. Large linewidth enhancement factor α will increase the number of laser oscillating modes, sideband modes, the spectral components, and enhance the dispersion effect, which will also weaken the information about outer cavity and improve the complexity of chaos. In addition, the above-mentioned chaos properties can be enhanced by injecting the chaos output from a nanolaser subjected to optical feedback into another (slave) nanolaser, which is due to the nonlinear interaction between the driving chaotic signal and the internal electric field of the slave nanolaser. Finally, two-dimensional maps depicting high unpredictability and TDS concealment in the parameter space of the frequency detuning and the injection strength are obtained. It can be found that unpredictability degree can be enhanced by choosing high detuning frequency and intermediate injection strength in the non-injection locking area. The numerical results pave the way for generating the high-quality chaotic sources on a chip or the photonic integrated circuits based on novel semiconductor nanolaser and its related applications.
-
Keywords:
- nanolasers /
- chaos /
- unpredictability /
- time delay signature
[1] Argyris A, Syvridis D, Larger L, Annovazzi-Lodi V, Colet P, Fischer I, García-Ojalvo J, Mirasso C R, Pesquera L, Shore K A 2005 Nature 438 343
Google Scholar
[2] Sciamanna M, Shore K A 2015 Nat. Photonics 9 151
Google Scholar
[3] Uchida A, Amano K, Inoue M, Hirano K, Naito S, Someya H, Oowada I, Kurashige T, Shiki M, Yoshimori S, Yoshimura K, Davis P 2008 Nat. Photonics 2 728
Google Scholar
[4] Li N Q, Kim B, Chizhevsky V N, Locquet A, Bloch M, Citrin D S, Pan W 2014 Opt. Express 22 6634
Google Scholar
[5] Lin F Y, Liu J M 2004 IEEE J. Sel. Top. Quantum Electron. 10 991
Google Scholar
[6] Lin F Y, Liu J M 2004 IEEE J. Quantum Electron. 40 815
Google Scholar
[7] Locquet A, Kim B, Choi D, Li N Q, Citrin D S 2017 Phy. Rev. A 95 023801
Google Scholar
[8] Rontani D, Locquet A, Sciamanna M, Citrin D S 2007 Opt. Lett. 32 2960
Google Scholar
[9] Zhao Q C, Wang Y C, Wang A B 2009 Appl. Opt. 48 3515
Google Scholar
[10] Kanno K, Uchida A, Bunsen M 2016 Phy. Rev. E 93 032206
Google Scholar
[11] Li N Q, Pan W, Xiang S Y, Zhao Q C, Zhang L Y, Mu P H 2014 IEEE J. Quantum Electron. 50 766
Google Scholar
[12] Keller K, Sinn M 2010 Phy. D 239 997
Google Scholar
[13] Bandt C, Pompe B 2002 Phy. Rev. Lett. 88 174102
Google Scholar
[14] Xiang S Y, Pan W, Yan L S, Luo B, Zou X H, Jiang N, Wen K H 2011 Opt. Lett. 36 310
Google Scholar
[15] Xiang S Y, Pan W, Luo B, Yan L S, Zou X H, Jiang N, Yang L, Zhu H N 2011 J. Lightwave Technol. 29 2173
Google Scholar
[16] Xiang S Y, Pan W, Luo B, Yan L S, Zou X H, Jiang N, Yang L, Li N Q 2011 IEEE J. Quantum Electron. 47 1354
Google Scholar
[17] Xiang S Y, Pan W, Luo B, Yan L S, Zou X H, Jiang N, Zhu H N 2012 IEEE J. Quantum Electron. 48 1069
Google Scholar
[18] Xiang S Y, Pan W, Li N Q, Zhang L Y, Zhu H N 2013 Opt. Commun. 311 294
Google Scholar
[19] Guo X X, Xiang S Y, Zhang Y H, Wen A J, Hao Y 2018 IEEE J. Quantum Electron. 54 2000308
Google Scholar
[20] Zhang H, Xiang S Y, Zhang Y H, Guo X X 2017 Appl. Opt. 56 6728
Google Scholar
[21] Li N Q, Pan W, Locquet A, Citrin D S 2015 Opt. Lett. 40 4416
Google Scholar
[22] Li N Q, Pan W, Xiang S Y, Yan L S, Luo B, Zou X H, Zhang L Y 2013 Opt. Laser Technol. 53 45
Google Scholar
[23] Hill M T, Oei Y S, Smalbrugge B, Zhu Y C, Vries T D, Veldhoven P J V, Otten F W M V, Eijkemans T J, Turkiewicz J P, Waardt H D, Geluk E J, Kwon S H, Lee Y H, Nötzel R, Smit M K 2007 Nat. Photonics 1 589
Google Scholar
[24] Lau E K, Lakhani A, Tucker R S, Wu M C 2009 Opt. Express 17 7790
Google Scholar
[25] Sattar Z A, Shore K A 2015 J. Lightwave Technol. 33 3028
Google Scholar
[26] Sattar Z A, Shore K A 2015 IEEE J. Sel. Top. Quantum Electron. 21 1800106
Google Scholar
[27] Sattar Z A, Shore K A 2016 IEEE J. Quantum Electron. 52 1100108
Google Scholar
[28] Sattar Z A, Kamel N A, Shore K A 2016 IEEE J. Quantum Electron. 52 1200108
Google Scholar
[29] Han H, Shore K A 2018 IET Optoelectron. 12 25
Google Scholar
[30] Han H, Shore K A 2016 IEEE J. Quantum Electron. 52 2000306
Google Scholar
[31] Elsonbaty A, Hegazy S F, Obayya S S A 2018 Opt. Laser. Eng. 107 342
Google Scholar
[32] Qu Y, Xiang S Y, Wang Y, Lin L, Wen A J, Hao Y 2019 IEEE J. Quantum Electron. 55 2000407
Google Scholar
[33] Jiang P, Zhou P, Li N Q, Mu P H, Li X F 2020 Opt. Express 28 26421
Google Scholar
[34] Chao M, Wang D M, Wang L S, Sun Y C, Han H, Guo Y Y, Jia Z W, Wang Y C, Wang A B 2020 Opt. Commun. 456 124702
Google Scholar
[35] 阎娟, 潘炜, 李念强, 张力月, 刘庆喜 2016 65 204203
Google Scholar
Yan J, Pan W, Li N Q, Zhang L Y, Liu Q X 2016 Acta Phys. Sin. 65 204203
Google Scholar
[36] Zhou P, Fang Q, Li N Q 2020 Opt. Lett. 45 399
Google Scholar
[37] 苏斌斌, 陈建军, 吴正茂, 夏光琼 2017 66 244206
Google Scholar
Su B B, Chen J J, Wu Z M, Xia G Q 2017 Acta. Phys. Sin. 66 244206
Google Scholar
[38] Uchida A 2012 Optical Communication with Chaotic Lasers: Applications of Nonlinear Dynamics and Synchronization (Berlin: Wiley) p195
-
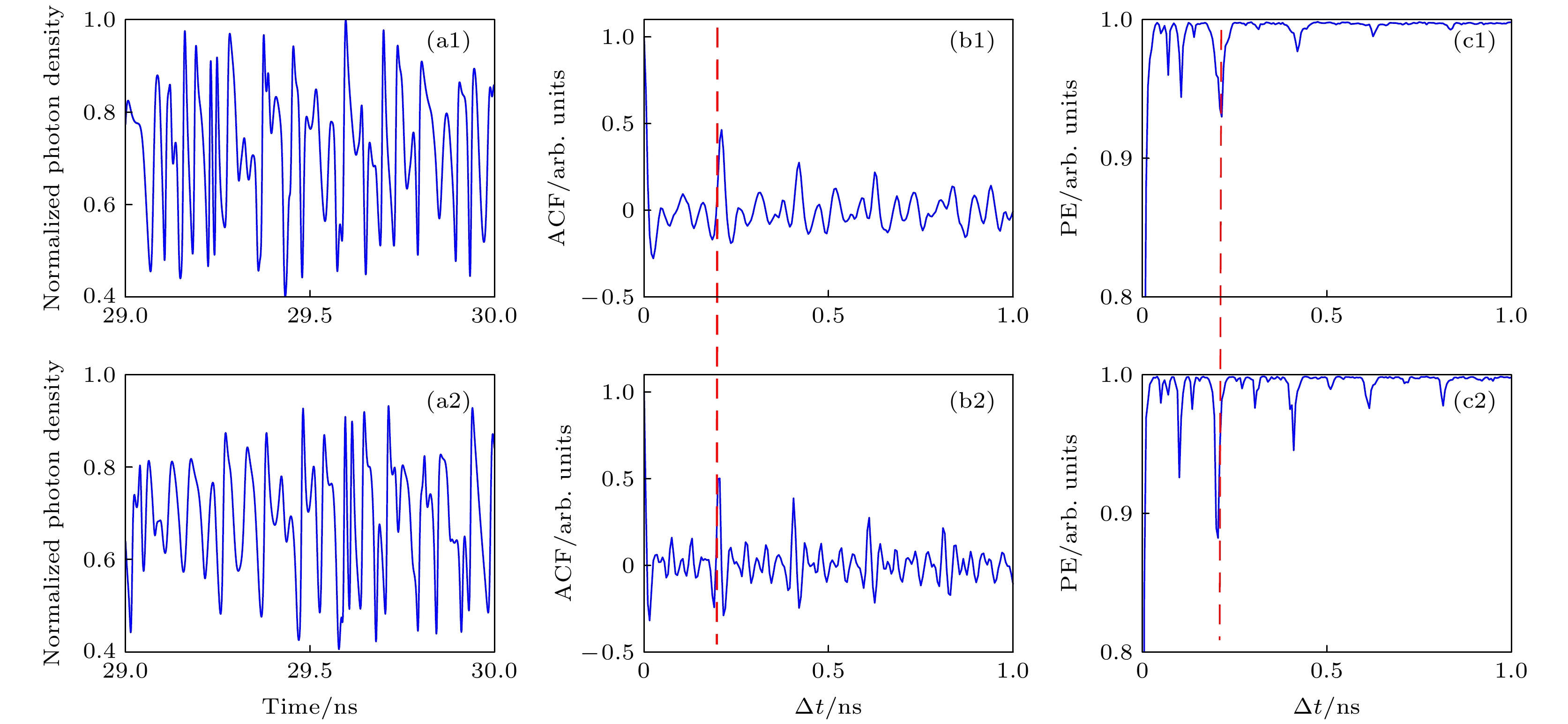
图 1 (a1), (a2)光反馈下的纳米激光器时序; (b1), (b2) ACF曲线; (c1), (c2) PE曲线. 反馈耦合因子: (a1)—(c1)
$f = 0.02$ ; (a2)—(c2)$ f = 0.06$ Fig. 1. (a1), (a2) Time series; (b1), (b2) ACF curve; (c1), (c2) PE curve of a nanolaser under optical feedback. The feedback coupling fraction: (a1)–(c1)
$ f = 0.02 $ ; (a2)–(c2)$ f = 0.06 $ .
图 2 光反馈纳米激光器 (a) TDS与 (b) H[P ]随着
$ \alpha $ ,$ \varepsilon $ 的变化Fig. 2. (a) TDS and (b) H[P ] of a nanolaser subjected to optical feedback as functions of
$ \alpha $ ,$ \varepsilon $ .
图 3 光反馈纳米激光器 (a) TDS与 (b) H[P] 随着
$ F $ 的变化Fig. 3. (a) TDS and (b) H[P] of a nanolaser subjected to optical feedback as functions of
$ F$ .
图 4 光反馈纳米激光器 (a) TDS与 (b) H[P] 随着偏置电流的变化
Fig. 4. (a) TDS and (b) H[P] of a nanolaser subjected to optical feedback as functions of the bias current.
图 5 混沌光注入下从纳米激光器的 (a1), (a2)时序; (b1), (b2)ACF曲线; (c1), (c2) PE曲线. 注入强度(a1)—(c1)
$ {k_{\rm{r}}} = 100\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ; (a2)—(c2)$ {k_{\rm{r}}} = 200\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ;$ \Delta f = 25\;{\rm{GHz}} $ Fig. 5. (a1), (a2) Time series; (b1), (b2) ACF curve; (c1), (c2) PE curve of the slave nanolaser under chaotic optical injection. The injection strength (a1)–(c1)
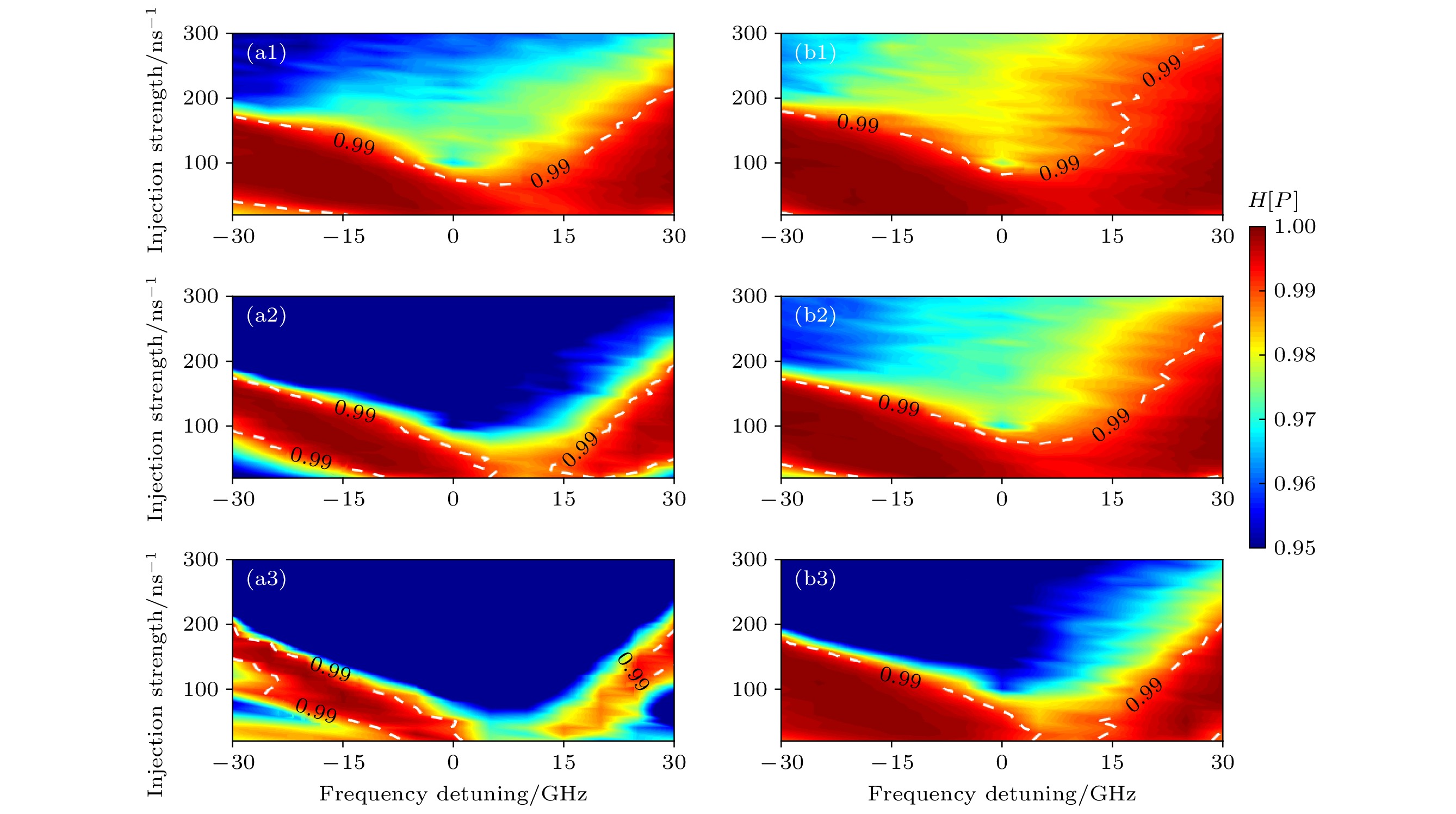
$ {k_{\rm{r}}} = 100\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ; (a2)–(c2)$ {k_{\rm{r}}} = 200\;{\rm{n}}{{\rm{s}}^{ - 1}} $ ;$ \Delta f = 25\;{\rm{GHz}} $ .
图 6 在不同F, β及偏置电流下, 从纳米激光器混沌输出的H[P ]随失谐频率及注入强度变化的二维映射 (a1)—(a3)
${I_{{\rm{dc}}}} = $ $ 2{I_{{\rm{th}}}}$ ; (b1)—(b3)$ {I_{{\rm{dc}}}} = 4{I_{{\rm{th}}}} $ . (a1), (b1)F = 14, β = 0.05; (a2), (b2)F = 14, β = 0.1; (a3), (b3)F = 30, β = 0.1Fig. 6. Two-dimensional maps of H[P ] in the parameter space of the frequency detuning and injection strength under different values of F, β and injection current for the slave nanolaser: (a1)–(a3)
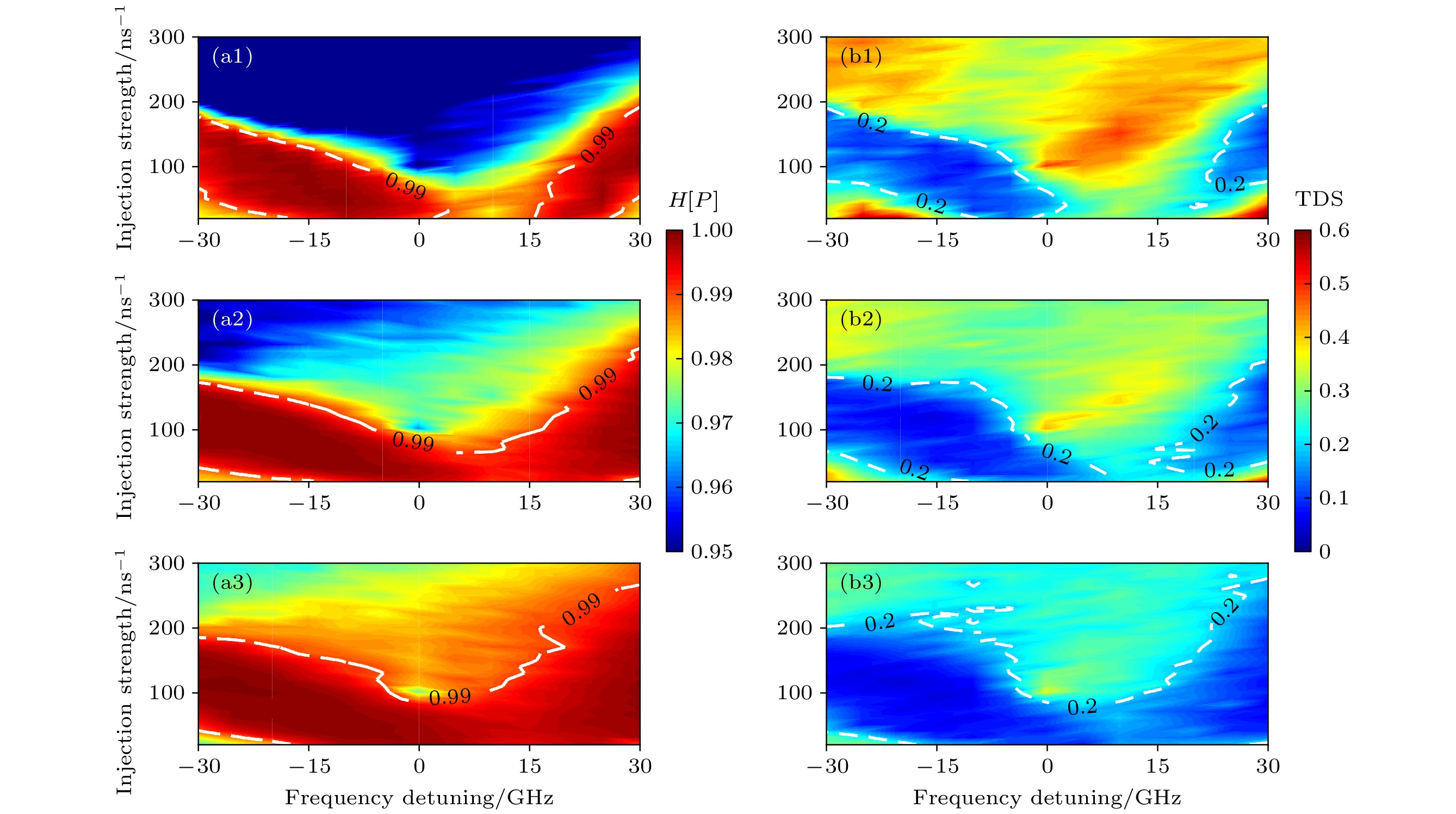
$ {I_{{\rm{dc}}}} = 2{I_{{\rm{th}}}} $ ; (b1)–(b3)$ {I_{{\rm{dc}}}} = 4{I_{{\rm{th}}}} $ . (a1), (b1) F = 14, β = 0.05; (a2), (b2) F = 14, β = 0.1; (a3), (b3) F = 30, β = 0.1.
图 7 在不同线宽增强因子下, 从纳米激光器混沌输出的 (a1)—(a3)H[P ]及(b1)—(b3)时延特征峰值随失谐频率及注入强度变化的二维映射. (a1), (b1)
$ \alpha=4 $ ; (a2), (b2)$ \alpha=5 $ ; (a3), (b3)$ \alpha=6 $ Fig. 7. Two-dimensional maps of (a1)–(a3) H[P ] and (b1)–(b3) TDS in the parameter space of the frequency detuning and injection strength under different values of the linewidth enhancement factor for the slave nanolaser. (a1), (b1)
$ \alpha=4 $ ; (a2), (b2)$ \alpha=5 $ ; (a3), (b3)$ \alpha=6 $ . -
[1] Argyris A, Syvridis D, Larger L, Annovazzi-Lodi V, Colet P, Fischer I, García-Ojalvo J, Mirasso C R, Pesquera L, Shore K A 2005 Nature 438 343
Google Scholar
[2] Sciamanna M, Shore K A 2015 Nat. Photonics 9 151
Google Scholar
[3] Uchida A, Amano K, Inoue M, Hirano K, Naito S, Someya H, Oowada I, Kurashige T, Shiki M, Yoshimori S, Yoshimura K, Davis P 2008 Nat. Photonics 2 728
Google Scholar
[4] Li N Q, Kim B, Chizhevsky V N, Locquet A, Bloch M, Citrin D S, Pan W 2014 Opt. Express 22 6634
Google Scholar
[5] Lin F Y, Liu J M 2004 IEEE J. Sel. Top. Quantum Electron. 10 991
Google Scholar
[6] Lin F Y, Liu J M 2004 IEEE J. Quantum Electron. 40 815
Google Scholar
[7] Locquet A, Kim B, Choi D, Li N Q, Citrin D S 2017 Phy. Rev. A 95 023801
Google Scholar
[8] Rontani D, Locquet A, Sciamanna M, Citrin D S 2007 Opt. Lett. 32 2960
Google Scholar
[9] Zhao Q C, Wang Y C, Wang A B 2009 Appl. Opt. 48 3515
Google Scholar
[10] Kanno K, Uchida A, Bunsen M 2016 Phy. Rev. E 93 032206
Google Scholar
[11] Li N Q, Pan W, Xiang S Y, Zhao Q C, Zhang L Y, Mu P H 2014 IEEE J. Quantum Electron. 50 766
Google Scholar
[12] Keller K, Sinn M 2010 Phy. D 239 997
Google Scholar
[13] Bandt C, Pompe B 2002 Phy. Rev. Lett. 88 174102
Google Scholar
[14] Xiang S Y, Pan W, Yan L S, Luo B, Zou X H, Jiang N, Wen K H 2011 Opt. Lett. 36 310
Google Scholar
[15] Xiang S Y, Pan W, Luo B, Yan L S, Zou X H, Jiang N, Yang L, Zhu H N 2011 J. Lightwave Technol. 29 2173
Google Scholar
[16] Xiang S Y, Pan W, Luo B, Yan L S, Zou X H, Jiang N, Yang L, Li N Q 2011 IEEE J. Quantum Electron. 47 1354
Google Scholar
[17] Xiang S Y, Pan W, Luo B, Yan L S, Zou X H, Jiang N, Zhu H N 2012 IEEE J. Quantum Electron. 48 1069
Google Scholar
[18] Xiang S Y, Pan W, Li N Q, Zhang L Y, Zhu H N 2013 Opt. Commun. 311 294
Google Scholar
[19] Guo X X, Xiang S Y, Zhang Y H, Wen A J, Hao Y 2018 IEEE J. Quantum Electron. 54 2000308
Google Scholar
[20] Zhang H, Xiang S Y, Zhang Y H, Guo X X 2017 Appl. Opt. 56 6728
Google Scholar
[21] Li N Q, Pan W, Locquet A, Citrin D S 2015 Opt. Lett. 40 4416
Google Scholar
[22] Li N Q, Pan W, Xiang S Y, Yan L S, Luo B, Zou X H, Zhang L Y 2013 Opt. Laser Technol. 53 45
Google Scholar
[23] Hill M T, Oei Y S, Smalbrugge B, Zhu Y C, Vries T D, Veldhoven P J V, Otten F W M V, Eijkemans T J, Turkiewicz J P, Waardt H D, Geluk E J, Kwon S H, Lee Y H, Nötzel R, Smit M K 2007 Nat. Photonics 1 589
Google Scholar
[24] Lau E K, Lakhani A, Tucker R S, Wu M C 2009 Opt. Express 17 7790
Google Scholar
[25] Sattar Z A, Shore K A 2015 J. Lightwave Technol. 33 3028
Google Scholar
[26] Sattar Z A, Shore K A 2015 IEEE J. Sel. Top. Quantum Electron. 21 1800106
Google Scholar
[27] Sattar Z A, Shore K A 2016 IEEE J. Quantum Electron. 52 1100108
Google Scholar
[28] Sattar Z A, Kamel N A, Shore K A 2016 IEEE J. Quantum Electron. 52 1200108
Google Scholar
[29] Han H, Shore K A 2018 IET Optoelectron. 12 25
Google Scholar
[30] Han H, Shore K A 2016 IEEE J. Quantum Electron. 52 2000306
Google Scholar
[31] Elsonbaty A, Hegazy S F, Obayya S S A 2018 Opt. Laser. Eng. 107 342
Google Scholar
[32] Qu Y, Xiang S Y, Wang Y, Lin L, Wen A J, Hao Y 2019 IEEE J. Quantum Electron. 55 2000407
Google Scholar
[33] Jiang P, Zhou P, Li N Q, Mu P H, Li X F 2020 Opt. Express 28 26421
Google Scholar
[34] Chao M, Wang D M, Wang L S, Sun Y C, Han H, Guo Y Y, Jia Z W, Wang Y C, Wang A B 2020 Opt. Commun. 456 124702
Google Scholar
[35] 阎娟, 潘炜, 李念强, 张力月, 刘庆喜 2016 65 204203
Google Scholar
Yan J, Pan W, Li N Q, Zhang L Y, Liu Q X 2016 Acta Phys. Sin. 65 204203
Google Scholar
[36] Zhou P, Fang Q, Li N Q 2020 Opt. Lett. 45 399
Google Scholar
[37] 苏斌斌, 陈建军, 吴正茂, 夏光琼 2017 66 244206
Google Scholar
Su B B, Chen J J, Wu Z M, Xia G Q 2017 Acta. Phys. Sin. 66 244206
Google Scholar
[38] Uchida A 2012 Optical Communication with Chaotic Lasers: Applications of Nonlinear Dynamics and Synchronization (Berlin: Wiley) p195
下载:
计量
- 文章访问数: 4327
- PDF下载量: 70
- 被引次数: 0
