-
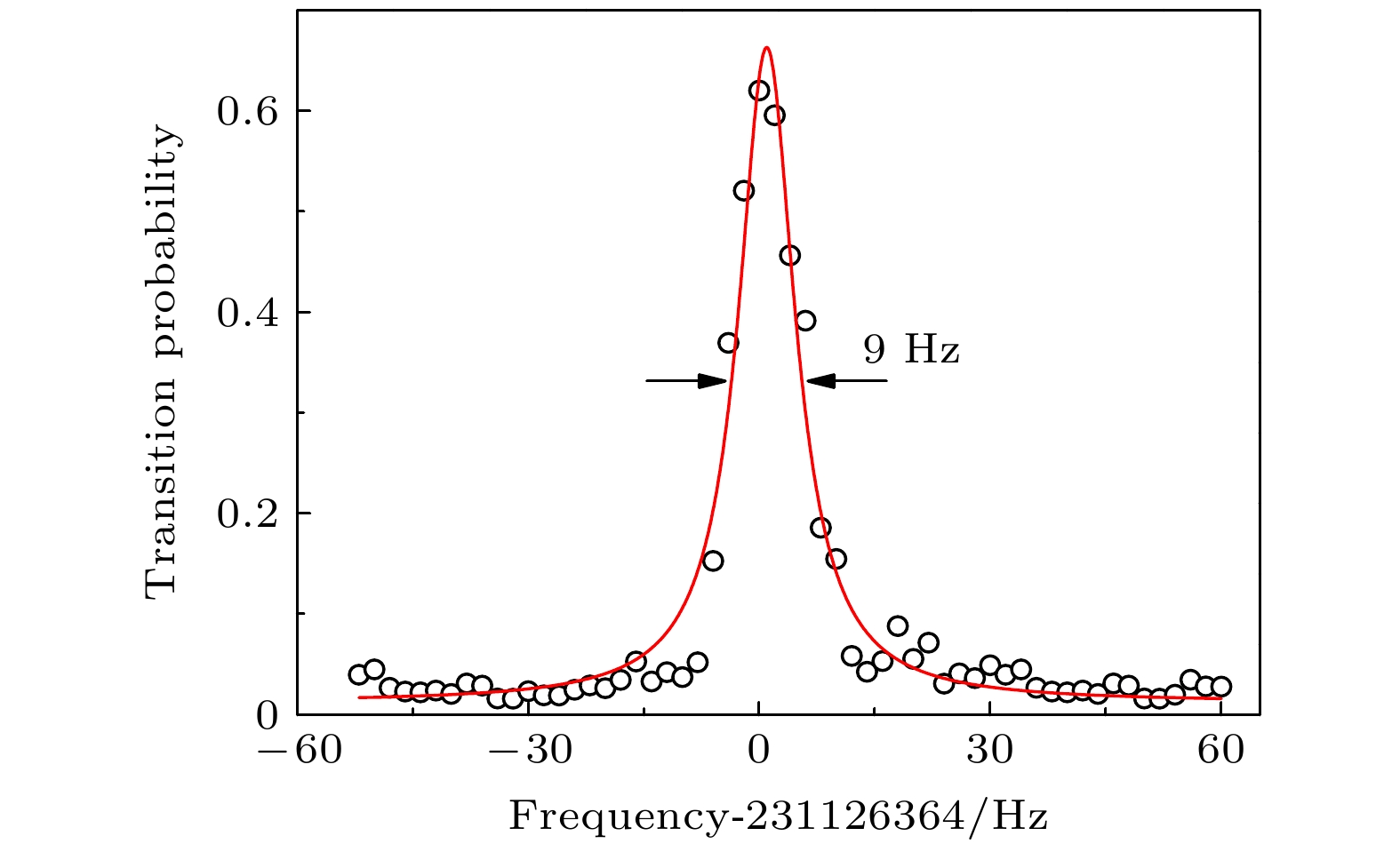
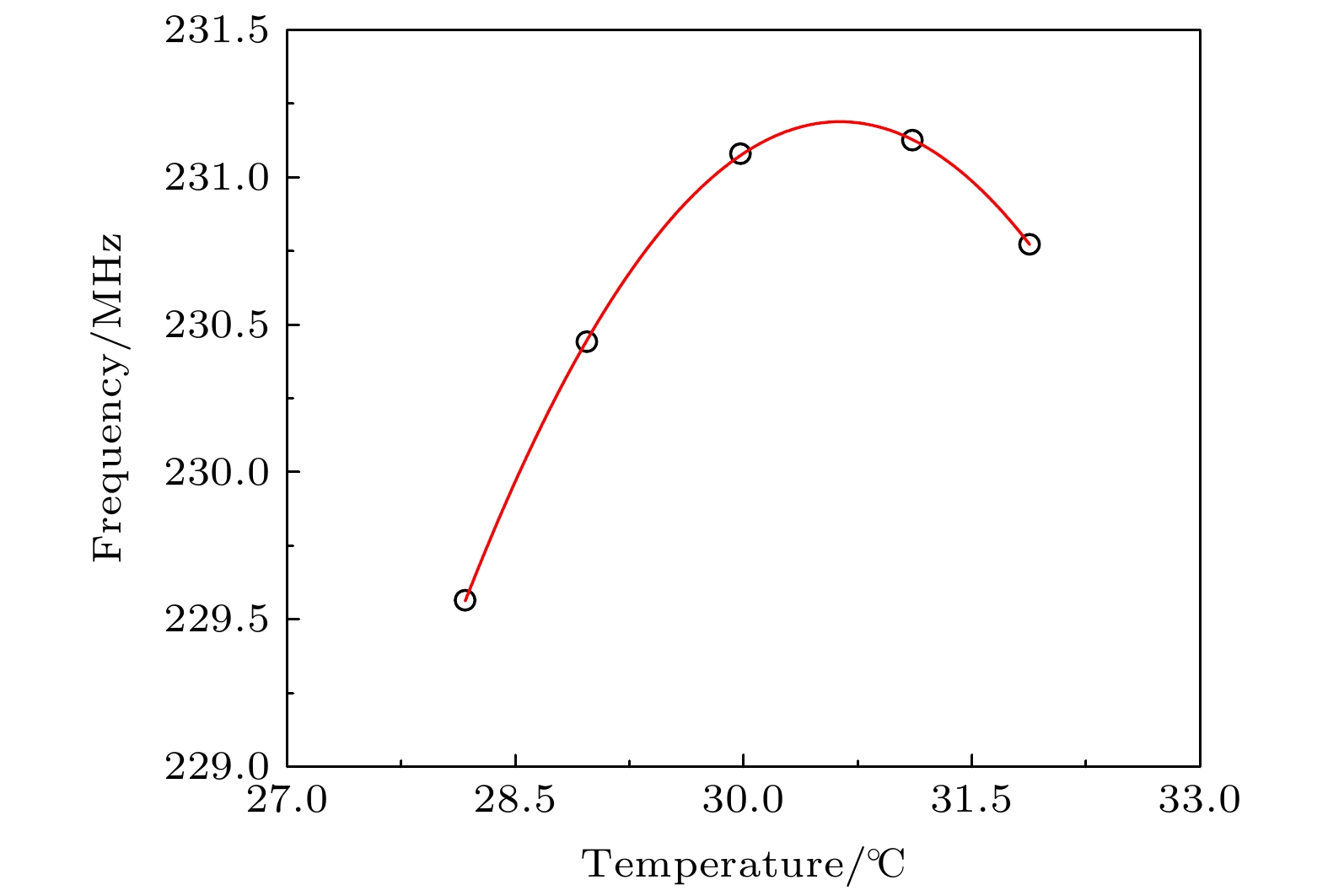
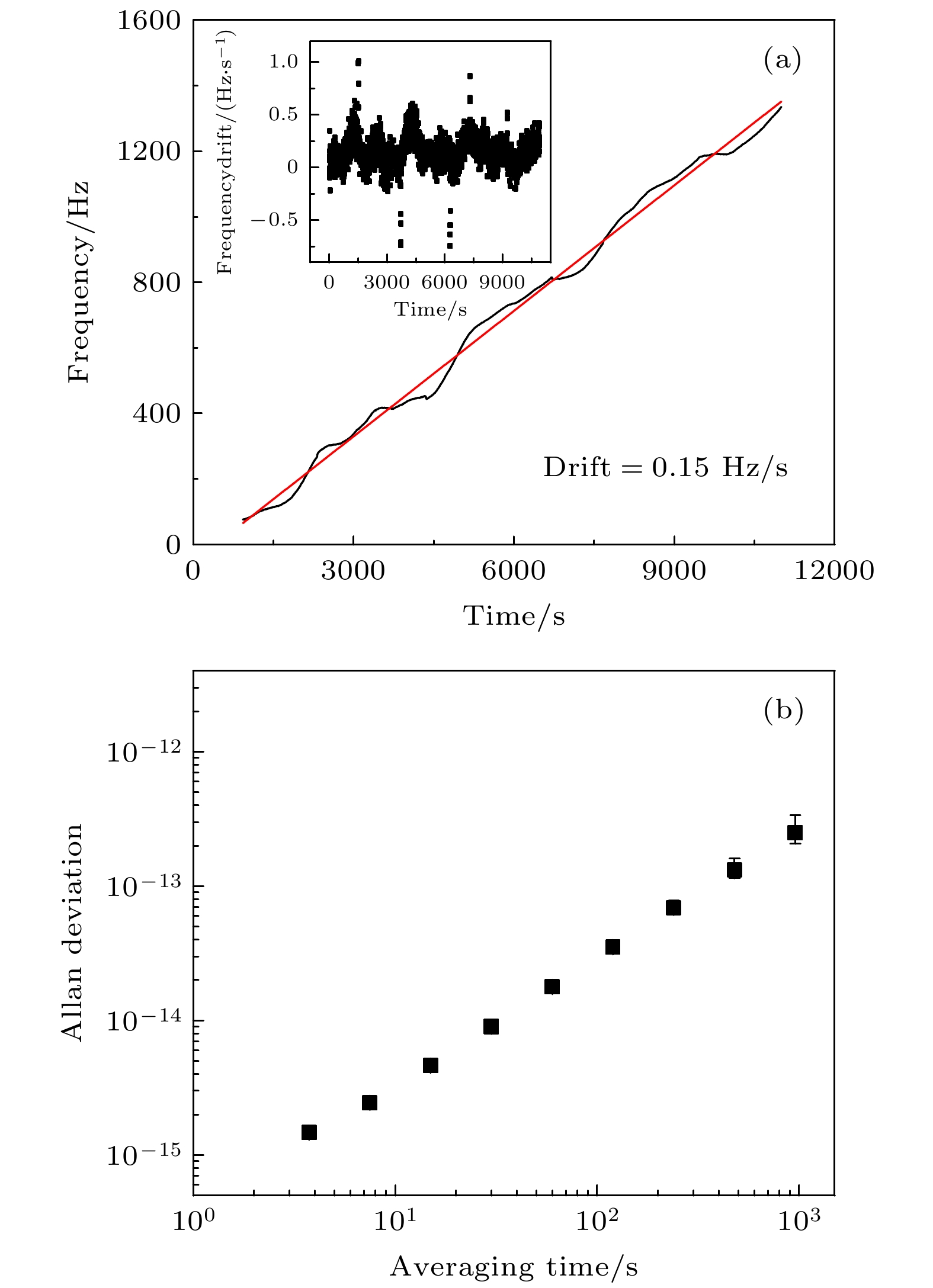
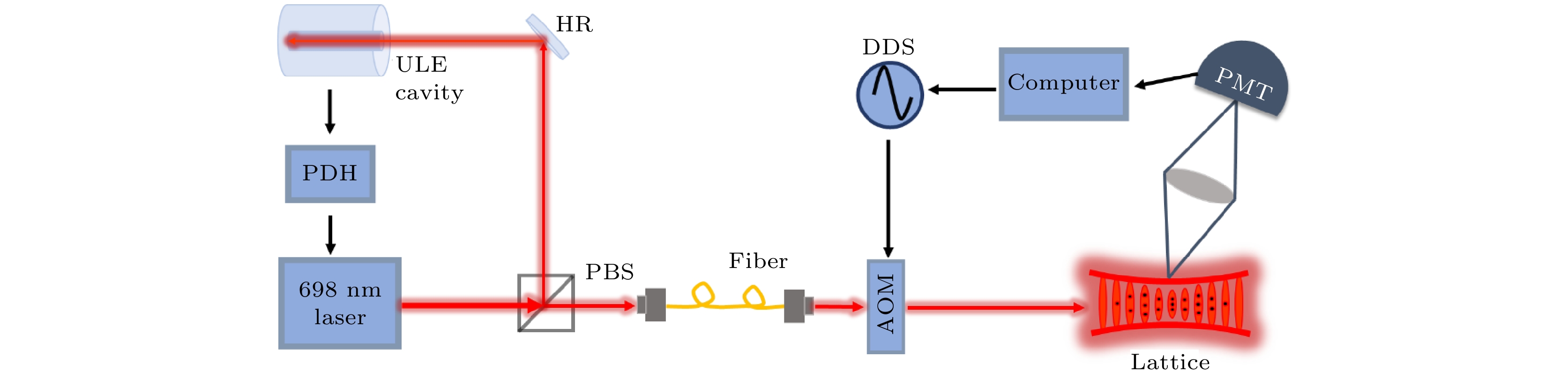
在87Sr光晶格钟实验系统中, 通过将自由运转的698 nm激光频率锁定在由超低膨胀系数的玻璃材料构成的超稳光学参考腔上, 从而获得短期频率稳定性较好的超稳窄线宽激光. 超稳光学参考腔的腔长稳定性决定了最终激光频率的稳定度. 为了降低腔长对温度的敏感性, 使激光频率具有更好的稳定度和更小的频率漂移, 利用锶原子光晶格钟的钟跃迁谱线, 测量了698 nm超稳窄线宽激光系统中超稳光学参考腔的零温漂点. 通过对钟跃迁谱线中心频率随温度的变化曲线进行二阶多项式拟合, 得到698 nm超稳窄线宽激光系统的零温漂点为30.63 ℃. 利用锶原子光晶格钟的闭环锁定, 测得零温漂点处698 nm超稳窄线宽激光系统的线性频率漂移率为0.15 Hz/s, 频率不稳定度为1.6 × 10–15@3.744 s.In an experimental system of 87Sr atomic optical lattice clock, the free-running 698 nm diode laser is locked in an ultra-stable optical reference cavity to obtain the ultra-stable narrow linewidth laser with good short-term frequency stability. The ultra-stable optical reference cavity, which is usually composed of glass material doped with titanium dioxide for ultra-low thermal expansion coefficient and two highly reflective fused quartz mirrors, is called ULE cavity. The cavity length is prone to being affected by mechanical vibration, temperature change, airflow, etc. The stability of the cavity length determines the stability of the final laser frequency. Near the room temperature, there exists a special temperature point for the ultra-low expansion glass material, at which temperature its thermal expansion coefficient becomes zero, which is called the zero-crossing temperature. At the zero-crossing temperature, the length of the ULE cavity is not sensitive to the temperature fluctuation, reaching a minimum value, and the laser locked to the ULE cavity has a minimum frequency drift. In order to reduce the influence of temperature on the laser frequency instability, the zero-crossing temperature of the ultra-stable optical reference cavity of 698 nm ultra-stable narrow linewidth laser system is measured by using the clock transition spectrum of the strontium atomic optical lattice clock. The frequency drift and frequency instability of the 698 nm ultra-stable narrow linewidth laser system at zero-crossing temperature are measured by using the change of the in-loop locked clock frequency of strontium atomic optical lattice clock. By scanning the atomic clock transition frequencies at different temperatures, the clock transition spectra at different temperatures are obtained. The second order polynomial fitting of the central frequency of the clock transition spectrum with the change curve of temperature is carried out, and the zero-crossing temperature of the 698 nm ultra-stable narrow linewidth laser system ULE cavity is measured to be 30.63 ℃. At the zero-crossing temperature, the 698 nm ultra-stable narrow linewidth laser frequency is used for in-loop locking of 87Sr atomic optical lattice clock. The linear drift rate of the ULE cavity in the 698 nm ultra-stable narrow linewidth laser system is measured to be 0.15 Hz/s, and the frequency instability of the 698 nm ultra-stable narrow linewidth laser system is 1.6 × 10–15 at an average time of 3.744 s. The determination of ULE cavity zero-crossing temperature for the 698 nm ultra-stable narrow linewidth laser system is of great significance in helping to not only improve the instability of the laser system, but also increase the instability of 87Sr optical lattice clock system. In the future, we will improve the temperature control system of the ULE cavity in the 698 nm clock laser system, enhancing the temperature control accuracy of the ULE cavity and reducing the measurement error, thus achieving a more accurate zero-crossing temperature and further improving the frequency instability of the 698 nm ultra-stable narrow linewidth laser system.
-
Keywords:
- ultra-stable optical reference cavity /
- frequency drift /
- clock transition spectra /
- zero-crossing temperature
[1] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
 Google Scholar
Google Scholar
[2] Blatt S, Ludlow A D, Campbell G K, et al. 2008 Phys. Rev. Lett. 100 140801
 Google Scholar
Google Scholar
[3] Godun R M, Nisbet-Jones P B R, Jones J M, King S A, Johnson L A, Margolis H S, Szymaniec K, Lea S N, Bongs K, Gill P 2014 Phys. Rev. Lett. 113 210801
 Google Scholar
Google Scholar
[4] Huntemann N, Lipphardt B, Tamm C, Gerginov V, Weyers S, Peik E 2014 Phys. Rev. Lett. 113 210802
 Google Scholar
Google Scholar
[5] Derevianko A, Pospelov M 2014 Nat. Phys. 10 933
 Google Scholar
Google Scholar
[6] Wcisło P, Morzyński P, Bober M, Cygan A, Lisak D, Ciuryło R, Zawada M 2016 Nat. Astron. 1 0009
[7] Hees A, Guéna J, Abgrall M, Bize S, Wolf P 2016 Phys. Rev. Lett. 117 061301
 Google Scholar
Google Scholar
[8] Roberts B M, Blewitt G, Dailey C, Murphy M, Pospelov M, Rollings A, Sherman J, Williams W, Derevianko A 2017 Nat.Commun. 8 1195
 Google Scholar
Google Scholar
[9] Adhikari R X 2014 Rev. Mod. Phys. 86 121
 Google Scholar
Google Scholar
[10] Kolkowitz S, Pikovski I, Langellier N, Lukin M D, Walsworth R L, Ye J 2016 Phys. Rev. D 94 124043
 Google Scholar
Google Scholar
[11] Fox R W 2008 Proc. SPIE, Photonics North 7099 70991R
 Google Scholar
Google Scholar
[12] Jiang Y Y, Ludlow A D, Lemke N D, Fox R W, Sherman J A, Ma L S, Oates C W 2011 Nat. Photonics 5 158
 Google Scholar
Google Scholar
[13] Liu H, Jiang K L, Wang J Q, Xiong Z X, He L X, Lü B L 2018 Chin. Phys. B 27 053201
 Google Scholar
Google Scholar
[14] 林弋戈, 方占军 2018 67 160604
 Google Scholar
Google Scholar
Lin Y G, Fang Z J 2018 Acta Phys. Sin. 67 160604
 Google Scholar
Google Scholar
[15] Muller H, Peters A, Chu S 2010 Nature 463 926
 Google Scholar
Google Scholar
[16] Wang C, Ji Z, Gong T, et al. 2019 J. Phys. D: Appl. Phys. 52 455104
 Google Scholar
Google Scholar
[17] Thomas L, Thomas K, Uwe S 2010 J. Opt. Soc. Am. B 27 914
 Google Scholar
Google Scholar
[18] Zhang J, Luo Y X, Ouyang B, Deng K, Lu Z H, Luo J 2013 Eur. Phys. J. D 67 46
 Google Scholar
Google Scholar
[19] Berthold J W, Jacobs S F 1976 Appl. Opt. 15 2334
[20] 卢晓同, 李婷, 孔德欢, 王叶兵, 常宏 2019 68 233401
 Google Scholar
Google Scholar
Lu X T, Li T, Kong D H, Wang Y B, Chang H 2019 Acta Phys. Sin. 68 233401
 Google Scholar
Google Scholar
[21] Lu X T, Yin M J, Li T, Wang Y B, Chang H 2020 Appl. Sci. 10 1440
 Google Scholar
Google Scholar
[22] 高峰, 刘辉, 许鹏, 王叶兵, 田晓, 常宏 2014 63 140704
 Google Scholar
Google Scholar
Gao F, Liu H, Xu P, Wang Y B, Tian X, Chang H 2014 Acta Phys. Sin. 63 140704
 Google Scholar
Google Scholar
[23] Drever R W P, Hall J L, Kowalski F V, Hough J, Ford G M, Munley A J, Ward H 1983 Appl. Phys. B 31 97
[24] Wang Y B, Yin M J, Ren J, Xu Q F, Lu B Q, Han J X, Guo Y, Chang H 2018 Chin. Phys. B 27 023701
 Google Scholar
Google Scholar
-
-
[1] Ludlow A D, Boyd M M, Ye J, Peik E, Schmidt P O 2015 Rev. Mod. Phys. 87 637
 Google Scholar
Google Scholar
[2] Blatt S, Ludlow A D, Campbell G K, et al. 2008 Phys. Rev. Lett. 100 140801
 Google Scholar
Google Scholar
[3] Godun R M, Nisbet-Jones P B R, Jones J M, King S A, Johnson L A, Margolis H S, Szymaniec K, Lea S N, Bongs K, Gill P 2014 Phys. Rev. Lett. 113 210801
 Google Scholar
Google Scholar
[4] Huntemann N, Lipphardt B, Tamm C, Gerginov V, Weyers S, Peik E 2014 Phys. Rev. Lett. 113 210802
 Google Scholar
Google Scholar
[5] Derevianko A, Pospelov M 2014 Nat. Phys. 10 933
 Google Scholar
Google Scholar
[6] Wcisło P, Morzyński P, Bober M, Cygan A, Lisak D, Ciuryło R, Zawada M 2016 Nat. Astron. 1 0009
[7] Hees A, Guéna J, Abgrall M, Bize S, Wolf P 2016 Phys. Rev. Lett. 117 061301
 Google Scholar
Google Scholar
[8] Roberts B M, Blewitt G, Dailey C, Murphy M, Pospelov M, Rollings A, Sherman J, Williams W, Derevianko A 2017 Nat.Commun. 8 1195
 Google Scholar
Google Scholar
[9] Adhikari R X 2014 Rev. Mod. Phys. 86 121
 Google Scholar
Google Scholar
[10] Kolkowitz S, Pikovski I, Langellier N, Lukin M D, Walsworth R L, Ye J 2016 Phys. Rev. D 94 124043
 Google Scholar
Google Scholar
[11] Fox R W 2008 Proc. SPIE, Photonics North 7099 70991R
 Google Scholar
Google Scholar
[12] Jiang Y Y, Ludlow A D, Lemke N D, Fox R W, Sherman J A, Ma L S, Oates C W 2011 Nat. Photonics 5 158
 Google Scholar
Google Scholar
[13] Liu H, Jiang K L, Wang J Q, Xiong Z X, He L X, Lü B L 2018 Chin. Phys. B 27 053201
 Google Scholar
Google Scholar
[14] 林弋戈, 方占军 2018 67 160604
 Google Scholar
Google Scholar
Lin Y G, Fang Z J 2018 Acta Phys. Sin. 67 160604
 Google Scholar
Google Scholar
[15] Muller H, Peters A, Chu S 2010 Nature 463 926
 Google Scholar
Google Scholar
[16] Wang C, Ji Z, Gong T, et al. 2019 J. Phys. D: Appl. Phys. 52 455104
 Google Scholar
Google Scholar
[17] Thomas L, Thomas K, Uwe S 2010 J. Opt. Soc. Am. B 27 914
 Google Scholar
Google Scholar
[18] Zhang J, Luo Y X, Ouyang B, Deng K, Lu Z H, Luo J 2013 Eur. Phys. J. D 67 46
 Google Scholar
Google Scholar
[19] Berthold J W, Jacobs S F 1976 Appl. Opt. 15 2334
[20] 卢晓同, 李婷, 孔德欢, 王叶兵, 常宏 2019 68 233401
 Google Scholar
Google Scholar
Lu X T, Li T, Kong D H, Wang Y B, Chang H 2019 Acta Phys. Sin. 68 233401
 Google Scholar
Google Scholar
[21] Lu X T, Yin M J, Li T, Wang Y B, Chang H 2020 Appl. Sci. 10 1440
 Google Scholar
Google Scholar
[22] 高峰, 刘辉, 许鹏, 王叶兵, 田晓, 常宏 2014 63 140704
 Google Scholar
Google Scholar
Gao F, Liu H, Xu P, Wang Y B, Tian X, Chang H 2014 Acta Phys. Sin. 63 140704
 Google Scholar
Google Scholar
[23] Drever R W P, Hall J L, Kowalski F V, Hough J, Ford G M, Munley A J, Ward H 1983 Appl. Phys. B 31 97
[24] Wang Y B, Yin M J, Ren J, Xu Q F, Lu B Q, Han J X, Guo Y, Chang H 2018 Chin. Phys. B 27 023701
 Google Scholar
Google Scholar
计量
- 文章访问数: 6948
- PDF下载量: 138
- 被引次数: 0













 下载:
下载: