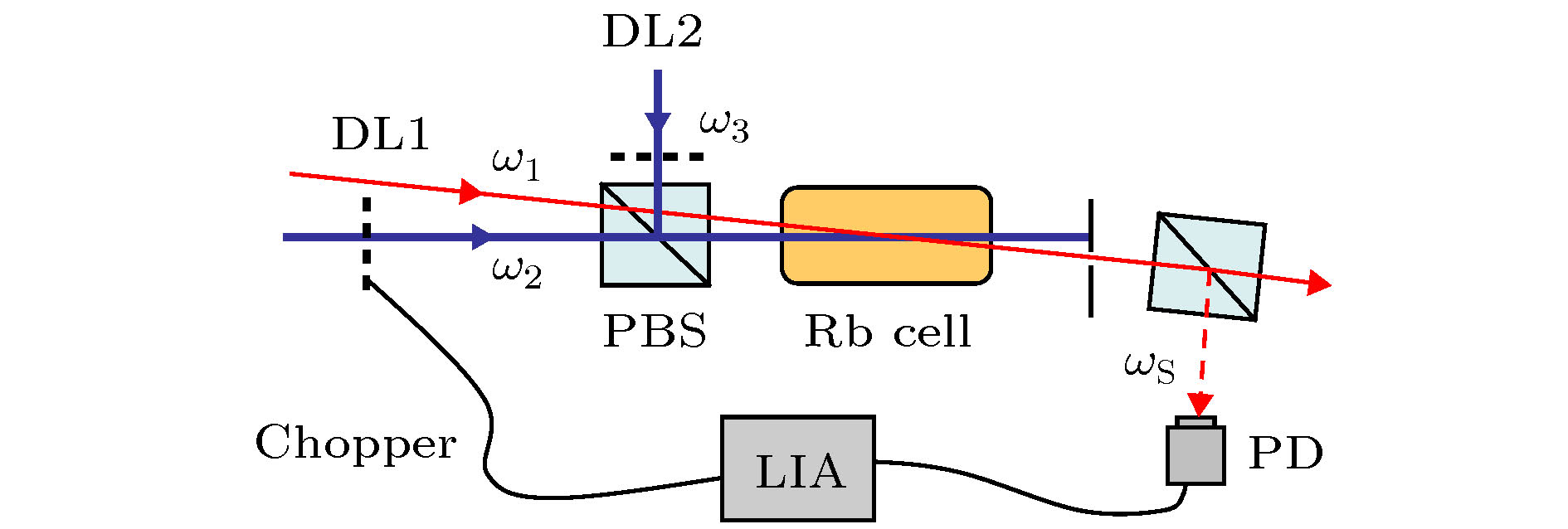
-
We observe experimentally huge enhanced four-wave mixing based on Raman resonance in an 85Rb atomic vapor system. With the decrease of coupling field power or the increase of experimental temperature, the signal tends to be narrowed down in linewidth, and be basically the same spectrum as the stimulated Raman spectroscopy. It is found that the macroscopic polarization interference effect plays a crucial role in determining the nonlinear spectra. Further more, in the Doppler-broadened Λ-type energy level system, there is a strong relationship among electromagnetically induced transparency, four-wave mixing and stimulated Raman spectroscopy. The sharp transparent window in electromagnetically induced transparency can be interpreted as the suppression of Raman gain on the linear absorption of the probe field. However, the four-wave mixing signal is a new field generated by the atomic vapor system, and it comes from the Raman gain which is affected and modified by the absorption and dispersion of the nonlinear optical medium. It shows that in a Λ-type Doppler-broadened system, in essence, both the electromagnetically induced transparency and enhanced four-wave mixing stem from stimulated Raman scattering based on the third-order nonlinear processes, just the spectra of which are from different ways and objects of detection.
-
Keywords:
- stimulated Raman spectroscopy /
- four-wave mixing /
- electromagnetically induced transparency /
- polarization interference
[1] Harris S E, Field J E, Imamoglu A 1990 Phys. Rev. Lett. 64 1107
Google Scholar
[2] Harris S E 1997 Phys. Today 50 36
[3] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[4] Kang H, Zhu Y F 2003 Phys. Rev. Lett. 91 093601
Google Scholar
[5] Wang H, Goorskey D, Xiao M 2001 Phys. Rev. Lett. 87 073601
Google Scholar
[6] Wang Z B, Marzlin K P, Sanders B C 2006 Phys. Rev. Lett. 97 063901
Google Scholar
[7] Pack M V, Camacho R M, Howell J C 2007 Phys. Rev. A 76 033835
Google Scholar
[8] Pei L Y, Lu X G, Wang R Q, Wu L A, Zuo Z C, Fu P M 2013 Phys. Rev. A 87 063822
Google Scholar
[9] 裴丽娅, 王如泉, 左战春, 吴令安, 傅盘铭 2013 62 124208
Google Scholar
Pei L Y, Wang R Q, Zuo Z C, Wu L A, Fu P M 2013 Acta Phys. Sin. 62 124208
Google Scholar
[10] 裴丽娅, 左战春, 吴令安, 傅盘铭 2013 62 184209
Google Scholar
Pei L Y, Zuo Z C, Wu L A, Fu P M 2013 Acta Phys. Sin. 62 184209
Google Scholar
[11] Jiang Q, Mi X, Yu Z H, Wang Y B, Wang L J, Fu P M 2001 Chin. Phys. Lett. 18 54
Google Scholar
[12] Zibrov A S, Matsko A B, Scully M O 2002 Phys. Rev. Lett. 89 103601
Google Scholar
[13] Liu J, Wei D, Wang J W, Yu Y, Hu H J, Gao H, Li F L 2016 Chin. Phys. B 25 114204
Google Scholar
[14] Carrasco-Sanz A, Martin-Lopez S, Gonzalez-Herraez M, Corredera P, Hernanz M L, Abrardi L 2008 Opt. Commun. 281 2948
Google Scholar
[15] Vanholsbeeck F, Emplit P, Coen S 2003 Opt. Lett. 28 1960
Google Scholar
[16] Michaud F, Gattobigio G L, Tabosa J W R, Kaiser R 2007 J. Opt. Soc. Am. B 24 A40
Google Scholar
[17] Silva N A, Muga N J, Pinto A N 2009 J. Lightwave. Technol. 27 4979
Google Scholar
[18] Romanov G, O’Brien C, Novikova I 2016 J. Mod. Optic. 63 2048
Google Scholar
[19] Parniak M, Leszczynski A, Wasilewski W 2016 Phys. Rev. A 93 053821
Google Scholar
[20] Lee C Y, Wu B H, Wang G, Chen Y F, Chen Y C, Yu I A 2016 Opt. Express 24 001008
Google Scholar
[21] Dudin Y O, Li L, Kuzmich A 2013 Phys. Rev. A 87 031801(R)
Google Scholar
[22] Ma L J, Slattery O, Tang X 2017 J. Optics-UK 19 043001
Google Scholar
[23] 顾世杰 1984 33 593
Google Scholar
Gu S J 1984 Acta Phys. Sin. 33 593
Google Scholar
[24] Fleischhauer M, Imamoglu A, Marangos J P 2005 Reviews of Modern Physics 77 633
-
图 2 实验装置简图. 其中, DL1和DL2: 半导体激光器; Chopper: 斩波器; PBS: 偏振分束器; PD: 光电探测器; LIA: 锁相放大器
Fig. 2. Experimental setup. DL1 and DL2, diode lasers; PBS, polarizing beam splitter; PD, photodetector; LIA, lock-in amplifier.
图 3 (a) 耦合光共振(
${\varDelta _2} = 0$ )和(b) 耦合光失谐(${\varDelta _2} = 350\;{\rm{MHz}}$ )下的弱探测光吸收谱(黑色实线)和窄线宽FWM信号(红色实线). (注意: 实验中失谐条件下的信号较小, 这里为了看图清楚, 图(b)的光谱强度相应地均增大到实际强度的2.5倍)Fig. 3. Experimental results for the transmission intensity of the weak probe beam (black solid line) and the FWM signal with narrow linewidth (red solid line) as a function of Δ1: (a) Δ2 = 0; (b) Δ2 = 350 MHz. (Note that in order to see the details clearly, the spectral intensity in Fig. (b) is the result of magnification to 2.5 times the actual situation.)
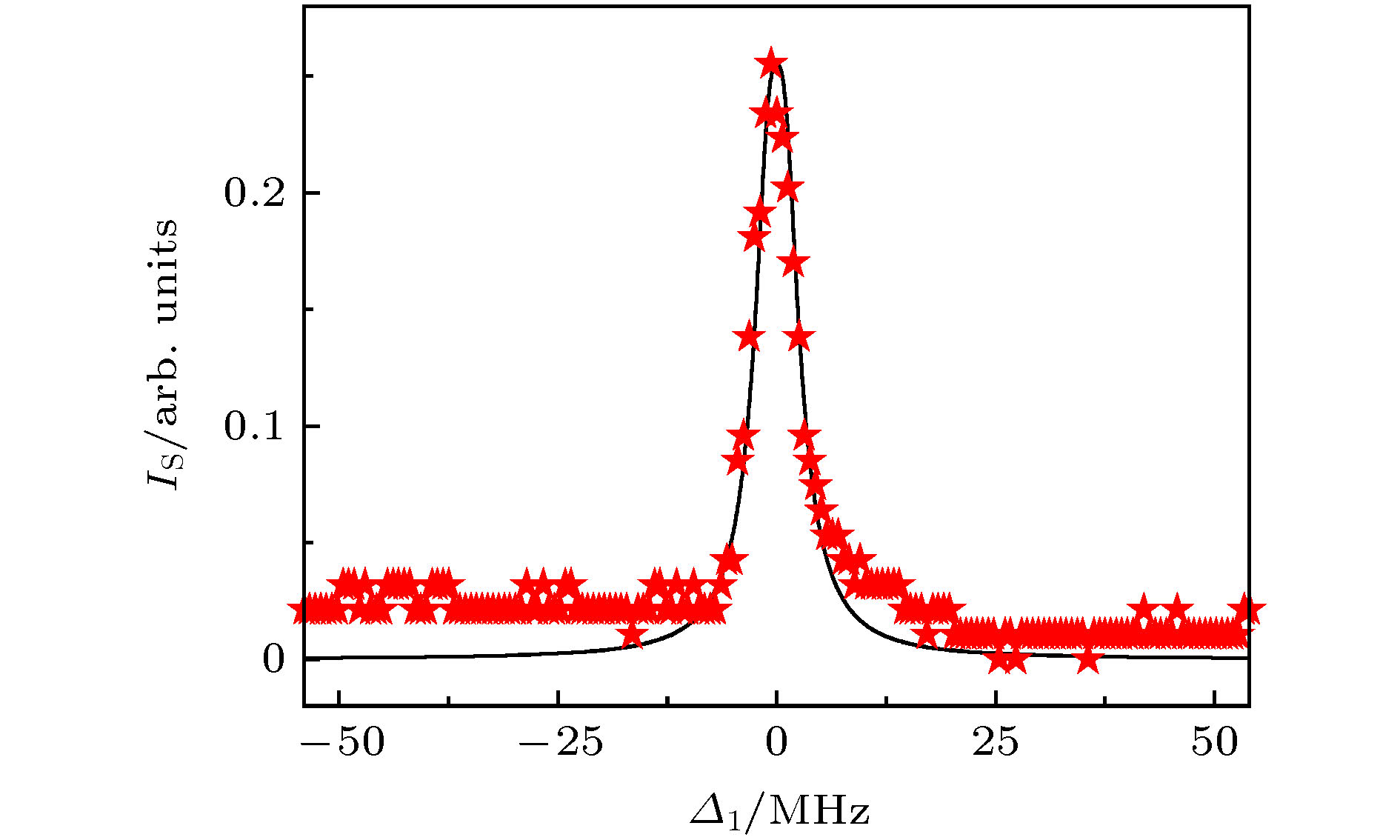
图 4 扫描弱探测光频率时, FWM实验信号(红色-星星)和理论拟合(黑色-实线). 实验采用的耦合光强度I2 = 1.97 mW, 控制光强度I3 = 7.4 mW; 理论模拟采用的参数是:
${\varGamma _{10}} = 7.2\;{\rm{MHz}}$ ,${\varGamma _{20}} = 0.72\;{\rm{MHz}}$ ,${G_2} = 10.8\;{\rm{MHz}}$ ,${G_3} = 20.4\;{\rm{MHz}}$ )Fig. 4. Experimental results (red star) and theoretical fitting (black solid line) for the FWM signal. The coupling field intensity I2 = 1.97 mW and the control field intensity I3 = 7.4 mW are used in the experiment. The parameters used in the theoretical simulation are
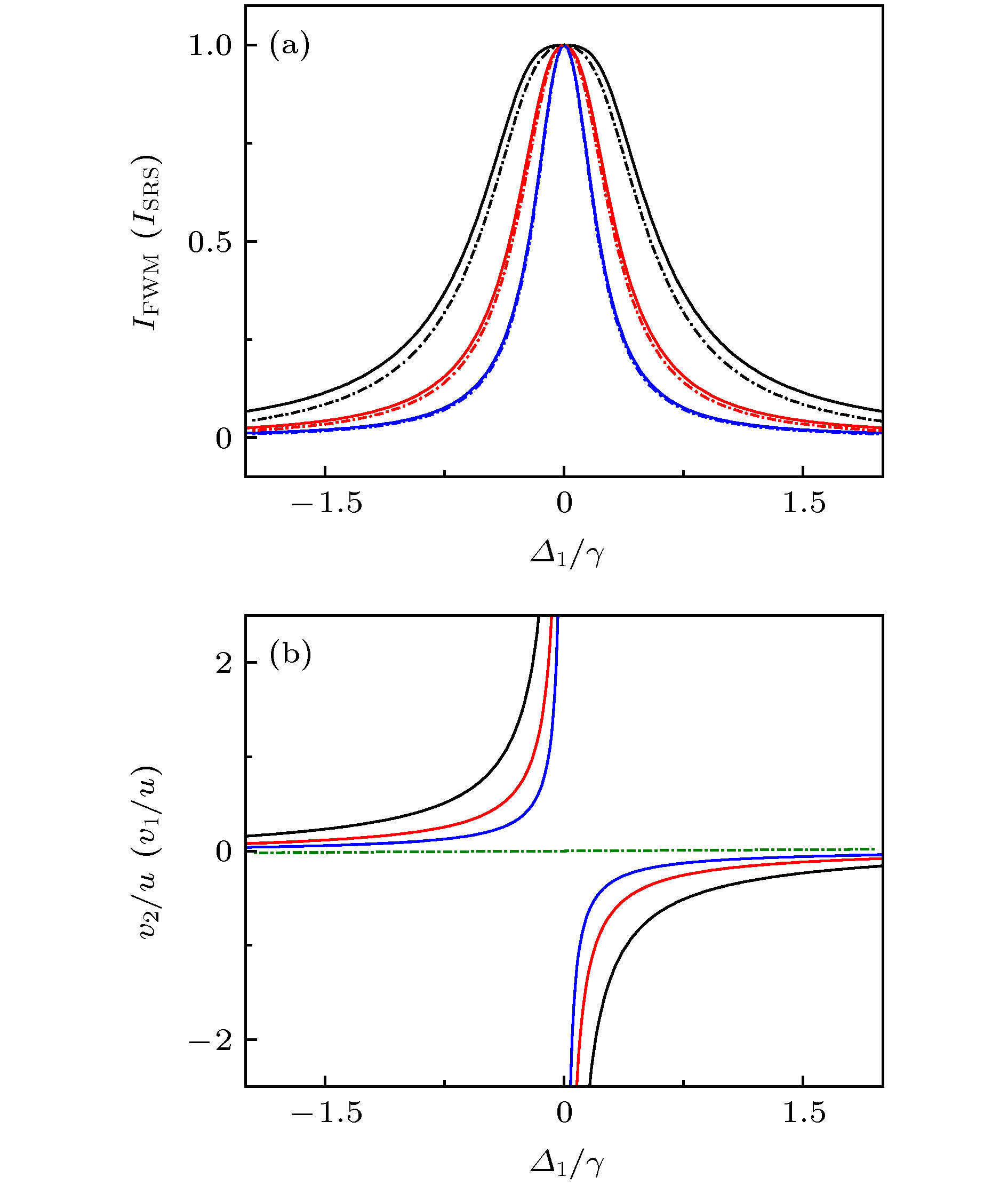
${\varGamma _{10}} = 7.2\;{\rm{MHz}}$ ,${\varGamma _{20}} = 0.72\;{\rm{MHz}}$ ,${G_2} = 10.8\;{\rm{MHz}}$ ,${G_3} = 20.4\;{\rm{MHz}}$ .
图 5 变化耦合光强度(I2)条件下的(a)FWM光谱(实线)和SRS光谱(虚线), 和(b)原子共振速度
${v_2}/u$ (实线)和${v_1}/u$ (虚线). 所取理论参数为:${G_2}/\gamma =0.5$ (黑线), 2.5(红线), 4.0(蓝线)Fig. 5. (a) FWM (solid line) and SRS (dotted line), and (b) corresponding resonant velocities
${v_2}/u$ (solid line) and${v_1}/u$ (dotted line) as a function of${\varDelta _1}/\gamma$ when${G_2}/\gamma = 0.5$ (black), 2.5(red), 4.0(blue).
图 6 变化多普勒展宽线宽(ku)条件下的(a) FWM光谱(实线)和SRS光谱(虚线), 和(b) 原子共振速度
${v_2}/u$ (实线)和${v_1}/u$ (虚线). 所取理论参数为:$ku/\gamma =50.7$ (黑线), 101.4(红线), 202.8(蓝线)Fig. 6. (a) FWM (solid line) and SRS (dotted line), and (b) corresponding resonant velocities
${v_2}/u$ (solid line) and${v_1}/u$ (dotted line) as a function of${\varDelta _1}/\gamma$ when$ku/\gamma =$ 50.7 (black), 101.4(red), 202.8(blue). -
[1] Harris S E, Field J E, Imamoglu A 1990 Phys. Rev. Lett. 64 1107
Google Scholar
[2] Harris S E 1997 Phys. Today 50 36
[3] Fleischhauer M, Imamoglu A, Marangos J P 2005 Rev. Mod. Phys. 77 633
Google Scholar
[4] Kang H, Zhu Y F 2003 Phys. Rev. Lett. 91 093601
Google Scholar
[5] Wang H, Goorskey D, Xiao M 2001 Phys. Rev. Lett. 87 073601
Google Scholar
[6] Wang Z B, Marzlin K P, Sanders B C 2006 Phys. Rev. Lett. 97 063901
Google Scholar
[7] Pack M V, Camacho R M, Howell J C 2007 Phys. Rev. A 76 033835
Google Scholar
[8] Pei L Y, Lu X G, Wang R Q, Wu L A, Zuo Z C, Fu P M 2013 Phys. Rev. A 87 063822
Google Scholar
[9] 裴丽娅, 王如泉, 左战春, 吴令安, 傅盘铭 2013 62 124208
Google Scholar
Pei L Y, Wang R Q, Zuo Z C, Wu L A, Fu P M 2013 Acta Phys. Sin. 62 124208
Google Scholar
[10] 裴丽娅, 左战春, 吴令安, 傅盘铭 2013 62 184209
Google Scholar
Pei L Y, Zuo Z C, Wu L A, Fu P M 2013 Acta Phys. Sin. 62 184209
Google Scholar
[11] Jiang Q, Mi X, Yu Z H, Wang Y B, Wang L J, Fu P M 2001 Chin. Phys. Lett. 18 54
Google Scholar
[12] Zibrov A S, Matsko A B, Scully M O 2002 Phys. Rev. Lett. 89 103601
Google Scholar
[13] Liu J, Wei D, Wang J W, Yu Y, Hu H J, Gao H, Li F L 2016 Chin. Phys. B 25 114204
Google Scholar
[14] Carrasco-Sanz A, Martin-Lopez S, Gonzalez-Herraez M, Corredera P, Hernanz M L, Abrardi L 2008 Opt. Commun. 281 2948
Google Scholar
[15] Vanholsbeeck F, Emplit P, Coen S 2003 Opt. Lett. 28 1960
Google Scholar
[16] Michaud F, Gattobigio G L, Tabosa J W R, Kaiser R 2007 J. Opt. Soc. Am. B 24 A40
Google Scholar
[17] Silva N A, Muga N J, Pinto A N 2009 J. Lightwave. Technol. 27 4979
Google Scholar
[18] Romanov G, O’Brien C, Novikova I 2016 J. Mod. Optic. 63 2048
Google Scholar
[19] Parniak M, Leszczynski A, Wasilewski W 2016 Phys. Rev. A 93 053821
Google Scholar
[20] Lee C Y, Wu B H, Wang G, Chen Y F, Chen Y C, Yu I A 2016 Opt. Express 24 001008
Google Scholar
[21] Dudin Y O, Li L, Kuzmich A 2013 Phys. Rev. A 87 031801(R)
Google Scholar
[22] Ma L J, Slattery O, Tang X 2017 J. Optics-UK 19 043001
Google Scholar
[23] 顾世杰 1984 33 593
Google Scholar
Gu S J 1984 Acta Phys. Sin. 33 593
Google Scholar
[24] Fleischhauer M, Imamoglu A, Marangos J P 2005 Reviews of Modern Physics 77 633
下载:
计量
- 文章访问数: 6328
- PDF下载量: 106
- 被引次数: 0
