平带光子微结构中的新颖现象:从模式局域到实空间拓扑

夏世强; 唐莉勤; 夏士齐; 马继娜; 燕文超; 宋道红; 胡毅; 许京军; 陈志刚

doi:10.7498/aps.69.20200384

摘要

近年来, 凝聚态物理中平带局域与拓扑等概念与光学体系的有机结合, 使得平带光子学系统的研究迎来了极为快速的发展, 催生了一系列新颖的光物理现象与潜在的应用前景. 目前, 平带结构在光子晶体、光学超构材料以及光子晶格(倏逝波耦合的光学波导阵列)等多种人工光子微结构中得到了实现, 并在其中观察到了很多凝聚态系统中难以直接实现的物理现象. 本文简要综述光子微结构中关于平带物理的最新研究进展. 以光诱导和激光直写光子晶格系统为例, 包括Lieb, Kagome 和超级蜂窝晶格等, 特别介绍平带模式局域与实空间拓扑效应等新颖物理现象. 光子微结构为研究平带物理和拓扑效应提供了一个可调控的平台, 同时其研究结果也对探究电子、声子、等离激元、腔极化子与超冷原子等系统中相关的基本物理问题和应用具有借鉴作用.

关键词:

Abstract

In recent years, flatband systems have aroused considerable interest in different branches of physics, from condensed-matter physics to engineered flatband structures such as in ultracold atoms, various metamaterials, electronic materials, and photonic waveguide arrays. Flatband localization, as an important phenomenon in solid state physics, is of broad interest in the exploration of many fundamental physics of many-body systems. We briefly review the recent experimental advances in light localization in engineered flatband lattices, with the emphasis on the optical induction technique of various photonic lattices and unconventional flatband states. The photonic lattices, established by various optical induction techniques, include quasi-one-dimensional diamond lattices and two-dimensional super-honeycomb, Lieb and Kagome lattices. Nontrivial flatband line states, independent of linear superpositions of conventional compact localized states, are demonstrated in photonic Lieb and super-honeycomb lattices, and they can be considered as an indirect illustration of the non-contractible loop states. Furthermore, we discuss alternative approaches to directly observing the non-contractible loop states in photonic Kagome lattices. These robust loop states are direct manifestation of real-space topology in such flatband systems. In this paper we do not intend to comprehensively account the vast flatband literature, but we briefly review the relevant work on photonic lattices mainly from our group. We hope that the mentioned concepts and techniques can be further explored and developed for subsequent applications in other structured photonic media such as photonic crystals, metamaterials, and other synthetic nanophotonic materials.

Keywords:

作者及机构信息

1.
南开大学物理科学学院, 泰达应用物理研究院, 天津　300457

2.
河南师范大学物理学院, 新乡　453007

3.
山西大学极端光学协同创新中心, 太原　030006

通信作者: 宋道红, songdaohong@nankai.edu.cn ; 许京军, jjxu@nankai.edu.cn ; 陈志刚, zgchen@nankai.edu.cn

基金项目: 国家级-国家自然科学基金( 批准号: 2017YFA0303800)

Authors and contacts

1.
TEDA Institute of Applied Physics, School of Physics, Nankai University, Tianjin 300457, China

2.
School of Physics, Henan Normal University, Xinxiang 453007, China

3.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Song Dao-Hong, songdaohong@nankai.edu.cn ; Xu Jing-Jun, jjxu@nankai.edu.cn ; Chen Zhi-Gang, zgchen@nankai.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Ramirez A P 1994 Annu. Rev. Mater. Sci. 24 453 Google Scholar
[2]	Huse D A, Rutenberg A D 1992 Phys. Rev. B 45 7536 Google Scholar
[3]	Chalker J T, Holdsworth P C, Shender E F 1992 Phys. Rev. Lett. 68 855 Google Scholar
[4]	Moessner R, Chalker J T 1998 Phys. Rev. B 58 12049 Google Scholar
[5]	Moessner R, Ramirez A P 2006 Phys. Today 59 24
[6]	Bergman D L, Wu C, Balents L 2008 Phys. Rev. B 78 125104 Google Scholar
[7]	Huber S D, Altman E 2010 Phys. Rev. B 82 184502 Google Scholar
[8]	Nixon M, Ronen E, Friesem A A, Davidson N 2013 Phys. Rev. Lett. 110 184102 Google Scholar
[9]	Möller G, Cooper N R 2012 Phys. Rev. Lett. 108 045306 Google Scholar
[10]	Yin J X, Zhang S S, Li H, Jiang K, Chang G, Zhang B, Lian B, Xiang C, Belopolski I, Zheng H, Cochran T A, Xu S Y, Bian G, Liu K, Chang T R, Lin H, Lu Z Y, Wang Z, Jia S, Wang W, Hasan M Z 2018 Nature 562 91 Google Scholar
[11]	Yin J X, Zhang S S, Chang G, Wang Q, Tsirkin S S, Guguchia Z, Lian B, Zhou H, Jiang K, Belopolski I, Shumiya N, Multer D, Litskevich M, Cochran T A, Lin H, Wang Z, Neupert T, Jia S, Lei H, Hasan M Z 2019 Nat. Phys. 15 443 Google Scholar
[12]	Xie Y, Lian B, Jäck B, Liu X, Chiu C L, Watanabe K, Taniguchi T, Bernevig B A, Yazdani A 2019 Nature 572 101 Google Scholar
[13]	Tang E, Mei J W, Wen X G 2011 Phys. Rev. Lett. 106 236802 Google Scholar
[14]	Sun K, Gu Z, Katsura H, Sarma S D 2011 Phys. Rev. Lett. 106 236803 Google Scholar
[15]	Neupert T, Santos L, Chamon C, Mudry C 2011 Phys. Rev. Lett. 106 236804 Google Scholar
[16]	Sheng D N, Gu Z C, Sun K, Sheng L 2011 Nat. Commun. 2 389 Google Scholar
[17]	Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C, Jarillo-Herrero P 2018 Nature 556 80 Google Scholar
[18]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43 Google Scholar
[19]	Kopnin N B, Heikkilä T T, Volovik G E 2011 Phys. Rev. B 83 220503 Google Scholar
[20]	Tang E, Fu L 2014 Nat. Phys. 10 964 Google Scholar
[21]	Iglovikov V I, Hébert F, Grémaud B, Batrouni G G, Scalettar R T 2014 Phys. Rev. B 90 094506 Google Scholar
[22]	Fleischer J W, Segev M, Efremidis N K, Christodoulides D N 2003 Nature 422 147 Google Scholar
[23]	Efremidis N K, Sears S, Christodoulides D N, Fleischer J W, Segev M 2002 Phys. Rev. E 66 046602 Google Scholar
[24]	Chen Z, Segev M, Christodoulides D N 2012 Rep. Prog. Phys. 75 086401 Google Scholar
[25]	Longhi S, Marangoni M, Lobino M, Ramponi R, Laporta P, Cianci E, Foglietti V 2006 Phys. Rev. Lett. 96 243901 Google Scholar
[26]	Szameit A, Garanovich I L, Heinrich M, Sukhorukov A A, Dreisow F, Pertsch T, Nolte S, Tünnermann A, Kivshar Y S 2009 Nat. Phys. 5 271 Google Scholar
[27]	Schwartz T, Bartal G, Fishman S, Segev M 2007 Nature 446 52 Google Scholar
[28]	Lahini Y, Avidan A, Pozzi F, Sorel M, Morandotti R, Christodoulides D N, Silberberg Y 2008 Phys. Rev. Lett. 100 013906 Google Scholar
[29]	Sutherland B 1986 Phys. Rev. B 34 5208 Google Scholar
[30]	Arai M, Tokihiro T, Fujiwara T, Kohmoto M 1988 Phys. Rev. B 38 1621
[31]	Lieb E H 1989 Phys. Rev. Lett. 62 1201 Google Scholar
[32]	Mielke A 1991 J. Phys. A: Math. Gen. 24 L73 Google Scholar
[33]	Mielke A 1991 J. Phys. A: Math. Gen. 24 3311 Google Scholar
[34]	Mielke A 1999 Phys. Rev. Lett. 82 4312 Google Scholar
[35]	Tasaki H 1992 Phys. Rev. Lett. 69 1608 Google Scholar
[36]	Tasaki H 1998 Prog. Theor. Phys. 99 489 Google Scholar
[37]	Aoki H, Ando M, Matsumura H 1996 Phys. Rev. B 54 R17296 Google Scholar
[38]	Slot M R, Gardenier T S, Jacobse P H, van Miert G C, Kempkes S N, Zevenhuizen S J, Smith C M, Vanmaekelbergh D, Swart I 2017 Nat. Phys. 13 672 Google Scholar
[39]	Jo G B, Guzman J, Thomas C K, Hosur P, Vishwanath A, Stamper-Kurn D M 2012 Phys. Rev. Lett. 108 045305 Google Scholar
[40]	Taie S, Ozawa H, Ichinose T, Nishio T, Nakajima S, Takahashi Y 2015 Sci. Adv. 1 e1500854 Google Scholar
[41]	Guzmán-Silva D, Mejía-Cortés C, Bandres M A, Rechtsman M C, Weimann S, Nolte S, Segev M, Szameit A, Vicencio R A 2014 New J. Phys. 16 063061 Google Scholar
[42]	Makasyuk I, Chen Z, Yang J 2006 Phys. Rev. Lett. 96 223903 Google Scholar
[43]	Flach S, Leykam D, Bodyfelt J D, Matthies P, Desyatnikov A S 2014 Europhys. Lett. 105 30001 Google Scholar
[44]	Ramachandran A, Andreanov A, Flach S 2017 Phys. Rev. B 96 161104 Google Scholar
[45]	Li J, White T P, O’Faolain L, Gomez-Iglesias A, Krauss T F 2008 Opt. Express 16 6227 Google Scholar
[46]	Schulz S A, Upham J, O’Faolain L, Boyd R W 2017 Opt. Lett. 42 3243 Google Scholar
[47]	Myoung N, Park H C, Ramachandran A, Lidorikis E, Ryu J W 2019 Sci. Rep. 9 2862 Google Scholar
[48]	Nakata Y, Okada T, Nakanishi T, Kitano M 2012 Phys. Rev. B 85 205128 Google Scholar
[49]	Kajiwara S, Urade Y, Nakata Y, Nakanishi T, Kitano M 2016 Phys. Rev. B 93 075126 Google Scholar
[50]	Huang X, Lai Y, Hang Z H, Zheng H, Chan C T 2011 Nat. Mater. 10 582 Google Scholar
[51]	Baboux F, Ge L, Jacqmin T, Biondi M, Galopin E, Lemaître A, Gratiet L L, Sagnes I, Schmidt S, Türeci H E, Amo A, Bloch J 2016 Phys. Rev. Lett. 116 066402 Google Scholar
[52]	Whittaker C E, Cancellieri E, Walker P M, Gulevich D R, Schomerus H, Vaitiekus D, Royall B, Whittaker D M, Clarke E, Iorsh I V, Shelykh I A, Skolnick M S, Krizhanovskii D N 2018 Phys. Rev. Lett. 120 097401 Google Scholar
[53]	Harder T H, Egorov O A, Beierlein J, Gagel P, Michl J, Emmerling M, Schneider C, Peschel U, Höfling S, Klembt S 2020 arXiv 2002.05405
[54]	Milićević M, Montambaux G, Ozawa T, Jamadi O, Real B, Sagnes I, Lemaître A, Gratiet L L, Harouri A, Bloch J, Amo A 2019 Phys. Rev. X 9 031010
[55]	Leykam D, Andreanov A, Flach S 2018 Adv. Phys. X 3 1473052
[56]	Leykam D, Flach S 2018 APL Photonics 3 070901 Google Scholar
[57]	Pertsch T, Peschel U, Lederer F, Burghoff J, Will M, Nolte S, Tuennermann A 2004 Opt. Lett. 29 468 Google Scholar
[58]	Szameit A, Blömer D, Burghoff J, Schreiber T, Pertsch T, Nolte S, Tünnermann A, Lederer F 2005 Opt. Express 13 10552 Google Scholar
[59]	Plotnik Y, Rechtsman M C, Song D, Heinrich M, Zeuner J M, Nolte S, Lumer Y, Malkova N, Xu J, Szameit A, Chen Z, Segev M 2014 Nat. Mater. 13 57 Google Scholar
[60]	Rechtsman M C, Zeuner J M, Tünnermann A, Nolte S, Segev M, Szameit A 2013 Nat. Photonics 7 153 Google Scholar
[61]	Rechtsman M C, Zeuner J M, Plotnik Y, Lumer Y, Podolsky D, Dreisow F, Nolte S, Segev M, Szameit A 2013 Nature 496 196 Google Scholar
[62]	Rechtsman M C, Plotnik Y, Zeuner J M, Song D, Chen Z, Szameit A, Segev M 2013 Phys. Rev. Lett. 111 103901 Google Scholar
[63]	Ivanov S K, Zhang Y, Kartashov Y V, Skryabin D V 2019 APL Photonics 4 126101 Google Scholar
[64]	Mukherjee S, Spracklen A, Choudhury D, Goldman N, Öhberg P, Andersson E, Thomson R R 2015 Phys. Rev. Lett. 114 245504 Google Scholar
[65]	Vicencio R A, Cantillano C, Morales-Inostroza L, Real B, Mejía-Cortés C, Weimann S, Szameit A, Molina M I 2015 Phys. Rev. Lett. 114 245503 Google Scholar
[66]	EI Hassan A, Kunst F K, Moritz A, Andler G, Emil J. Bergholtz E J, Bourennane M 2019 Nat. Photonics 13 697 Google Scholar
[67]	Mukherjee S, Di Liberto M, Öhberg P, Thomson R R, Goldman N 2018 Phys. Rev. Lett. 121 075502 Google Scholar
[68]	Kremer M, Petrides I, Meyer E, Heinrich M, Zilberberg O, Szameit A2018 arXiv 1805.05209
[69]	Zyuzin A A, Zyuzin A Y 2018 Phys. Rev. B 97 041203 Google Scholar
[70]	Ramezani H 2017 Phys. Rev. A 96 011802 Google Scholar
[71]	Leykam D, Flach S, Chong Y D 2017 Phys. Rev. B 96 064305 Google Scholar
[72]	Qi B, Zhang L, Ge L 2018 Phys. Rev. Lett. 120 093901 Google Scholar
[73]	Ge L 2018 Photonics Res 6 A10 Google Scholar
[74]	Ge L 2015 Phys. Rev. A 92 052103 Google Scholar
[75]	Molina M I 2015 Phys. Rev. A 92 063813 Google Scholar
[76]	Biesenthal T, Kremer M, Heinrich M, Szameit A 2019 Phys. Rev. Lett. 123 183601 Google Scholar
[77]	Chen Z, Klinger J, Christodoulides D N 2002 Phys. Rev. E 66 066601 Google Scholar
[78]	Martin H, Eugenieva E D, Chen Z, Christodoulides D N 2004 Phys. Rev. Lett. 92 123902 Google Scholar
[79]	Song D, Leykam D, Su J, Liu X, Tang L, Liu S, Zhao J, Efremidis N K, Xu J, Chen Z 2019 Phys. Rev. Lett. 122 123903 Google Scholar
[80]	Song D, Paltoglou V, Liu S, Zhu Y, Gallardo D, Tang L, Xu J, Ablowitz M, Efremidis N K, Chen Z 2015 Nat. Commun. 6 6272 Google Scholar
[81]	Song D, Liu S, Paltoglou V, Gallardo D, Tang L, Zhao J, Xu J, Efremidis N K Chen Z 2015 2D Mater. 2 034007
[82]	Boguslawski M, Rose P, Denz C 2011 Phys. Rev. A 84 013832 Google Scholar
[83]	Gao Y, Song D, Chu S, Chen Z 2014 IEEE Photonics J. 6 2201806
[84]	Shen R, Shao L B, Wang B, Xing D Y 2010 Phys. Rev. B 81 041410 Google Scholar
[85]	Xia S, Hu Y, Song D, Zong Y, Tang L, Chen Z 2016 Opt. Lett. 41 1435 Google Scholar
[86]	Malkova N, Hromada I, Wang X, Bryant G, Chen Z 2009 Opt. Lett. 34 1633 Google Scholar
[87]	Malkova N, Hromada I, Wang X, Bryant G, Chen Z 2009 Phys. Rev. A 80 043806 Google Scholar
[88]	Boguslawski M, Kelberer A, Rose P, Denz C 2012 Opt. Express 20 27331 Google Scholar
[89]	Xia S, Ramachandran A, Xia S, Li D, Liu X, Tang L, Hu Y, Song D, Xu J, Leykam D, Flach S, Chen Z 2018 Phys. Rev. Lett. 121 263902 Google Scholar
[90]	Ma J, Rhim J W, Tang L, Xia S, Wang H, Zheng X, Xia S, Song D, Hu Y, Li Y, Yang B J, Leykam D, Chen Z 2020 Phys. Rev. Lett. 124 183901
[91]	Yan W, Zhong H, Song D, Zhang Y, Xia S, Tang L, Leykam D, Chen Z 2020 Adv. Optical Mater. 8 1902174
[92]	Xia S, Danieli C, Yan W, Li D, Xia S, Ma J, Lu H, Song D, Tang L, Flach S, Chen Z 2020 APL Photonics 5 016107 Google Scholar
[93]	Travkin E, Diebel F, Denz C 2017 Appl. Phys. Lett. 111 011104 Google Scholar
[94]	Diebel F, Leykam D, Kroesen S, Denz C, Desyatnikov A S 2016 Phys. Rev. Lett. 116 183902 Google Scholar
[95]	Leykam D, Bahat-Treidel O, Desyatnikov A S 2012 Phys. Rev. A 86 031805 Google Scholar
[96]	Bandres M A, Rechtsman M C, Szameit A, Segev M 2014 Conference on Lasers and Electro-Optics (CLEO)-Laser Science to Photonic Applications San Jose, CA, USA, June 8−13, 2014 p. FF2D.3.
[97]	Goda M, Nishino S, Matsuda H 2006 Phys. Rev. Lett. 96 126401 Google Scholar
[98]	Leykam D, Flach S, Bahat-Treidel O, Desyatnikov A S 2013 Phys. Rev. B 88 224203 Google Scholar
[99]	Bodyfelt J D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403 Google Scholar
[100]	Gligorić G, Maluckov A, Hadžievski L, Flach S, Malomed B A 2016 Phys. Rev. B 94 144302 Google Scholar
[101]	Leykam D, Bodyfelt J D, Desyatnikov A S, Flach S 2017 Eur. Phys. J. B 90 1 Google Scholar
[102]	Vicencio R A, Johansson M 2013 Phys. Rev. A 87 061803 Google Scholar
[103]	Vicencio R A, Mejía-Cortés C 2014 J. Opt. 16 015706
[104]	Zong Y, Xia S, Tang L, Song D, Hu Y, Pei Y, Su J, Li Y, Chen Z 2016 Opt. Express 24 8877 Google Scholar
[105]	Guo H, Shen S Q, Feng S 2012 Phys. Rev. B 86 085124 Google Scholar
[106]	Weeks C, Franz M 2012 Phys. Rev. B 85 041104
[107]	Liu Z, Bergholtz E J, Fan H, Läuchli A M 2012 Phys. Rev. Lett. 109 186805 Google Scholar
[108]	Bergholtz E J, Liu Z 2013 Int. J. Mod. Phys. B 27 1330017 Google Scholar
[109]	Kalesaki E, Delerue C, Smith C M, Beugeling W, Allan G, Vanmaekelbergh D 2014 Phys. Rev. X 4 011010
[110]	Pal B 2018 Phys. Rev. B 98 245116 Google Scholar
[111]	Khomeriki R, Flach S 2016 Phys. Rev. Lett. 116 245301 Google Scholar
[112]	Long Y, Ren J 2017 arXiv 1706.01107
[113]	Mukherjee S, Thomson R R 2017 Opt. Lett. 42 2243 Google Scholar
[114]	Kolovsky A R, Ramachandran A, Flach S 2018 Phys. Rev. B 97 045120 Google Scholar
[115]	Yulin A V, Konotop V V 2013 Opt. Lett. 38 4880 Google Scholar
[116]	Longhi S 2014 Opt. Lett. 39 5892 Google Scholar
[117]	Mukherjee S, Thomson R R 2015 Opt. Lett. 40 5443 Google Scholar
[118]	Rhim J W, Yang B J 2019 Phys. Rev. B 99 045107 Google Scholar
[119]	Shima N, Aoki H 1993 Phys. Rev. Lett. 71 4389 Google Scholar
[120]	Zhong H, Zhang Y, Zhu Y, Zhang D, Li C, Zhang Y, Li F, Belić M R, Xiao M 2017 Ann. Phys. 529 1600258 Google Scholar
[121]	Longhi S 2019 Opt. Lett. 44 287 Google Scholar
[122]	Lim L K, Fuchs J N, Piéchon F, Montambaux G 2020 Phys. Rev. B 101 045131 Google Scholar
[123]	Jiang W, Kang M, Huang H, Xu H, Low T, Liu F 2019 Phys. Rev. B 99 125131 Google Scholar
[124]	Wang P, Zheng Y, Chen X, Huang C, Kartashov Y V, Torner L, Konotop V V, Ye F 2020 Nature 577 42 Google Scholar
[125]	Abouelkomsan A, Liu Z, Bergholtz E J 2020 Phys. Rev. Lett. 124 106803 Google Scholar

施引文献

图 1 几种典型的平带晶格结构　(a) 菱形晶格; (b) Lieb晶格; (c) Kagome晶格; (d) 超级蜂窝型晶格; 彩色点为常规紧凑排列的局域本征模式示意图, 灰色点振幅为0, 红色点代表振幅为1, 蓝色点为–1, 即两者振幅大小相同而相位差为π

Fig. 1. Typical examples of flatband lattices: (a) Quasi-one-dimensional (1D) rhombic lattice; (b) Lieb lattice; (c) Kagome lattice; (d) super-honeycomb lattice (sHCL). Compact localized states (CLSs) are depicted as colored sites, where zero amplitudes are denoted by gray color, and those with non-zero amplitudes of opposite phase are denoted by red and blue colors.

下载: 全尺寸图片幻灯片

图 2 光子系统中平带研究的典型实例　(a) 左图为表面等离激元平带的金属Kagome超构材料, 右图为对应的太赫兹波透射图, 存在一个全角度的无辐射平带(水平虚线所示)^[48]; (b) 左图为四方结构的全介质零折射率超构材料实现隐身效应实验装置, 右图为适当介质参数时得到的四方结构色散关系, 含有一个狄拉克锥与一个无色散平带^[50]; (c) 一维“枕”型结构的微柱光学腔及其色散关系, 中间为平带^[51]

Fig. 2. Examples of photonic flatband structures: (a) Kagome lattice for terahertz spoof plasmons, displaying an omnidirectional minimum in the transmission at the flatband frequency (dashed line) in the right panel^[48]; (b) experimental setup exposing the zero-refractive-index all-dielectric metamaterials with a square lattice to realize cloaking inside a channel with the Dirac point, and the right panel shows corresponding three-dimensional dispersion diagrams consisting of a Dirac cone and a flatband^[50]; (c) structured microcavity forming a 1D stub lattice and its photoluminescence spectrum, revealing a flatband in the middle^[51].

下载: 全尺寸图片幻灯片

图 3 利用飞秒激光直写技术制备的平带光子晶格　(a) 用于研究平带局域模式的Lieb光子晶格^[64,65]; (b) 用于研究拓扑角态的Kagome光子晶格^[66]; (c) 用于实现Aharonov-Bohm效应的纵向弯曲菱形光子晶格^[67,68]

Fig. 3. Examples of femtosecond laser-writing flatband photonic lattices: (a) A photonic Lieb lattice for demonstration of flatband compact localized states^[64,65]; (b) a photonic Kagome lattice established for demonstration of topological corner states^[66]; (c) a driven photonic rhombic lattice for experimental observation of Aharonov-Bohm cages^[67,68].

下载: 全尺寸图片幻灯片

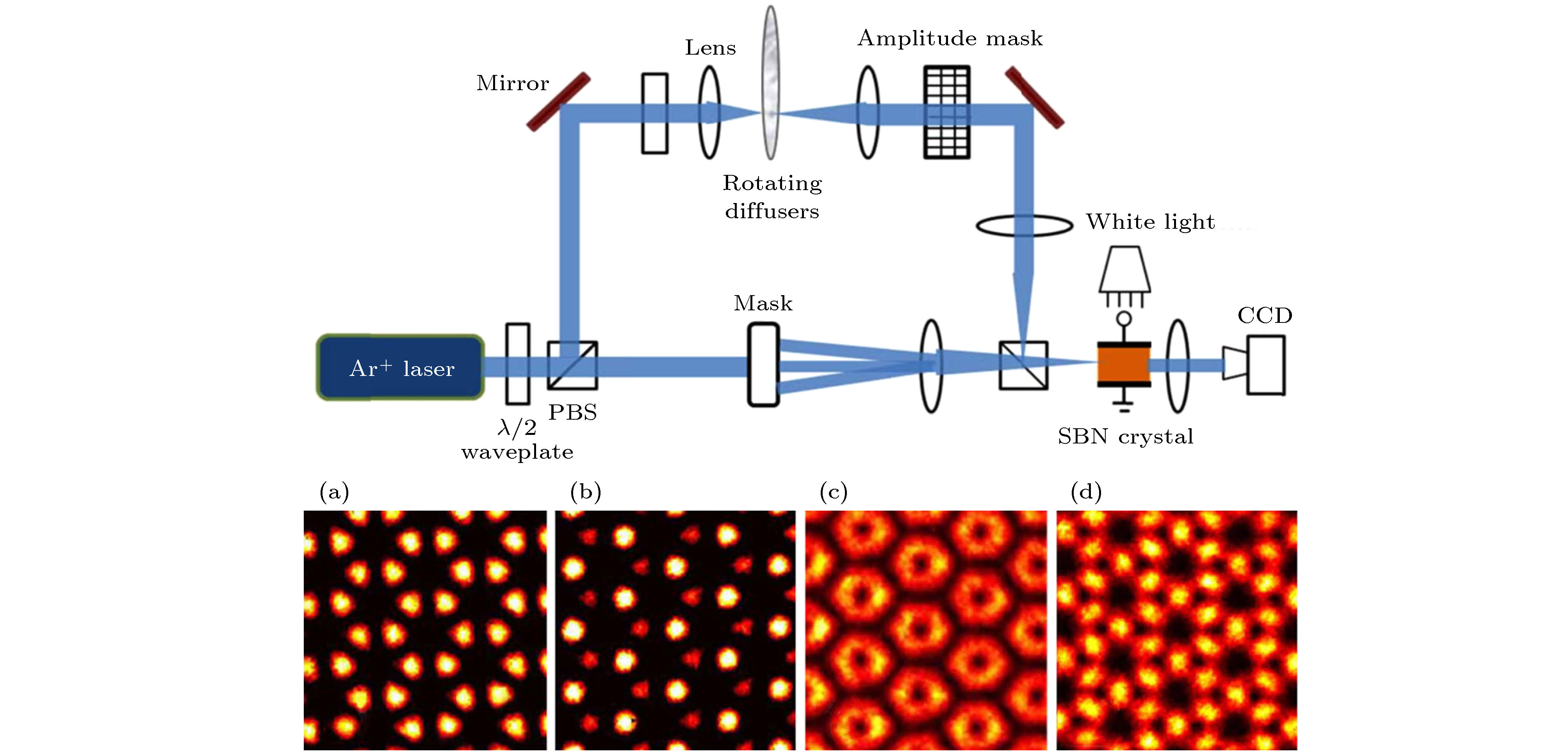
图 4 多光束干涉光诱导技术制备光子晶格^[80,83], 其中第一排为实验光路图(PBS, 偏振分光棱镜; Mask, 掩膜板; SBN, 铌酸锶钡晶体); 第二排为实验制作的典型光子晶格　(a) 蜂窝型光子晶格; (b) 对称破缺的蜂窝型光子晶格; (c) 涡旋晶格; (d) Kagome晶格

Fig. 4. Examples of photonic lattices created by multiple-beam optical induction method^[80,83]. Top panel shows schematic of experimental setup. PBS, polarized beam splitter; SBN, strontium barium niobite. Bottom panel shows typical examples of photonic lattices realized in experiment: (a) A “perfect” honeycomb lattice; (b) an inversion-symmetry-breaking honeycomb lattice; (c) a vortex lattice; (d) a Kagome lattice.

下载: 全尺寸图片幻灯片

图 5 连续激光直写技术制备不同平带光子晶格, 其中, 第一排为实验光路图(SLM, 空间光调制器; BS, 分光棱镜; FM, 傅里叶掩膜板); 第二排为典型的直写光子晶格　(a)“胡须”边界(“bearded” edges)的Lieb光子晶格^[89]; (b) 平滑边界的Kagome光子晶格^[90]; (c) 超级蜂窝晶格^[91]; (d) 横向折射率梯度变化的菱形光子晶格^[92]

Fig. 5. Examples of photonic lattices created by direct cw-laser-writing technique in a nonlinear bulk crystal. Top panel shows illustration of experimental setup. SLM, spatial light modulator; BS, beam splitter; FM, Fourier mask. Bottom panel shows typical examples of photonic lattices created by direct cw-laser-writing method: (a) A photonic Lieb lattice with “bearded” edges^[89]; (b) a photonic Kagome lattice with flat boundary^[90]; (c) a photonic sHCL^[91]; (d) a driven photonic rhombic lattice with refractive index gradient parallel to the ribbon^[92].

下载: 全尺寸图片幻灯片

图 6 平带光子晶格常规紧凑局域模式的实验结果(从左至右: 实验制备的光诱导光子晶格结构、紧束缚近似下能带结构、入射面探测光、同相位输出以及反相位输出)　(a) Lieb光子晶格中基于平带模式的图像传输^[85]; (b) Kagome光子晶格中的平带局域模式^[104]; (c) 折射率梯度场下菱形光子晶格中U = 2的局域本征模式^[92]

Fig. 6. Experimental results of CLSs in flatband lattices: (a) Linear image (formed by CLSs) propagation through an optically induced Lieb photonic lattice^[85]; (b) a bound-state transmission in a Kagome photonic lattice^[104]; (c) observation of a quincunx-shaped (U = 2) compact localized state which spans over two-unit cells in a photonic rhombic lattice^[92]. From left to right: shown are the lattices, calculated band structures in the tight-binding approximation, probe beam inputs, and their in-phase and out-of-phase outputs.

下载: 全尺寸图片幻灯片

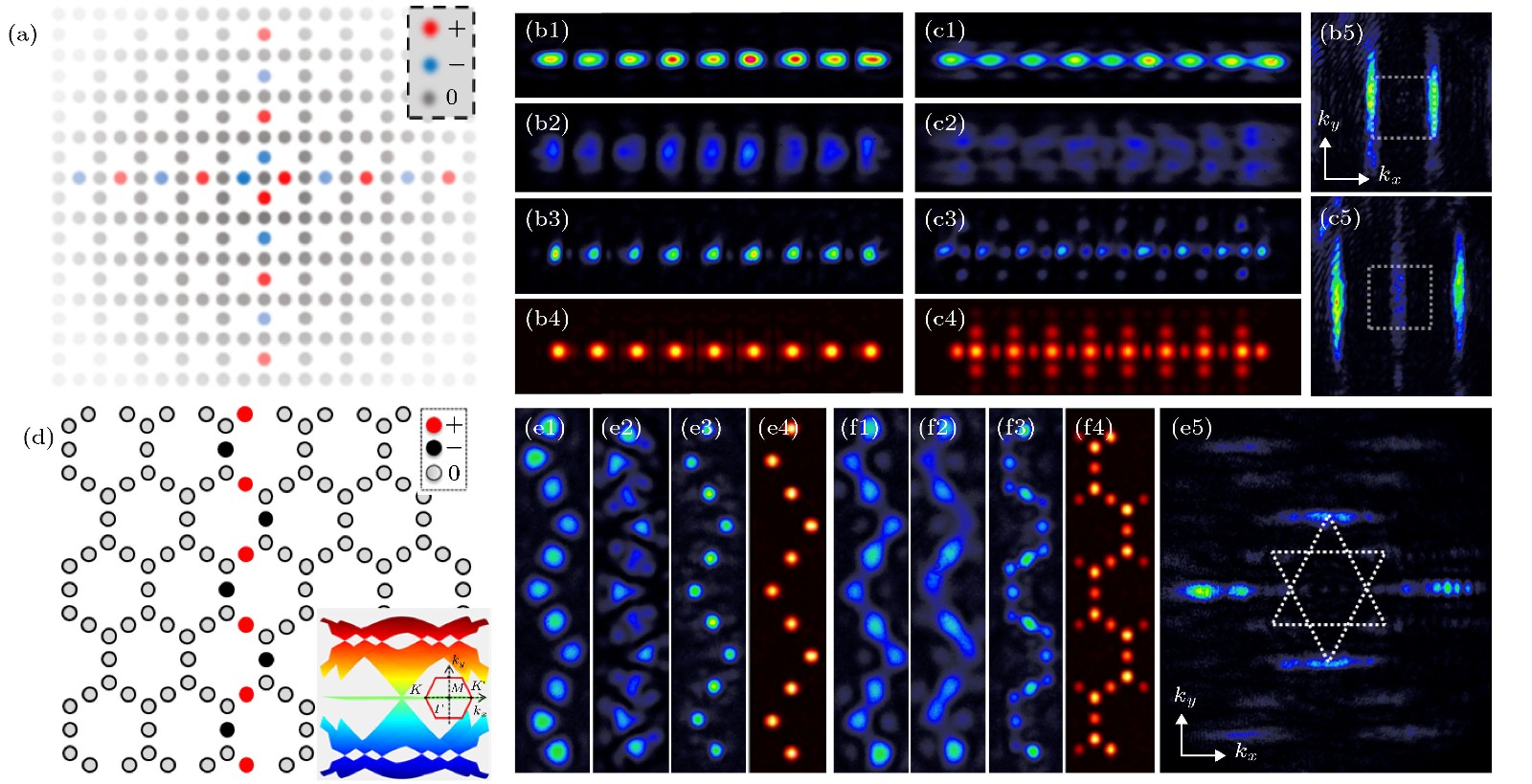
图 7 Lieb与超级蜂窝光子晶格中非常规线形平带模式的实验结果^[89,91]　(a), (d)非常规线形平带局域模式的示意图, 其中图(d)右下插图为能带结构; (b1), (e1) 反相位入射的探测光; (b2), (e2) 无晶格时的输出; (b3), (e3) 有晶格时的输出; (b4), (e4) 长距离传输的数值模拟结果; 图(c1)−(c4)完全对应(b1)−(b4), 但为探测光同相位入射时的结果; 图(f1)−(f4)对应(e1)−(e4), 但为探测光同相位入射时的结果; (b5), (c5)为对应(b3), (c3)的k空间能谱, 虚线框为第一布里渊区边界; (e5) 为对应于图(e3)的k空间能量分布, 其中虚线框表示第一与第二布里渊区边界

Fig. 7. Demonstration of unconventional line state in photonic Lieb and super-honeycomb lattices^[89,91]: (a), (d) Schematic of flatband line states in infinite lattices, and insect in (d) shows the band structure of sHCL; (b1), (e1) out-of-phase input line beam; (b2), (e2) out-of-phase output without the lattice; (b3), (e3) out-of-phase output through the lattice; (b4), (e4) simulation results showing the out-of-phase line beam remains intact but the in-phase line deteriorates after propagating a long distance through the lattice; (b5) measured k-space spectrum of (b3) with a dashed square marking the first Brillouin zone (BZ); (c1)−(c5) the same as in (b1)−(b5), and (f1)−(f4) the same as in (e1)−(e4) except that the line beam is in in-phase excitation condition; (e5) momentum space spectrum of (e3), where the white dashed lines outline the first and second BZs.

下载: 全尺寸图片幻灯片

图 8 (a) Kagome晶格中两种不可压缩环形态示意图; (b) 模拟无限Kagome晶格两个不可压缩环形态的圆环面; (c) 在平滑边界的Kagome晶格中两种稳定的平带边界局域模, 橘黄色线代表模式一, 绿色虚线代表模式二; (d) Corbino-Kagome结构示意图, 橘黄色圆环代表不可压缩的局域环形态; (e) 从左至右, (e1), (e2) 边界模式一的反相位输出与对应数值模拟结果; (e3), (e4) 边界模式二的反相位输出与对应数值模拟结果; (f1) 实验制备的Corbino-Kagome光子晶格; (f2), (f3)反相位激发的不可压缩环形态及其对应数值模拟结果; (f4) 40 mm传输时数值模拟结果; 图中所有插图均代表输入探测光; 同相位激发破坏所有平带局域模式的形成^[90]

Fig. 8. (a) Illustration of the noncontractible loop states (NLSs) in an infinitely extended Kagome lattice; (b) a torus showing two NLSs mimicking the 2D infinite lattice; (c) two robust boundary modes (RBMs) in a Kagome lattice with flat cutting edges, where black sites are of zero-amplitude, while blue and red ones distinguish non-zero sites with opposite phase; (d) schematic diagram of the Corbino-shaped Kagome lattice, where the NLS is illustrated by the orange circle; (e) from left to right (e1), (e3) experimental results of RBM1 and RBM2 under out-of-phase condition; (e2), (e4) simulation result corresponding to (e1) and (e3); (f1) experimentally established finite-sized Kagome lattice in a Corbino-geometry; (f2)－(f4) the NLS observed in (f2) experiment and (f3) simulations after propagation to 10 mm and (f4) 40 mm under out-of-phase condition. All insets are from input ring necklace of the probe beam. In-phase excitation destroys all localized states^[90].

下载: 全尺寸图片幻灯片

map

[1]	Ramirez A P 1994 Annu. Rev. Mater. Sci. 24 453 Google Scholar
[2]	Huse D A, Rutenberg A D 1992 Phys. Rev. B 45 7536 Google Scholar
[3]	Chalker J T, Holdsworth P C, Shender E F 1992 Phys. Rev. Lett. 68 855 Google Scholar
[4]	Moessner R, Chalker J T 1998 Phys. Rev. B 58 12049 Google Scholar
[5]	Moessner R, Ramirez A P 2006 Phys. Today 59 24
[6]	Bergman D L, Wu C, Balents L 2008 Phys. Rev. B 78 125104 Google Scholar
[7]	Huber S D, Altman E 2010 Phys. Rev. B 82 184502 Google Scholar
[8]	Nixon M, Ronen E, Friesem A A, Davidson N 2013 Phys. Rev. Lett. 110 184102 Google Scholar
[9]	Möller G, Cooper N R 2012 Phys. Rev. Lett. 108 045306 Google Scholar
[10]	Yin J X, Zhang S S, Li H, Jiang K, Chang G, Zhang B, Lian B, Xiang C, Belopolski I, Zheng H, Cochran T A, Xu S Y, Bian G, Liu K, Chang T R, Lin H, Lu Z Y, Wang Z, Jia S, Wang W, Hasan M Z 2018 Nature 562 91 Google Scholar
[11]	Yin J X, Zhang S S, Chang G, Wang Q, Tsirkin S S, Guguchia Z, Lian B, Zhou H, Jiang K, Belopolski I, Shumiya N, Multer D, Litskevich M, Cochran T A, Lin H, Wang Z, Neupert T, Jia S, Lei H, Hasan M Z 2019 Nat. Phys. 15 443 Google Scholar
[12]	Xie Y, Lian B, Jäck B, Liu X, Chiu C L, Watanabe K, Taniguchi T, Bernevig B A, Yazdani A 2019 Nature 572 101 Google Scholar
[13]	Tang E, Mei J W, Wen X G 2011 Phys. Rev. Lett. 106 236802 Google Scholar
[14]	Sun K, Gu Z, Katsura H, Sarma S D 2011 Phys. Rev. Lett. 106 236803 Google Scholar
[15]	Neupert T, Santos L, Chamon C, Mudry C 2011 Phys. Rev. Lett. 106 236804 Google Scholar
[16]	Sheng D N, Gu Z C, Sun K, Sheng L 2011 Nat. Commun. 2 389 Google Scholar
[17]	Cao Y, Fatemi V, Demir A, Fang S, Tomarken S L, Luo J Y, Sanchez-Yamagishi J D, Watanabe K, Taniguchi T, Kaxiras E, Ashoori R C, Jarillo-Herrero P 2018 Nature 556 80 Google Scholar
[18]	Cao Y, Fatemi V, Fang S, Watanabe K, Taniguchi T, Kaxiras E, Jarillo-Herrero P 2018 Nature 556 43 Google Scholar
[19]	Kopnin N B, Heikkilä T T, Volovik G E 2011 Phys. Rev. B 83 220503 Google Scholar
[20]	Tang E, Fu L 2014 Nat. Phys. 10 964 Google Scholar
[21]	Iglovikov V I, Hébert F, Grémaud B, Batrouni G G, Scalettar R T 2014 Phys. Rev. B 90 094506 Google Scholar
[22]	Fleischer J W, Segev M, Efremidis N K, Christodoulides D N 2003 Nature 422 147 Google Scholar
[23]	Efremidis N K, Sears S, Christodoulides D N, Fleischer J W, Segev M 2002 Phys. Rev. E 66 046602 Google Scholar
[24]	Chen Z, Segev M, Christodoulides D N 2012 Rep. Prog. Phys. 75 086401 Google Scholar
[25]	Longhi S, Marangoni M, Lobino M, Ramponi R, Laporta P, Cianci E, Foglietti V 2006 Phys. Rev. Lett. 96 243901 Google Scholar
[26]	Szameit A, Garanovich I L, Heinrich M, Sukhorukov A A, Dreisow F, Pertsch T, Nolte S, Tünnermann A, Kivshar Y S 2009 Nat. Phys. 5 271 Google Scholar
[27]	Schwartz T, Bartal G, Fishman S, Segev M 2007 Nature 446 52 Google Scholar
[28]	Lahini Y, Avidan A, Pozzi F, Sorel M, Morandotti R, Christodoulides D N, Silberberg Y 2008 Phys. Rev. Lett. 100 013906 Google Scholar
[29]	Sutherland B 1986 Phys. Rev. B 34 5208 Google Scholar
[30]	Arai M, Tokihiro T, Fujiwara T, Kohmoto M 1988 Phys. Rev. B 38 1621
[31]	Lieb E H 1989 Phys. Rev. Lett. 62 1201 Google Scholar
[32]	Mielke A 1991 J. Phys. A: Math. Gen. 24 L73 Google Scholar
[33]	Mielke A 1991 J. Phys. A: Math. Gen. 24 3311 Google Scholar
[34]	Mielke A 1999 Phys. Rev. Lett. 82 4312 Google Scholar
[35]	Tasaki H 1992 Phys. Rev. Lett. 69 1608 Google Scholar
[36]	Tasaki H 1998 Prog. Theor. Phys. 99 489 Google Scholar
[37]	Aoki H, Ando M, Matsumura H 1996 Phys. Rev. B 54 R17296 Google Scholar
[38]	Slot M R, Gardenier T S, Jacobse P H, van Miert G C, Kempkes S N, Zevenhuizen S J, Smith C M, Vanmaekelbergh D, Swart I 2017 Nat. Phys. 13 672 Google Scholar
[39]	Jo G B, Guzman J, Thomas C K, Hosur P, Vishwanath A, Stamper-Kurn D M 2012 Phys. Rev. Lett. 108 045305 Google Scholar
[40]	Taie S, Ozawa H, Ichinose T, Nishio T, Nakajima S, Takahashi Y 2015 Sci. Adv. 1 e1500854 Google Scholar
[41]	Guzmán-Silva D, Mejía-Cortés C, Bandres M A, Rechtsman M C, Weimann S, Nolte S, Segev M, Szameit A, Vicencio R A 2014 New J. Phys. 16 063061 Google Scholar
[42]	Makasyuk I, Chen Z, Yang J 2006 Phys. Rev. Lett. 96 223903 Google Scholar
[43]	Flach S, Leykam D, Bodyfelt J D, Matthies P, Desyatnikov A S 2014 Europhys. Lett. 105 30001 Google Scholar
[44]	Ramachandran A, Andreanov A, Flach S 2017 Phys. Rev. B 96 161104 Google Scholar
[45]	Li J, White T P, O’Faolain L, Gomez-Iglesias A, Krauss T F 2008 Opt. Express 16 6227 Google Scholar
[46]	Schulz S A, Upham J, O’Faolain L, Boyd R W 2017 Opt. Lett. 42 3243 Google Scholar
[47]	Myoung N, Park H C, Ramachandran A, Lidorikis E, Ryu J W 2019 Sci. Rep. 9 2862 Google Scholar
[48]	Nakata Y, Okada T, Nakanishi T, Kitano M 2012 Phys. Rev. B 85 205128 Google Scholar
[49]	Kajiwara S, Urade Y, Nakata Y, Nakanishi T, Kitano M 2016 Phys. Rev. B 93 075126 Google Scholar
[50]	Huang X, Lai Y, Hang Z H, Zheng H, Chan C T 2011 Nat. Mater. 10 582 Google Scholar
[51]	Baboux F, Ge L, Jacqmin T, Biondi M, Galopin E, Lemaître A, Gratiet L L, Sagnes I, Schmidt S, Türeci H E, Amo A, Bloch J 2016 Phys. Rev. Lett. 116 066402 Google Scholar
[52]	Whittaker C E, Cancellieri E, Walker P M, Gulevich D R, Schomerus H, Vaitiekus D, Royall B, Whittaker D M, Clarke E, Iorsh I V, Shelykh I A, Skolnick M S, Krizhanovskii D N 2018 Phys. Rev. Lett. 120 097401 Google Scholar
[53]	Harder T H, Egorov O A, Beierlein J, Gagel P, Michl J, Emmerling M, Schneider C, Peschel U, Höfling S, Klembt S 2020 arXiv 2002.05405
[54]	Milićević M, Montambaux G, Ozawa T, Jamadi O, Real B, Sagnes I, Lemaître A, Gratiet L L, Harouri A, Bloch J, Amo A 2019 Phys. Rev. X 9 031010
[55]	Leykam D, Andreanov A, Flach S 2018 Adv. Phys. X 3 1473052
[56]	Leykam D, Flach S 2018 APL Photonics 3 070901 Google Scholar
[57]	Pertsch T, Peschel U, Lederer F, Burghoff J, Will M, Nolte S, Tuennermann A 2004 Opt. Lett. 29 468 Google Scholar
[58]	Szameit A, Blömer D, Burghoff J, Schreiber T, Pertsch T, Nolte S, Tünnermann A, Lederer F 2005 Opt. Express 13 10552 Google Scholar
[59]	Plotnik Y, Rechtsman M C, Song D, Heinrich M, Zeuner J M, Nolte S, Lumer Y, Malkova N, Xu J, Szameit A, Chen Z, Segev M 2014 Nat. Mater. 13 57 Google Scholar
[60]	Rechtsman M C, Zeuner J M, Tünnermann A, Nolte S, Segev M, Szameit A 2013 Nat. Photonics 7 153 Google Scholar
[61]	Rechtsman M C, Zeuner J M, Plotnik Y, Lumer Y, Podolsky D, Dreisow F, Nolte S, Segev M, Szameit A 2013 Nature 496 196 Google Scholar
[62]	Rechtsman M C, Plotnik Y, Zeuner J M, Song D, Chen Z, Szameit A, Segev M 2013 Phys. Rev. Lett. 111 103901 Google Scholar
[63]	Ivanov S K, Zhang Y, Kartashov Y V, Skryabin D V 2019 APL Photonics 4 126101 Google Scholar
[64]	Mukherjee S, Spracklen A, Choudhury D, Goldman N, Öhberg P, Andersson E, Thomson R R 2015 Phys. Rev. Lett. 114 245504 Google Scholar
[65]	Vicencio R A, Cantillano C, Morales-Inostroza L, Real B, Mejía-Cortés C, Weimann S, Szameit A, Molina M I 2015 Phys. Rev. Lett. 114 245503 Google Scholar
[66]	EI Hassan A, Kunst F K, Moritz A, Andler G, Emil J. Bergholtz E J, Bourennane M 2019 Nat. Photonics 13 697 Google Scholar
[67]	Mukherjee S, Di Liberto M, Öhberg P, Thomson R R, Goldman N 2018 Phys. Rev. Lett. 121 075502 Google Scholar
[68]	Kremer M, Petrides I, Meyer E, Heinrich M, Zilberberg O, Szameit A2018 arXiv 1805.05209
[69]	Zyuzin A A, Zyuzin A Y 2018 Phys. Rev. B 97 041203 Google Scholar
[70]	Ramezani H 2017 Phys. Rev. A 96 011802 Google Scholar
[71]	Leykam D, Flach S, Chong Y D 2017 Phys. Rev. B 96 064305 Google Scholar
[72]	Qi B, Zhang L, Ge L 2018 Phys. Rev. Lett. 120 093901 Google Scholar
[73]	Ge L 2018 Photonics Res 6 A10 Google Scholar
[74]	Ge L 2015 Phys. Rev. A 92 052103 Google Scholar
[75]	Molina M I 2015 Phys. Rev. A 92 063813 Google Scholar
[76]	Biesenthal T, Kremer M, Heinrich M, Szameit A 2019 Phys. Rev. Lett. 123 183601 Google Scholar
[77]	Chen Z, Klinger J, Christodoulides D N 2002 Phys. Rev. E 66 066601 Google Scholar
[78]	Martin H, Eugenieva E D, Chen Z, Christodoulides D N 2004 Phys. Rev. Lett. 92 123902 Google Scholar
[79]	Song D, Leykam D, Su J, Liu X, Tang L, Liu S, Zhao J, Efremidis N K, Xu J, Chen Z 2019 Phys. Rev. Lett. 122 123903 Google Scholar
[80]	Song D, Paltoglou V, Liu S, Zhu Y, Gallardo D, Tang L, Xu J, Ablowitz M, Efremidis N K, Chen Z 2015 Nat. Commun. 6 6272 Google Scholar
[81]	Song D, Liu S, Paltoglou V, Gallardo D, Tang L, Zhao J, Xu J, Efremidis N K Chen Z 2015 2D Mater. 2 034007
[82]	Boguslawski M, Rose P, Denz C 2011 Phys. Rev. A 84 013832 Google Scholar
[83]	Gao Y, Song D, Chu S, Chen Z 2014 IEEE Photonics J. 6 2201806
[84]	Shen R, Shao L B, Wang B, Xing D Y 2010 Phys. Rev. B 81 041410 Google Scholar
[85]	Xia S, Hu Y, Song D, Zong Y, Tang L, Chen Z 2016 Opt. Lett. 41 1435 Google Scholar
[86]	Malkova N, Hromada I, Wang X, Bryant G, Chen Z 2009 Opt. Lett. 34 1633 Google Scholar
[87]	Malkova N, Hromada I, Wang X, Bryant G, Chen Z 2009 Phys. Rev. A 80 043806 Google Scholar
[88]	Boguslawski M, Kelberer A, Rose P, Denz C 2012 Opt. Express 20 27331 Google Scholar
[89]	Xia S, Ramachandran A, Xia S, Li D, Liu X, Tang L, Hu Y, Song D, Xu J, Leykam D, Flach S, Chen Z 2018 Phys. Rev. Lett. 121 263902 Google Scholar
[90]	Ma J, Rhim J W, Tang L, Xia S, Wang H, Zheng X, Xia S, Song D, Hu Y, Li Y, Yang B J, Leykam D, Chen Z 2020 Phys. Rev. Lett. 124 183901
[91]	Yan W, Zhong H, Song D, Zhang Y, Xia S, Tang L, Leykam D, Chen Z 2020 Adv. Optical Mater. 8 1902174
[92]	Xia S, Danieli C, Yan W, Li D, Xia S, Ma J, Lu H, Song D, Tang L, Flach S, Chen Z 2020 APL Photonics 5 016107 Google Scholar
[93]	Travkin E, Diebel F, Denz C 2017 Appl. Phys. Lett. 111 011104 Google Scholar
[94]	Diebel F, Leykam D, Kroesen S, Denz C, Desyatnikov A S 2016 Phys. Rev. Lett. 116 183902 Google Scholar
[95]	Leykam D, Bahat-Treidel O, Desyatnikov A S 2012 Phys. Rev. A 86 031805 Google Scholar
[96]	Bandres M A, Rechtsman M C, Szameit A, Segev M 2014 Conference on Lasers and Electro-Optics (CLEO)-Laser Science to Photonic Applications San Jose, CA, USA, June 8−13, 2014 p. FF2D.3.
[97]	Goda M, Nishino S, Matsuda H 2006 Phys. Rev. Lett. 96 126401 Google Scholar
[98]	Leykam D, Flach S, Bahat-Treidel O, Desyatnikov A S 2013 Phys. Rev. B 88 224203 Google Scholar
[99]	Bodyfelt J D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403 Google Scholar
[100]	Gligorić G, Maluckov A, Hadžievski L, Flach S, Malomed B A 2016 Phys. Rev. B 94 144302 Google Scholar
[101]	Leykam D, Bodyfelt J D, Desyatnikov A S, Flach S 2017 Eur. Phys. J. B 90 1 Google Scholar
[102]	Vicencio R A, Johansson M 2013 Phys. Rev. A 87 061803 Google Scholar
[103]	Vicencio R A, Mejía-Cortés C 2014 J. Opt. 16 015706
[104]	Zong Y, Xia S, Tang L, Song D, Hu Y, Pei Y, Su J, Li Y, Chen Z 2016 Opt. Express 24 8877 Google Scholar
[105]	Guo H, Shen S Q, Feng S 2012 Phys. Rev. B 86 085124 Google Scholar
[106]	Weeks C, Franz M 2012 Phys. Rev. B 85 041104
[107]	Liu Z, Bergholtz E J, Fan H, Läuchli A M 2012 Phys. Rev. Lett. 109 186805 Google Scholar
[108]	Bergholtz E J, Liu Z 2013 Int. J. Mod. Phys. B 27 1330017 Google Scholar
[109]	Kalesaki E, Delerue C, Smith C M, Beugeling W, Allan G, Vanmaekelbergh D 2014 Phys. Rev. X 4 011010
[110]	Pal B 2018 Phys. Rev. B 98 245116 Google Scholar
[111]	Khomeriki R, Flach S 2016 Phys. Rev. Lett. 116 245301 Google Scholar
[112]	Long Y, Ren J 2017 arXiv 1706.01107
[113]	Mukherjee S, Thomson R R 2017 Opt. Lett. 42 2243 Google Scholar
[114]	Kolovsky A R, Ramachandran A, Flach S 2018 Phys. Rev. B 97 045120 Google Scholar
[115]	Yulin A V, Konotop V V 2013 Opt. Lett. 38 4880 Google Scholar
[116]	Longhi S 2014 Opt. Lett. 39 5892 Google Scholar
[117]	Mukherjee S, Thomson R R 2015 Opt. Lett. 40 5443 Google Scholar
[118]	Rhim J W, Yang B J 2019 Phys. Rev. B 99 045107 Google Scholar
[119]	Shima N, Aoki H 1993 Phys. Rev. Lett. 71 4389 Google Scholar
[120]	Zhong H, Zhang Y, Zhu Y, Zhang D, Li C, Zhang Y, Li F, Belić M R, Xiao M 2017 Ann. Phys. 529 1600258 Google Scholar
[121]	Longhi S 2019 Opt. Lett. 44 287 Google Scholar
[122]	Lim L K, Fuchs J N, Piéchon F, Montambaux G 2020 Phys. Rev. B 101 045131 Google Scholar
[123]	Jiang W, Kang M, Huang H, Xu H, Low T, Liu F 2019 Phys. Rev. B 99 125131 Google Scholar
[124]	Wang P, Zheng Y, Chen X, Huang C, Kartashov Y V, Torner L, Konotop V V, Ye F 2020 Nature 577 42 Google Scholar
[125]	Abouelkomsan A, Liu Z, Bergholtz E J 2020 Phys. Rev. Lett. 124 106803 Google Scholar

[1]	于欣如, 崔继峰, 陈小刚, 慕江勇, 乔煜然. 平行板微通道中一类不可压缩微极性流体在高Zeta势下的时间周期电渗流. , 2024, 73(16): 164701. doi: 10.7498/aps.73.20240591
[2]	陆展鹏, 徐志浩. 具有平带的一维十字型晶格中重返局域化现象. , 2024, 73(3): 037202. doi: 10.7498/aps.73.20231393
[3]	古杰, 马立国. 莫尔晶格中的激子绝缘体. , 2023, 72(6): 067101. doi: 10.7498/aps.72.20230079
[4]	郑雅欣, 那仁满都拉. 可压缩液体中气泡的声空化特性. , 2022, 71(1): 014301. doi: 10.7498/aps.71.20211266
[5]	孙海明. 一维螺旋型Se原子链中的Rashba效应和平带性质. , 2022, 71(14): 147102. doi: 10.7498/aps.71.20220646
[6]	王仲锐, 姜宇航. 转角二维量子材料中平带相关的新奇电子态物性. , 2022, 71(12): 127202. doi: 10.7498/aps.71.20220064
[7]	张若寒, 任慧莹, 何林. 二维材料平带的实现及其新奇量子物态. , 2022, 71(12): 127302. doi: 10.7498/aps.71.20220225
[8]	郑雅欣, 那仁满都拉. 可压缩液体中气泡的声空化特性. , 2021, (): . doi: 10.7498/aps.70.20211266
[9]	胡嘉懿, 张文欢, 柴振华, 施保昌, 汪一航. 三维不可压缩流的12速多松弛格子Boltzmann模型. , 2019, 68(23): 234701. doi: 10.7498/aps.68.20190984
[10]	邱流潮. 基于不可压缩光滑粒子动力学的黏性液滴变形过程仿真. , 2013, 62(12): 124702. doi: 10.7498/aps.62.124702
[11]	王立锋, 叶文华, 李英骏. 二维不可压缩流体Kelvin-Helmholtz不稳定性的二次谐波产生. , 2008, 57(5): 3038-3043. doi: 10.7498/aps.57.3038
[12]	王新军, 王玲玲, 黄维清, 唐黎明, 邹炳锁, 陈克求. 三元合金缺陷层对有限超晶格中局域界面光学声子模的影响. , 2007, 56(1): 429-436. doi: 10.7498/aps.56.429
[13]	龚志强, 贺梦冬. 两耦合半无限超晶格中的局域界面声子-极化激元. , 2007, 56(11): 6600-6607. doi: 10.7498/aps.56.6600
[14]	张大成, 王鹿霞, 刘德胜, 韩圣浩, 解士杰. 扰动对一维局域模的影响. , 2003, 52(12): 3191-3196. doi: 10.7498/aps.52.3191
[15]	周光辉, 夏庆林, 颜家壬. 一维金刚石结构晶格的非线性局域模. , 2000, 49(9): 1741-1746. doi: 10.7498/aps.49.1741
[16]	俞慧丹, 赵凯华. 模拟可压缩流体的格子Boltzmann模型. , 1999, 48(8): 1470-1476. doi: 10.7498/aps.48.1470
[17]	丁建文, 颜晓红, 方显承, 段祝平. 纳米结构链的hopping电导实空间重正化群方法. , 1999, 48(2): 314-319. doi: 10.7498/aps.48.314
[18]	蒋祺, 陶瑞宝. 有任意带满的紧束缚哈密顿量的实空间重整化群研究. , 1989, 38(11): 1778-1784. doi: 10.7498/aps.38.1778
[19]	熊诗杰, 蔡建华. 非均匀无序系统中Anderson局域化的标度理论——实空间重整化群途径. , 1985, 34(12): 1530-1538. doi: 10.7498/aps.34.1530
[20]	卢鹤绂. 可压缩流体之散逸函数. , 1951, 8(2): 143-149. doi: 10.7498/aps.8.143

计量

文章访问数: 13536
PDF下载量: 776
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

平带光子微结构中的新颖现象:从模式局域到实空间拓扑