-
玻璃化转变的本质是现代凝聚态物理中最有趣的问题之一. 有理论认为高分子玻璃化转变的本质是: 当主链原子的扩散运动概率P小于
$ {{\rm{e}}^{ - 2{{\rm{e}}^3}}}$ 时, 必有比例不小于1 + 2e3/lnP的主链原子扩散运动被冻结. 以该理论的模量温度公式拟合文献的聚苯乙烯模量温度曲线, 得到聚苯乙烯的自由体积膨胀系数值在(0.00045, 0.00052)之间. 以此理论为基础推导得到了玻璃化转变中的比热温度公式: 玻璃化转变中的材料是橡胶和玻璃的混合物, 其中橡胶的比例是自由体积分数的链段中主链原子数次方, 总比热等于两组分各自的比热和比例之积的和. 用聚苯乙烯检验了该比热温度公式, 将计算得到的聚苯乙烯自由体积膨胀系数代入比热温度公式, 不需拟合任何参数公式就能够精准地定量描述聚苯乙烯玻璃化转变中的比热温度关系. 据分析, 聚苯乙烯的玻璃化转变过程是主链原子的扩散运动被激活或者被冻结的过程, 这和非晶合金相关研究结论一致. 以主链原子为摩尔计量单元时, 聚苯乙烯转变中的比热变化为1.61R (R为气体常数), 这和非晶合金玻璃化转变中比热变化约为1.5R的规律一致. 这些一致的结论预示非晶合金的玻璃化转变和聚苯乙烯的玻璃化转变具有相同的本质, 以此出发, 提出并证明了非晶合金Pd40Ni10Cu30P20和聚苯乙烯的比热温度公式是一致的.The nature of glass transition is one of the most interesting problems in modern condensed matter physics. There is a theory that shows that when the particle's diffusion motion probability P is less than $ {{\rm{e}}^{ - 2{{\rm{e}}^3}}}$ , the proportion of particles whose diffusion motion is frozen is not less than 1 + 2e3/lnP. Based on the modulus temperature formula of this theory and the experimental modulus-temperature curve of polystyrene in the literature, the free volume expansion coefficient of polystyrene is determined to be in a range of 0.00045－0.00052.In this paper, we first quantitatively study the specific heat temperature relationship in the glass transition of polystyrene. Based on this theory, the specific heat-temperature formula in the glass transition region is derived. The material in the glass transition region is a mixture of rubber and glass, and this two-component (rubber and glass) system’s total specific heat is the product of the specific heat of the rubber and the percentage of rubber in the two-component system plus the product of the specific heat of the glass and the percentage of glass in the two-component system. Let b be the number of atoms in the main chain of the segment, then the proportion of rubber will be the b-th power of free volume fraction. This specific heat-temperature formula with polystyrene is tested. By substituting the obtained free volume expansion coefficient of the polystyrene into the specific heat-temperature formula, the resulting formula can accurately and quantitatively describe the specific heat-temperature relationship in the glass transition of polystyrene without fitting any parameters. In this paper, we also study the change of motion in the glass transition of polystyrene. According to the analysis, the glass transition process of polystyrene is a process in which the diffusion movement of the main chain atoms is activated or frozen, which is consistent with the conclusions of relevant research on amorphous alloys. When the main chain atom is used as the molar unit of measurement, the specific heat change in the glass transition of polystyrene is 1.61R (R is the gas constant), which is consistent with the law, i.e. “the specific heat change in the glass transition of the amorphous alloy is about 1.5R”. These consistent conclusions predict that the glass transitions of amorphous alloys and glass transitions of polystyrene have the same essence. Based on this idea, the specific heat temperature formulas of the amorphous alloy Pd40Ni10Cu30P20 and polystyrene are verified and prove to be consistent. -
Keywords:
- glass transition /
- specific heat-temperature formula /
- amorphous alloy /
- polystyrene
[1] 金肖, 王利民 2017 66 176406
Google Scholar
Jin X, Wang L M 2017 Acta Phys. Sin. 66 176406
Google Scholar
[2] Angell C A 1995 Science 267 1924
Google Scholar
[3] 汪卫华 2013 物理学进展 33 177
Wang W H 2013 Progress in Physics 33 177
[4] Ke H B, Wen P, Zhao D Q, Wang W H 2010 Appl. Phys. Lett. 96 251902
Google Scholar
[5] Ke H B, Wen P, Zhao Z F, Wang W H 2012 Chin. Phys. Lett. 29 046402
Google Scholar
[6] Ke H B, Wen P, Wang W H 2012 AIP Adv. 2 041404
Google Scholar
[7] 李健, 张烨, 张声春 1996 45 1359
Google Scholar
Li J, Zhang Y, Zhang C S 1996 Acta Phys. Sin. 45 1359
Google Scholar
[8] 闻平 2017 66 176407
Google Scholar
Wen P 2017 Acta Phys. Sin. 66 176407
Google Scholar
[9] 任景莉, 于利萍, 张李盈 2017 66 176401
Google Scholar
Ren J L, Yu L P, Zhang L Y 2017 Acta Phys. Sin. 66 176401
Google Scholar
[10] Angell C A, Ngai K L, McKenna G B, McMillan P F, Martin S W 2000 J. Appl. Phys. 88 3113
Google Scholar
[11] 刘国栋, 张福强, 张丽娇, 王艳丽, 范留彬 2010 高分子学报 54 1065
Google Scholar
Liu G D, Zhang F Q, Zhang L J, Wang Y L, Fan L B 2010 Acta Polym. Sin. 54 1065
Google Scholar
[12] 卢新亚, 姜炳政 1990 高分子学报 34 434
Lu X Y, Jiang B Z 1990 Acta Polym. Sin. 34 434
[13] 何曼君, 陈维孝, 董西侠 1990 高分子物理(修订版)(上海: 复旦大学出版社) 第224−237页
He M J, Chen W X, Dong X X 1990 Polymer Physics (Rev. ed.) (Shanghai: Fudan University Press) pp224−237 (in Chinese)
[14] 卓启疆 1987 聚合物自由体积 (成都: 成都科技大学出版社) 第138−144页
Zhuo Q J 1987 Free Volume of Polymer (Chengdu: Chengdu University of Science And Technology Press) pp138−144 (in Chinese)
[15] 姜文龙 2019 玻璃化转变中高弹模量的定量研究 (北京: 中国科技论文在线) [2019-07-05]
Jiang W L 2019 Numerical Study of Plateau Modulus in Glass Transition (Beijing: Sciencepaper Online) [2019-07-05] (in Chinese)
[16] 傅献彩, 沈文霞, 姚天扬, 侯文华 2005 物理化学(上册, 第五版) (北京: 高等教育出版社) 第396−397页
Fu X C, Shen W X, Yao T Y, Hou W H 2005 Physical Chemistry (Vol. 1, 5th Ed.) (Beijing: Higher Education Press) pp396−397 (in Chinese)
[17] 于同隐, 何曼君, 卜海山, 胡家璁, 张炜 1986 高聚物的粘弹性 (上海: 上海科学技术出版社) 第38−44页
Yu T Y, He M J, Bo H S, He J C, Zhang W 1986 Viscoelasticity of Polymers (Shanghai: Shanghai Science & Technology Publishers) pp38−44 (in Chinese)
[18] Mark J E 1999 Polymer Data Handbook (Oxford: Oxford University Press) pp830−836
[19] 林晶晶, 左阳, 刘国栋 2014 河北工业大学学报 43 33
Lin J J, Zuo Y, Liu G D 2014 Journal of Hebei University of Technology 43 33
[20] 李丽霞, 赵冬梅, 范留彬, 刘国栋 2011 河北大学学报(自然科学版) 31 617
Li L X, Zhao D M, Fan L B, Liu G D 2011 Journal of Hebei University (Natural Science Edition) 31 617
-
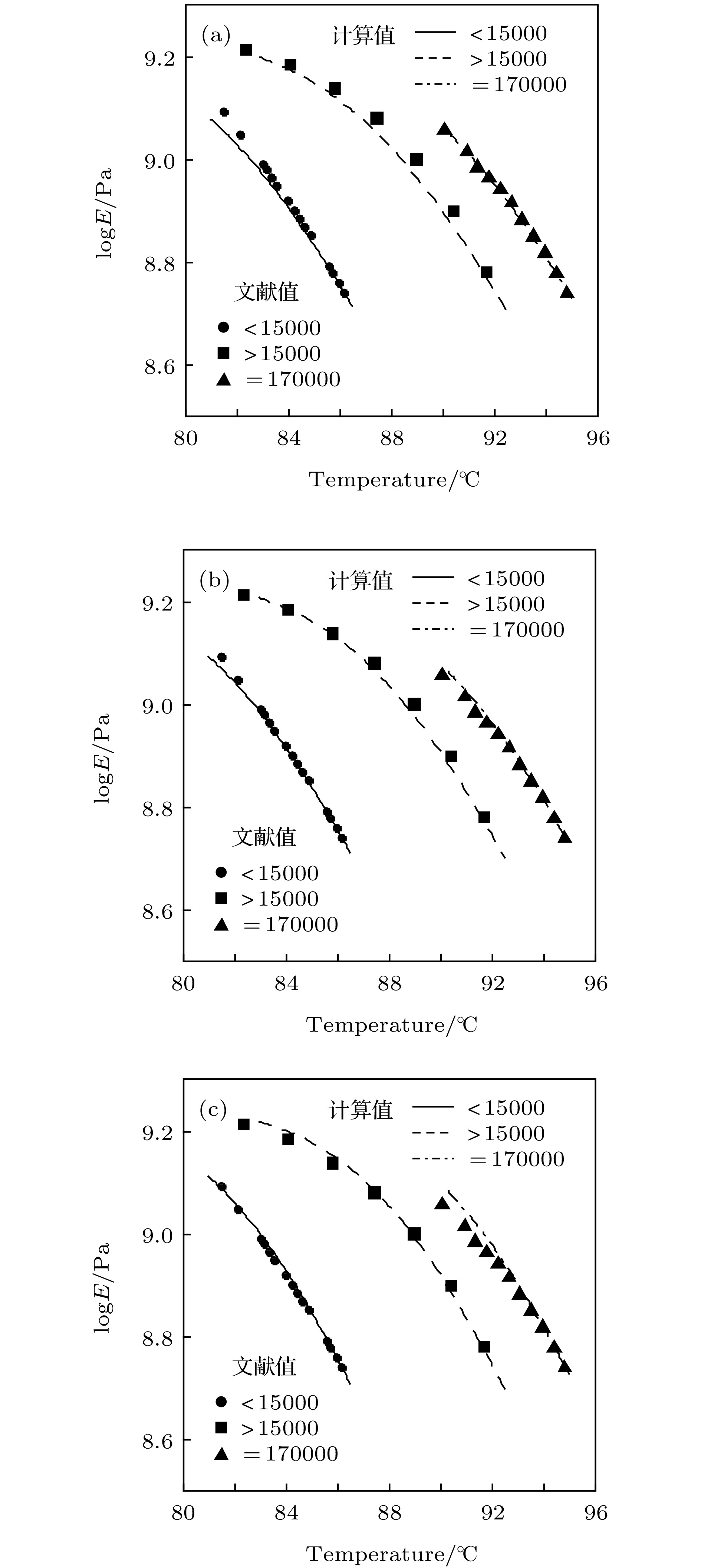
图 1 以不同
${a_{\rm{f}}}$ 值拟合的不同分子量的聚苯乙烯的模量-温度曲线(文献值的原数据取自文献[17]) (a)${a_{\rm{f}}}=0.00045$ ; (b)${a_{\rm{f}}}=0.00048$ ; (c)${a_{\rm{f}}}=0.00052$ Fig. 1. Modulus-temperature curves of polystyrene at different molecular weight under different
${a_{\rm{f}}}$ (The source data of the reference values marked in panel are extracted from Ref. [17]): (a)${a_{\rm{f}}}=0.00045$ ; (b)${a_{\rm{f}}}=0.00048$ ; (c)${a_{\rm{f}}}=$ 0.00052
图 3 不同
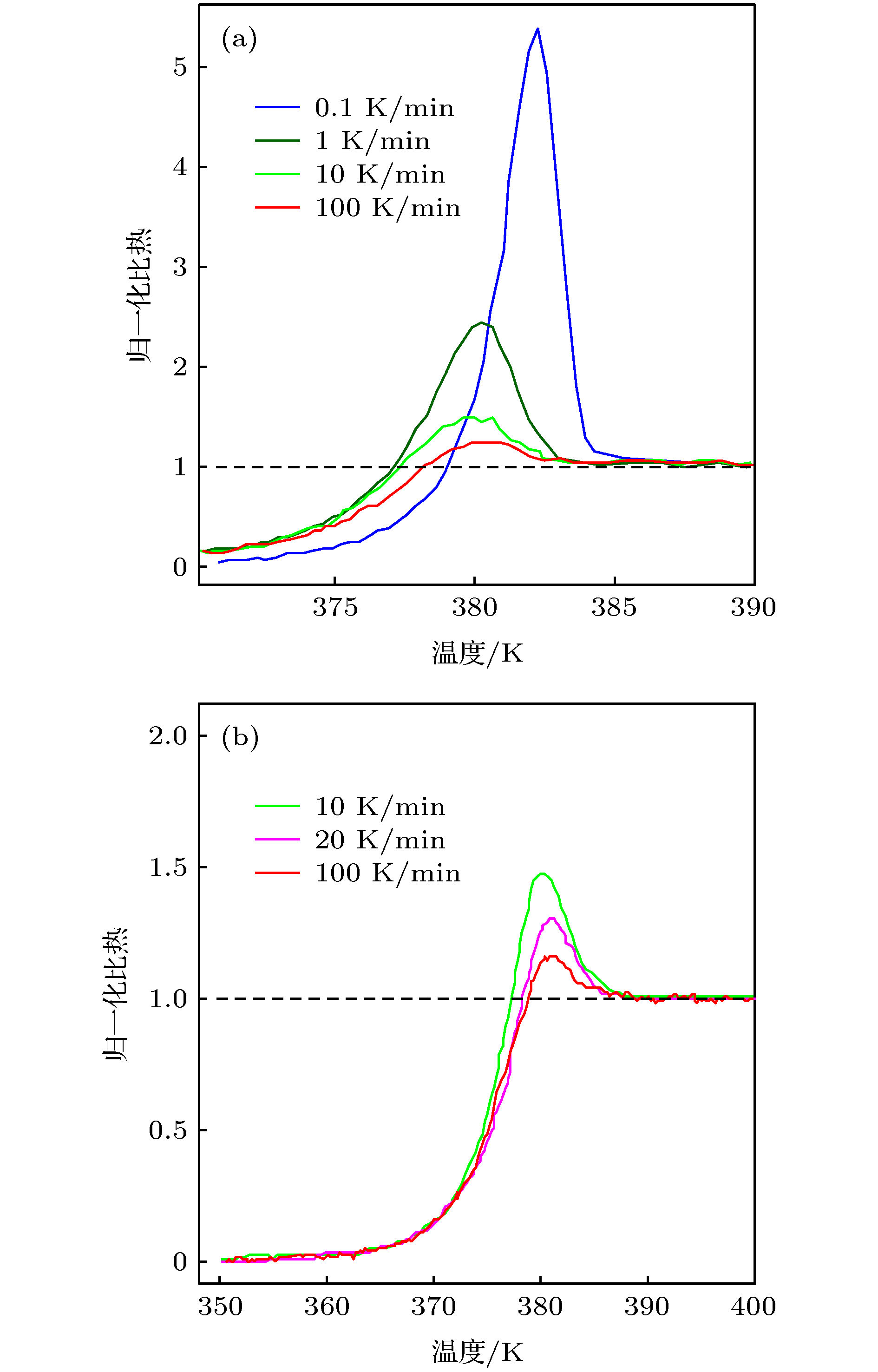
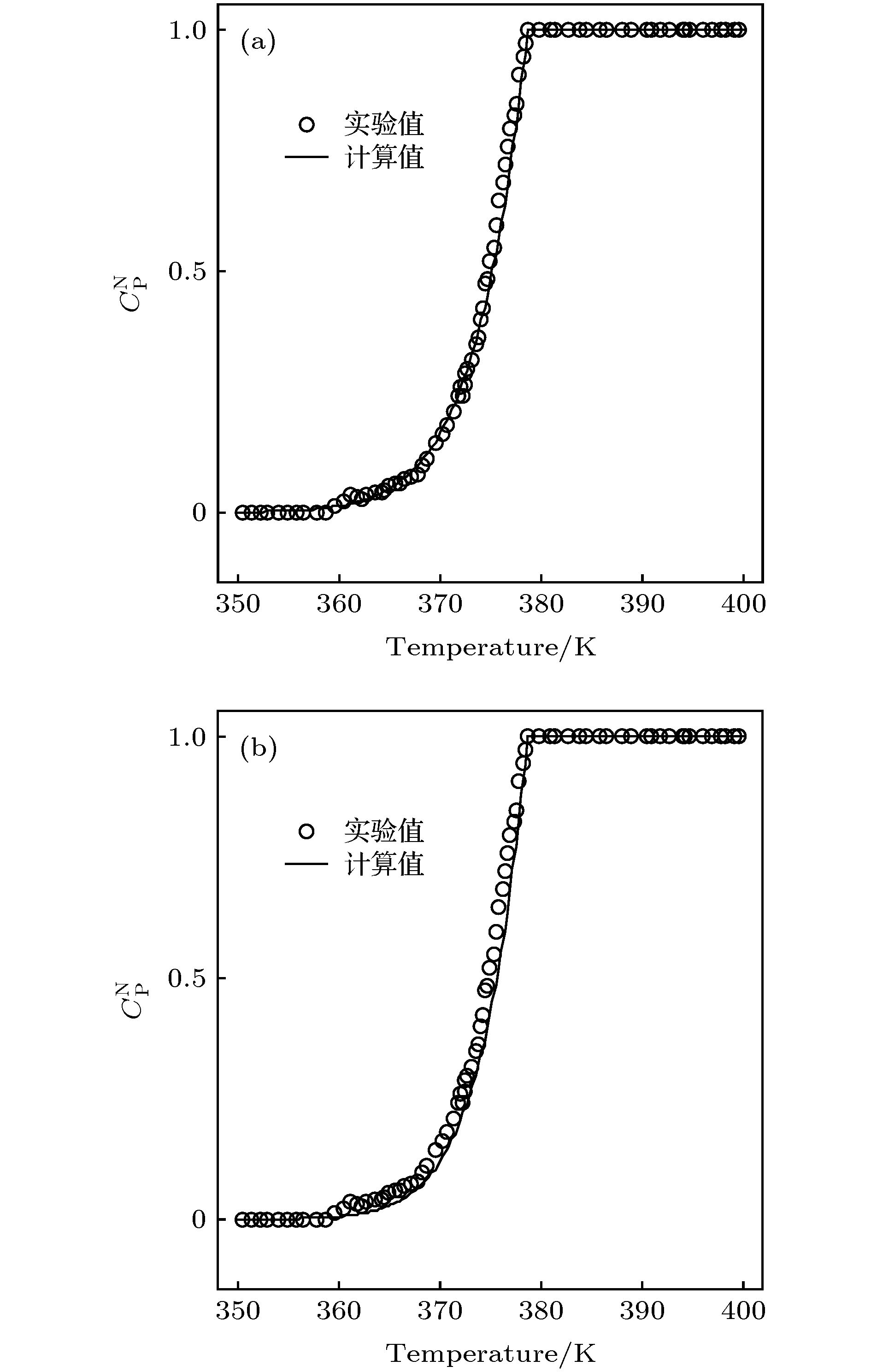
${a_{\rm{f}}}$ 值的聚苯乙烯的$C_{\rm{p}}^{\rm{N}}$ 的实验值和计算值(实验值的原数据取自文献[20]) (a)${a_{\rm{f}}}$ = 0.00045; (b)${a_{\rm{f}}}$ = 0.00052Fig. 3. Experimental and predicted
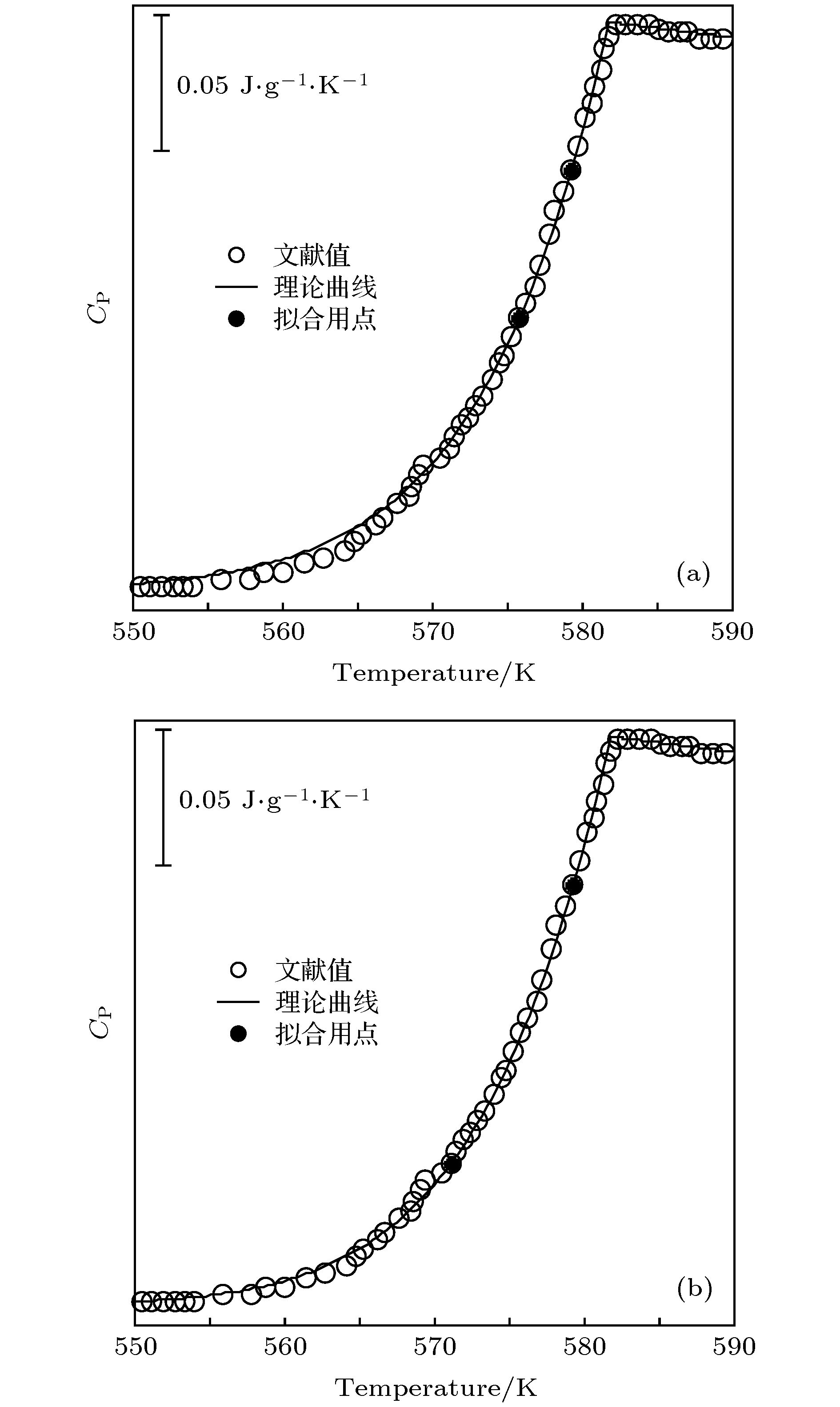
$C_{\rm{p}}^{\rm{N}}$ of PS at different${a_{\rm{f}}}$ (The source data of the experimental values marked in panel are extracted from Ref. [20]): (a)${a_{\rm{f}}}$ = 0.00045; (b) af = 0.00052.
图 4 Pd40Ni10Cu30P20的比热温度曲线(文献值的原数据取自文献[4]) (a) af = 0.00027, b = 11.57; (b) af = 0.00043, b = 7.20
Fig. 4. Specific heat-temperature curves of Pd40Ni10Cu30P20 (The source data of the reference values marked in panel are extracted from Ref. [4]): (a) af = 0.00027, b = 11.57; (b) af = 0.00043, b = 7.20.
-
[1] 金肖, 王利民 2017 66 176406
Google Scholar
Jin X, Wang L M 2017 Acta Phys. Sin. 66 176406
Google Scholar
[2] Angell C A 1995 Science 267 1924
Google Scholar
[3] 汪卫华 2013 物理学进展 33 177
Wang W H 2013 Progress in Physics 33 177
[4] Ke H B, Wen P, Zhao D Q, Wang W H 2010 Appl. Phys. Lett. 96 251902
Google Scholar
[5] Ke H B, Wen P, Zhao Z F, Wang W H 2012 Chin. Phys. Lett. 29 046402
Google Scholar
[6] Ke H B, Wen P, Wang W H 2012 AIP Adv. 2 041404
Google Scholar
[7] 李健, 张烨, 张声春 1996 45 1359
Google Scholar
Li J, Zhang Y, Zhang C S 1996 Acta Phys. Sin. 45 1359
Google Scholar
[8] 闻平 2017 66 176407
Google Scholar
Wen P 2017 Acta Phys. Sin. 66 176407
Google Scholar
[9] 任景莉, 于利萍, 张李盈 2017 66 176401
Google Scholar
Ren J L, Yu L P, Zhang L Y 2017 Acta Phys. Sin. 66 176401
Google Scholar
[10] Angell C A, Ngai K L, McKenna G B, McMillan P F, Martin S W 2000 J. Appl. Phys. 88 3113
Google Scholar
[11] 刘国栋, 张福强, 张丽娇, 王艳丽, 范留彬 2010 高分子学报 54 1065
Google Scholar
Liu G D, Zhang F Q, Zhang L J, Wang Y L, Fan L B 2010 Acta Polym. Sin. 54 1065
Google Scholar
[12] 卢新亚, 姜炳政 1990 高分子学报 34 434
Lu X Y, Jiang B Z 1990 Acta Polym. Sin. 34 434
[13] 何曼君, 陈维孝, 董西侠 1990 高分子物理(修订版)(上海: 复旦大学出版社) 第224−237页
He M J, Chen W X, Dong X X 1990 Polymer Physics (Rev. ed.) (Shanghai: Fudan University Press) pp224−237 (in Chinese)
[14] 卓启疆 1987 聚合物自由体积 (成都: 成都科技大学出版社) 第138−144页
Zhuo Q J 1987 Free Volume of Polymer (Chengdu: Chengdu University of Science And Technology Press) pp138−144 (in Chinese)
[15] 姜文龙 2019 玻璃化转变中高弹模量的定量研究 (北京: 中国科技论文在线) [2019-07-05]
Jiang W L 2019 Numerical Study of Plateau Modulus in Glass Transition (Beijing: Sciencepaper Online) [2019-07-05] (in Chinese)
[16] 傅献彩, 沈文霞, 姚天扬, 侯文华 2005 物理化学(上册, 第五版) (北京: 高等教育出版社) 第396−397页
Fu X C, Shen W X, Yao T Y, Hou W H 2005 Physical Chemistry (Vol. 1, 5th Ed.) (Beijing: Higher Education Press) pp396−397 (in Chinese)
[17] 于同隐, 何曼君, 卜海山, 胡家璁, 张炜 1986 高聚物的粘弹性 (上海: 上海科学技术出版社) 第38−44页
Yu T Y, He M J, Bo H S, He J C, Zhang W 1986 Viscoelasticity of Polymers (Shanghai: Shanghai Science & Technology Publishers) pp38−44 (in Chinese)
[18] Mark J E 1999 Polymer Data Handbook (Oxford: Oxford University Press) pp830−836
[19] 林晶晶, 左阳, 刘国栋 2014 河北工业大学学报 43 33
Lin J J, Zuo Y, Liu G D 2014 Journal of Hebei University of Technology 43 33
[20] 李丽霞, 赵冬梅, 范留彬, 刘国栋 2011 河北大学学报(自然科学版) 31 617
Li L X, Zhao D M, Fan L B, Liu G D 2011 Journal of Hebei University (Natural Science Edition) 31 617
下载:
计量
- 文章访问数: 7145
- PDF下载量: 57
- 被引次数: 0
