螺旋波等离子体中螺旋波与Trivelpiece-Gould波模式耦合及线性能量沉积特性参量分析

李文秋; 赵斌; 王刚; 相东

doi:10.7498/aps.69.20200062

摘要

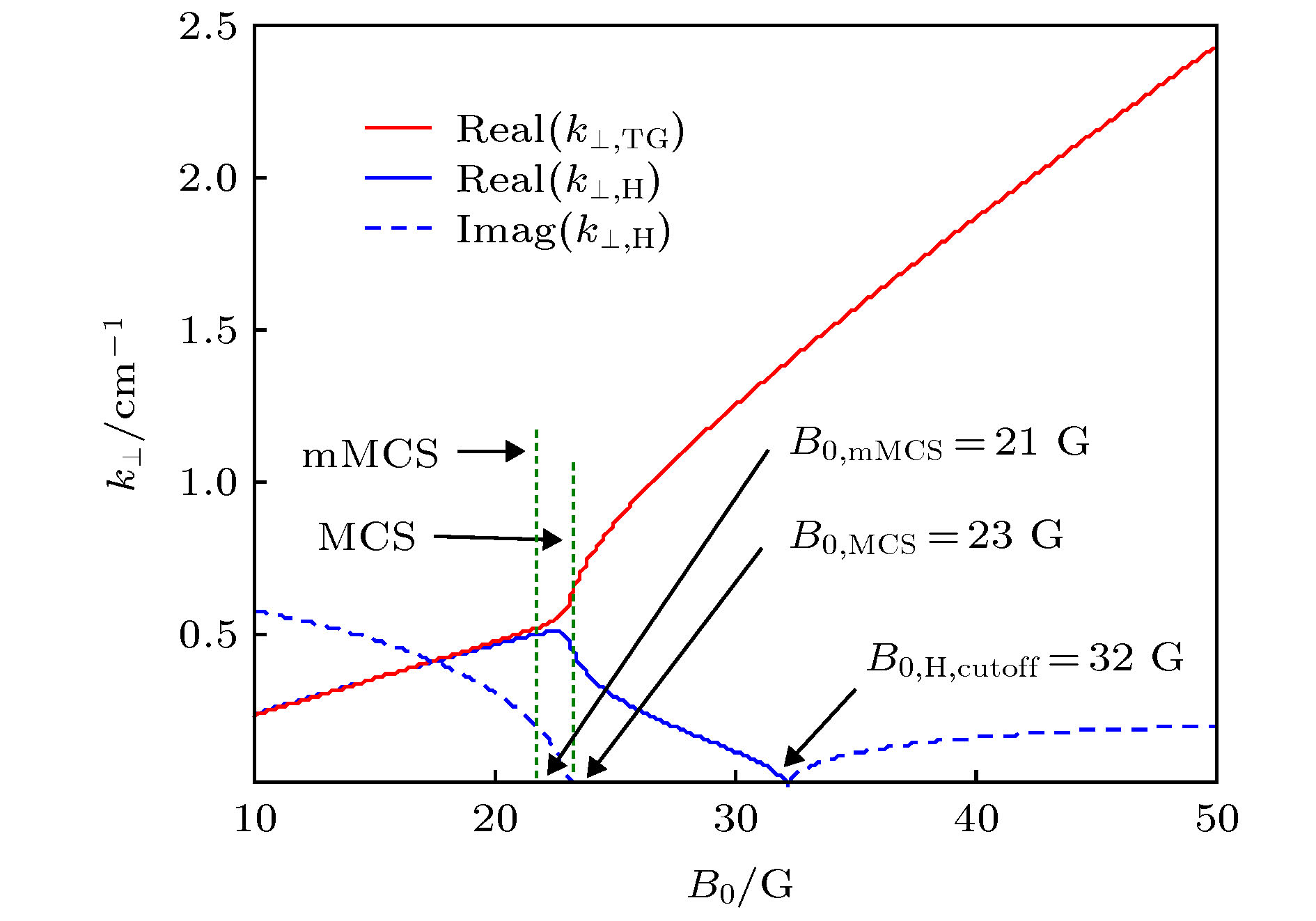
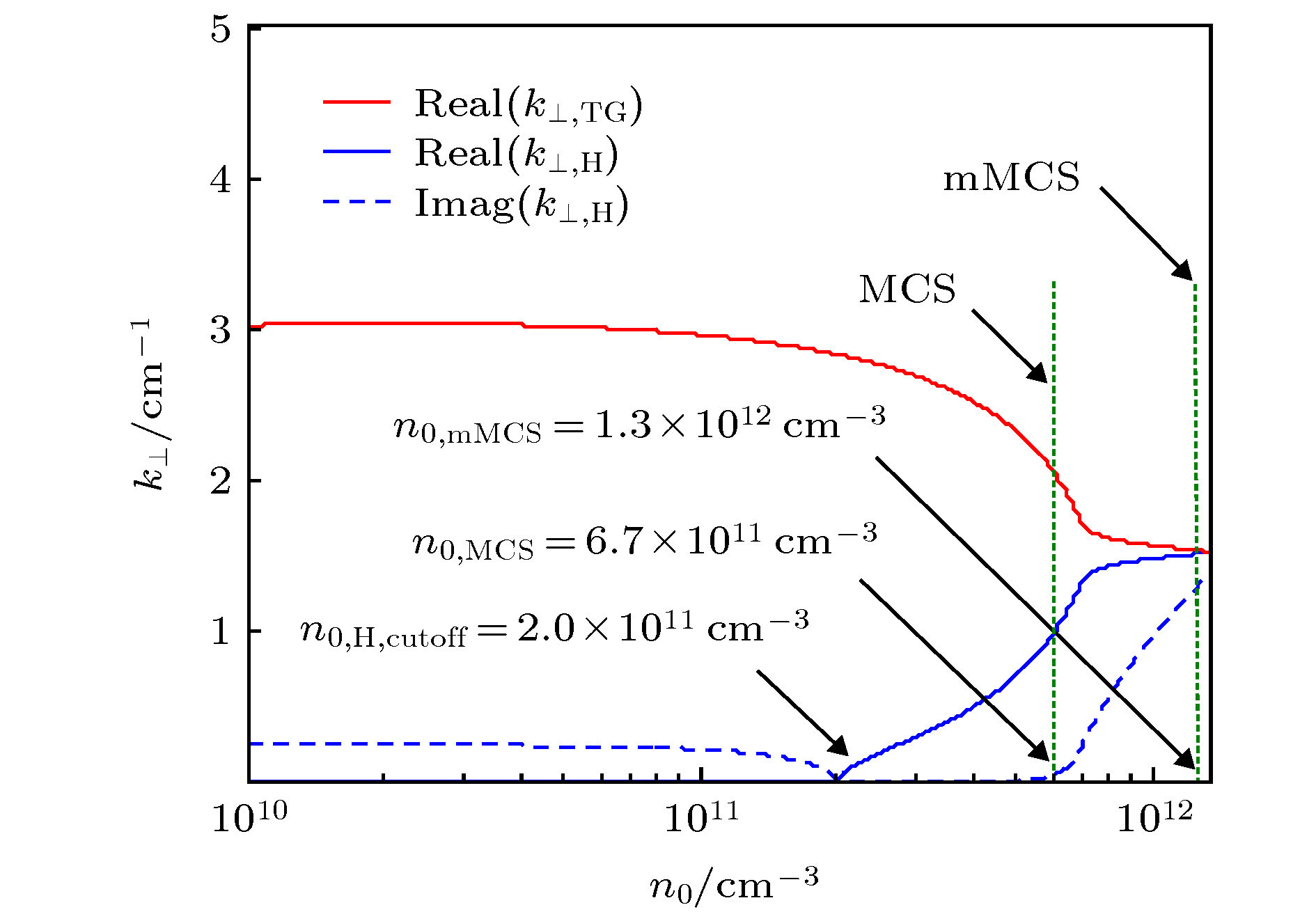
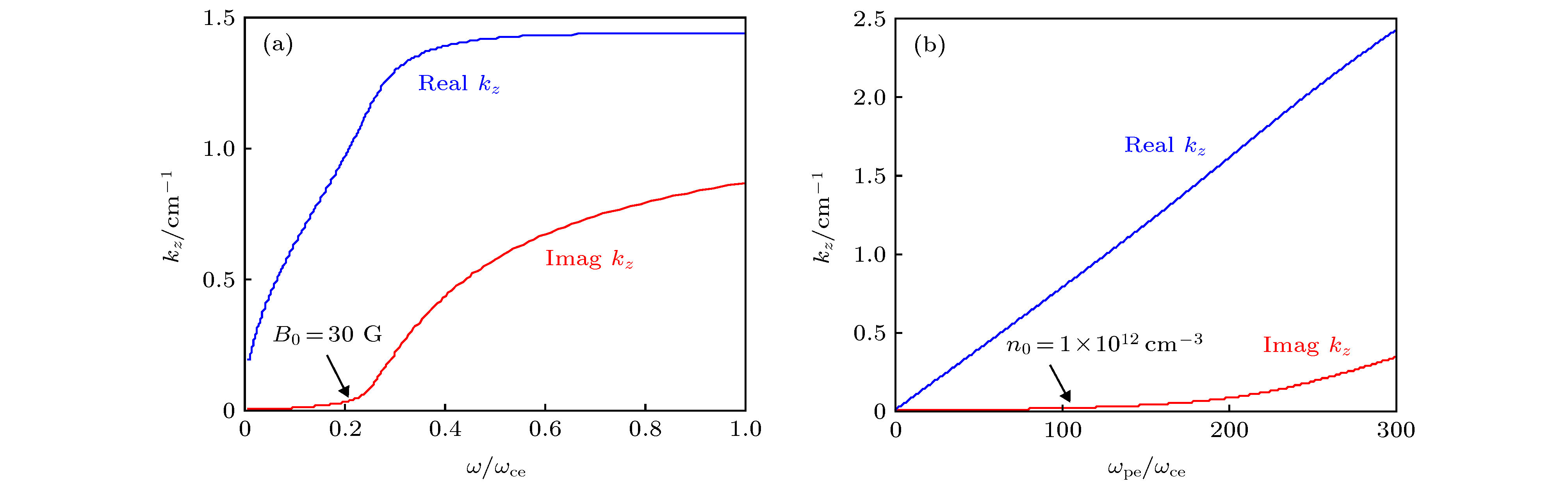
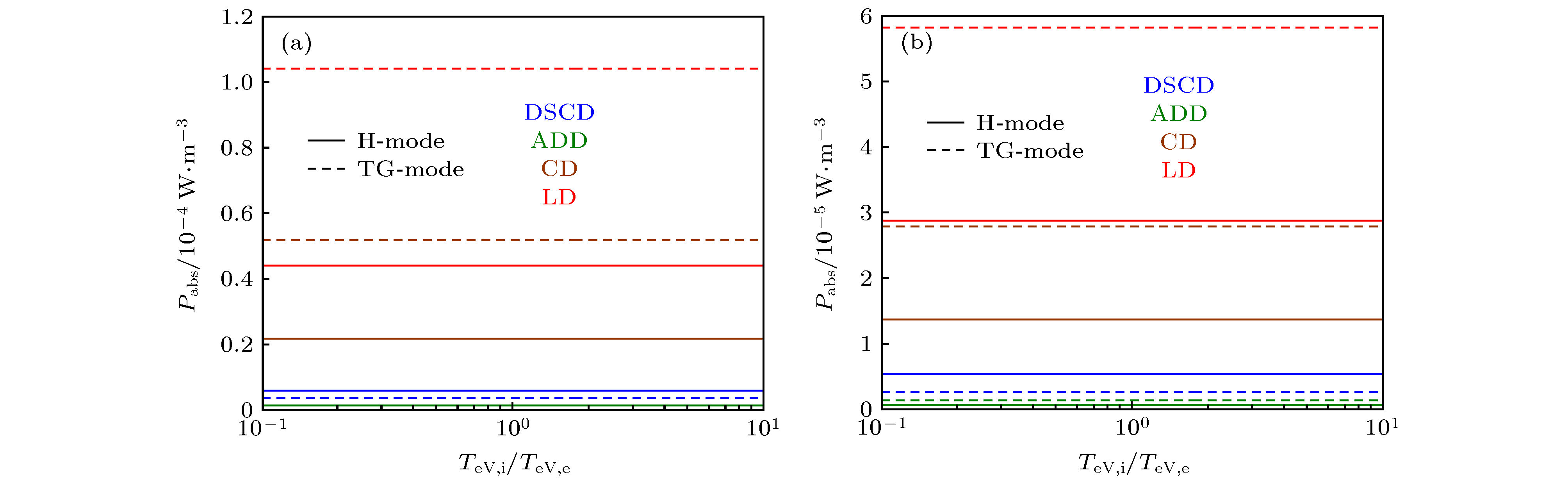
采用有限温度等离子体介电张量模型, 在考虑粒子热效应情形下, 通过求解传导边界条件下等离子体柱中本征模的色散关系, 分析了螺旋波等离子体中典型参量条件下螺旋波与Trivelpiece-Gould (TG) 波的耦合特性及线性能量沉积特性. 在ω/(2π) = 13.56 MHz和T_eV,i = 0.1T_eV,e参量条件下计算结果表明: 对于螺旋波, 存在截止静磁场B_0,H,cutoff与截止等离子体密度n_0,H,cutoff, 在B₀ > B_0,H,cutoff或n₀ < n_0,H,cutoff条件下, 螺旋波变为消逝波; 在ω/ω_ce ∈ (0.01, 0.10)范围内, 对于m = 0 角向模, TG波Landau阻尼致使的能量沉积占主导地位, 而对于m = 1角向模, 螺旋波Landau阻尼或TG波Landau阻尼致使的能量沉积哪个占据主导地位则取决于B₀的大小; 在ω_pe/ω_ce ∈ (3, 100)范围内, TG波Landau阻尼致使的能量沉积占主导地位; 在整体能量沉积过程中, 对于m = 0模和m = 1模, Landau阻尼致使的能量沉积均占据主导地位.

关键词:

Abstract

Based on the finite temperature plasma dielectric tensor model which contains the particle thermal effect, by numerically solving the eigenmode dispersion relation of electromagnetic waves propagating in radially uniform and magnetized warm plasma column which is surrounded by conducting boundary, the mode coupling characteristic and liner damping mechanism induced wave power deposition properties of helicon and Trivelpiece-Gould (TG) waves are parametrically analyzed. The detailed investigations show as follows. Under typical helicon plasma parameter conditions, i.e. wave frequency ω/(2π) = 13.56 MHz, ion temperature is much smaller than electron temperature, for the helicon wave, there exist a cut-off magnetic field B_0,H,cutoff and a cut-off plasma density n_0,H,cutoff, for which under the conditions of B₀ > B_0,H,cutoff or n₀ < n_0,H,cutoff, the helicon wave becomes an evanescent wave. When the magnetic field intensity changes from 48.4 to 484 G, i.e., ω/ω_ce ranges from 0.01 to 0.1, for the power deposition intensity, Landau damping of TG wave dominates for the m = 0 mode, meanwhile, for the m = 1 mode, which wave, i.e. helicon wave or TG wave, plays a major role in power deposition mainly depends on the magnitude of the magnetic field. On the other hand, for a given magnetic field B₀ = 100 G, when ω_pe/ω_ce changes from 3 to 100, for both the m = 0 mode and the m = 1 mode, the power deposition induced by Landau damping of TG wave plays a major role, further, one may notice that the power deposition of TG wave decreases while the power deposition of the helicon wave increases as plasma density increases. Finally, for both the m = 0 mode and the m = 1 mode, the power deposition due to the Landau damping plays a dominant role. All these conclusions provide us with some useful clues to better understanding the high ionization mechanism of helicon wave discharges.

Keywords:

作者及机构信息

1.
中国科学院空天信息创新研究院, 北京　100094

2.
普林斯顿大学, 普林斯顿等离子体物理实验室, 新泽西　08543, 美国

3.
中国科学院大学电子电气与通信工程学院, 北京　100049

4.
北京微电子技术研究所, 北京　100094

通信作者: 李文秋, beiste@163.com

基金项目: 国家级-国家“万人计划”科技创新领军人才(Y8BF130272)

Authors and contacts

1.
Aerospace Information Research Institute, Chinese Academy of Sciences, Beijing 100094, China

2.
Princeton Plasma Physics Laboratory, Princeton University, New Jersey 08543, USA

3.
School of Electronic, Electrical and Communication Engineering, University of Chinese Academy of Sciences, Beijing 100049, China

4.
Beijing Institute of Aerospace Micro-electromechanical Technology, Beijing 100094, China

Corresponding author: Li Wen-Qiu, beiste@163.com

文章全文 : translate this paragraph

参考文献

[1]	Chen F F 2015 Plasma Sources Sci. Technol. 24 014001 Google Scholar
[2]	Isayama S, Shinohara S, Hada T 2018 Plasma Fusion Res. 13 1101014 Google Scholar
[3]	Shinohara S 2018 Adv. Phys.: X 3 1420424 Google Scholar
[4]	Aigrain P 1960 Proceedings of the International Conference on Semiconductor Physics Prague, Czech Republic, August 4–8, 1960 p224
[5]	Chen F F 1991 Plasma Phys. Controlled Fusion 33 339 Google Scholar
[6]	Shamrai K P, Taranov V B 1996 Plasma Sources Sci. Technol. 5 474 Google Scholar
[7]	Shamrai K P, Taranov V B 1994 Plasma Phys. Controlled Fusion 36 1719 Google Scholar
[8]	Shamrai K P 1998 Plasma Sources Sci. Technol. 7 499 Google Scholar
[9]	Chen F F, Blackwell D D 1999 Phys. Rev. Lett. 82 2677 Google Scholar
[10]	Blackwell D D, Chen F F 2001 Plasma Sources Sci. Technol. 10 226 Google Scholar
[11]	Kline J, Scime E 2003 Phys. Plasmas 10 135 Google Scholar
[12]	Kim S, Hwang Y 2008 Plasma Phys. Controlled Fusion 50 035007 Google Scholar
[13]	Isayama S, Hada T, Shinohara S, et al. 2016 Phys. Plasmas 23 063513 Google Scholar
[14]	成玉国, 程谋森, 王墨戈等 2014 63 035203 Google Scholar Cheng Y G, Cheng M S, Wang M G, et al. 2014 Acta Phys. Sin. 63 035203 Google Scholar
[15]	平兰兰, 张新军, 杨桦等 2019 68 205201 Google Scholar Ping L L, Zhang X J, Yang H, et al. 2019 Acta Phys.Sin. 68 205201 Google Scholar
[16]	Chen F F, Arnush D 1997 Phys. Plasmas 4 3411 Google Scholar
[17]	Arnush D, Chen F F 1998 Phys. Plasmas 5 1239 Google Scholar
[18]	Arnush D 2000 Phys. Plasmas 7 3042 Google Scholar
[19]	Sakawa Y, Kunimatsu H, Kikuchi H, et al. 2003 Phys. Rev. Lett. 90 105001 Google Scholar
[20]	Vey B 1984 PFC/RR-84-12 (Cambridge: Massachusetts Institute of Technology) pp30–31
[21]	Niemi K, Krämer M 2008 Phys. Plasmas 15 073503 Google Scholar
[22]	Shamrai K P, Shinohara S 2001 Phys. Plasmas 8 4659 Google Scholar
[23]	Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[24]	Fried B D, Conte S D 2015 The Plasma Dispersion Function: the Hilbert Transform of the Gaussian (New York: Academic Press) pp1–3
[25]	Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253 Google Scholar
[26]	Shoji T, Sakawa Y, Nakazawa S, et al. 1993 Plasma Sources Sci. Technol. 2 5 Google Scholar
[27]	Swanson D G 1989 Plasma Waves (New York: Academic Press) pp375–376
[28]	Lafleur T, Charles C, Boswell R 2010 Phys. Plasmas 17 073508 Google Scholar

施引文献

图 1 被传导边界包裹的等离子体柱横向截面示意图

Fig. 1. Cross section of plasma column surround by conducting boundary

下载: 全尺寸图片幻灯片

图 2 粒子温度对螺旋波与TG波耦合色散关系的影响　(a)电子温度的影响; (b)离子温度的影响

Fig. 2. Influence of particle temperature on dispersion relation between helicon and TG waves: (a) Electron temperature effect; (b) ion temperature effect.

下载: 全尺寸图片幻灯片

图 3 螺旋波与TG波横向波数对轴向静磁场的依赖关系

Fig. 3. The perpendicular wave number of helicon and TG waves given as functions of axial static magnetic field.

下载: 全尺寸图片幻灯片

图 4 螺旋波与TG波横向波数对等离子体密度的依赖关系

Fig. 4. The perpendicular wave number of helicon and TG waves given as functions of plasma density.

下载: 全尺寸图片幻灯片

图 5 螺旋波轴向波数随参量变化情况　(a)轴向波数随轴向静磁场变化; (b)轴向静磁场随等离子体密度变化

Fig. 5. The axial wave number of the right hand polarized wave is given as a function of (a) axial static magnetic field and (b) plasma density.

下载: 全尺寸图片幻灯片

图 6 螺旋波与TG波径向功率沉积分布　(a) m = 0 角向对称模; (b) m = 1 角向对称模

Fig. 6. Radial power deposition profiles of the helicon and TG waves for: (a) m = 0 mode; (b) m = 1 mode.

下载: 全尺寸图片幻灯片

图 7 螺旋波与TG波功率沉积随电子温度的变化关系　(a) m = 0 模; (b) m = 1 模

Fig. 7. Power deposition profiles of helicon and TG waves are given as functions of electron temperature for: (a) m = 0 mode; (b) m = 1 mode.

下载: 全尺寸图片幻灯片

图 8 螺旋波与TG波功率沉积随离子温度的变化关系　(a) m = 0 模; (b) m = 1 模

Fig. 8. Power deposition profiles of helicon and TG waves are given as functions of ion temperature for: (a) m = 0 mode; (b) m = 1 mode.

下载: 全尺寸图片幻灯片

图 9 螺旋波与TG波功率沉积随轴向静磁场的变化关系　(a) m = 0 模; (b) m = 1 模

Fig. 9. Power deposition profiles of helicon and TG waves are given as functions of axial static magnetic field for: (a) m = 0 mode; (b) m = 1 mode.

下载: 全尺寸图片幻灯片

图 10 螺旋波与TG波功率沉积随等离子体密度的变化关系　(a) m = 0 模; (b) m = 1 模

Fig. 10. Power deposition profiles of helicon and TG waves are given as functions of plasma density for: (a) m = 0 mode; (b) m = 1 mode.

下载: 全尺寸图片幻灯片

map

[1]	Chen F F 2015 Plasma Sources Sci. Technol. 24 014001 Google Scholar
[2]	Isayama S, Shinohara S, Hada T 2018 Plasma Fusion Res. 13 1101014 Google Scholar
[3]	Shinohara S 2018 Adv. Phys.: X 3 1420424 Google Scholar
[4]	Aigrain P 1960 Proceedings of the International Conference on Semiconductor Physics Prague, Czech Republic, August 4–8, 1960 p224
[5]	Chen F F 1991 Plasma Phys. Controlled Fusion 33 339 Google Scholar
[6]	Shamrai K P, Taranov V B 1996 Plasma Sources Sci. Technol. 5 474 Google Scholar
[7]	Shamrai K P, Taranov V B 1994 Plasma Phys. Controlled Fusion 36 1719 Google Scholar
[8]	Shamrai K P 1998 Plasma Sources Sci. Technol. 7 499 Google Scholar
[9]	Chen F F, Blackwell D D 1999 Phys. Rev. Lett. 82 2677 Google Scholar
[10]	Blackwell D D, Chen F F 2001 Plasma Sources Sci. Technol. 10 226 Google Scholar
[11]	Kline J, Scime E 2003 Phys. Plasmas 10 135 Google Scholar
[12]	Kim S, Hwang Y 2008 Plasma Phys. Controlled Fusion 50 035007 Google Scholar
[13]	Isayama S, Hada T, Shinohara S, et al. 2016 Phys. Plasmas 23 063513 Google Scholar
[14]	成玉国, 程谋森, 王墨戈等 2014 63 035203 Google Scholar Cheng Y G, Cheng M S, Wang M G, et al. 2014 Acta Phys. Sin. 63 035203 Google Scholar
[15]	平兰兰, 张新军, 杨桦等 2019 68 205201 Google Scholar Ping L L, Zhang X J, Yang H, et al. 2019 Acta Phys.Sin. 68 205201 Google Scholar
[16]	Chen F F, Arnush D 1997 Phys. Plasmas 4 3411 Google Scholar
[17]	Arnush D, Chen F F 1998 Phys. Plasmas 5 1239 Google Scholar
[18]	Arnush D 2000 Phys. Plasmas 7 3042 Google Scholar
[19]	Sakawa Y, Kunimatsu H, Kikuchi H, et al. 2003 Phys. Rev. Lett. 90 105001 Google Scholar
[20]	Vey B 1984 PFC/RR-84-12 (Cambridge: Massachusetts Institute of Technology) pp30–31
[21]	Niemi K, Krämer M 2008 Phys. Plasmas 15 073503 Google Scholar
[22]	Shamrai K P, Shinohara S 2001 Phys. Plasmas 8 4659 Google Scholar
[23]	Huba J D 2016 NRL Plasma Formulary (Washington: Naval Research Laboratory) p34
[24]	Fried B D, Conte S D 2015 The Plasma Dispersion Function: the Hilbert Transform of the Gaussian (New York: Academic Press) pp1–3
[25]	Mouzouris Y, Scharer J E 1998 Phys. Plasmas 5 4253 Google Scholar
[26]	Shoji T, Sakawa Y, Nakazawa S, et al. 1993 Plasma Sources Sci. Technol. 2 5 Google Scholar
[27]	Swanson D G 1989 Plasma Waves (New York: Academic Press) pp375–376
[28]	Lafleur T, Charles C, Boswell R 2010 Phys. Plasmas 17 073508 Google Scholar

[1]	李文秋, 唐彦娜, 刘雅琳, 王刚. 电子温度各向异性对螺旋波m = 1角向模功率沉积特性的影响. , 2024, 73(7): 075202. doi: 10.7498/aps.73.20231759
[2]	李文秋, 唐彦娜, 刘雅琳, 马维聪, 王刚. 各向同性等离子体覆盖金属天线辐射增强现象. , 2023, 72(13): 135202. doi: 10.7498/aps.72.20230101
[3]	李文秋, 唐彦娜, 刘雅琳, 王刚. 电子温度各向异性对螺旋波等离子体中电磁模式的传播及功率沉积特性的影响. , 2023, 72(5): 055202. doi: 10.7498/aps.72.20222048
[4]	苏瑞霞, 黄霞, 郑志刚. 耦合Frenkel-Kontorova双链的格波解及其色散关系. , 2022, 71(15): 154401. doi: 10.7498/aps.71.20212362
[5]	季佩宇, 黄天源, 陈佳丽, 诸葛兰剑, 吴雪梅. 螺旋波等离子体制备多种碳基薄膜原位诊断研究. , 2021, 70(9): 097201. doi: 10.7498/aps.70.20201809
[6]	杨建荣, 毛杰键, 吴奇成, 刘萍, 黄立. 强碰撞磁化尘埃等离子体中的漂移波. , 2020, 69(17): 175201. doi: 10.7498/aps.69.20200468
[7]	李文秋, 赵斌, 王刚. 电子温度对螺旋波等离子体中电磁模式能量沉积特性的影响. , 2020, 69(21): 215201. doi: 10.7498/aps.69.20201018
[8]	平兰兰, 张新军, 杨桦, 徐国盛, 苌磊, 吴东升, 吕虹, 郑长勇, 彭金花, 金海红, 何超, 甘桂华. 螺旋波等离子体原型实验装置中天线的优化设计与功率沉积. , 2019, 68(20): 205201. doi: 10.7498/aps.68.20182107
[9]	张凯, 杜春光, 高健存. 长程表面等离子体的增强效应. , 2017, 66(22): 227302. doi: 10.7498/aps.66.227302
[10]	李文秋, 王刚, 苏小保. 非磁化冷等离子体柱中的模式辐射特性分析. , 2017, 66(5): 055201. doi: 10.7498/aps.66.055201
[11]	李小泽, 滕雁, 王建国, 宋志敏, 张黎军, 张余川, 叶虎. 过模结构表面波振荡器模式选择. , 2013, 62(8): 084103. doi: 10.7498/aps.62.084103
[12]	刘三秋, 国洪梅. 极端相对论快电子分布等离子体中横振荡色散关系. , 2011, 60(5): 055203. doi: 10.7498/aps.60.055203
[13]	刘炳灿, 逯志欣, 于丽. 金属和Kerr非线性介质界面上表面等离子体激元的色散关系. , 2010, 59(2): 1180-1184. doi: 10.7498/aps.59.1180
[14]	季沛勇, 鲁楠, 祝俊. 量子等离子体中波的色散关系以及朗道阻尼. , 2009, 58(11): 7473-7478. doi: 10.7498/aps.58.7473
[15]	王亮, 曹金祥, 王艳, 牛田野, 王舸, 朱颖. 电磁脉冲在实验室等离子体中传播时间的实验研究. , 2007, 56(3): 1429-1433. doi: 10.7498/aps.56.1429
[16]	赵国伟, 徐跃民, 陈诚. 等离子体天线色散关系和辐射场数值计算. , 2007, 56(9): 5298-5303. doi: 10.7498/aps.56.5298
[17]	周国成, 曹晋滨, 王德驹, 蔡春林. 无碰撞等离子体电流片中的低频波. , 2004, 53(8): 2644-2653. doi: 10.7498/aps.53.2644
[18]	谢鸿全, 刘濮鲲, 李承跃, 鄢　扬, 刘盛纲. 等离子体填充波纹波导中低频模式特性分析. , 2004, 53(9): 3114-3118. doi: 10.7498/aps.53.3114
[19]	于威, 刘丽辉, 侯海虹, 丁学成, 韩理, 傅广生. 螺旋波等离子体增强化学气相沉积氮化硅薄膜. , 2003, 52(3): 687-691. doi: 10.7498/aps.52.687
[20]	喻胜, 李宏福, 谢仲怜, 罗勇. 渐变复合腔回旋管高次谐波注-波互作用非线性模拟. , 2000, 49(12): 2455-2459. doi: 10.7498/aps.49.2455

计量

文章访问数: 6293
PDF下载量: 96
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

螺旋波等离子体中螺旋波与Trivelpiece-Gould波模式耦合及线性能量沉积特性参量分析