Verwey相变处Fe<sub>3</sub>O<sub>4</sub>的结构、磁性和电输运特性

刘祥; 米文博

doi:10.7498/aps.69.20191763

摘要

作为典型的金属–绝缘体转变, Fe₃O₄的Verwey相变蕴涵的丰富物理现象与微观机制, 因而受到了人们的广泛关注. 在Verwey相变处, Fe₃O₄的晶体结构、电子结构以及磁各向异性等均发生转变, 但其磁基态并未发生改变. 与其他强关联体系相比, Fe₃O₄的Verwey相变不需要考虑磁交换耦合作用的变化, 有利于揭示强关联体系中金属–绝缘体转变的物理本质. 本文从晶体结构、电荷有序、电输运特性、磁性和铁电特性等方面简要地介绍了Fe₃O₄的Verwey相变的研究历史和现状.

关键词:

Abstract

As the first known metal-insulator transition, Verwey transition of Fe₃O₄ attracts much attention due to its fascinating physics. With the decreasing temperature across Verwey temperature, Fe₃O₄ undergoes the transition of lattice distortion, charge ordering, electricity, magnetic anisotropy, etc, but the magnetic ground state keeps the ferrimagnetism. The comprehension of the underlying physics in Verwey transition facilitates the understanding of metal–insulator transition in other strongly-correlated systems. Nevertheless, the mechanism of Verwey transition is still debated after the first glimpse of Verwey transition. In this paper, we summarize the research history and current status of Verwey transition in Fe₃O₄. The investigations of lattice structure, charge ordering, electronic transport, magnetic and ferroelectric properties of Fe₃O₄ across Verwey transition are reviewed. Finally, the summary and outlook are given.

Keywords:

作者及机构信息

刘祥,
米文博

天津大学理学院应用物理学系, 天津市低维功能材料物理与制备技术重点实验室, 天津　300354

通信作者: 米文博, miwenbo@tju.edu.cn

Authors and contacts

Tianjin Key Laboratory of Low Dimensional Materials Physics and Preparation Technology, School of Science, Tianjin University, Tianjin 300354, China

Corresponding author: Mi Wen-Bo, miwenbo@tju.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Verwey E J W 1939 Nature 144 327
[2]	Renger K 1913 Ph. D. Dissertation (Zürich: Swiss Federal Institute of Technology Zürich)
[3]	Parks G S, Kelly K K 1926 J. Phys. Chem. 30 47 Google Scholar
[4]	Millar R W 1929 J. Am. Chem. Soc. 51 215 Google Scholar
[5]	Okamura T 1932 Sci. Rep. Tohoku Imp. Univ. 21 231
[6]	Ellefson B S, Taylor N W 1934 J. Chem. Phys. 2 58 Google Scholar
[7]	Weiss P, Forrer R 1929 Ann. Phys. 12 279
[8]	Bragg W H 1915 Philos. Mag. 30 305 Google Scholar
[9]	Bragg W H and Brown G B 1926 Z. Kristallogr. 63 122
[10]	Claassen A 1926 Proc. Phys. Soc. 38 482
[11]	Néel L 1948 Ann. Phys. 3 137
[12]	Verwey E J W, Heilmann E L 1948 J. Chem. Phys. 16 1091 Google Scholar
[13]	Verwey E J W, Haayman P W, Romeijn F C 1947 J. Chem. Phys. 15 181 Google Scholar
[14]	Westrum E F, Grønvold F 1969 J. Chem. Thermodyn. 1 543 Google Scholar
[15]	Cullen J R, Callen E R 1971 Solid State Commun. 9 1041 Google Scholar
[16]	Evans B J, Westrum E F 1972 Phys. Rev. B 5 3791 Google Scholar
[17]	Cullen J R, Callen E R 1973 Phys. Rev. B 7 397 Google Scholar
[18]	Chakraverty B K 1974 Solid State Commun. 15 1271 Google Scholar
[19]	Buckwald R A, Hirsch A A 1975 Solid State Commun. 17 621 Google Scholar
[20]	Bartel J J, Westrum E F, Haas J L 1976 J. Chem. Thermodyn. 8 575 Google Scholar
[21]	Matsui M, Todo S, Chikazumi S 1977 J. Phys. Soc. Jpn. 42 1517 Google Scholar
[22]	Rigo M O, Kleinclauss J 1980 Philos. Mag. B 42 393 Google Scholar
[23]	Senn M S, Wright J P, Attfield J P 2012 Nature 481 173 Google Scholar
[24]	Miles P A, Westphal W B, von Hippel A 1957 Rev. Mod. Phys. 29 279 Google Scholar
[25]	Wright J P, Attfield J P, Radaelli P G 2001 Phys. Rev. Lett. 87 266401 Google Scholar
[26]	Bohra M, Agarwal N, Singh V 2019 J. Nanomater. 2019 8457383
[27]	Bickford Jr L R 1950 Phys. Rev. 78 449 Google Scholar
[28]	Kato K, Iida S 1981 J. Phys. Soc. Jpn. 50 2844 Google Scholar
[29]	Chikazumi S, Chiba K, Suzuki K and Chikazumi S 1970 Proceedings of the International Conference on Ferrites Kyoto, Japan, July 6−15, 1970 p595
[30]	Iida S, Yamamoto M, Umemura S 1974 AIP Conf. Proc. 18 913
[31]	Vieland L J 1975 Acta Crystallogr., Sect. A: Found. Crystallogr. 31 753
[32]	Shirane G, Chikazumi S, Akimitsu J, Chiba K, Matsui M, Fujii Y 1975 J. Phys. Soc. Jpn. 39 949 Google Scholar
[33]	Iizumi M, Shirane G 1975 Solid State Commun. 17 433 Google Scholar
[34]	Iizumi M, Koetzle T F, Shirane G, Chikazumi S, Matsui M, Todo S 1982 Acta Crystallogr., Sect. B: Struct. Sci. 38 2121 Google Scholar
[35]	Wright J P, Attfield J P, Radaelli P G 2002 Phys. Rev. B 66 214422 Google Scholar
[36]	Jeng H T, Guo G Y, Huang D J 2006 Phys. Rev. B 74 195115 Google Scholar
[37]	Senn M S, Loa I, Wright J P, Attfield J P 2012 Phys. Rev. B 85 125119 Google Scholar
[38]	Anderson P W 1956 Phys. Rev. 102 1008 Google Scholar
[39]	Weng S C, Lee Y R, Chen C G, Chu C H, Soo Y L, Chang S L 2012 Phys. Rev. Lett. 108 146404 Google Scholar
[40]	de Jong S, Kukreja R, Trabant C, Pontius N, Chang C F, Kachel T, Beye M, Sorgenfrei F, Back C H, Bräuer B, Schlotter W F, Turner J J, Krupin O, Doehler M, Zhu D, Hossain M A, Scherz A O, Fausti D, Novelli F, Esposito M, Lee W S, Chuang Y D, Lu D H, Moore R G, Yi M, Trigo M, Kirchmann P, Pathey L, Golden M S, Buchholz M, Metcalf P, Parmigiani F, Wurth W, Föhlisch A, Schüßler-Langeheine C, Dürr H A 2013 Nat. Mater. 12 882 Google Scholar
[41]	Mi W B, Guo Z B, Wang Q X, Yang Y, Bai H L 2013 Scr. Mater. 68 972 Google Scholar
[42]	Margulies D T, Parker F T, Spada F E, Goldman R S, Li J, Sinclair R, Berkowitz A E 1996 Phys. Rev. B 53 9175 Google Scholar
[43]	Liu X, Mi W B, Zhang Q, Zhang X X 2018 Appl. Phys. Lett. 113 012401 Google Scholar
[44]	Margulies D T, Parker F T, Rudee M L, Spada F E, Chapman J N, Aitchison P R, Berkowitz A E 1997 Physical Review Letters 79 5162
[45]	Fitzgerald A G, May T G 1976 Thin Solid Films 35 201 Google Scholar
[46]	Celotto S, Eerenstein W, Hibma T 2003 Eur. Phys. J. B 36 271 Google Scholar
[47]	Liu X H, Liu W, Zhang Z D 2017 Phys. Rev. B 96 094405 Google Scholar
[48]	McKenna K P, Hofer F, Gilks D, Lazarov V K, Chen C, Wang Z C, Ikuhara Y 2014 Nat. Commun. 5 6740
[49]	Kasama T, Church N S, Feinberg J M Dunin-Borkowski R E, Harrison R J 2010 Earth Planet. Sci. Lett. 297 10 Google Scholar
[50]	Kasama T, Harrison R J, Church N S, Nagao M, Feinberg J M, Dunin-Borkowski R E 2013 Phase Transitions 86 67 Google Scholar
[51]	de la Figuera J, Novotny Z, Setvin M, Liu T J, Mao Z Q, Chen G, N’Diaye T A, Schmid M, Diebold U, Schmid K A, S.Parkinson G 2013 Phys. Rev. B 88 161410 Google Scholar
[52]	Chen C L, Li H P, Seki T, Yin D Q, Sanchez-Santolino G, Inoue K, Shibata N, Ikuhara Y 2018 ACS Nano 12 2662 Google Scholar
[53]	Attfield J P 2014 J. Jpn. Soc. Powder Powder Metall. 61 S43 Google Scholar
[54]	Jeng H T, Guo G Y, Huang D J 2004 Phys. Rev. Lett. 93 156403 Google Scholar
[55]	Liu X, Yin L, Mi W B 2017 Sci. Rep. 7 43403 Google Scholar
[56]	Verwey E J W, Haayman P W 1941 Physica 8 979 Google Scholar
[57]	Cullen J R, Callen E 1970 J. Appl. Phys. 41 879 Google Scholar
[58]	Mott N F 1990 Metal-insulator transitions (2nd Ed.) (London: Taylor and Francis) p68
[59]	Chakraverty B K 1980 Philos. Mag. B 42 473 Google Scholar
[60]	Seo H, Ogata M, Fukuyama H 2002 Phys. Rev. B 65 085107 Google Scholar
[61]	van den Brink J, Khomskii D I 2008 J. Phys. Condens. Matter 20 434217 Google Scholar
[62]	García J, Subías G, Proietti M G, Blasco J, Renevier H, Hodeau J L, Joly Y 2001 Phys. Rev. B 63 054110 Google Scholar
[63]	Nazarenko E, Lorenzo J E, Joly Y, Hodeau J L, Mannix D, Marin C 2006 Phys. Rev. Lett. 97 056403 Google Scholar
[64]	Leonov I, Yaresko A N, Antonov V N, Korotin M A, Anisimov V I 2004 Phys. Rev. Lett. 93 146404 Google Scholar
[65]	Liu X H, Chang C F, Rata A D, Komarek A C, Tjeng L H 2016 npj Quantum Mater. 1 16027 Google Scholar
[66]	Calhoun B A 1954 Phys. Rev. 94 1577 Google Scholar
[67]	Palmer W 1963 Phys. Rev. 131 1057 Google Scholar
[68]	Domenicali C A 1950 Phys. Rev. 78 458 Google Scholar
[69]	Balberg I 1970 Phys. Rev. Lett. 25 1294 Google Scholar
[70]	Kostopoulos D 1972 Phys. Status Solidi 9 523 Google Scholar
[71]	Gong G Q, Gupta A, Xiao G, Qian W, Dravid V P 1997 Phys. Rev. B 56 5096 Google Scholar
[72]	Rozenberg G K, Hearne G R, Pasternak M P, Metcalf P A, Honig J M 1996 Phys. Rev. B 53 6482 Google Scholar
[73]	Ziese M, Blythe H J 2000 J. Phys. Condens. Matter 12 13 Google Scholar
[74]	Feng J S Y, Pashley R D, Nicolet M A 1975 J. Phys. C: Solid State Phys. 8 1010 Google Scholar
[75]	Margulies D T, Parker F T, Rudee M L, Spada F E, Chapman J N, Aitchison P R, Berkowitz A E 1997 Phys. Rev. Lett. 79 5162 Google Scholar
[76]	Voogt F C, Palstra T T M, Niesen L, Rogojanu O C, James M A, Hibma T 1998 Phys. Rev. B 57 R8107 Google Scholar
[77]	Eerenstein W, Palstra T T M, Saxena S S Hibma T 2002 Phys. Rev. Lett. 88 247204 Google Scholar
[78]	Ramos A V, Moussy J B, Guittet M J, Bataille A M, Gautier-Soyer M 2006 J. Appl. Phys. 100 103902 Google Scholar
[79]	Li P, Zhang L T, Mi W B, Jiang E Y, Bai H L 2009 J. Appl. Phys. 106 033908 Google Scholar
[80]	Sofin R G S, Arora S K, Shvets I V 2011 Phys. Rev. B 83 134436 Google Scholar
[81]	Ramos R, Arora S K, Shvets I V 2008 Phys. Rev. B 78 214402 Google Scholar
[82]	Li P, Jiang E Y, Bai H L 2010 Appl. Phys. Lett. 96 092502 Google Scholar
[83]	Hu C R, Zhu J, Chen G, Li J X, Wu Y Z 2012 Phys. Lett. A 376 3317 Google Scholar
[84]	Ding Z, Li J X, Zhu J, Ma T P, Won C, Wu Y Z 2013 J. Appl. Phys. 113 17B
[85]	Liu X, Mi W B, Zhang Q, Zhang X X 2017 Phys. Rev. B 96 214434 Google Scholar
[86]	Rado G T, Ferrari J M 1975 Phys. Rev. B 12 5166 Google Scholar
[87]	Iwauchi K, Kita Y, Koizumi N 1980 J. Phys. Soc. Jpn. 49 1328 Google Scholar
[88]	Kato K, Iida S 1982 J. Phys. Soc. Jpn 51 1335 Google Scholar
[89]	Kato K, Iida S, Yanai K, Mizushima K 1983 J. Magn. Magn. Mater. 83 783
[90]	Miyamoto Y, Ishiyama K 1993 Solid State Commun. 87 581 Google Scholar
[91]	Miyamoto Y, Ishihara S, Hirano T, Tkada M, Suzuki N 1994 Solid State Commun. 89 51 Google Scholar
[92]	Alexe M, Ziese M, Hesse D, Esquinazi P, Yamauchi K, Fukushima T, Picozzi S, Gösele U 2009 Adv. Mater. 21 4452 Google Scholar
[93]	Yamauchi K, Fukushima T, Picozzi S 2009 Phys. Rev. B 79 212404 Google Scholar
[94]	Liu X, Mi W B 2018 Front. Phys. 13 134204 Google Scholar

施引文献

图 1 Fe₃O₄的电阻率随温度的变化关系. 样品I中FeO∶Fe₂O₃ = 1∶1.025, 样品II中FeO:Fe₂O₃ = 1∶1.08^[1]

Fig. 1. Temperature-dependent resistivity of Fe₃O₄ sample I with FeO∶Fe₂O₃ = 1∶1.025 and sample II with FeO∶Fe₂O₃ = 1∶1.08^[1].

下载: 全尺寸图片幻灯片

图 2 尖晶石晶胞　(a)次晶格的堆叠方式; (b)晶体结构^[24]

Fig. 2. Spinel unit cell: (a) Stacking pattern of sub-lattices; (b) crystal structure^[24].

下载: 全尺寸图片幻灯片

图 3 空间群为$Fd\overline 3 m$, P2/m, P2/c和Cc的Fe₃O₄单胞^[35]

Fig. 3. Relationship between the unit cells referred to the structure with space group $Fd\overline 3 m$, P2/m, P2/c and Cc^[35].

下载: 全尺寸图片幻灯片

图 4 (a)三极化子和(b)三极化子分布的示意图^[23]

Fig. 4. Schematic diagram of (a) trimeron and (b) distribution of trimeron^[23].

下载: 全尺寸图片幻灯片

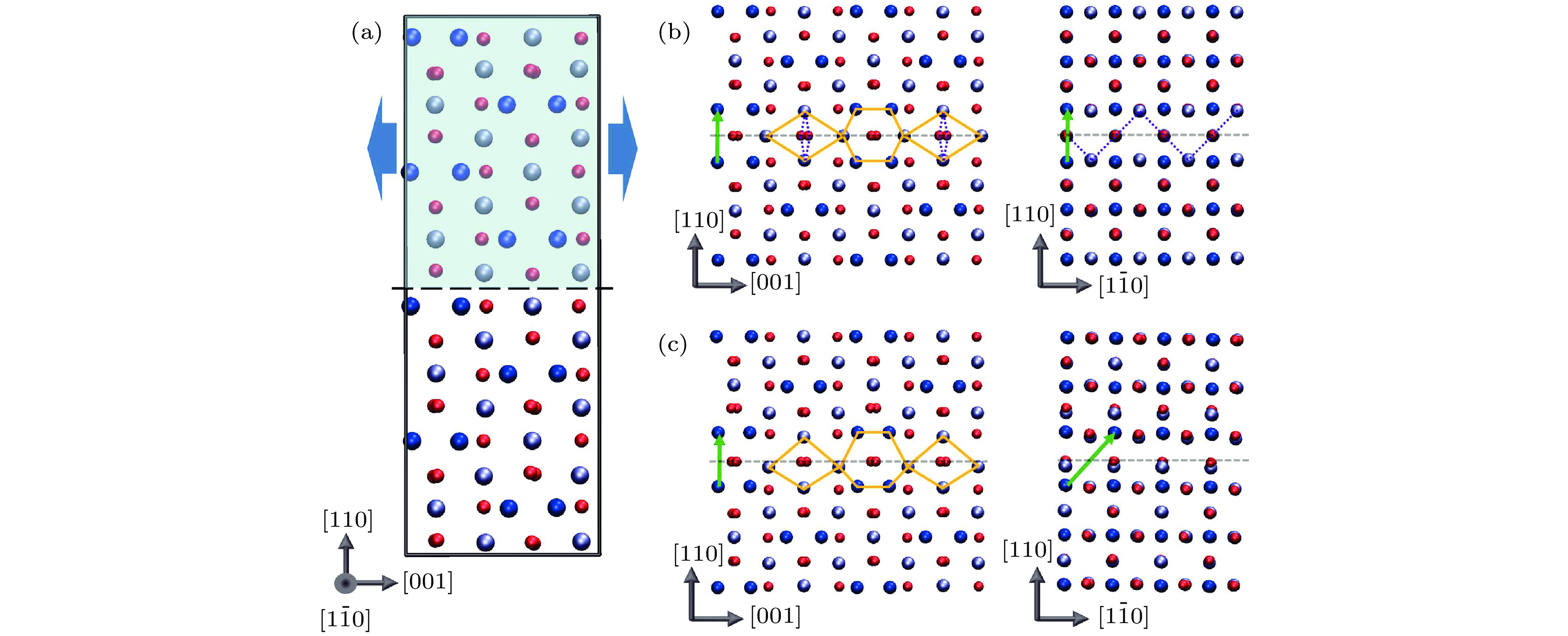
图 5 (a)−(d) Fe₃O₄(001)薄膜的TEM研究结果; (e)−(h) Fe₃O₄(111)薄膜的TEM研究结果. 室温和95 K的衍射斑点分别由室温相和低温相Fe₃O₄密勒指数标注. 图(g)中黄字为Al₂O₃密勒指数. 图(b)和图(f)棕球和红球分别代表Fe和O原子^[41,43]

Fig. 5. TEM results of ((a)−(d)) Fe₃O₄(001) and ((e)−(h)) Fe₃O₄(111) films. White Miller index above (below) T_V are marked with cubic (monoclinic) Fe₃O₄. Yellow Miller index in Fig. (g) indicates Al₂O₃. Brown and red spheres in Fig. (b) and Fig. (f) represent Fe and O^[41,43].

下载: 全尺寸图片幻灯片

图 6 Fe₃O₄(110)面上APB的结构　(a)理想情况下Fe₃O₄的结构; (b)第一类APB(APB–I); (c)第二类APB(APB–II). APB的平移方向由绿色箭头表示, 红球为O原子, 蓝球为Fe_A离子, 灰球为Fe_B离子^[48]

Fig. 6. {110} APB defects in Fe₃O₄: (a) The ideal cubic Fe₃O₄ structure; (b) APB-I; (c) APB-II. The APB crystal translations are indicated by green vectors. Red, blue and gray spheres represent the oxygen atoms, tetrahedral Fe and octahedral Fe atoms^[48].

下载: 全尺寸图片幻灯片

图 7 立方相和单斜相Fe₃O₄晶格的相关性^[49]

Fig. 7. Symmetrically distinct crystallographic relationships between cubic and monoclinic phases of magnetite^[49].

下载: 全尺寸图片幻灯片

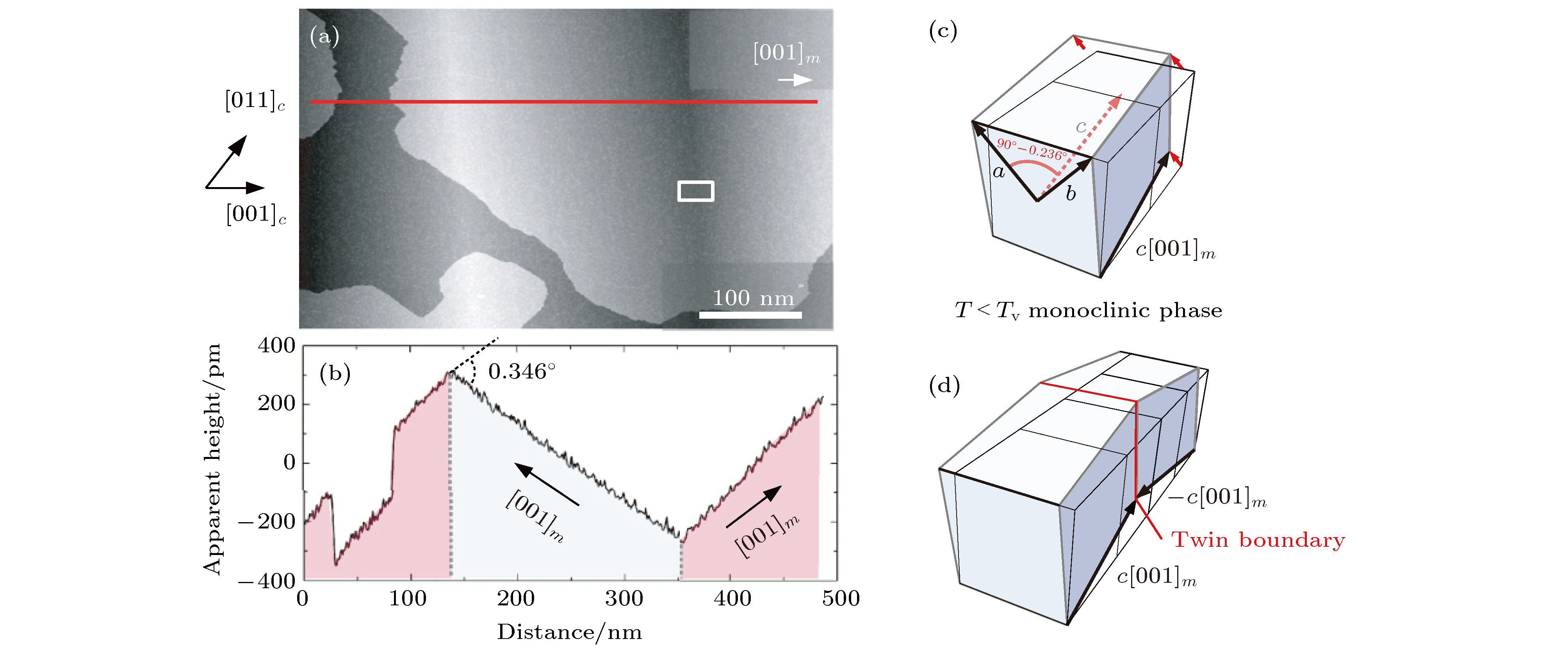
图 8 (a) Fe₃O₄薄膜的扫描隧道显微镜图像; (b)沿(a)中红线标记方向上的高度变化; (c)单斜结构Fe₃O₄; (d)由镜面对称单斜结构形成的Fe₃O₄^[51]

Fig. 8. (a) STM image of Fe₃O₄(100) surface at 78 K; (b) profile along the line marked in red of (a); (c) the monoclinic unit cell of Fe₃O₄; (d) two mirrored monoclinic cells with opposite monoclinic c axis at a twin boundary^[51].

下载: 全尺寸图片幻灯片

图 9 Fe₃O₄孪晶界处的自旋极化态密度图(density of states, DOS)　(a) I型; (b) II型; (c) III型. 费米能级由红色虚线表示. 图中给出了弛豫后的模型. 态密度表明I型孪晶界处为铁磁耦合, II型和III型为反铁磁耦合^[52]

Fig. 9. Spin-polarized DOS of Fe₃O₄ twin boundaries (TBs): (a) Type I TB; (b) Type II TB; (c) Type III TB. E_F is represented by the red dashed lines. The relaxed atomistic models are also given for reference. The DOS suggest that the magnetic coupling across the type I TB is ferromagnetic and those across the type II and III TBs are antiferromagnetic^[52].

下载: 全尺寸图片幻灯片

图 10 Fe₃O₄中Fe离子的3d电子轨道排布和磁耦合示意图^[53]

Fig. 10. Sketch map of the electronic ground state of Fe 3d electrons and magnetic couplings in Fe₃O₄^[53].

下载: 全尺寸图片幻灯片

图 11 Fe₃O₄的磁各向异性常数K₁随温度的变化关系^[27]

Fig. 11. Temperature dependent Anisotropy constant K₁ of Fe₃O₄^[27].

下载: 全尺寸图片幻灯片

图 12 Fe₃O₄的Fe_B位的电子局域模型　(a) Verwey提出的简单四面体Fe²⁺/Fe³⁺电荷有序模型; (b)包含两个Fe²⁺和两个Fe³⁺的安德森四面体模型; (c) Fe_B₄四面体内的键二聚化, 电子局域化在两个距离相近的Fe_B–Fe_B内, 由粗线表示^[53]

Fig. 12. Models for electron localization on Fe_B sites of Fe₃O₄: (a) Verwey’s tetragonal model of Fe²⁺/Fe³⁺ charge order; (b) an Anderson tetrahedron of two Fe²⁺ and two Fe³⁺ ions; (c) bond-dimerization in the Fe_B₄ tetrahedron, where the electrons are localized in two shortened Fe_B-Fe_B distances, shown as bold lines^[53].

下载: 全尺寸图片幻灯片

图 13 Fe₃O₄中Fe_B离子的态密度图, 费米能级位于E_F = 0 eV处^[54]

Fig. 13. DOS of Fe₃O₄ with the monoclinic structure projected onto the Fe_B d orbitals. Fermi level E_F is set at 0 eV^[54].

下载: 全尺寸图片幻灯片

图 14 δ₁₂和δ₃₄置信因子的等值图. 最佳值为δ₁₂ = 0.12 ± 0.025, δ₃₄ = 0.10 ± 0.06. Fe₁电子占据数为5.38和5.62, Fe₄电子占据数为5.40和5.60^[63]

Fig. 14. Isovalue of the confidence factor. The best agreement is obtained for δ₁₂ = 0.12 ± 0.025 electrons and δ₃₄ = 0.10 ± 0.06 electrons, where the charge occupancies of Fe₁ and Fe₄ are 5.38, 5.62 and 5.40, 5.60, respectively^[63].

下载: 全尺寸图片幻灯片

图 15 150和660 nm厚的Fe₃O₄外延薄膜的ρ–T曲线及300 Oe磁场下660 nm厚的Fe₃O₄外延薄膜的磁化强度随温度的变化关系^[71]

Fig. 15. Temperature dependent resistivity of 150 and 660-nm thick Fe₃O₄ films in the temperature range of 60–350 K. The temperature dependent magnetization of 660-nm thick film at a magnetic field of 300 Oe^[71].

下载: 全尺寸图片幻灯片

图 16 (a) 70 K和(b) 115 K下, 660 nm厚的Fe₃O₄薄膜的磁电阻随磁场变化关系; (c) 0.5, 1, 2和4 T磁场下磁电阻随温度的变化关系^[71]

Fig. 16. Magnetoresistance of 660 nm thick Fe₃O₄ films at (a) 70 K and (b) 115 K; (c) Temperature dependent magnetoresistance of 660-nm thick Fe₃O₄ film at the magnetic fields of 0.5, 1, 2, 4 T. The dotted lines are simulations using Mott’s formula^[71].

下载: 全尺寸图片幻灯片

图 17 块体Fe₃O₄和200, 50和15 nm厚的Fe₃O₄薄膜的(a)磁化强度和(b)零场电阻率随温度的变化关系^[73]

Fig. 17. Temperature dependent (a) magnetization and (b) zero-field resistivity of Fe₃O₄ single crystal and films with the thickness of 200, 50 and 15 nm^[73].

下载: 全尺寸图片幻灯片

图 18 在磁场作用下, Fe₃O₄薄膜反相边界处的磁矩分布^[77]

Fig. 18. Spin orientation of two ferromagnetic chains with antiferromagnetic coupling at an atomically sharp boundary at a magnetic field^[77].

下载: 全尺寸图片幻灯片

图 19 在5 T磁场下, (a) 67 nm厚的Fe₃O₄薄膜和(b) Fe₃O₄块体的AMR^[81]

Fig. 19. AMR of the (a) 67 nm thick Fe₃O₄ film and (b) Fe₃O₄ single crystal at a magnetic field of 5 T^[81].

下载: 全尺寸图片幻灯片

图 20 外延Fe₃O₄(100)薄膜的AMR　(a) 50 kOe下AMR随温度的变化; (b) 110 K和(c)80 K下AMR随磁场的变化^[85]

Fig. 20. AMR of the epitaxial Fe₃O₄(100) film: (a) Temperature-dependent AMR at a 50 kOe magnetic field; AMR at (b) 110 K and (c) 80 K^[85].

下载: 全尺寸图片幻灯片

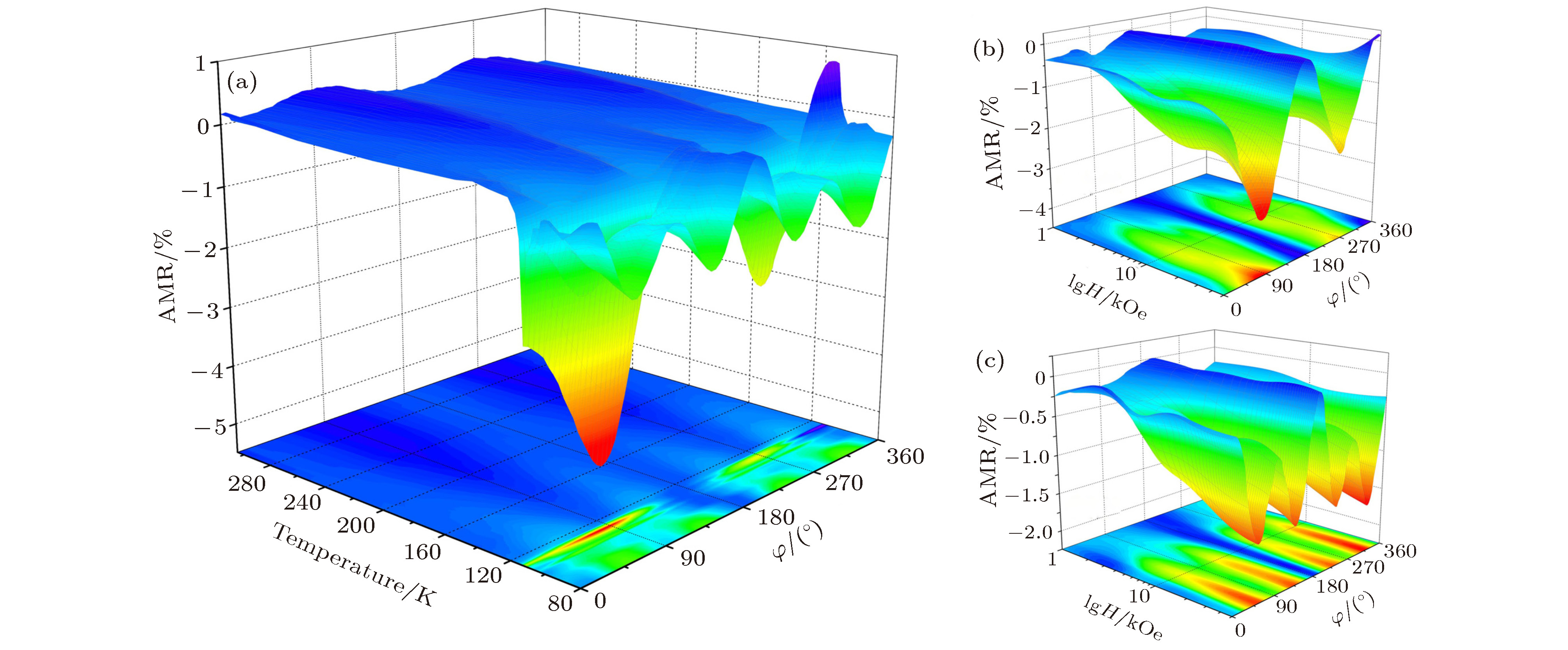
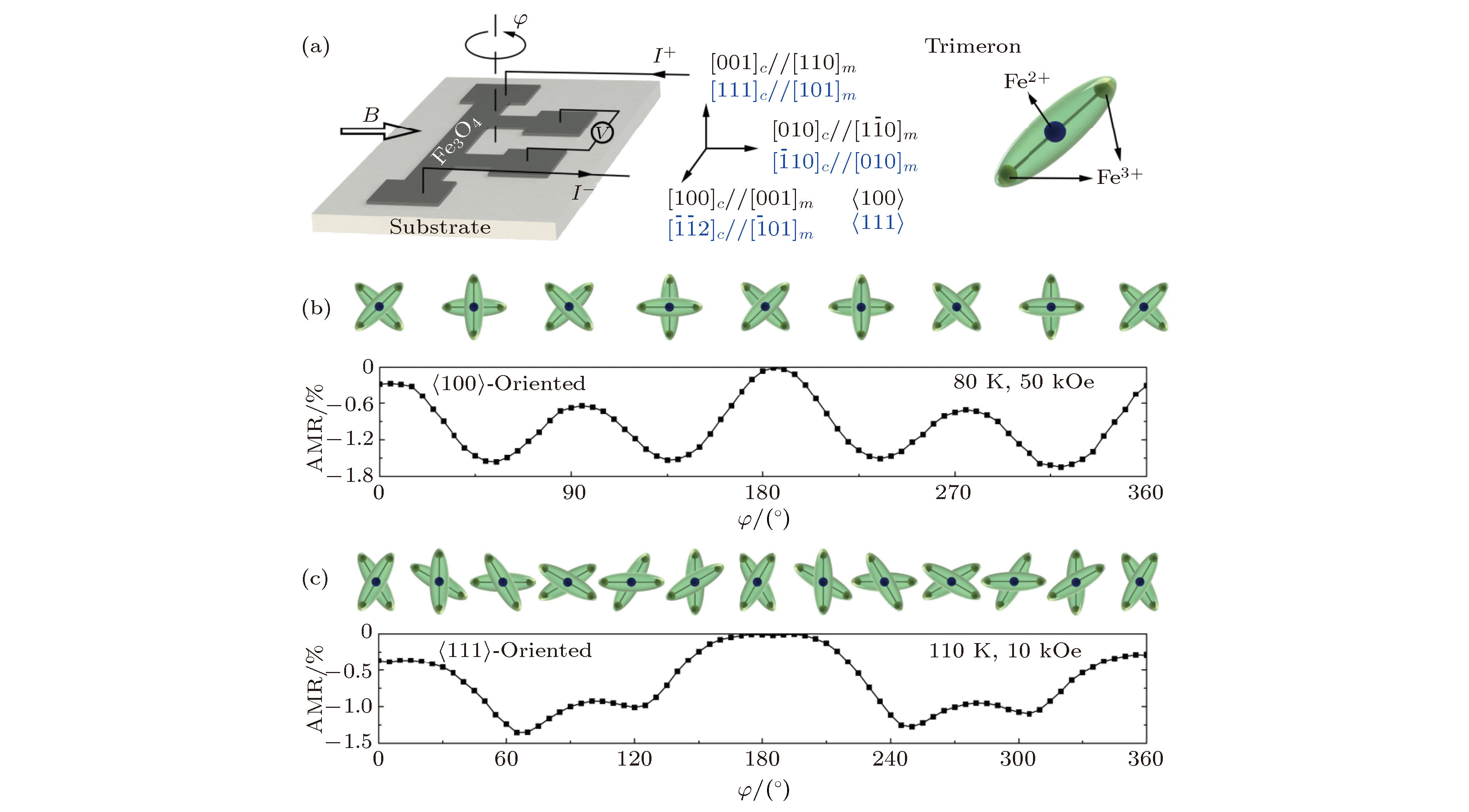
图 21 (a)测试示意图; (b) 80 K和50 kOe下, Fe₃O₄(100)薄膜的AMR与三极化子分布的关系; (c) 110 K和10 kOe下, Fe₃O₄(111)薄膜的AMR与三极化子分布的关系. 三极化子示意图如右上角所示^[85]

Fig. 21. (a) Schematic of the measurements; (b) relation between AMR and distribution of in-plane trimeron of Fe₃O₄(100) film at 80 K and 50 kOe; (c) relation between AMR and distribution of in-plane trimeron of Fe₃O₄(111) film at 110 K and 10 kOe. The trimeron is shown in the upper right corner^[85].

下载: 全尺寸图片幻灯片

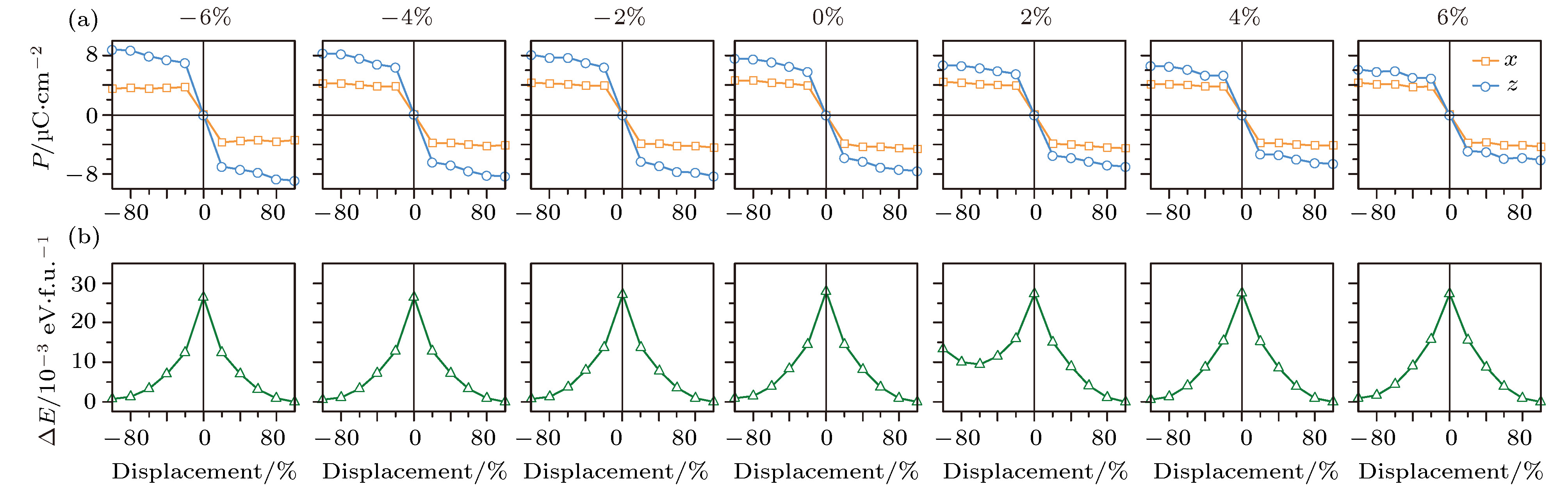
图 22 (a) Pd/Fe₃O₄/Nd:SrTiO₃异质结构的电滞回线^[92]; (b) P2/c (左图)和Cc空间群(右图)的Fe_B离子结构. 橙色和蓝色球表示Fe²⁺和Fe³⁺. 红色箭头表示电荷转移引起的电偶极矩^[93]

Fig. 22. (a) Dielectric hysteresis loop of Pd/Fe₃O₄/Nd:SrTiO₃ heterostructure^[92]; (b) ionic structure of Fe octahedral sites with P2/c (left) and Cc (right) space groups. Orange and blue balls represent the Fe²⁺ and Fe³⁺ ions. Electric dipole moments caused by charge shifts are indicated by red arrows^[93].

下载: 全尺寸图片幻灯片

图 23 (a)低温相Fe₃O₄铁电极化在x, z轴方向的分量; (b)体系总能随应力的变化^[94]

Fig. 23. (a) Ferroelectric polarization along the x and z axes; (b) strain dependent total energy^[94].

下载: 全尺寸图片幻灯片

表 1 外延Fe₃O₄(001)薄膜中APB处的磁交换相互作用^[46]

Table 1. Magnetic exchange interaction across APBs in the epitaxial Fe₃O₄(001) films^[46].

交换相互作用	类型和角度	磁性和强度	出现位置
Fe_B-O-Fe_B	超交换, 180°	反铁磁, 强	APB处
Fe_A-O-Fe_A	超交换, 约140°	反铁磁, 强	APB处
Fe_B-O-Fe_A	超交换, 约120°	反铁磁, 强	块体和APB处
Fe_B-O-Fe_B	超交换, 90°	铁磁, 弱	块体和APB处
Fe_A-O-Fe_A	超交换, 约70°	反铁磁, 弱	APB处
Fe_B-Fe_B	直接	铁磁, 弱	块体和APB处
Fe_A-Fe_A	直接	反铁磁, 弱	APB处
Fe_B-Fe_A	直接	铁磁, 弱	APB处

下载: 导出CSV

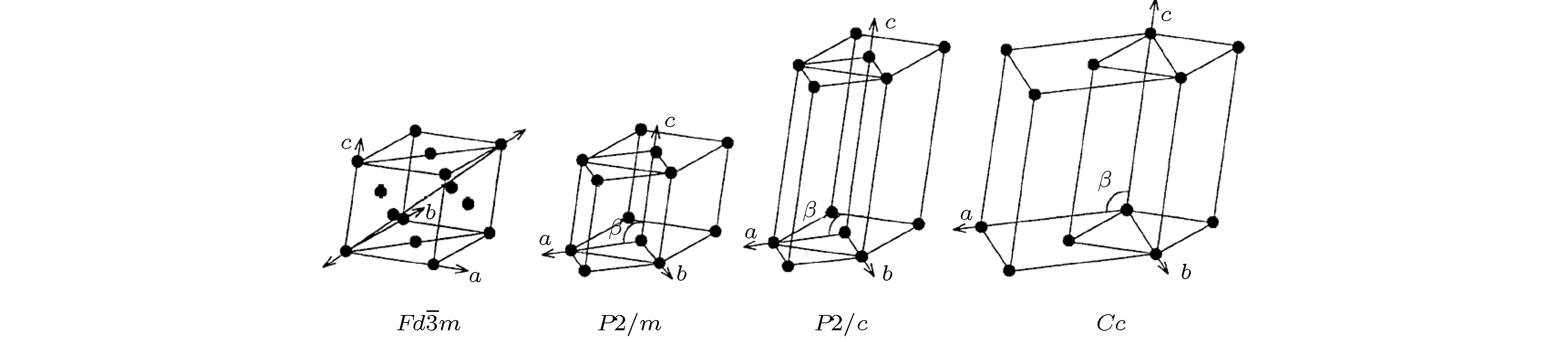
表 2 在P2/c和$Fd\overline 3 m$空间群下, ${{{a_c}}/{\sqrt 2 }} \times {{{a_c}}/{\sqrt 2 }} \times 2{a_c}$晶胞Fe₃O₄的电荷差(CS)、轨道有序度(OO)及总能量E_t^[36]

Table 2. Calculated charge separations (CS), orbital ordering (OO) and the total energy (E_t) of Fe₃O₄ with ${{{a_c}}/{\sqrt 2 }} \times {{{a_c}}/{\sqrt 2 }} \times 2{a_c}$ unit cell in monoclinic P2/c and cubic phase^[36].

U/eV	P2/c				$Fd\overline 3 m$
U/eV	↓gap/eV	CS/e	OO(P)	E_t/eV·(f.u.)^–1	↓gap/eV	CS/e	OO(P)	E_t/eV·(f.u.)^–1
0.0	No	0.00	No(0.55)	–0.15	No	0.00	No(0.34)	0.00
4.0	No	0.11	Yes(0.98)	–0.15	No	0.10	Yes(0.96)	–0.22
4.5	0.2	0.15	Yes(0.98)	–0.53	No	0.12	Yes(0.96)	–0.27
5.0	0.42	0.17	Yes(0.97)	–0.75	0.11	0.16	Yes(0.96)	–0.35
5.5	0.63	0.19	Yes(0.96)	–0.85	0.28	0.19	Yes(0.91)	–0.47

下载: 导出CSV

map

[1]	Verwey E J W 1939 Nature 144 327
[2]	Renger K 1913 Ph. D. Dissertation (Zürich: Swiss Federal Institute of Technology Zürich)
[3]	Parks G S, Kelly K K 1926 J. Phys. Chem. 30 47 Google Scholar
[4]	Millar R W 1929 J. Am. Chem. Soc. 51 215 Google Scholar
[5]	Okamura T 1932 Sci. Rep. Tohoku Imp. Univ. 21 231
[6]	Ellefson B S, Taylor N W 1934 J. Chem. Phys. 2 58 Google Scholar
[7]	Weiss P, Forrer R 1929 Ann. Phys. 12 279
[8]	Bragg W H 1915 Philos. Mag. 30 305 Google Scholar
[9]	Bragg W H and Brown G B 1926 Z. Kristallogr. 63 122
[10]	Claassen A 1926 Proc. Phys. Soc. 38 482
[11]	Néel L 1948 Ann. Phys. 3 137
[12]	Verwey E J W, Heilmann E L 1948 J. Chem. Phys. 16 1091 Google Scholar
[13]	Verwey E J W, Haayman P W, Romeijn F C 1947 J. Chem. Phys. 15 181 Google Scholar
[14]	Westrum E F, Grønvold F 1969 J. Chem. Thermodyn. 1 543 Google Scholar
[15]	Cullen J R, Callen E R 1971 Solid State Commun. 9 1041 Google Scholar
[16]	Evans B J, Westrum E F 1972 Phys. Rev. B 5 3791 Google Scholar
[17]	Cullen J R, Callen E R 1973 Phys. Rev. B 7 397 Google Scholar
[18]	Chakraverty B K 1974 Solid State Commun. 15 1271 Google Scholar
[19]	Buckwald R A, Hirsch A A 1975 Solid State Commun. 17 621 Google Scholar
[20]	Bartel J J, Westrum E F, Haas J L 1976 J. Chem. Thermodyn. 8 575 Google Scholar
[21]	Matsui M, Todo S, Chikazumi S 1977 J. Phys. Soc. Jpn. 42 1517 Google Scholar
[22]	Rigo M O, Kleinclauss J 1980 Philos. Mag. B 42 393 Google Scholar
[23]	Senn M S, Wright J P, Attfield J P 2012 Nature 481 173 Google Scholar
[24]	Miles P A, Westphal W B, von Hippel A 1957 Rev. Mod. Phys. 29 279 Google Scholar
[25]	Wright J P, Attfield J P, Radaelli P G 2001 Phys. Rev. Lett. 87 266401 Google Scholar
[26]	Bohra M, Agarwal N, Singh V 2019 J. Nanomater. 2019 8457383
[27]	Bickford Jr L R 1950 Phys. Rev. 78 449 Google Scholar
[28]	Kato K, Iida S 1981 J. Phys. Soc. Jpn. 50 2844 Google Scholar
[29]	Chikazumi S, Chiba K, Suzuki K and Chikazumi S 1970 Proceedings of the International Conference on Ferrites Kyoto, Japan, July 6−15, 1970 p595
[30]	Iida S, Yamamoto M, Umemura S 1974 AIP Conf. Proc. 18 913
[31]	Vieland L J 1975 Acta Crystallogr., Sect. A: Found. Crystallogr. 31 753
[32]	Shirane G, Chikazumi S, Akimitsu J, Chiba K, Matsui M, Fujii Y 1975 J. Phys. Soc. Jpn. 39 949 Google Scholar
[33]	Iizumi M, Shirane G 1975 Solid State Commun. 17 433 Google Scholar
[34]	Iizumi M, Koetzle T F, Shirane G, Chikazumi S, Matsui M, Todo S 1982 Acta Crystallogr., Sect. B: Struct. Sci. 38 2121 Google Scholar
[35]	Wright J P, Attfield J P, Radaelli P G 2002 Phys. Rev. B 66 214422 Google Scholar
[36]	Jeng H T, Guo G Y, Huang D J 2006 Phys. Rev. B 74 195115 Google Scholar
[37]	Senn M S, Loa I, Wright J P, Attfield J P 2012 Phys. Rev. B 85 125119 Google Scholar
[38]	Anderson P W 1956 Phys. Rev. 102 1008 Google Scholar
[39]	Weng S C, Lee Y R, Chen C G, Chu C H, Soo Y L, Chang S L 2012 Phys. Rev. Lett. 108 146404 Google Scholar
[40]	de Jong S, Kukreja R, Trabant C, Pontius N, Chang C F, Kachel T, Beye M, Sorgenfrei F, Back C H, Bräuer B, Schlotter W F, Turner J J, Krupin O, Doehler M, Zhu D, Hossain M A, Scherz A O, Fausti D, Novelli F, Esposito M, Lee W S, Chuang Y D, Lu D H, Moore R G, Yi M, Trigo M, Kirchmann P, Pathey L, Golden M S, Buchholz M, Metcalf P, Parmigiani F, Wurth W, Föhlisch A, Schüßler-Langeheine C, Dürr H A 2013 Nat. Mater. 12 882 Google Scholar
[41]	Mi W B, Guo Z B, Wang Q X, Yang Y, Bai H L 2013 Scr. Mater. 68 972 Google Scholar
[42]	Margulies D T, Parker F T, Spada F E, Goldman R S, Li J, Sinclair R, Berkowitz A E 1996 Phys. Rev. B 53 9175 Google Scholar
[43]	Liu X, Mi W B, Zhang Q, Zhang X X 2018 Appl. Phys. Lett. 113 012401 Google Scholar
[44]	Margulies D T, Parker F T, Rudee M L, Spada F E, Chapman J N, Aitchison P R, Berkowitz A E 1997 Physical Review Letters 79 5162
[45]	Fitzgerald A G, May T G 1976 Thin Solid Films 35 201 Google Scholar
[46]	Celotto S, Eerenstein W, Hibma T 2003 Eur. Phys. J. B 36 271 Google Scholar
[47]	Liu X H, Liu W, Zhang Z D 2017 Phys. Rev. B 96 094405 Google Scholar
[48]	McKenna K P, Hofer F, Gilks D, Lazarov V K, Chen C, Wang Z C, Ikuhara Y 2014 Nat. Commun. 5 6740
[49]	Kasama T, Church N S, Feinberg J M Dunin-Borkowski R E, Harrison R J 2010 Earth Planet. Sci. Lett. 297 10 Google Scholar
[50]	Kasama T, Harrison R J, Church N S, Nagao M, Feinberg J M, Dunin-Borkowski R E 2013 Phase Transitions 86 67 Google Scholar
[51]	de la Figuera J, Novotny Z, Setvin M, Liu T J, Mao Z Q, Chen G, N’Diaye T A, Schmid M, Diebold U, Schmid K A, S.Parkinson G 2013 Phys. Rev. B 88 161410 Google Scholar
[52]	Chen C L, Li H P, Seki T, Yin D Q, Sanchez-Santolino G, Inoue K, Shibata N, Ikuhara Y 2018 ACS Nano 12 2662 Google Scholar
[53]	Attfield J P 2014 J. Jpn. Soc. Powder Powder Metall. 61 S43 Google Scholar
[54]	Jeng H T, Guo G Y, Huang D J 2004 Phys. Rev. Lett. 93 156403 Google Scholar
[55]	Liu X, Yin L, Mi W B 2017 Sci. Rep. 7 43403 Google Scholar
[56]	Verwey E J W, Haayman P W 1941 Physica 8 979 Google Scholar
[57]	Cullen J R, Callen E 1970 J. Appl. Phys. 41 879 Google Scholar
[58]	Mott N F 1990 Metal-insulator transitions (2nd Ed.) (London: Taylor and Francis) p68
[59]	Chakraverty B K 1980 Philos. Mag. B 42 473 Google Scholar
[60]	Seo H, Ogata M, Fukuyama H 2002 Phys. Rev. B 65 085107 Google Scholar
[61]	van den Brink J, Khomskii D I 2008 J. Phys. Condens. Matter 20 434217 Google Scholar
[62]	García J, Subías G, Proietti M G, Blasco J, Renevier H, Hodeau J L, Joly Y 2001 Phys. Rev. B 63 054110 Google Scholar
[63]	Nazarenko E, Lorenzo J E, Joly Y, Hodeau J L, Mannix D, Marin C 2006 Phys. Rev. Lett. 97 056403 Google Scholar
[64]	Leonov I, Yaresko A N, Antonov V N, Korotin M A, Anisimov V I 2004 Phys. Rev. Lett. 93 146404 Google Scholar
[65]	Liu X H, Chang C F, Rata A D, Komarek A C, Tjeng L H 2016 npj Quantum Mater. 1 16027 Google Scholar
[66]	Calhoun B A 1954 Phys. Rev. 94 1577 Google Scholar
[67]	Palmer W 1963 Phys. Rev. 131 1057 Google Scholar
[68]	Domenicali C A 1950 Phys. Rev. 78 458 Google Scholar
[69]	Balberg I 1970 Phys. Rev. Lett. 25 1294 Google Scholar
[70]	Kostopoulos D 1972 Phys. Status Solidi 9 523 Google Scholar
[71]	Gong G Q, Gupta A, Xiao G, Qian W, Dravid V P 1997 Phys. Rev. B 56 5096 Google Scholar
[72]	Rozenberg G K, Hearne G R, Pasternak M P, Metcalf P A, Honig J M 1996 Phys. Rev. B 53 6482 Google Scholar
[73]	Ziese M, Blythe H J 2000 J. Phys. Condens. Matter 12 13 Google Scholar
[74]	Feng J S Y, Pashley R D, Nicolet M A 1975 J. Phys. C: Solid State Phys. 8 1010 Google Scholar
[75]	Margulies D T, Parker F T, Rudee M L, Spada F E, Chapman J N, Aitchison P R, Berkowitz A E 1997 Phys. Rev. Lett. 79 5162 Google Scholar
[76]	Voogt F C, Palstra T T M, Niesen L, Rogojanu O C, James M A, Hibma T 1998 Phys. Rev. B 57 R8107 Google Scholar
[77]	Eerenstein W, Palstra T T M, Saxena S S Hibma T 2002 Phys. Rev. Lett. 88 247204 Google Scholar
[78]	Ramos A V, Moussy J B, Guittet M J, Bataille A M, Gautier-Soyer M 2006 J. Appl. Phys. 100 103902 Google Scholar
[79]	Li P, Zhang L T, Mi W B, Jiang E Y, Bai H L 2009 J. Appl. Phys. 106 033908 Google Scholar
[80]	Sofin R G S, Arora S K, Shvets I V 2011 Phys. Rev. B 83 134436 Google Scholar
[81]	Ramos R, Arora S K, Shvets I V 2008 Phys. Rev. B 78 214402 Google Scholar
[82]	Li P, Jiang E Y, Bai H L 2010 Appl. Phys. Lett. 96 092502 Google Scholar
[83]	Hu C R, Zhu J, Chen G, Li J X, Wu Y Z 2012 Phys. Lett. A 376 3317 Google Scholar
[84]	Ding Z, Li J X, Zhu J, Ma T P, Won C, Wu Y Z 2013 J. Appl. Phys. 113 17B
[85]	Liu X, Mi W B, Zhang Q, Zhang X X 2017 Phys. Rev. B 96 214434 Google Scholar
[86]	Rado G T, Ferrari J M 1975 Phys. Rev. B 12 5166 Google Scholar
[87]	Iwauchi K, Kita Y, Koizumi N 1980 J. Phys. Soc. Jpn. 49 1328 Google Scholar
[88]	Kato K, Iida S 1982 J. Phys. Soc. Jpn 51 1335 Google Scholar
[89]	Kato K, Iida S, Yanai K, Mizushima K 1983 J. Magn. Magn. Mater. 83 783
[90]	Miyamoto Y, Ishiyama K 1993 Solid State Commun. 87 581 Google Scholar
[91]	Miyamoto Y, Ishihara S, Hirano T, Tkada M, Suzuki N 1994 Solid State Commun. 89 51 Google Scholar
[92]	Alexe M, Ziese M, Hesse D, Esquinazi P, Yamauchi K, Fukushima T, Picozzi S, Gösele U 2009 Adv. Mater. 21 4452 Google Scholar
[93]	Yamauchi K, Fukushima T, Picozzi S 2009 Phys. Rev. B 79 212404 Google Scholar
[94]	Liu X, Mi W B 2018 Front. Phys. 13 134204 Google Scholar

[1]	柯少秋, 叶先峰, 张昊俊, 聂晓蕾, 陈天天, 刘承姗, 朱婉婷, 魏平, 赵文俞. 正负磁阻共存的Fe/Bi_0.5Sb_1.5Te₃热电磁薄膜. , 2024, 73(22): 227301. doi: 10.7498/aps.73.20240701
[2]	任延英, 李雅宁, 柳洪盛, 徐楠, 郭坤, 徐朝辉, 陈鑫, 高峻峰. 过渡金属元素掺杂对磁铁矿磁矩及磁各向异性的调控. , 2024, 73(6): 066104. doi: 10.7498/aps.73.20231744
[3]	樊晓筝, 李怡莲, 吴怡, 陈俊彩, 徐国亮, 安义鹏. 二维磁性半导体笼目晶格Nb₃Cl₈单层的磁性及自旋电子输运性质. , 2023, 72(24): 247503. doi: 10.7498/aps.72.20231163
[4]	肖忆瑶, 何佳豪, 陈南锟, 王超, 宋宁宁. 基于负载Fe₃O₄纳米微球的大尺寸单层二维Ti₃C₂T_x微波吸收性能. , 2023, 72(21): 217501. doi: 10.7498/aps.72.20231200
[5]	卿煜林, 彭小莉, 胡爱元. 自旋为1的双层平方晶格阻挫模型的相变. , 2022, 71(4): 047501. doi: 10.7498/aps.71.20211685
[6]	孟婧, 冯心薇, 邵倾蓉, 赵佳鹏, 谢亚丽, 何为, 詹清峰. 具有不同交换偏置方向的外延FeGa/IrMn双层膜的磁各向异性与磁化翻转. , 2022, 71(12): 127501. doi: 10.7498/aps.71.20220166
[7]	杨雪, 杨青慧, 张怀武, 文岐业, 白飞明, 钟智勇, 张鼎, 黄建涛. 面外取向的(BiTm)₃(GaFe)₅O₁₂磁光单晶薄膜制备及取向机理分析. , 2021, 70(10): 107801. doi: 10.7498/aps.70.20202209
[8]	文林, 胡爱元. 双二次交换作用和各向异性对反铁磁体相变温度的影响. , 2020, 69(10): 107501. doi: 10.7498/aps.69.20200077
[9]	姜兴东, 管兴胤, 黄娟娟, 范小龙, 薛德胜. N⁺注入修复外延Fe膜面内六重磁对称. , 2019, 68(12): 126102. doi: 10.7498/aps.68.20190131
[10]	肖嘉星, 鲁军, 朱礼军, 赵建华. 垂直磁各向异性L10-Mn1.67Ga超薄膜分子束外延生长与磁性研究. , 2016, 65(11): 118105. doi: 10.7498/aps.65.118105
[11]	王强. 电子自旋共振研究Bi0.2Ca0.8MnO3纳米晶粒的电荷有序和自旋有序. , 2015, 64(18): 187501. doi: 10.7498/aps.64.187501
[12]	张辉, 曾德长. Tb0.3Dy0.7Fe2单晶中巨磁致伸缩的逆效应. , 2010, 59(4): 2808-2814. doi: 10.7498/aps.59.2808
[13]	刘宁, 严国清, 毛强, 王桂英, 郭焕银. La0.3Ca0.7Mn1－xVxO3体系的有序相和再入型自旋玻璃行为研究. , 2010, 59(8): 5759-5765. doi: 10.7498/aps.59.5759
[14]	王桂英, 郭焕银, 毛强, 杨刚, 彭振生. V替代Mn对La0.45Ca0.55MnO3电荷有序相及自旋玻璃态的影响. , 2010, 59(12): 8883-8889. doi: 10.7498/aps.59.8883
[15]	王强. Bi0.5Ca0.5Mn1-xCoxO3体系中的电荷有序和相分离. , 2010, 59(9): 6569-6574. doi: 10.7498/aps.59.6569
[16]	李晓娟, 王强. 晶粒尺寸对Bi0.2Ca0.8MnO3电荷有序的影响. , 2009, 58(9): 6482-6486. doi: 10.7498/aps.58.6482
[17]	郭玉献, 王劼, 徐彭寿, 李红红, 蔡建旺. Co0.9Fe0.1薄膜面内元素分辨的磁各向异性. , 2007, 56(2): 1121-1126. doi: 10.7498/aps.56.1121
[18]	郭焕银, 刘宁, 蔡之让, 张裕恒. Mn位W掺杂对La0.3Ca0.7MnO3体系磁结构的影响. , 2006, 55(2): 865-872. doi: 10.7498/aps.55.865
[19]	俞坚, 张金仓, 曹桂新, 王仕鹏, 敬超, 曹世勋. 相分离Nd0.5Ca0.5MnO3体系的再入型自旋玻璃行为和电荷有序. , 2006, 55(4): 1914-1920. doi: 10.7498/aps.55.1914
[20]	王仕鹏, 张金仓, 曹桂新, 俞坚, 敬超, 曹世勋. 半掺杂Sm0.5Ca0.5MnO3体系的电荷有序和再入型自旋玻璃行为. , 2006, 55(1): 367-371. doi: 10.7498/aps.55.367

计量

文章访问数: 19592
PDF下载量: 603
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

Verwey相变处Fe₃O₄的结构、磁性和电输运特性

Structure, magnetic and transport properties of Fe₃O₄ near verwey transition

摘要

Abstract

作者及机构信息

天津大学理学院应用物理学系, 天津市低维功能材料物理与制备技术重点实验室, 天津　300354

通信作者: 米文博, miwenbo@tju.edu.cn

Authors and contacts

Tianjin Key Laboratory of Low Dimensional Materials Physics and Preparation Technology, School of Science, Tianjin University, Tianjin 300354, China

Corresponding author: Mi Wen-Bo, miwenbo@tju.edu.cn

文章全文 : translate this paragraph

参考文献

施引文献

目录

计量

作者中心

审稿中心

关于期刊

关于我们

搜索

留言板

Verwey相变处Fe3O4的结构、磁性和电输运特性

Structure, magnetic and transport properties of Fe3O4 near verwey transition

摘要

Abstract

作者及机构信息

天津大学理学院应用物理学系, 天津市低维功能材料物理与制备技术重点实验室, 天津 300354

通信作者: 米文博, miwenbo@tju.edu.cn

Authors and contacts

Tianjin Key Laboratory of Low Dimensional Materials Physics and Preparation Technology, School of Science, Tianjin University, Tianjin 300354, China

Corresponding author: Mi Wen-Bo, miwenbo@tju.edu.cn

文章全文 : translate this paragraph

参考文献

施引文献

目录

计量

出版历程

作者中心

审稿中心

关于期刊

关于我们

Verwey相变处Fe₃O₄的结构、磁性和电输运特性

Structure, magnetic and transport properties of Fe₃O₄ near verwey transition

天津大学理学院应用物理学系, 天津市低维功能材料物理与制备技术重点实验室, 天津　300354