动态复杂网络中节点影响力的研究进展

任卓明

doi:10.7498/aps.69.20190830

摘要

节点影响力的识别和预测具有重要的理论意义和应用价值, 是复杂网络的热点研究领域. 目前大多数研究方法都是针对静态网络或动态网络某一时刻的快照进行的, 然而在实际应用场景中, 社会、生物、信息、技术等复杂网络都是动态演化的. 因此在动态复杂网络中评估节点影响力以及预测节点未来影响力, 特别是在网络结构变化之前的预测更具意义. 本文系统地总结了动态复杂网络中节点影响力算法面临的三类挑战, 即在增长网络中, 节点影响力算法的计算复杂性和时间偏见; 网络实时动态演化时, 节点影响力算法的适应性; 网络结构微扰或突变时, 节点影响力算法的鲁棒性, 以及利用网络结构演变阐释经济复杂性涌现的问题. 最后总结了这一研究方向几个待解决的问题并指出未来可能的发展方向.

关键词:

Abstract

Crucial to the physicists’ strong interest in the field is the fact that such macroscopic properties typically arise as the result of a myriad of interactions between the system constituents. Network science aims at simplifying the study of a given complex system by representing it as a network, a collection of nodes and edges interconnecting them. Nowadays, it is widely recognized that some of the structural traits of networks are in fact ubiquitous properties in real systems. The identification and prediction of node influence are of great theoretical and practical significance to be known as a hot research field of complex networks. Most of current research advance is focused on static network or a snapshot of dynamic networks at a certain moment. However, in practical application scenarios, mostly complex networks extracted from society, biology, information, technology are evolving dynamically. Therefore, it is more meaningful to evaluate the node's influence in the dynamic network and predict the future influence of the node, especially before the change of the network structure. In this summary, we contribute on reviewing the improvement of node influence in dynamical networks, which involves three tasks: algorithmic complexity and time bias in growing networks; algorithmic applicability in time varying networks; algorithmic robustness in a dynamical network with small or sharp perturbation. Furthermore, we overview the framework of economic complexity based on dynamical network structure. Lastly, we point out the forefront as well as critical challenges of the field.

Keywords:

作者及机构信息

任卓明

杭州师范大学阿里巴巴商学院复杂科学研究中心, 杭州　311121

通信作者: 任卓明, zhuoming.ren@hznu.edu.cn

基金项目: 国家级-基于雪崩电离的磁阻效应及其机理研究(61673151，61873080，61803137)

Authors and contacts

Ren Zhuo-Ming

Research Center for Complexity Sciences, Alibaba Business School, Hangzhou Normal University, Hangzhou 311121, China

Corresponding author: Ren Zhuo-Ming, zhuoming.ren@hznu.edu.cn

文章全文 : translate this paragraph

参考文献

[1]	Clauset A, Larremore D B, Sinatra R 2017 Science 355 477 Google Scholar
[2]	Ren Z M, Zeng A, Zhang Y C 2018 Phys. Rep. 750 1 Google Scholar
[3]	Lü L, Chen D, Ren X L, Zhang Q M, Zhang Y C, Zhou T 2016 Phys. Rep. 650 1 Google Scholar
[4]	Lynch C 2008 Nature 455 28 Google Scholar
[5]	Mariani M S, Ren Z M, Bascompte J, Tessone C J 2019 Physics Reports 813 1
[6]	Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175 Google Scholar
[7]	Wang W, Tang M, Stanley H E, Braunstein L A 2017 Rep. Prog. Phys. 80 036603 Google Scholar
[8]	Zhang Z K, Liu C, Zhan X X, Lu X, Zhang C X, Zhang Y C 2016 Phys. Rep. 651 1 Google Scholar
[9]	Zeng A, Shen Z, Zhou J, Wu J, Fan Y, Wang Y, Stanley H E 2017 Phys. Rep. 714 1 Google Scholar
[10]	Schweitzer F, Fagiolo G, Sornette D, Vega-Redondo F, Vespignani A, White D R 2009 Science 325 422 Google Scholar
[11]	高见, 周涛 2016 电子科技大学学报 45 625 Google Scholar Gao J, Zhou T 2016 J. Univ. Elec. Sci. Tech. China 45 625 Google Scholar
[12]	Hidalgo C A 2018 Nat. Phys. 14 9 Google Scholar
[13]	Borgatti S P, Mehra A, Brass D J, Labianca G 2009 Science 323 892 Google Scholar
[14]	Newman M E J 2003 SIAM Rev. 45 167 Google Scholar
[15]	Gert S 1966 Psychometrika 31 581
[16]	Goh K I, Oh E, Kahng B, Kim D 2003 Phys. Rev. E 67 017101 Google Scholar
[17]	Borgatti S P 2005 Soc. Net. 27 55 Google Scholar
[18]	Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E 2010 Nat. Phys. 6 888 Google Scholar
[19]	任卓明, 邵凤, 刘建国, 郭强, 汪秉宏 2013 262 128901 Google Scholar Ren Z M, Shao F, Liu J G, Guo Q, Wang B H 2013 Acta Phys. Sin. 262 128901 Google Scholar
[20]	Chen D, Lü L, Shang M S, Zhang Y C, Zhou T 2012 Physica A 391 1777 Google Scholar
[21]	Zhang J, Xu X K, Li P, Zhang K, Small M 2011 Chaos 21 016107 Google Scholar
[22]	Comin C H, da Fontoura Costa L 2011 Phys. Rev. E 84 056105 Google Scholar
[23]	Poulin R, Boily M C, Masse B R 2000 Soc. Net. 22 187 Google Scholar
[24]	Pei S, Morone F, Makse H A 2018 Theories for Influencer Identification in Complex Networks. In: Lehmann S, Ahn YY. (Ed.) Complex Spreading Phenomena in Social Systems. Computational Social Sciences. Springer, Cham pp125–148
[25]	Garas A, Schweitzer F, Havlin S 2012 New J. Phys. 14 083030 Google Scholar
[26]	Zeng A, Zhang C J 2013 Phys. Lett. A 377 1031 Google Scholar
[27]	Lü L, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168 Google Scholar
[28]	Travenolo B A N, Costa L F 2008 Phys. Lett. A 373 89 Google Scholar
[29]	Chen D B, Xiao R, Zeng A, Zhang Y C 2014 EPL 104 68006
[30]	Ren Z M, Zeng A, Chen D B, Liao H, Liu J G 2014 EPL 106 48005 Google Scholar
[31]	Bryan K, Leise T 2006 SIAM Rev. 48 569 Google Scholar
[32]	Berkhin P 2005 Internet Math. 2 73 Google Scholar
[33]	Lü L, Zhang Y C, Yeung C H, Zhou T 2011 PloS One 6 e21202 Google Scholar
[34]	Kleinberg J M 1999 JACM 46 604 Google Scholar
[35]	Newman M E J 2016 New Palg. Dict. Econ. 2016 1
[36]	Da Silva R A P, Viana M P, da Fontoura Costa L 2012 J. Stat. Mech. 2012 P07005 Google Scholar
[37]	任卓明, 刘建国, 邵凤, 胡兆龙, 郭强 2013 62 108902 Google Scholar Ren Z M, Liu J G, Shao F, Hu Z L, Guo Q 2013 Acta Phys. Sin. 62 108902 Google Scholar
[38]	刘建国, 任卓明, 郭强, 汪秉宏 2013 62 178901 Google Scholar Liu J G, Ren Z M, Guo Q, Wang B H 2013 Acta Phys. Sin. 62 178901 Google Scholar
[39]	任晓龙, 吕琳媛 2014 科学通报 59 1175 Google Scholar Ren X L, Lü L Y 2014 Chin. Sci. Bull. 59 1175 Google Scholar
[40]	Pei S, Makse H A 2013 J. Stat. Mech. 2013 P12002 Google Scholar
[41]	Holme P, Saramaki J 2012 Phys. Rep. 519 97 Google Scholar
[42]	Liao H, Mariani M S, Medo M, Zhang Y C, Zhou M Y 2017 Phys. Rep. 689 1 Google Scholar
[43]	Ercsey-Ravasz M, Toroczkai Z 2010 Phys. Rev. Lett. 105 038701 Google Scholar
[44]	Ercsey-Ravasz M, Lichtenwalter R N, Chawla N V, Toroczkai Z 2012 Phys. Rev. E 85 066103 Google Scholar
[45]	Lü L, Jin C H, Zhou T 2009 Phys. Rev. E 80 046122 Google Scholar
[46]	Mariani M S, Medo M, Zhang Y C 2015 Sci. Rep. 5 16181 Google Scholar
[47]	Mariani M S, Medo M, Zhang Y C 2016 J. Informetr. 10 1207 Google Scholar
[48]	Vaccario G, Medo M, Wider N, Mariani M S 2017 J. Informetr. 11 766 Google Scholar
[49]	Wasserman M, Zeng X H T, Amaral L A N 2015 PNAS 112 1281 Google Scholar
[50]	Wasserman M, Mukherjee S, Scott K, Zeng X H, Radicchi F, Amaral L A 2015 J. Asso. Info. Sci. Tech. 66 858 Google Scholar
[51]	Walker D, Xie H, Yan K K, Maslov S 2007 J. Stat. Mech. 2007 P06010 Google Scholar
[52]	Ren Z M, Mariani M S, Zhang Y C, Medo M 2018 Phys. Rev. E 97 052311 Google Scholar
[53]	Ren Z M 2018 Physica A 513 325 Google Scholar
[54]	Watts D J, Strogatz S H 1998 Nature 393 440 Google Scholar
[55]	Newman M E J 2003 Phys. Rev. E 67 026126 Google Scholar
[56]	Foster J G, Foster DV, Grassberger P, Paczuski M 2010 PNAS 107 10815 Google Scholar
[57]	Tian L, Bashan A, Shi D N, Liu Y Y 2017 Nat. Commun. 8 14223 Google Scholar
[58]	Arenas A, Diaz−Guilera A, Kurths J, Moreno Y, Zhou C 2008 Phys. Rep. 469 93 Google Scholar
[59]	Klemm K, Serrano M A, Eguiluz V M, San Miguel M 2012 Sci. Rep. 2 292 Google Scholar
[60]	Aral S, Walker D 2012 Science 337 337 Google Scholar
[61]	Centola D 2010 Science 329 1194 Google Scholar
[62]	Bond R M, Fariss C J, Jones J J, Kramer A D, Marlow C, Settle J E, Fowler J H 2012 Nature 489 295 Google Scholar
[63]	宋玉萍, 倪静 2016 65 028901 Google Scholar Song Y P, Ning J 2016 Acta Phys. Sin. 65 028901 Google Scholar
[64]	Ma S J, Ren Z M, Ye C M, Guo Q, Liu J G 2014 Inter. J. Mod. Phys. C 25 1450065 Google Scholar
[65]	邵凤, 郭强, 曾诗奇, 刘建国 2014 电子科技大学学报 43 174 Google Scholar Shao F, Guo Q, Zeng S Q, Liu J G 2014 J. Univ. Elec. Sci. Tech. China 43 174 Google Scholar
[66]	Lambiotte R, Rosvall M, Scholtes I 2018 arXiv preprint arXiv 1806 05977
[67]	Perri V, Scholtes I 2019 arXiv preprint arXiv 1908 05976
[68]	Xu J, Wickramarathne T L, Chawla N V 2016 Sci. Adv. 2 e1600028 Google Scholar
[69]	Tao J, Xu J, Wang C, Chawla N V 2017 IEEE Paci. Vis. Symp. (PacificVis) 2 1
[70]	Ghoshal G, Barabasi A L 2011 Nat. Commun. 2 394 Google Scholar
[71]	Lü L, Pan L, Zhou T, Zhang Y C, Stanley H E 2015 PNAS 112 2325 Google Scholar
[72]	Tacchella A, Mazzilli D, Pietronero L 2018 Nat. Phys. 14 861 Google Scholar
[73]	Cristelli M, Tacchella A, Pietronero L 2015 PloS One 10 e0117174 Google Scholar
[74]	Tacchella A, Cristelli M, Caldarelli G, Gabrielli A, Pietronero L 2012 Sci. Rep. 2 723 Google Scholar
[75]	Jara-Figueroa C, Jun B, Glaeser E L, Hidalgo C A 2018 PNAS 115 12646 Google Scholar
[76]	Hidalgo C A, Hausmann R 2009 PNAS 106 10570 Google Scholar
[77]	Hidalgo C A, Klinger B, Barabasi A L, Hausmann R 2007 Science 317 482 Google Scholar
[78]	Mariani M S, Vidmer A, Medo M, Zhang Y C 2015 Eur. Phys. J. B 88 293 Google Scholar
[79]	Wu R J, Shi G Y, Zhang Y C, Mariani M S 2016 Physica A 460 254 Google Scholar
[80]	Gao J, Zhou T 2018 Physica A 492 1591 Google Scholar
[81]	Gao J, Zhang Y C, Zhou T 2019 Phys. Rep. 817 1 Google Scholar
[82]	Almeida−Neto M, Guimaraes P, Guimaraes Jr P R, Loyola R D, Ulrich W 2008 Oikos 117 1227 Google Scholar
[83]	Mariani M S, Ren Z M, Bascompte J, Tessone C J 2019 Phys. Rep. 813 1 Google Scholar
[84]	Bustos S, Gomez C, Hausmann R, Hidalgo C A 2012 PloS One 7 e49393 Google Scholar
[85]	Liu J G, Lin J H, Guo Q, Zhou T 2016 Sci. Rep. 6 21380 Google Scholar
[86]	Barzel B, Barabasi A L 2013 Nat. Phys. 9 673 Google Scholar
[87]	Barzel B, Barabasi A L 2016 Nature 530 307 Google Scholar
[88]	Medo M 2014 Phys. Rev. E 89 032801 Google Scholar
[89]	Medo M, Cimini G, Gualdi S 2011 Phys. Rev. Lett. 107 238701 Google Scholar
[90]	Ren Z M, Shi Y Q, Liao H 2016 Physica A 453 236 Google Scholar

施引文献

图 1 动态网络示意图

Fig. 1. An example of the dynamic network

下载: 全尺寸图片幻灯片

图 2 局部到全局的渐进式算法的示意图　(a) 全局算法; (b) 渐进式算法

Fig. 2. The diagram of local to global progressive algorithm: (a) Global algorithm; (b) The local to global progressive algorithm.

下载: 全尺寸图片幻灯片

图 3 实时动态网络　(a) 含有一段时间的网络; (b) 动态演化网络

Fig. 3. An example of the time-variant dynamic network: (a) A network with a period of time; (b) the time-variant dynamic network.

下载: 全尺寸图片幻灯片

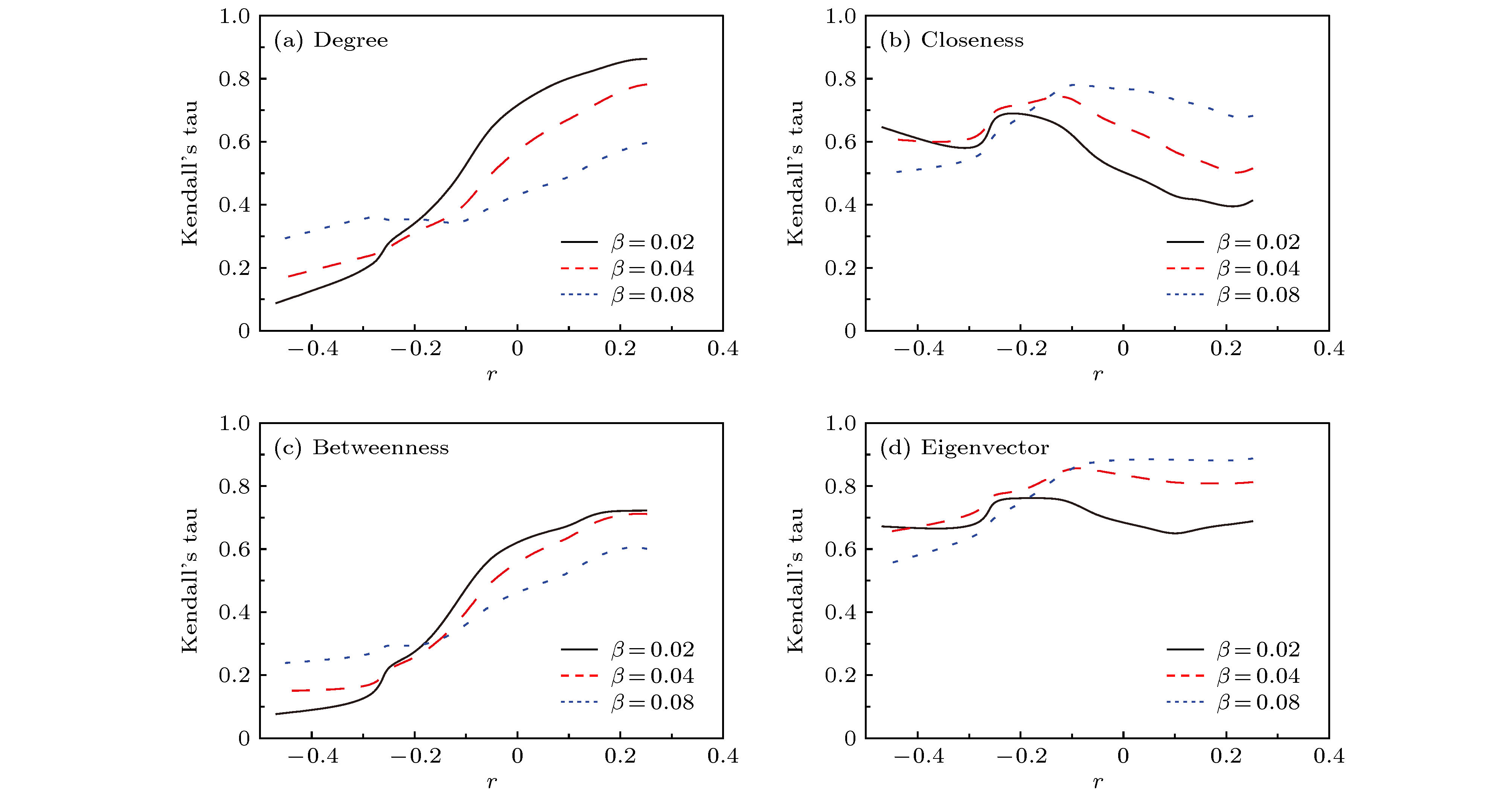
图 4 4种经典节点影响力算法(度、紧密度、介数、特征向量中心性)在可变度-度相关性的无标度网络中准确性, 其中β表示传播参数, r表示可变度-度相关性的无标度网络中的度- 度相关性参数, Kendall's tau值大小表示节点影响力方法的准确性

Fig. 4. The accuracy analysis of four centrality (degree, closeness, betweenness, eigenvector) methods on the scale-free network model with tunable assortative coefficient r and different infectious rate β.

下载: 全尺寸图片幻灯片

图 5 邻接矩阵的嵌套性示意图　(a) 邻接矩阵的嵌套值为0; (b) 邻接矩阵的嵌套值为0.5; (c) 邻接矩阵的嵌套值为1

Fig. 5. The nestedness of the adjacency matrix: (a) The nestedness of the adjacency matrix is 0; (b)the nestedness of the adjacency matrix is 0.5; (c)the nestedness of the adjacency matrix is 1.

下载: 全尺寸图片幻灯片

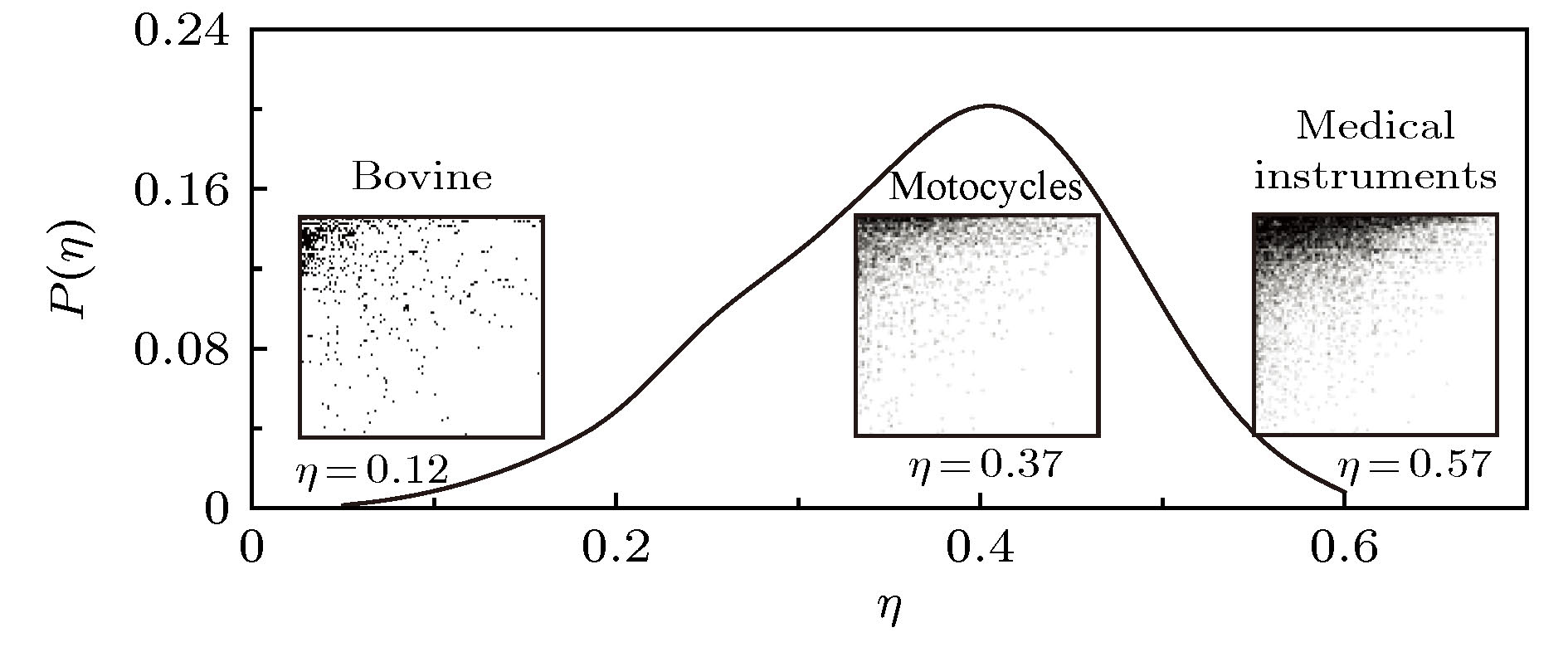
图 6 786类商品国际贸易网络的嵌套性分布图, 其中子图为牛肉、摩托车、医疗器械三类不同商品的国际贸易网络的可视化邻接矩阵

Fig. 6. Distribution of the nestedness in the international trade networks with 786 kinds of goods. (subgraphs) The matrices are representations of the different layer of world trade networks which respectively corresponds to the network of Bovine, Motorcycles, and Medical Instruments.

下载: 全尺寸图片幻灯片

map

[1]	Clauset A, Larremore D B, Sinatra R 2017 Science 355 477 Google Scholar
[2]	Ren Z M, Zeng A, Zhang Y C 2018 Phys. Rep. 750 1 Google Scholar
[3]	Lü L, Chen D, Ren X L, Zhang Q M, Zhang Y C, Zhou T 2016 Phys. Rep. 650 1 Google Scholar
[4]	Lynch C 2008 Nature 455 28 Google Scholar
[5]	Mariani M S, Ren Z M, Bascompte J, Tessone C J 2019 Physics Reports 813 1
[6]	Boccaletti S, Latora V, Moreno Y, Chavez M, Hwang D U 2006 Phys. Rep. 424 175 Google Scholar
[7]	Wang W, Tang M, Stanley H E, Braunstein L A 2017 Rep. Prog. Phys. 80 036603 Google Scholar
[8]	Zhang Z K, Liu C, Zhan X X, Lu X, Zhang C X, Zhang Y C 2016 Phys. Rep. 651 1 Google Scholar
[9]	Zeng A, Shen Z, Zhou J, Wu J, Fan Y, Wang Y, Stanley H E 2017 Phys. Rep. 714 1 Google Scholar
[10]	Schweitzer F, Fagiolo G, Sornette D, Vega-Redondo F, Vespignani A, White D R 2009 Science 325 422 Google Scholar
[11]	高见, 周涛 2016 电子科技大学学报 45 625 Google Scholar Gao J, Zhou T 2016 J. Univ. Elec. Sci. Tech. China 45 625 Google Scholar
[12]	Hidalgo C A 2018 Nat. Phys. 14 9 Google Scholar
[13]	Borgatti S P, Mehra A, Brass D J, Labianca G 2009 Science 323 892 Google Scholar
[14]	Newman M E J 2003 SIAM Rev. 45 167 Google Scholar
[15]	Gert S 1966 Psychometrika 31 581
[16]	Goh K I, Oh E, Kahng B, Kim D 2003 Phys. Rev. E 67 017101 Google Scholar
[17]	Borgatti S P 2005 Soc. Net. 27 55 Google Scholar
[18]	Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E 2010 Nat. Phys. 6 888 Google Scholar
[19]	任卓明, 邵凤, 刘建国, 郭强, 汪秉宏 2013 262 128901 Google Scholar Ren Z M, Shao F, Liu J G, Guo Q, Wang B H 2013 Acta Phys. Sin. 262 128901 Google Scholar
[20]	Chen D, Lü L, Shang M S, Zhang Y C, Zhou T 2012 Physica A 391 1777 Google Scholar
[21]	Zhang J, Xu X K, Li P, Zhang K, Small M 2011 Chaos 21 016107 Google Scholar
[22]	Comin C H, da Fontoura Costa L 2011 Phys. Rev. E 84 056105 Google Scholar
[23]	Poulin R, Boily M C, Masse B R 2000 Soc. Net. 22 187 Google Scholar
[24]	Pei S, Morone F, Makse H A 2018 Theories for Influencer Identification in Complex Networks. In: Lehmann S, Ahn YY. (Ed.) Complex Spreading Phenomena in Social Systems. Computational Social Sciences. Springer, Cham pp125–148
[25]	Garas A, Schweitzer F, Havlin S 2012 New J. Phys. 14 083030 Google Scholar
[26]	Zeng A, Zhang C J 2013 Phys. Lett. A 377 1031 Google Scholar
[27]	Lü L, Zhou T, Zhang Q M, Stanley H E 2016 Nat. Commun. 7 10168 Google Scholar
[28]	Travenolo B A N, Costa L F 2008 Phys. Lett. A 373 89 Google Scholar
[29]	Chen D B, Xiao R, Zeng A, Zhang Y C 2014 EPL 104 68006
[30]	Ren Z M, Zeng A, Chen D B, Liao H, Liu J G 2014 EPL 106 48005 Google Scholar
[31]	Bryan K, Leise T 2006 SIAM Rev. 48 569 Google Scholar
[32]	Berkhin P 2005 Internet Math. 2 73 Google Scholar
[33]	Lü L, Zhang Y C, Yeung C H, Zhou T 2011 PloS One 6 e21202 Google Scholar
[34]	Kleinberg J M 1999 JACM 46 604 Google Scholar
[35]	Newman M E J 2016 New Palg. Dict. Econ. 2016 1
[36]	Da Silva R A P, Viana M P, da Fontoura Costa L 2012 J. Stat. Mech. 2012 P07005 Google Scholar
[37]	任卓明, 刘建国, 邵凤, 胡兆龙, 郭强 2013 62 108902 Google Scholar Ren Z M, Liu J G, Shao F, Hu Z L, Guo Q 2013 Acta Phys. Sin. 62 108902 Google Scholar
[38]	刘建国, 任卓明, 郭强, 汪秉宏 2013 62 178901 Google Scholar Liu J G, Ren Z M, Guo Q, Wang B H 2013 Acta Phys. Sin. 62 178901 Google Scholar
[39]	任晓龙, 吕琳媛 2014 科学通报 59 1175 Google Scholar Ren X L, Lü L Y 2014 Chin. Sci. Bull. 59 1175 Google Scholar
[40]	Pei S, Makse H A 2013 J. Stat. Mech. 2013 P12002 Google Scholar
[41]	Holme P, Saramaki J 2012 Phys. Rep. 519 97 Google Scholar
[42]	Liao H, Mariani M S, Medo M, Zhang Y C, Zhou M Y 2017 Phys. Rep. 689 1 Google Scholar
[43]	Ercsey-Ravasz M, Toroczkai Z 2010 Phys. Rev. Lett. 105 038701 Google Scholar
[44]	Ercsey-Ravasz M, Lichtenwalter R N, Chawla N V, Toroczkai Z 2012 Phys. Rev. E 85 066103 Google Scholar
[45]	Lü L, Jin C H, Zhou T 2009 Phys. Rev. E 80 046122 Google Scholar
[46]	Mariani M S, Medo M, Zhang Y C 2015 Sci. Rep. 5 16181 Google Scholar
[47]	Mariani M S, Medo M, Zhang Y C 2016 J. Informetr. 10 1207 Google Scholar
[48]	Vaccario G, Medo M, Wider N, Mariani M S 2017 J. Informetr. 11 766 Google Scholar
[49]	Wasserman M, Zeng X H T, Amaral L A N 2015 PNAS 112 1281 Google Scholar
[50]	Wasserman M, Mukherjee S, Scott K, Zeng X H, Radicchi F, Amaral L A 2015 J. Asso. Info. Sci. Tech. 66 858 Google Scholar
[51]	Walker D, Xie H, Yan K K, Maslov S 2007 J. Stat. Mech. 2007 P06010 Google Scholar
[52]	Ren Z M, Mariani M S, Zhang Y C, Medo M 2018 Phys. Rev. E 97 052311 Google Scholar
[53]	Ren Z M 2018 Physica A 513 325 Google Scholar
[54]	Watts D J, Strogatz S H 1998 Nature 393 440 Google Scholar
[55]	Newman M E J 2003 Phys. Rev. E 67 026126 Google Scholar
[56]	Foster J G, Foster DV, Grassberger P, Paczuski M 2010 PNAS 107 10815 Google Scholar
[57]	Tian L, Bashan A, Shi D N, Liu Y Y 2017 Nat. Commun. 8 14223 Google Scholar
[58]	Arenas A, Diaz−Guilera A, Kurths J, Moreno Y, Zhou C 2008 Phys. Rep. 469 93 Google Scholar
[59]	Klemm K, Serrano M A, Eguiluz V M, San Miguel M 2012 Sci. Rep. 2 292 Google Scholar
[60]	Aral S, Walker D 2012 Science 337 337 Google Scholar
[61]	Centola D 2010 Science 329 1194 Google Scholar
[62]	Bond R M, Fariss C J, Jones J J, Kramer A D, Marlow C, Settle J E, Fowler J H 2012 Nature 489 295 Google Scholar
[63]	宋玉萍, 倪静 2016 65 028901 Google Scholar Song Y P, Ning J 2016 Acta Phys. Sin. 65 028901 Google Scholar
[64]	Ma S J, Ren Z M, Ye C M, Guo Q, Liu J G 2014 Inter. J. Mod. Phys. C 25 1450065 Google Scholar
[65]	邵凤, 郭强, 曾诗奇, 刘建国 2014 电子科技大学学报 43 174 Google Scholar Shao F, Guo Q, Zeng S Q, Liu J G 2014 J. Univ. Elec. Sci. Tech. China 43 174 Google Scholar
[66]	Lambiotte R, Rosvall M, Scholtes I 2018 arXiv preprint arXiv 1806 05977
[67]	Perri V, Scholtes I 2019 arXiv preprint arXiv 1908 05976
[68]	Xu J, Wickramarathne T L, Chawla N V 2016 Sci. Adv. 2 e1600028 Google Scholar
[69]	Tao J, Xu J, Wang C, Chawla N V 2017 IEEE Paci. Vis. Symp. (PacificVis) 2 1
[70]	Ghoshal G, Barabasi A L 2011 Nat. Commun. 2 394 Google Scholar
[71]	Lü L, Pan L, Zhou T, Zhang Y C, Stanley H E 2015 PNAS 112 2325 Google Scholar
[72]	Tacchella A, Mazzilli D, Pietronero L 2018 Nat. Phys. 14 861 Google Scholar
[73]	Cristelli M, Tacchella A, Pietronero L 2015 PloS One 10 e0117174 Google Scholar
[74]	Tacchella A, Cristelli M, Caldarelli G, Gabrielli A, Pietronero L 2012 Sci. Rep. 2 723 Google Scholar
[75]	Jara-Figueroa C, Jun B, Glaeser E L, Hidalgo C A 2018 PNAS 115 12646 Google Scholar
[76]	Hidalgo C A, Hausmann R 2009 PNAS 106 10570 Google Scholar
[77]	Hidalgo C A, Klinger B, Barabasi A L, Hausmann R 2007 Science 317 482 Google Scholar
[78]	Mariani M S, Vidmer A, Medo M, Zhang Y C 2015 Eur. Phys. J. B 88 293 Google Scholar
[79]	Wu R J, Shi G Y, Zhang Y C, Mariani M S 2016 Physica A 460 254 Google Scholar
[80]	Gao J, Zhou T 2018 Physica A 492 1591 Google Scholar
[81]	Gao J, Zhang Y C, Zhou T 2019 Phys. Rep. 817 1 Google Scholar
[82]	Almeida−Neto M, Guimaraes P, Guimaraes Jr P R, Loyola R D, Ulrich W 2008 Oikos 117 1227 Google Scholar
[83]	Mariani M S, Ren Z M, Bascompte J, Tessone C J 2019 Phys. Rep. 813 1 Google Scholar
[84]	Bustos S, Gomez C, Hausmann R, Hidalgo C A 2012 PloS One 7 e49393 Google Scholar
[85]	Liu J G, Lin J H, Guo Q, Zhou T 2016 Sci. Rep. 6 21380 Google Scholar
[86]	Barzel B, Barabasi A L 2013 Nat. Phys. 9 673 Google Scholar
[87]	Barzel B, Barabasi A L 2016 Nature 530 307 Google Scholar
[88]	Medo M 2014 Phys. Rev. E 89 032801 Google Scholar
[89]	Medo M, Cimini G, Gualdi S 2011 Phys. Rev. Lett. 107 238701 Google Scholar
[90]	Ren Z M, Shi Y Q, Liao H 2016 Physica A 453 236 Google Scholar

[1]	李江, 刘影, 王伟, 周涛. 识别高阶网络传播中最有影响力的节点. , 2024, 73(4): 048901. doi: 10.7498/aps.73.20231416
[2]	韩忠明, 李胜男, 郑晨烨, 段大高, 杨伟杰. 基于动态网络表示的链接预测. , 2020, 69(16): 168901. doi: 10.7498/aps.69.20191162
[3]	康玲, 项冰冰, 翟素兰, 鲍中奎, 张海峰. 基于区域密度曲线识别网络上的多影响力节点. , 2018, 67(19): 198901. doi: 10.7498/aps.67.20181000
[4]	王雨, 郭进利. 基于多重影响力矩阵的有向加权网络节点重要性评估方法. , 2017, 66(5): 050201. doi: 10.7498/aps.66.050201
[5]	阮逸润, 老松杨, 王竣德, 白亮, 侯绿林. 一种改进的基于信息传播率的复杂网络影响力评估算法. , 2017, 66(20): 208901. doi: 10.7498/aps.66.208901
[6]	韩忠明, 陈炎, 李梦琪, 刘雯, 杨伟杰. 一种有效的基于三角结构的复杂网络节点影响力度量模型. , 2016, 65(16): 168901. doi: 10.7498/aps.65.168901
[7]	胡庆成, 张勇, 许信辉, 邢春晓, 陈池, 陈信欢. 一种新的复杂网络影响力最大化发现方法. , 2015, 64(19): 190101. doi: 10.7498/aps.64.190101
[8]	闵磊, 刘智, 唐向阳, 陈矛, 刘三(女牙). 基于扩展度的复杂网络传播影响力评估算法. , 2015, 64(8): 088901. doi: 10.7498/aps.64.088901
[9]	舒盼盼, 王伟, 唐明, 尚明生. 花簇分形无标度网络中节点影响力的区分度. , 2015, 64(20): 208901. doi: 10.7498/aps.64.208901
[10]	苏晓萍, 宋玉蓉. 利用邻域“结构洞”寻找社会网络中最具影响力节点. , 2015, 64(2): 020101. doi: 10.7498/aps.64.020101
[11]	赵佳, 喻莉, 李静茹. 社交网络中基于贝叶斯和半环代数模型的节点影响力计算机理. , 2013, 62(13): 130201. doi: 10.7498/aps.62.130201
[12]	胡庆成, 尹龑燊, 马鹏斐, 高旸, 张勇, 邢春晓. 一种新的网络传播中最有影响力的节点发现方法. , 2013, 62(14): 140101. doi: 10.7498/aps.62.140101
[13]	苑卫国, 刘云, 程军军, 熊菲. 微博双向关注网络节点中心性及传播影响力的分析. , 2013, 62(3): 038901. doi: 10.7498/aps.62.038901
[14]	赵岩岩, 蒋国平. 一类输出耦合时延复杂动态网络故障诊断研究. , 2011, 60(11): 110206. doi: 10.7498/aps.60.110206
[15]	卢静, 张荣, 徐振源. 振幅耦合动态网络中相邻结点间的相同步. , 2010, 59(9): 5949-5953. doi: 10.7498/aps.59.5949
[16]	闫小勇, 王明生. 增长速度对合作网络参与者节点度分布的影响. , 2010, 59(2): 851-858. doi: 10.7498/aps.59.851
[17]	熊菲, 刘云, 司夏萌, 丁飞. 基于Web 2.0的边与节点同时增长网络模型. , 2010, 59(10): 6889-6895. doi: 10.7498/aps.59.6889
[18]	罗群, 高雅, 齐雅楠, 吴桐, 许欢, 李丽香, 杨义先. 融合复杂动态网络的模型参考自适应同步研究. , 2009, 58(10): 6809-6817. doi: 10.7498/aps.58.6809
[19]	高洋, 李丽香, 彭海朋, 杨义先, 张小红. 多重边融合复杂动态网络的自适应同步. , 2008, 57(4): 2081-2091. doi: 10.7498/aps.57.2081
[20]	李季, 汪秉宏, 蒋品群, 周涛, 王文旭. 节点数加速增长的复杂网络生长模型. , 2006, 55(8): 4051-4057. doi: 10.7498/aps.55.4051

计量

文章访问数: 13127
PDF下载量: 409
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

动态复杂网络中节点影响力的研究进展