-
利用自旋噪声谱技术研究了无缓冲气体133Cs原子气室的自旋动力学和展宽机制. 在宏观原子气室中, 自旋弛豫速率失谐频率谱的线型为高斯分布; 在空间局域较强的微米气室中, 自旋弛豫速率失谐频率谱的线型为洛伦兹分布. 实验测量得到的自旋弛豫速率失谐频率谱的展宽约4 GHz, 明显大于宏观原子气室中约500 MHz的多普勒非均匀展宽. 同时, 研究了两种气室的总噪声的失谐频率谱. 在宏观原子气室中, 总噪声强度强烈依赖于激光相对于原子共振跃迁的频率失谐; 在微米气室中, 由于较强的均匀展宽, 总噪声的失谐频率谱中心处出现明显的凹陷. 通过建立简化的物理模型来计算微米气室的展宽机制, 在实验与理论中解释了原子的均匀展宽特性.In this paper, the spin dynamics and broadening mechanism of cesium vapor in cells without buffer gas is investigated by means of spin noise spectroscopy. In a macro atomic vapor cell, the lineshape of detuning frequency spectrum of spin relaxation rate is of Gaussian distribution. For a micron-scaled vapor cell with strong spatial locality, the lineshape of detuning frequency spectrum of spin relaxation rate is of Lorentzian distribution. The parameter dependence of detuning frequency spectrum of spin relaxation rate, such as temperature, is studied quantitatively. The detuning frequency spectrum of the spin relaxation rate is measured experimentally to be broadened by
$ \sim $ 4 GHz, which is obviously larger than the unhomogeneous Doppler broadening of$ \sim $ 500 MHz for a macro atomic vapor cell. At the same time, the detuning frequency spectrum of total noise in the two atomic vapor cells is studied. In the macro atomic vapor cell, the total noise intensity strongly relies on the detuning frequency of the laser with respect to the atomic resonance transition. In the micron-scaled vapor cell, due to the strong homogeneous broadening, the center of the detuning frequency spectrum of the total noise is observed to dip. Finally, a simplified physical model is established to compute the broadening of the micron-scaled vapor cell. The homogeneous broadening of atoms is explained experimentally and theoretically in the micron-scaled vapor cell.[1] Kubo R 1966 Rep. Prog. Phys. 29 255
Google Scholar
[2] Römer M, Hübner J, Oestreich M 2007 Rev. Sci. Instrum. 78 103903
Google Scholar
[3] Sørensen J L, Hald J, Polzik E S 1998 Phys Rev. Lett. 80 3487
Google Scholar
[4] Crooker S A, Rickel D G, Balatsky A V, Smith D L 2004 Nature 431 49
Google Scholar
[5] Oestreich M, Römer M, Haug R J, Hägele D 2005 Phys. Rev. Lett. 95 216603
Google Scholar
[6] Sterin P, Wiegand J, Hübner Jens, Oestreich M 2018 Phys. Rev. Appl. 9 034003
Google Scholar
[7] Lucivero V G, Jiménez-Martínez Ricardo, Kong J, Mitchell M W 2016 Phys. Rev. A. 93 053802
Google Scholar
[8] 史平, 马健, 钱轩, 姬杨, 李伟 2017 66 017201
Google Scholar
Shi P, Ma J, Qian X, Ji Y, Li W 2017 Acta Phys. Sin. 66 017201
Google Scholar
[9] Roy D, Yang L, Crooker S A, Sinitsyn N A 2015 Sci. Rep. 5 9573
Google Scholar
[10] Petrov M Y, Kamenskii A N, Zapasskii V S, Bayer M, Greilich A 2018 Phys. Rev. B 97 125202
Google Scholar
[11] Cronenberger S, Scalbert D 2016 Rev. Sci. Instrum. 87 093111
Google Scholar
[12] 李晨, 丁畅, 张桐耀, 曹丹华, 吴裕斌, 陈院森 2017 量子光学学报 23 228
Li C, Ding C, Zhang T Y, Cao D H, Wu Y B, Chen Y S 2017 J. Quant. Opt. 23 228
[13] Müller G M, Römer M, Hübner J, Oestreich M 2010 App. Phys. Lett. 97 192109
Google Scholar
[14] Poltavtsev S V, Ryzhov I I, Glazov M M, Kozlov G G, Zapasskii V S, Kavokin A V, Lagoudakis P G, Smirnov D S, Ivchenko E L 2014 Phys. Rev. B 89 081304
Google Scholar
[15] Pershin Y V, Slipko V A, Roy D, Sinitsyn N A 2013 Appl. Phys. Lett. 102 202405
Google Scholar
[16] Dahbashi R, Hübner J, Berski F, Pierz K, Oestreich M 2014 Phys. Rev. Lett. 112 156601
Google Scholar
[17] Yang L, Glasenapp P, Greilich A, Reuter D, Wieck A D, Yakovlev D R, Bayer M, Crooker S A 2014 Nat. Commun. 5 4949
Google Scholar
[18] Crooker S A, Brandt J, Sandfort C, Greilich A, Yakovlev D R, Reuter D, Wieck A D, Bayer M 2010 Phys. Rev. Lett. 104 036601
Google Scholar
[19] Kozlov G G, Ryzhov I I, Zapasskii V S 2017 Phys. Rev. A 95 043810
Google Scholar
[20] Kozlov G G, Ryzhov I I, Zapasskii V S 2018 Phys. Rev. A 97 013848
Google Scholar
[21] Keaveney J 2013 Ph. D. Dissertation (Durham: Durham University)
[22] Ma J, Shi P, Qian X, Li W, Ji Y 2016 Chin. Phys. B 25 117203
Google Scholar
[23] Hübner J, Berski F, Dahbashi R, Oestreich M 2014 Phys. Status. Solidi. 251 1824
Google Scholar
[24] Petrov M Y, Ryzhov I I, Smirnov D S, Belyaev L Y, Potekhin R A, Glazov M M, Kulyasov V N, Kozlov G G, Aleksandrov E B, Zapasskii1 V S 2018 Phys. Rev. A 97 032502
Google Scholar
[25] Zapasskii V S, Greilich A, Crooker S A, Li Y, Kozlov G G, Yakovlev D R, Reuter D, Wieck A D, Bayer M 2013 Phys. Rev. Lett. 110 176601
Google Scholar
[26] Ghosh R K 2009 Ph. D. Dissertation (Princeton: Princeton University)
[27] Rajroop J 2018 Ph. D. Dissertation (London: University College London)
[28] Christopher J F 2005 Atomic Physics (Oxford: Oxford University Press) p142
[29] Ma J, Shi P, Qian X, Shang Y, Ji Y 2017 Sci. Rep. 7 10238
Google Scholar
[30] Buckingham A D, Stephens P J 1966 Annu. Rev. Phys. Chem. 17 399
Google Scholar
[31] Zapasskii V S 2013 Adv. Opt. Photon. 5 131
Google Scholar
[32] 尚雅轩, 马健, 史平, 钱轩, 李伟, 姬杨 2018 67 087201
Google Scholar
Shang Y X, Ma J, Shi P, Qian X, Li W, Ji Y 2018 Acta Phys. Sin. 67 087201
Google Scholar
[33] Chalupczak W, Godun R M 2011 Phys. Rev. A. 83 032512
Google Scholar
[34] Zhang W J, You L X, Li H, Huang J, Lv C L, Zhang L, Liu X Y, Wu J J, Wang Z, Xie X M 2017 Sci: China Phys. Mech. Astron. 60 120314
Google Scholar
[35] Yang W H, Shi S P, Wang Y J, Ma W G, Zheng Y H, Peng K C 2017 Opt. Lett. 42 21
Google Scholar
-
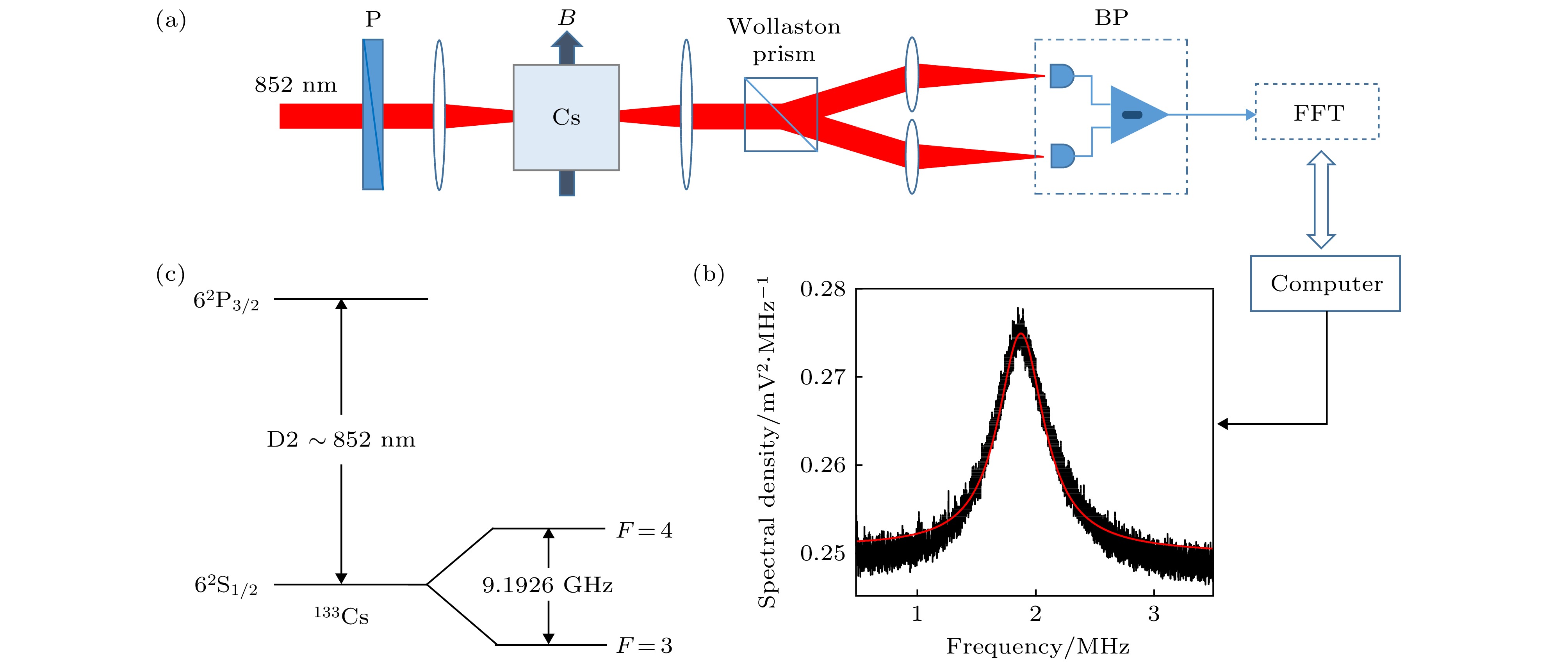
图 1 (a)自旋噪声谱的实验原理图(P是偏振片, B是外加磁场, Wollaston prism是沃拉斯顿棱镜, BP是平衡零拍探测器, FFT是快速傅里叶变换); (b)气室1中经典的133Cs自旋噪声谱(激光失谐频率ΩD2 = + 600 MHz于D2线(62S1/2 (F = 4) → 62P3/2), 原子气室温度T = 296 K, 激光功率P = 500 μW, 外加磁场B = 5 G); (c) 133Cs的D2跃迁线和基态超精细结构
Fig. 1. (a) Schematic of the experimental apparatus (P-polarizer, B-magnetic fields, BP-balanced homodyne detector, FFT-fast Fourier transform); (b) typical spin noise spectrum of 133Cs in cell 1 (the laser is detuned ΩD2 = + 600 MHz from the D2 transition (62S1/2 (F = 4) → 62P3/2). The temperature of atomic cell is 296 K. The laser power P = 500 μW. Magnetic field B = 5 G); (c) D2 line transition and ground-state hyperfine structure of 133Cs.
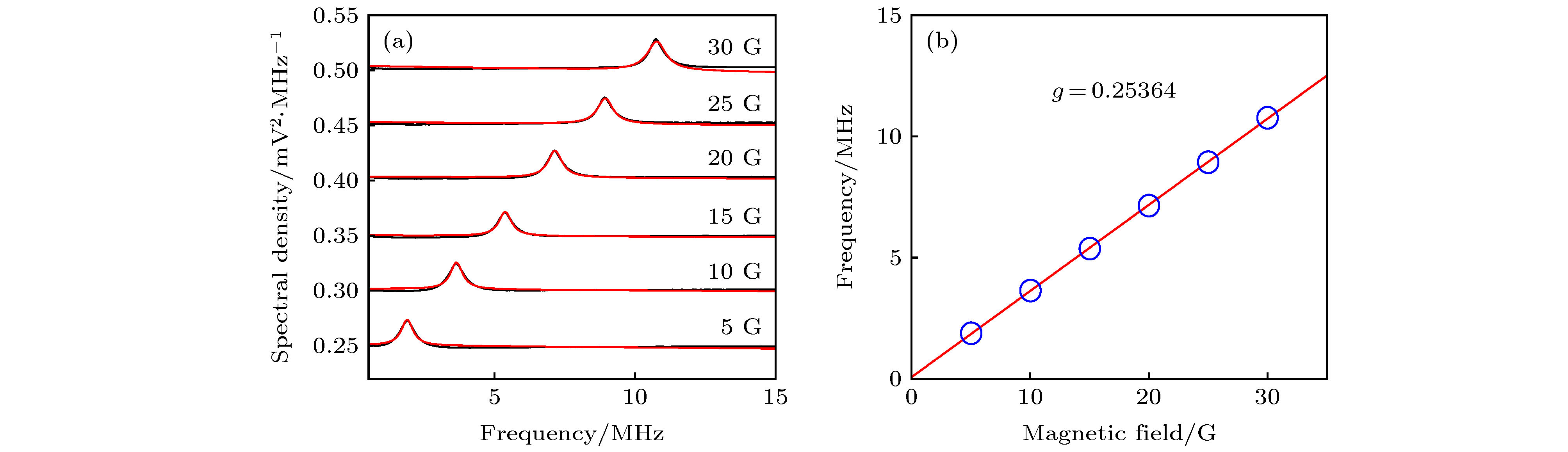
图 2 气室1中磁场相关的自旋噪声谱 (a)不同磁场下的自旋噪声谱(黑线)和拟合曲线(红线); (b)自旋噪声谱中心频率(蓝圆圈)与外场关系图, 以及拟合曲线(红线); 激光失谐频率ΩD2 = + 600 MHz于D2线(62S1/2 (F = 4) → 62P3/2), 激光功率为P = 500 μW, 原子气室温度T = 296 K
Fig. 2. Magnetic-field dependent spin noise spectrum in cell 1: (a) Spin noise spectrum (black lines) and fitting curve (red lines) versus the magnetic fields; (b) dependence of center frequency of spin noise spectrum on magnetic fields. The blue circles are the experimental data. The red line is the fitting curve. The laser is detuned ΩD2 = + 600 MHz from the D2 transition (62S1/2 (F = 4) → 62P3/2). The laser power P = 500 μW. The temperature of atomic cell is 296 K.
图 3 气室1中自旋噪声谱的失谐频率依赖关系 (a)自旋弛豫速率与失谐频率的对应关系图; (b)总噪声与失谐频率的对应关系图; 激光失谐频率在D2线(62S1/2 (F = 3) → 62P3/2)附近, 激光功率P = 500 μW, 外磁场B = 15 G, 实验数据为(蓝圆圈)和拟合曲线(红线), 原子气室温度T = 296 K
Fig. 3. Detuning frequency dependent spin noise spectrum in cell 1: (a) Spin relaxation rate versus the detuning frequency; (b) total noise versus the detuning frequency. The laser is detuned from the D2 transition (62S1/2 (F = 3) → 62P3/2). The laser power P = 500 μW. Magnetic field B = 15 G. The blue circles are the experimental data. The red line is the fitting curve. The temperature of atomic cell is 296 K.
图 4 气室2中自旋噪声谱的失谐频率依赖关系 (a) T = 387 K时自旋弛豫速率与失谐频率的关系; (b) T = 431 K时自旋弛豫速率与失谐频率的关系; (c) T = 387 K时总噪声与失谐频率的关系; (d) T = 431 K时总噪声与失谐频率的关系; 激光失谐频率在D2线(62S1/2 (F = 3) → 2P3/2)附近, 激光功率为P = 5 mW, 蓝圆圈表示实验数据, 红线为拟合曲线
Fig. 4. The detuning frequency dependent spin noise spectrum in cell 2: (a) Spin relaxation rate versus the detuning frequency at T = 387 K; (b) spin relaxation rate versus the detuning frequency at T = 431 K; (c) total noise versus the detuning frequency at T = 387 K; (d) total noise versus the detuning frequency at T = 431 K. The laser is detuned from the D2 transition (62S1/2 (F = 3) → 62P3/2). The laser power P = 5 mW. The blue circles are the experimental data, and the red line is the fitting curve.
-
[1] Kubo R 1966 Rep. Prog. Phys. 29 255
Google Scholar
[2] Römer M, Hübner J, Oestreich M 2007 Rev. Sci. Instrum. 78 103903
Google Scholar
[3] Sørensen J L, Hald J, Polzik E S 1998 Phys Rev. Lett. 80 3487
Google Scholar
[4] Crooker S A, Rickel D G, Balatsky A V, Smith D L 2004 Nature 431 49
Google Scholar
[5] Oestreich M, Römer M, Haug R J, Hägele D 2005 Phys. Rev. Lett. 95 216603
Google Scholar
[6] Sterin P, Wiegand J, Hübner Jens, Oestreich M 2018 Phys. Rev. Appl. 9 034003
Google Scholar
[7] Lucivero V G, Jiménez-Martínez Ricardo, Kong J, Mitchell M W 2016 Phys. Rev. A. 93 053802
Google Scholar
[8] 史平, 马健, 钱轩, 姬杨, 李伟 2017 66 017201
Google Scholar
Shi P, Ma J, Qian X, Ji Y, Li W 2017 Acta Phys. Sin. 66 017201
Google Scholar
[9] Roy D, Yang L, Crooker S A, Sinitsyn N A 2015 Sci. Rep. 5 9573
Google Scholar
[10] Petrov M Y, Kamenskii A N, Zapasskii V S, Bayer M, Greilich A 2018 Phys. Rev. B 97 125202
Google Scholar
[11] Cronenberger S, Scalbert D 2016 Rev. Sci. Instrum. 87 093111
Google Scholar
[12] 李晨, 丁畅, 张桐耀, 曹丹华, 吴裕斌, 陈院森 2017 量子光学学报 23 228
Li C, Ding C, Zhang T Y, Cao D H, Wu Y B, Chen Y S 2017 J. Quant. Opt. 23 228
[13] Müller G M, Römer M, Hübner J, Oestreich M 2010 App. Phys. Lett. 97 192109
Google Scholar
[14] Poltavtsev S V, Ryzhov I I, Glazov M M, Kozlov G G, Zapasskii V S, Kavokin A V, Lagoudakis P G, Smirnov D S, Ivchenko E L 2014 Phys. Rev. B 89 081304
Google Scholar
[15] Pershin Y V, Slipko V A, Roy D, Sinitsyn N A 2013 Appl. Phys. Lett. 102 202405
Google Scholar
[16] Dahbashi R, Hübner J, Berski F, Pierz K, Oestreich M 2014 Phys. Rev. Lett. 112 156601
Google Scholar
[17] Yang L, Glasenapp P, Greilich A, Reuter D, Wieck A D, Yakovlev D R, Bayer M, Crooker S A 2014 Nat. Commun. 5 4949
Google Scholar
[18] Crooker S A, Brandt J, Sandfort C, Greilich A, Yakovlev D R, Reuter D, Wieck A D, Bayer M 2010 Phys. Rev. Lett. 104 036601
Google Scholar
[19] Kozlov G G, Ryzhov I I, Zapasskii V S 2017 Phys. Rev. A 95 043810
Google Scholar
[20] Kozlov G G, Ryzhov I I, Zapasskii V S 2018 Phys. Rev. A 97 013848
Google Scholar
[21] Keaveney J 2013 Ph. D. Dissertation (Durham: Durham University)
[22] Ma J, Shi P, Qian X, Li W, Ji Y 2016 Chin. Phys. B 25 117203
Google Scholar
[23] Hübner J, Berski F, Dahbashi R, Oestreich M 2014 Phys. Status. Solidi. 251 1824
Google Scholar
[24] Petrov M Y, Ryzhov I I, Smirnov D S, Belyaev L Y, Potekhin R A, Glazov M M, Kulyasov V N, Kozlov G G, Aleksandrov E B, Zapasskii1 V S 2018 Phys. Rev. A 97 032502
Google Scholar
[25] Zapasskii V S, Greilich A, Crooker S A, Li Y, Kozlov G G, Yakovlev D R, Reuter D, Wieck A D, Bayer M 2013 Phys. Rev. Lett. 110 176601
Google Scholar
[26] Ghosh R K 2009 Ph. D. Dissertation (Princeton: Princeton University)
[27] Rajroop J 2018 Ph. D. Dissertation (London: University College London)
[28] Christopher J F 2005 Atomic Physics (Oxford: Oxford University Press) p142
[29] Ma J, Shi P, Qian X, Shang Y, Ji Y 2017 Sci. Rep. 7 10238
Google Scholar
[30] Buckingham A D, Stephens P J 1966 Annu. Rev. Phys. Chem. 17 399
Google Scholar
[31] Zapasskii V S 2013 Adv. Opt. Photon. 5 131
Google Scholar
[32] 尚雅轩, 马健, 史平, 钱轩, 李伟, 姬杨 2018 67 087201
Google Scholar
Shang Y X, Ma J, Shi P, Qian X, Li W, Ji Y 2018 Acta Phys. Sin. 67 087201
Google Scholar
[33] Chalupczak W, Godun R M 2011 Phys. Rev. A. 83 032512
Google Scholar
[34] Zhang W J, You L X, Li H, Huang J, Lv C L, Zhang L, Liu X Y, Wu J J, Wang Z, Xie X M 2017 Sci: China Phys. Mech. Astron. 60 120314
Google Scholar
[35] Yang W H, Shi S P, Wang Y J, Ma W G, Zheng Y H, Peng K C 2017 Opt. Lett. 42 21
Google Scholar
下载:
计量
- 文章访问数: 9674
- PDF下载量: 142
- 被引次数: 0
