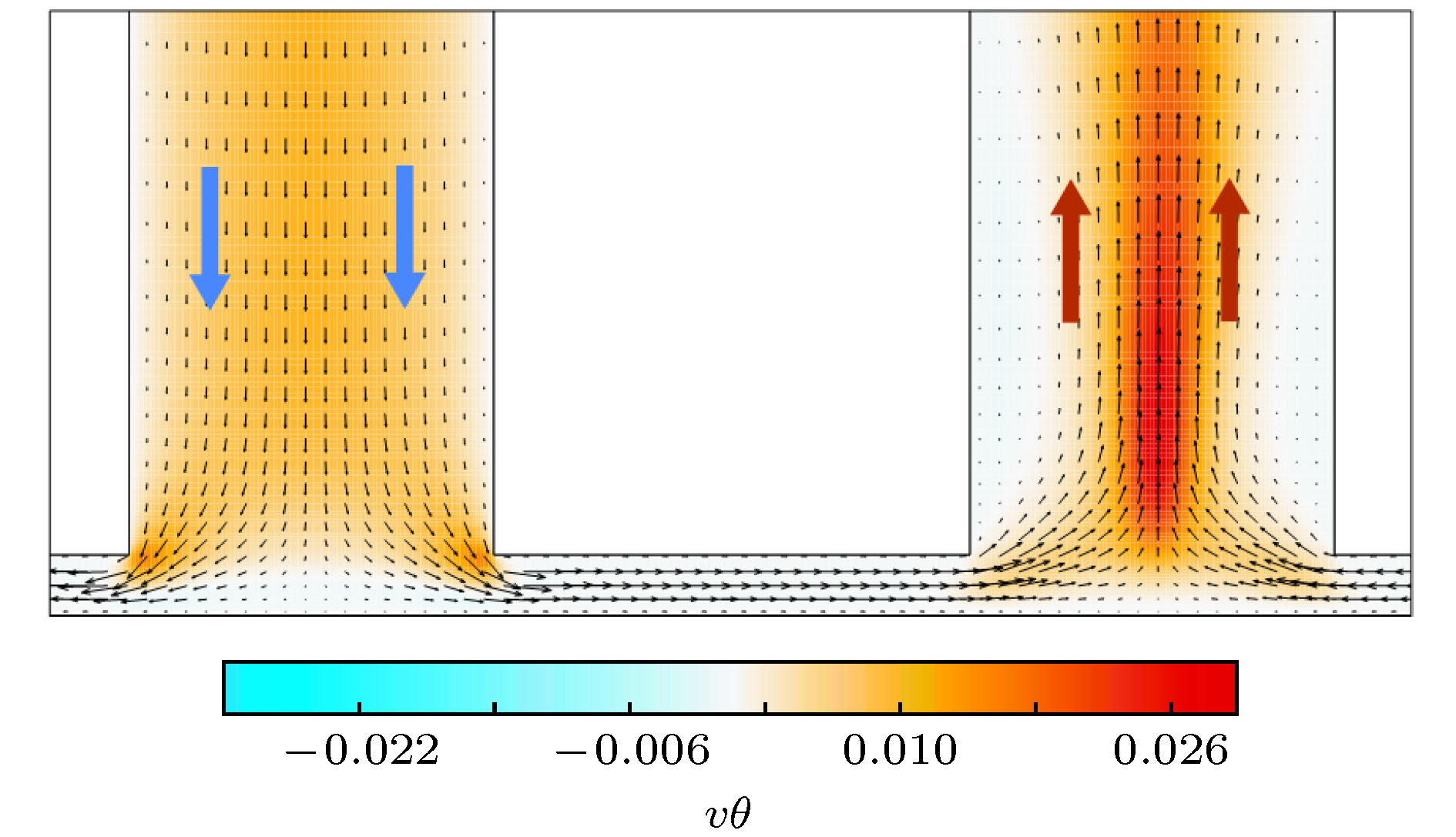
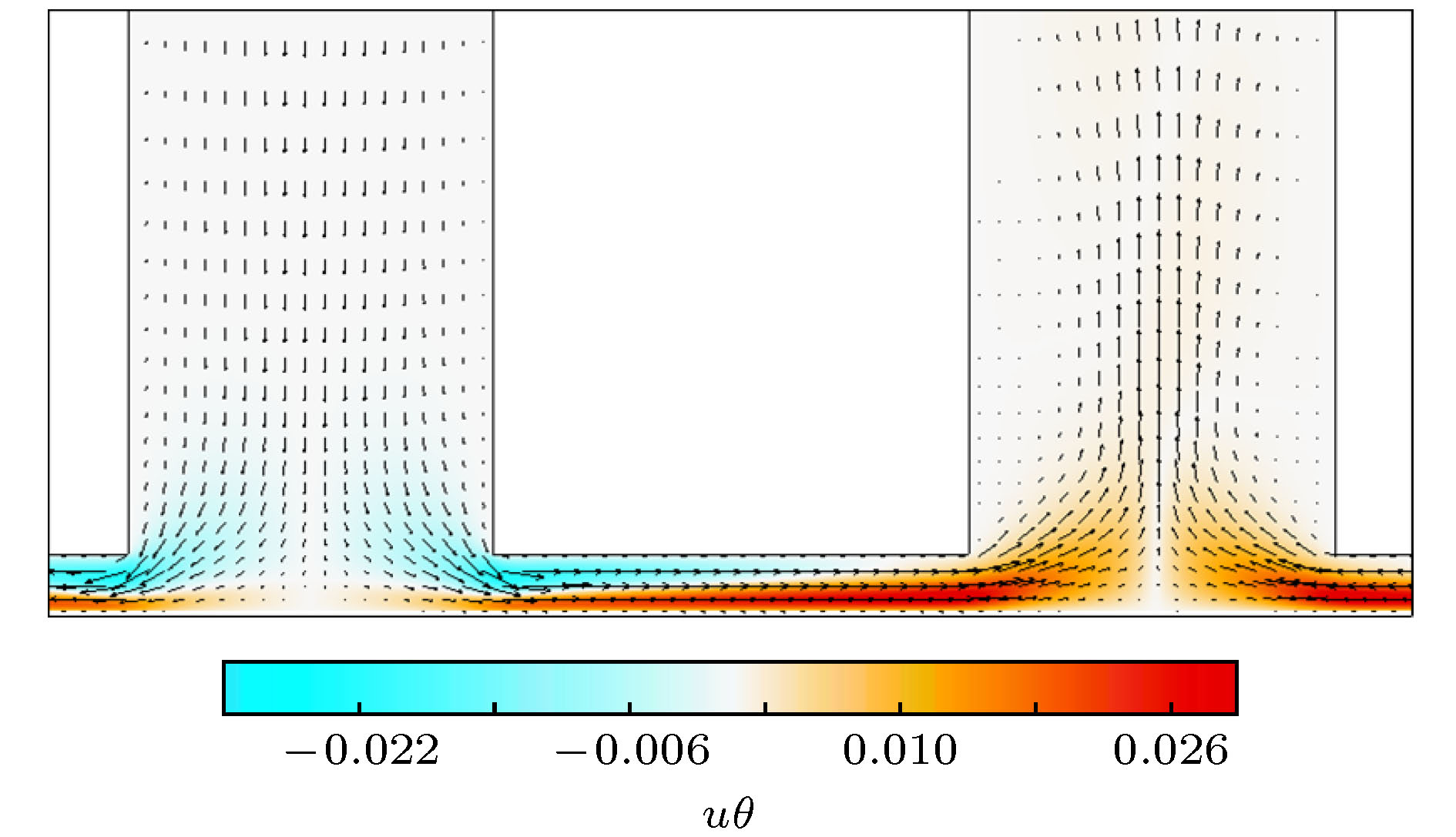
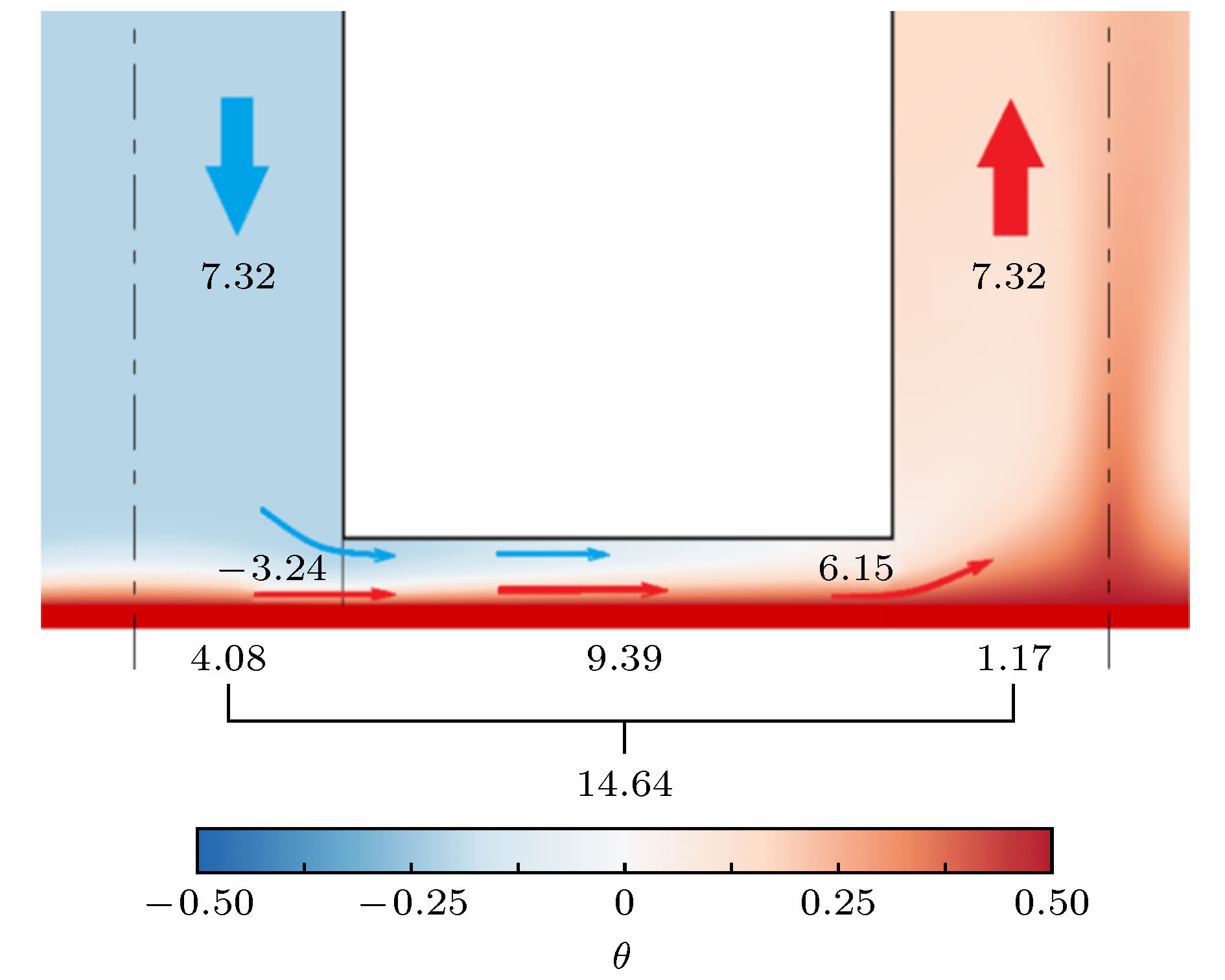
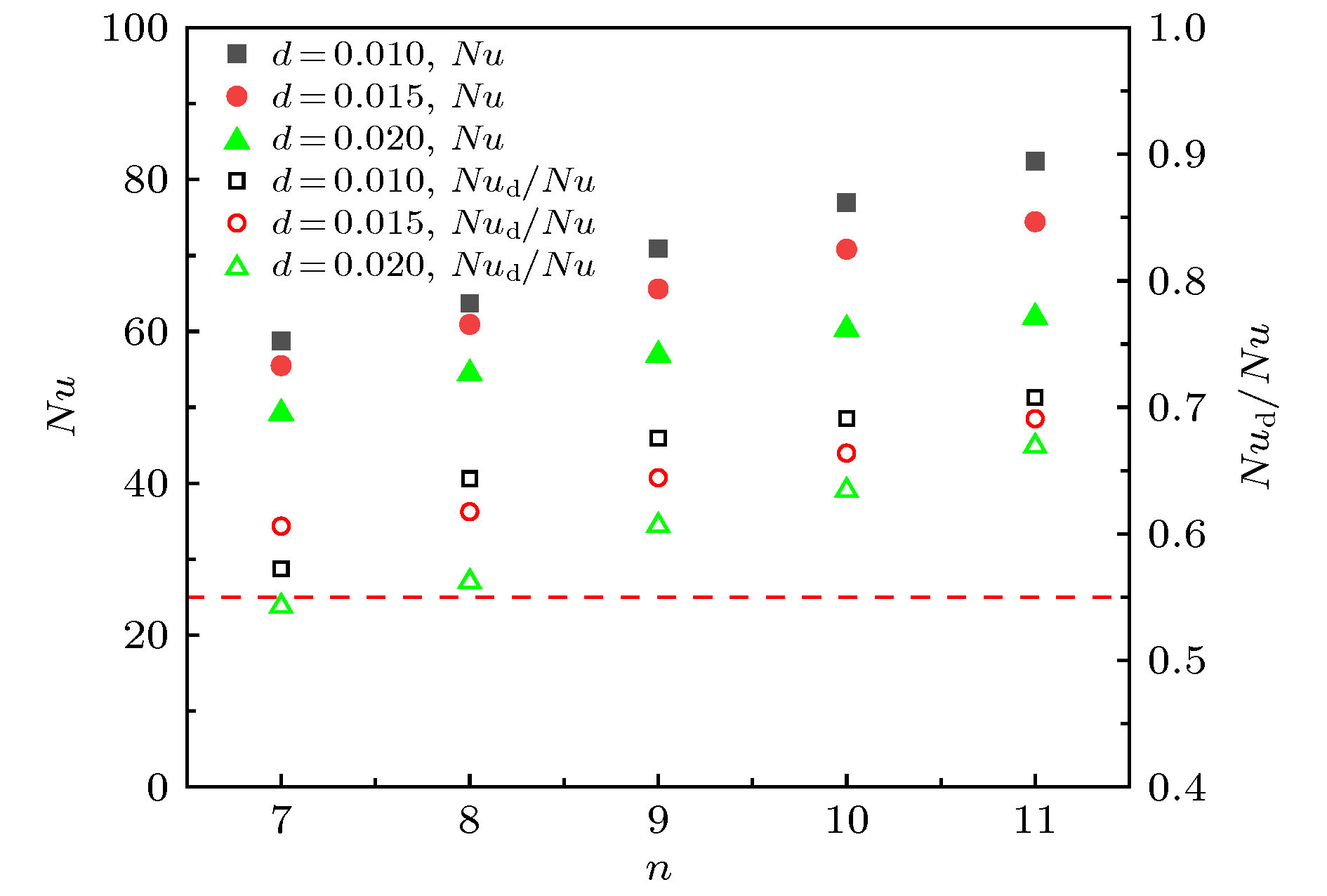
-
采用DNS方法对隔板对流装置进行模拟计算, 研究系统中热流特性以及热量输入与传递特性. 讨论了热流的纵向和横向输运特性, 在此基础上对传热通道和狭缝区域的热通量以及对应底板外界输入热通量进行了定量化分析. 研究结果表明, 通道中低温流体向下冲击底板而后转入水平运动, 流入狭缝区域并不断被加热, 只进行水平的热量输运. 流出狭缝后的高温流体在传热通道中汇聚形成向上喷流, 进行热量传递. 水平热量输运的区域对应的底板外界输入的热通量很大, 占总输入热通量的92%, 狭缝区域底板外界输入热通量占总量的64%, 纵向热量传递区域对应底板外界输入热通量很小. 不同几何参数隔板对流系统都具有增强传热效果, 狭缝高度较小时对应的增强效果较强. 隔板数n = 11及狭缝高度d = 0.01时系统传热Nu数值最大, 是无隔板时的3倍以上.How to improve the heat transfer efficiency of the system is always a hot issue in thermal convection research field. It is found that when the partitions are added at equal distances to the classical physical model -- Rayleigh-Bénard convection system and gaps are left between the horizontal plates and partitions, the heat transfer efficiency of the system increases significantly with the number of partitions increasing. The heat transfer efficiency can reach up to 3.1 times that of the non-partition device with the specific geometric parameters. In this paper, the Direct Numerical Simulation (DNS) method is used to simulate the partitioned convection system. The mechanism of the heat transfer enhancement of the system is analyzed by studying the characteristics of the heat flow as well as the heat conduction and transport in the system. After the flow in partitioned convection system is fully developed, the fluid in each channel moves vertically in alternating direction and the upward(downward) channel has a higher(lower) temperature than the average temperature of the cell. Due to the symmetry of the system, only the bottom region of the low temperature channel, the bottom region of the high temperature channel and the gap region connecting these two channels are selected for research. By discussing the lateral and longitudinal transport processes of heat flow in the above three regions, the heat flux in the channels and gap areas of the system are studied by quantitative analysis. The results show that the low-temperature fluid in the channel impacts on the bottom plate and then moves into the gap area; the fluid is continuously heated by the bottom plate and flows out of gap area with high temperature. Finally, the fluid converges in the heat transfer channel and forms a longitudinal jet. The external input heat flux of the area that has only horizontal heat transport is large, accounting for 92% of the total heat flux which is obtained from the bottom plate. The heat flux of gap area accounts for 64% of the total heat flux, but the external input heat flux of the area that has only longitudinal heat transport is smaller. The convection system with different geometric parameters has the effect of enhancing heat transfer efficiency, and enhancement capability of the system is stronger when the height of gaps is smaller. When the number of partitions n = 11 and the height of gap d = 0.01, the value of the global Nu number is largest, Nu = 82, which is more than three times that of the system without partitions.
-
Keywords:
- partitioned convection system /
- heat flow /
- heat flux /
- heat conduction and transport /
- enhancement of heat transfer
[1] Lappa M 2005 Cryst. Res. Technol. 40 531
Google Scholar
[2] Bodenschatz E, Pesch W, Ahlers G 2000 Annu. Rev. Fluid Mech. 32 709
Google Scholar
[3] Ahlers G, Grossmann S, Lohse D 2009 Rev. Mod. Phys. 81 503
Google Scholar
[4] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[5] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[6] Shishkina O, Horn S, Wagner S, Ching E S C 2015 Phys. Rev. Lett. 114 114302
Google Scholar
[7] Weiss S, He X, Ahlers G, Bodenschatz E, Shishkina O 2018 J. Fluid Mech. 851 374
Google Scholar
[8] Zhao J, Cai W, Jiang Y 2019 Int. J. Heat Mass Transfer 129 599
Google Scholar
[9] Urban P, Hanzelka P, Králík T, Macek M, Musilová V, Skrbek L 2019 Phys. Rev. E 99 011101
Google Scholar
[10] Zhong J Q, Stevens R J, Clercx H J, Verzicco R, Lohse D, Ahlers G 2009 Phys. Rev. Lett. 102 044502
Google Scholar
[11] Stevens R J, Clercx H J, Lohse D 2013 Eur. J. Mech. Fluids 40 41
Google Scholar
[12] Liu Y, Ecke R E 1997 Phys. Rev. Lett. 79 2257
Google Scholar
[13] Kunnen R P J, Clercx H J H, Geurts B J 2006 Phys. Rev. E 74 056306
Google Scholar
[14] Kunnen R P J, Clercx H J H, Geurts B J 2008 Europhys. Lett. 84 24001
Google Scholar
[15] Du Y B, Tong P 1998 Phys. Rev. Lett. 81 987
Google Scholar
[16] Stringano G, Pascazio G, Verzicco R 2006 J. Fluid Mech. 557 307
Google Scholar
[17] Xu F, Patterson J C, Lei C 2009 Int. J. Heat Mass Transfer 52 620
Google Scholar
[18] Bao Y, Chen J, Liu B F, She Z S, Zhang J, Zhou Q 2015 J. Fluid Mech. 784 R5
[19] 包芸, 林泽鹏, 丁广裕 2017 计算机辅助工程 26 57
Bao Y, Lin Z P, Ding G Y 2017 Comput. Aided Eng. 26 57
[20] 林泽鹏, 包芸 2018 中国科学: 物理学 力学 天文学 48 054702
Lin Z P, Bao Y 2018 Sci. Sin. Phys. Mech. Astron. 48 054702
[21] 林泽鹏, 包芸 2018 中国科学: 物理学 力学 天文学 48 104702
Lin Z P, Bao Y 2018 Sci. Sin. Phys. Mech. Astron. 48 104702
[22] 林泽鹏, 徐圣卓, 包芸 2019 水动力学研究与进展(A辑) 34 193
Google Scholar
Lin Z P, Xu S Z, Bao Y 2019 Chin. J. Hydrodynam. 34 193
Google Scholar
[23] 包芸, 林泽鹏, 何鹏 2019 中国科学: 物理学 力学 天文学 49 044701
Bao Y, Lin Z P, He P 2019 Sci. Sin. Phys. Mech. Astron. 49 044701
[24] Lin Z P, Bao Y 2019 Chin. Phys. B 28 094701
Google Scholar
-
图 1 对流系统中的温度场和流线图
Fig. 1. Temperature field and streamline of partitioned convection system
图 2 隔板对流系统中不同传热通道的热通量
Fig. 2. The heat flux of different heat transfer channels in partitioned convection system.
图 3 隔板对流系统局部区域纵向热流分布特性
Fig. 3. An enlarged portion of the vertical heat flow field in partitioned convection system, the arrows represent the direction of the flow.
图 4 隔板对流系统局部区域横向热流分布特性
Fig. 4. An enlarged portion of the horizontal heat flow field in partitioned convection system.
图 5 系统局部区域热流热通量变化及底板传热特性定量表示
Fig. 5. Change of heat flux and heat flow in partial area of the system and quantitative representation of the heat transfer on the bottom plate.
图 6 狭缝高度d = 0.015时隔板数n = 9 (a), n = 11 (b)及d = 0.01时隔板数n = 9 (c), n = 11 (d)的局部温度场和局部传热大小
Fig. 6. Partial temperature field and magnitude of local heat flux under different number of partitions n = 9 (a) and n = 11 (b) when the height of gap is d = 0.015 and n = 9 (c) and n = 11 (d) when the height of gap is d = 0.01
图 7 不同狭缝高度下传热Nu数与Nud/Nu随隔板数的变化, 红色线表示无隔板时系统的传热
Fig. 7. Nu and Nud/Nu with the change of the partition number n under different height of gaps, the horizontal red dashed line represents the system without partitions.
-
[1] Lappa M 2005 Cryst. Res. Technol. 40 531
Google Scholar
[2] Bodenschatz E, Pesch W, Ahlers G 2000 Annu. Rev. Fluid Mech. 32 709
Google Scholar
[3] Ahlers G, Grossmann S, Lohse D 2009 Rev. Mod. Phys. 81 503
Google Scholar
[4] Grossmann S, Lohse D 2000 J. Fluid Mech. 407 27
Google Scholar
[5] Grossmann S, Lohse D 2001 Phys. Rev. Lett. 86 3316
Google Scholar
[6] Shishkina O, Horn S, Wagner S, Ching E S C 2015 Phys. Rev. Lett. 114 114302
Google Scholar
[7] Weiss S, He X, Ahlers G, Bodenschatz E, Shishkina O 2018 J. Fluid Mech. 851 374
Google Scholar
[8] Zhao J, Cai W, Jiang Y 2019 Int. J. Heat Mass Transfer 129 599
Google Scholar
[9] Urban P, Hanzelka P, Králík T, Macek M, Musilová V, Skrbek L 2019 Phys. Rev. E 99 011101
Google Scholar
[10] Zhong J Q, Stevens R J, Clercx H J, Verzicco R, Lohse D, Ahlers G 2009 Phys. Rev. Lett. 102 044502
Google Scholar
[11] Stevens R J, Clercx H J, Lohse D 2013 Eur. J. Mech. Fluids 40 41
Google Scholar
[12] Liu Y, Ecke R E 1997 Phys. Rev. Lett. 79 2257
Google Scholar
[13] Kunnen R P J, Clercx H J H, Geurts B J 2006 Phys. Rev. E 74 056306
Google Scholar
[14] Kunnen R P J, Clercx H J H, Geurts B J 2008 Europhys. Lett. 84 24001
Google Scholar
[15] Du Y B, Tong P 1998 Phys. Rev. Lett. 81 987
Google Scholar
[16] Stringano G, Pascazio G, Verzicco R 2006 J. Fluid Mech. 557 307
Google Scholar
[17] Xu F, Patterson J C, Lei C 2009 Int. J. Heat Mass Transfer 52 620
Google Scholar
[18] Bao Y, Chen J, Liu B F, She Z S, Zhang J, Zhou Q 2015 J. Fluid Mech. 784 R5
[19] 包芸, 林泽鹏, 丁广裕 2017 计算机辅助工程 26 57
Bao Y, Lin Z P, Ding G Y 2017 Comput. Aided Eng. 26 57
[20] 林泽鹏, 包芸 2018 中国科学: 物理学 力学 天文学 48 054702
Lin Z P, Bao Y 2018 Sci. Sin. Phys. Mech. Astron. 48 054702
[21] 林泽鹏, 包芸 2018 中国科学: 物理学 力学 天文学 48 104702
Lin Z P, Bao Y 2018 Sci. Sin. Phys. Mech. Astron. 48 104702
[22] 林泽鹏, 徐圣卓, 包芸 2019 水动力学研究与进展(A辑) 34 193
Google Scholar
Lin Z P, Xu S Z, Bao Y 2019 Chin. J. Hydrodynam. 34 193
Google Scholar
[23] 包芸, 林泽鹏, 何鹏 2019 中国科学: 物理学 力学 天文学 49 044701
Bao Y, Lin Z P, He P 2019 Sci. Sin. Phys. Mech. Astron. 49 044701
[24] Lin Z P, Bao Y 2019 Chin. Phys. B 28 094701
Google Scholar
下载:
计量
- 文章访问数: 6746
- PDF下载量: 59
- 被引次数: 0
