HgTe/CdTe量子阱中自旋拓扑态的退相干效应

闫婕; 魏苗苗; 邢燕霞

doi:10.7498/aps.68.20191072

摘要

HgTe/CdTe量子阱是一种特殊的二维拓扑材料, 其中的量子自旋霍尔效应在自旋电子器件应用方面极有潜力. “工”字形四端口体系纵向非局域电阻阻值为$0.25\;h/e^{2}$的特殊的量子化平台是判别量子自旋霍尔效应的有力证据. 本文基于二维HgTe/CdTe量子阱模型, 利用非平衡格林函数理论及Landauer-Büttiker公式计算非局域电阻, 进而研究自旋拓扑态在非静态杂质作用下的退相干效应. 计算同时考虑磁交换场和磁场的影响. 研究发现, 尽管磁交换场和外磁场会破坏时间反演对称性, 但它们都仅改变拓扑带隙的宽度和相对位置, 并不影响螺旋边缘态的拓扑性. 而退相干杂质对自旋拓扑边缘态的影响则完全不同于铁磁和弱磁场. 退相干效应不会影响拓扑带隙的位置和宽度, 但是会影响拓扑边缘态的稳定性. 其中, 自旋不守恒的退相干杂质对螺旋边缘态的影响更为明显, 轻微的退相干效应便会引起自旋翻转, 从而引起自旋相反的背散射, 最终破坏自旋霍尔边缘态.

关键词:

Abstract

HgTe/CdTe quantum well is a typical two dimensional topological material which supports the helical edge states and quantum spin Hall effect that is imposing in applying of spin electronic devices. The special plateau valued with $0.25\;h/e^{2}$ of nonlocal resistance in H-shaped four terminal devices can be used as the fingerprint of quantum spin Hall effect. Based on the HgTe/CdTe quantum well, with the aid of nonequilibrium Green's function theory and multi-terminal Landauer-Büttiker formula, we calculate the nonlocal resistance and study the dephasing effect of spin topological states in the presence of exchange field and external magnetic field. It is found the dephasing processes play a role completely different from exchange field and external magnetic field. The latter destroy time reversal symmetry and change the width and relative position of topological gap, but do not influent the topological stability of helical edge states. In the contrary, dephasing processes don't change the width and relative position, however, they broke the topological stability. We consider two kinds of dephasing: normal dephasing and spin dephasing. In the first kind, the carriers lose only the phase memory while maintaining the spin memory. In the second kind, the carriers lose both phase and spin memories. Because of the spin locking properties, normal dephasing almost have no influence on the helical edge states. While the spin dephasing will induce spin flip backscattering and finally destroy helical edge states seriously.

Keywords:

作者及机构信息

北京理工大学物理学院, 先进光电量子结构设计与测量教育部重点实验室, 纳米光子学与超精密光电系统北京市重点实验室, 北京　100081

通信作者: 邢燕霞, xingyanxia@bit.edu.cn

基金项目: 国家自然科学基金(批准号: 11674024)资助的课题

Authors and contacts

Key Laboratory of Advanced Optoelectronic Quantum Architecture and Measurement, Micronano Centre, Beijing Key Laboratory of Nanophotonics and Ultrafine Optoelectronic Systems, School of Physics, Beijing Institute of Technology, Beijing 100081, China

Corresponding author: Xing Yan-Xia, xingyanxia@bit.edu.cn

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11674024)

文章全文 : translate this paragraph

参考文献

[1]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[2]	Zhang F, Zhou J, Xiao D, Yao Y 2017 Phys. Rev. Lett. 119 266804 Google Scholar
[3]	Schindler F, Cook A M, Vergniory M G, Wang Z, Parkin S S, Bernevig B A, Neupert T 2018 Sci. Adv. 4 eaat0346 Google Scholar
[4]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[5]	Alexandradinata A, Wang Z, Bernevig B A 2016 Phys. Rev. X 6 021008
[6]	König M, Wiedmann S, Brüne C, Roth A, Buhmann H, Molenkamp L W, Qi X L, Zhang S C 2007 Science 318 766 Google Scholar
[7]	Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757 Google Scholar
[8]	Yang W, Chang K, Zhang S C 2008 Phys. Rev. Lett. 100 056602 Google Scholar
[9]	Liu C C, Feng W, Yao Y 2011 Phys. Rev. Lett. 107 076802 Google Scholar
[10]	Xu Y, Yan B, Zhang H J, Wang J, Xu G, Tang P, Duan W, Zhang S C 2013 Phys. Rev. Lett. 111 136804 Google Scholar
[11]	Hsieh D, Qian D, Wray L, Xia Y, Hor Y S, Cava R J, Hasan M Z 2008 Nature 452 970 Google Scholar
[12]	Chen Y L, Analytis J G, Chu J H, Liu Z K, Mo S K, Qi X L, Zhang H J, Lu D H, Dai X, Fang Z, Zhang S C, Fisher I R, Hussain Z, Shen Z X 2009 Science 325 178 Google Scholar
[13]	Zhang L, Zhuang J, Xing Y, Li J, Wang J, Guo H 2014 Phys. Rev. B 89 245107 Google Scholar
[14]	Xing Y, Xu F, Cheung K T, Sun Q F, Wang J, Yao Y 2018 New J. Phys 20 043011 Google Scholar
[15]	Xing Y, Xu F, Sun Q F, Wang J, Yao Y G 2018 J. Phys. Condens. Mat. 30 435303 Google Scholar
[16]	Wada M, Murakami S, Freimuth F, Bihlmayer G 2011 Phys. Rev. B 83 121310 Google Scholar
[17]	Chang K, Lou W K 2011 Phys. Rev. Lett. 106 206802 Google Scholar
[18]	Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2008 Phys. Rev. Lett. 101 146802
[19]	Xing Y, Sun Q F 2014 Phys. Rev. B 89 085309 Google Scholar
[20]	Hinz J, Buhmann H, Schäfer M, Hock V, Becker C, Molenkamp L 2006 Semicond. Sci. Tech. 21 501 Google Scholar
[21]	Piatrusha S, Khrapai V, Kvon Z, Mikhailov N, Dvoretsky S, Tikhonov E 2017 Phys. Rev. B 96 245417 Google Scholar
[22]	Xue F, MacDonald A H 2018 Phys. Rev. Lett. 120 186802 Google Scholar
[23]	Dolcetto G, Sassetti M, Schmidt T L 2015 arXiv preprint: 1511.06141
[24]	Sticlet D, Cayssol J 2014 Phys. Rev. B 90 201303 Google Scholar
[25]	Väyrynen J I, Pikulin D I, Alicea J 2018 Phys. Rev. Lett. 121 106601 Google Scholar
[26]	Zhou B, Lu H Z, Chu R L, Shen S Q, Niu Q 2008 Phys. Rev. Lett. 101 246807 Google Scholar
[27]	Dai X, Hughes T L, Qi X L, Fang Z, Zhang S C 2008 Phys. Rev. B 77 125319 Google Scholar
[28]	Ohyama Y, Tsuchiura H, Sakuma A 2011 Journal of Physics: Conference Series 266 012103 Google Scholar
[29]	Xing Y, Yang Z L, Sun Q F, Wang J 2014 Phys. Rev. B 90 075435 Google Scholar
[30]	Zhang L B, Cheng F, Zhai F, Chang K 2011 Phys. Rev. B 83 081402 Google Scholar
[31]	Xing Y, Zhang L, Wang J 2011 Phys. Rev. B 84 035110 Google Scholar
[32]	Ren Y, Zeng J, Wang K, Xu F, Qiao Z 2017 Phys. Rev. B 96 155445 Google Scholar
[33]	Wang K T, Xu F, Xing Y, Zhao H K 2018 Front. Phys. 13 1 Google Scholar
[34]	Abanin D A, Morozov S V, Ponomarenko L A, Gorbachev R V, Mayorov A S, Katsnelson M L, Watanabe K, Taniguchi T, Novoselov K S, Levitov L S, Geim A K 2011 Science 332 328 Google Scholar
[35]	Wang Z, Liu H, Jiang H, Xie X C 2016 Phys. Rev. B 94 035409 Google Scholar
[36]	Renard J, Studer M, Folk J A 2014 Phys. Rev. Lett. 112 116601 Google Scholar
[37]	Shimazaki Y, Yamamoto M, Borzenets I V, Watanabe K, Taniguchi T, Tarucha S 2015 Nat. Phys. 11 1032 Google Scholar
[38]	Sui M, Chen G, Ma L, Shan W Y, Tian D, Watanabe K, Taniguchi T, Jin X, Yao W, Xiao D, Zhang Y 2015 Nat. Phys. 11 1027 Google Scholar
[39]	Wang J, Lian B, Zhang H, Zhang S C 2013 Phys. Rev. Lett. 111 086803 Google Scholar
[40]	Brüne C, Roth A, Buhmann H, Hankiewicz E M, Molenkamp L W, Maciejko J, Qi X L, Zhang S C 2012 Nat. Phys. 8 485 Google Scholar
[41]	Krishtopenko S, Teppe F 2018 Phys. Rev. B 97 165408 Google Scholar
[42]	Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2008 Phys. Rev. Lett. 101 146802 Google Scholar
[43]	Ahn J, Yang B J 2017 Phys. Rev. Lett. 118 156401 Google Scholar
[44]	Sun Q F, Xie X C 2010 Phys. Rev. Lett. 104 066805 Google Scholar
[45]	Xing Y, Sun Q F, Wang J 2008 Phys. Rev. B 77 115346 Google Scholar
[46]	Jiang H, Cheng S, Sun Q F, Xie X C 2009 Phys. Rev. Lett. 103 036803 Google Scholar
[47]	Qi J, Liu H, Jiang H, Xie X C 2019 Front. Phys. 14 43403 Google Scholar
[48]	Golizadeh-Mojarad R, Datta S 2007 Phys. Rev. B 75 081301 Google Scholar
[49]	Zhang L, Yu Z, Xu F, Wang J 2018 Carbon 126 183 Google Scholar
[50]	Datta S 1995 Electronic Transport in Mesoscopic Systems (1st ed.) (New York: Cambridge university press) pp79–93
[51]	Jiang H, Wang L, Sun Q F, Xie X C 2009 Phys. Rev. B 80 165316 Google Scholar
[52]	Sun Q F, Li Y X, Long W, Wang J 2011 Phys. Rev. B 83 115315 Google Scholar

施引文献

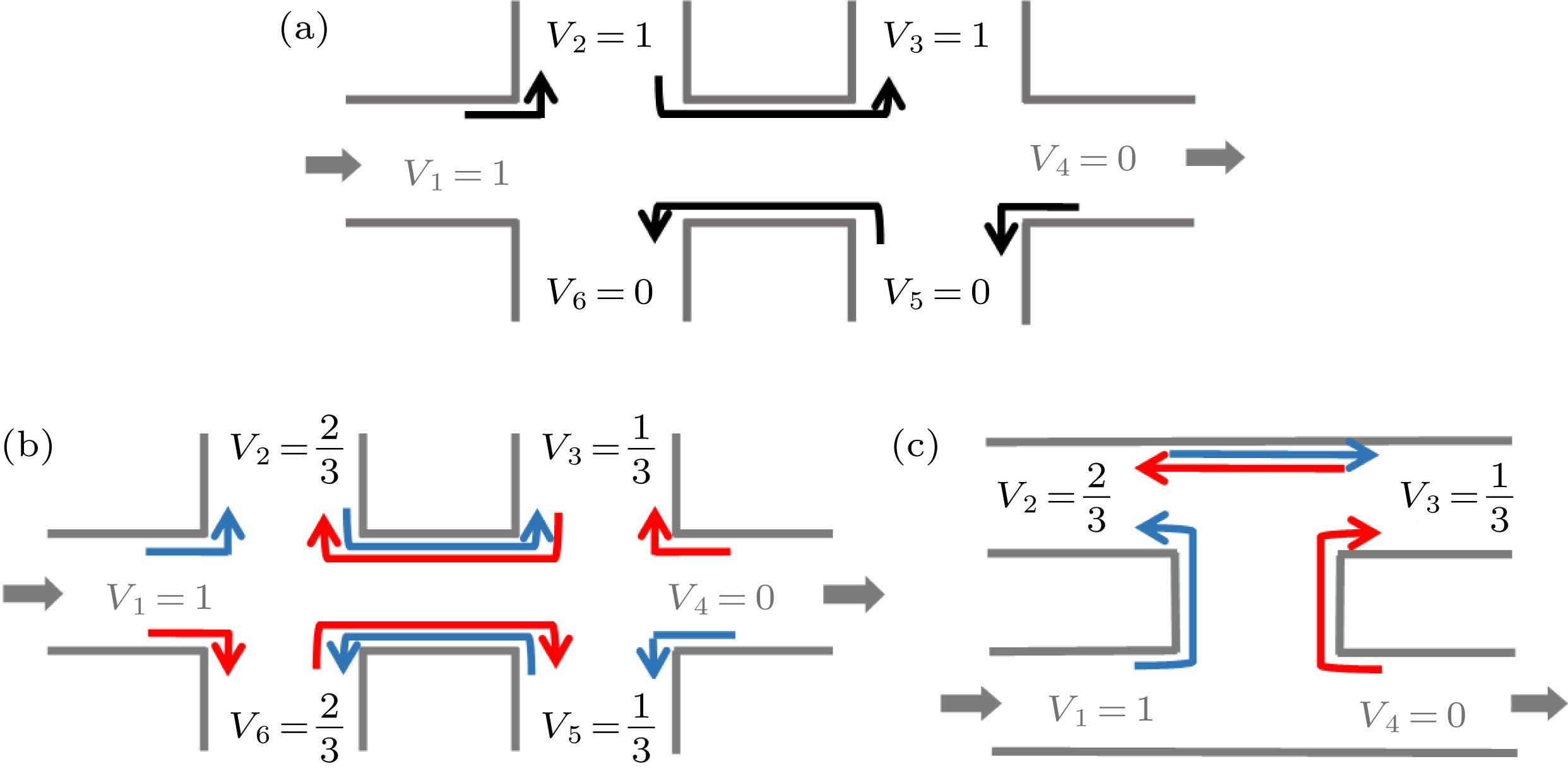
图 1 (a) 四端口HgTe/CdTe量子阱模型, 其中1、4端口为电流输入端口, 2、3端口为电压测量端口. 图中蓝色和绿色区域分别由两个独立的门电压控制, 通过调节门电压, 两个区域可分别独立地在图(b)中所示的三个区间自由切换； (b) HgTe/CdTe量子阱二维系统的能带结构, 包含简并的螺旋边缘态和明显不对称的价带和导带. 体带隙分割出三个区域: 量子自旋霍尔区(QSH), n型自旋霍尔区(n-SH)和p型自旋霍尔区(n-SH)

Fig. 1. (a) Four-terminal device based on HgTe/CdTe quantum well with two current terminals 1, 4 and two voltage terminals 2, 3; the blue region and green region can be independently tuned into the three region shown in panel (b); (b) band structure of 2 D HgTe/CdTe quantum well. Bulk energy gap divides three region: QSH region, n-SH region and p-SH region.

下载: 全尺寸图片幻灯片

图 2 手性边缘态和螺旋边缘态在多端口体系中的电压降示意图

Fig. 2. Sketch map of voltage drop induced by chiral edge states and helical edge states in multi-terminal system.

下载: 全尺寸图片幻灯片

图 3 纵向非局域电阻$R_{23, 14}$和部分透射系数$T_{14}$和$T_{41}$随电流输入区(图1绿色区)在位能$E_1$的变化. 左右两栏分别对应铁磁交换场$M=0$和$M=5\;{\rm{meV}}$的情况, 探测区(图1蓝色区)在位能$E_2=0$. 为便于比较, 顶栏给出了相应能量区间的能带图. 能带图中, 蓝色和红色分别表示自旋上和自旋下的能带

Fig. 3. Nonlocal resistors $R_{23, 14}$ and transmission coefficient $T_{14}$ and $T_{41}$ vs energy $ E_1 $ with energy of detector region $E_2=0$. left and right panels are for $ M= 0$ and $ M=5 \;{\rm{meV}} $, respectively. Top panels are band structure of infinite ribbon, the blue lines and red lines correspond to spin up and spin down, respectively.

下载: 全尺寸图片幻灯片

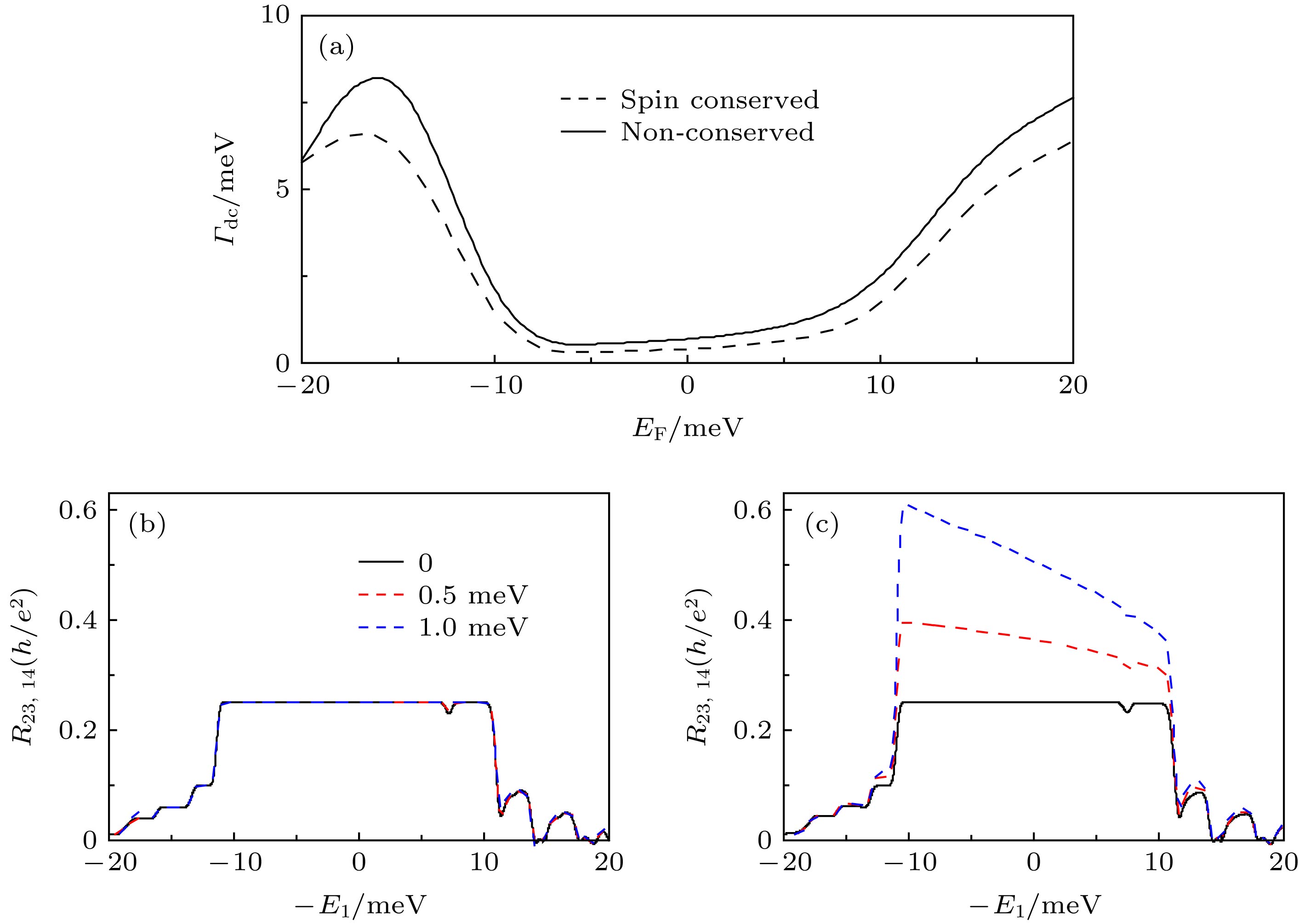
图 4 (a)不同退相干条件下$\varGamma_{\rm {dc}}$随费米能的变化; (b)和(c): 在普通退相干(图(b))和自旋退相干(图(c))作用下, 纵向非局域电阻$R_{23, 14}$随入射端能量$E_1$的变化, 不同曲线对应不同的退相干强度. 图(b)和图(c)共享图例

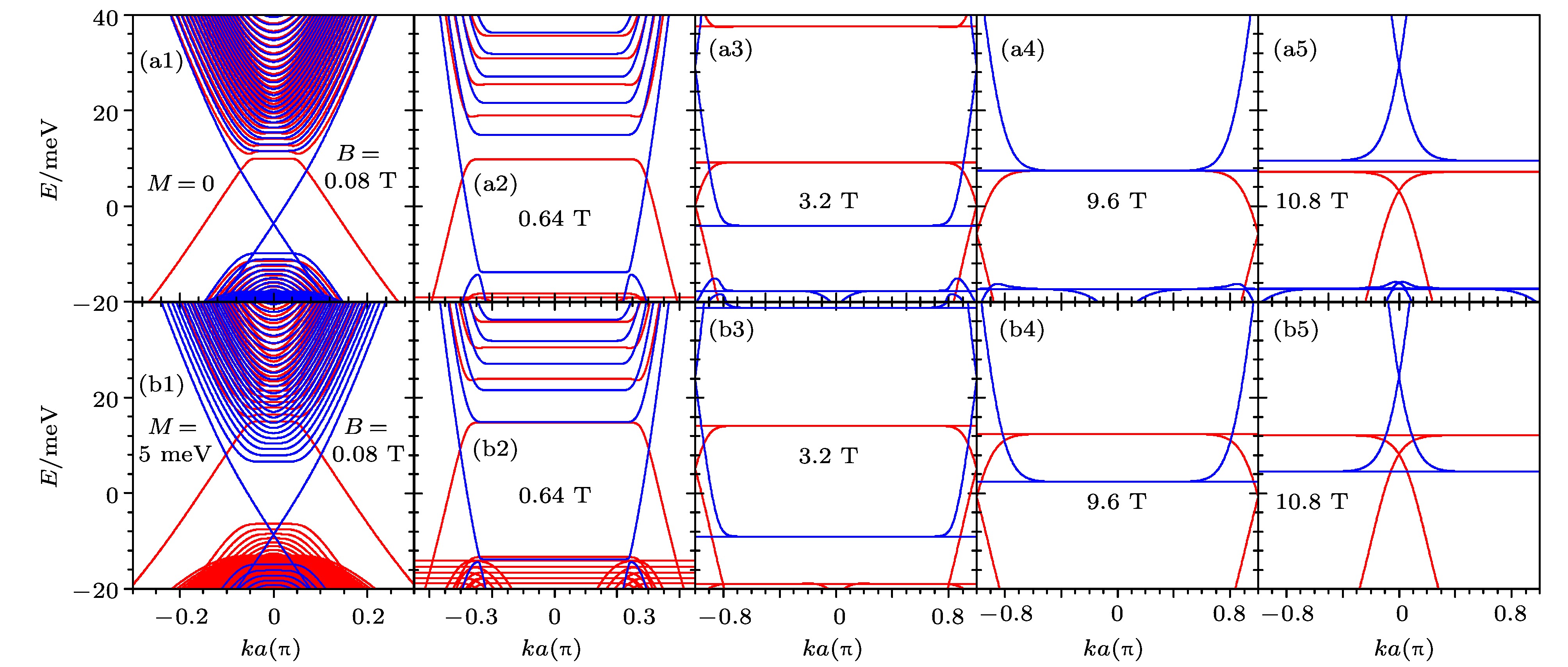
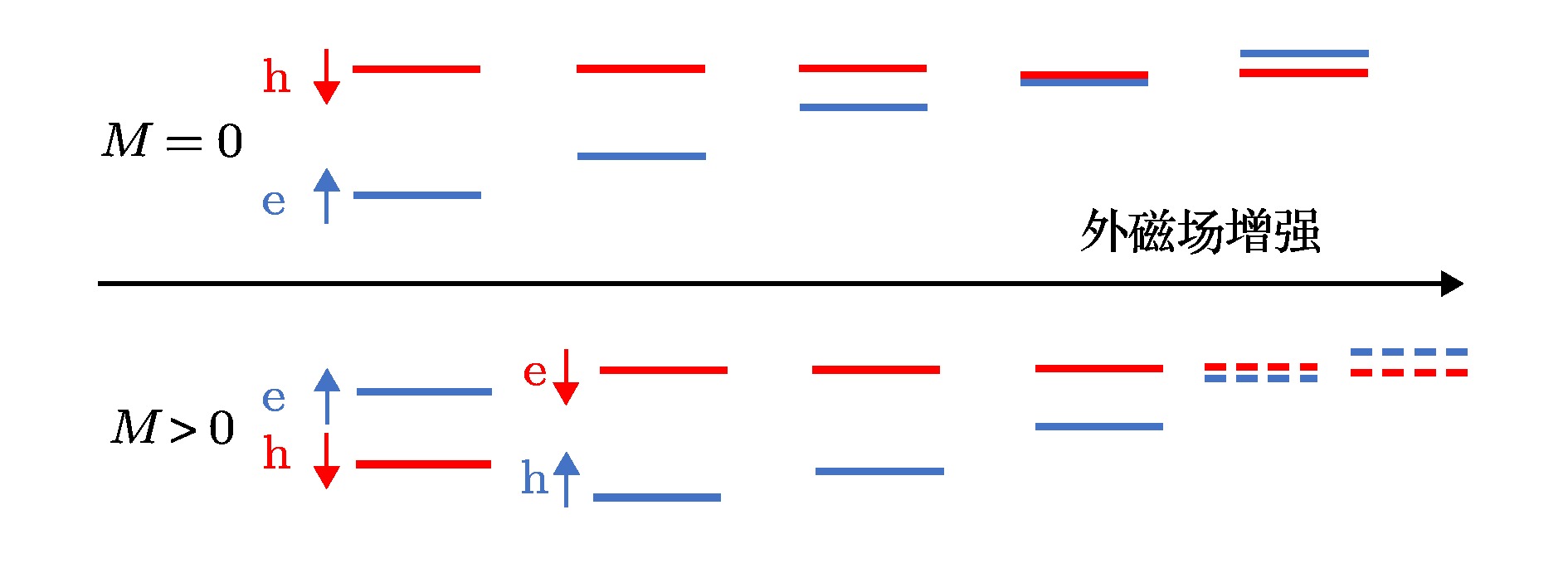
Fig. 4. Panel (a) $\varGamma_{\rm {dc}}$ vs energy $E_1$. Panel (b) and (c): longitudinal non-local resistance $R_{23, 14}$ vs energy $E_1$ with different $\varGamma_d$ for normal dephasing [panel (b)] and spin dephasing [panel (c)].

下载: 全尺寸图片幻灯片

图 5 磁场从弱到强作用下无穷长条带在零磁交换场(上栏)和非零磁交换场(下栏)条件下的能带演化

Fig. 5. Band structures of infinite ribbon with various magnetic field B for exchange field $M=0$(top panels) and $5\rm {\;meV}$(bottom panels). Red lines denotes the chiral edge states. The red lines and blue lines are correspond to the states of spin up and spin down.

下载: 全尺寸图片幻灯片

图 6 零磁交换场和非零磁交换场能带随外磁场的演化趋势示意图

Fig. 6. Schematic diagram of the developing tendency of band structure in the presence of magnetic field for the zero exchange field (top panels) and nonzero exchange field (bottom panels).

下载: 全尺寸图片幻灯片

图 7 普通退相干和磁场作用下, 纵向非局域电阻$R_{23, 14}$随入射端能量$E_1$的变化. 左栏: 零磁交换场; 右栏: 非零磁交换场. 上下两栏共享图例

Fig. 7. $R_{23, 14}$ vs energy $E_1$ for different normal dephasing strength $\varGamma_{\rm d}$ with (right panels) or without (left panels) exchange field. The gray region signs the energy gap in zero magnetic field.

下载: 全尺寸图片幻灯片

图 8 自旋退相干作用下的纵向非局域电阻, 其余参数设置同图7

Fig. 8. $R_{23, 14}$ vs energy $E_1$, the dephasing precesses are spin non-conserved. The other parameters are the same as Fig. 7

下载: 全尺寸图片幻灯片

map

[1]	Kane C L, Mele E J 2005 Phys. Rev. Lett. 95 226801 Google Scholar
[2]	Zhang F, Zhou J, Xiao D, Yao Y 2017 Phys. Rev. Lett. 119 266804 Google Scholar
[3]	Schindler F, Cook A M, Vergniory M G, Wang Z, Parkin S S, Bernevig B A, Neupert T 2018 Sci. Adv. 4 eaat0346 Google Scholar
[4]	Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 Google Scholar
[5]	Alexandradinata A, Wang Z, Bernevig B A 2016 Phys. Rev. X 6 021008
[6]	König M, Wiedmann S, Brüne C, Roth A, Buhmann H, Molenkamp L W, Qi X L, Zhang S C 2007 Science 318 766 Google Scholar
[7]	Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757 Google Scholar
[8]	Yang W, Chang K, Zhang S C 2008 Phys. Rev. Lett. 100 056602 Google Scholar
[9]	Liu C C, Feng W, Yao Y 2011 Phys. Rev. Lett. 107 076802 Google Scholar
[10]	Xu Y, Yan B, Zhang H J, Wang J, Xu G, Tang P, Duan W, Zhang S C 2013 Phys. Rev. Lett. 111 136804 Google Scholar
[11]	Hsieh D, Qian D, Wray L, Xia Y, Hor Y S, Cava R J, Hasan M Z 2008 Nature 452 970 Google Scholar
[12]	Chen Y L, Analytis J G, Chu J H, Liu Z K, Mo S K, Qi X L, Zhang H J, Lu D H, Dai X, Fang Z, Zhang S C, Fisher I R, Hussain Z, Shen Z X 2009 Science 325 178 Google Scholar
[13]	Zhang L, Zhuang J, Xing Y, Li J, Wang J, Guo H 2014 Phys. Rev. B 89 245107 Google Scholar
[14]	Xing Y, Xu F, Cheung K T, Sun Q F, Wang J, Yao Y 2018 New J. Phys 20 043011 Google Scholar
[15]	Xing Y, Xu F, Sun Q F, Wang J, Yao Y G 2018 J. Phys. Condens. Mat. 30 435303 Google Scholar
[16]	Wada M, Murakami S, Freimuth F, Bihlmayer G 2011 Phys. Rev. B 83 121310 Google Scholar
[17]	Chang K, Lou W K 2011 Phys. Rev. Lett. 106 206802 Google Scholar
[18]	Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2008 Phys. Rev. Lett. 101 146802
[19]	Xing Y, Sun Q F 2014 Phys. Rev. B 89 085309 Google Scholar
[20]	Hinz J, Buhmann H, Schäfer M, Hock V, Becker C, Molenkamp L 2006 Semicond. Sci. Tech. 21 501 Google Scholar
[21]	Piatrusha S, Khrapai V, Kvon Z, Mikhailov N, Dvoretsky S, Tikhonov E 2017 Phys. Rev. B 96 245417 Google Scholar
[22]	Xue F, MacDonald A H 2018 Phys. Rev. Lett. 120 186802 Google Scholar
[23]	Dolcetto G, Sassetti M, Schmidt T L 2015 arXiv preprint: 1511.06141
[24]	Sticlet D, Cayssol J 2014 Phys. Rev. B 90 201303 Google Scholar
[25]	Väyrynen J I, Pikulin D I, Alicea J 2018 Phys. Rev. Lett. 121 106601 Google Scholar
[26]	Zhou B, Lu H Z, Chu R L, Shen S Q, Niu Q 2008 Phys. Rev. Lett. 101 246807 Google Scholar
[27]	Dai X, Hughes T L, Qi X L, Fang Z, Zhang S C 2008 Phys. Rev. B 77 125319 Google Scholar
[28]	Ohyama Y, Tsuchiura H, Sakuma A 2011 Journal of Physics: Conference Series 266 012103 Google Scholar
[29]	Xing Y, Yang Z L, Sun Q F, Wang J 2014 Phys. Rev. B 90 075435 Google Scholar
[30]	Zhang L B, Cheng F, Zhai F, Chang K 2011 Phys. Rev. B 83 081402 Google Scholar
[31]	Xing Y, Zhang L, Wang J 2011 Phys. Rev. B 84 035110 Google Scholar
[32]	Ren Y, Zeng J, Wang K, Xu F, Qiao Z 2017 Phys. Rev. B 96 155445 Google Scholar
[33]	Wang K T, Xu F, Xing Y, Zhao H K 2018 Front. Phys. 13 1 Google Scholar
[34]	Abanin D A, Morozov S V, Ponomarenko L A, Gorbachev R V, Mayorov A S, Katsnelson M L, Watanabe K, Taniguchi T, Novoselov K S, Levitov L S, Geim A K 2011 Science 332 328 Google Scholar
[35]	Wang Z, Liu H, Jiang H, Xie X C 2016 Phys. Rev. B 94 035409 Google Scholar
[36]	Renard J, Studer M, Folk J A 2014 Phys. Rev. Lett. 112 116601 Google Scholar
[37]	Shimazaki Y, Yamamoto M, Borzenets I V, Watanabe K, Taniguchi T, Tarucha S 2015 Nat. Phys. 11 1032 Google Scholar
[38]	Sui M, Chen G, Ma L, Shan W Y, Tian D, Watanabe K, Taniguchi T, Jin X, Yao W, Xiao D, Zhang Y 2015 Nat. Phys. 11 1027 Google Scholar
[39]	Wang J, Lian B, Zhang H, Zhang S C 2013 Phys. Rev. Lett. 111 086803 Google Scholar
[40]	Brüne C, Roth A, Buhmann H, Hankiewicz E M, Molenkamp L W, Maciejko J, Qi X L, Zhang S C 2012 Nat. Phys. 8 485 Google Scholar
[41]	Krishtopenko S, Teppe F 2018 Phys. Rev. B 97 165408 Google Scholar
[42]	Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2008 Phys. Rev. Lett. 101 146802 Google Scholar
[43]	Ahn J, Yang B J 2017 Phys. Rev. Lett. 118 156401 Google Scholar
[44]	Sun Q F, Xie X C 2010 Phys. Rev. Lett. 104 066805 Google Scholar
[45]	Xing Y, Sun Q F, Wang J 2008 Phys. Rev. B 77 115346 Google Scholar
[46]	Jiang H, Cheng S, Sun Q F, Xie X C 2009 Phys. Rev. Lett. 103 036803 Google Scholar
[47]	Qi J, Liu H, Jiang H, Xie X C 2019 Front. Phys. 14 43403 Google Scholar
[48]	Golizadeh-Mojarad R, Datta S 2007 Phys. Rev. B 75 081301 Google Scholar
[49]	Zhang L, Yu Z, Xu F, Wang J 2018 Carbon 126 183 Google Scholar
[50]	Datta S 1995 Electronic Transport in Mesoscopic Systems (1st ed.) (New York: Cambridge university press) pp79–93
[51]	Jiang H, Wang L, Sun Q F, Xie X C 2009 Phys. Rev. B 80 165316 Google Scholar
[52]	Sun Q F, Li Y X, Long W, Wang J 2011 Phys. Rev. B 83 115315 Google Scholar

[1]	丁锦廷, 胡沛佳, 郭爱敏. 线缺陷石墨烯纳米带的电输运研究. , 2023, 72(15): 157301. doi: 10.7498/aps.72.20230502
[2]	高建华, 盛欣力, 王群, 庄鹏飞. 费米子的相对论自旋输运理论. , 2023, 72(11): 112501. doi: 10.7498/aps.72.20222470
[3]	刘天, 李宗良, 张延惠, 蓝康. 耗散环境单量子点体系输运过程的量子速度极限研究. , 2023, 72(4): 047301. doi: 10.7498/aps.72.20222159
[4]	方静云, 孙庆丰. 石墨烯p-n结在磁场中的电输运热耗散. , 2022, 71(12): 127203. doi: 10.7498/aps.71.20220029
[5]	胡海涛, 郭爱敏. 双层硼烯纳米带的量子输运研究. , 2022, 71(22): 227301. doi: 10.7498/aps.71.20221304
[6]	巩龙延, 杨慧, 赵生妹. 中间测量对受驱单量子比特统计复杂度的影响. , 2020, 69(23): 230301. doi: 10.7498/aps.69.20200802
[7]	白旭芳, 陈磊, 额尔敦朝鲁. 电磁场中施主中心量子点内磁极化子态寿命与qubit退相干. , 2020, 69(14): 147802. doi: 10.7498/aps.69.20200242
[8]	吴歆宇, 韩伟华, 杨富华. 硅纳米结构晶体管中与杂质量子点相关的量子输运. , 2019, 68(8): 087301. doi: 10.7498/aps.68.20190095
[9]	闫瑞, 吴泽文, 谢稳泽, 李丹, 王音. 导线非共线的分子器件输运性质的第一性原理研究. , 2018, 67(9): 097301. doi: 10.7498/aps.67.20172221
[10]	王孜博, 江华, 谢心澄. 多端口石墨烯系统中的非局域电阻. , 2017, 66(21): 217201. doi: 10.7498/aps.66.217201
[11]	常锋, 王晓茜, 盖永杰, 严冬, 宋立军. 光与物质相互作用系统中的量子Fisher信息和自旋压缩. , 2014, 63(17): 170302. doi: 10.7498/aps.63.170302
[12]	党文佳, 曾晓东, 冯喆珺. 目标粗糙对合成孔径激光雷达回波的退相干效应. , 2013, 62(2): 024204. doi: 10.7498/aps.62.024204
[13]	张浩亮, 贾芳, 徐学翔, 郭琴, 陶向阳, 胡利云. 光子增减叠加相干态在热环境中的退相干. , 2013, 62(1): 014208. doi: 10.7498/aps.62.014208
[14]	赵虎, 李铁夫, 刘建设, 陈炜. 基于超导量子比特的电磁感应透明研究进展. , 2012, 61(15): 154214. doi: 10.7498/aps.61.154214
[15]	张彩霞, 郭虹, 杨致, 骆游桦. 三明治结构Tan(B3N3H6)n+1 团簇的磁性和量子输运性质. , 2012, 61(19): 193601. doi: 10.7498/aps.61.193601
[16]	赵文垒, 王建忠, 豆福全. 混沌微扰导致的量子退相干. , 2012, 61(24): 240302. doi: 10.7498/aps.61.240302
[17]	付邦, 邓文基. 任意正多边形量子环自旋输运的普遍解. , 2010, 59(4): 2739-2745. doi: 10.7498/aps.59.2739
[18]	李鹏, 邓文基. 正多边形量子环自旋输运的严格解. , 2009, 58(4): 2713-2719. doi: 10.7498/aps.58.2713
[19]	尹永琦, 李华, 马佳宁, 贺泽龙, 王选章. 多端耦合量子点分子桥的量子输运特性研究. , 2009, 58(6): 4162-4167. doi: 10.7498/aps.58.4162
[20]	刘绍鼎, 程木田, 周慧君, 李耀义, 王取泉, 薛其坤. 双激子和浸润层泄漏以及俄歇俘获对量子点Rabi振荡衰减的影响. , 2006, 55(5): 2122-2127. doi: 10.7498/aps.55.2122

计量

文章访问数: 10929
PDF下载量: 149
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

HgTe/CdTe量子阱中自旋拓扑态的退相干效应