基于压电材料的薄膜声学超材料隔声性能研究

贺子厚; 赵静波; 姚宏; 蒋娟娜; 陈鑫

doi:10.7498/aps.68.20190245

摘要

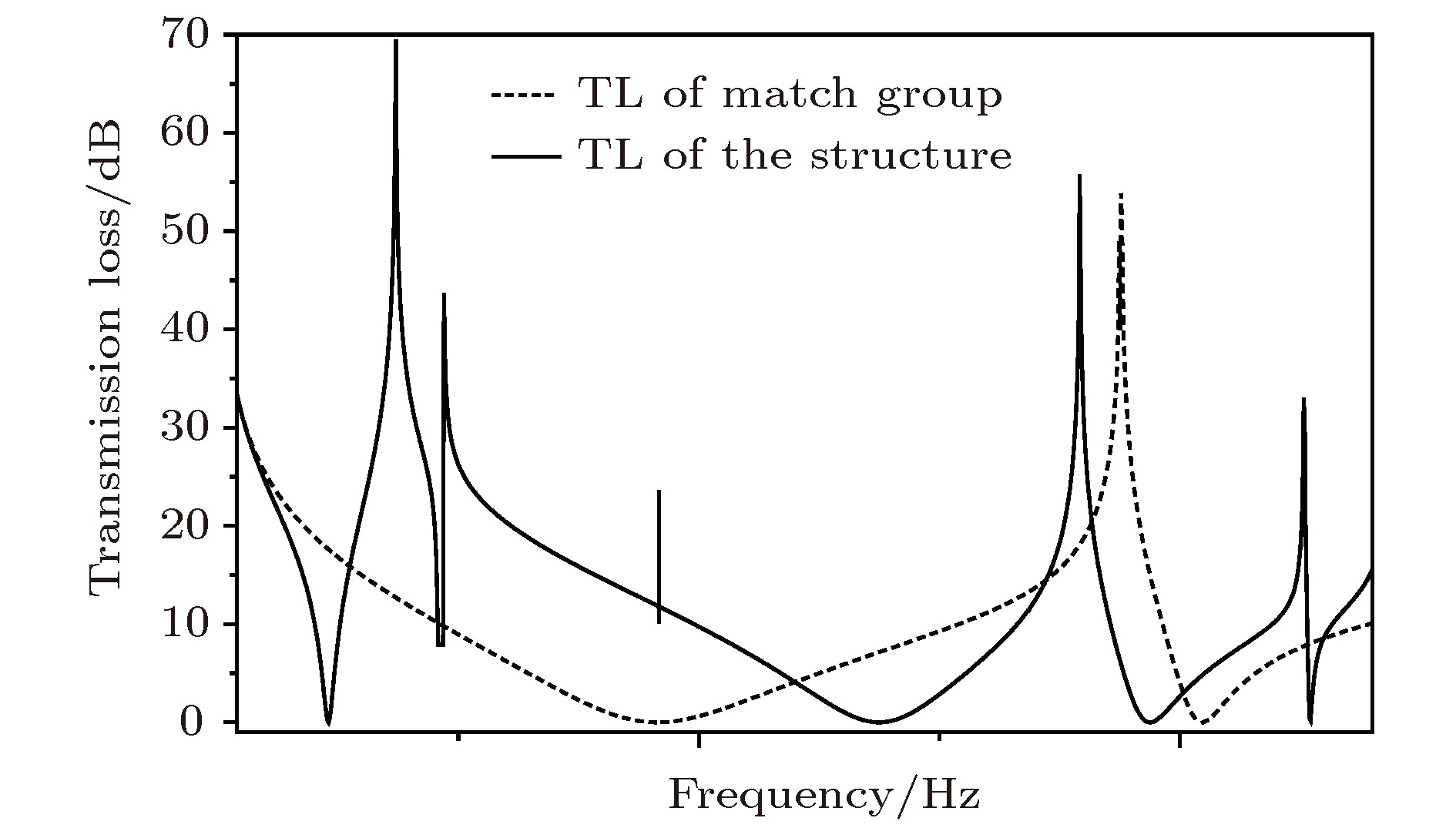
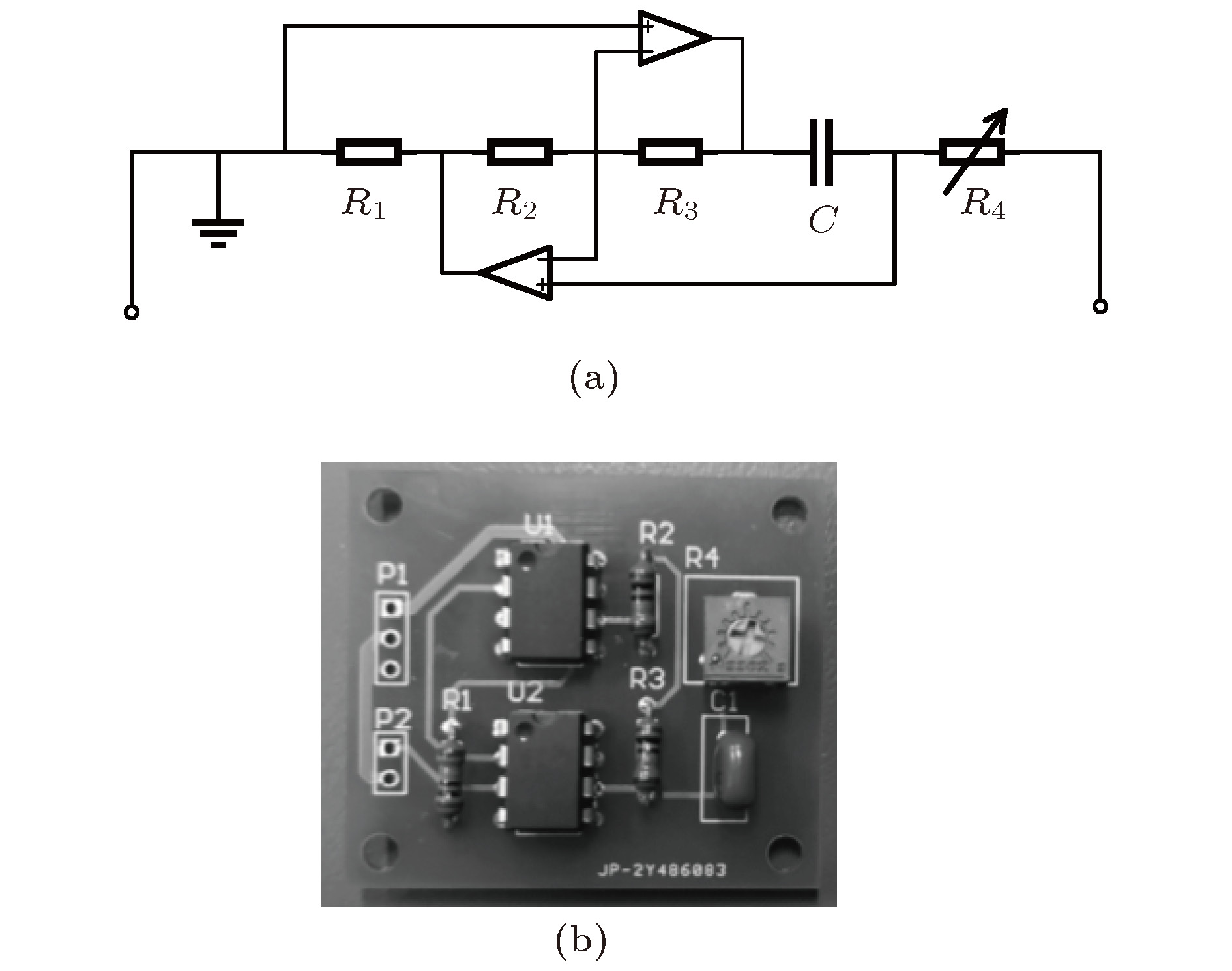
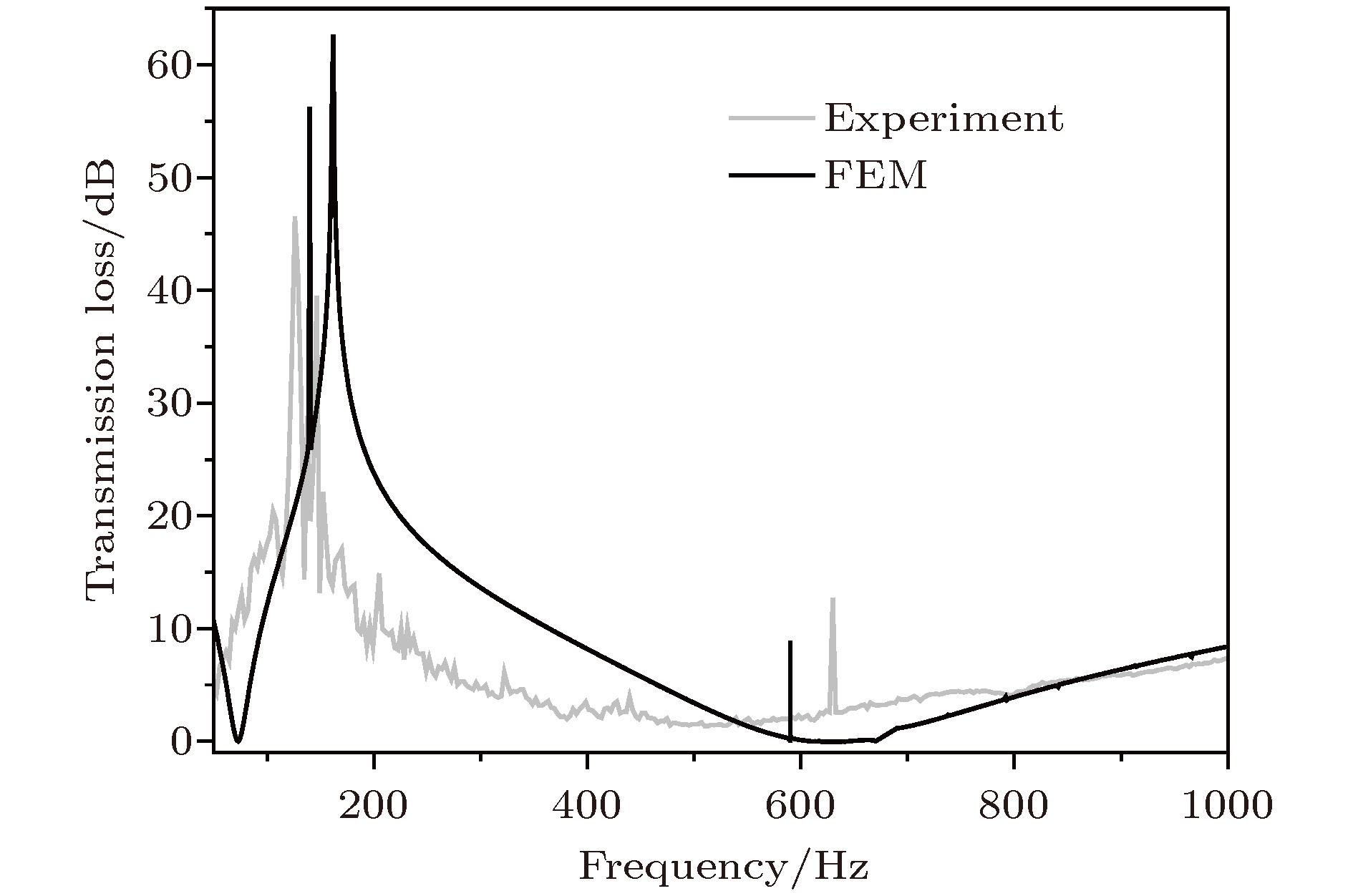
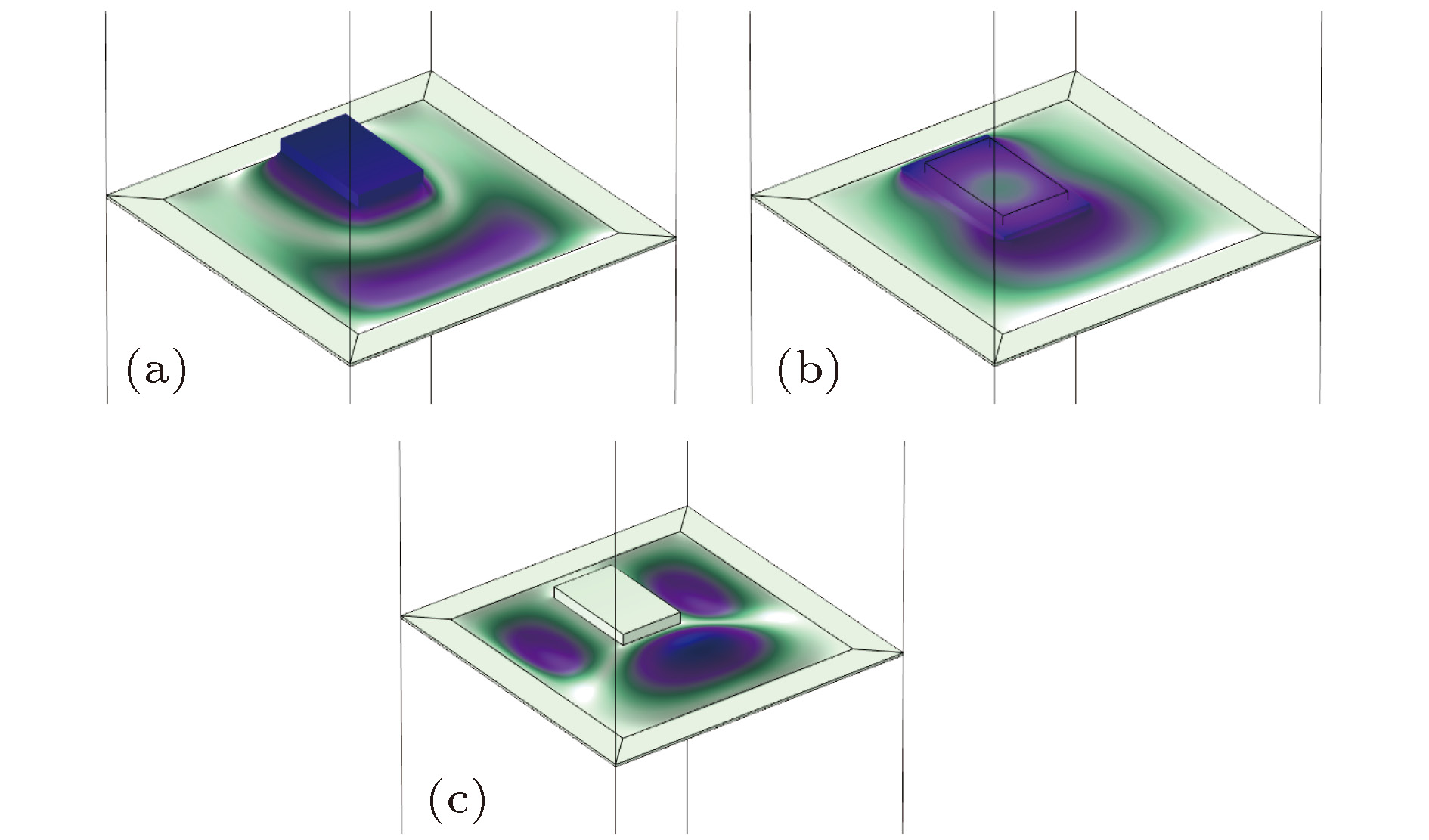
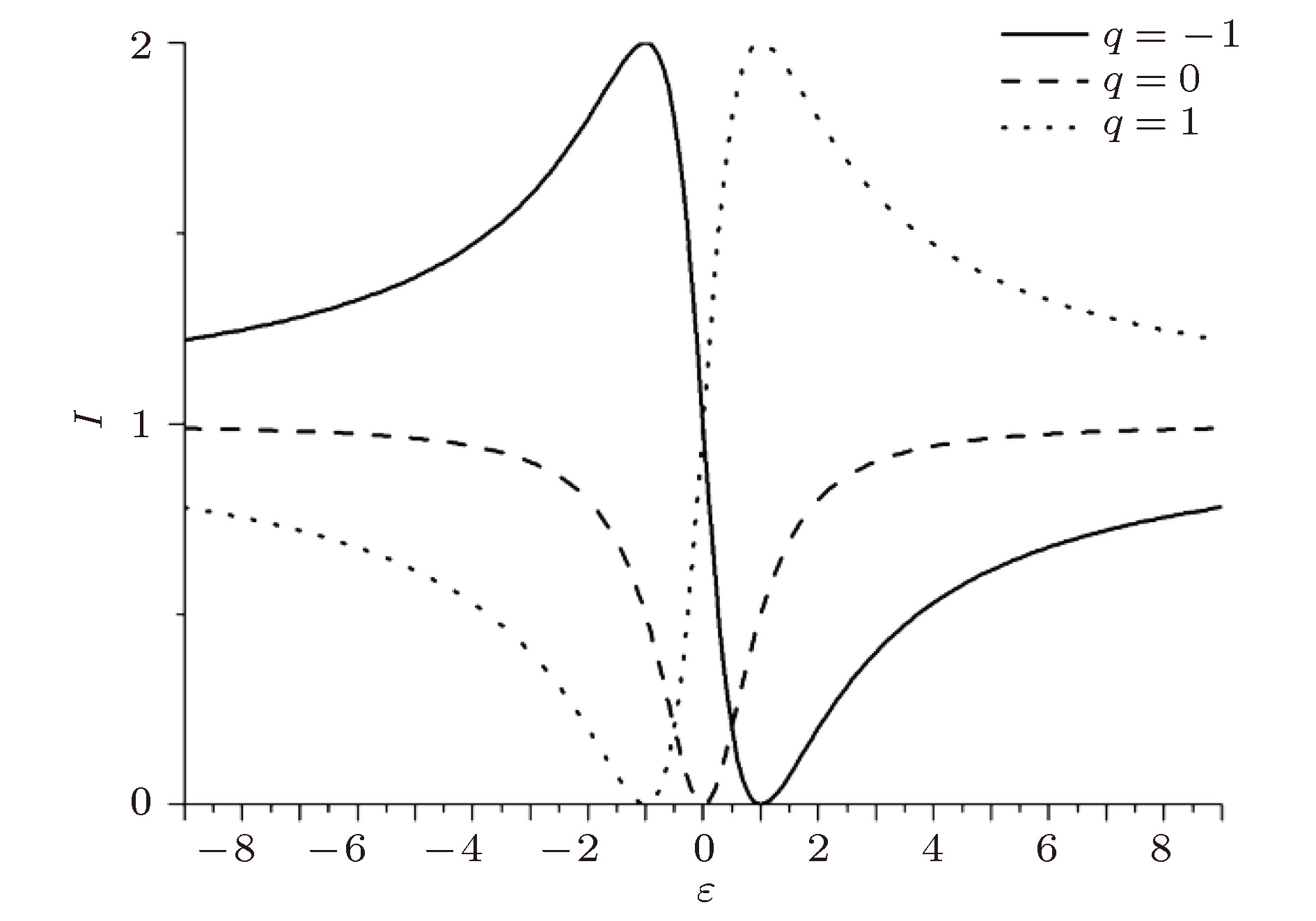
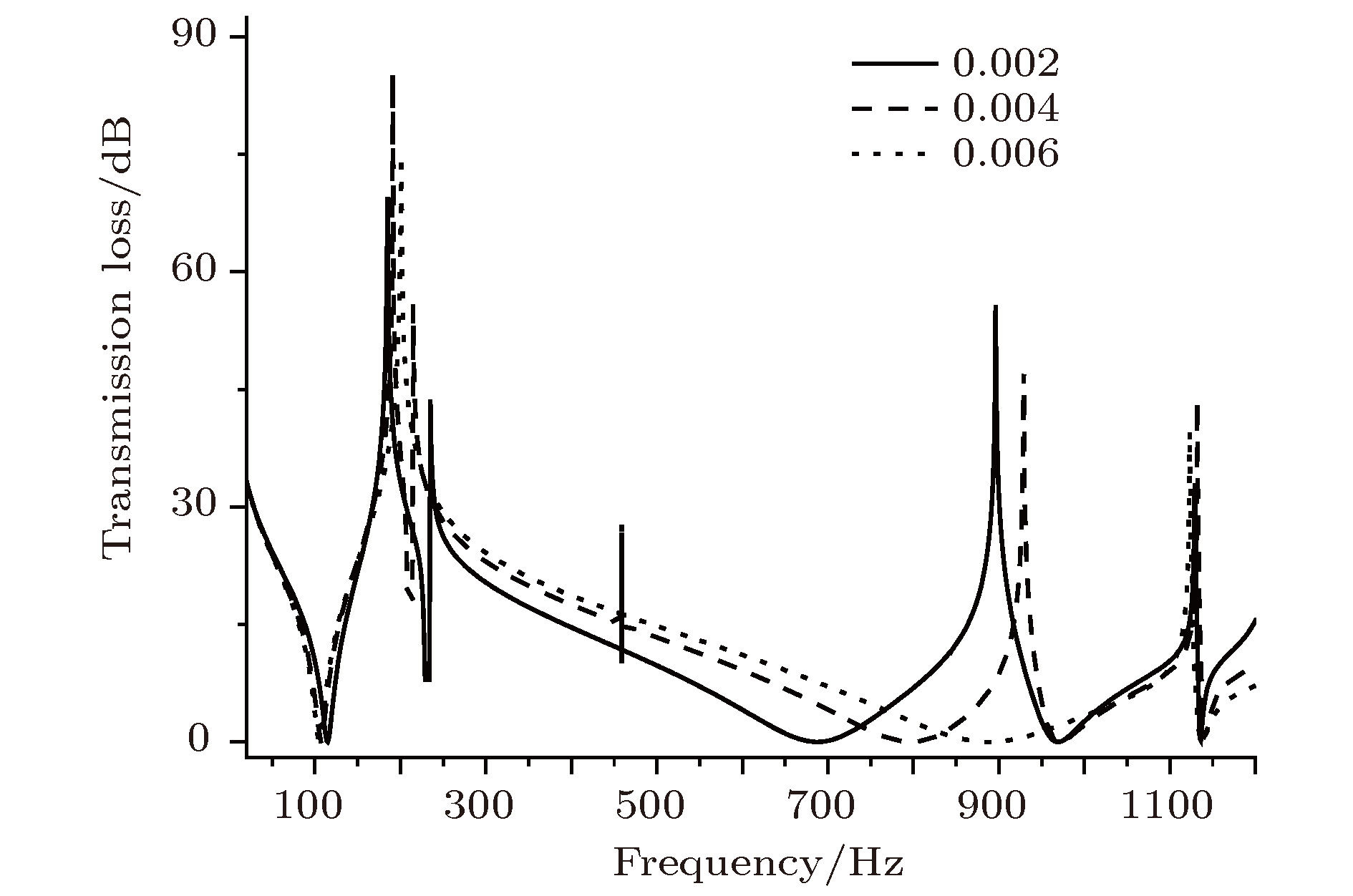
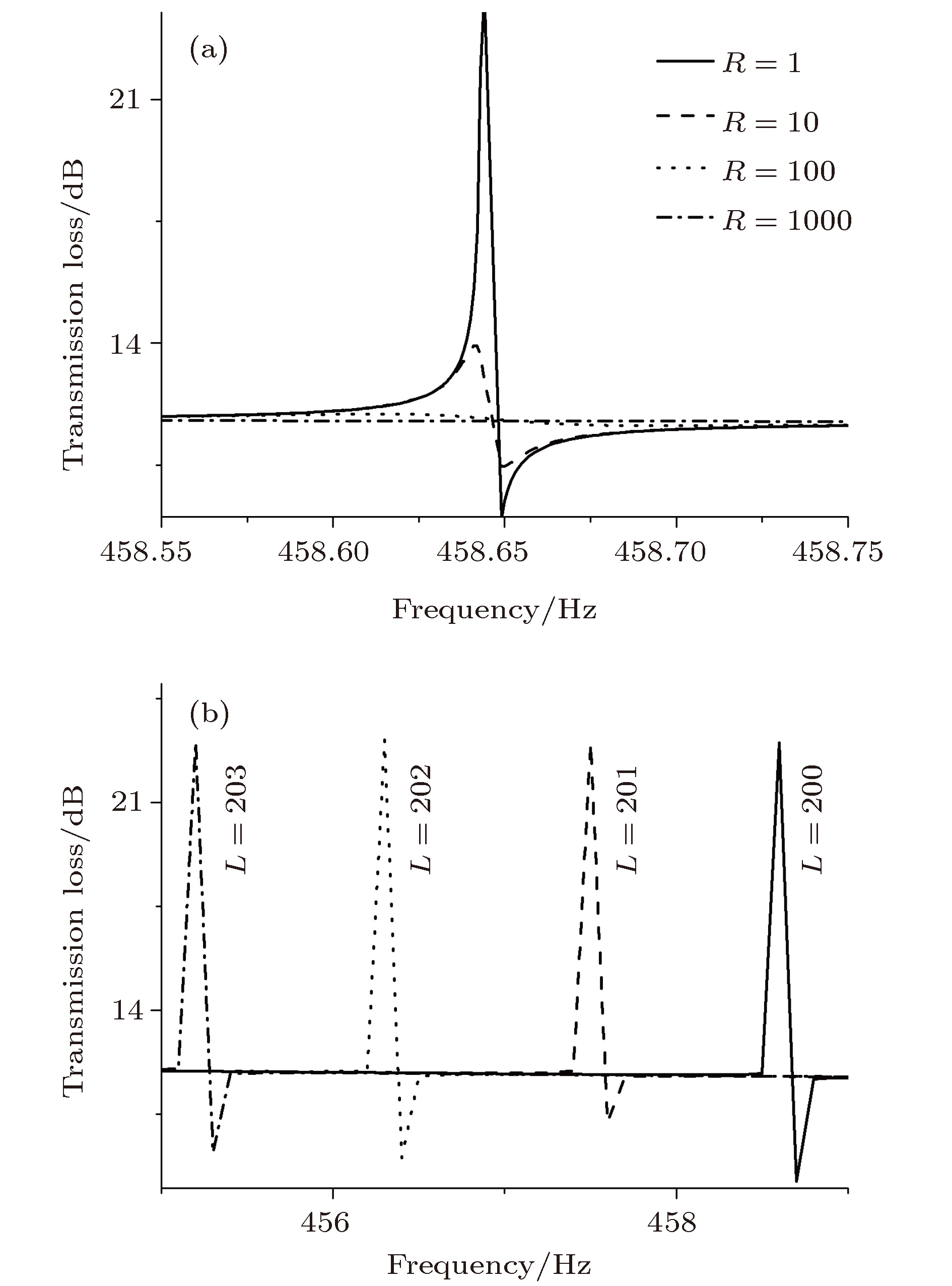
针对低频噪声的隔离问题, 设计了一种基于压电材料的可调控薄膜声学超材料, 该材料由压电质量块嵌入弹性薄膜制成. 建立了材料的有限元分析模型, 并且计算了材料的各阶特征频率与20—1200 Hz频段的传输损失曲线, 并通过实验验证了有限元计算的真实性. 计算结果表明: 此声学超材料在20—1200 Hz频段内隔声性能良好, 存在两个50 dB以上的隔声峰与一个可调式的隔声峰. 通过分析简单结构的首阶共振模态并构建其等效模型, 从理论上探究了结构参数对薄膜声学超材料隔声性能的影响, 并通过有限元计算验证了其等效模型的正确性; 综合分析材料的特征频率与传输损失曲线, 进一步讨论了结构的隔声机理, 分析结果表明, 在特征频率处, 薄膜的“拍动”会导致声波在其后的传播过程中干涉相消, 实现声波的衰减; 通过Fano共振理论, 探究了各共振点处传输损失曲线特征不同的原因; 压电质量块与外接电路组成LC振荡电路, 在电路的共振频率处, 压电材料的振动可以吸收声波的能量从而造成一个隔声峰, 同时可以改变外接电路的参数来调整电路的共振频率, 从而实现对隔声性能的调控. 最后, 探究了压电质量块偏心量对材料性能的影响, 并通过有限元计算验证了材料隔声性能的可调性. 研究结果为可调式薄膜声学超材料的设计提供了理论参考.

关键词:

Abstract

Aiming at the isolation of low-frequency sound, a kind of thin-film acoustic metamaterialis designed and obtained by implanting PZT into thin film. The finite element method (FEM) of the structure is built, and 1^st–14^th order eigenfrequencies and transmission loss between 20–1200 Hz are calculated. The reliability of finite element calculation is verified experimentally and the existence of adjustable sound insulation peak is monitored in the experiment. The results show that the acoustic metamaterial has good sound insulation performance in a frequency range between 20 and 1200 Hz, and has two sound insulation peaks of more than 50 dB, and there is a sound insulation peak which can be changed by adjusting the parameters of the outer circuit. By analyzing the first resonance mode of simple structure and building its equivalent model, the effect of structural parameter on the sound insulation performance of thin film acoustic metamaterial is investigated theoretically, and the rationality of the equivalent model is verified by the finite element calculation. The sound insulation mechanism of the structure is further illustrated by taking into consideration the eigenfrequencies, transmission loss curve and vibration mode diagrams at various frequencies. It is found that at the resonance frequency, the flapping motion of the film will cause the sound wave in the subsequent propagation to cancell the interference, therefore realizing the attenuation of the sound wave. Based on Fano resonance theory, the reasons for the different characteristics of transmission loss curves at different resonance points are investigated. The PZT and outer circuit can form a LC oscillator. At the resonant frequency of the oscillator, the vibration of the piezoelectric material can absorb the energy of sound wave to cause a sound insolation peak. The resonant frequency of the circuit can be adjusted by changing the parameters of the outer circuit, thereby realizing the adjustability of the sound insulation performance. The influence of eccentricity of piezoelectric mass block on sound insulation performance of material is explored, proving that the sound insulation performance can be further optimized by improving structure. And through the finite element calculation, it is proved that the sound insulation performance of material is adjustable by changing the parameters of the outer circuit. The results provide a theoretical reference for designing the thin film acoustic metamaterials.

Keywords:

作者及机构信息

1.
空军工程大学研究生院, 西安　710051

2.
空军工程大学基础部, 西安　710051

通信作者: 赵静波, chjzjb@163.com

基金项目: 国家自然科学基金(批准号: 11504429)资助的课题.

Authors and contacts

1.
Graduate School, Air Force Engineering University, Xi'an 710051, China

2.
Department of Basic, Air Force Engineering University, Xi'an 710051, China

Corresponding author: Zhao Jing-Bo, chjzjb@163.com

Funds: Project supported by the National Natural Science Foundation of China (Grant No. 11504429).

文章全文 : translate this paragraph

参考文献

[1]	邓吉宏, 王柯, 陈国平 2008 航空学报 29 1581 Google Scholar Deng J H, Wang K, Chen G P 2008 Acta Aeronaut. Astronaut. Sin. 29 1581 Google Scholar
[2]	Bolton J S, Shiau N M, Kang Y 1996 JSV 191 317 Google Scholar
[3]	Liu Z, Zhang X X, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[4]	张思文, 吴九汇 2013 62 134302 Google Scholar Zhang S W, Wu J H 2013 Acta Phys. Sin. 62 134302 Google Scholar
[5]	张帅, 郭书祥, 姚宏, 赵静波, 蒋娟娜, 贺子厚 2018 压电与声光 40 754 Google Scholar Zhang S, Guo S X, Yao H, Zhao J B, Jiang J N, He Z H 2018 Piezoelectr. Acoustoopt. 40 754 Google Scholar
[6]	赵甜甜, 林书玉, 段祎林 2018 67 224207 Google Scholar Zhao T T, Lin S Y, Duan W L 2018 Acta Phys. Sin. 67 224207 Google Scholar
[7]	王莎, 林书玉 2019 68 024303 Wang S, Lin S Y 2019 Acta Phys. Sin. 68 024303
[8]	张振方, 郁殿龙, 刘江伟, 温激鸿 2018 67 074301 Google Scholar Zhang Z F, Yu D L, Liu J W, Wen J H 2018 Acta Phys. Sin. 67 074301 Google Scholar
[9]	杜春阳, 郁殿龙, 刘江伟, 温激鸿 2017 66 140701 Google Scholar Du C Y, Yu D L, Liu J W, Wen J H 2017 Acta Phys. Sin. 66 140701 Google Scholar
[10]	Mei J, Yang M, Yang Z Y, Chan N H, Shen P 2018 Phys. Rev. Lett. 101 204301
[11]	Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Shen P 2012 Nat. Commun. 3 756 Google Scholar
[12]	梅军, 马冠聪, 杨旻 2012 物理 41 425 Google Scholar Mei J, Ma G C, Yang M 2012 Physics 41 425 Google Scholar
[13]	Chen Y, Huang G, Zhou X, Hu G, Sun C 2014 J. Acoust. Soc. Am. 136 969 Google Scholar
[14]	Langfeldt F, Gleine W, von Estorff O 2015 JSV 349 315 Google Scholar
[15]	张佳龙, 姚宏, 杜军, 赵静波, 董亚科, 祁鹏山 2016 人工晶体学报 45 2549 Google Scholar Zhang J L, Yao H, Du J, Zhao J B, Dong Y K, Qi P S 2016 J. Synth. Cryst. 45 2549 Google Scholar
[16]	叶超, 苏继龙 2017 噪声与振动控制 37 163 Google Scholar Ye C, Su J L 2017 Noise Vibr. Control 37 163 Google Scholar
[17]	周榕, 吴卫国, 闻轶凡 2017 声学技术 36 297 Zhou Y, Wu W G, Wen Y F 2017 Tech. Acoust. 36 297
[18]	邢拓, 李贤徽, 盖晓玲, 张斌, 谢鹏 2016 声学技术 35 2 Xing T, Li X H, Gai X L, Zhang B, Xie P 2016 Tech. Acoust. 35 2
[19]	Zhang Y, Wen J 2012 JASA 131 3372
[20]	Preumont A 2011 Vibration Control of Active Structures (Berlin: Springer) pp21–59
[21]	Chen S B, Wen J H, Yu D L, Wang G, Wen X 2011 Chin. Phys. B 20 014301 Google Scholar
[22]	Zhang H, Wen J, Xiao Y, Wang G, Wen X 2015 JSV 343 104 Google Scholar
[23]	董亚科, 姚宏, 杜军, 赵静波, 姜久龙 2018 压电与声光 40 860 Google Scholar Dong Y K, Yao H, Du J, Zhao J B, Jiang J L 2018 Piezoelectr. Acoustoopt. 40 860 Google Scholar
[24]	廖涛, 孙小伟, 宋婷, 田俊红, 康太凤, 孙伟彬 2018 67 214208 Google Scholar Liao T, Sun X W, Song T, Tian J H, Kang T F, Sun W B 2018 Acta Phys. Sin. 67 214208 Google Scholar
[25]	孙炜海, 张超群, 鞠桂玲, 潘晶雯 2018 67 194303 Google Scholar Sun W H, Zhang C Q, Jü G L, Pan J W 2018 Acta Phys. Sin. 67 194303 Google Scholar
[26]	Yubao S, Leping F, Jihong W, Dianlong Y, Xisen W 2015 Phys. Lett. A 379 1449 Google Scholar
[27]	陈圣兵 2014 博士学位论文(长沙: 国防科技大学) Chen S B 2014 Ph. D. Dissertation (Changsha: National University of Defense Technology)(in Chinese)
[28]	汪承灏, 赵哲英 1981 声学学报 4 263 Wang C H, Zhao Z Y 1981 Acta Acust. 4 263
[29]	贺子厚, 赵静波, 姚宏, 蒋娟娜, 张帅 2019 压电与声光 41 40 Google Scholar He Z H, Zhao J B, Yao H, Jiang J N, Zhang S 2019 Piezoelectr. Acoustoopt. 41 40 Google Scholar
[30]	Fano U 1961 Phys. Rev. 124 1866 Google Scholar
[31]	潘庭婷, 曹文, 邓彩松, 王鸣, 夏巍, 郝辉 2018 67 157301 Google Scholar Pan T T, Cao W, Deng C S, Wang M, Xia W, Hao H 2018 Acta Phys. Sin. 67 157301 Google Scholar
[32]	Mikhail F, Mikhail V, Alexander N, Yuri S 2017 Nat. Photon. 11 543 Google Scholar

施引文献

图 1 材料结构　(a)结构示意图; (b)结构参数

Fig. 1. Material structure: (a) Structural sketch; (b) structure parameter.

下载: 全尺寸图片幻灯片

图 2 腔体结构

Fig. 2. Cavity structure.

下载: 全尺寸图片幻灯片

图 3 传输损失曲线

Fig. 3. Transmission loss curve.

下载: 全尺寸图片幻灯片

图 4 实验示意图　(a)样件结构; (b)实验装置; (c)样件实物图

Fig. 4. Experimental schematic diagram: (a) Sample structure; (b) experimental facility; (c) physical samples.

下载: 全尺寸图片幻灯片

图 5 大电感　(a)电路图; (b)实物图

Fig. 5. Large inductance: (a) Circuit diagram; (b) physical diagram.

下载: 全尺寸图片幻灯片

图 6 传输损失曲线

Fig. 6. Transmission loss curve.

下载: 全尺寸图片幻灯片

图 7 简化结构示意图

Fig. 7. Simplified structure sketch.

下载: 全尺寸图片幻灯片

图 8 贝塞尔函数曲线

Fig. 8. Bessel function curve.

下载: 全尺寸图片幻灯片

图 9 等效模型示意图

Fig. 9. Schematic diagram of equivalent model.

下载: 全尺寸图片幻灯片

图 10 首阶特征频率

Fig. 10. First natural frequency.

下载: 全尺寸图片幻灯片

图 11 消声原理图

Fig. 11. Anechoic schematic diagram.

下载: 全尺寸图片幻灯片

图 12 隔声峰处的振动模式图　(a) 185 Hz; (b) 485.6 Hz; (c) 896 Hz

Fig. 12. Vibration mode diagram at sound insulation peak: (a) 185 Hz; (b) 485.6 Hz; (c) 969 Hz.

下载: 全尺寸图片幻灯片

图 13 隔声谷处的振动模式图　(a) 115 Hz; (b) 457Hz

Fig. 13. Vibration mode diagram at sound insulation peak: (a) 115 Hz; (b) 457Hz.

下载: 全尺寸图片幻灯片

图 14 隔声谷与传输损失突变处的振动模式图　(a) 687 Hz; (b) 969 Hz; (c) 1129 Hz; (d) 1136 Hz

Fig. 14. Vibration mode diagram at TL peak and TL sudden change: (a) 687 Hz; (b) 969 Hz; (c) 1129 Hz; (d) 1136 Hz

下载: 全尺寸图片幻灯片

图 15 传输损失突变处的振动模式图　(a) 229 Hz; (b) 235 Hz

Fig. 15. Vibration mode diagram at TL sudden change: (a) 229 Hz; (b) 235 Hz.

下载: 全尺寸图片幻灯片

图 16 Fano共振

Fig. 16. Fano resonance.

下载: 全尺寸图片幻灯片

图 17 传输损失曲线m = 0.001, 0.004, 0.006 m

Fig. 17. TL curve m = 0.001, 0.004, 0.006 m.

下载: 全尺寸图片幻灯片

图 18 特征频率

Fig. 18. Eigen frequencies.

下载: 全尺寸图片幻灯片

图 19 第五阶共振模态　(a) m = 0.002 m; (b) m = 0.004 m; (c) m = 0.006 m

Fig. 19. Fifth order vibration: (a) m = 0.002 m; (b) m = 0.004 m; (c) m = 0.006 m.

下载: 全尺寸图片幻灯片

图 20 电路参数不同时隔声量的变化 (a)不同电阻; (b)不同电感

Fig. 20. TL with different circuit parameters: (a) Different resistors; (b) different inductances.

下载: 全尺寸图片幻灯片

表 1 压电材料参数

Table 1. Piezoelectric material parameters.

ρ/kg·m^–3 $s_{11}^{\rm{E}}/{{\rm{m}}^3} \cdot {{\rm{N}}^{ - 1}}$ d₃₁/C·m^–2 $\varepsilon _{33}^{\rm{T}}/{\rm{F}} \cdot {{\rm{m}}^{ - 1}}$

7500 1.65 × 10^–11 –2.74 × 10^–10 3.01 × 10^–8

下载: 导出CSV

表 2 材料参数

Table 2. Material parameters.

Material ρ/kg·m^–3 E/10¹⁰ Pa Possion rate

Silastic 1300 1.175 × 10^–5 0.469
Steel 7780 21.06 0.3

下载: 导出CSV

表 3 模态图

Table 3. Modal diagram.

阶数频率/Hz 模态图阶数频率/Hz 模态图

1 111.77 8 689.74
2 135.84 9 793.01
3 147.67 10 835.10
4 185.63 11 842.97
5 201.65 12 945.92
6 231.21 13 981.43
7 458.62 14 1148.40

下载: 导出CSV

map

[1]	邓吉宏, 王柯, 陈国平 2008 航空学报 29 1581 Google Scholar Deng J H, Wang K, Chen G P 2008 Acta Aeronaut. Astronaut. Sin. 29 1581 Google Scholar
[2]	Bolton J S, Shiau N M, Kang Y 1996 JSV 191 317 Google Scholar
[3]	Liu Z, Zhang X X, Chan C T, Sheng P 2000 Science 289 1734 Google Scholar
[4]	张思文, 吴九汇 2013 62 134302 Google Scholar Zhang S W, Wu J H 2013 Acta Phys. Sin. 62 134302 Google Scholar
[5]	张帅, 郭书祥, 姚宏, 赵静波, 蒋娟娜, 贺子厚 2018 压电与声光 40 754 Google Scholar Zhang S, Guo S X, Yao H, Zhao J B, Jiang J N, He Z H 2018 Piezoelectr. Acoustoopt. 40 754 Google Scholar
[6]	赵甜甜, 林书玉, 段祎林 2018 67 224207 Google Scholar Zhao T T, Lin S Y, Duan W L 2018 Acta Phys. Sin. 67 224207 Google Scholar
[7]	王莎, 林书玉 2019 68 024303 Wang S, Lin S Y 2019 Acta Phys. Sin. 68 024303
[8]	张振方, 郁殿龙, 刘江伟, 温激鸿 2018 67 074301 Google Scholar Zhang Z F, Yu D L, Liu J W, Wen J H 2018 Acta Phys. Sin. 67 074301 Google Scholar
[9]	杜春阳, 郁殿龙, 刘江伟, 温激鸿 2017 66 140701 Google Scholar Du C Y, Yu D L, Liu J W, Wen J H 2017 Acta Phys. Sin. 66 140701 Google Scholar
[10]	Mei J, Yang M, Yang Z Y, Chan N H, Shen P 2018 Phys. Rev. Lett. 101 204301
[11]	Mei J, Ma G C, Yang M, Yang Z Y, Wen W J, Shen P 2012 Nat. Commun. 3 756 Google Scholar
[12]	梅军, 马冠聪, 杨旻 2012 物理 41 425 Google Scholar Mei J, Ma G C, Yang M 2012 Physics 41 425 Google Scholar
[13]	Chen Y, Huang G, Zhou X, Hu G, Sun C 2014 J. Acoust. Soc. Am. 136 969 Google Scholar
[14]	Langfeldt F, Gleine W, von Estorff O 2015 JSV 349 315 Google Scholar
[15]	张佳龙, 姚宏, 杜军, 赵静波, 董亚科, 祁鹏山 2016 人工晶体学报 45 2549 Google Scholar Zhang J L, Yao H, Du J, Zhao J B, Dong Y K, Qi P S 2016 J. Synth. Cryst. 45 2549 Google Scholar
[16]	叶超, 苏继龙 2017 噪声与振动控制 37 163 Google Scholar Ye C, Su J L 2017 Noise Vibr. Control 37 163 Google Scholar
[17]	周榕, 吴卫国, 闻轶凡 2017 声学技术 36 297 Zhou Y, Wu W G, Wen Y F 2017 Tech. Acoust. 36 297
[18]	邢拓, 李贤徽, 盖晓玲, 张斌, 谢鹏 2016 声学技术 35 2 Xing T, Li X H, Gai X L, Zhang B, Xie P 2016 Tech. Acoust. 35 2
[19]	Zhang Y, Wen J 2012 JASA 131 3372
[20]	Preumont A 2011 Vibration Control of Active Structures (Berlin: Springer) pp21–59
[21]	Chen S B, Wen J H, Yu D L, Wang G, Wen X 2011 Chin. Phys. B 20 014301 Google Scholar
[22]	Zhang H, Wen J, Xiao Y, Wang G, Wen X 2015 JSV 343 104 Google Scholar
[23]	董亚科, 姚宏, 杜军, 赵静波, 姜久龙 2018 压电与声光 40 860 Google Scholar Dong Y K, Yao H, Du J, Zhao J B, Jiang J L 2018 Piezoelectr. Acoustoopt. 40 860 Google Scholar
[24]	廖涛, 孙小伟, 宋婷, 田俊红, 康太凤, 孙伟彬 2018 67 214208 Google Scholar Liao T, Sun X W, Song T, Tian J H, Kang T F, Sun W B 2018 Acta Phys. Sin. 67 214208 Google Scholar
[25]	孙炜海, 张超群, 鞠桂玲, 潘晶雯 2018 67 194303 Google Scholar Sun W H, Zhang C Q, Jü G L, Pan J W 2018 Acta Phys. Sin. 67 194303 Google Scholar
[26]	Yubao S, Leping F, Jihong W, Dianlong Y, Xisen W 2015 Phys. Lett. A 379 1449 Google Scholar
[27]	陈圣兵 2014 博士学位论文(长沙: 国防科技大学) Chen S B 2014 Ph. D. Dissertation (Changsha: National University of Defense Technology)(in Chinese)
[28]	汪承灏, 赵哲英 1981 声学学报 4 263 Wang C H, Zhao Z Y 1981 Acta Acust. 4 263
[29]	贺子厚, 赵静波, 姚宏, 蒋娟娜, 张帅 2019 压电与声光 41 40 Google Scholar He Z H, Zhao J B, Yao H, Jiang J N, Zhang S 2019 Piezoelectr. Acoustoopt. 41 40 Google Scholar
[30]	Fano U 1961 Phys. Rev. 124 1866 Google Scholar
[31]	潘庭婷, 曹文, 邓彩松, 王鸣, 夏巍, 郝辉 2018 67 157301 Google Scholar Pan T T, Cao W, Deng C S, Wang M, Xia W, Hao H 2018 Acta Phys. Sin. 67 157301 Google Scholar
[32]	Mikhail F, Mikhail V, Alexander N, Yuri S 2017 Nat. Photon. 11 543 Google Scholar

[1]	胥强荣, 朱洋, 林康, 沈承, 卢天健. 一种具有动态磁负刚度薄膜声学超材料的低频隔声特性. , 2022, 71(21): 214301. doi: 10.7498/aps.71.20221058
[2]	徐琦, 孙小伟, 宋婷, 温晓东, 刘禧萱, 王羿文, 刘子江. 不同缺陷态下具有高光力耦合率的新型一维光力晶体纳米梁. , 2021, 70(22): 224210. doi: 10.7498/aps.70.20210925
[3]	曹明鹏, 吴晓鹏, 管宏山, 单光宝, 周斌, 杨力宏, 杨银堂. 基于对偶单元法的三维集成微系统电热耦合分析. , 2021, 70(7): 074401. doi: 10.7498/aps.70.20201628
[4]	姚宽明, 姚靖仪, 海照, 李登峰, 解兆谦, 于欣格. 用于触觉感知的自供能可拉伸压电橡胶皮肤电子器件. , 2020, 69(17): 178701. doi: 10.7498/aps.69.20200664
[5]	孙伟彬, 王婷, 孙小伟, 康太凤, 谭自豪, 刘子江. 新型二维三组元压电声子晶体板的缺陷态及振动能量回收. , 2019, 68(23): 234206. doi: 10.7498/aps.68.20190260
[6]	李林利, 薛春霞. 压电材料双曲壳热弹耦合作用下的混沌运动. , 2019, 68(1): 010501. doi: 10.7498/aps.68.20181714
[7]	贺子厚, 赵静波, 姚宏, 陈鑫. 薄膜底面Helmholtz腔声学超材料的隔声性能. , 2019, 68(21): 214302. doi: 10.7498/aps.68.20191131
[8]	廖涛, 孙小伟, 宋婷, 田俊红, 康太凤, 孙伟彬. 新型二维压电声子晶体板带隙可调性研究. , 2018, 67(21): 214208. doi: 10.7498/aps.67.20180611
[9]	赵运进, 田锰, 黄勇刚, 王小云, 杨红, 米贤武. 基于有限元法的光子并矢格林函数重整化及其在自发辐射率和能级移动研究中的应用. , 2018, 67(19): 193102. doi: 10.7498/aps.67.20180898
[10]	汤立国. 压电材料全矩阵材料常数超声谐振谱反演技术中的变温模式识别. , 2017, 66(2): 027703. doi: 10.7498/aps.66.027703
[11]	陈艳, 周桂耀, 夏长明, 侯峙云, 刘宏展, 王超. 具有双模特性的大模场面积微结构光纤的设计. , 2014, 63(1): 014701. doi: 10.7498/aps.63.014701
[12]	王玥, 刘丽炜, 胡思怡, 李其扬, 孙振皓, 苗馨卉, 杨小川, 张喜和. 基于COMSOL Multiphysics对Cu2S量子点的表面等离激元共振模拟研究. , 2013, 62(19): 197803. doi: 10.7498/aps.62.197803
[13]	于歌, 韩奇钢, 李明哲, 贾晓鹏, 马红安, 李月芬. 新型圆角式高压碳化钨硬质合金顶锤的有限元分析. , 2012, 61(4): 040702. doi: 10.7498/aps.61.040702
[14]	齐跃峰, 乔汉平, 毕卫红, 刘燕燕. 热激法光子晶体光纤光栅制备工艺中热传导特性研究. , 2011, 60(3): 034214. doi: 10.7498/aps.60.034214
[15]	陈蕾, 李平, 文玉梅, 王东. 高磁导率材料FeCuNbSiB对超磁致伸缩/压电层合材料磁电性能的影响. , 2011, 60(6): 067501. doi: 10.7498/aps.60.067501
[16]	刘全喜, 钟鸣. 激光二极管阵列端面抽运复合棒状激光器热效应的有限元法分析. , 2010, 59(12): 8535-8541. doi: 10.7498/aps.59.8535
[17]	韩奇钢, 马红安, 肖宏宇, 李瑞, 张聪, 李战厂, 田宇, 贾晓鹏. 基于有限元法分析宝石级金刚石的合成腔体温度场. , 2010, 59(3): 1923-1927. doi: 10.7498/aps.59.1923
[18]	韩奇钢, 贾晓鹏, 马红安, 李瑞, 张聪, 李战厂, 田宇. 基于三维有限元法模拟分析六面顶顶锤的热应力. , 2009, 58(7): 4812-4816. doi: 10.7498/aps.58.4812
[19]	卞雷祥, 文玉梅, 李平. 磁致伸缩/压电叠层复合材料磁-机-电耦合系数分析. , 2009, 58(6): 4205-4213. doi: 10.7498/aps.58.4205
[20]	袁玲, 沈中华, 倪晓武, 陆建. 激光在近表面弹性性质梯度变化的材料中激发超声波的数值分析. , 2007, 56(12): 7058-7063. doi: 10.7498/aps.56.7058

计量

文章访问数: 12368
PDF下载量: 309
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

基于压电材料的薄膜声学超材料隔声性能研究