-
当声波在含气泡的液体中传播时会出现共振传播现象, 即在气泡的共振频率附近声衰减和声速会显著地增大,这是声空化领域的一个重要现象.以往的研究一般假设液体中只存在单一种类的气泡, 因此忽略了声波共振传播的某些重要信息. 本文研究了含混合气泡液体中声波的共振传播, 混合气泡是指液体中包含多种静态半径不同的气泡. 结果显示:在这种系统中存在声波共振传播的抑制效应, 即与含单一种类气泡的系统相比, 在含混合气泡的系统中声波的共振衰减和共振声速会明显变小. 对于两种气泡混合、多种气泡混合以及气泡满足某种连续分布的系统, 研究了抑制效应的本质和主要特征, 此外还探究了黏性和空化率等对抑制效应的影响. 本文的研究结果是对该领域现有知识的必要补充.There is the resonant propagation phenomenon of acoustic wave in bubbly liquid, i.e., the attenuation coefficient and the velocity of acoustic wave in range of resonant frequencies of bubbles can become very large. In previous papers, generally adopted was a simplified assumption that there is a single type of bubble in a liquid. It restricts our understanding of the resonant propagation phenomenon. In this paper the resonant propagation of acoustic wave in a liquid with mixed bubbles is studied. Here, static radii of bubbles are different from each other. Research results show that there is a restraining effect of the resonant propagation of acoustic wave in liquid with mixed bubbles. The attenuation coefficient and the velocity of acoustic wave in the liquid with mixed bubbles are obviously less than those in the liquid containing bubbles with the same static radius. The nature of the restraining effect is that the resonant vibration of bubbles is weakened due to the interaction between bubbles with different static radii. Some important properties of the restraining effect are investigated for all kinds of liquid systems with mixed bubbles. Moreover, the effect of the viscosity and the rate of cavitation on the restraining effect are also studied. Research results are shown as follows. 1) Comparing with bigger bubbles, resonant characteristic quantities (such as the attenuation coefficient and the velocity of acoustic wave) caused by smaller bubbles can be reduced more obviously; 2) the efficiency of the restraining effect increases with the number of types of bubbles increasing, however, it will gradually reach to a stable value when the number of types of bubbles is large; 3) the bandwidth of the resonant absorption of acoustic wave is dramatically affected by the distribution function of the percentage of the number of bubbles. The bandwidth of the resonant absorption will become large as the percentage of the number of smaller bubbles increases.
-
Keywords:
- mixed bubbles /
- acoustic cavitation /
- attenuation coefficient /
- linear acoustic wave
[1] 陈伟中 2014 声空化物理 (北京: 科学出版社)第371−421页
Chen W Z 2014 Acoustic Cavitation Physics (Beijing: Science Press) pp371−421 (in Chinese)
[2] Christopher E B 1995 Cavitation and Bubble Dynamics (Oxford: OxfordvUniversity Press) pp15−47
[3] 应崇福 2008 应用声学 27 333
Google Scholar
Ying C F 2008 J. Appl. Acoust. 27 333
Google Scholar
[4] 王寻, 陈伟中, 杨景 2015 声学技术 34 33
Wang X, Chen W Z, Yang J 2015 Tech. Acoust. 34 33
[5] Commander K W, Prosperetti A 1989 J. Acoust. Soc. Am. 85 732
Google Scholar
[6] 徐贞, 张迪, 陈时, 等 2018 中国科学: 物理学 力学 天文学 48 044301
Xu Z, Zhang D, Chen S, et al. 2018 Sci. Sin. Phys. Mech. Astron. 48 044301
[7] 王勇, 林书玉, 张小丽 2013 62 064304
Wang Y, Lin S Y, Zhang X L 2013 Acta Phys. Sin. 62 064304
[8] 王成会, 林书玉 2008 陕西师范大学学报 36 30
Google Scholar
Wang C H, Lin S Y 2008 J. Shaanxi Norm. Univ. 36 30
Google Scholar
[9] 王勇, 林书玉, 张小丽 2014 63 034301
Google Scholar
Wang Y, Lin S Y, Zhang X L 2014 Acta Phys. Sin. 63 034301
Google Scholar
[10] 陈伟中 2018 应用声学 37 675
Google Scholar
Chen W Z 2018 J. Appl. Acoust. 37 675
Google Scholar
[11] 朱哲民, 杜功焕 1995 声学学报 6 425
Zhu Z M, Du H G 1995 Acta Acust. 6 425
[12] An Y 2012 Phys. Rev. E 85 016305
Google Scholar
[13] Vanhille C, Campospozuelo C 2013 Ultrason. Sonochem. 20 963
Google Scholar
[14] Vanhille C, Campospozuelo C 2012 Ultrason. Sonochem. 19 217
Google Scholar
[15] Lebon G S B, Tzanakis I, Djambazov G, et al. 2017 Ultrason. Sonochem. 37 660
Google Scholar
[16] Zhang Y, Guo Z, Du X 2018 Appl. Therm. Eng. 133 483
Google Scholar
[17] Zhang Y, Du X 2015 Ultrason. Sonochem. 26 119
Google Scholar
[18] Trujillo F J 2018 Ultrason. Sonochem. 47 75
Google Scholar
[19] 张鹏利, 林书玉, 张涛 2013 中国科学: 物理学 力学 天文学 43 249
Zhang P L, Lin S Y, Zhang T 2013 Sci. Sin. Phys. Mech. Astron. 43 249
[20] 苗博雅, 安宇 2015 64 225
Google Scholar
Miao B Y, An Y 2015 Acta Phys. Sin. 64 225
Google Scholar
[21] 王德鑫, 那仁满都拉 2018 67 037802
Google Scholar
Wang D X, Naranmandula 2018 Acta Phys. Sin. 67 037802
Google Scholar
[22] Keller J B, Kolodner I I 1956 J. Appl. Phys. 2 71152
-
图 1 含两种混合气泡的液体中声波的衰减谱
Fig. 1. Attenuation spectrums of acoustic waves in liquids with two kinds of bubbles.
图 2 含两种混合气泡的液体中声波衰减谱的相对峰值和相对带宽与
${\theta _1}$ (或者${\theta _2}$ )的关系Fig. 2. Relationships between
${\theta _1}$ (${\theta _2}$ )and relative peak values or bandwidths of attenuation spectrums of acoustic waves in liquids with two kinds of bubbles.
图 3 在含两种混合气泡的液体中, 不同
${\theta _1}$ (或者${\theta _2}$ )对应的声波的声速谱 图中${\theta _1}$ 分别是0, 0.20, 0.40, 0.60, 0.80, 0.90, 0.95, 1.00, 或者${\theta _2}$ 分别是0, 0.05, 0.10, 0.20, 0.40, 0.60, 0.80, 1.00. 左边的箭头表示${\theta _2}$ 增加的方向, 右边的箭头表示${\theta _1}$ 增加的方向Fig. 3. Speed spectrums for different
${\theta _1}$ (or${\theta _2}$ ) in liquids with two kinds of bubbles. Here${\theta _1}$ is 0, 0.20, 0.40, 0.60, 0.80, 0.90, 0.95 and 1.00, respectively.${\theta _2}$ is 0, 0.05, 0.10, 0.20, 0.40, 0.60, 0.80 and 1.00, respectively. The white arrow indicates the direction of increase of${\theta _2}$ , the gray arrow indicates the direction of increase of${\theta _1}$ .
图 4 在含两种混合气泡的液体中,
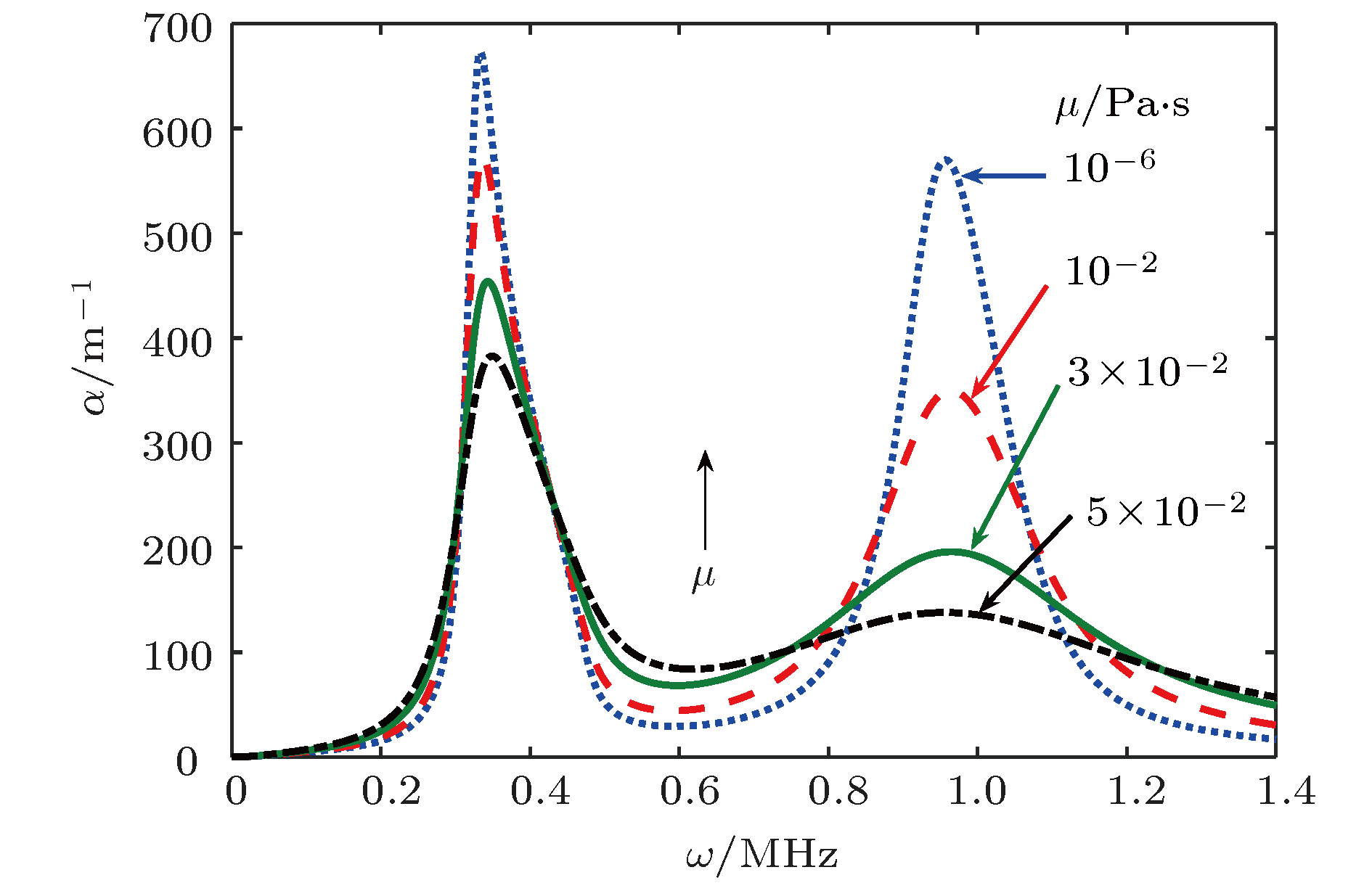
${\beta _0}$ 不同时声波的相对衰减谱 图中${\theta _1} = 0.8$ ,${\beta _0}$ 分别是${10^{ - 6}}$ ,${10^{ - 4}}$ ,${10^{ - 3}}$ 和${10^{ - 2}}$ , 箭头表示该角频率区域${\beta _0}$ 增加的方向Fig. 4. Attenuation spectrums for different
${\beta _0}$ in liquids with two kinds of bubbles. Here,${\theta _1} = 0.8$ ,${\beta _0}$ is${10^{ - 6}}$ ,${10^{ - 4}}$ ,${10^{ - 3}}$ and${10^{ - 2}}$ , respectively. The arrow indicates the direction of increase of${\beta _0}$ .
图 5 在含两种混合气泡的液体中,
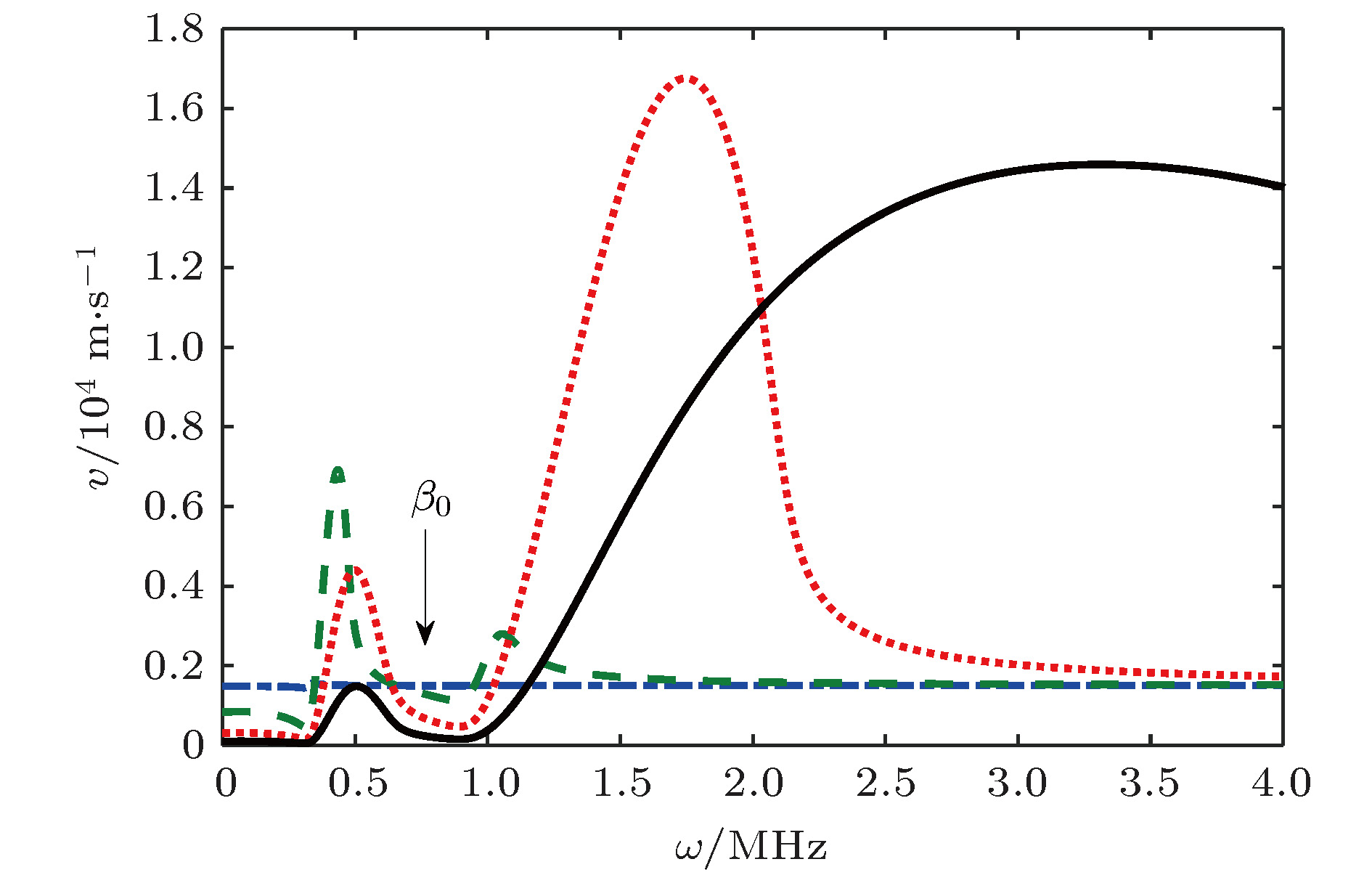
${\beta _0}$ 不同时声波的声速谱 图中${\theta _1} = 0.8$ ,${\beta _0}$ 分别是${10^{ - 6}}$ ,${10^{ - 4}}$ ,${10^{ - 3}}$ 和${10^{ - 2}}$ , 箭头表示该角频率区域${\beta _0}$ 增加的方向Fig. 5. Speed spectrums for different
${\beta _0}$ in liquids with two kinds of bubbles. Here,${\theta _1} = 0.8$ ,${\beta _0}$ is${10^{ - 6}}$ ,${10^{ - 4}}$ ,${10^{ - 3}}$ and${10^{ - 2}}$ , respectively. The arrow indicates the direction of increase of${\beta _0}$ .
图 6 在两种混合气泡的液体中黏度不同时声波的衰减谱
Fig. 6. Attenuation spectrums for different viscosity in liquids with two kinds of bubbles.
图 7 在含多种混合气泡的液体中气泡的种类数不同时声波的衰减谱. 图中
${\theta _j} = 1/M$ ,${R_j} = 20 \!+ \!40\left( {j\! -\! 1} \right)/\left( {M \!-\! 1} \right)$ $\left( {{\text{μ}}{\rm{m}}} \right)$ ($j = 1, 2, \cdots, M$ ).Fig. 7. Attenuation spectrums for different
$M$ . Here,${\theta _j} = 1/M$ ,${R_j} = 20 + 40\left( {j - 1} \right)/\left( {M - 1} \right)\left( {{\text{μ}}{\rm{m}}} \right)$ ,$j = 1, 2, $ $\cdots, M$ .
图 8 气泡满足不同分布时声波的衰减谱 细实线是参考曲线, 它对应着存在两种混合气泡的情况; 对其他曲线而言, 各个气泡的静态半径分别是R = 20 + 40(j – 1)/
$\left( {M - 1} \right)\left( {{\text{μ}}{\rm{m}}} \right)$ ,$j = 1, 2, \cdots, M$ ,$M = 21$ Fig. 8. Attenuation spectrums for different distribution functions of bubble number. The thin solid line indicates the systems with two kinds of bubbles. Here, R =
$ 20 + 40\left( {j - 1} \right)/\left( {M - 1} \right)\left( {{\text{μ}}{\rm{m}}} \right)$ ,$j = 1, 2, \cdots, M$ . -
[1] 陈伟中 2014 声空化物理 (北京: 科学出版社)第371−421页
Chen W Z 2014 Acoustic Cavitation Physics (Beijing: Science Press) pp371−421 (in Chinese)
[2] Christopher E B 1995 Cavitation and Bubble Dynamics (Oxford: OxfordvUniversity Press) pp15−47
[3] 应崇福 2008 应用声学 27 333
Google Scholar
Ying C F 2008 J. Appl. Acoust. 27 333
Google Scholar
[4] 王寻, 陈伟中, 杨景 2015 声学技术 34 33
Wang X, Chen W Z, Yang J 2015 Tech. Acoust. 34 33
[5] Commander K W, Prosperetti A 1989 J. Acoust. Soc. Am. 85 732
Google Scholar
[6] 徐贞, 张迪, 陈时, 等 2018 中国科学: 物理学 力学 天文学 48 044301
Xu Z, Zhang D, Chen S, et al. 2018 Sci. Sin. Phys. Mech. Astron. 48 044301
[7] 王勇, 林书玉, 张小丽 2013 62 064304
Wang Y, Lin S Y, Zhang X L 2013 Acta Phys. Sin. 62 064304
[8] 王成会, 林书玉 2008 陕西师范大学学报 36 30
Google Scholar
Wang C H, Lin S Y 2008 J. Shaanxi Norm. Univ. 36 30
Google Scholar
[9] 王勇, 林书玉, 张小丽 2014 63 034301
Google Scholar
Wang Y, Lin S Y, Zhang X L 2014 Acta Phys. Sin. 63 034301
Google Scholar
[10] 陈伟中 2018 应用声学 37 675
Google Scholar
Chen W Z 2018 J. Appl. Acoust. 37 675
Google Scholar
[11] 朱哲民, 杜功焕 1995 声学学报 6 425
Zhu Z M, Du H G 1995 Acta Acust. 6 425
[12] An Y 2012 Phys. Rev. E 85 016305
Google Scholar
[13] Vanhille C, Campospozuelo C 2013 Ultrason. Sonochem. 20 963
Google Scholar
[14] Vanhille C, Campospozuelo C 2012 Ultrason. Sonochem. 19 217
Google Scholar
[15] Lebon G S B, Tzanakis I, Djambazov G, et al. 2017 Ultrason. Sonochem. 37 660
Google Scholar
[16] Zhang Y, Guo Z, Du X 2018 Appl. Therm. Eng. 133 483
Google Scholar
[17] Zhang Y, Du X 2015 Ultrason. Sonochem. 26 119
Google Scholar
[18] Trujillo F J 2018 Ultrason. Sonochem. 47 75
Google Scholar
[19] 张鹏利, 林书玉, 张涛 2013 中国科学: 物理学 力学 天文学 43 249
Zhang P L, Lin S Y, Zhang T 2013 Sci. Sin. Phys. Mech. Astron. 43 249
[20] 苗博雅, 安宇 2015 64 225
Google Scholar
Miao B Y, An Y 2015 Acta Phys. Sin. 64 225
Google Scholar
[21] 王德鑫, 那仁满都拉 2018 67 037802
Google Scholar
Wang D X, Naranmandula 2018 Acta Phys. Sin. 67 037802
Google Scholar
[22] Keller J B, Kolodner I I 1956 J. Appl. Phys. 2 71152
下载:
计量
- 文章访问数: 7114
- PDF下载量: 70
- 被引次数: 0
