中性原子量子计算研究进展

许鹏; 何晓东; 刘敏; 王谨; 詹明生

doi:10.7498/aps.68.20182133

摘要

相互作用可控、相干时间较长的中性单原子体系具备在1 mm²的面积上提供成千上万个量子比特的规模化集成的优势, 是进行量子模拟、实现量子计算的有力候选者. 近几年中性单原子体系在实验上取得了快速的发展, 完成了包括50个单原子的确定性装载、二维和三维阵列中单个原子的寻址和操控、量子比特相干时间的延长、基于里德伯态的两比特量子门的实现和原子态的高效读出等, 这些工作极大地推动了该体系在量子模拟和量子计算方面的应用. 本文综述了该体系在量子计算方面的研究进展, 并介绍了我们在其中所做的两个贡献: 一是实现了“魔幻强度光阱”, 克服了光阱中原子退相干的首要因素, 将原子相干时间提高了百倍, 使得相干时间与比特操作时间的比值高达10⁵; 二是利用异核原子共振频率的差异建立了低串扰的异核单原子体系, 并利用里德伯阻塞效应首次实现了异核两原子的量子受控非门和量子纠缠, 将量子计算的实验研究拓展至异核领域. 最后, 分析了中性单原子体系在量子模拟和量子计算方面进一步发展面临的挑战与瓶颈.

关键词:

Abstract

As an important candidate for quantum simulation and quantum computation, a microscopic array of single atoms confined in optical dipole traps is advantageous in controlled interaction, long coherence time, and scalability of providing thousands of qubits in a small footprint of less than 1 mm². Recently, several breakthroughs have greatly advanced the applications of neutral atom system in quantum simulation and quantum computation, such as atom-by-atom assembling of defect-free arbitrary atomic arrays, single qubit addressing and manipulating in two-dimensional and three-dimensional arrays, extending coherence time of atomic qubits, controlled-NOT (C-NOT) gate based on Rydberg interactions, high fidelity readout, etc.In this paper, the experimental progress of quantum computation based on trapped single neutral atoms is reviewed, along with two contributions done by single atom group in Wuhan Institute of Physics and Mathematics of Chinese Academy of Sciences. First, a magic-intensity trapping technique is developed and used to mitigate the detrimental decoherence effects which are induced by light shift and substantially enhance the coherence time to 225 ms which is 100 times as large as our previous coherence time thus amplifying the ratio between coherence time and single qubit operation time to 10⁵. Second, the difference in resonant frequency between the two atoms of different isotopes is used to avoid crosstalking between individually addressing and manipulating nearby atoms. Based on this heteronuclear single atom system, the heteronuclear C-NOT quantum gate and entanglement of an Rb-85 atom and an Rb-87 atom are demonstrated via Rydberg blockade for the first time. These results will trigger the quests for new protocols and schemes to use the double species for quantum computation with neutral atoms. In the end, the challenge and outlook for further developing the neutral atom system in quantum simulation and quantum computation are also reviewed.

Keywords:

作者及机构信息

1.
中国科学院武汉物理与数学研究所, 波谱与原子分子物理国家重点实验室, 武汉　430071

2.
中国科学院冷原子物理中心, 武汉　430071

通信作者: 詹明生, mszhan@wipm.ac.cn

基金项目: 国家重点研发计划(批准号: 2016YFA0302800, 2017YFA0304501)、中国科学院先导专项(批准号: XDB21010100)和国家自然科学基金(批准号: 11674361, 11774389)资助的课题.

Authors and contacts

1.
State Key Laboratory of Magnetic Resonance and Atomic and Molecular Physics, Wuhan Institute of Physics and Mathematics, Chinese Academy of Sciences, Wuhan 430071, China

2.
Center for Cold Atom Physics, Chinese Academy of Sciences, Wuhan 430071, China

Corresponding author: Zhan Ming-Sheng, mszhan@wipm.ac.cn

Funds: Project supported by the National Key Research and Development Program of China (Grant Nos. 2016YFA0302800, 2017YFA0304501), the Strategic Priority Research Program of the Chinese Academy of Sciences, China (Grant No. XDB21010100), and the National Natural Science Foundation of China (Grant Nos. 11674361, 11774389).

文章全文 : translate this paragraph

参考文献

[1]	Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien J L 2010 Nature 464 45 Google Scholar
[2]	Benhelm J, Kirchmair G, Roos C F, Blatt R 2008 Nat. Phys. 4 463 Google Scholar
[3]	Wendin G 2017 Rep. Prog. Phys. 80 106001 Google Scholar
[4]	O’Brien J L 2007 Science 318 1567 Google Scholar
[5]	Veldhorst M, Yang C H, Hwang J C C, Huang W, Dehollain J P, Muhonen J T, Simmons S, Laucht A, Hudson F E, Itoh K M, Morello A, Dzurak A S 2015 Nature 526 410 Google Scholar
[6]	Childress L, Hanson R 2013 MRS Bulletin 38 134 Google Scholar
[7]	Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313 Google Scholar
[8]	周正威, 陈巍, 孙方稳, 项国勇, 李传锋 2012 科学通报 57 1498 Google Scholar Zhou Z W, Chen W, Sun F W, Xiang G Y, Li C F 2012 Chin. Sci. Bull. 57 1498 Google Scholar
[9]	Wu T Y, Kumar A, Mejia F G, Weiss D S 2018 arxiv: 1809.09197 [physics.atom-ph]
[10]	Saffman M 2018 Nat. Sci. Rev. nwy088 Google Scholar
[11]	Saffman M 2016 J. Phys. B: At. Mol. Opt. Phys. 49 202001 Google Scholar
[12]	Barredo D, Lienhard V, de Léséleuc S, Lahaye T, Browaeys A 2018 Nature 561 79 Google Scholar
[13]	Barredo D, de Léséleuc S, Lienhard V, Lahaye T, Browaeys A 2016 Science 354 1021 Google Scholar
[14]	Endres M, Bernien H, Keesling A, Levine H, Anschuetz E R, Krajenbrink A, Senko C, Vuletic V, Greiner M, Lukin M D 2016 Science 354 1024 Google Scholar
[15]	Wang Y, Kumar A, Wu T Y, Weiss D S 2016 Science 352 1562 Google Scholar
[16]	Xia T, Lichtman M, Maller K, Carr A W, Piotrowicz M J, Isenhower L, Saffman M 2015 Phys. Rev. Lett. 114 100503 Google Scholar
[17]	Yang J H, He X D, Guo R J, Xu P, Wang K P, Sheng C, Liu M, Wang J, Derevianko A, Zhan M S 2016 Phys. Rev. Lett. 117 123201 Google Scholar
[18]	Li G, Zhang S, Isenhower L, Maller K, Saffman M 2012 Opt. Lett. 37 851 Google Scholar
[19]	Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503 Google Scholar
[20]	Zeng Y, Xu P, He X D, Liu Y Y, Liu M, Wang J, Papoular D J, Shlyapnikov G V, Zhan M S 2017 Phys. Rev. Lett. 119 160502 Google Scholar
[21]	Kwon M, Ebert M F, Walker T G, Saffman M 2017 Phys. Rev. Lett. 119 180504 Google Scholar
[22]	Martinez-Dorantes M, Alt W, Gallego J, Ghosh S, Ratschbacher L, Völzke Y, Meschede D 2017 Phys. Rev. Lett. 119 180503 Google Scholar
[23]	DiVincenzo D P 2000 Fortschr. Phys. 48 771 Google Scholar
[24]	Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39 Google Scholar
[25]	Schlosser N, Reymond G, Protsenko I, Grangier P 2001 Nature 411 1024 Google Scholar
[26]	Kim H, Lee W, Lee H, Jo H, Song Y, Ahn J 2016 Nat. Commun. 7 13317 Google Scholar
[27]	Kumar A, Wu T Y, Giraldo F, Weiss D S 2018 Nature 561 83 Google Scholar
[28]	Walker T G, Saffman M 2012 Adv. At. Mol. Opt. Phys. 61 81 Google Scholar
[29]	Kuhr S, Alt W, Schrader D, Dotsenko I, Miroshnychenko Y, Rauschenbeutel A, Meschede D 2005 Phys. Rev. A 72 023406 Google Scholar
[30]	Wang Y, Zhang X L, Corcovilos T A, Kumar A, Weiss D S 2015 Phys. Rev. Lett. 115 043003 Google Scholar
[31]	Yavuz D D, Kulatunga P B, Urban E, Johnson T A, Proite N, Henage T, Walker T G, Saffman M 2006 Phys. Rev. Lett. 96 063001 Google Scholar
[32]	Schrader D, Dotsenko I, Khudaverdyan M, Miroshnychenko Y, Rauschenbeutel A, Meschede D 2004 Phys. Rev. Lett. 93 150501 Google Scholar
[33]	Bakr W S, Gillen J T, Peng A, Fölling S, Greiner M 2009 Nature 462 74 Google Scholar
[34]	Sherson J F, Weitenberg C, Endres M, Cheneau M, Bloch I, Kuhr S 2010 Nature 467 68 Google Scholar
[35]	Haller E, Hudson J, Kelly A, Cotta D A, Peaudecerf B, Bruce G D, Kuhr S 2015 Nat. Phys. 11 738 Google Scholar
[36]	Weitenberg C, Endres M, Sherson J F, Cheneau M, Schauẞ P, Fukuhara T, Bloch I, Kuhr S 2011 Nature 471 319 Google Scholar
[37]	Knill E, Leibfried D, Reichle R, Britton J, Blakestad R B, Jost J D, Langer C, Ozeri R, Seidelin S, Wineland D J 2008 Phys. Rev. A 77 012307 Google Scholar
[38]	Volz J, Weber M, Schlenk D, Rosenfeld W, Vrana J, Saucke K, Kurtsiefer C, Weinfurter H 2006 Phys. Rev. Lett. 96 030404 Google Scholar
[39]	Hofmann J, Krug M, Ortegel N, Gérard L, Weber M, Rosenfeld W, Weinfurter H 2012 Science 337 72 Google Scholar
[40]	Jaksch D, Briegel H J, Cirac J I, Gardiner C W, Zoller P 1999 Phys. Rev. Lett. 82 1975 Google Scholar
[41]	Strauch F W, Edwards M, Tiesinga E, Williams C, Clark C W 2008 Phys. Rev. A 77 050304 Google Scholar
[42]	Mandel O, Greiner M, Widera A, Rom T, Hänsch T W, Bloch I 2003 Nature 425 937 Google Scholar
[43]	Anderlini M, Lee P J, Brown B L, Strabley J S, Phillips W D, Porto J V 2007 Nature 448 452 Google Scholar
[44]	Kaufman A M, Lester B J, Regal C A 2012 Phys. Rev. X 2 041014 Google Scholar
[45]	Thompson J D, Tiecke T G, Zibrov A S, Vuletic′ V, Lukin M D 2013 Phys. Rev. Lett. 110 133001 Google Scholar
[46]	Kaufman A M, Lester B J, Foss-Feig M, Wall M L, Rey A M, Regal C A 2015 Nature 527 208 Google Scholar
[47]	Jaksch D, Cirac J I, Zoller P, Rolston S L, Cote R, Lukin M D 2000 Phys. Rev. Lett. 85 2208 Google Scholar
[48]	Petrosyan D, Motzoi F, Saffman M, MØlmer K 2017 Phys. Rev. A 96 042306 Google Scholar
[49]	Keating T, Cook R L, Hankin A M, Jau Y Y, Biedermann G W, Deutsch I H 2015 Phys. Rev. A 91 012337 Google Scholar
[50]	Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110 Google Scholar
[51]	Gaëtan A, Miroshnychenko M, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nat. Phys. 5 115 Google Scholar
[52]	Wilk T, Gaëtan A, Evellin C, Wolters J, Miroshnychenko J, Grangier P, Browaeys A 2010 Phys. Rev. Lett. 104 010502 Google Scholar
[53]	Zhang X L, Isenhower L, Gill A T, Walker T G, Saffman M 2010 Phys. Rev. A 82 030306 Google Scholar
[54]	Maller K M, Lichtman M T, Xia T, Sun Y, Piotrowicz M J, Carr A W, Isenhower L, Saffman M 2015 Phys. Rev. A 92 022336 Google Scholar
[55]	Kuhr S, Alt W, Schrader D, Dotsenko I, Miroshnychenko Y, Rosenfeld W, Khudaverdyan M, Gomer V, Rauschenbeutel A, Meschede D 2003 Phys. Rev. Lett. 91 213002 Google Scholar
[56]	Fuhrmanek A, Bourgain R, Sortais Y R P, Browaeys A 2011 Phys. Rev. Lett. 106 133003 Google Scholar
[57]	Gibbons M J, Hamley C D, Shi C Y, Chapman M S 2011 Phys. Rev. Lett. 106 133002 Google Scholar
[58]	He J, Yang B D, Zhang T C, Wang J M 2011 Phys. Scr. 84 025302 Google Scholar
[59]	Dai H N, Yang B, Reingruber A, Xu X F, Jiang X, Chen Y A, Yuan Z S, Pan J W 2016 Nat. Phys. 12 783 Google Scholar
[60]	Yu S, He X D, Xu P, Liu M, Wang J, Zhan M S 2012 Chin. Sci. Bull. 57 1931 Google Scholar
[61]	詹明生 2015 物理 44 518 Google Scholar Zhan M S 2015 Physics 44 518 Google Scholar
[62]	Yu S, Xu P, He X D, Liu M, Wang J, Zhan M S 2013 Opt. Express 21 32130 Google Scholar
[63]	Yu S, Xu P, Liu M, He X D, Wang J, Zhan M S 2014 Phys. Rev. A 90 062335 Google Scholar
[64]	Derevianko A 2010 Phys. Rev. A 81 051606 Google Scholar
[65]	Lundblad N, Schlosser M, Porto J V 2010 Phys. Rev. A 81 031611 Google Scholar
[66]	Carr A W, Saffman M 2016 Phys. Rev. Lett. 117 150801 Google Scholar
[67]	Beterov I I, Saffman M 2015 Phys. Rev. A 92 042710 Google Scholar
[68]	Auger J M, Bergamini S, Browne D E 2017 Phys. Rev. A 96 052320 Google Scholar
[69]	Tan T R, Gaebler J P, Lin Y, Wan Y, Bowler T, Leibfried D, Wineland D J 2015 Nature 528 380 Google Scholar
[70]	Ballance C J, Schäfer V M, Home J P, Szwer D J, Webster S C, Allcock D T, Linke N M, Harty T P, Aude Craik D P, Stacey D N, Steane A M, Lucas D M 2015 Nature 528 384 Google Scholar
[71]	Weimer H, Müller M, Lesanovsky I, Zoller P, Büchler H P 2010 Nat. Phys. 6 382 Google Scholar
[72]	Qian J, Zhang L, Zhai J J, Zhang W P 2015 Phys. Rev. A 92 063407 Google Scholar
[73]	Wang J Y, Bai J D, He J, Wang J M 2016 J. Opt. Soc. Am. B 33 2020 Google Scholar
[74]	Naber J B, Vos J, Rengelink R J, Nusselder R J, Davtyan D 2016 Eur. Phys. J. Spec. Top. 225 2785 Google Scholar
[75]	Legaie R, Picken C J, Pritchard J D 2018 J. Opt. Soc. Am. B 35 892 Google Scholar
[76]	Zeng Y, Wang K P, Lui Y Y, He X D, Liu M, Xu P, Wang J, Zhan M S 2018 Journal of the Optical Society of America B 35 454 Google Scholar
[77]	Hankin A M, Jau Y Y, Parazzoli L P, Chou C W, Armstrong D J, Landahl A J, Biedermann G W 2014 Phys. Rev. A 89 033416 Google Scholar
[78]	Beguin L 2013 Ph. D. Dissertation (Palaiseau: Institut d’Optique Graduate School)
[79]	Sedlacek J A, Kim E, Rittenhouse S T, Weck P F, Sadeghpour H R, Shaffer J P 2016 Phys. Rev. Lett. 116 133201 Google Scholar
[80]	Xu P, Yang J H, Liu M, He X D, Zeng Y, Wang K P, Wang J, Papoular D J, Shlyapnikov G V, Zhan M S 2015 Nat. Commun. 6 7803 Google Scholar
[81]	de Léséleuc S, Barredo D, Lienhard V, Browaeys A, Lahaye T 2018 Phys. Rev. A 97 053803 Google Scholar
[82]	Levine H, Keesling A, Omran A, Bernien H, Schwartz S, Zibrov A S, Endres M, Greiner M, Vuletić V, Lukin M D 2018 Phys. Rev. Lett. 121 123603 Google Scholar
[83]	Harrow A W, Montanaro A 2017 Nature 549 203 Google Scholar
[84]	Chen Z Y, Zhou Q, Xue C, Yang X, Guo G C, Guo G P 2018 Sci. Bull. 63 964 Google Scholar
[85]	Bravyi1 S, Gosset D, König R 2018 Science 362 308 Google Scholar
[86]	Sheng C, He X D, Xu P, Guo R J, Wang K P, Xiong Z Y, Liu M, Wang J, Zhan M S 2018 Phys. Rev. Lett. 121 240501 Google Scholar
[87]	Labuhn H, Barredo D, Ravets S, de Léséleuc S, Macrì T, Lahaye T and Browaeys A 2016 Nature 534 667 Google Scholar
[88]	Bernien H, Schwartz S, Keesling A, Levine H, Omran A, Pichler H, Choi S, Zibrov A S, Endres M, Greiner M, Vuletić V, Lukin M D 2017 Nature 551 579 Google Scholar
[89]	Schauss P 2018 Quantum Sci. Technol. 3 023001 Google Scholar
[90]	Das S, Grankin A, Iakoupov I, Brion E, Borregaard J, Boddeda R, Usmani I, Ourjoumtsev A, Grangier P, Sørensen A S 2016 Phys. Rev. A 93 040303(R)Google Scholar
[91]	Wade A C J, Mattioli M, Mølmer K 2016 Phys. Rev. A 94 053830 Google Scholar
[92]	Sun Y, Chen P X 2018 Optica 5 1492 Google Scholar

施引文献

图 1 中性单原子量子计算的概念架构

Fig. 1. Conceptual architecture for a neutral atom quantum computer.

下载: 全尺寸图片幻灯片

图 2 远红失谐光聚焦形成的偶极阱和偶极阱中收集的单原子荧光信号

Fig. 2. The optical dipole trap formed by strongly focusing far red-detuned laser. The fluorescence of single atoms trapped by the dipole trap.

下载: 全尺寸图片幻灯片

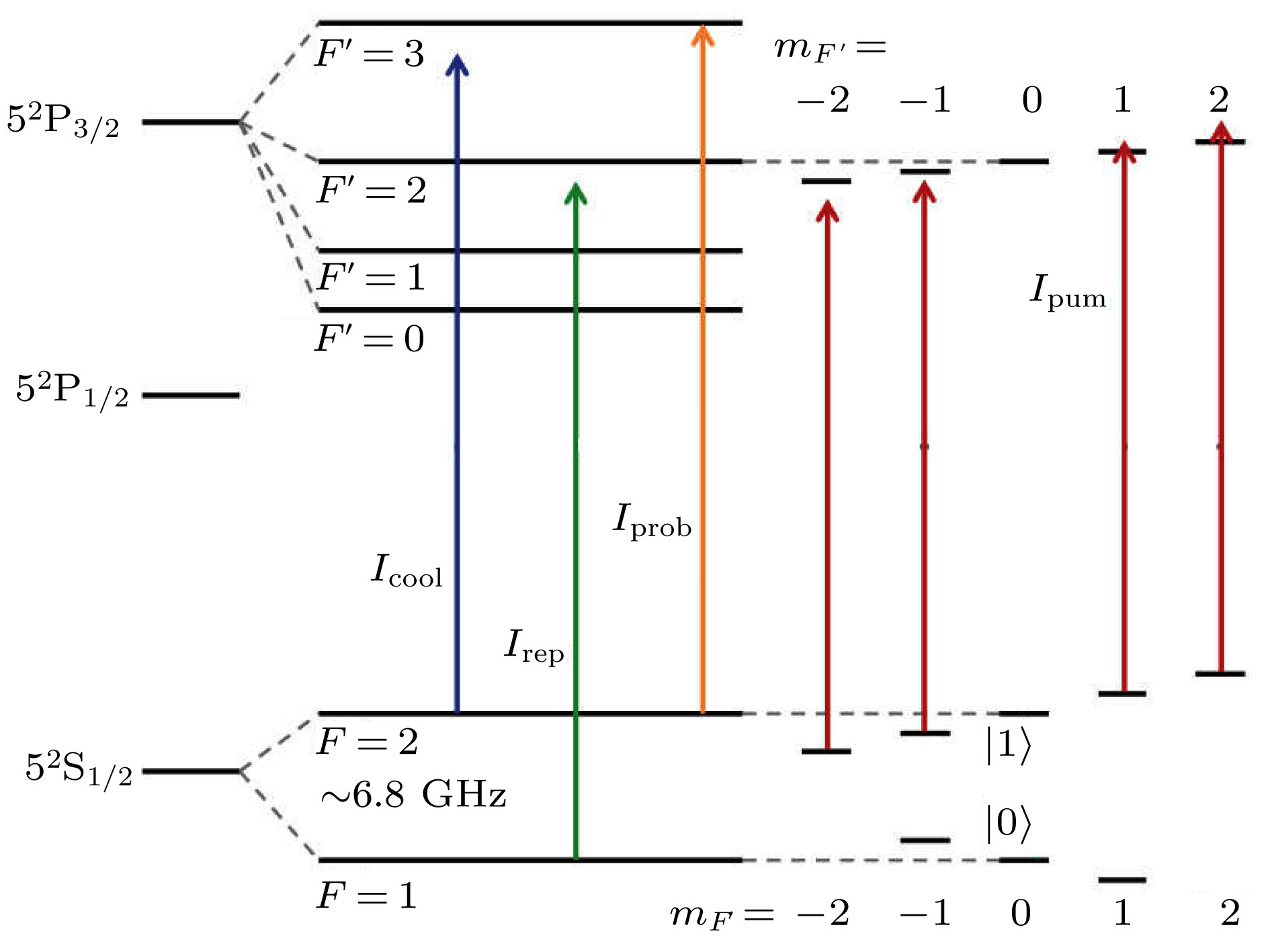
图 3 $ ^{87}{\rm Rb} $原子能级和相关的冷却光$ I_{\rm cool} $、回泵光$ I_{\rm rep} $、态制备光$ I_{\rm pum} $和态探测光$ I_{\rm prob} $对应的跃迁(量子比特的$ |0\rangle $态和$ |1\rangle $态编码在 $ F=1 $,$ m_F $ = 0和$ F=2 $, $ m_F=0 $上)

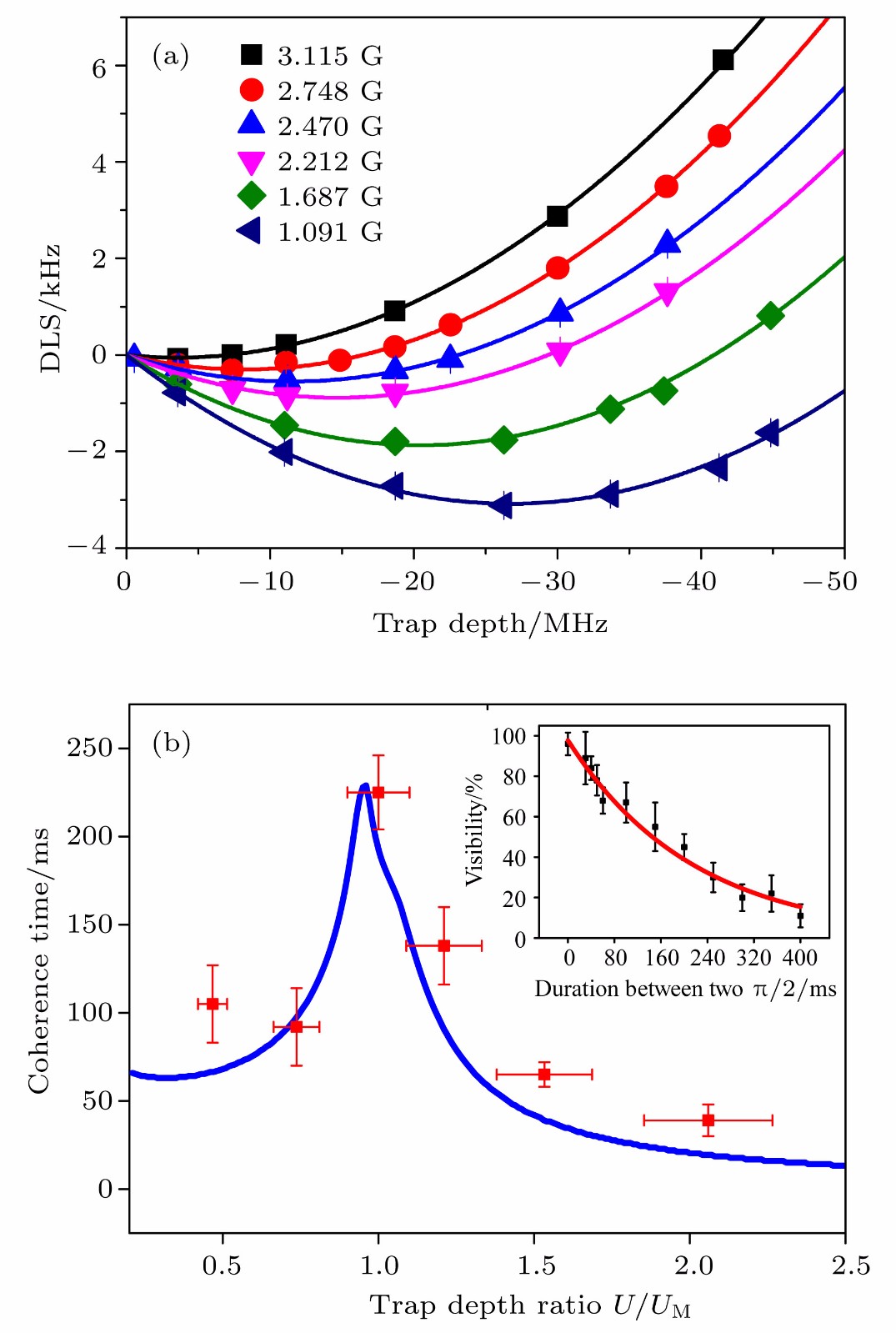
Fig. 3. The energy levels and lasers used for cooling, repumpiup ng, optical pumpiup ng, and state detection of $ ^{87}{\rm Rb} $. The ground hyperfine states of $ F=1 $, $ m_F=0 $ and $ F=2 $, $ m_F=0 $ are used for encoding the qubit.

下载: 全尺寸图片幻灯片

图 4 (a)超极化率不可忽略情况下, 原子量子比特的微分光频移在不同磁场下随偶极阱势深的变化; (b)原子量子比特相干时间在不同偶极阱势深下的实验值, 蓝色实线为理论值; 内插图显示了阱深为$ U_{\rm M} $时, 通过拟合Ramsey条纹的对比度得到相干时间为$ \tau= (225 \pm 21) $ ms^[17]

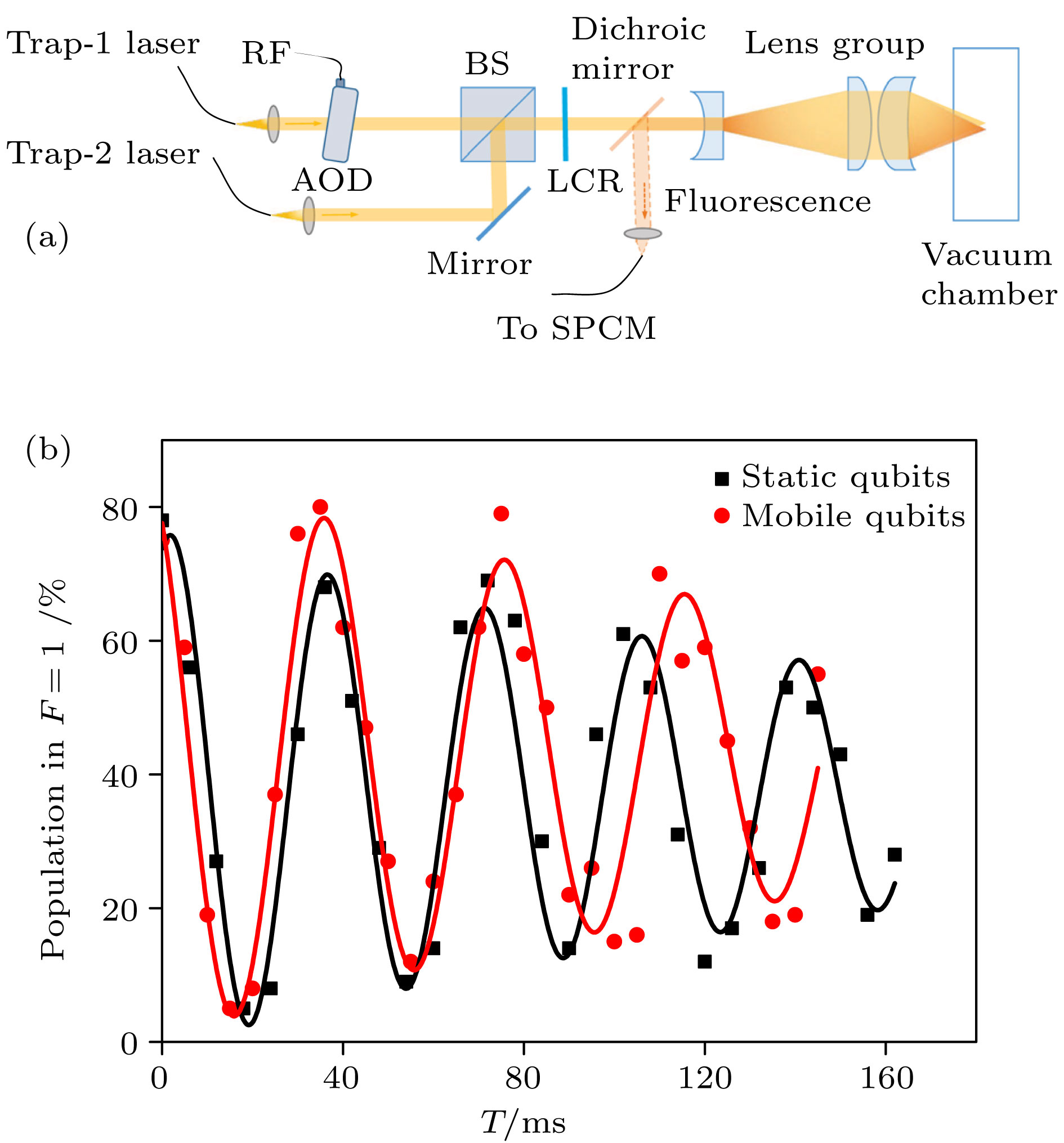
Fig. 4. (a) In the presence of hyperpolarizability, the differential light shift (DLS) of a qubit in the circularly polarized trap is measured as a function of trap depths at various magnetic field strengths; (b) coherence time $ \tau $ and its dependence on normalized ratios $ U/U_{\rm M} $ obtained from experiment. The solid blue line is the theoretical curve. A coherence time is extracted from a decay time of the envelope of Ramsey visibility, as shown as in the inset. At $ U_a= U_{\rm M} $, $ \tau= (225 \pm 21) $ ms^[17].

下载: 全尺寸图片幻灯片

图 5 (a)原子量子比特相干转移的实验装置示意图(Trap 1是可移动阱, 其在焦平面上的位置由2D声光偏转器控制; Trap 2是静止阱; 两阱的偏振可以通过液晶相位片(Thorlabs LCR-1-NIR)实时控制); (b) 原子量子比特在两阱中不转移(黑色方块)和转移(红色圆点)时的Ramsey条纹(实验数据中每个点是100多次实验的平均值; 通过衰减的正弦函数拟合(实线部分), 可以得到静止量子比特和转移量子比特的相干时间分别是(206 $ \pm $ 69) ms和(205 $ \pm $ 74) ms^[17]

Fig. 5. (a) Experimental setup for coherent transfer of atomic qubit. Trap 1 is a movable trap which can be shiftted in two orthogonal diretions by an AOD. Trap 2 is a static one. Both of their polarizations can be actively controlled by a liquid crystal retarder (LCR). (b) Measured Ramsey signals for single static qubits (black squares) and single mobile qubits (red dots) at $ B = 3.115 $ G. Every point is an average over 100 experimental runs. The solid curves are fits to the damped sinusoidal function, with coherence times of static qubits and mobile qubits are (206 $ \pm $ 69) ms and (205 $ \pm $ 74) ms, respectively^[17].

下载: 全尺寸图片幻灯片

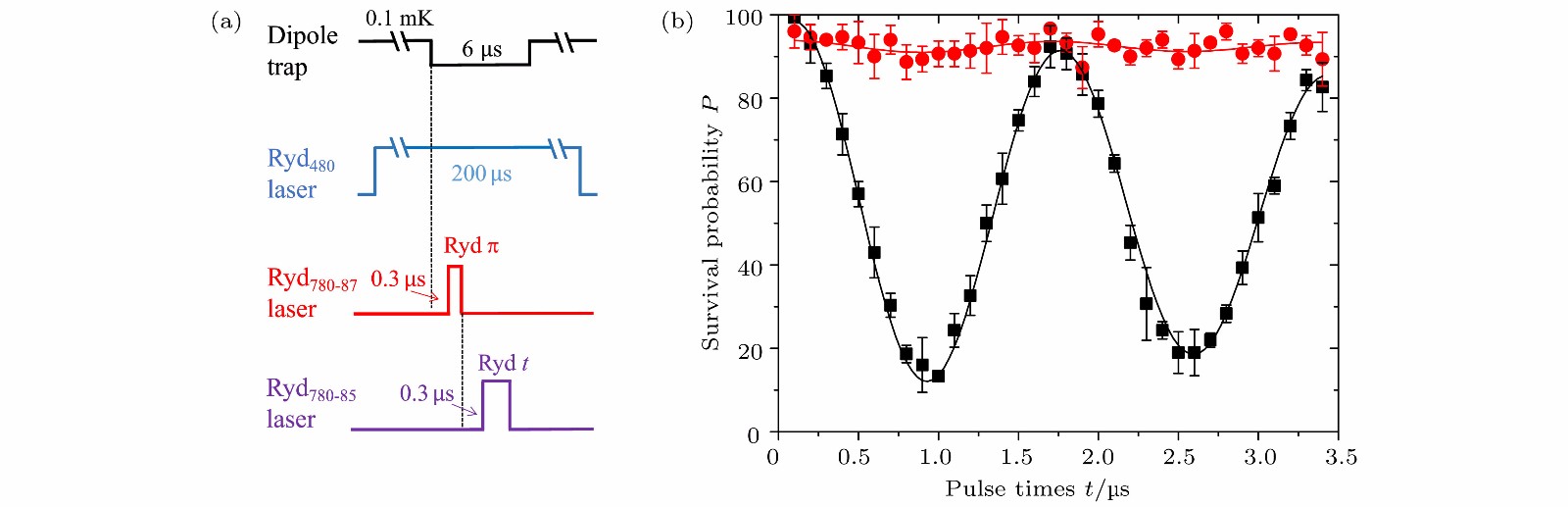
图 6 (a) $ ^{85}{\rm Rb} $和$ ^{87}{\rm Rb} $的能级及相应的激光; (b) 实验光路示意图; (c)$ ^{87}{\rm Rb} $原子在$ |\!\!\uparrow\rangle $和$ |r\rangle $态间的相干Rabi振荡; 里德伯态激发光同时作用到$ ^{85} {\rm Rb}$, 由于频率的差别, $ ^{85}{\rm Rb} $没有任何激发, 两原子间操作的串扰可忽略^[20]

Fig. 6. (a) Energy levels and lasers of $ ^{85}{\rm Rb} $ and $ ^{87}{\rm Rb} $; (b) experimental setup; (c) the coherent Rabi oscillation between $ |\!\!\uparrow\rangle $ and $ |r\rangle $ of $ ^{87}{\rm Rb} $, there is no excitation of $ ^{85}{\rm Rb} $ although the Rydberg excitation lasers also act on it which shows negligible crosstalk between two atoms^[20].

下载: 全尺寸图片幻灯片

图 7 (a) 异核里德伯阻塞的时序; (b) 异核里德伯阻塞. 没有$ ^{87}{\rm Rb} $时, $ ^{85}{\rm Rb} $展示了很好的基态到里德伯态的相干Rabi振荡, 当$ ^{87}{\rm Rb} $激发到里德伯态时, 由于异核里德伯阻塞, $ ^{85}{\rm Rb} $几乎没有Rabi振荡^[20]

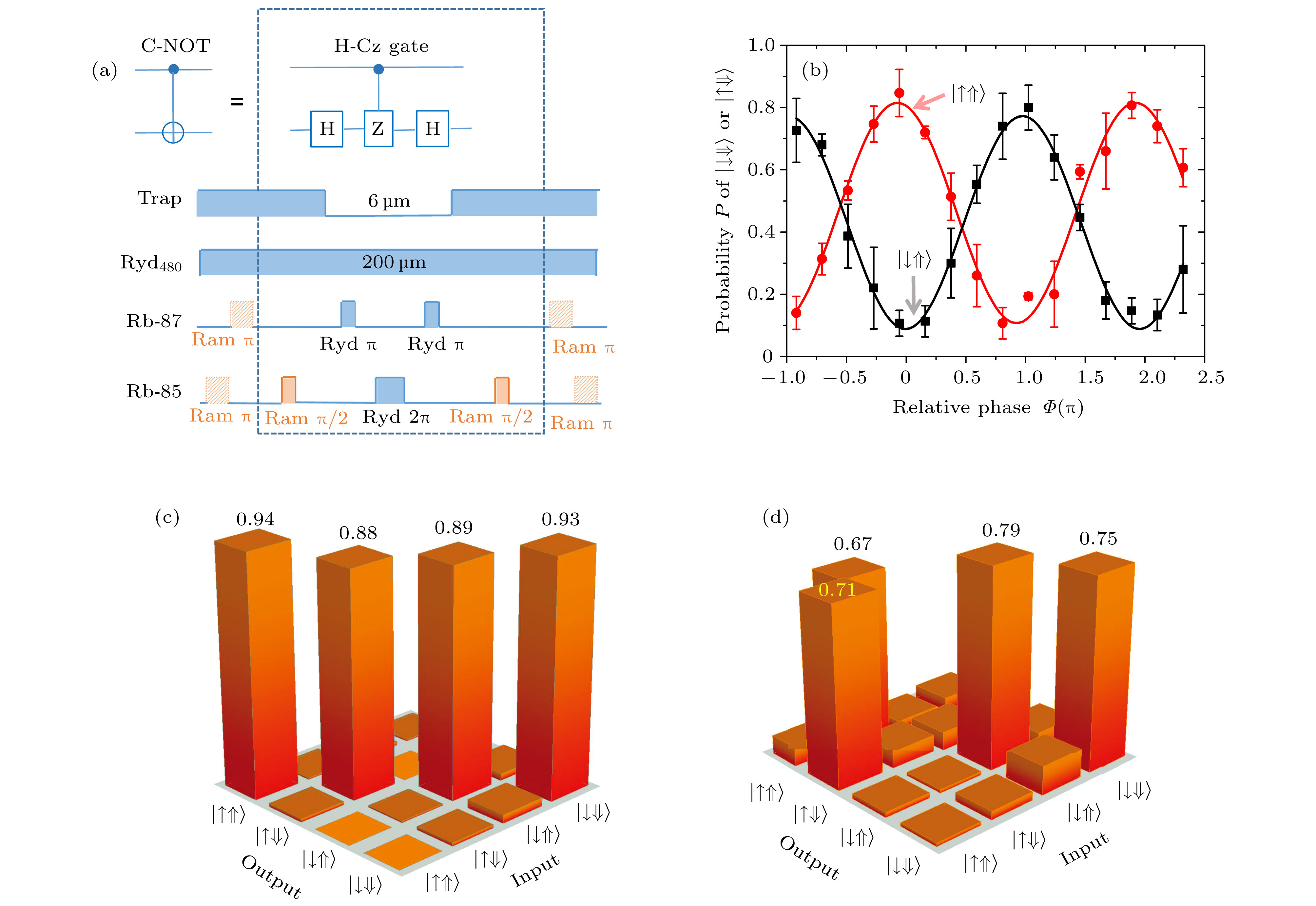
Fig. 7. (a) Time sequence for heteronuclear Rydberg blockade; (b) Rabi oscillations between the $ ^{85}{\rm Rb} $ $ {\rm 5S_{1/2}}, F=3, m_F=0 $ and $ {\rm 79D_{5/2}}, m_j=5/2 $ states with and without $ ^{87}{\rm Rb} $ in Rydberg state^[20].

下载: 全尺寸图片幻灯片

图 8 (a) 异核C-NOT门的时序; (b) 不同输入态$ |\!\!\downarrow\Uparrow\rangle $(黑色方块)和$ |\!\!\uparrow\Uparrow\rangle $(红色圆点)时, 输出态的布居随两个Raman $ {\text{π}}/2 $ 脉冲的振荡; 用正弦函数拟合后, 两个振荡间的相位差为$ (0.94 \pm 0.01) {\text{π}} $; (c) 初态制备的真值表; (d) 两个Raman $ {\text{π}}/2 $脉冲的相对相位设为0时, 测得的H-Cz型的C-NOT门的真值表^[20]

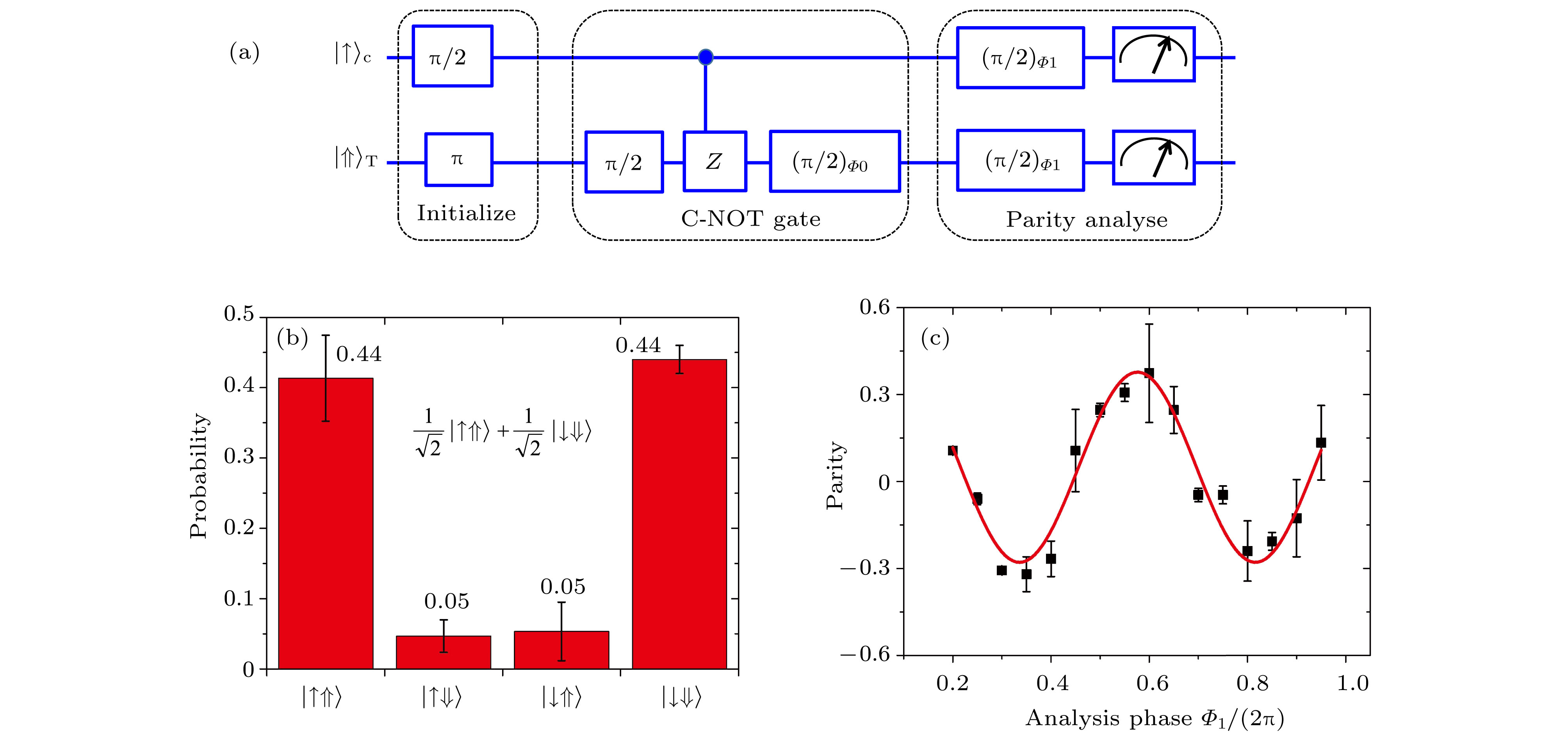
Fig. 8. (a) Experimental time sequence of H-Cz C-NOT gate; (b) output states as a function of the relative phase between the Raman $ {\text{π}}/2 $ pulses, for the initial states $ |\!\!\downarrow\Uparrow\rangle $ (black squares) and $ |\!\!\uparrow\Uparrow\rangle $ (red circles). The solid curves are sinusoidal fits yielding the phase difference of $ (0.94 \pm 0.01){\text{π}}$ between the two signals; (c) truth table matrix for the initial state preparation; (d) set the relative phase to be 0, the measured truth table matrix for H-Cz C-NOT gate^[20]..

下载: 全尺寸图片幻灯片

图 9 (a) 制备和测量异核两原子纠缠的时序; (b) 纠缠态的布居; (c) 宇称信号随测量脉冲相对相位的振荡, 拟合得到$ |C_{1}|= 0.16 \pm 0.01 $^[20]

Fig. 9. (a) Time sequence for generating and verifying entanglement of two heteronuclear atoms; (b) measured probabilities for the entangled state; (c) the parity signal $ P $; the solid curve is a sinusoidal fit with $ |C_{1}|= 0.16 \pm 0.01 $^[20].

下载: 全尺寸图片幻灯片

表 1 魔幻光强偶极阱中的退相干机制

Table 1. The mechanisms of decoherence in magic intensity optical trap.

⁸⁷Rb	退相干机制	参数	无转移时$T_2 $	转移后$T_2 $
均匀退相时间$T'_{2} $ (Homogeneous dephasing time)	磁场起伏	$ \sigma_B=0.019 $%	300 ms	300 ms
	偶极光功率起伏	$ \sigma_I=0.0015 $	200 s	200 s
	偶极光重合及指向抖动	$ \sigma_{\rm{point}}=0.06 $	—	30 s
	微波频率起伏	$ \sigma_{\rm MW} < 1 $ mHz	$ > 300 $ s	$ > 300 $ s
	原子加热	2 μK/s	34 s	34 s
非均匀退相时间$T^{*}_{2} $ (Inhomogeneous dephasing time)	原子热运动	约8 μK	2 s	—
非均匀退相时间$T^{*}_{2} $ (Inhomogeneous dephasing time)	转移引起的加热	$ < 10\;{\text{μ}}{\rm K} $	—	$ > 1.2 $ s
自旋翻转时间$T_{1} $	偶极光引起的自旋翻转	0.66 $ {\rm s}\cdot {\rm mK}$	4 s	4 s
总的退相干时间T	$ T=1/(1/T_{1}+1/T^{*}_{2}+1/T^{'}_{2}) $	—	约242 ms	约222 ms
实验值			约200 ms	约200 ms

下载: 导出CSV

map

[1]	Ladd T D, Jelezko F, Laflamme R, Nakamura Y, Monroe C, O’Brien J L 2010 Nature 464 45 Google Scholar
[2]	Benhelm J, Kirchmair G, Roos C F, Blatt R 2008 Nat. Phys. 4 463 Google Scholar
[3]	Wendin G 2017 Rep. Prog. Phys. 80 106001 Google Scholar
[4]	O’Brien J L 2007 Science 318 1567 Google Scholar
[5]	Veldhorst M, Yang C H, Hwang J C C, Huang W, Dehollain J P, Muhonen J T, Simmons S, Laucht A, Hudson F E, Itoh K M, Morello A, Dzurak A S 2015 Nature 526 410 Google Scholar
[6]	Childress L, Hanson R 2013 MRS Bulletin 38 134 Google Scholar
[7]	Saffman M, Walker T G, Mølmer K 2010 Rev. Mod. Phys. 82 2313 Google Scholar
[8]	周正威, 陈巍, 孙方稳, 项国勇, 李传锋 2012 科学通报 57 1498 Google Scholar Zhou Z W, Chen W, Sun F W, Xiang G Y, Li C F 2012 Chin. Sci. Bull. 57 1498 Google Scholar
[9]	Wu T Y, Kumar A, Mejia F G, Weiss D S 2018 arxiv: 1809.09197 [physics.atom-ph]
[10]	Saffman M 2018 Nat. Sci. Rev. nwy088 Google Scholar
[11]	Saffman M 2016 J. Phys. B: At. Mol. Opt. Phys. 49 202001 Google Scholar
[12]	Barredo D, Lienhard V, de Léséleuc S, Lahaye T, Browaeys A 2018 Nature 561 79 Google Scholar
[13]	Barredo D, de Léséleuc S, Lienhard V, Lahaye T, Browaeys A 2016 Science 354 1021 Google Scholar
[14]	Endres M, Bernien H, Keesling A, Levine H, Anschuetz E R, Krajenbrink A, Senko C, Vuletic V, Greiner M, Lukin M D 2016 Science 354 1024 Google Scholar
[15]	Wang Y, Kumar A, Wu T Y, Weiss D S 2016 Science 352 1562 Google Scholar
[16]	Xia T, Lichtman M, Maller K, Carr A W, Piotrowicz M J, Isenhower L, Saffman M 2015 Phys. Rev. Lett. 114 100503 Google Scholar
[17]	Yang J H, He X D, Guo R J, Xu P, Wang K P, Sheng C, Liu M, Wang J, Derevianko A, Zhan M S 2016 Phys. Rev. Lett. 117 123201 Google Scholar
[18]	Li G, Zhang S, Isenhower L, Maller K, Saffman M 2012 Opt. Lett. 37 851 Google Scholar
[19]	Isenhower L, Urban E, Zhang X L, Gill A T, Henage T, Johnson T A, Walker T G, Saffman M 2010 Phys. Rev. Lett. 104 010503 Google Scholar
[20]	Zeng Y, Xu P, He X D, Liu Y Y, Liu M, Wang J, Papoular D J, Shlyapnikov G V, Zhan M S 2017 Phys. Rev. Lett. 119 160502 Google Scholar
[21]	Kwon M, Ebert M F, Walker T G, Saffman M 2017 Phys. Rev. Lett. 119 180504 Google Scholar
[22]	Martinez-Dorantes M, Alt W, Gallego J, Ghosh S, Ratschbacher L, Völzke Y, Meschede D 2017 Phys. Rev. Lett. 119 180503 Google Scholar
[23]	DiVincenzo D P 2000 Fortschr. Phys. 48 771 Google Scholar
[24]	Greiner M, Mandel O, Esslinger T, Hänsch T W, Bloch I 2002 Nature 415 39 Google Scholar
[25]	Schlosser N, Reymond G, Protsenko I, Grangier P 2001 Nature 411 1024 Google Scholar
[26]	Kim H, Lee W, Lee H, Jo H, Song Y, Ahn J 2016 Nat. Commun. 7 13317 Google Scholar
[27]	Kumar A, Wu T Y, Giraldo F, Weiss D S 2018 Nature 561 83 Google Scholar
[28]	Walker T G, Saffman M 2012 Adv. At. Mol. Opt. Phys. 61 81 Google Scholar
[29]	Kuhr S, Alt W, Schrader D, Dotsenko I, Miroshnychenko Y, Rauschenbeutel A, Meschede D 2005 Phys. Rev. A 72 023406 Google Scholar
[30]	Wang Y, Zhang X L, Corcovilos T A, Kumar A, Weiss D S 2015 Phys. Rev. Lett. 115 043003 Google Scholar
[31]	Yavuz D D, Kulatunga P B, Urban E, Johnson T A, Proite N, Henage T, Walker T G, Saffman M 2006 Phys. Rev. Lett. 96 063001 Google Scholar
[32]	Schrader D, Dotsenko I, Khudaverdyan M, Miroshnychenko Y, Rauschenbeutel A, Meschede D 2004 Phys. Rev. Lett. 93 150501 Google Scholar
[33]	Bakr W S, Gillen J T, Peng A, Fölling S, Greiner M 2009 Nature 462 74 Google Scholar
[34]	Sherson J F, Weitenberg C, Endres M, Cheneau M, Bloch I, Kuhr S 2010 Nature 467 68 Google Scholar
[35]	Haller E, Hudson J, Kelly A, Cotta D A, Peaudecerf B, Bruce G D, Kuhr S 2015 Nat. Phys. 11 738 Google Scholar
[36]	Weitenberg C, Endres M, Sherson J F, Cheneau M, Schauẞ P, Fukuhara T, Bloch I, Kuhr S 2011 Nature 471 319 Google Scholar
[37]	Knill E, Leibfried D, Reichle R, Britton J, Blakestad R B, Jost J D, Langer C, Ozeri R, Seidelin S, Wineland D J 2008 Phys. Rev. A 77 012307 Google Scholar
[38]	Volz J, Weber M, Schlenk D, Rosenfeld W, Vrana J, Saucke K, Kurtsiefer C, Weinfurter H 2006 Phys. Rev. Lett. 96 030404 Google Scholar
[39]	Hofmann J, Krug M, Ortegel N, Gérard L, Weber M, Rosenfeld W, Weinfurter H 2012 Science 337 72 Google Scholar
[40]	Jaksch D, Briegel H J, Cirac J I, Gardiner C W, Zoller P 1999 Phys. Rev. Lett. 82 1975 Google Scholar
[41]	Strauch F W, Edwards M, Tiesinga E, Williams C, Clark C W 2008 Phys. Rev. A 77 050304 Google Scholar
[42]	Mandel O, Greiner M, Widera A, Rom T, Hänsch T W, Bloch I 2003 Nature 425 937 Google Scholar
[43]	Anderlini M, Lee P J, Brown B L, Strabley J S, Phillips W D, Porto J V 2007 Nature 448 452 Google Scholar
[44]	Kaufman A M, Lester B J, Regal C A 2012 Phys. Rev. X 2 041014 Google Scholar
[45]	Thompson J D, Tiecke T G, Zibrov A S, Vuletic′ V, Lukin M D 2013 Phys. Rev. Lett. 110 133001 Google Scholar
[46]	Kaufman A M, Lester B J, Foss-Feig M, Wall M L, Rey A M, Regal C A 2015 Nature 527 208 Google Scholar
[47]	Jaksch D, Cirac J I, Zoller P, Rolston S L, Cote R, Lukin M D 2000 Phys. Rev. Lett. 85 2208 Google Scholar
[48]	Petrosyan D, Motzoi F, Saffman M, MØlmer K 2017 Phys. Rev. A 96 042306 Google Scholar
[49]	Keating T, Cook R L, Hankin A M, Jau Y Y, Biedermann G W, Deutsch I H 2015 Phys. Rev. A 91 012337 Google Scholar
[50]	Urban E, Johnson T A, Henage T, Isenhower L, Yavuz D D, Walker T G, Saffman M 2009 Nat. Phys. 5 110 Google Scholar
[51]	Gaëtan A, Miroshnychenko M, Wilk T, Chotia A, Viteau M, Comparat D, Pillet P, Browaeys A, Grangier P 2009 Nat. Phys. 5 115 Google Scholar
[52]	Wilk T, Gaëtan A, Evellin C, Wolters J, Miroshnychenko J, Grangier P, Browaeys A 2010 Phys. Rev. Lett. 104 010502 Google Scholar
[53]	Zhang X L, Isenhower L, Gill A T, Walker T G, Saffman M 2010 Phys. Rev. A 82 030306 Google Scholar
[54]	Maller K M, Lichtman M T, Xia T, Sun Y, Piotrowicz M J, Carr A W, Isenhower L, Saffman M 2015 Phys. Rev. A 92 022336 Google Scholar
[55]	Kuhr S, Alt W, Schrader D, Dotsenko I, Miroshnychenko Y, Rosenfeld W, Khudaverdyan M, Gomer V, Rauschenbeutel A, Meschede D 2003 Phys. Rev. Lett. 91 213002 Google Scholar
[56]	Fuhrmanek A, Bourgain R, Sortais Y R P, Browaeys A 2011 Phys. Rev. Lett. 106 133003 Google Scholar
[57]	Gibbons M J, Hamley C D, Shi C Y, Chapman M S 2011 Phys. Rev. Lett. 106 133002 Google Scholar
[58]	He J, Yang B D, Zhang T C, Wang J M 2011 Phys. Scr. 84 025302 Google Scholar
[59]	Dai H N, Yang B, Reingruber A, Xu X F, Jiang X, Chen Y A, Yuan Z S, Pan J W 2016 Nat. Phys. 12 783 Google Scholar
[60]	Yu S, He X D, Xu P, Liu M, Wang J, Zhan M S 2012 Chin. Sci. Bull. 57 1931 Google Scholar
[61]	詹明生 2015 物理 44 518 Google Scholar Zhan M S 2015 Physics 44 518 Google Scholar
[62]	Yu S, Xu P, He X D, Liu M, Wang J, Zhan M S 2013 Opt. Express 21 32130 Google Scholar
[63]	Yu S, Xu P, Liu M, He X D, Wang J, Zhan M S 2014 Phys. Rev. A 90 062335 Google Scholar
[64]	Derevianko A 2010 Phys. Rev. A 81 051606 Google Scholar
[65]	Lundblad N, Schlosser M, Porto J V 2010 Phys. Rev. A 81 031611 Google Scholar
[66]	Carr A W, Saffman M 2016 Phys. Rev. Lett. 117 150801 Google Scholar
[67]	Beterov I I, Saffman M 2015 Phys. Rev. A 92 042710 Google Scholar
[68]	Auger J M, Bergamini S, Browne D E 2017 Phys. Rev. A 96 052320 Google Scholar
[69]	Tan T R, Gaebler J P, Lin Y, Wan Y, Bowler T, Leibfried D, Wineland D J 2015 Nature 528 380 Google Scholar
[70]	Ballance C J, Schäfer V M, Home J P, Szwer D J, Webster S C, Allcock D T, Linke N M, Harty T P, Aude Craik D P, Stacey D N, Steane A M, Lucas D M 2015 Nature 528 384 Google Scholar
[71]	Weimer H, Müller M, Lesanovsky I, Zoller P, Büchler H P 2010 Nat. Phys. 6 382 Google Scholar
[72]	Qian J, Zhang L, Zhai J J, Zhang W P 2015 Phys. Rev. A 92 063407 Google Scholar
[73]	Wang J Y, Bai J D, He J, Wang J M 2016 J. Opt. Soc. Am. B 33 2020 Google Scholar
[74]	Naber J B, Vos J, Rengelink R J, Nusselder R J, Davtyan D 2016 Eur. Phys. J. Spec. Top. 225 2785 Google Scholar
[75]	Legaie R, Picken C J, Pritchard J D 2018 J. Opt. Soc. Am. B 35 892 Google Scholar
[76]	Zeng Y, Wang K P, Lui Y Y, He X D, Liu M, Xu P, Wang J, Zhan M S 2018 Journal of the Optical Society of America B 35 454 Google Scholar
[77]	Hankin A M, Jau Y Y, Parazzoli L P, Chou C W, Armstrong D J, Landahl A J, Biedermann G W 2014 Phys. Rev. A 89 033416 Google Scholar
[78]	Beguin L 2013 Ph. D. Dissertation (Palaiseau: Institut d’Optique Graduate School)
[79]	Sedlacek J A, Kim E, Rittenhouse S T, Weck P F, Sadeghpour H R, Shaffer J P 2016 Phys. Rev. Lett. 116 133201 Google Scholar
[80]	Xu P, Yang J H, Liu M, He X D, Zeng Y, Wang K P, Wang J, Papoular D J, Shlyapnikov G V, Zhan M S 2015 Nat. Commun. 6 7803 Google Scholar
[81]	de Léséleuc S, Barredo D, Lienhard V, Browaeys A, Lahaye T 2018 Phys. Rev. A 97 053803 Google Scholar
[82]	Levine H, Keesling A, Omran A, Bernien H, Schwartz S, Zibrov A S, Endres M, Greiner M, Vuletić V, Lukin M D 2018 Phys. Rev. Lett. 121 123603 Google Scholar
[83]	Harrow A W, Montanaro A 2017 Nature 549 203 Google Scholar
[84]	Chen Z Y, Zhou Q, Xue C, Yang X, Guo G C, Guo G P 2018 Sci. Bull. 63 964 Google Scholar
[85]	Bravyi1 S, Gosset D, König R 2018 Science 362 308 Google Scholar
[86]	Sheng C, He X D, Xu P, Guo R J, Wang K P, Xiong Z Y, Liu M, Wang J, Zhan M S 2018 Phys. Rev. Lett. 121 240501 Google Scholar
[87]	Labuhn H, Barredo D, Ravets S, de Léséleuc S, Macrì T, Lahaye T and Browaeys A 2016 Nature 534 667 Google Scholar
[88]	Bernien H, Schwartz S, Keesling A, Levine H, Omran A, Pichler H, Choi S, Zibrov A S, Endres M, Greiner M, Vuletić V, Lukin M D 2017 Nature 551 579 Google Scholar
[89]	Schauss P 2018 Quantum Sci. Technol. 3 023001 Google Scholar
[90]	Das S, Grankin A, Iakoupov I, Brion E, Borregaard J, Boddeda R, Usmani I, Ourjoumtsev A, Grangier P, Sørensen A S 2016 Phys. Rev. A 93 040303(R)Google Scholar
[91]	Wade A C J, Mattioli M, Mølmer K 2016 Phys. Rev. A 94 053830 Google Scholar
[92]	Sun Y, Chen P X 2018 Optica 5 1492 Google Scholar

[1]	陈锋, 任刚. 基于纠缠态表象的双模耦合谐振子量子特性分析. , 2024, 73(23): 230302. doi: 10.7498/aps.73.20241303
[2]	白健男, 韩嵩, 陈建弟, 韩海燕, 严冬. 超级里德伯原子间的稳态关联集体激发与量子纠缠. , 2023, 72(12): 124202. doi: 10.7498/aps.72.20222030
[3]	仲银银, 潘晓州, 荆杰泰. 级联四波混频相干反馈控制系统量子纠缠特性. , 2020, 69(13): 130301. doi: 10.7498/aps.69.20200042
[4]	李翔艳, 王志辉, 李少康, 田亚莉, 李刚, 张鹏飞, 张天才. 蓝移阱中单个铯原子基态磁不敏感态的相干操控. , 2020, 69(8): 080301. doi: 10.7498/aps.69.20192001
[5]	李晓康, 贾凤东, 余方晨, 李明阳, 薛平, 许祥源, 钟志萍. 一价镧离子高n里德伯态. , 2019, 68(4): 043201. doi: 10.7498/aps.68.20181980
[6]	张秦榕, 王彬彬, 张孟龙, 严冬. 稀薄里德伯原子气体中的两体纠缠. , 2018, 67(3): 034202. doi: 10.7498/aps.67.20172052
[7]	安志云, 李志坚. 逾渗分立时间量子行走的传输及纠缠特性. , 2017, 66(13): 130303. doi: 10.7498/aps.66.130303
[8]	裴栋梁, 何军, 王杰英, 王家超, 王军民. 铯原子里德伯态精细结构测量. , 2017, 66(19): 193701. doi: 10.7498/aps.66.193701
[9]	丛美艳, 杨晶, 黄燕霞. 在不同初态下Dzyaloshinskii-Moriya相互作用及内禀退相干对海森伯系统的量子纠缠的影响. , 2016, 65(17): 170301. doi: 10.7498/aps.65.170301
[10]	汪仲清, 赵小奇, 周贤菊. 原子在弱相干场光纤耦合腔系统中的纠缠特性. , 2013, 62(22): 220302. doi: 10.7498/aps.62.220302
[11]	孙江, 孙娟, 王颖, 苏红新. 双光子共振非简并四波混频测量Ba原子里德伯态的碰撞展宽和频移. , 2012, 61(11): 114214. doi: 10.7498/aps.61.114214
[12]	孙江, 刘鹏, 孙娟, 苏红新, 王颖. 双光子共振非简并四波混频测量钡原子里德伯态碰撞展宽中的伴线研究. , 2012, 61(12): 124205. doi: 10.7498/aps.61.124205
[13]	陈宇, 邹健, 李军刚, 邵彬. 耗散环境下三原子之间稳定纠缠的量子反馈控制. , 2010, 59(12): 8365-8370. doi: 10.7498/aps.59.8365
[14]	刘小娟, 刘一曼, 周并举. 原子与双模相干强场依赖强度耦合多光子过程中纠缠量度与制备. , 2010, 59(12): 8518-8525. doi: 10.7498/aps.59.8518
[15]	单传家, 夏云杰. Tavis-Cummings模型中两纠缠原子纠缠的演化特性. , 2006, 55(4): 1585-1590. doi: 10.7498/aps.55.1585
[16]	熊恒娜, 郭红, 江健, 陈俊, 唐丽艳. 原子间纠缠和光场模间纠缠的对应关系. , 2006, 55(6): 2720-2725. doi: 10.7498/aps.55.2720
[17]	胡要花, 方卯发, 廖湘萍, 郑小娟. 二项式光场与级联三能级原子的量子纠缠. , 2006, 55(9): 4631-4637. doi: 10.7498/aps.55.4631
[18]	孙江, 左战春, 郭庆林, 王英龙, 怀素芳, 王颖, 傅盘铭. 应用双光子共振非简并四波混频测量Ba原子里德伯态. , 2006, 55(1): 221-225. doi: 10.7498/aps.55.221
[19]	周青春, 祝世宁. Λ型三能级原子与数态单模光场互作用系统的纠缠特性. , 2005, 54(5): 2043-2048. doi: 10.7498/aps.54.2043
[20]	王成志, 方卯发. 双模压缩真空态与原子相互作用中的量子纠缠和退相干. , 2002, 51(9): 1989-1995. doi: 10.7498/aps.51.1989

计量

文章访问数: 15614
PDF下载量: 689
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板