两腔级联纠缠增强的理论分析

周瑶瑶; 田剑锋; 闫智辉; 贾晓军

doi:10.7498/aps.68.20182079

摘要

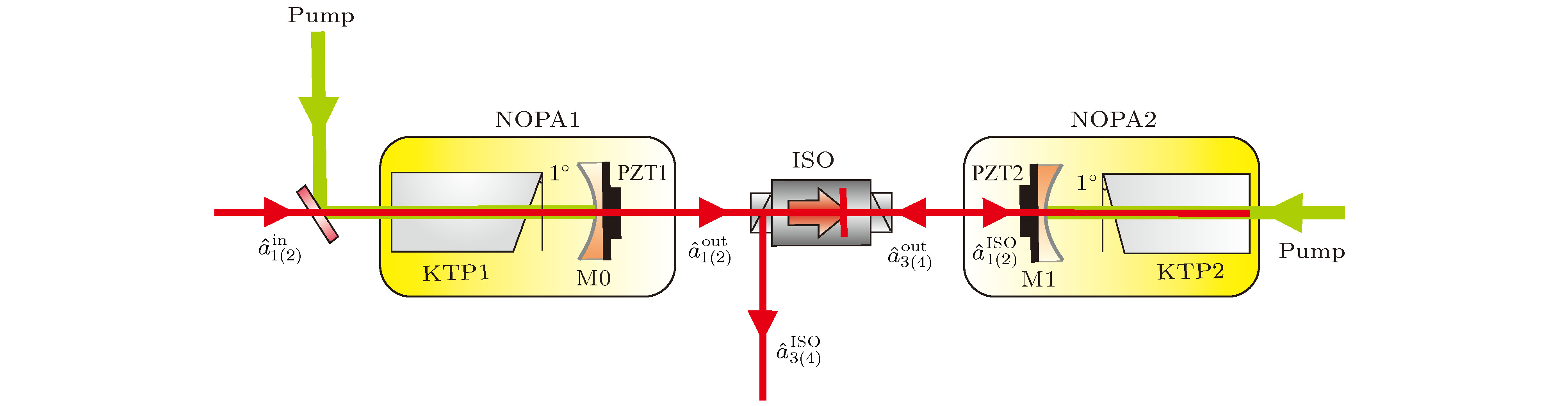
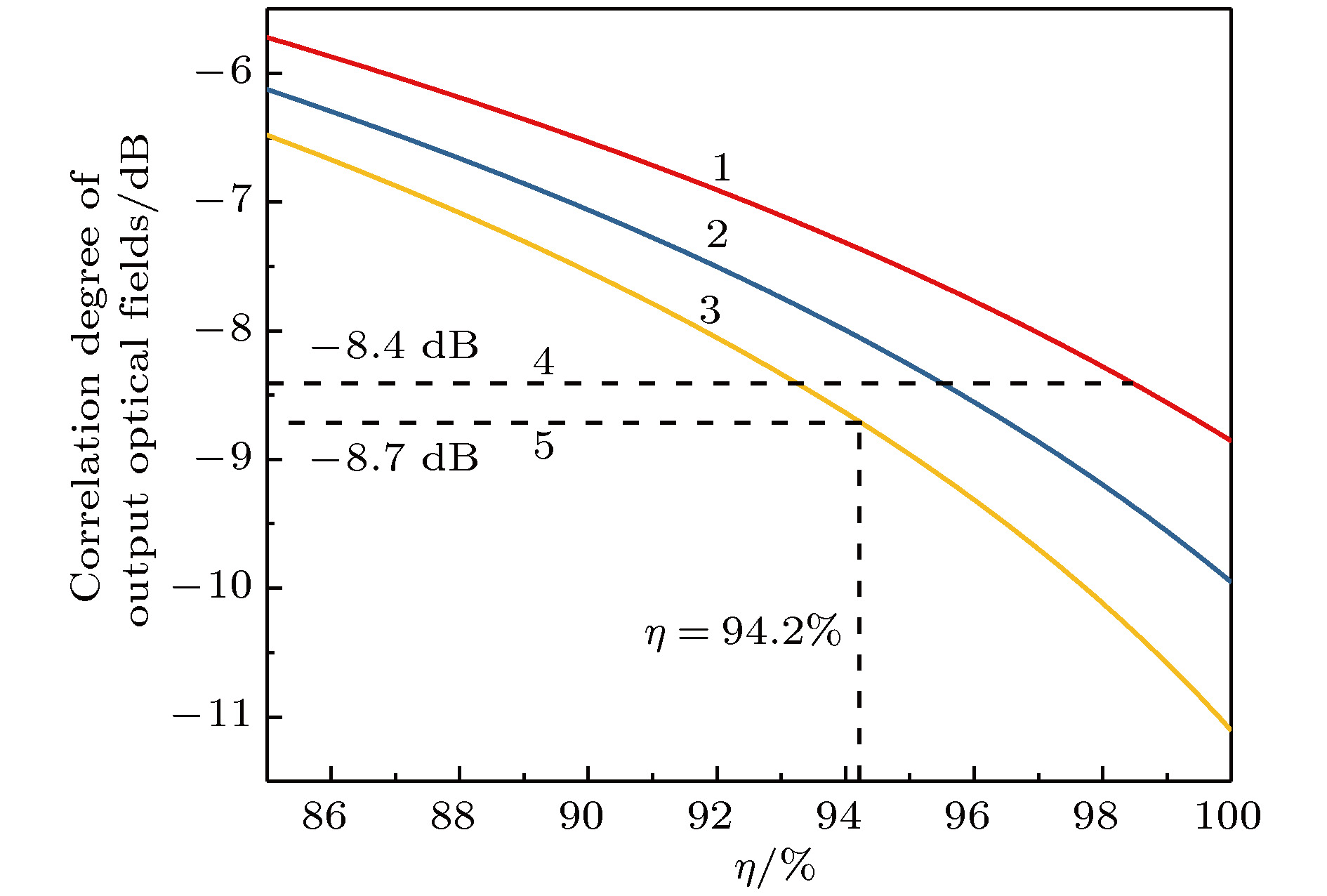
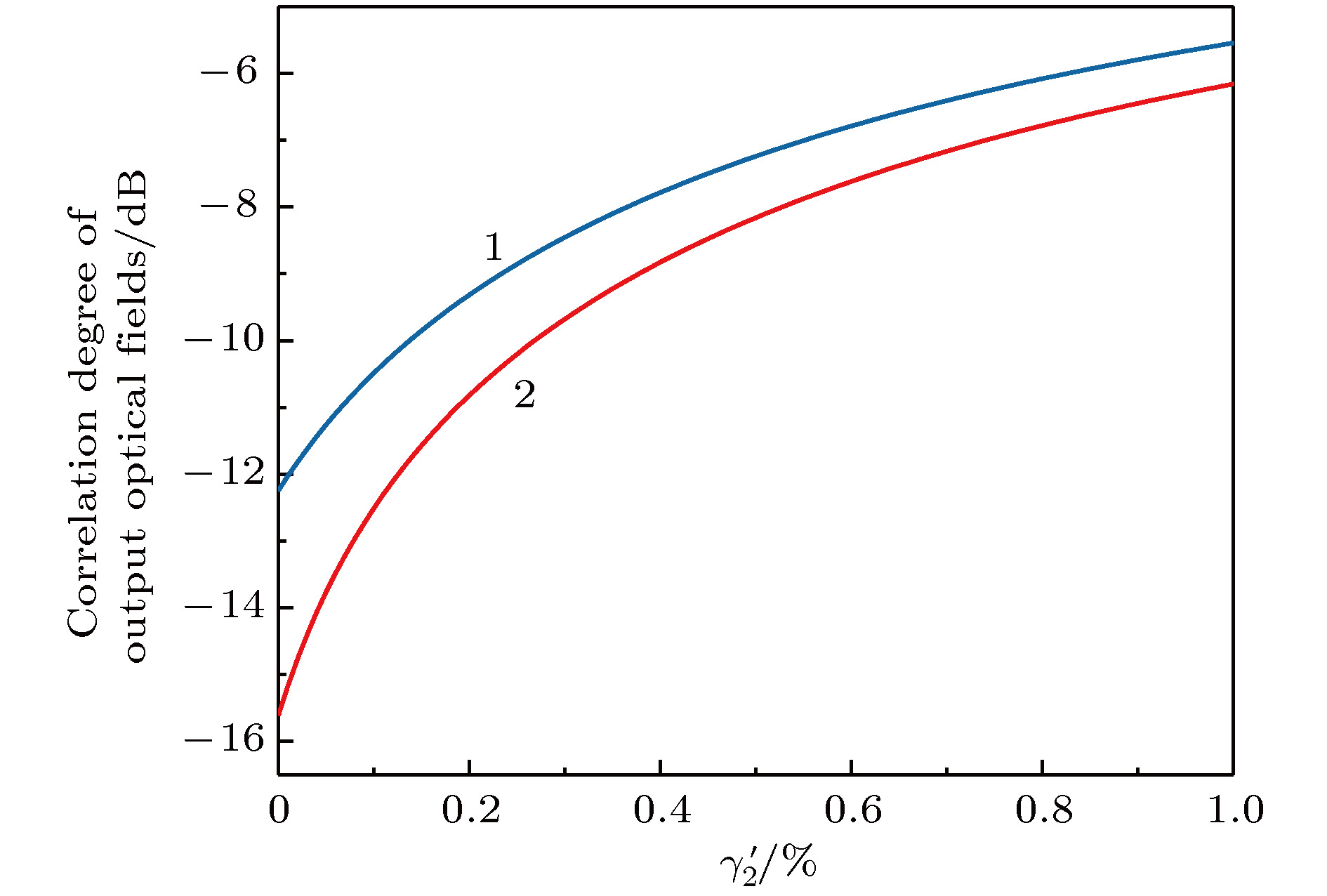
高纠缠度的纠缠源是实现高保真度量子信息传输与处理的保障, 因为受到光学元器件自身性能不完美的限制, 通过有效的操控手段来提高光场的纠缠度是十分必要的. 连续变量Einstein-Podolsky-Rosen纠缠态光场可以利用工作在阈值以下的非简并光学参量放大器来获得. 将两个非简并光学参量放大器级联, 可以利用第二个光学腔来操控第一个光学腔输出的纠缠态光场, 在一定条件下实现光场的纠缠增强. 本文通过理论分析设计出两种光学腔级联的实验系统, 其中, 纠缠产生装置采用具有三共振结构的半整块驻波腔, 输出到目前为止世界上单腔获得两组份纠缠态光场纠缠度的最高值, 操控光学腔采用驻波腔或四镜环形腔的结构. 详细对比分析了不同结构的操控腔对纠缠增强效果的影响, 得出利用不同腔形作为操控腔的最佳实验方案. 同时分析了级联腔输出光场的纠缠度随不同物理参量的变化关系, 得出进一步优化的最佳实验系统参量, 为实验获得更高纠缠度的纠缠态光场提供了依据.

关键词:

Abstract

Entanglement source with high entanglement degree is the guarantee for accomplishing the quantum information transmission and process with higher fidelity. Continuous variable Einstein-Podolsky-Rosen (EPR) entangled optical field with quantum correlation of amplitude and phase quadrature is a basic and important quantum resource in the quantum information science area, which can be obtained by a non-degenerate optical parametric amplifier (NOPA) operated below the threshold pump power. Because of the limitation of the imperfect performance of optical components in optical cavity, we should find efficient methods of implementing quantum manipulation to improve the entanglement degree of the entangled state of light. Connecting NOPA1 and NOPA2 in series, the entangled state of light output from the NOPA1 can be manipulated by NOPA2, and the entanglement degree can be enhanced under certain conditions. To improve the entanglement degree to a greater extent, the structure of the NOPA1 is chosen as a half-monolithic standing-wave optical resonator with the triple resonance of the pump and two subharmonic modes. The NOPA1 is able to output the entangled optical fields with an entanglement degree of 8.4 dB, which is the highest entanglement generated by a single device so far. The structure of the NOPA2 can be chosen as a standing-wave optical cavity or a four-mirror ring optical cavity. According to the different structures of the NOPA2, we theoretically design two kinds of optical systems with two cascaded cavities and compare the effects of the two optical systems on the continuous variable EPR entanglement cascaded enhancement in detail. Based on the above contrastive analysis, when the entanglement degree of the input optical fields is 8.4 dB and the transmissivity of the output coupler is lower, the structure of a four-mirror ring optical cavity for NOPA2 cannot enhance the entanglement degree, so the optical system including NOPA2 with standing wave cavity structure and the optical isolator with high transmission efficiency is appropriate. When the transmissivity of the output coupler and transmission efficiency of the optical isolator are higher, the structure of the NOPA2 should be chosen as a standing-wave optical cavity, otherwise the structure of the NOPA2 should be chosen as a four-mirror ring optical cavity. We also theoretically analyze the dependence of the correlation degree of output optical fields on physical parameters. The results show that under the conditions of higher input and output coupling efficiency, higher transmission efficiency and lower intro-cavity loss, the entangled state of light with higher entanglement degree can be obtained experimentally. This provides the reference for obtaining entangled optical fields with higher entanglement degree in the future.

Keywords:

Einstein-Podolsky-Rosen entangled optical fields /
manipulated optical cavity /
entanglement enhancement

作者及机构信息

1.
太原师范学院物理系, 晋中　030619

2.
山西大学光电研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

3.
山西大学, 极端光学协同创新中心, 太原　030006

通信作者: 周瑶瑶, zhouyaoyaofangxia@163.com

基金项目: 国家重点研发计划(批准号: 2016YFA0301402)、国家自然科学基金(批准号: 11804246, 61775127, 11474190, 11654002)、山西青年三晋学者项目、山西省回国留学人员科研资助项目、山西省“1331工程”重点学科建设计划和山西省高等学校创新人才支持计划.

Authors and contacts

1.
Department of Physics, Taiyuan Normal University, Jinzhong 030619, China

2.
Institute of Opto-Electronics, State Key Laboratory of Quantum Optics and Quantum Optics Devices, Shanxi University, Taiyuan 030006, China

3.
Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

Corresponding author: Zhou Yao-Yao, zhouyaoyaofangxia@163.com

Funds: Project supported by the National Key R&D Program of China (Grant No. 2016YFA0301402), the National Natural Science Foundation of China (Grant Nos. 11804246, 61775127, 11474190, 11654002), the Program for Sanjin Scholars of Shanxi Province, China, the Shanxi Scholarship Council of China, the Fund for Shanxi “1331 Project” Key Subjects Construction, China, and the Program for the Outstanding Innovative Teams of Higher Learning Institutions of Shanxi, China.

文章全文 : translate this paragraph

参考文献

[1]	Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575 Google Scholar
[2]	Furusawa A, Sorensen J L, Braustein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706 Google Scholar
[3]	Boschi D, Branca S, Marini F D, Hardy L, Popescu S 1998 Phys. Rev. Lett. 80 1121 Google Scholar
[4]	Vaidman L 1994 Phys. Rev. A 49 1473 Google Scholar
[5]	Braunstein S L, Kimble H J 1998 Phys. Rev. Lett. 80 869 Google Scholar
[6]	Bowen W P, Schnabel R, Lam P K, Ralph T C 2004 Phys. Rev. A 69 012304 Google Scholar
[7]	Eberle T, Händchen V, Duhme J, Franz T, Werner R F, Schnabel R 2011 Phys. Rev. A 83 052329 Google Scholar
[8]	Mizuno J, Wakui K, Furusawa A, Sasaki M 2005 Phys. Rev. A 71 012304 Google Scholar
[9]	Stoler D 1970 Phys. Rev. D 1 3217 Google Scholar
[10]	Mehmet M, Vahlbruch H, Lastzka N, Danzmann K, Schnabel R 2010 Phys. Rev. A 81 013814 Google Scholar
[11]	Mehmet M, Ast S, Eberle T, Steinlechner S, Vahlbruch H, Schnabel R 2011 Opt. Express 19 25763 Google Scholar
[12]	Eberle T, Steinlechner S, Bauchrowitz J, Händchen V, Vahlbruch H, Mehmet M, Muller-Ebhardt H, Schnabel R 2010 Phys. Rev. Lett. 104 251102 Google Scholar
[13]	Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801 Google Scholar
[14]	彭堃墀, 贾晓军, 苏晓龙, 谢常德 2011 光学学报 31 09001071 Peng K C, Jia X J, Su X L, Xie C D 2011 Acta Opt. Sin. 31 09001071
[15]	贾晓军, 苏晓龙, 潘庆, 谢常德, 彭堃墀 2005 54 2717 Google Scholar Jia X J, Su X L, Pan Q, Xie C D, Peng K C 2005 Acta Phys. Sin. 54 2717 Google Scholar
[16]	赵超樱, 谭维翰 2005 54 4526 Google Scholar Zhao C Y, Tan W H 2005 Acta Phys. Sin. 54 4526 Google Scholar
[17]	Wang Y, Su X L, Shen H, Tan A H, Xie C D, Peng K C 2010 Phys. Rev. A 81 022311 Google Scholar
[18]	Ou Z Y, Pereira S F, Kimble H J, Peng K C 1992 Phys. Rev. Lett. 68 3663 Google Scholar
[19]	Zhang Y, Wang H, Li X Y, Jing J T, Xie C D, Peng K C 2000 Phys. Rev. A 62 023813 Google Scholar
[20]	Laurat J, Coudreau T, Keller G, Treps N, Fabre C 2004 Phys. Rev. A 70 042315 Google Scholar
[21]	Takei N, Yonezawa H, Aoki T, Furusawa A 2005 Phys. Rev. Lett. 94 220502 Google Scholar
[22]	Wang Y, Shen H, Jin X L, Su X L, Xie C D, Peng K C 2010 Opt. Express 18 6149 Google Scholar
[23]	Gottesman D, Preskill J 2001 Phys. Rev. A 63 022309 Google Scholar
[24]	Yukawa M, Benichi H, Furusawa A 2008 Phys. Rev. A 77 022314 Google Scholar
[25]	Li X Y, Pan Q, Jing J T, Zhang J, Xie C D, Peng K C 2002 Phys. Rev. Lett. 88 047904 Google Scholar
[26]	Mattle K, Weinfurter H, Kwiat P G, Zeilinger A 1996 Phys. Rev. Lett. 76 4656 Google Scholar
[27]	Braunstein S L, Kimble H J 2000 Phys. Rev. A 61 042302 Google Scholar
[28]	Zhang J, Peng K C 2000 Phys. Rev. A 62 064302 Google Scholar
[29]	Zhou Y Y, Jia X J, Li F, Xie C D, Peng K C 2015 Opt. Express 23 4952 Google Scholar
[30]	Chen H X, Zhang J 2009 Phys. Rev. A 79 063826 Google Scholar
[31]	Shang Y N, Jia X J, Shen Y M, Xie C D, Peng K C 2010 Opt. Lett. 35 853 Google Scholar
[32]	Yan Z H, Jia X J, Su X L, Duan Z Y, Xie C D, Peng K C 2012 Phys. Rev. A 85 040305(R)Google Scholar
[33]	Duan L M, Giedke G, Cirac J I, Zoller P 2000 Phys. Rev. Lett. 84 2722 Google Scholar
[34]	Simon R 2000 Phys. Rev. Lett. 84 2726 Google Scholar
[35]	周瑶瑶, 蔚娟, 闫智辉, 贾晓军 2018 38 0727001 Zhou Y Y, Yu J, Yan Z H, Jia X J 2018 Acta Opt. Sin. 38 0727001

施引文献

图 1 驻波腔与四镜环形腔级联的光学系统

Fig. 1. Optical system of connecting a standing wave cavity and a four-mirror ring cavity in series.

下载: 全尺寸图片幻灯片

图 2 输出光场的量子关联噪声随输出镜对信号光场和闲置光场透射率之差的变化

Fig. 2. Quantum correlation variances of two output beams versus the transmissivity differences of the output coupler for idle and signal fields.

下载: 全尺寸图片幻灯片

图 3 两驻波腔级联的光学系统

Fig. 3. Optical system of two cascaded standing wave optical cavities.

下载: 全尺寸图片幻灯片

图 4 输出光场的纠缠度随光学隔离器传输效率的变化

Fig. 4. Dependences of correlation degree of output optical fields on transmission efficiency of the optical isolator.

下载: 全尺寸图片幻灯片

图 5 输出光场的纠缠度随输入EPR纠缠态光场纠缠度的变化

Fig. 5. Dependences of correlation degree of output optical fields on correlation degree of input EPR entanglement optical fields.

下载: 全尺寸图片幻灯片

图 6 输出光场的纠缠度随内腔损耗的变化

Fig. 6. Dependences of correlation degree of output optical fields on intracavity loss.

下载: 全尺寸图片幻灯片

map

[1]	Bouwmeester D, Pan J W, Mattle K, Eibl M, Weinfurter H, Zeilinger A 1997 Nature 390 575 Google Scholar
[2]	Furusawa A, Sorensen J L, Braustein S L, Fuchs C A, Kimble H J, Polzik E S 1998 Science 282 706 Google Scholar
[3]	Boschi D, Branca S, Marini F D, Hardy L, Popescu S 1998 Phys. Rev. Lett. 80 1121 Google Scholar
[4]	Vaidman L 1994 Phys. Rev. A 49 1473 Google Scholar
[5]	Braunstein S L, Kimble H J 1998 Phys. Rev. Lett. 80 869 Google Scholar
[6]	Bowen W P, Schnabel R, Lam P K, Ralph T C 2004 Phys. Rev. A 69 012304 Google Scholar
[7]	Eberle T, Händchen V, Duhme J, Franz T, Werner R F, Schnabel R 2011 Phys. Rev. A 83 052329 Google Scholar
[8]	Mizuno J, Wakui K, Furusawa A, Sasaki M 2005 Phys. Rev. A 71 012304 Google Scholar
[9]	Stoler D 1970 Phys. Rev. D 1 3217 Google Scholar
[10]	Mehmet M, Vahlbruch H, Lastzka N, Danzmann K, Schnabel R 2010 Phys. Rev. A 81 013814 Google Scholar
[11]	Mehmet M, Ast S, Eberle T, Steinlechner S, Vahlbruch H, Schnabel R 2011 Opt. Express 19 25763 Google Scholar
[12]	Eberle T, Steinlechner S, Bauchrowitz J, Händchen V, Vahlbruch H, Mehmet M, Muller-Ebhardt H, Schnabel R 2010 Phys. Rev. Lett. 104 251102 Google Scholar
[13]	Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801 Google Scholar
[14]	彭堃墀, 贾晓军, 苏晓龙, 谢常德 2011 光学学报 31 09001071 Peng K C, Jia X J, Su X L, Xie C D 2011 Acta Opt. Sin. 31 09001071
[15]	贾晓军, 苏晓龙, 潘庆, 谢常德, 彭堃墀 2005 54 2717 Google Scholar Jia X J, Su X L, Pan Q, Xie C D, Peng K C 2005 Acta Phys. Sin. 54 2717 Google Scholar
[16]	赵超樱, 谭维翰 2005 54 4526 Google Scholar Zhao C Y, Tan W H 2005 Acta Phys. Sin. 54 4526 Google Scholar
[17]	Wang Y, Su X L, Shen H, Tan A H, Xie C D, Peng K C 2010 Phys. Rev. A 81 022311 Google Scholar
[18]	Ou Z Y, Pereira S F, Kimble H J, Peng K C 1992 Phys. Rev. Lett. 68 3663 Google Scholar
[19]	Zhang Y, Wang H, Li X Y, Jing J T, Xie C D, Peng K C 2000 Phys. Rev. A 62 023813 Google Scholar
[20]	Laurat J, Coudreau T, Keller G, Treps N, Fabre C 2004 Phys. Rev. A 70 042315 Google Scholar
[21]	Takei N, Yonezawa H, Aoki T, Furusawa A 2005 Phys. Rev. Lett. 94 220502 Google Scholar
[22]	Wang Y, Shen H, Jin X L, Su X L, Xie C D, Peng K C 2010 Opt. Express 18 6149 Google Scholar
[23]	Gottesman D, Preskill J 2001 Phys. Rev. A 63 022309 Google Scholar
[24]	Yukawa M, Benichi H, Furusawa A 2008 Phys. Rev. A 77 022314 Google Scholar
[25]	Li X Y, Pan Q, Jing J T, Zhang J, Xie C D, Peng K C 2002 Phys. Rev. Lett. 88 047904 Google Scholar
[26]	Mattle K, Weinfurter H, Kwiat P G, Zeilinger A 1996 Phys. Rev. Lett. 76 4656 Google Scholar
[27]	Braunstein S L, Kimble H J 2000 Phys. Rev. A 61 042302 Google Scholar
[28]	Zhang J, Peng K C 2000 Phys. Rev. A 62 064302 Google Scholar
[29]	Zhou Y Y, Jia X J, Li F, Xie C D, Peng K C 2015 Opt. Express 23 4952 Google Scholar
[30]	Chen H X, Zhang J 2009 Phys. Rev. A 79 063826 Google Scholar
[31]	Shang Y N, Jia X J, Shen Y M, Xie C D, Peng K C 2010 Opt. Lett. 35 853 Google Scholar
[32]	Yan Z H, Jia X J, Su X L, Duan Z Y, Xie C D, Peng K C 2012 Phys. Rev. A 85 040305(R)Google Scholar
[33]	Duan L M, Giedke G, Cirac J I, Zoller P 2000 Phys. Rev. Lett. 84 2722 Google Scholar
[34]	Simon R 2000 Phys. Rev. Lett. 84 2726 Google Scholar
[35]	周瑶瑶, 蔚娟, 闫智辉, 贾晓军 2018 38 0727001 Zhou Y Y, Yu J, Yan Z H, Jia X J 2018 Acta Opt. Sin. 38 0727001

[1]	郝景晨, 杜培林, 孙恒信, 刘奎, 张静, 杨荣国, 郜江瑞. 双端腔Ⅱ类倍频产生四组份纠缠光场. , 2024, 73(7): 074203. doi: 10.7498/aps.73.20231630
[2]	余胜, 刘焕章, 刘胜帅, 荆杰泰. 基于四波混频过程和线性分束器产生四组份纠缠. , 2020, 69(9): 090303. doi: 10.7498/aps.69.20200040
[3]	李娟, 李佳明, 蔡春晓, 孙恒信, 刘奎, 郜江瑞. 优化抽运空间分布实现连续变量超纠缠的纠缠增强. , 2019, 68(3): 034204. doi: 10.7498/aps.68.20181625
[4]	田聪, 鹿翔, 张英杰, 夏云杰. 纠缠相干光场对量子态最大演化速率的操控. , 2019, 68(15): 150301. doi: 10.7498/aps.68.20190385
[5]	杨荣国, 张超霞, 李妮, 张静, 郜江瑞. 级联四波混频系统中纠缠增强的量子操控. , 2019, 68(9): 094205. doi: 10.7498/aps.68.20181837
[6]	周瑶瑶, 李鹏飞, 闫智辉, 贾晓军. 基于相干反馈操控的纠缠源的分析. , 2019, 68(23): 234203. doi: 10.7498/aps.68.20191168
[7]	邢贵超, 夏云杰. 与热库耦合的光学腔内三原子间的纠缠动力学. , 2018, 67(7): 070301. doi: 10.7498/aps.67.20172546
[8]	张秀龙, 鲍倩倩, 杨明珠, 田雪松. 双腔光力学系统中输出光场纠缠特性的研究. , 2018, 67(10): 104203. doi: 10.7498/aps.67.20172467
[9]	任宝藏, 邓富国. 光子两自由度超并行量子计算与超纠缠态操控. , 2015, 64(16): 160303. doi: 10.7498/aps.64.160303
[10]	梁艳, 吴奇成, 计新. 在非惯性系中处于热库中的两个腔的纠缠动力学. , 2014, 63(2): 020301. doi: 10.7498/aps.63.020301
[11]	卢道明. 弱相干场耦合腔系统中的纠缠特性. , 2013, 62(3): 030302. doi: 10.7498/aps.62.030302
[12]	闫智辉, 贾晓军, 谢常德, 彭堃墀. 利用非简并光学参量振荡腔产生连续变量三色三组分纠缠态. , 2012, 61(1): 014206. doi: 10.7498/aps.61.014206
[13]	卢道明. 腔外原子操作控制腔内原子的纠缠特性. , 2010, 59(12): 8359-8364. doi: 10.7498/aps.59.8359
[14]	姜春蕾, 方卯发, 吴珍珍. 双纠缠原子在耗散腔场中的纠缠动力学. , 2006, 55(9): 4647-4651. doi: 10.7498/aps.55.4647
[15]	周青春, 祝世宁. Λ型三能级原子与数态单模光场互作用系统的纠缠特性. , 2005, 54(5): 2043-2048. doi: 10.7498/aps.54.2043
[16]	宋军, 曹卓良. 两纠缠原子与二项式光场相互作用的动力学. , 2005, 54(2): 696-702. doi: 10.7498/aps.54.696
[17]	贾晓军, 苏晓龙, 潘庆, 谢常德, 彭堃墀. 具有经典相干性的两组EPR纠缠态光场的实验产生. , 2005, 54(6): 2717-2722. doi: 10.7498/aps.54.2717
[18]	赖振讲, 杨志勇, 白晋涛, 孙中禹. 二能级原子与相干态腔场相互作用过程中的纠缠交换. , 2004, 53(11): 3733-3738. doi: 10.7498/aps.53.3733
[19]	戴宏毅, 陈平形, 梁林梅, 李承祖. 利用Λ型原子与光场的纠缠态传送腔场的奇偶相干态的叠加态. , 2004, 53(2): 441-444. doi: 10.7498/aps.53.441
[20]	宋克慧. 利用原子腔场的Raman相互作用制备多种形式的原子纠缠态. , 2000, 49(3): 441-444. doi: 10.7498/aps.49.441

计量

文章访问数: 6711
PDF下载量: 70
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

两腔级联纠缠增强的理论分析