相干与信息守恒及其在Mach-Zehnder干涉中的应用

傅双双; 骆顺龙; 孙源

doi:10.7498/aps.68.20181778

摘要

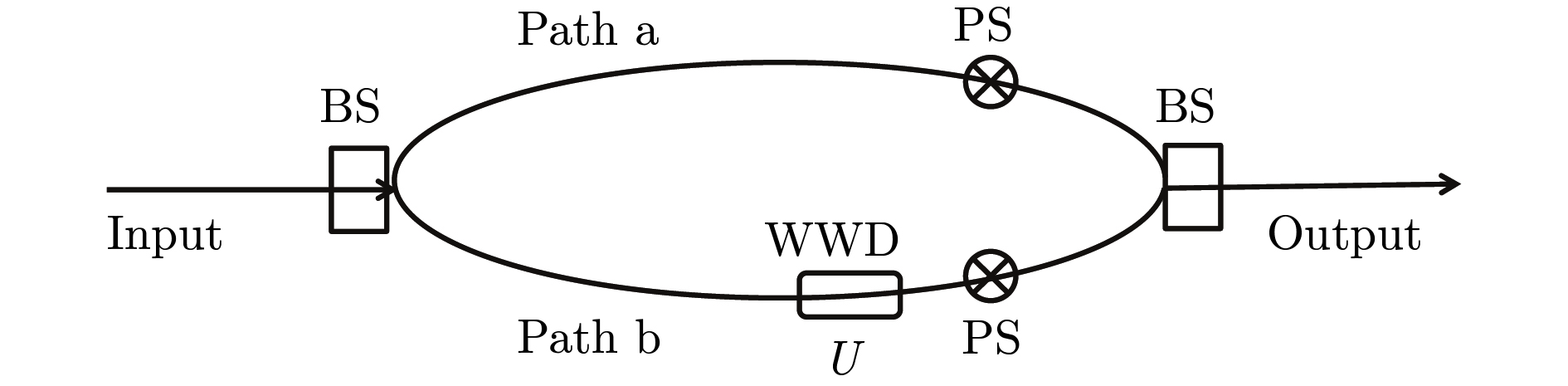
自量子力学诞生以来, 相干性和互补性一直是被广泛而深入研究的两个重要课题. 随着量子信息近年来的发展, 人们引入了若干度量来定量地刻画相干性和互补性. 本文建立两个信息守恒关系式, 分别基于“Bures距离-保真度”和“对称-非对称”, 并且利用它们来刻画相干性和互补性. 具体来说, 首先从信息守恒的观点解释Bures距离和保真度的互补关系, 并由此自然推导出Mach-Zehnder 干涉仪中的Englert“干涉-路径”互补关系. 其次在量子态和信道相互作用的一般框架中讨论“对称-非对称”信息守恒关系, 并揭示其与Bohr互补性和量子相干性的内在联系. 最后, 在Mach-Zehnder干涉仪中探讨相干、退相干及互补性, 刻画两个信息守恒关系之间的密切联系.

关键词:

Abstract

Coherence and complementarity are two important themes in quantum mechanics, which have been widely and thoroughly investigated. Recently, with the rapid development of quantum information theory, various measures have been introduced for quantitatively studying the coherence and complementarity. However, most of these studies are independent of each other in that they focus on only one theme, for example, the wave-particle duality and Heisenberg uncertainty principle are usually regarded as manifestation of Bohr’s complementary principle, while coherence is a quantum feature closely related to quantum superposition. During the past few years, there has been a flurry of research interest in the study of quantum coherence from the quantum resource-theoretic point of view. In this paper, we establish two information conservation relations and employ them to characterize complementarity and quantum coherence. As an illustration of the main results, we discuss these two themes in the Mach-Zehnder interferometer. Our study reveals that these two quantum themes are closely related to each other. Our main results are listed as follows. Firstly, we establish two information conservation relations, one is based on " Bures distance versus fidelity” and the other based on " symmetry versus asymmetry”. Then we employ these information conservation relations to investigate coherence and complementarity. Specifically, we provide an explanation of the " Bures distance versus fidelity” trade-off relation from the information conservation perspective, establish the link between the information conservation relation and wave-particle duality, and derive the famous Englert inequality concerning " fringe visibility versus path distinguishability” from the information conservation relation. Furthermore, in the general framework of state-channel interaction, we derive " symmetry versus asymmetry” trade-off relation and explain it as an information conservation relation, reveal its intrinsic relations with coherence and complementarity. Lastly, we demonstrate that the two information conservation relations are closely interrelated, and we also discuss the coherence, decoherence and complementarity in the Mach-Zehnder interferometer, explicitly, we reveal that the Bures distance can be regarded as a lower bound of the asymmetry of state-channel interaction while fidelity is an upper bound of the symmetry of state-channel interaction. We expect that our information conservation relation can provide a unified framework for the study of coherence and complementarity.

Keywords:

作者及机构信息

1.
北京科技大学数理学院, 北京　100083

2.
中国科学院数学与系统科学研究院, 北京　100190

3.
中国科学院大学数学学院, 北京　100049

通信作者: 骆顺龙, luosl@amt.ac.cn

基金项目: 北京市自然科学基金(批准号: 1174017)、国家自然科学基金青年科学基金(批准号: 11605006)、国家自然科学基金(批准号: 11875317)、国家数学与交叉科学中心(批准号: Y029152K51)和中国科学院随机复杂结构与数据科学重点实验室(批准号: 2008DP173182)资助的课题.

Authors and contacts

1.
School of Mathematics and Physics, University of Science and Technology Beijing, Beijing 100083, China

2.
Academy of Mathematics and Systems Science, Chinese Academy of Sciences, Beijing 100190, China

3.
School of Mathematical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

Corresponding author: Luo Shun-Long, luosl@amt.ac.cn

Funds: Project supported by the Natural Science Foundation of Beijing, China (Grant No. 1174017), the Young Scientists Fund of the National Natural Science Foundation of China (Grant No. 11605006), the National Natural Science Foundation of China (Grant No. 11875317), the National Center for Mathematics and Interdisciplinary Sciences, Chinese Academy of Sciences, China (Grant No. Y029152K51), and the Key Laboratory of Random Complex Structures and Data Science, Chinese Academy of Sciences, China (Grant No. 2008DP173182).

文章全文 : translate this paragraph

参考文献

[1]	Bohr N 1937 Phil. Sci. 4 289 Google Scholar
[2]	Heisenberg W 1927 Zeit. Physik 43 172 Google Scholar
[3]	Heisenberg W 1930 The Physical Principles of the Quantum Theory (Chicago: The University of Chicago Press) pp13–39
[4]	Wootters W K, Zurek W H 1979 Phys. Rev. D 19 473 Google Scholar
[5]	Scully M O, Englert B G, Walther H 1991 Nature 351 111 Google Scholar
[6]	Mandel L 1991 Opt. Lett. 16 1882 Google Scholar
[7]	Jaeger G, Horne M A, Shimony A 1993 Phys. Rev. A 48 1023 Google Scholar
[8]	Englert B G 1996 Phys. Rev. Lett. 77 2154 Google Scholar
[9]	Busch P, Shilladay C 2006 Phys. Rep. 435 1 Google Scholar
[10]	Coles P J, Kaniewski J, Wehner S 2014 Nat. Commun. 5 5814 Google Scholar
[11]	Coles P J, Berta M, Tomamichel M, Wehner S 2017 Rev. Mod. Phys. 89 015002 Google Scholar
[12]	Jaeger G, Shimony A, Vaidmann L 1995 Phys. Rev. A 51 54 Google Scholar
[13]	Åberg J 2006 arXiv:quant-ph/0612146
[14]	Levi F, Mintert F 2014 New J. Phys. 16 033007 Google Scholar
[15]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[16]	Girolami D 2014 Phys. Rev. Lett. 113 170401 Google Scholar
[17]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[18]	Pires D P, Celeri L C, Soares-Pinto D O 2015 Phys. Rev. A 91 042330 Google Scholar
[19]	Yao Y, Xiao X, Ge L, Sun C P 2015 Phys. Rev. A 92 022112 Google Scholar
[20]	Winter A, Yang D 2016 Phys. Rev. Lett. 116 120404 Google Scholar
[21]	Ma J, Yadin B, Girolami D, Vedral V, Gu M 2016 Phys. Rev. Lett. 116 160407 Google Scholar
[22]	Chang L, Luo S, Sun Y 2017 Commun. Theor. Phys. 68 565 Google Scholar
[23]	Streltsov A, Adesso G, Plenio M B 2017 Rev. Mod. Phys. 89 041003 Google Scholar
[24]	Luo S, Sun Y 2017 Phys. Rev. A 96 022130 Google Scholar
[25]	Luo S, Sun Y 2017 Phys. Rev. A 96 022136 Google Scholar
[26]	Yao Y, Dong G H, Xiao X, Li M, Sun C P 2017 Phys. Rev. A 96 052322 Google Scholar
[27]	Zhao H, Yu C 2018 Sci. Rep. 8 299 Google Scholar
[28]	Jin Z X, Fei S M 2018 Phys. Rev. A 97 062342 Google Scholar
[29]	Horodecki M, Oppenheim J 2013 Nat. Commun. 4 2059 Google Scholar
[30]	Narasimhachar V, Gour G 2015 Nat. Commun. 6 7689 Google Scholar
[31]	Lloyd S 2011 J. Phys. Conf. Ser. 302 012037 Google Scholar
[32]	Marvian I, Spekkens R W 2014 Nat. Commun. 5 3821 Google Scholar
[33]	Marvian I, Spekkens R W 2016 Phys. Rev. A 94 052324 Google Scholar
[34]	Fang Y N, Dong G H, Zhou D L, Sun C P 2016 Commun. Theor. Phys. 65 423 Google Scholar
[35]	Yao Y, Dong G H., Xiao X, Sun C P 2016 Sci. Rep. 6 32010 Google Scholar
[36]	Bagan E, Bergou J A, Cottrell S S, Hillery M 2016 Phys. Rev. Lett. 116 160406 Google Scholar
[37]	Bera M N, Qureshi T, Siddiqui M A, Pati A K 2015 Phys. Rev. A 92 012118 Google Scholar
[38]	Hu M L, Hu X , Wang J C, Peng Yi, Zhang Y R, Fan H 2018 arXiv:1703.01852 [quant-ph]
[39]	Luo S, Sun Y 2018 Phys. Rev. A 98 012113 Google Scholar
[40]	Nielsen, M A, Chuang I L 2000 Quantum Computation and Quantum Information (10th Anniversary Edition) (New York: Cambridge University Press) pp60–111, 399–416
[41]	Bures D 1969 Trans. Amer. Math. Soc. 135 199-212 Google Scholar
[42]	Hubner M 1993 Phys. Lett. A 179 226 Google Scholar
[43]	Fuchs C A, Caves C M 1995 Open Sys. Inf. Dyn. 3 345 Google Scholar
[44]	Barnum H, Caves C M, Fuchs C A, Jozsa R, Schumacher B 1996 Phys. Rev. Lett. 76 2818 Google Scholar
[45]	Uhlmann A 2000 Phys. Rev. A 62 032307 Google Scholar
[46]	Dodd J L, Nielsen M A 2002 Phys. Rev. A 66 044301 Google Scholar
[47]	Luo S, Zhang Q 2004 Phys. Rev. A 69 032106 Google Scholar

施引文献

图 1 对称MZI (BS, 50 : 50分束器; PS, 相移器; WWD, 路径探测器)

Fig. 1. A schematic sketch of the symmetric Mach-Zehnder interferometer. BS, 50:50 beam splitter; PS, phase shifter; WWD, which-way detector.

下载: 全尺寸图片幻灯片

map

[1]	Bohr N 1937 Phil. Sci. 4 289 Google Scholar
[2]	Heisenberg W 1927 Zeit. Physik 43 172 Google Scholar
[3]	Heisenberg W 1930 The Physical Principles of the Quantum Theory (Chicago: The University of Chicago Press) pp13–39
[4]	Wootters W K, Zurek W H 1979 Phys. Rev. D 19 473 Google Scholar
[5]	Scully M O, Englert B G, Walther H 1991 Nature 351 111 Google Scholar
[6]	Mandel L 1991 Opt. Lett. 16 1882 Google Scholar
[7]	Jaeger G, Horne M A, Shimony A 1993 Phys. Rev. A 48 1023 Google Scholar
[8]	Englert B G 1996 Phys. Rev. Lett. 77 2154 Google Scholar
[9]	Busch P, Shilladay C 2006 Phys. Rep. 435 1 Google Scholar
[10]	Coles P J, Kaniewski J, Wehner S 2014 Nat. Commun. 5 5814 Google Scholar
[11]	Coles P J, Berta M, Tomamichel M, Wehner S 2017 Rev. Mod. Phys. 89 015002 Google Scholar
[12]	Jaeger G, Shimony A, Vaidmann L 1995 Phys. Rev. A 51 54 Google Scholar
[13]	Åberg J 2006 arXiv:quant-ph/0612146
[14]	Levi F, Mintert F 2014 New J. Phys. 16 033007 Google Scholar
[15]	Baumgratz T, Cramer M, Plenio M B 2014 Phys. Rev. Lett. 113 140401 Google Scholar
[16]	Girolami D 2014 Phys. Rev. Lett. 113 170401 Google Scholar
[17]	Streltsov A, Singh U, Dhar H S, Bera M N, Adesso G 2015 Phys. Rev. Lett. 115 020403 Google Scholar
[18]	Pires D P, Celeri L C, Soares-Pinto D O 2015 Phys. Rev. A 91 042330 Google Scholar
[19]	Yao Y, Xiao X, Ge L, Sun C P 2015 Phys. Rev. A 92 022112 Google Scholar
[20]	Winter A, Yang D 2016 Phys. Rev. Lett. 116 120404 Google Scholar
[21]	Ma J, Yadin B, Girolami D, Vedral V, Gu M 2016 Phys. Rev. Lett. 116 160407 Google Scholar
[22]	Chang L, Luo S, Sun Y 2017 Commun. Theor. Phys. 68 565 Google Scholar
[23]	Streltsov A, Adesso G, Plenio M B 2017 Rev. Mod. Phys. 89 041003 Google Scholar
[24]	Luo S, Sun Y 2017 Phys. Rev. A 96 022130 Google Scholar
[25]	Luo S, Sun Y 2017 Phys. Rev. A 96 022136 Google Scholar
[26]	Yao Y, Dong G H, Xiao X, Li M, Sun C P 2017 Phys. Rev. A 96 052322 Google Scholar
[27]	Zhao H, Yu C 2018 Sci. Rep. 8 299 Google Scholar
[28]	Jin Z X, Fei S M 2018 Phys. Rev. A 97 062342 Google Scholar
[29]	Horodecki M, Oppenheim J 2013 Nat. Commun. 4 2059 Google Scholar
[30]	Narasimhachar V, Gour G 2015 Nat. Commun. 6 7689 Google Scholar
[31]	Lloyd S 2011 J. Phys. Conf. Ser. 302 012037 Google Scholar
[32]	Marvian I, Spekkens R W 2014 Nat. Commun. 5 3821 Google Scholar
[33]	Marvian I, Spekkens R W 2016 Phys. Rev. A 94 052324 Google Scholar
[34]	Fang Y N, Dong G H, Zhou D L, Sun C P 2016 Commun. Theor. Phys. 65 423 Google Scholar
[35]	Yao Y, Dong G H., Xiao X, Sun C P 2016 Sci. Rep. 6 32010 Google Scholar
[36]	Bagan E, Bergou J A, Cottrell S S, Hillery M 2016 Phys. Rev. Lett. 116 160406 Google Scholar
[37]	Bera M N, Qureshi T, Siddiqui M A, Pati A K 2015 Phys. Rev. A 92 012118 Google Scholar
[38]	Hu M L, Hu X , Wang J C, Peng Yi, Zhang Y R, Fan H 2018 arXiv:1703.01852 [quant-ph]
[39]	Luo S, Sun Y 2018 Phys. Rev. A 98 012113 Google Scholar
[40]	Nielsen, M A, Chuang I L 2000 Quantum Computation and Quantum Information (10th Anniversary Edition) (New York: Cambridge University Press) pp60–111, 399–416
[41]	Bures D 1969 Trans. Amer. Math. Soc. 135 199-212 Google Scholar
[42]	Hubner M 1993 Phys. Lett. A 179 226 Google Scholar
[43]	Fuchs C A, Caves C M 1995 Open Sys. Inf. Dyn. 3 345 Google Scholar
[44]	Barnum H, Caves C M, Fuchs C A, Jozsa R, Schumacher B 1996 Phys. Rev. Lett. 76 2818 Google Scholar
[45]	Uhlmann A 2000 Phys. Rev. A 62 032307 Google Scholar
[46]	Dodd J L, Nielsen M A 2002 Phys. Rev. A 66 044301 Google Scholar
[47]	Luo S, Zhang Q 2004 Phys. Rev. A 69 032106 Google Scholar

[1]	吕鑫. 相干与路径信息. , 2020, 69(7): 070301. doi: 10.7498/aps.69.20191084
[2]	程君妮. 基于光纤锥和纤芯失配的Mach-Zehnder干涉湿度传感器. , 2018, 67(2): 024212. doi: 10.7498/aps.67.20171677
[3]	兰斌, 冯国英, 张涛, 梁井川, 周寿桓. 用于透明平板平行度和均匀性测量的单元件干涉仪. , 2017, 66(6): 069501. doi: 10.7498/aps.66.069501
[4]	秦晨, 余辉, 叶乔波, 卫欢, 江晓清. 基于绝缘体上硅的一种改进的Mach-Zehnder声光调制器. , 2016, 65(1): 014304. doi: 10.7498/aps.65.014304
[5]	谭林秋, 华灯鑫, 汪丽, 高飞, 狄慧鸽. Mach-Zehnder干涉仪条纹成像多普勒激光雷达风速反演及视场展宽技术. , 2014, 63(22): 224205. doi: 10.7498/aps.63.224205
[6]	李成强, 王挺峰, 张合勇, 谢京江, 刘立生, 郭劲. 光源参数及大气湍流对电磁光束传输偏振特性的影响. , 2014, 63(10): 104201. doi: 10.7498/aps.63.104201
[7]	张颖, 刘兰琴, 王文义, 黄晚晴, 耿远超, 谢旭东, 朱启华. 激光脉冲前后沿相干叠加对多程放大的影响. , 2014, 63(18): 184205. doi: 10.7498/aps.63.184205
[8]	李辉栋, 傅海威, 邵敏, 赵娜, 乔学光, 刘颖刚, 李岩, 闫旭. 基于光纤气泡和纤芯失配的Mach-Zehnder干涉液体折射率传感器. , 2013, 62(21): 214209. doi: 10.7498/aps.62.214209
[9]	殷丽梅, 张伟刚, 薛晓琳, 白志勇, 魏石磊. 飞秒激光刻蚀非平行壁光纤微腔Mach-Zehnder干涉仪特性及其流体传感研究. , 2012, 61(17): 170701. doi: 10.7498/aps.61.170701
[10]	程治明, 吴逢铁, 方翔, 范丹丹, 朱健强. 圆顶轴棱锥产生多个局域空心光束. , 2012, 61(21): 214201. doi: 10.7498/aps.61.214201
[11]	齐晓庆, 高春清. 螺旋相位光束轨道角动量态测量的实验研究. , 2011, 60(1): 014208. doi: 10.7498/aps.60.014208
[12]	邓勇, Meglinski Igor. Monte Carlo方法模拟光在生物组织中传播的新进展. , 2010, 59(2): 1396-1401. doi: 10.7498/aps.59.1396
[13]	郑力明, 王发强, 刘颂豪. 光声互作用模型中的Pancharatnam相位. , 2009, 58(5): 2884-2888. doi: 10.7498/aps.58.2884
[14]	商娅娜, 王东, 闫智辉, 王文哲, 贾晓军, 彭堃墀. 利用非平衡光纤Mach-Zehnder干涉仪探测频率非简并纠缠态光场. , 2008, 57(6): 3514-3518. doi: 10.7498/aps.57.3514
[15]	郑无敌, 张国平, 王琛, 孙今人, 方智恒, 顾援, 傅思祖. 用X射线激光M-Z干涉仪诊断点聚焦CH等离子体电子密度. , 2007, 56(7): 3984-3989. doi: 10.7498/aps.56.3984
[16]	柴路, 何铁英, 杨胜杰, 王清月, 张志刚. 光谱位相干涉仪参数的优化选取. , 2004, 53(1): 114-118. doi: 10.7498/aps.53.114
[17]	刘婷婷, 王大威, 陆伟新, 孙泉, 杨宏, 蒋红兵, 龚旗煌. 双光束相干控制产生多次谐波的实验验证. , 2003, 52(4): 864-869. doi: 10.7498/aps.52.864
[18]	郭红霞, 陈雨生, 张义门, 周辉, 龚建成, 韩福斌, 关颖, 吴国荣. 稳态、瞬态X射线辐照引起的互补性金属-氧化物-半导体器件剂量增强效应研究. , 2001, 50(12): 2279-2283. doi: 10.7498/aps.50.2279
[19]	庄松林, 郑权. 部分相干信息处理中的逆源问题. , 1985, 34(4): 439-446. doi: 10.7498/aps.34.439
[20]	激光干涉研究小组. 以巨脉冲红宝石激光为光源的Mach-Zehnder干涉仪应用于θ收缩等离子体的研究. , 1974, 23(1): 1-16. doi: 10.7498/aps.23.1

计量

文章访问数: 7940
PDF下载量: 148
被引次数: 0

姓名
邮箱
手机号码
标题
留言内容
验证码

搜索

留言板

相干与信息守恒及其在Mach-Zehnder干涉中的应用