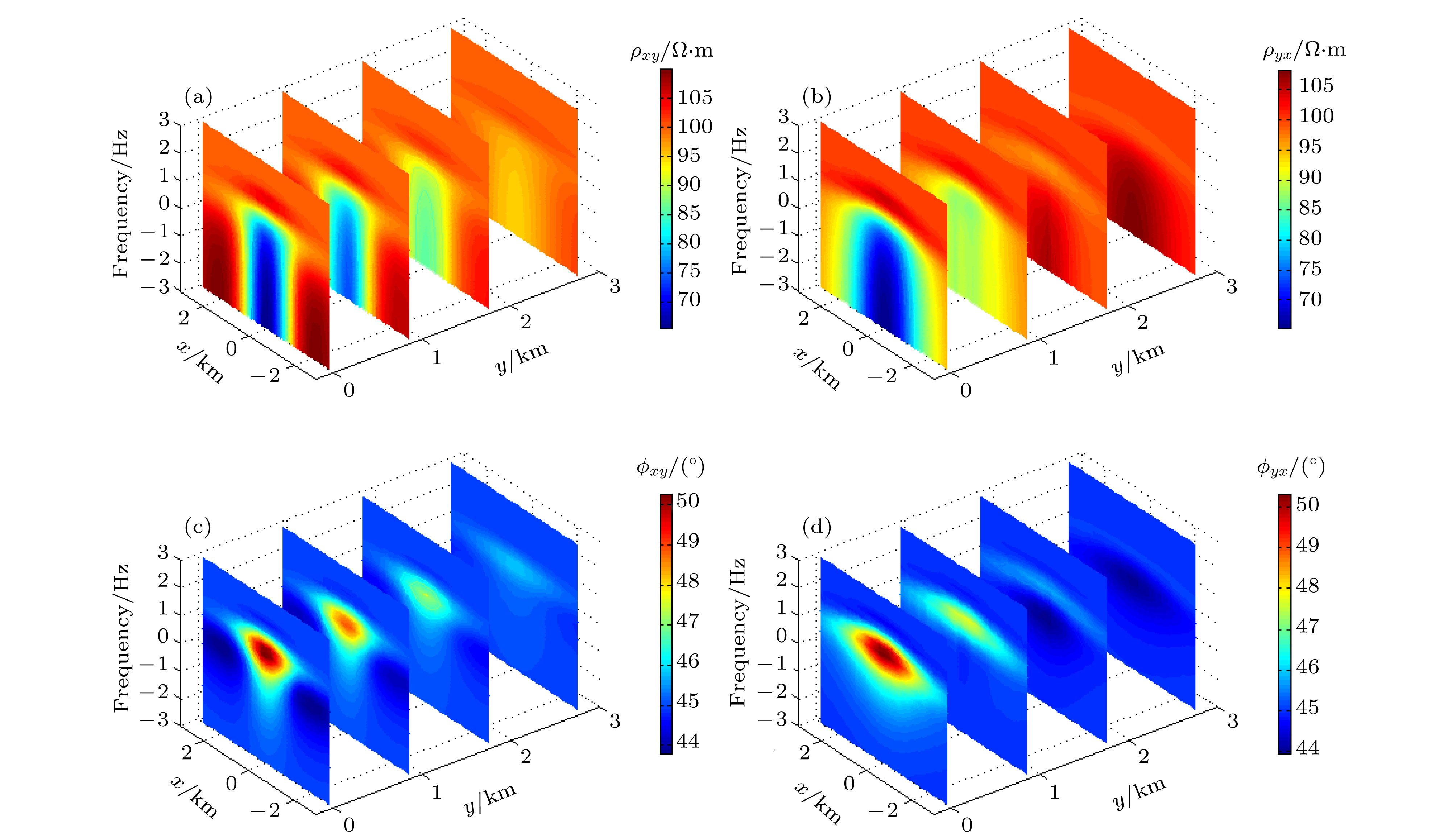
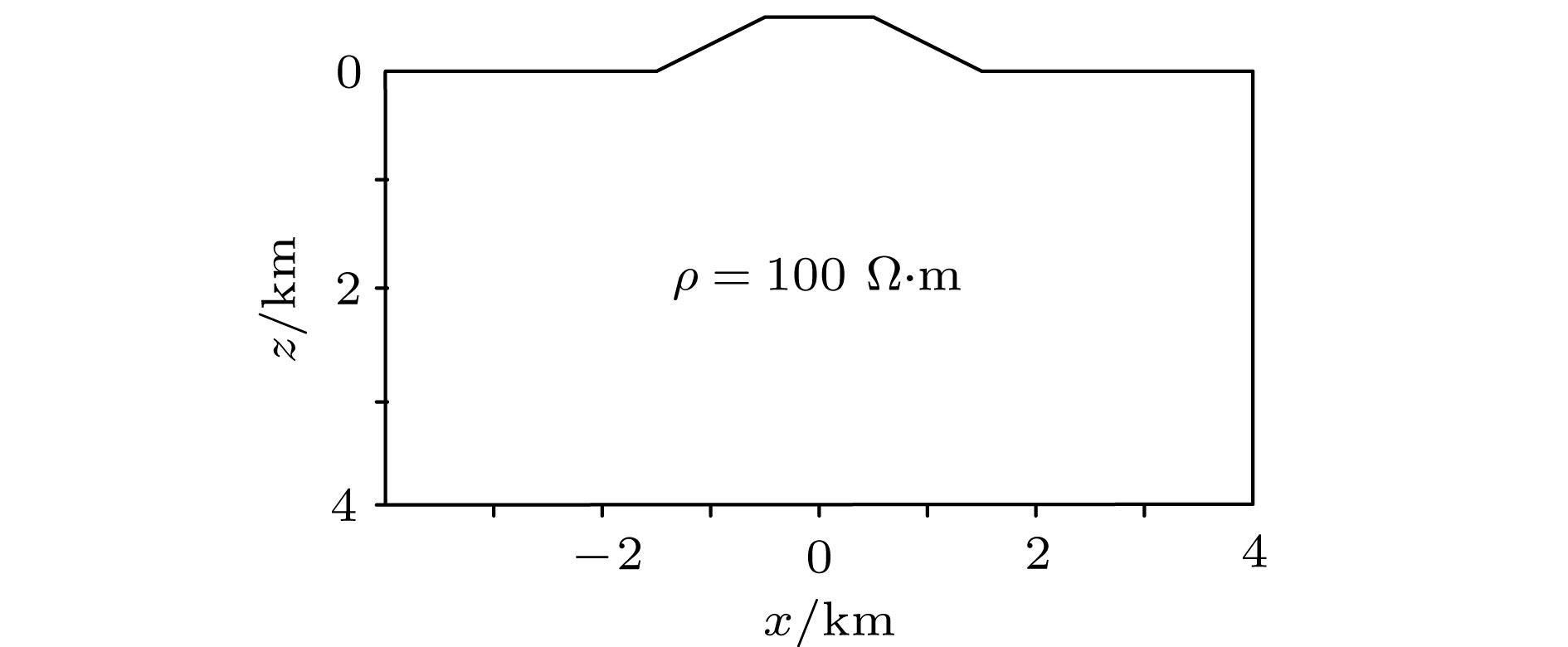
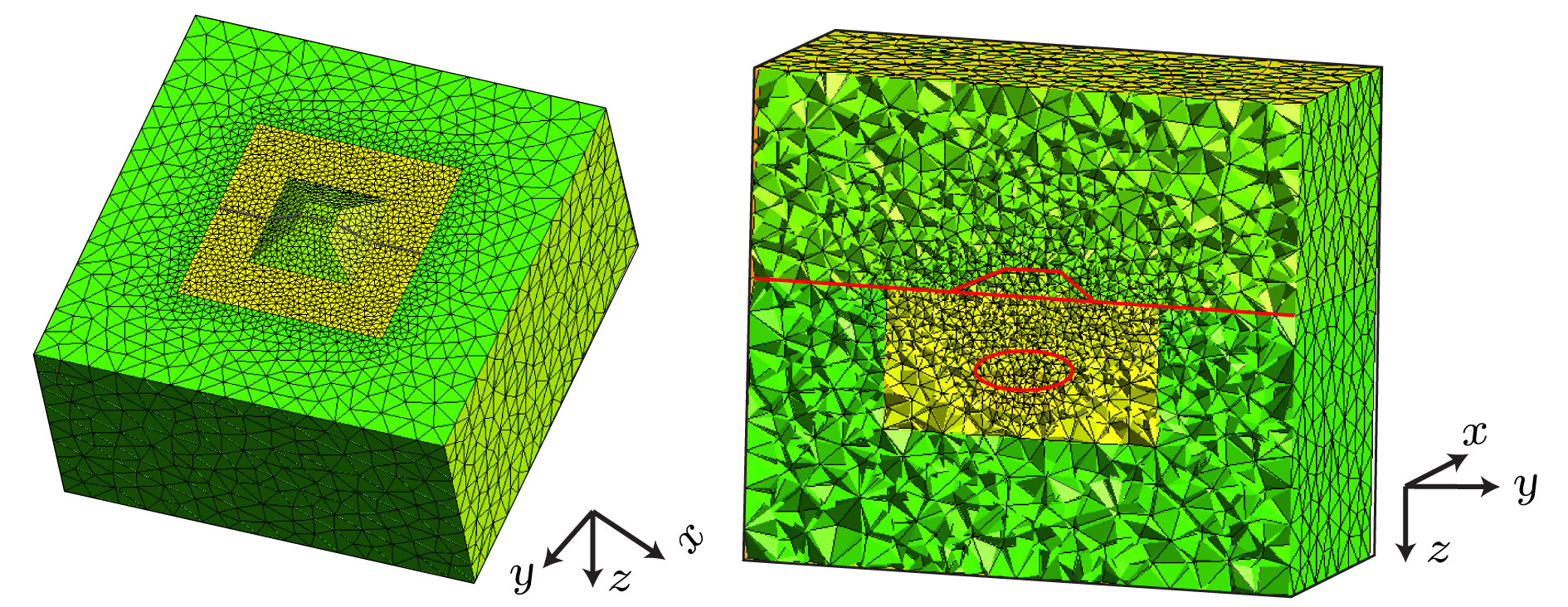
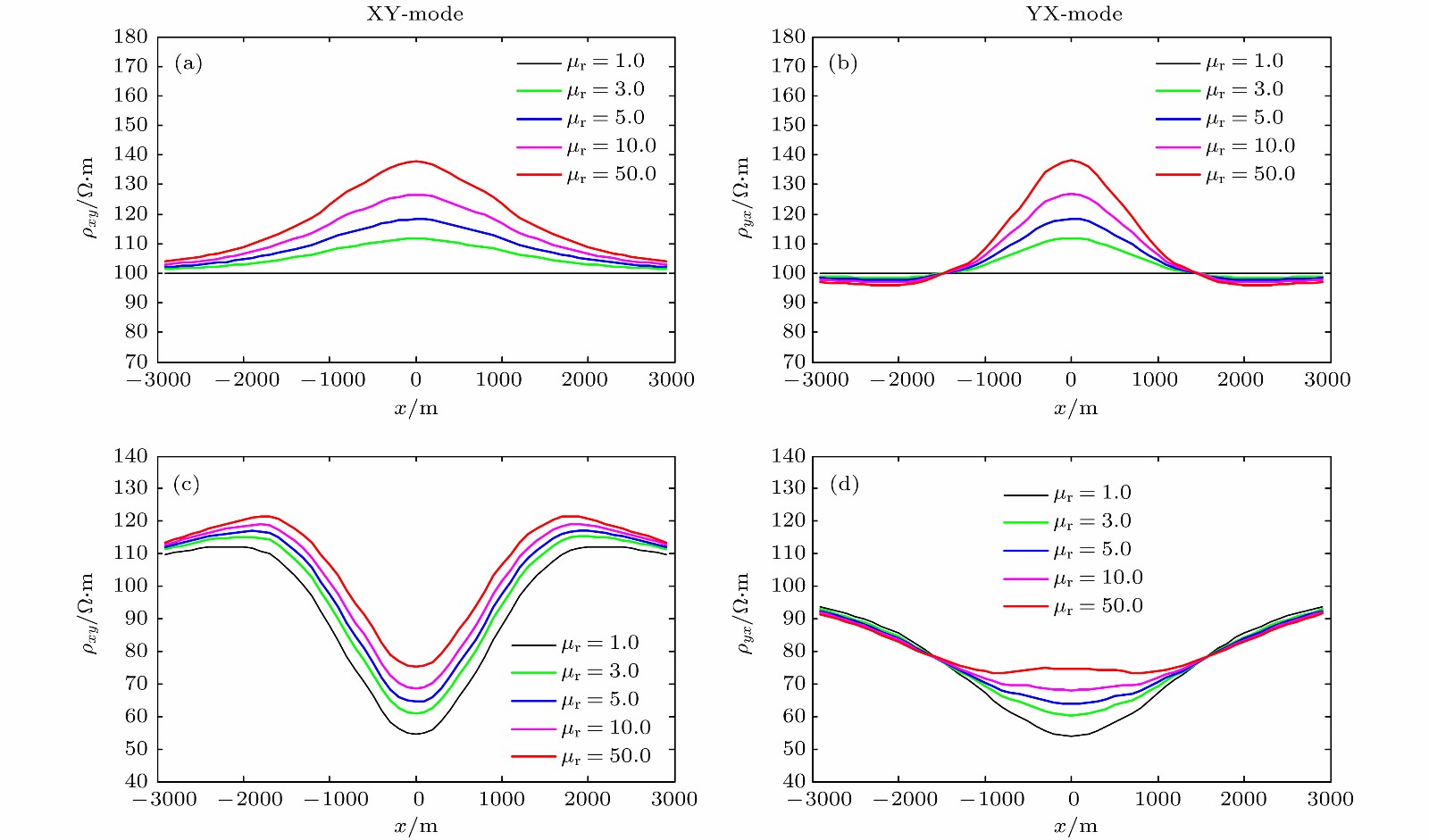
-
采用矢量有限元法实现了三维电磁扩散场数值模拟, 并成功将其应用在大地电磁的正演研究中. 为灵活精确地拟合起伏地形和地下不规则构造, 采用由不规则四面体单元组成的非结构化网格, 可根据模型设计的需要调整网格的大小. 引入了基于二次场理论, 将解析的一次场从总场中扣除, 直接计算二次场, 使得误差仅局限于相对较小的二次场, 以提高总场计算精度. 常规的节点有限元法不满足电性分界面上法向电场不连续和无源区单元内电流密度无散, 违反麦克斯韦方程组. 为克服节点有限元法的弊端, 使用矢量有限元法求解基于二次电场的偏微分方程. 另外, 在算法设计中, 考虑了磁导率参数的变化, 可以模拟磁导率不均匀的模型. 通过与COMMEMI模型已发表的结果对比, 证明了本文算法的正确性和精确性. 为突显非结构网格优势, 计算了椭球异常体模型和任意地形模型的MT响应, 并详细讨论了地形和磁化效应对三维数值模拟结果的影响.We present a newly developed algorithm for three-dimensional (3D) magnetotelluric model based on the vector finite element method. In this paper, unstructured grids which are composed of irregular tetrahedrons are used in our finite element model, which can be refined locally and adaptively according to the complex geometry of computational domain or subsurface structure. For obtaining more accurate solutions, secondary field rather than total field is numerically computed, which makes the errors limited to relatively small secondary field. Traditional node-based finite element method does not satisfy the condition that the normal electrical field is discontinuous at the interface of electric separatrix and the electrical current density is divergence-free throughout the regions without source, which obviously violates Maxwell equations. In order to overcome these drawbacks of node-based finite element, vector finite element method is employed to solve the secondary field-based partial differential equation. Moreover, in this study, the heterogeneous permeability is taken into consideration in our algorithm, as a consequence, which can deal with heterogeneous permeability model. The accuracy of our approach is verified by comparing with previously published numerical simulations of a COMMEMI-3D model. The advantages of our approach are also illustrated by the numerical simulations of model with arbitrary topography and complicated anomalous body. In addition, the simulation results of the irregular anomaly and the complex model of arbitrary terrain are both ideal results. It proves that the effect of 3D terrain is more serious and complex than that of two-dimensional (2D) terrain, and dealing with 3D models or data with 2D algorithm may bring in large errors. In the area where the magnetic permeability is abnormal, the magnetic permeability has an important influence on the numerical simulation results, and the magnetic permeability must be treated as an independent parameter in the magnetotellurics survey.
-
Keywords:
- electromagnetic diffusion /
- vector finite element method /
- numerical simulation /
- magnetization /
- magnetotellurics
[1] Hohmann G W 1983 Surv. Geophys. 6 27
Google Scholar
[2] Zhdanov M S, Lee S K, Yoshioka K 2006 Geophysics 71 G333
Google Scholar
[3] 陈桂波, 汪宏年, 姚敬金, 韩子夜 2009 58 3848
Google Scholar
Chen G B, Wang H N, Yao J J, Han Z Y 2009 Acta Phys. Sin. 58 3848
Google Scholar
[4] 谭捍东, 余钦范, John B 2003 地球 46 705
Google Scholar
Tang H D, Yu Q F, John B 2003 Chin. J. Geophys. 46 705
Google Scholar
[5] Streich R 2009 Geophysics 74 F95
Google Scholar
[6] Smith J T 1996 Geophysics 61 1308
Google Scholar
[7] Wang W, Wu X P, Spitzer K 2013 Geophys. J. Int. 193 734
Google Scholar
[8] Coggon J H 1971 Geophysics 36 132
Google Scholar
[9] Fox R C, Hohmann G W, Killpack T J 1980 Geophysics 45 75
Google Scholar
[10] Wannamaker P E, Stodt J A, Rijo L 1987 Geophys. J. Int. 88 277
Google Scholar
[11] 李勇, 吴小平, 林品荣 2013 地球物理学进展 27 2452
Li Y, Wu X P, Lin P R 2013 Prog. Geophys. 27 2452
[12] Liu C, Ren Z, Tang J 2008 Appl. Geophys. 5 170
Google Scholar
[13] Key K, Weiss C 2006 Geophysics 71 G291
Google Scholar
[14] Franke A, Börner R U, Spitzer K 2007 Geophys. J. Int. 171 71
Google Scholar
[15] Jin J 2002 The Finite Element Method in Electromagnetics (New York: John Wiley & Sons)
[16] 柳建新, 童孝忠, 郭荣文 2012 大地电磁测深法勘探 (北京: 科学出版社) 第48−50页
Liu J X, Tong X Z, Guo R W 2012 The Magnetotelluric Sounding Method (Beijing: Science Press) pp48−50
[17] Unsworth M J 2010 Surv. Geophys. 31 137
Google Scholar
[18] Rao C K, Jones A G, Moorkamp M 2014 Geophys. J. Int. 198 737
Google Scholar
[19] Juanatey M, Hubert J, Tryggvason A 2013 Geophys. Prospect. 61 200
Google Scholar
[20] Egger A E, Jonathan M G, Glen J M G 2014 Geol. Soc. Am. Bull. 126 523
Google Scholar
[21] Abdelzaher M, Nishijima J, Saibi H 2012 Pure Appl. Geophys. 169 1679
Google Scholar
[22] 徐世浙 1994 地球物理中的有限单元法 (北京: 科学出版社) 第220−224页
Xu S Z 1994 FEM in Geophysics (Beijing: Science Press) pp220−224 (in Chinese)
[23] Farquharson C G, Miensopust M P 2011 J, Appl. Geophys. 75 699
Google Scholar
[24] Zhdanov M S, Varentsov I M, Weaver J T 1997 J. Appl. Geophys. 37 133
Google Scholar
[25] Mitsuhata Y, Uchida T 2004 Geophysics 69 108
Google Scholar
[26] Ren Z, Kalscheuer, Greenhalgh S 2014 Geophysics 79 E255
Google Scholar
[27] Mukherjee S, Everett M E 2011 Geophysics 76 F215
Google Scholar
-
图 2 四面体单元及其棱边编号示意图
Fig. 2. Schematic diagram for tetrahedral element and edge numbers.
图 4 基于总场和二次场的二次插值的模拟结果与解析解的对比T为周期) (a) 视电阻率
${\rho _{\rm{s}}}$ ; (b) 相位$\phi $ Fig. 4. Comparisons of modelling results of quadratic interpolation and analytical solutions based on total fields and secondary fields: (a) Apparent resistivity
${\rho _{\rm{s}}}$ ; (b) phase$\phi $ .
图 5 COMMEMI-3D1模型, 其中(a)图中虚线为x和y测线
Fig. 5. COMMEMI-3D1 model. The dashed lines in (a) are the x and y survey lines.
图 10 椭球体模型 (a) xy剖面; (b) xz剖面
Fig. 10. Ellipsoidal model: (a) xy profile; (b) xz profile.
图 11 椭球体模型模拟结果切片图 (a) XY模式视电阻率; (b) YX模式视电阻率; (c) XY模式相位; (d) YX模式相位
Fig. 11. Slices of modelling results for ellipse model: (a) XY-mode apparent resistivities; (b) YX-mode apparent resistivities; (c) XY-mode phase; (d) YX-mode phase.
图 13 三维和二维模拟结果对比
Fig. 13. Comparisions of three-dimensional and two-dimensional modelling results.
图 14 山峰模型及其非结构化网格剖分(左图点为测线)
Fig. 14. Peak model and discretization using unstructured grids (the points in left diagram are survey line).
图 15 三维和二维模拟结果对比 (a), (b)山峰模型; (c), (d)山谷模型
Fig. 15. Comparisions of three-dimensional and two-dimensional modelling results: (a), (b) Peak model; (c), (d) valley model.
图 16 不同磁导率模拟结果对比 (a), (b)无电性异常模型; (c), (d)含电性异常模型
Fig. 16. Comparisons of modelling results for different magnetic permeability: (a), (b) Model without electrical anomaly; (c), (d) model with electrical anomaly.
-
[1] Hohmann G W 1983 Surv. Geophys. 6 27
Google Scholar
[2] Zhdanov M S, Lee S K, Yoshioka K 2006 Geophysics 71 G333
Google Scholar
[3] 陈桂波, 汪宏年, 姚敬金, 韩子夜 2009 58 3848
Google Scholar
Chen G B, Wang H N, Yao J J, Han Z Y 2009 Acta Phys. Sin. 58 3848
Google Scholar
[4] 谭捍东, 余钦范, John B 2003 地球 46 705
Google Scholar
Tang H D, Yu Q F, John B 2003 Chin. J. Geophys. 46 705
Google Scholar
[5] Streich R 2009 Geophysics 74 F95
Google Scholar
[6] Smith J T 1996 Geophysics 61 1308
Google Scholar
[7] Wang W, Wu X P, Spitzer K 2013 Geophys. J. Int. 193 734
Google Scholar
[8] Coggon J H 1971 Geophysics 36 132
Google Scholar
[9] Fox R C, Hohmann G W, Killpack T J 1980 Geophysics 45 75
Google Scholar
[10] Wannamaker P E, Stodt J A, Rijo L 1987 Geophys. J. Int. 88 277
Google Scholar
[11] 李勇, 吴小平, 林品荣 2013 地球物理学进展 27 2452
Li Y, Wu X P, Lin P R 2013 Prog. Geophys. 27 2452
[12] Liu C, Ren Z, Tang J 2008 Appl. Geophys. 5 170
Google Scholar
[13] Key K, Weiss C 2006 Geophysics 71 G291
Google Scholar
[14] Franke A, Börner R U, Spitzer K 2007 Geophys. J. Int. 171 71
Google Scholar
[15] Jin J 2002 The Finite Element Method in Electromagnetics (New York: John Wiley & Sons)
[16] 柳建新, 童孝忠, 郭荣文 2012 大地电磁测深法勘探 (北京: 科学出版社) 第48−50页
Liu J X, Tong X Z, Guo R W 2012 The Magnetotelluric Sounding Method (Beijing: Science Press) pp48−50
[17] Unsworth M J 2010 Surv. Geophys. 31 137
Google Scholar
[18] Rao C K, Jones A G, Moorkamp M 2014 Geophys. J. Int. 198 737
Google Scholar
[19] Juanatey M, Hubert J, Tryggvason A 2013 Geophys. Prospect. 61 200
Google Scholar
[20] Egger A E, Jonathan M G, Glen J M G 2014 Geol. Soc. Am. Bull. 126 523
Google Scholar
[21] Abdelzaher M, Nishijima J, Saibi H 2012 Pure Appl. Geophys. 169 1679
Google Scholar
[22] 徐世浙 1994 地球物理中的有限单元法 (北京: 科学出版社) 第220−224页
Xu S Z 1994 FEM in Geophysics (Beijing: Science Press) pp220−224 (in Chinese)
[23] Farquharson C G, Miensopust M P 2011 J, Appl. Geophys. 75 699
Google Scholar
[24] Zhdanov M S, Varentsov I M, Weaver J T 1997 J. Appl. Geophys. 37 133
Google Scholar
[25] Mitsuhata Y, Uchida T 2004 Geophysics 69 108
Google Scholar
[26] Ren Z, Kalscheuer, Greenhalgh S 2014 Geophysics 79 E255
Google Scholar
[27] Mukherjee S, Everett M E 2011 Geophysics 76 F215
Google Scholar
下载:
计量
- 文章访问数: 8850
- PDF下载量: 73
- 被引次数: 0
