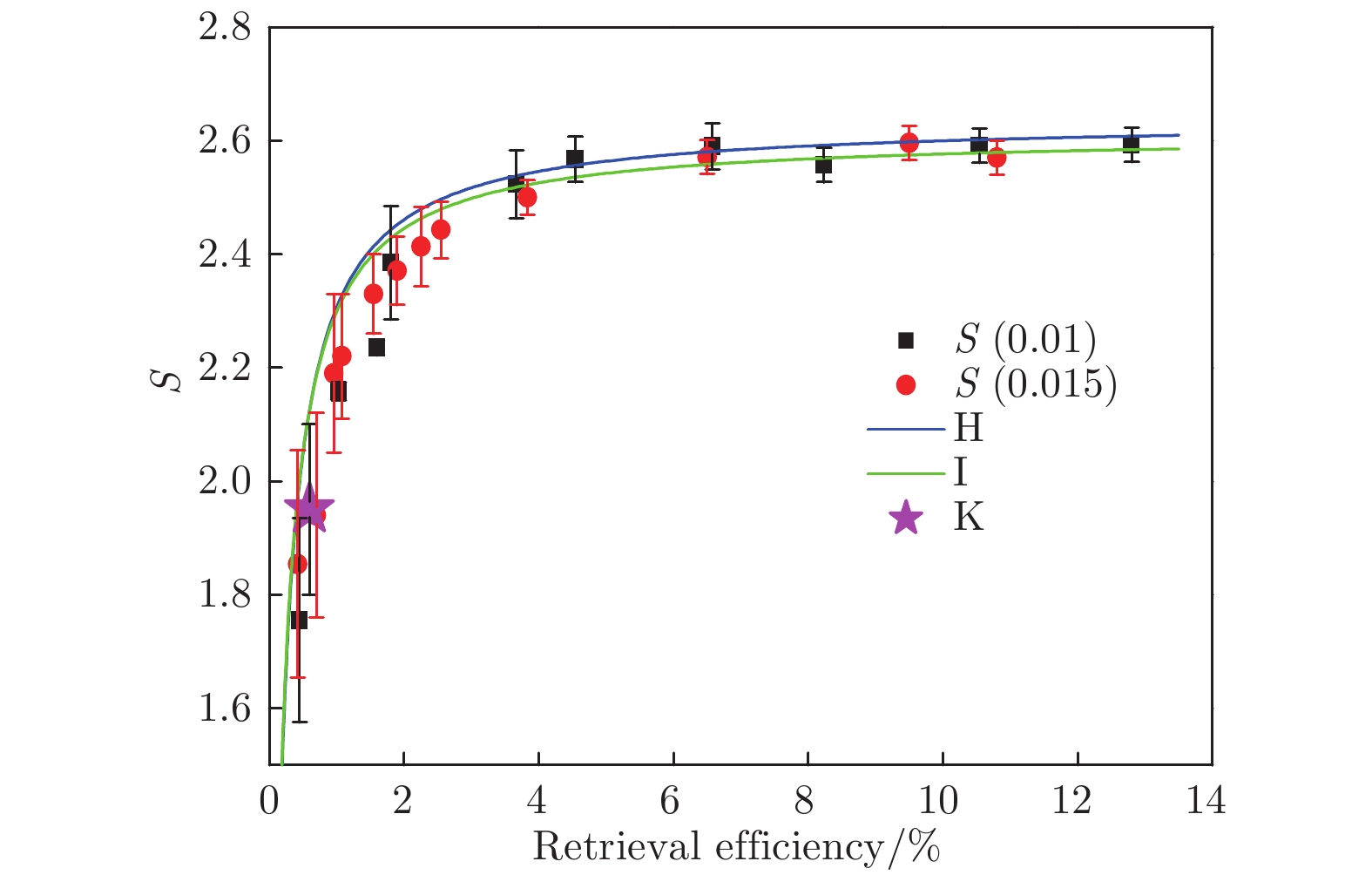
-
The photon-atom interface is a basic component of quantum repeater, quantum network, and linear optical quantum computing. Different approaches have been tested in the last decade to develop quantum interface, such as quantum dots, single atoms and ions, color centers and cold atomic ensemble. In the cold atomic ensemble, a normal way to produce photon-atom interface is the Duan-Lukin-Cirac-Zoller (DLCZ) protocol. Used in the DLCZ protocol is an atomic ensemble that can emit single photons while creating a single atomic excitation, which is stored in the ensemble. The atomic excitation can be converted into a photon due to the collective interference. The influences of the retrieval efficiency on the atom-photon entanglement source have been studied in various experiments. But no one has studied the retrieval efficiency threshold of entanglement generation. In our experiment we study the retrieval efficiency dependence on read power and OD. Setting the power of the repump light beam to be 12.2 mW, 5.0 mW, 2.0 mW, 0.5 mW and 0.3 mW, OD of the cold atom ensemble is measured to be 20, 17, 10, 2, and 1, respectively. As we expected, the retrieval efficiency increases with increasing OD value and read power, the curve shows that the retrieval efficiency increases sharply with increasing the OD value and read power, then after a while slowly increases with increasing the OD values and read power. Then we measure the Bell parameter with increasing the retrieval efficiency by increasing the read power. It shows that the Bell parameter sharply increases for retrieval efficiency values ranging from 0 to 3%, but changes very small for retrieval efficiency values ranging from 3% to 18.3%. The maximum Bell parameter is 2.6. We further analysis the result, finding that the Bell parameter can be expressed as
$S = \dfrac{{{S_{{\rm{MAX}}}}r}}{{(1 + 2\chi )r + 2B}}$ . Fitting parameters to the curve are$\chi$ = 1%, B = 0.073%. To avoid of multi-excitation the write power kept low that$\chi$ at 1% level. Then we can find out from the function that the signal-to-noise ratio is bigger than 6∶1 the Bell parameter will reach 2. The theoretical analysis and experimental results fit very well. So the further reason that alter the Bell parameter is the signal-to-noise ratio. We should decrease the noise while increasing the retrieval efficiency. This paper will help with rise the quality of entanglement generation through photon-atom interface.-
Keywords:
- cold atomic ensemble /
- spontaneous Raman scattering /
- retrieval efficiency /
- photon-atom entanglement
[1] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
Google Scholar
[2] Hensen B, Bernien H, Dreau A E, Reiserer A, Kalb N, Blok M S, Ruitenberg J, Vermeulen R F, Schouten R N, Abellan C, Amaya W, Pruneri V, Mitchell M W, Markham M, Twitchen D J, Elkouss D, Wehner S, Taminiau T H, Hanson R 2015 Nature 526 682
Google Scholar
[3] Volz J, Weber M, Schlenk D, Rosenfeld W, Vrana J, Saucke K, Kurtsiefer C, Weinfurter H 2006 Phys. Rev. Lett. 96 030404
Google Scholar
[4] Hofmann J, Krug M, Ortegel N, Gérard L, Weber M, Rosenfeld W, Weinfurter H 2012 Science 337 72
Google Scholar
[5] Rosenfeld W, Burchardt D, Garthoff R, Redeker K, Ortegel N, Rau M, Weinfurter H 2017 Phys. Rev. Lett. 119 010402
Google Scholar
[6] Blinov B B, Moehring D L, Duan L M, Monroe C 2004 Nature 428 153
Google Scholar
[7] Moehring D L, Maunz P, Olmschenk S, Younge K C, Matsukevich D N, Duan L M, Monroe C 2007 Nature 449 68
Google Scholar
[8] Kuzmich A, Bowen W P, Boozer A D, Boca A, Chou C W, Duan L M, Kimble H J 2003 Nature 423 731
Google Scholar
[9] van der Wal C H, Eisaman M D, André A, Walsworth R L, Phillips D F, Zibrov A S, Lukin M D 2003 Science 301 196
Google Scholar
[10] Matsukevich D N, Chaneliere T, Bhattacharya M, Lan S Y, Jenkins S D, Kennedy T A B, Kuzmich A 2005 Phys. Rev. Lett. 95 040405
Google Scholar
[11] Yan H, Zhang S, Chen J F, Loy M M, Wong G K, Du S 2011 Phys. Rev. Lett. 106 033601
Google Scholar
[12] Yang S J, Wang X J, Li J, Rui J, Bao X H, Pan J W 2015 Phys. Rev. Lett. 114 210501
Google Scholar
[13] Ding D S, Zhang W, Zhou Z Y, Shi S, Shi B S, Guo G C 2015 Nat. Photon. 9 332
Google Scholar
[14] Xu Z X, Wu Y L, Liu H L, Li S J, Wang H 2013 Phys. Rev. A 88 013423
Google Scholar
[15] Jenkins S D, Matsukevich D N, Chanelière T, Kuzmich A, Kennedy T A B 2006 Phys. Rev. A 73 021803
Google Scholar
[16] Matsukevich D N, Chaneliere T, Jenkins S D, Lan S Y, Kennedy T A, Kuzmich A 2006 Phys. Rev. Lett. 96 033601
Google Scholar
[17] Gorshkov A V, André A, Lukin M D, Sørensen A S 2007 Phys. Rev. A 76 033804
Google Scholar
[18] Felinto D, Chou C W, de Riedmatten H, Polyakov S V, Kimble H J 2015 Phys. Rev. A 72 053809
[19] Chen S, Chen Y A, Strassel T, Yuan Z S, Zhao B, Schmiedmayer J, Pan J W 2006 Phys. Rev. Lett. 97 173004
Google Scholar
[20] de Riedmatten H, Laurat J, Chou C W, Schomburg E W, Felinto D, Kimble H J 2006 Phys. Rev. Lett. 97 113603
Google Scholar
[21] Zhao B, Chen Y A, Bao X H, Strassel T, Chuu C S, Jin X M, Schmiedmayer J, Yuan Z S, Chen S, Pan J W 2008 Nat. Phys. 5 95
[22] 张常睿, 王圣智, 徐忠孝, 李淑静, 王海 2018 量子光学学报 24 333
Zhang C R, Wang S Z, Xu Z X, Li S J, Wang H 2018 Acta Sinica Quantum Optica 24 333
[23] Lettner M, Mucke M, Riedl S, Vo C, Hahn C, Baur S, Bochmann J, Ritter S, Durr S, Rempe G 2011 Phys. Rev. Lett. 106 210503
Google Scholar
[24] Fu Z, Wang P, Chai S, Huang L, Zhang J 2011 Phys. Rev. A 84 043609
Google Scholar
-
图 1 实验能级图 (a)和(b)分别为自发拉曼散射的写过程和读过程, σ+ (σ−)代表右旋圆偏振(左旋圆偏振)的斯托克斯光场和反斯托克斯光场; W表示写光, R表示读光
Fig. 1. Relevant 87Rb atomic levels: (a) and (b) are writing process and reading process of the SRS process. σ+ (σ−) represents right (left) polarization of emitted photon. W (R) represents writing(reading) field.
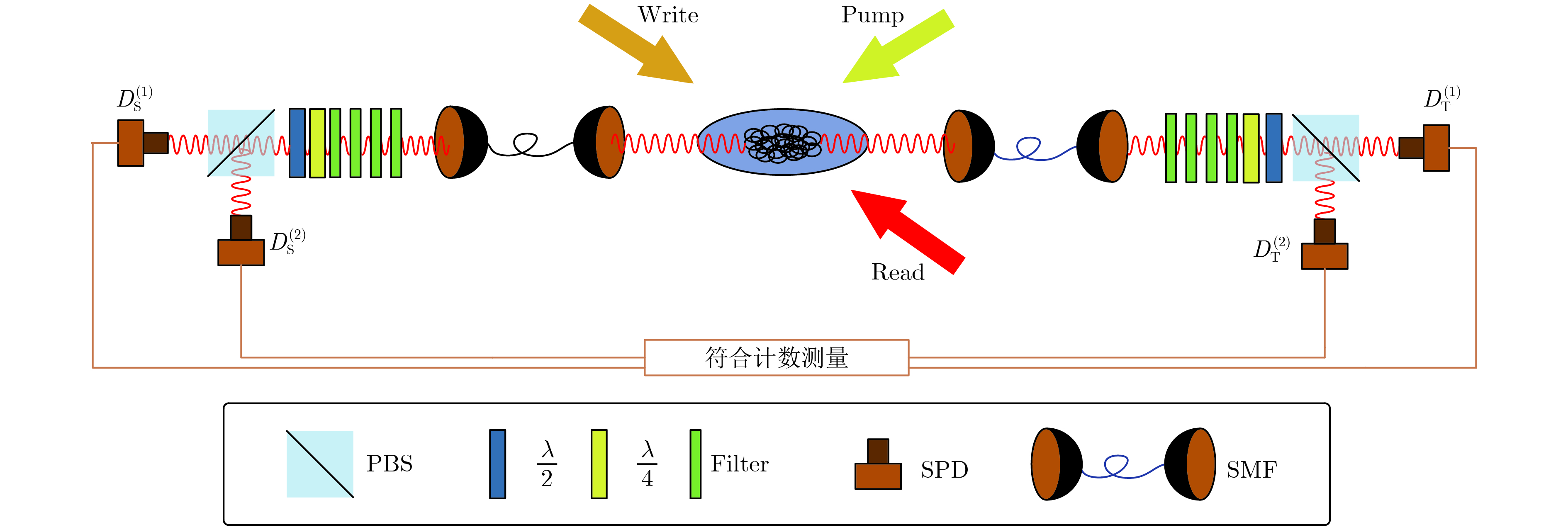
图 2 实验装置, 其中PBS为偏振分束棱镜, SMF为单模光纤, SPD为单光子探测器,
$\frac{\lambda }{2}$ 为二分之一波片,$\frac{\lambda }{4}$ 为四分之一波片, Filter为滤波器Fig. 2. Experimental setup. PBS, polarization beam splitter; SMF, single mode fiber; SPD, single photon detector;
$\frac{\lambda }{2}$ , half wave plate;$\frac{\lambda }{4}$ , quarter wave plate; Filter, F-P etalon.
图 3 实验时序图 (图中Trig表示触发信号, C表示态清洗过程, W和R分别代表写过程与读过程, MOT代表冷原子制备过程)
Fig. 3. Time sequence of experiment (Trig represents the trigger signal, C represents the state cleaning process, W and R represent the writing and reading process, and MOT represents the cold atom preparation process).
图 5 读出效率及
$\scriptstyle N_{\rm AS}$ 随读光功率变化Fig. 5. The retrieval efficiency and
$\scriptstyle N_{\rm AS}$ as the function of power of read light field.
图 6 Bell参量S随读出效率的变化
Fig. 6. The Bell parameter S as the function of quantum retrieval efficiency.
-
[1] Briegel H J, Dür W, Cirac J I, Zoller P 1998 Phys. Rev. Lett. 81 5932
Google Scholar
[2] Hensen B, Bernien H, Dreau A E, Reiserer A, Kalb N, Blok M S, Ruitenberg J, Vermeulen R F, Schouten R N, Abellan C, Amaya W, Pruneri V, Mitchell M W, Markham M, Twitchen D J, Elkouss D, Wehner S, Taminiau T H, Hanson R 2015 Nature 526 682
Google Scholar
[3] Volz J, Weber M, Schlenk D, Rosenfeld W, Vrana J, Saucke K, Kurtsiefer C, Weinfurter H 2006 Phys. Rev. Lett. 96 030404
Google Scholar
[4] Hofmann J, Krug M, Ortegel N, Gérard L, Weber M, Rosenfeld W, Weinfurter H 2012 Science 337 72
Google Scholar
[5] Rosenfeld W, Burchardt D, Garthoff R, Redeker K, Ortegel N, Rau M, Weinfurter H 2017 Phys. Rev. Lett. 119 010402
Google Scholar
[6] Blinov B B, Moehring D L, Duan L M, Monroe C 2004 Nature 428 153
Google Scholar
[7] Moehring D L, Maunz P, Olmschenk S, Younge K C, Matsukevich D N, Duan L M, Monroe C 2007 Nature 449 68
Google Scholar
[8] Kuzmich A, Bowen W P, Boozer A D, Boca A, Chou C W, Duan L M, Kimble H J 2003 Nature 423 731
Google Scholar
[9] van der Wal C H, Eisaman M D, André A, Walsworth R L, Phillips D F, Zibrov A S, Lukin M D 2003 Science 301 196
Google Scholar
[10] Matsukevich D N, Chaneliere T, Bhattacharya M, Lan S Y, Jenkins S D, Kennedy T A B, Kuzmich A 2005 Phys. Rev. Lett. 95 040405
Google Scholar
[11] Yan H, Zhang S, Chen J F, Loy M M, Wong G K, Du S 2011 Phys. Rev. Lett. 106 033601
Google Scholar
[12] Yang S J, Wang X J, Li J, Rui J, Bao X H, Pan J W 2015 Phys. Rev. Lett. 114 210501
Google Scholar
[13] Ding D S, Zhang W, Zhou Z Y, Shi S, Shi B S, Guo G C 2015 Nat. Photon. 9 332
Google Scholar
[14] Xu Z X, Wu Y L, Liu H L, Li S J, Wang H 2013 Phys. Rev. A 88 013423
Google Scholar
[15] Jenkins S D, Matsukevich D N, Chanelière T, Kuzmich A, Kennedy T A B 2006 Phys. Rev. A 73 021803
Google Scholar
[16] Matsukevich D N, Chaneliere T, Jenkins S D, Lan S Y, Kennedy T A, Kuzmich A 2006 Phys. Rev. Lett. 96 033601
Google Scholar
[17] Gorshkov A V, André A, Lukin M D, Sørensen A S 2007 Phys. Rev. A 76 033804
Google Scholar
[18] Felinto D, Chou C W, de Riedmatten H, Polyakov S V, Kimble H J 2015 Phys. Rev. A 72 053809
[19] Chen S, Chen Y A, Strassel T, Yuan Z S, Zhao B, Schmiedmayer J, Pan J W 2006 Phys. Rev. Lett. 97 173004
Google Scholar
[20] de Riedmatten H, Laurat J, Chou C W, Schomburg E W, Felinto D, Kimble H J 2006 Phys. Rev. Lett. 97 113603
Google Scholar
[21] Zhao B, Chen Y A, Bao X H, Strassel T, Chuu C S, Jin X M, Schmiedmayer J, Yuan Z S, Chen S, Pan J W 2008 Nat. Phys. 5 95
[22] 张常睿, 王圣智, 徐忠孝, 李淑静, 王海 2018 量子光学学报 24 333
Zhang C R, Wang S Z, Xu Z X, Li S J, Wang H 2018 Acta Sinica Quantum Optica 24 333
[23] Lettner M, Mucke M, Riedl S, Vo C, Hahn C, Baur S, Bochmann J, Ritter S, Durr S, Rempe G 2011 Phys. Rev. Lett. 106 210503
Google Scholar
[24] Fu Z, Wang P, Chai S, Huang L, Zhang J 2011 Phys. Rev. A 84 043609
Google Scholar
下载:
计量
- 文章访问数: 7389
- PDF下载量: 40
- 被引次数: 0
