光场调控的活性粒子体系的动态自组装

郭思航; 杨光宇; 孟国庆; 王英英; 潘俊星; 张进军

doi:10.7498/aps.74.20241556

摘要

活性粒子体系是一类由自驱动布朗粒子组成的非平衡系统, 体系粒子之间通过相互作用可以表现出众多奇特的集体行为. 本文基于布朗动力学模拟, 研究了光场调控的活性粒子体系有序结构的形成和转变机制. 研究发现, 活性粒子在光场调控下发生了大尺度的相分离行为, 形成了特定的有序结构, 并实现了多种有序结构的动态转变. 本文系统地探讨了光场对这一动态相转变的影响和调控机制. 研究结果为活性体系群体结构的精确调控以及微纳米智能器件的制造提供了重要参考.

关键词:

Abstract

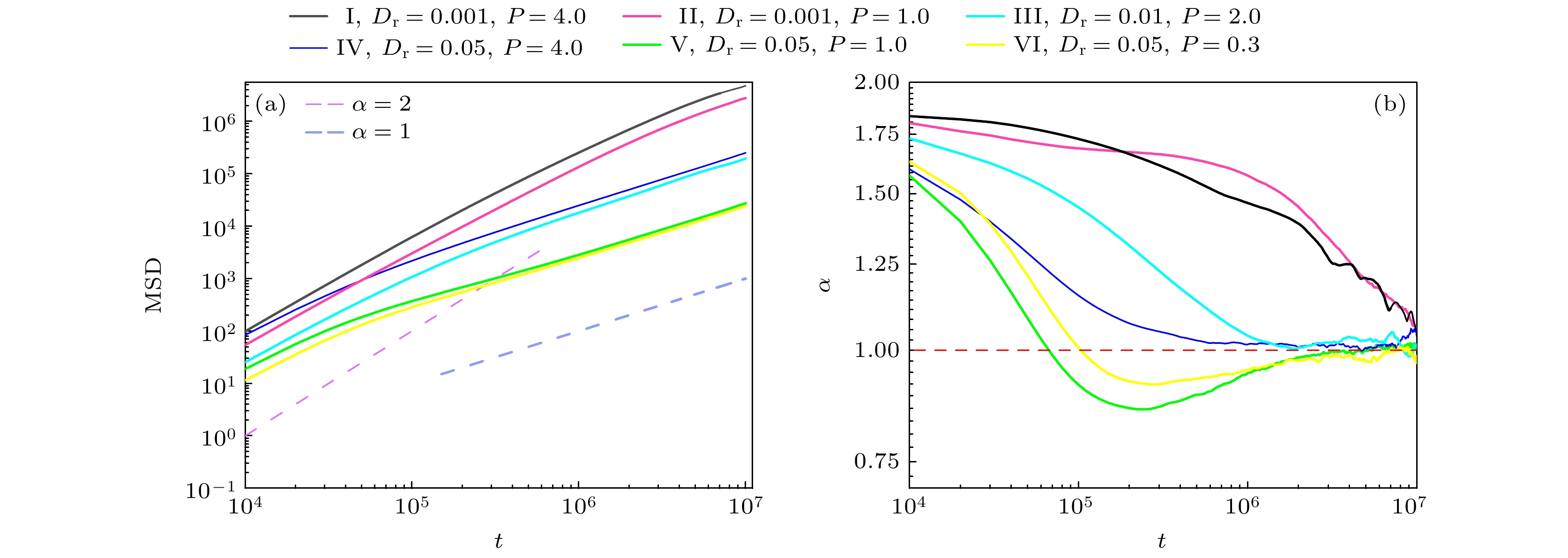
Active particle systems are nonequilibrium systems composed of self-propelled Brownian particles, where interactions between particles can give rise to various collective behaviors. This study, based on Brownian dynamics simulations, explores the effects of light intensity, rotational diffusion coefficient, and the width and spacing of illuminated regions on the aggregation structures of the system. First, this study examines the influence of light intensity on aggregation structures under different rotational diffusion coefficients, finding that as the rotational diffusion coefficient increases, the system gradually stabilizes. This stabilization is attributed to the reduced collision effects among particles at higher diffusion coefficients. Under suitable rotational diffusion coefficients, gradually increasing the ratio of longitudinal to transverse light-induced self-propulsion forces leads to a transition in the system’s aggregation structure from a transverse stripe structure configuration to a tic-tac-toe structure, ultimately resulting in a longitudinal stripe structure. This indicates that the system’s aggregation structure can be effectively controlled by changing the relative light intensity of the longitudinal and transverse illumination. From a dynamical perspective, an unstable structure consistently exhibits a super-diffusive behavior throughout the simulations, while stable structure transitions from initial super-diffusion to normal diffusion, indicating that under steady state conditions, particles aggregate in the shaded regions, exhibiting Brownian motion. To further investigate the influence of light field on collective particle behavior, in this study the width of the illuminated region and the spacing between adjacent illuminated regions are systematically varied, finding that the overall trends are consistent with previous conclusions. It is also observed that wider illumination regions with narrower spacing contribute to the formation of tic-tac-toe structures, while narrower illumination regions with wider spacing give rise to a novel structure—checkerboard structures. This study investigates the phase separation behavior of particles in complex optical field environments, providing some valuable ideas for controlling aggregation states in active particle systems.

Keywords:

作者及机构信息

山西师范大学物理与信息工程学院, 太原　030032

通信作者: 潘俊星, panjx@sxnu.edu.cn ; 张进军, zhangjinjun@sxnu.edu.cn

基金项目: 山西省基础研究计划(批准号: 202103021223245, 202303021212148)、山西省研究生科研创新项目(批准号: 2024KY452)和山西师范大学研究生科研创新项目(批准号: 2024XSY36)资助的课题.

Authors and contacts

School of Physics and Information Engineering, Shanxi Normal University, Taiyuan 030032, China

Corresponding author: PAN Junxing, panjx@sxnu.edu.cn ; ZHANG Jinjun, zhangjinjun@sxnu.edu.cn

Funds: Project supported by the Fundamental Research Program of Shanxi Province, China (Grant Nos. 202103021223245, 202303021212148), the Postgraduate Education Innovation Program of Shanxi Province, China (Grant No. 2024KY452), and the Postgraduate Education Innovation Program of Shanxi Normal University, China (Grant No.2024XSY36).

文章全文

补充材料

2025年第74卷090501---SV1 不稳定团簇结构.mp4

2025年第74卷090501---SV2 振荡结构.mp4

2025年第74卷090501---SV3 横向条形结构.mp4

2025年第74卷090501---SV4 井字结构.mp4

2025年第74卷090501---SV5 纵向条形结构.mp4

2025年第74卷090501---SV6 条形格状混合结构.mp4

2025年第74卷090501---SV7 条形格状混合结构.mp4

2025年第74卷090501---SV8 棋盘状结构.mp4

参考文献

[1]	Ramaswamy S 2017 J. Stat. Mech. 5 054002 Google Scholar
[2]	Ramaswamy S 2010 Annu. Rev. Condens. Mater Phys. 1 323 Google Scholar
[3]	Tailleur J, Cates M E 2008 Phys. Rev. Lett. 100 218103 Google Scholar
[4]	Martinez R, Alarcon F, Rodriguez D R, Aragones J L, Valeriani C 2018 Eur. Phys. J. E 41 91 Google Scholar
[5]	Vladescu I D, Marsden E J, Schwarz-Linek J, Martinez V A, Arlt J, Morozov A N, Marenduzzo D, Cates M E, Poon W C 2014 Phys. Rev. Lett. 113 268101 Google Scholar
[6]	Schweitzer F, Tilch B, Ebeling W 2000 Eur. Phys. J. B 14 157 Google Scholar
[7]	Erdmann U, Ebeling W, Schimansky-Geier L, Schweitzer F 2000 Eur. Phys. J. B 15 105 Google Scholar
[8]	Schweitzer F, Ebeling W, Tilch B 1998 Phys. Rev. Lett. 80 5044 Google Scholar
[9]	Yang X, Manning M L, Marchetti M C 2014 Soft Matter 10 6477 Google Scholar
[10]	Stenhammar J, Tiribocchi A, Allen R J, Marenduzzo D, Cates M E 2013 Phys. Rev. Lett. 111 145702 Google Scholar
[11]	Stenhammar J, Wittkowski R, Marenduzzo D, Cates M E 2015 Phys. Rev. Lett. 114 018301 Google Scholar
[12]	Dolai P, Simha A, Mishra S 2017 Soft Matter 14 6137 Google Scholar
[13]	高艺雯, 王影, 田文得, 陈康 2022 71 240501 Google Scholar Gao Y W, Wang Y, Tian W D, Chen K 2022 Acta Phys. Sin. 71 240501 Google Scholar
[14]	Fernandez-Rodriguez M A, Grillo F, Alvarez L, Rathlef M, Buttinoni L, Volpe G, Isa L 2020 Nat. Commun. 11 4223 Google Scholar
[15]	Vutukuri H R, Lisicki M, Lauga E, Vermant J 2020 Nat. Commun. 11 2628 Google Scholar
[16]	Hernández R J, Sevilla F J, Mazzulla A, Pagliusi P, Pellizzi N, Cipparrone G 2020 Soft Matter 16 7704 Google Scholar
[17]	Zhang J H, Guo J J, Mou F Z, Guan J G 2018 Micromachines 9 88 Google Scholar
[18]	Bäuerle T, Fischer A, Speck T, Bechinger C 2018 Nat. Commun. 9 3232 Google Scholar
[19]	Wang G, Phan T V, Li S, Wombacher M, Qu J, Peng Y, Chen G, Goldman D I, Levin S A, Austin R H, Liu L Y 2021 Phys. Rev. Lett. 126 108002 Google Scholar
[20]	Liu Y P, Wang G, Wang P L, Yuan D M, Hou S X, Jin Y K, Wang J, Liu L Y 2023 Chin. Phys. B 32 068701 Google Scholar
[21]	Humphrey W, Dalke A, Schulten K 1996 J. Mol. Graphics 14 33 Google Scholar
[22]	Ning H P, Zhang Y, Zhu H, Ingham A, Huang G S, Mei Y F, Solovev A A 2018 Micromachines 9 75 Google Scholar
[23]	Chen H X, Zhao Q L, Du X M 2018 Micromachines 9 41 Google Scholar
[24]	Xu L L, Mou F Z, Gong H T, Luo M, Guan J G 2017 Chem. Soc. Rev. 46 6905 Google Scholar
[25]	Wang W, Duan W T, Ahmed S, Sen A, Mallouk T E 2015 Acc. Chem. Res. 48 1938 Google Scholar
[26]	Chen C R, Mou F Z, Xu L L, Wang S F, Guan J G, Feng Z P, Wang Q W, Kong L, Li W, Wang J, Zhang Q J 2017 Adv. Mater. 29 3 Google Scholar
[27]	Tang S S, Zhang F Y, Zhao J, Talaat W, Soto F, Karshalev E, Chen C R, Hu Z H, Lu X L, Li J X, Lin Z H, Dong H F, Zhang X J, Nourhani A, Wang J 2019 Adv. Funct. Mater. 29 1809003 Google Scholar
[28]	Sun Y Y, Liu Y, Zhang D M, Zhang H, Jiang J W, Duan R M, Xiao J J, Xing J, Zhang D F, Dong B 2019 ACS Appl. Mater. Interfaces 11 40533 Google Scholar
[29]	Singh D P, Choudhury U, Fischer P, Mark A G 2017 Adv Mater. 29 32 Google Scholar
[30]	Lin Z, Si T, Wu Z, Gao C, Lin X, He Q 2017 Angew. Chem. Int. Ed. 56 13517 Google Scholar
[31]	Wang Y, Shen Z L, Xia Y Q, Feng G Q, Tian W D 2020 Chin. Phys. B 29 053103 Google Scholar
[32]	Pan J X, Wei H, Qi M J, Wang H F, Zhang J J, Tian W D, Chen K 2020 Soft Matter 16 5545 Google Scholar
[33]	Ye S M, Liu P, Wei Z X, Ye F F, Yang M C, Chen K 2020 Chin. Phys. B 29 058201 Google Scholar
[34]	Zhou X L, Wang Y Z, Xu B J, Liu Y P, Lu D, Luo J, Yang Z Y 2023 AIP Adv. 13 065332 Google Scholar
[35]	Chen J M, Zhou X L, Zhang L X 2018 Chin. Phys. B 27 118701 Google Scholar
[36]	Quillen A C, Smucker J P, Peshkov A 2020 Phys. Rev. E 101 052618 Google Scholar
[37]	Liu P, Ye S M, Ye F F, Chen K, Yang M C 2020 Phys. Rev. Lett. 124 158001 Google Scholar
[38]	Das S, Ghosh S, Chelakkot R 2020 Phys. Rev. E 102 032619 Google Scholar
[39]	Das S, Chelakkot R 2020 Soft Matter 16 7250 Google Scholar
[40]	Knežević M, Stark H 2020 New J. Phys 22 113025 Google Scholar
[41]	Chen X G, Lin L H, Li Z C, Sun H J 2022 Adv. Funct. Mater. 32 2104649 Google Scholar
[42]	Volpe G, Buttinoni I, Vogt D, Kuemmerer H J, Bechinger C 2011 Soft Matter. 7 8810 Google Scholar
[43]	Jahanshahi S, Lozano C, Liebchen B, Löwen H, Bechinger C 2020 Commun. Phys. 3 127 Google Scholar
[44]	Palacci J, Sacanna S, Steinberg A P, Pine D J, Chaikin P M 2013 Science 339 936 Google Scholar
[45]	Xia Y Q, Shen Z L, Tian W D, Chen K 2019 J. Chem. Phys. 150 154903 Google Scholar
[46]	Wang C, Li H S, Ma Y Q, Tian W D, Chen K 2018 J. Chem. Phys. 149 164902 Google Scholar
[47]	Shan W J, Zhang F, Tian W D, Chen K 2019 Soft Matter 15 4761 Google Scholar
[48]	石子璇, 金燕, 金奕扬, 田文得, 张天辉, 陈康 2024 73 170501 Google Scholar Shi Z X, Jin Y, Jin Y Y, Tian W D, Zhang T H, Chen K 2024 Acta Phys. Sin. 73 170501 Google Scholar
[49]	王晶, 焦阳, 田文得, 陈康 2023 72 190501 Google Scholar Wang J, Jiao Y, Tian W D, Chen K 2023 Acta Phys. Sin. 72 190501 Google Scholar
[50]	Tiwari C, Singh P S 2024 Soft Matter 20 4816 Google Scholar
[51]	Shen Y F, Hu H X, Luo M B 2024 Soft Matter 20 621 Google Scholar
[52]	Cates M E, Tailleur J 2015 Annu. Rev. Condens. Matter Phys. 6 219 Google Scholar
[53]	Gomez-Solano J R, Samin S, Lozano C, Ruedas-Batuecas P, van Roij R, Bechinger C 2017 Sci Rep. 7 14891 Google Scholar
[54]	Caprini L, Marini Bettolo Marconi U, Wittmann R, Löwen H 2022 Soft Matter 8 1412 Google Scholar
[55]	Takatori S C, Yan W, Brady J F 2014 Phys. Rev. Lett. 113 028103 Google Scholar
[56]	Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006 Google Scholar

施引文献

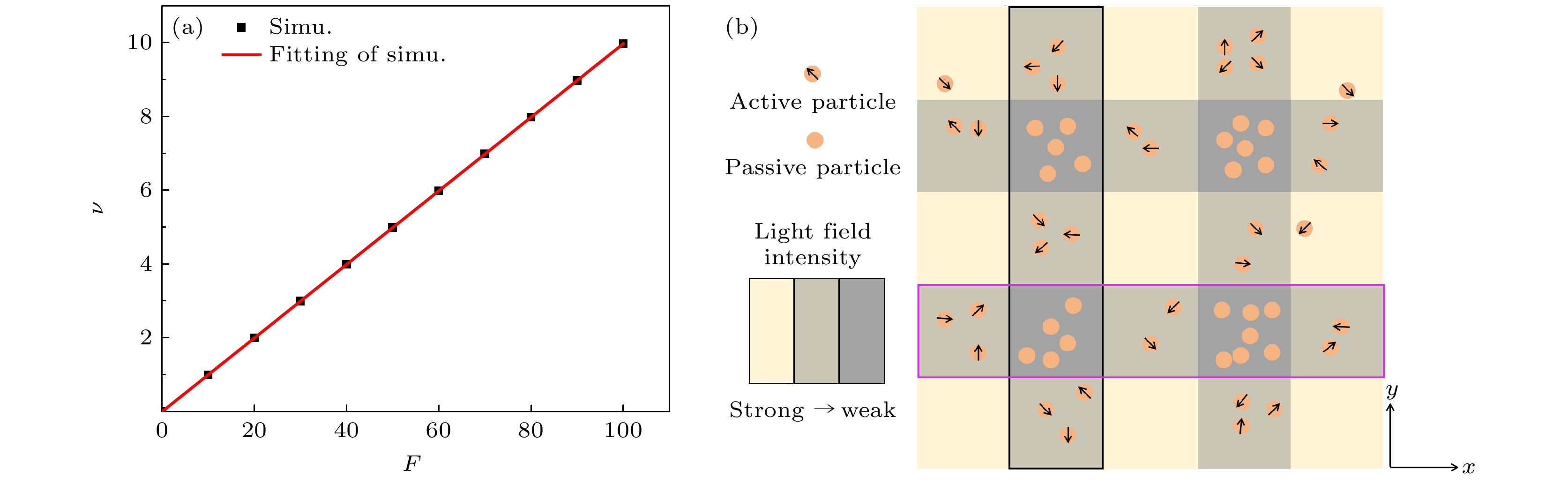
图 1 (a)均匀光场中活性粒子速度v与自驱力F关系; (b)周期性条形光场驱动活性粒子模型示意图; 黑色方框标注的区域为I区, 代表一个纵向遮光区; 紫色方框标注的区域为II区, 代表一个横向遮光区

Fig. 1. (a) Relationship between the velocity v of active particles and the self-propulsive force F in a uniform light field; (b) model schematic of active particles driven by the periodic striped light field. The region marked by the black box is Zone I, representing a longitudinal shaded region, while the region marked by the purple box is Zone II, representing a transverse shaded region.

下载: 全尺寸图片幻灯片

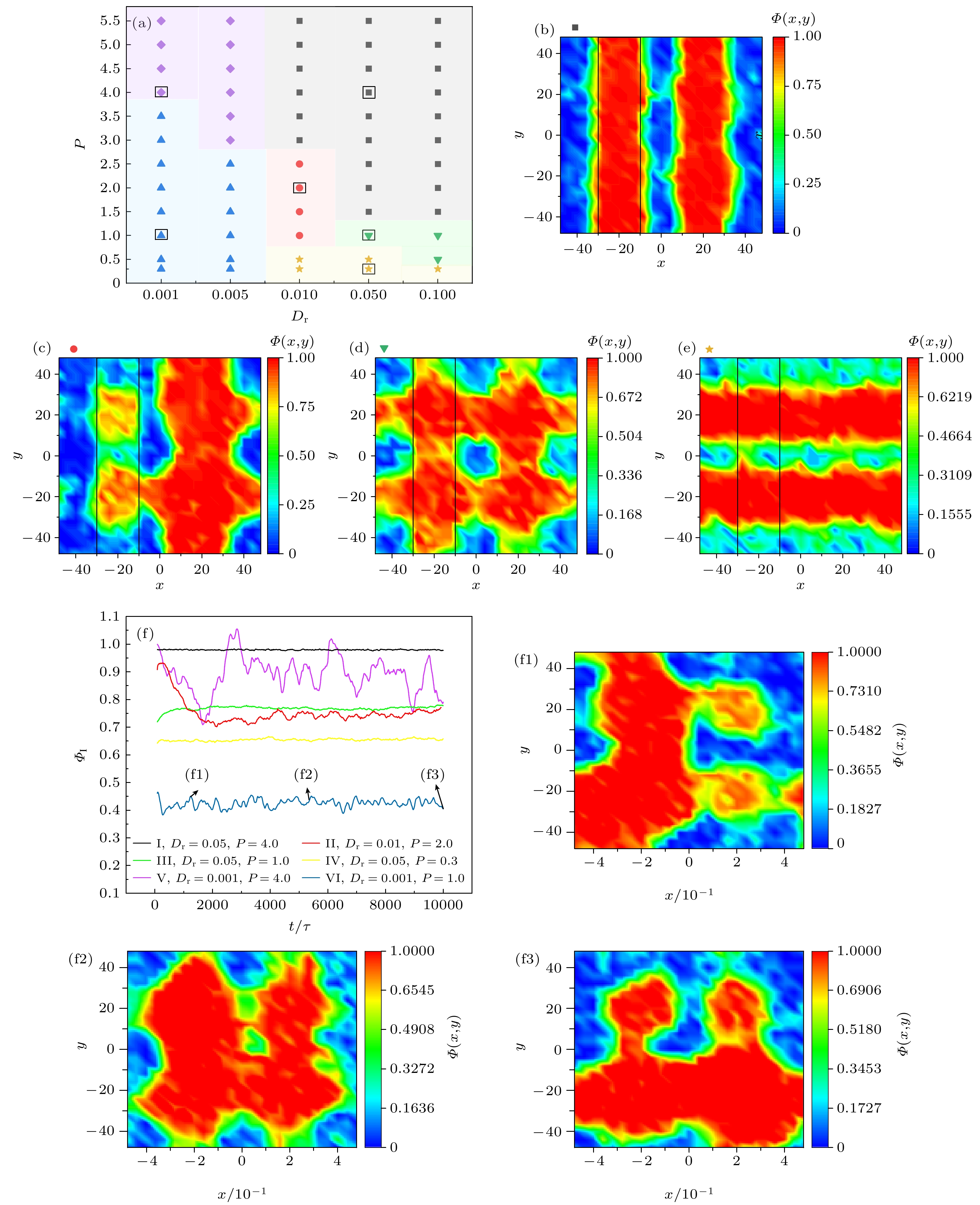
图 2 (a)体系聚集结构相图分布, 其中◆代表振荡结构; ▲代表不稳定团簇结构; ■代表纵向条形结构; ●代表条形格状混合结构; ▼代表井字结构; ★代表横向条形结构; (b), (c), (d), (e)为代表性结构的密度分布图, 图中黑色方框代表纵向遮光区I; (f)不同结构下纵向遮光区I粒子数密度随时间的演化

Fig. 2. (a) Phase diagram of the system’s aggregation structures. ◆ represents an oscillatory structure; ▲ represents an unstable cluster structure; ■ represents a longitudinal stripe structure; ● represents a mixed striped block-like hybrid structure; ▼ represents a tic-tac-toe structure; ★ represents a transverse stripe structure. (b), (c), (d), and (e) The density distribution of representative structures, with the black boxes indicating the longitudinal shading region I. (f) Temporal evolution of particle number density in region I for different structures.

下载: 全尺寸图片幻灯片

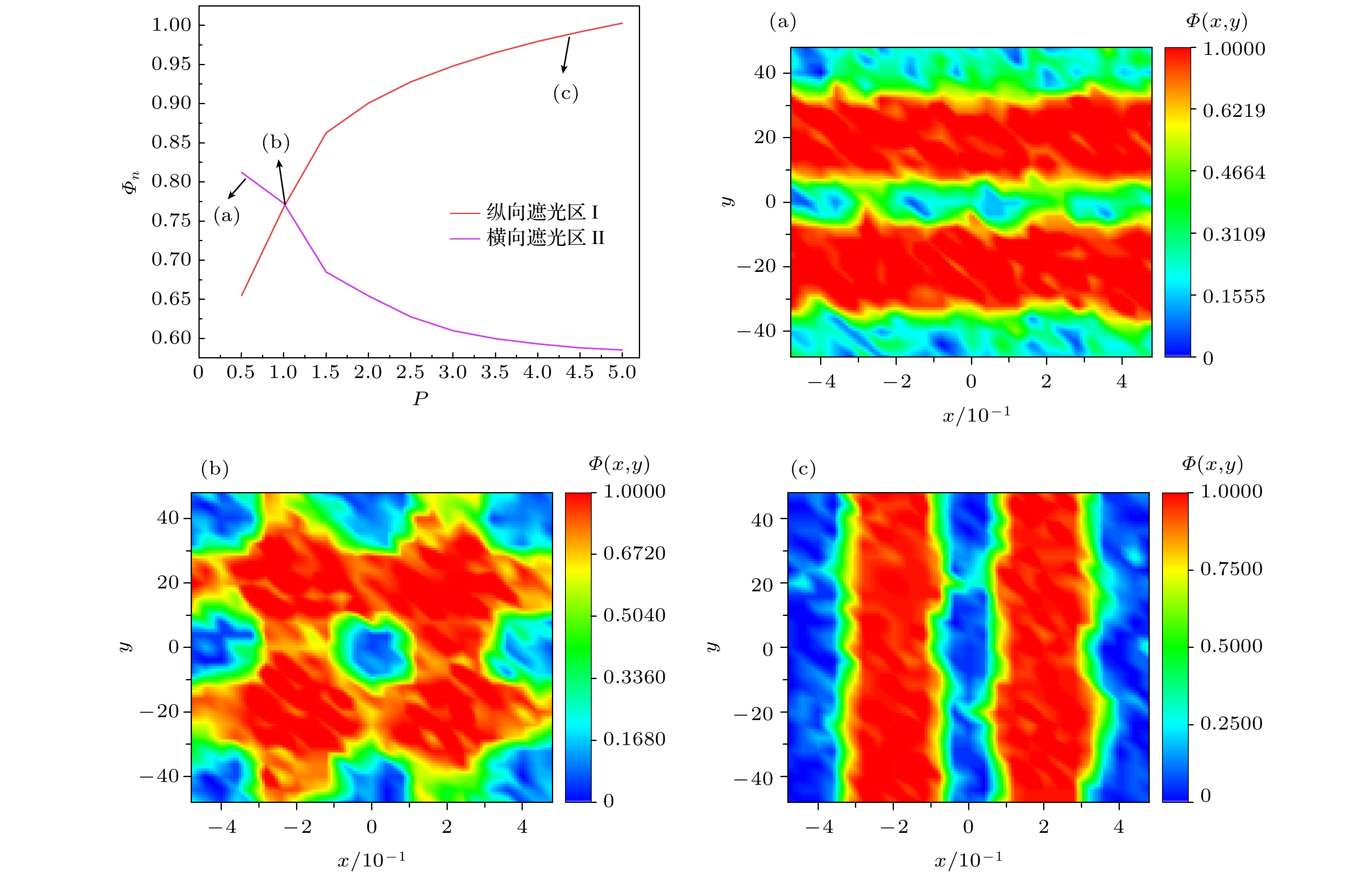
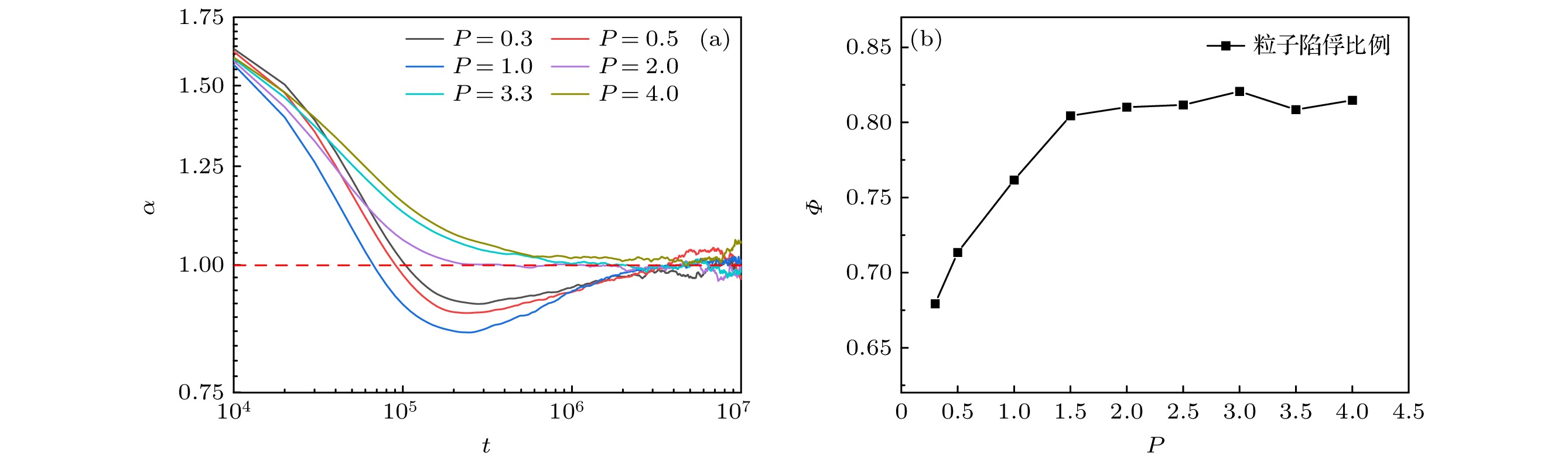
图 3 ${D_{\text{r}}} = 0.05$时纵向遮光区I、横向遮光区II中粒子数密度$ {\varPhi _{\text{n}}} $随纵向与横向光场自驱力比值P的变化

Fig. 3. Relationship between particle number density ($ {\varPhi _{\text{n}}} $) and the ratio P of longitudinal to transverse light-induced self-propulsion forces in the longitudinal shading region I and the transverse shaded region II at ${D_{\text{r}}} = 0.05$.

下载: 全尺寸图片幻灯片

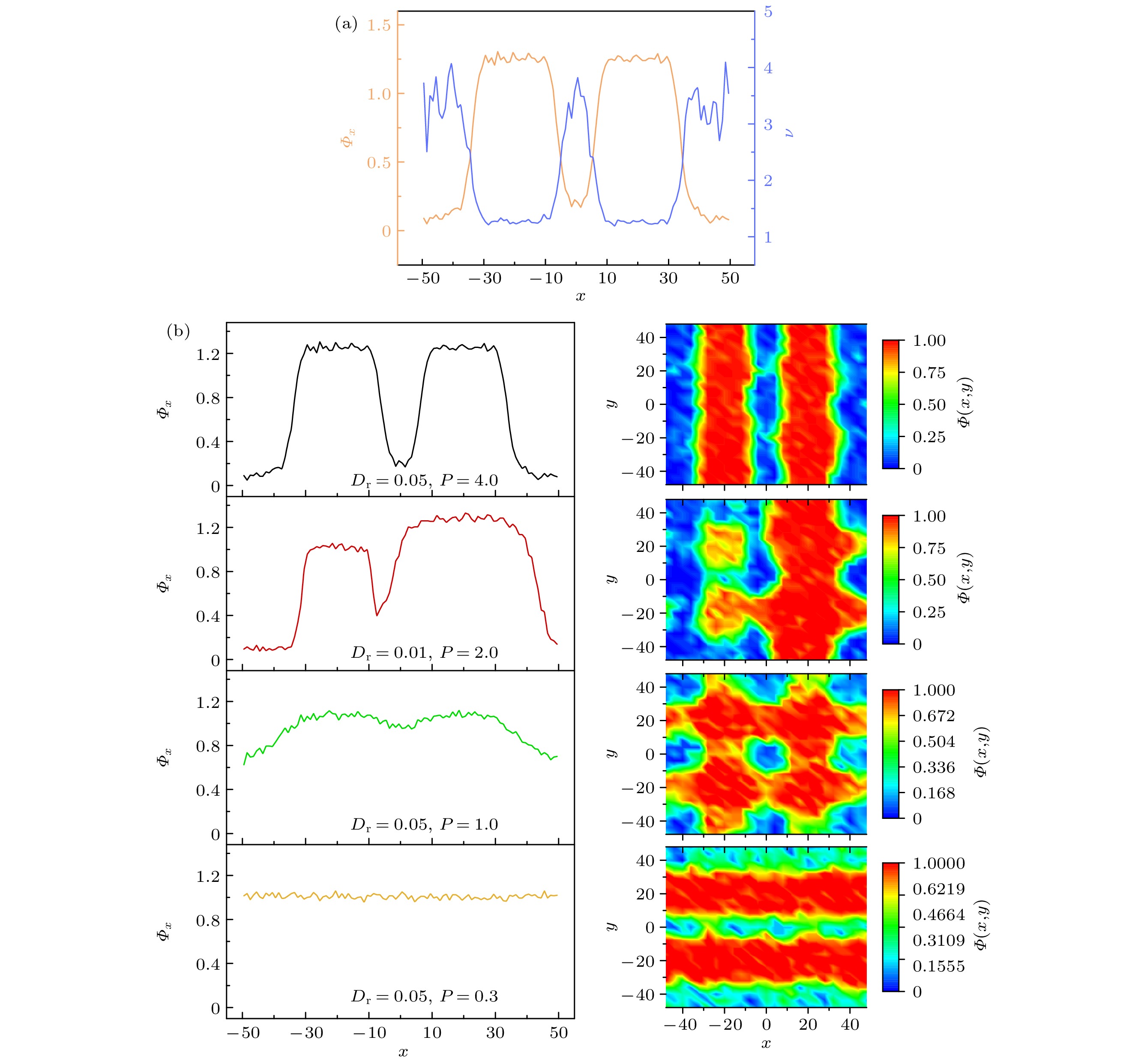
图 4 (a)纵向条形结构在横向遮光区(II)内沿x轴方向的粒子数密度和速度分布图; (b)四种稳定状态在横向遮光区(II)内沿x轴方向的粒子数密度分布图

Fig. 4. (a) Distributions of particle number density and velocity along the x-axis within the transverse shaded region (II) of the longitudinal stripe structure; (b) distributions of particle number density along the x-axis in the transverse shaded region (II) for four steady states.

下载: 全尺寸图片幻灯片

图 5 (a)粒子质心的均方位移MSD随时间t变化的双对数图; 虚线表示斜率为2.0或1.0; (b)标度指数α随时间的变化

Fig. 5. (a) Log-log plot of the mean squared displacement (MSD) of the particle center of mass as a function of time, where the dotted lines show slopes of 2.0 or 1.0; (b) scaling exponent α as a function of time.

下载: 全尺寸图片幻灯片

图 6 (a)不同比值P下, 标度指数α随时间的变化;(b) D_r = 0.05时, 不同比值P下遮光区内的粒子数密度变化情况

Fig. 6. (a) Variation of the scaling exponent α with time for different P ratios; (b) particle number density variation in the shadowed region as a function of ratio P at D_r = 0.05.

下载: 全尺寸图片幻灯片

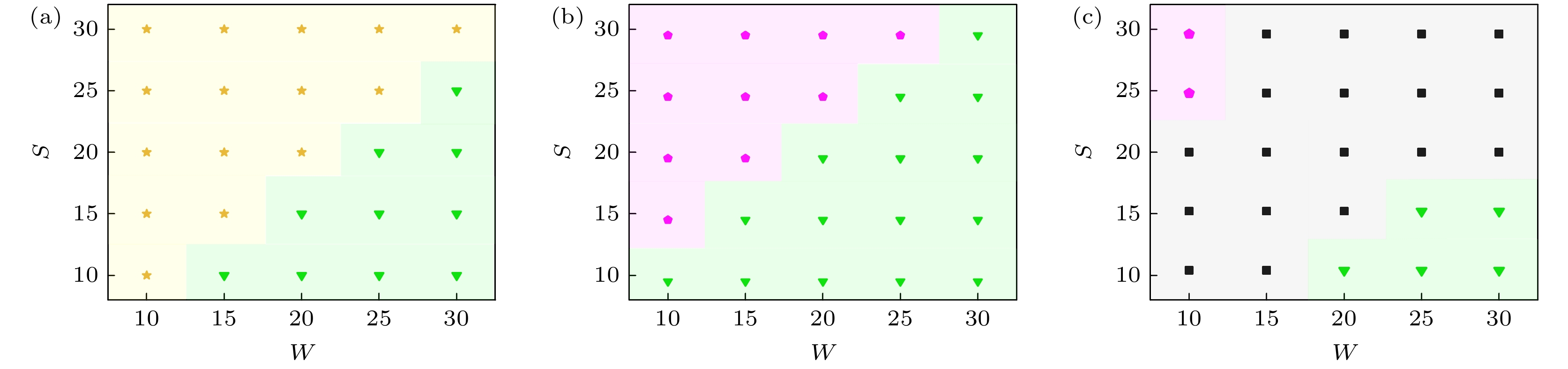
图 7 改变光照区域的宽度W和相邻光照区域间距S对体系聚集结构影响的相图(★代表横向条形结构; ▼代表井字结构; ●代表棋盘状结构; ■代表纵向条形结构)　(a) D_r = 0.05, P = 0.5; (b) D_r = 0.05, P = 1.0; (c) D_r = 0.05, P = 1.5

Fig. 7. Phase diagrams showing the effect of varying the illumination region width W and the spacing S between adjacent illuminated regions on the aggregation structure of the system: (a) D_r = 0.05, P = 0.5; (b) D_r = 0.05, P = 1.0; (c) D_r = 0.05, P =1.5. ★ represents the transverse stripe structure; ▼ represents the tic-tac-toe structure; ● represents the checkerboard-like structure; ■ represents the longitudinal stripe structure.

下载: 全尺寸图片幻灯片

map

[1]	Ramaswamy S 2017 J. Stat. Mech. 5 054002 Google Scholar
[2]	Ramaswamy S 2010 Annu. Rev. Condens. Mater Phys. 1 323 Google Scholar
[3]	Tailleur J, Cates M E 2008 Phys. Rev. Lett. 100 218103 Google Scholar
[4]	Martinez R, Alarcon F, Rodriguez D R, Aragones J L, Valeriani C 2018 Eur. Phys. J. E 41 91 Google Scholar
[5]	Vladescu I D, Marsden E J, Schwarz-Linek J, Martinez V A, Arlt J, Morozov A N, Marenduzzo D, Cates M E, Poon W C 2014 Phys. Rev. Lett. 113 268101 Google Scholar
[6]	Schweitzer F, Tilch B, Ebeling W 2000 Eur. Phys. J. B 14 157 Google Scholar
[7]	Erdmann U, Ebeling W, Schimansky-Geier L, Schweitzer F 2000 Eur. Phys. J. B 15 105 Google Scholar
[8]	Schweitzer F, Ebeling W, Tilch B 1998 Phys. Rev. Lett. 80 5044 Google Scholar
[9]	Yang X, Manning M L, Marchetti M C 2014 Soft Matter 10 6477 Google Scholar
[10]	Stenhammar J, Tiribocchi A, Allen R J, Marenduzzo D, Cates M E 2013 Phys. Rev. Lett. 111 145702 Google Scholar
[11]	Stenhammar J, Wittkowski R, Marenduzzo D, Cates M E 2015 Phys. Rev. Lett. 114 018301 Google Scholar
[12]	Dolai P, Simha A, Mishra S 2017 Soft Matter 14 6137 Google Scholar
[13]	高艺雯, 王影, 田文得, 陈康 2022 71 240501 Google Scholar Gao Y W, Wang Y, Tian W D, Chen K 2022 Acta Phys. Sin. 71 240501 Google Scholar
[14]	Fernandez-Rodriguez M A, Grillo F, Alvarez L, Rathlef M, Buttinoni L, Volpe G, Isa L 2020 Nat. Commun. 11 4223 Google Scholar
[15]	Vutukuri H R, Lisicki M, Lauga E, Vermant J 2020 Nat. Commun. 11 2628 Google Scholar
[16]	Hernández R J, Sevilla F J, Mazzulla A, Pagliusi P, Pellizzi N, Cipparrone G 2020 Soft Matter 16 7704 Google Scholar
[17]	Zhang J H, Guo J J, Mou F Z, Guan J G 2018 Micromachines 9 88 Google Scholar
[18]	Bäuerle T, Fischer A, Speck T, Bechinger C 2018 Nat. Commun. 9 3232 Google Scholar
[19]	Wang G, Phan T V, Li S, Wombacher M, Qu J, Peng Y, Chen G, Goldman D I, Levin S A, Austin R H, Liu L Y 2021 Phys. Rev. Lett. 126 108002 Google Scholar
[20]	Liu Y P, Wang G, Wang P L, Yuan D M, Hou S X, Jin Y K, Wang J, Liu L Y 2023 Chin. Phys. B 32 068701 Google Scholar
[21]	Humphrey W, Dalke A, Schulten K 1996 J. Mol. Graphics 14 33 Google Scholar
[22]	Ning H P, Zhang Y, Zhu H, Ingham A, Huang G S, Mei Y F, Solovev A A 2018 Micromachines 9 75 Google Scholar
[23]	Chen H X, Zhao Q L, Du X M 2018 Micromachines 9 41 Google Scholar
[24]	Xu L L, Mou F Z, Gong H T, Luo M, Guan J G 2017 Chem. Soc. Rev. 46 6905 Google Scholar
[25]	Wang W, Duan W T, Ahmed S, Sen A, Mallouk T E 2015 Acc. Chem. Res. 48 1938 Google Scholar
[26]	Chen C R, Mou F Z, Xu L L, Wang S F, Guan J G, Feng Z P, Wang Q W, Kong L, Li W, Wang J, Zhang Q J 2017 Adv. Mater. 29 3 Google Scholar
[27]	Tang S S, Zhang F Y, Zhao J, Talaat W, Soto F, Karshalev E, Chen C R, Hu Z H, Lu X L, Li J X, Lin Z H, Dong H F, Zhang X J, Nourhani A, Wang J 2019 Adv. Funct. Mater. 29 1809003 Google Scholar
[28]	Sun Y Y, Liu Y, Zhang D M, Zhang H, Jiang J W, Duan R M, Xiao J J, Xing J, Zhang D F, Dong B 2019 ACS Appl. Mater. Interfaces 11 40533 Google Scholar
[29]	Singh D P, Choudhury U, Fischer P, Mark A G 2017 Adv Mater. 29 32 Google Scholar
[30]	Lin Z, Si T, Wu Z, Gao C, Lin X, He Q 2017 Angew. Chem. Int. Ed. 56 13517 Google Scholar
[31]	Wang Y, Shen Z L, Xia Y Q, Feng G Q, Tian W D 2020 Chin. Phys. B 29 053103 Google Scholar
[32]	Pan J X, Wei H, Qi M J, Wang H F, Zhang J J, Tian W D, Chen K 2020 Soft Matter 16 5545 Google Scholar
[33]	Ye S M, Liu P, Wei Z X, Ye F F, Yang M C, Chen K 2020 Chin. Phys. B 29 058201 Google Scholar
[34]	Zhou X L, Wang Y Z, Xu B J, Liu Y P, Lu D, Luo J, Yang Z Y 2023 AIP Adv. 13 065332 Google Scholar
[35]	Chen J M, Zhou X L, Zhang L X 2018 Chin. Phys. B 27 118701 Google Scholar
[36]	Quillen A C, Smucker J P, Peshkov A 2020 Phys. Rev. E 101 052618 Google Scholar
[37]	Liu P, Ye S M, Ye F F, Chen K, Yang M C 2020 Phys. Rev. Lett. 124 158001 Google Scholar
[38]	Das S, Ghosh S, Chelakkot R 2020 Phys. Rev. E 102 032619 Google Scholar
[39]	Das S, Chelakkot R 2020 Soft Matter 16 7250 Google Scholar
[40]	Knežević M, Stark H 2020 New J. Phys 22 113025 Google Scholar
[41]	Chen X G, Lin L H, Li Z C, Sun H J 2022 Adv. Funct. Mater. 32 2104649 Google Scholar
[42]	Volpe G, Buttinoni I, Vogt D, Kuemmerer H J, Bechinger C 2011 Soft Matter. 7 8810 Google Scholar
[43]	Jahanshahi S, Lozano C, Liebchen B, Löwen H, Bechinger C 2020 Commun. Phys. 3 127 Google Scholar
[44]	Palacci J, Sacanna S, Steinberg A P, Pine D J, Chaikin P M 2013 Science 339 936 Google Scholar
[45]	Xia Y Q, Shen Z L, Tian W D, Chen K 2019 J. Chem. Phys. 150 154903 Google Scholar
[46]	Wang C, Li H S, Ma Y Q, Tian W D, Chen K 2018 J. Chem. Phys. 149 164902 Google Scholar
[47]	Shan W J, Zhang F, Tian W D, Chen K 2019 Soft Matter 15 4761 Google Scholar
[48]	石子璇, 金燕, 金奕扬, 田文得, 张天辉, 陈康 2024 73 170501 Google Scholar Shi Z X, Jin Y, Jin Y Y, Tian W D, Zhang T H, Chen K 2024 Acta Phys. Sin. 73 170501 Google Scholar
[49]	王晶, 焦阳, 田文得, 陈康 2023 72 190501 Google Scholar Wang J, Jiao Y, Tian W D, Chen K 2023 Acta Phys. Sin. 72 190501 Google Scholar
[50]	Tiwari C, Singh P S 2024 Soft Matter 20 4816 Google Scholar
[51]	Shen Y F, Hu H X, Luo M B 2024 Soft Matter 20 621 Google Scholar
[52]	Cates M E, Tailleur J 2015 Annu. Rev. Condens. Matter Phys. 6 219 Google Scholar
[53]	Gomez-Solano J R, Samin S, Lozano C, Ruedas-Batuecas P, van Roij R, Bechinger C 2017 Sci Rep. 7 14891 Google Scholar
[54]	Caprini L, Marini Bettolo Marconi U, Wittmann R, Löwen H 2022 Soft Matter 8 1412 Google Scholar
[55]	Takatori S C, Yan W, Brady J F 2014 Phys. Rev. Lett. 113 028103 Google Scholar
[56]	Bechinger C, Di Leonardo R, Löwen H, Reichhardt C, Volpe G, Volpe G 2016 Rev. Mod. Phys. 88 045006 Google Scholar

[1]	周雄峰, 陈彬, 刘坤. 氩气等离子体射流特性: 电压、气流、外磁场的综合影响. , 2024, 73(22): 225201. doi: 10.7498/aps.73.20241166
[2]	陆万利. 锥角调制的圆艾里涡旋光束构建光学针. , 2024, 73(17): 174203. doi: 10.7498/aps.73.20240878
[3]	李晨璞, 吴魏霞, 张礼刚, 胡金江, 谢革英, 郑志刚. 具有不同扩散系数的活性手征粒子分离. , 2024, 73(20): 200201. doi: 10.7498/aps.73.20240686
[4]	刘坤, 项红甫, 周雄峰, 夏昊天, 李华. 固定功率下大气压交流氩气等离子体射流的光谱特性. , 2023, 72(11): 115201. doi: 10.7498/aps.72.20230307
[5]	赵立芬, 哈静, 王非凡, 李庆, 何寿杰. 氧气空心阴极放电模拟. , 2022, 71(2): 025201. doi: 10.7498/aps.71.20211150
[6]	王晓雷, 赵洁惠, 李淼, 姜光科, 胡晓雪, 张楠, 翟宏琛, 刘伟伟. 基于人工表面等离激元探针实现太赫兹波的紧聚焦和场增强. , 2020, 69(5): 054201. doi: 10.7498/aps.69.20191531
[7]	廖晶晶, 蔺福军. 混合手征活性粒子在时间延迟反馈下的扩散和分离. , 2020, 69(22): 220501. doi: 10.7498/aps.69.20200505
[8]	陈卫军, 宋德, 李野, 王新, 秦旭磊, 刘春阳. 竞争型非线性介质中艾里-高斯光束交互作用的调控. , 2019, 68(9): 094206. doi: 10.7498/aps.68.20190042
[9]	郭宇琦, 潘俊星, 张进军, 孙敏娜, 王宝凤, 武海顺. 在光敏性三元聚合物混合物中构造多尺度有序图案. , 2016, 65(5): 056401. doi: 10.7498/aps.65.056401
[10]	何建平, 吕文中, 汪小红. Ba0.5Sr0.5TiO3有序构型的第一性原理研究. , 2011, 60(9): 097102. doi: 10.7498/aps.60.097102
[11]	孙转兰, 张晓青, 曹功勋, 王学文, 夏钟福. 有序结构氟聚合物压电驻极体的制备和压电性研究. , 2010, 59(7): 5061-5066. doi: 10.7498/aps.59.5061
[12]	曹功勋, 张晓青, 孙转兰, 王学文, 娄可行, 夏钟福. 人工调控微结构压电驻极体的热稳定性和电荷动态特性. , 2010, 59(9): 6514-6520. doi: 10.7498/aps.59.6514
[13]	宋庆功, 姜恩永, 裴海林, 康建海, 郭英. 插层化合物LixTiS2中Li离子-空位二维有序结构稳定性的第一性原理研究. , 2007, 56(8): 4817-4822. doi: 10.7498/aps.56.4817
[14]	张永炬, 余森江, 葛洪良, 邬良能, 崔玉建. 硅油基底表面铁薄膜的生长机理及表面有序结构. , 2006, 55(10): 5444-5450. doi: 10.7498/aps.55.5444
[15]	张永炬, 余森江. 准自由支撑铝薄膜中有序表面结构的自组织生长. , 2005, 54(10): 4867-4873. doi: 10.7498/aps.54.4867
[16]	夏阿根, 杨波, 金进生, 张亦文, 汤凡, 叶高翔. 液体基底表面金薄膜中的有序结构和自组装现象. , 2005, 54(1): 302-306. doi: 10.7498/aps.54.302
[17]	胡隐樵. 强迫耗散系统的有序结构和系统的发展(Ⅱ)，广义能量极小值原理和系统的发展. , 2003, 52(6): 1354-1359. doi: 10.7498/aps.52.1354
[18]	胡隐樵. 强迫耗散系统的有序结构和系统的发展(Ⅰ)，最小熵产生原理和有序结构. , 2003, 52(6): 1379-1384. doi: 10.7498/aps.52.1379
[19]	宋庆功, 丛选忠, 张庆军, 莫文玲, 戴占海. 六角蜂窝晶格的有序结构. , 2000, 49(10): 2011-2016. doi: 10.7498/aps.49.2011
[20]	宋庆功, 戴占海, 丛选忠, 魏环, 张庆军. 六方密堆二元合金的有序结构. , 2000, 49(11): 2201-2209. doi: 10.7498/aps.49.2201